Как найти фальшивую монету двумя взвешиваниями — логическая задача
Загадки на логику
Перед нами логическая задача, чтобы решить которую нужно немного пораскинуть мозгами.
Итак условия задачи следующие:
На столе лежат 9 монет. Известно, что одна из монет фальшивая. Фальшивая монета весит меньше чем остальные. У нас имеются весы для взвешивания.
Вопрос:
Как при помощи двух взвешиваний найти фальшивую монету?
Внимание!
Ниже приведен правильный ответ!
Правильный ответ:
Вначале на каждую чашу весов нужно положить по три монеты.
Если после этого весы приходят в равновесие, значит среди этих монет нет фальшивой, берем две из трех оставшихся монет, кладем на разные чаши весов. Если фальшивая монета среди этих двух, то мы поймем на какой она чаше, эта чаша поднимется выше.
А если весы снова придут в равновесие, значит фальшивая монета осталась на столе.
Если же при первом взвешивании весы не пришли в состояние равновесия, значит фальшивая монета уже находится на весах, берем 2 монеты из тех трех, что оказались легче, кладем по 1 на каждую чашу, если одна чаша поднялась выше, значит фальшивая монета на ней, если чаши уравновесились, значит фальшивая — оставшаяся третья.
Похожие новости

Все загадки
Все загадки

Все загадки
Все загадки
Все загадки
Все загадки
Время на прочтение
3 мин
Количество просмотров 204K
Сегодня я снова хочу вернуться к теме о задаче нахождении фальшивой монеты методом взвешивания на весах без циферблата.
Наиболее распространенные из таких задач — определение количества взвешиваний для выявления фальшивой монеты, если:
1) неизвестно какая она по весу;
2) известно, что она легче/тяжелее остальных.
Или обратная задача: можно ли за определенное количество взвешиваний выявить фальшивую из заданного количества монет.
1. Давайте сначала разберемся с 2 вариантом, который является частным случаем варианта 1.
Некоторое время назад, я на Хабре уже описывал решение такой задачи, но в одном из комментариев было замечание о немного странном первом разделении монет, по-этому предлагаю другой алгоритм решения. Хотя результат будет тот же и формула решения задачи остается та же:
N >= log3A,
где N — максимально необходимое количество взвешиваний, натуральное число, округленное в большую сторону;
A — количество монет.
Которая выведена на основании опытов (за 1 взвешивание можно найти одну фальшивую из 3-х монет, за 2 — из 9, за 3 — из 27 и т.д.)
Сам алгоритм решения простой, и я покажу его на примерах
1) Пусть у нас есть 26 монет. Нужно найти одну, которая легче/тяжелее
Первым действием буде разделение монет на три группы, в двух из которых число монет будет одинаковым, важно только что бы в третьей группе — остатке — было меньше монет, чем в каждой из двух других групп. То есть частое округляется к большему натуральному числу. То есть
A = 2 * B + C,
где A — количество монет;
B — частное от деления количества монет на 3, натуральное число, округленное в большую сторону;
C — остаток.
По условию задачи
26/3 = 8.666(6),
26 = 2 * 9 + 8,
При первом взвешивании будут сравниваться две группы: правая (ПГ) — 9 монет и левая (ЛГ) — 9 монет.
Далее у нас возможны два варианта:
1) фальшивая монета в левой/правой группе (9 монет)
2) фальшивая монета в остатке (8 монет)
для 1 варианта следующее деление на группы будет — 9 = 2 * 3 + 3;
для 2 варианта — 8 = 2 * 3 + 2
Ну и за одно взвешивание можно определить какая из 2 или 3 монет легче/тяжелее
Этот же результат я приведу в таблице
| № взвешивания | Число монет | ЛГ | ПГ | Остаток |
| 1 | 26 | 9 | 9 | 8 |
| 2 | 8 | 3 | 3 | 2 |
| 2 | 9 | 3 | 3 | 3 |
| 3 | 2 | 1 | 1 | 0 |
| 3 | 3 | 1 | 1 | 1 |
по формуле — log326 =2.9656 — соответственно количество взвешиваний — 3.
еще пример:
число монет- 71. По формуле log371 =3.8800 — количество взвешиваний — 4. Проверяем
| № взвешивания | Число монет | ЛГ | ПГ | Остаток |
| 1 | 71 | 24 | 24 | 23 |
| 2 | 23 | 8 | 8 | 7 |
| 2 | 24 | 8 | 8 | 8 |
| 3 | 7 | 3 | 3 | 1 |
| 3 | 8 | 3 | 3 | 2 |
| 4 | 2 | 1 | 1 | 0 |
| 4 | 3 | 1 | 1 | 1 |
Ну с алгоритм решения этих задач, я думаю, понятен.
2. Теперь перейдем к задачам, в которых не известно легче монета или тяжелее.
В данном случае я предлагаю такое первое действие: разделить монеты на четыре группы, три — с максимально одинаковым количеством монет, а в четвертой группе — остаток. Причем в остатке должны быть 1 или 2 монеты. То есть при делении на 3 частное округляется до меньшего натурального числа.
A = 3 * B + C,
где A — количество монет;
B — частное от деления количества монет на 3, натуральное число, округленное в меньшую сторону;
C — остаток.
Например, для 58-ми монет — это будет 58 = 3 * 19 + 1, для 23 = 3 * 7 + 2, для 15 = 3 * 5 + 0 и т. д.
Далее выполняем два взвешивания:
1) первая и вторая группы;
2) первая и третья группы;
и анализируем результат.
Здесь возможны четыре варианта:1, 2, 3 — это первая, вторая или третья группа отличаются по весу от двух остальных, или они равны, тогда нам повезло, так как фальшивая — в остатке. Так же два взвешивания помогают определить определить тяжелее фальшивая монета или легче. Кстати, если в остатке две монеты, то нужно выполнить еще 2 взвешивания для определения фальшивой монеты.
Теперь у нас есть задача: определить одну фальшивую монету из группы, которая легче/тяжелее.
Что касается формулы, то она примет следующий вид
N >= log3B + 2,
где N — максимально необходимое количество взвешиваний, натуральное число;
B — количество монет в группе после второго взвешивания.
А если учесть, что B = A/3, где A — количество всех монет, тогда получим:
log3B = log3A — 1,
N >= log3A + 1
Итог:
1) если известно, что фальшивая монета легче/тяжелее, тогда максимальное число взвешиваний определяется по формуле:
N >= log3A
2) если не известно, какая фальшивая, тогда максимальное число взвешиваний определяется по формуле:
N >= log3A + 1
где N — максимально необходимое количество взвешиваний, натуральное число, округленное в большую сторону;
А — количество монет.
|
Положите по три монеты на две чаши весов. Если равновесие, то фальшивая среди трех не взвешенных, если не равновесие, то среди тех, что на более легкой чаше. Теперь возьмите кучку их трех монет, среди которых фальшивая. Положите по одной из них на весы. Если равновесие — фальшивка у вас в руках, иначе фальшивка на более легкой чаше. автор вопроса выбрал этот ответ лучшим Грустный Роджер 8 лет назад Если заранее не известно, легче фальшивая или тяжелее, — то никак. Для этого понадобится минимум 4 взвешивания. И толькл когда ЗАРАНЕЕ известно, что фальшивая монета легче( или тяжелее) подлинных, — тогда да, тогда хватит двух взвешиваний. |

Димасик
Имеется 8 с виду одинаковых монет. Одна из них фальшивая и известно, что она легче настоящей. Как с помощью всего лишь двух взвешиваний найти фальшивую монету? В Вашем распоряжении аптекарские весы без гирь, которые показывают только легче-тяжелее.
весы
вид
помощь
гиря
распоряжение
монета
взвешивание
Ответы

Джива Атма
Делим монеты на две равные кучки. Из каждой кучки берем по 3 монеты, кладем на весы и взвешиваем. Если вес одинаковый, то взвешиваем оставшиеся 1 и 1 монеты и выявляем фальшивую (более легкую). Если же одна группа из трех монет легче другой, значит там есть фальшивая монета. Оставляем более легкую группу из трех монет и кладем на весы 1 и 1, и действуем по предыдущему алгоритму: если вес одинаков — значит, фальшивая третья, а если нет — то та, которая легче.
Димасик
давай завтра сейчас уже не соображаю
Димасик
напишите мне личное сообщение а я завтра в личке пришлю загадку

Вероника Колесник
Делим монеты на две равные кучки. Из каждой кучки берем по 3 монеты, кладем на весы и взвешиваем. Если вес одинаковый то взвешиваем оставшиеся 1и 1 монеты и выявляем фальшивую (более легкую). Если же одна группа из трех монет легче другой, значит там есть фальшивая монета. Оставляем более легкую группу из трех монет и кладем на весы 1и 1 и действуем по предыдущему алгоритму: если вес одинаков, значит фальшива третья, а если нет то та которая легче.

Саша
Делим монеты на две равные кучки. Из каждой кучки берем по 3 монеты, кладем на весы и взвешиваем. Если вес одинаковый то взвешиваем оставшиеся 1и 1 монеты и выявляем фальшивую (более легкую). Если же одна группа из трех монет легче другой, значит там есть фальшивая монета. Оставляем более легкую группу из трех монет и кладем на весы 1и 1 и действуем по предыдущему алгоритму: если вес одинаков, значит фальшива третья, а если нет то та которая легче

Татьяна ~
на чаши весов положить шесть монет (по три на кжд чашу). если чаши будут равны, то на чаши положить оставшиеся две монеты, одна из них фальшивая. если же при взвешивании шести монет в одной из чаш с тремя монетами будет фальшивая, то при второй попытке взвешивания надо будет взвесить любые две монеты из этих трех. если они будут равны, то невзвешиваемая монета и есть фальшивка. если не равны, то фальшивка при взвешивании будет обнаружена

Кто-То Из Толпы
1.Взвесить 6 монет (по 3 на каждой чашке)..если весы уравновешаны, значит фальшивка среди 2ух оставшихся, а какая именно, определим вторым взвешиванием оставшихся 2ух монет. 2.Если при взвешивании 6ти монет чашки на разном уровне, значит ищем среди них,взвесив монеты из чашки, которая оказалась легче(взвешиваем из этих 3ёх две монеты;если чашки не равны, то вопросов нет,какая из них легче, а если чашки равны,значит фальшивка-оставшаяся)

Евгения Алексеевна
1. Положить 3 на одну, 3 на другую — если есть разница, значит в одной из стопок фальшивая.
2. Если нет — фальшивая в руке.(одну стопку убираем, в другой оставляем монетку 1. Кладем на свободную чашу то одну, то вторую монету Где изменение в все — та поддельная).
3. Если весы показали разницу — поддельная в одной из сопок — убираем по 1 монете с каждой. Смотрим. Если сравнялись — повторяем п.2. Если разные — опять убираем. И так находим.
Димасик
нужно ток 2 взвешивания а у вас дофига получилось
Димасик
начало правильное по 3 взвешиваем если они равны то вторым взвешиванием 2 оставшихся монет определяем фальшивку если не равны тогда берем 2 монеты из более легкой стопки и взвешиваем если они равны то фальшивка третья монета если нет то та которая легче
Евгения Алексеевна
ах, там написано, что фальшивая легче! А я не заметила. Дело в том, что мне сестра без этого условия говорила — если они просто разного веса, но неизвестно кто легче, а кто тяжелей. Да, так правда.

Людмила
Кладем на каждую чашу весов по три монеты.
1. Если они весят одинаково, значит фальшивая — среди двух оставшихся. Взвешиваем их и находим более легкую.
2. Если три монеты на одной чаше весов легче, чем на другой, берем любые две монеты из этой кучки и взвешиваем.
2.1. Если они имеют одинаковый вес, значит фальшивая — третья.
2.2. Если они имеют разный вес, значит фальшивая — более легкая.
Димасик
перечитайте внимательно условия и объясните почему 7*0,15
НН
Натали Наталья
отложить две монеты, оставшиеся 6 разделить на две кучки по 3 штуки и взвесить. если по весу равны, то фальшивая в отложенных монетах.положить на весы по монете — и выяснится, какая.Если вес разнится, то выбрать кучку, которая легче, отложить оттуда одну монету и опять взвесить две . если одинаковые — то фальшивая отложенная))))

🇷🇺 Анжелика*
отложить 2 монеты и взвесить кучки по 3. Если кучки одинаково весят, значит, фальшивые в двух оставшихся. Вторым взвешиванием определим. Если одна кучка легче, значит, фальшивая там. На одну чашу весов кладем одну монету из трех + одну невзвешенную, на другую тоже одну из трех+ одну невзвешенную. Дальнейший ход понятен)
ВР
Вера Русакова
Ложим по 3 монеты на весы
Если равновесие, сравниваем оставшиеся две, какая легче та и фальшивая
Если нет равновесия берем с той чашки, где легче и сравниваем две любые
Если равновесие, то третья – фальшивая, если равновесия нет, то та что легче – та и фальшивая
Задачка со школьной программы))
ВР
Вера Русакова
поступила в пед училище, но не доучилась — вышла замуж, позже закончила техникум по специальности техник-технолог целлюлозно бумажной промышленности))
ВР
Вера Русакова
потвердила профессию, да и учиться после 30 — здорово, знаешь зачем и уже умеешь организовывать время, а потом это новые знакомства, ощущения, отвлечение от обыденности

Надежда
На весы положу по три монеты , если весы показывают поровну, на весы кладу 2 монеты с той стороны, которая полегче, если они равны, то третья будет легче, если нет, то нахожу сразу. Если 6 монет в равновесии, то вторым взвешиванием кладу оставшиеся две и выбираю ту, которая полегче
Димасик
да уже давно еще раньше этого
КЛ
Кэр Лаэда
Первый раз кладем по три монеты. Если вес один, то вторым сравниваем две оставшиеся, легкая- искомое. Если при первом взвешивании вес разный, то убираем три которые тяжелее и сравниваем любые две из трех легких. Если вес равный, то третья, если не равный то та что легче.

Николай Балакирев
Просто. Сначала случайно по четыре. Потом те, которые тяжелее, убрать в сторону. Остаются четыре. Взвесить по две. Нет, не получается. Если только за три взвешивания. Хотя, тут могут быть приёмчики, схожие с фокусами карточными, но нужно вспоминать
Димасик
когда вы добавляете то это считается за дополнительное взвешивание так что нет
Димасик
» и прибавить на сторону, где одна, одну из первого действия, про которую мы знаем, что она настоящая.» это добавление

Сергій
Берём шесть монет ложим по три на чаши весов, если вес одинаков, взвешиваем две оставшиеся, фальшивая там. Если нет то из трёх монет которые легче берём две и сравниваемых их вес, если одинаков то фальшивая третья, если нет то та что легче

Mass. Тerr
Кладём на весы по 3 монеты. Если одинаковый вес, то фальшивая одна из двух оставшихся, просто взвесим их. Если вес кучек разный, то из той, что легче. убираем одну монету, а две остальных сравниваем на весах.

Неизвестно Неизвестно
Долго писать. Очень примитивная задачка. Каждое взвешивание сужает круг «подозреваемых» монет в три раза. С помощью двух взвешиваний фальшивую монету можно найти среди максимум 9 монет. Давай посложнее.
ЕБ
Елена Борисова/ Гончарова
Делим монеты на две части и выкладываем на чаши весов, оставляем только те монеты которые легче, делим их опять на две части и так далее. Либо убираем по одной монетки с каждой чаши пока ни уровнем весы.
Ә(
Әруақ (Духи Предков) Ж.р.
А что если разделить монеты ровно на две части, то есть 4 слева и четыре справа. Затем в той что легче, взять тоже разделить на два, две слева и две справа. Затем из той, что легче и выбрать. ???
Димасик
это 3 взвешивания а нада только 2
Димасик
нет надо именно путем взвешивания

Счастливая Счастливая
Делим монеты пополам-взвешиваем.Где легче-там она.опять пополам -взвешиваем-где легче -там онаИ после 3 раза только можно узнать где она .Меньший вес делим пополам и -находим фальшивую.

Александр Жук Эстония Таллин
На весы кладем по три монеты оставив две если весы ушли в сторону значин там и более лёгкая и из него кладем по одной и одна остается либо весы в равновесии тогда лёгкая из оставшейся
Задача
Имеется 8 монет одинакового достоинства, одна из которых фальшивая. Фальшивая монета легче настоящей. Как с помощью всего лишь двух взвешиваний найти фальшивую монету? В вашем распоряжении аптекарские весы без гирь, которые показывают только легче-тяжелее.
Решение этой задачи состоит в том, что исходный набор монет надо разделить на три кучки, в двух из которых число монет обязательно должно быть равным.
Если мы взвесим на весах с двумя чашами две кучки с одинаковым числом монет одинакового достоинства и одна из них окажется легче, значит фальшивая монета в этой кучке, и уже её надо разделить на три части, в двух из которых число монет обязательно должно быть равным.
Если же у взвешенных двух кучек монет одинаковый вес, значит фальшивая монета в третьей кучке.
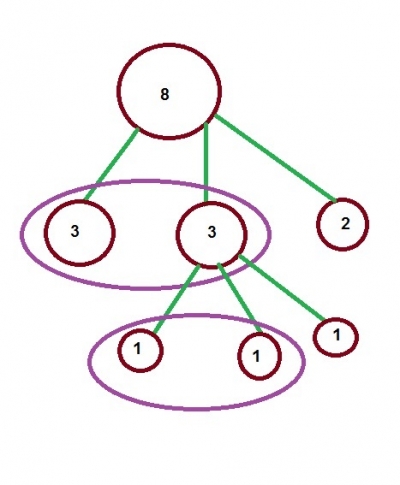
Покажем схему взвешивания для наших 8 монет:
Вначале у нас есть 8 монет. Мы делим их на кучки по 3, 3 и 2 монеты.
Взвешиваем две кучки по 3 монеты. Предположим, что одна из этих кучек оказалась легче. Значит, фальшивая монета в ней. Теперь делим эту кучку на три по 1 монете в каждой.
Теперь нам достаточно взвесить любые две монеты, чтобы определить, где фальшивая — она окажется или на весах, или это будет третья монета.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Задача
Имеется 10 монет одинакового достоинства, одна из которых фальшивая. Фальшивая монета легче настоящей. За какое минимально гарантированное количество взвешиваний можно найти фальшивую монету? В вашем распоряжении аптекарские весы без гирь, которые показывают только легче-тяжелее.
Это точно такая же задача, как и предыдущая, но в ней на 2 монеты больше, и взвешиваний будет на одно больше.
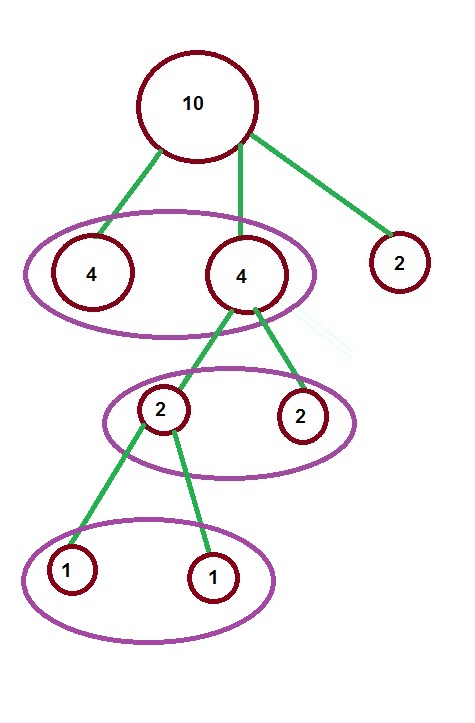
Вот схема взвешивания:
Как видим, на втором взвешивании у нас образовались кучки по две монеты, поэтому, когда мы определили, в какой из этих кучек находится фальшивая, то дальше смогли разделить её только на две «кучки» по 1 монете в каждой.
Дата публикации
17.04.2020


.jpg)