Как рекурсивно найти минимальное значение

Время на прочтение
3 мин

Количество просмотров 33K

Сегодня на Хабре появилась очень интересная статья, о поиске минимального (максимального) значения на отрезке в массиве. Так как статья оказалось интересной и популярной, я решил с вами поделиться ещё одним алгоритмом поиска в массиве некоторых «специальных» значений.

Наверняка каждому встречалась задача нахождения k-ого наименьшего элемента в массиве. k-ый элемент характеризуется тем, что он больше (или равен) k элементов массива и меньше или равен N-k оставшихся элементов (где N – число элементов в массиве).

Задача нахождения k-ого наименьшего элемента обычно связывается с задачей сортировки, так как очевидный метод нахождения этого элемента состоит в сортировке N элементов и выборе k-ого.

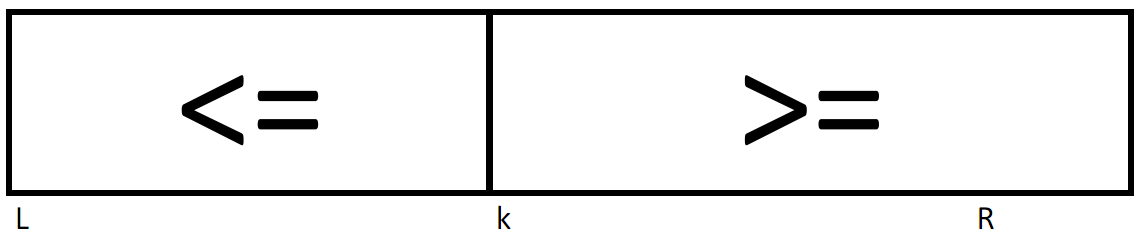
Но мы с вами пойдём немного другим путём. Я предполагаю, что читатели знают, как работает алгоритм быстрой сортировки, но на всякий случай напомню. В массиве выбирается случайный элемент x, и выполнется просмотр массива слева, пока не найдётся элемент a[i]>x, затем выполняется просмотр справа, пока не будет найден элемент a[j]<x. Как только два таких элемента найдены, выполняется их обмен и просмотр продолжается до тех пор, пока индексы i,j не станут равны где-то в середине массива. В результате получается массив левая часть которого содержит элементы <=x, а правая часть содержит элементы >=x. Описанная процедура применяется рекурсивно для левой и правой части и продолжается до тех пор, пока не будет получен полностью отсортированный массив. (Немного подробнее о эффективных алгоритмах сортировки).

Процедура разделения, используемая в быстрой сортировке, даёт потенциальную возможность находить искомый (k-ый) элемент гораздо быстрее.
Этот алгоритм работает следующим образом. На первом шаге вызывается процедура разделения с L=1 и R=N (т.е. разделение выполняется для всего массива), причём в качестве разделяющего значения x выбирается a[k]. После разделения получаются значения индексов i,j такие, что

a[h]<x для всех h<i
a[h]>x для всех h>j
i>j

Здесь возможны три случая:
•Разделяющее значение x оказалось слишком мало. В результате граница между двумя частями меньше нужного значения k. Тогда операцию разделения нужно повторить с элементами a[i]…a[R].

•Выбранное значение x оказалось слишком велико. Тогда операцию разделения нужно повторить с элементами a[L]…a[j].

•Элемент a[k] разбивает массив на две части в нужной пропорции и поэтому является искомым значением.

Операцию разделения нужно повторять, пока не реализуется случай 3. Этот цикл выражается следующим фрагментом (прошу прощения за Pascal, но мои ученики пока знают только его):

1. procedure Find(k: integer);
2. var
3. L,R,i,j: integer;
4. w,x: integer;
5. begin
6.   L:=1; R:=N;
7.   while L<R—1 do
8.   begin
9.     x:=a[k];
10.     i:=L;
11.     j:=R;
12.     REPEAT
13.       while a[i]<x do
14.         i:=i+1;
15.       while x<a[j] do
16.         j:=j—1;
17.       if i<=j then
18.       begin
19.         w:=a[i];
20.         a[i]:=a[j];
21.         a[j]:=w;
22.         i:=i+1;
23.         j:=j—1;
24.       end;
25.     UNTIL i>j;
26.     if j<k then
27.       L:=i;
28.     if k<i then
29.       R:=j;
30.   end;
31. end;

Если предположить, что в среднем каждое разбиение делит пополам размер части массива, в которой находится искомое значение, то необходимое число сравнений будет N+N/2+N/4+…+1=2N. Это объясняет эффективность приведённой процедуры для поиска медиан и прочих величин, а также объясняет её превосходство над простым методом, состоящем в предварительной сортировке всего массива с последующим выбором k-ого элемента (где наилучшее поведение имеет порядок N*log(N)).

Надеюсь, этот алгоритм поможет вам сделать ваши программы более эффективными и быстрыми. Спасибо за внимание.

Найти минимальный элемент массива очень просто. Если это упорядоченный массив, то достаточно вернуть первое или последнее значение, в зависимости от того, как отсортированы данные, от наименьшего к наибольшему или от наибольших к наименьшим. Это очень простая задача.

В случае с неотсортированным массивом, задача поиска минимального значения элемента сводиться к полному обходу всех элементов и выбора из них — минимума.

Код программы для поиска минимального, по значению, элемента неупорядоченного массива

{$CODEPAGE UTF8}
program Minimal;
const
  arrayLength = 10;
var
  inputArray : array [1..arrayLength] of integer;
  minimum, i: integer;
begin
  randomize;
  writeln ('Исходный массив: ');
  {заполнение случайными числами}
  for i := 1 to arrayLength do
  begin
    inputArray[i] := random(100);
    write (inputArray[i]:4);
  end;
  writeln;

  {поиск минимального значения}
  {считаем что первый элемент и есть минимальный}
  minimum := inputArray[1];
  for i := 2 to arrayLength do
    if minimum > inputArray[i] then         {если минимум больше текущего}
      minimum := inputArray[i];             {присваиваем ему текущее значение}

  write('Минимальный элемент массива ', minimum);
  readln;
end.

Найти минимальное значение, можно также, с использованием рекурсивного алгоритма.

Рекурсивный алгоритм поиска минимального элемента в одномерном массиве

{$CODEPAGE UTF8}
program MinimalElement;
const
  arrayLen = 10;
var
  inputArr : array [1..arrayLen] of integer;
  min, i: integer;

function MinElement(minimal, index: integer):integer;
begin
  if index > arrayLen then
    MinElement := minimal
  else
    begin
      if inputArr[index] < minimal then
        minimal := inputArr[index];
      MinElement := MinElement(minimal, index + 1); {рекурсивный вызов}
    end;
end;

begin
  randomize;
  writeln ('Исходные данные: ');
  for i := 1 to arrayLen do
  begin
    inputArr[i] := random(100);
    write (inputArr[i]:4);
  end;
  writeln;

  {рекуррентный поиск минимального значения}
  min := inputArr[1];
  min := MinElement(min, 2);

  write('Минимальный элемент ', min);
  readln;
end.