Как работает найти маршрут

Часть 1. Общий алгоритм поиска

Введение

Поиск пути — это одна из тех тем, которые обычно представляют самые большие сложности для разработчиков игр. Особенно плохо люди понимают алгоритм A*, и многим кажется, что это какая-то непостижимая магия.

Цель данной статьи — объяснить поиск пути в целом и A* в частности очень понятным и доступным образом, положив таким образом конец распространённому заблуждению о том, что эта тема сложна. При правильном объяснении всё достаточно просто.

Учтите, что в статье мы будем рассматривать поиск пути для игр; в отличие от более академических статей, мы опустим такие алгоритмы поиска, как поиск в глубину (Depth-First) или поиск в ширину (Breadth-First). Вместо этого мы постараемся как можно быстрее дойти от нуля до A*.

В первой части мы объясним простейшие концепции поиска пути. Разобравшись с этими базовыми концепциями, вы поймёте, что A* на удивление очевиден.

Простая схема

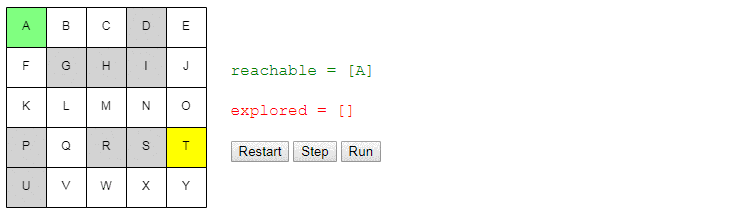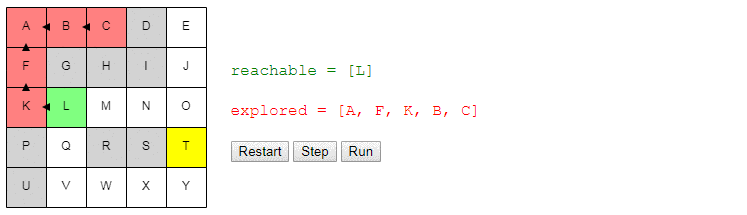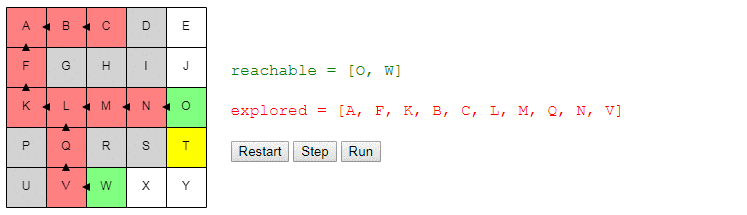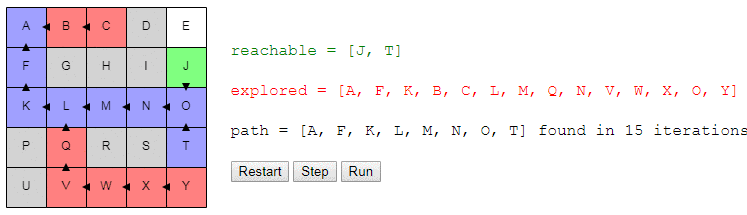
Хотя вы сможете применять эти концепции и к произвольным сложным 3D-средам, давайте всё-таки начнём с чрезвычайно простой схемы: квадратной сетки размером 5 x 5. Для удобства я пометил каждую ячейку заглавной буквой.

Простая сетка.

Самое первое, что мы сделаем — это представим эту среду в виде графа. Я не буду подробно объяснять, что такое граф; если говорить просто, то это набор кружков, соединённых стрелками. Кружки называются «узлами», а стрелки — «рёбрами».

Каждый узел представляет собой «состояние», в котором может находиться персонаж. В нашем случае состояние персонажа — это его позиция, поэтому мы создаём по одному узлу для каждой ячейки сетки:

Узлы, обозначающие ячейки сетки.

Теперь добавим рёбра. Они обозначают состояния, которых можно «достичь» из каждого заданного состояния; в нашем случае мы можем пройти из любой ячейки в соседнюю, за исключением заблокированных:

Дуги обозначают допустимые перемещения между ячейками сетки.

Если мы можем добраться из A в B, то говорим, что B является «соседним» с A узлом.

Стоит заметить, что рёбра имеют направление; нам нужны рёбра и из A в B, и из B в A. Это может показаться излишним, но не тогда, когда могут возникать более сложные «состояния». Например, персонаж может упасть с крыши на пол, но не способен допрыгнуть с пола на крышу. Можно перейти из состояния «жив» в состояние «мёртв», но не наоборот. И так далее.

Пример

Допустим, мы хотим переместиться из A в T. Мы начинаем с A. Можно сделать ровно два действия: пройти в B или пройти в F.

Допустим, мы переместились в B. Теперь мы можем сделать два действия: вернуться в A или перейти в C. Мы помним, что уже были в A и рассматривали варианты выбора там, так что нет смысла делать это снова (иначе мы можем потратить весь день на перемещения A → B → A → B…). Поэтому мы пойдём в C.

Находясь в C, двигаться нам некуда. Возвращаться в B бессмысленно, то есть это тупик. Выбор перехода в B, когда мы находились в A, был плохой идеей; возможно, стоит попробовать вместо него F?

Мы просто продолжаем повторять этот процесс, пока не окажемся в T. В этот момент мы просто воссоздадим путь из A, вернувшись по своим шагам. Мы находимся в T; как мы туда добрались? Из O? То есть конец пути имеет вид O → T. Как мы добрались в O? И так далее.

Учтите, что на самом деле мы не движемся; всё это было лишь мысленным процессом. Мы продолжаем стоять в A, и не сдвинемся из неё, пока не найдём путь целиком. Когда я говорю «переместились в B», то имею в виду «представьте, что мы переместились в B».

Общий алгоритм

Этот раздел — самая важная часть всей статьи. Вам абсолютно необходимо понять его, чтобы уметь реализовывать поиск пути; остальное (в том числе и A*) — это просто детали. В этом разделе вы будете разбираться, пока не поймёте смысл.

К тому же этот раздел невероятно прост.

Давайте попробуем формализовать наш пример, превратив его в псевдокод.

Нам нужно отслеживать узлы, которых мы знаем как достичь из начального узла. В начале это только начальный узел, но в процессе «исследования» сетки мы будем узнавать, как добираться до других узлов. Давайте назовём этот список узлов reachable:

reachable = [start_node]

Также нам нужно отслеживать уже рассмотренные узлы, чтобы не рассматривать их снова. Назовём их explored:

explored = []

Дальше я изложу ядро алгоритма: на каждом шаге поиска мы выбираем один из узлов, который мы знаем, как достичь, и смотрим, до каких новых узлов можем добраться из него. Если мы определим, как достичь конечного (целевого) узла, то задача решена! В противном случае мы продолжаем поиск.

Так просто, что даже разочаровывает? И это верно. Но из этого и состоит весь алгоритм. Давайте запишем его пошагово псевдокодом.

Мы продолжаем искать, пока или не доберёмся до конечного узла (в этом случае мы нашли путь из начального в конечный узел), или пока у нас не закончатся узлы, в которых можно выполнять поиск (в таком случае между начальным и конечным узлами пути нет).

while reachable is not empty:

Мы выбираем один из узлов, до которого знаем, как добраться, и который пока не исследован:

    node = choose_node(reachable)

Если мы только что узнали, как добраться до конечного узла, то задача выполнена! Нам просто нужно построить путь, следуя по ссылкам previous обратно к начальному узлу:

    if node == goal_node:
       path = []
       while node != None:
            path.add(node)
            node = node.previous
        
        return path

Нет смысла рассматривать узел больше одного раза, поэтому мы будем это отслеживать:

    reachable.remove(node)
    explored.add(node)

Мы определяем узлы, до которых не можем добраться отсюда. Начинаем со списка узлов, соседних с текущим, и удаляем те, которые мы уже исследовали:

    new_reachable = get_adjacent_nodes(node) - explored

Мы берём каждый из них:

    for adjacent in new_reachable:

Если мы уже знаем, как достичь узла, то игнорируем его. В противном случае добавляем его в список reachable, отслеживая, как в него попали:

        if adjacent not in reachable:
            adjacent.previous = node  # Remember how we got there.
            reachable.add(adjacent)

Нахождение конечного узла — это один из способов выхода из цикла. Второй — это когда reachable становится пустым: у нас закончились узлы, которые можно исследовать, и мы не достигли конечного узла, то есть из начального в конечный узел пути нет:

return None

И… на этом всё. Это весь алгоритм, а код построения пути выделен в отдельный метод:

function find_path (start_node, end_node):
    reachable = [start_node]
    explored = []

    while reachable is not empty:
        # Choose some node we know how to reach.
        node = choose_node(reachable)

        # If we just got to the goal node, build and return the path.
        if node == goal_node:
            return build_path(goal_node)

        # Don't repeat ourselves.
        reachable.remove(node)
        explored.add(node)

        # Where can we get from here?
        new_reachable = get_adjacent_nodes(node) - explored
        for adjacent in new_reachable:
            if adjacent not in reachable
                adjacent.previous = node  # Remember how we got there.
                reachable.add(adjacent)

    # If we get here, no path was found :(
    return None

Вот функция, которая строит путь, следуя по ссылкам previous обратно к начальному узлу:

function build_path (to_node):
    path = []
    while to_node != None:
        path.add(to_node)
        to_node = to_node.previous
    return path

Вот и всё. Это псевдокод каждого алгоритма поиска пути, в том числе и A*.

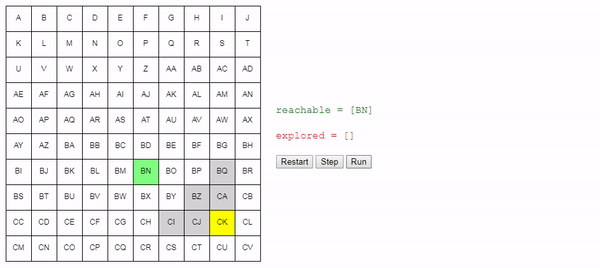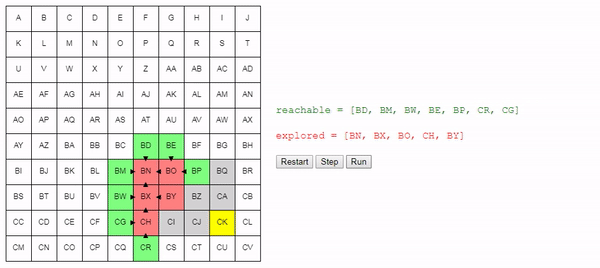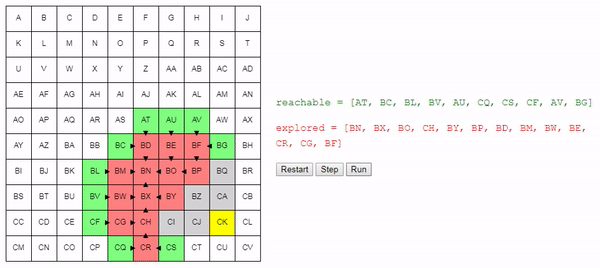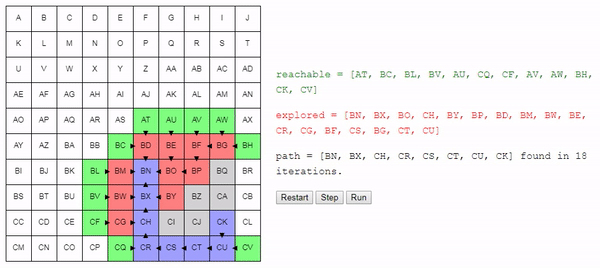
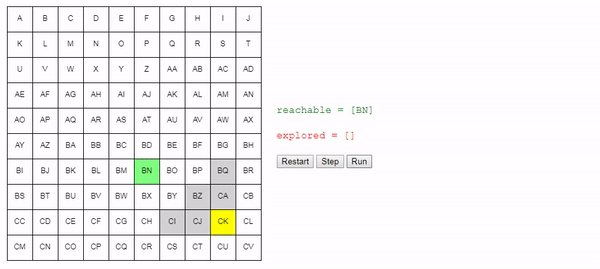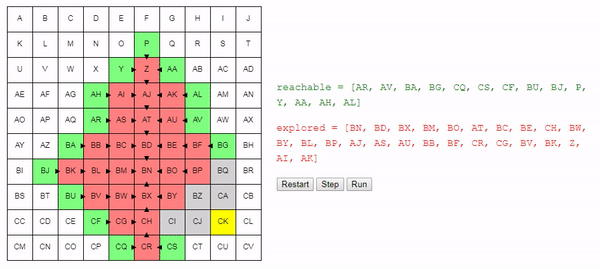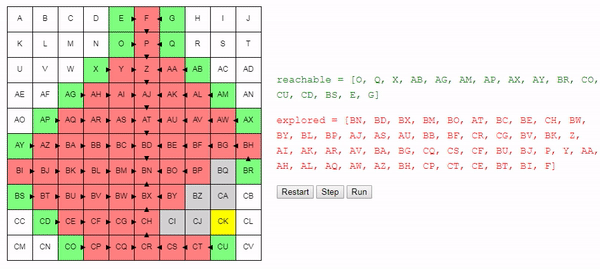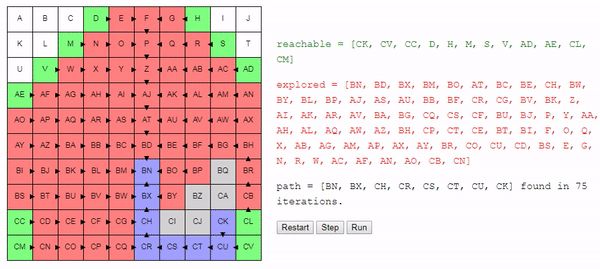
Перечитывайте этот раздел, пока не поймёте, как всё работает, и, что более важно, почему всё работает. Идеально будет нарисовать пример вручную на бумаге, но можете и посмотреть интерактивное демо:

Интерактивное демо

Вот демо и пример реализации показанного выше алгоритма (запустить его можно на странице оригинала статьи). choose_node просто выбирает случайный узел. Можете запустить алгоритм пошагово и посмотреть на список узлов reachable и explored, а также на то, куда указывают ссылки previous.

Заметьте, что поиск завершается, как только обнаруживается путь; может случиться так, что некоторые узлы даже не будут рассмотрены.

Заключение

Представленный здесь алгоритм — это общий алгоритм для любого алгоритма поиска пути.

Но что же отличает каждый алгоритм от другого, почему A* — это A*?

Вот подсказка: если запустить поиск в демо несколько раз, то вы увидите, что алгоритм на самом деле не всегда находит один и тот же путь. Он находит какой-то путь, и этот путь необязательно является кратчайшим. Почему?

Часть 2. Стратегии поиска

Если вы не полностью поняли описанный в предыдущем разделе алгоритм, то вернитесь к нему и прочтите заново, потому что он необходим для понимания дальнейшей информации. Когда вы в нём разберётесь, A* покажется вам совершенно естественным и логичным.

Секретный ингредиент

В конце предыдущей части я оставил открытыми два вопроса: если каждый алгоритм поиска использует один и тот же код, почему A* ведёт себя как A*? И почему демо иногда находит разные пути?

Ответы на оба вопроса связаны друг с другом. Хоть алгоритм и хорошо задан, я оставил нераскрытым один аспект, и как оказывается, он является ключевым для объяснения поведения алгоритмов поиска:

node = choose_node(reachable)

Именно эта невинно выглядящая строка отличает все алгоритмы поиска друг от друга. От способа реализации choose_node зависит всё.

Так почему же демо находит разные пути? Потому что его метод choose_node выбирает узел случайным образом.

Длина имеет значение

Прежде чем погружаться в различия поведений функции choose_node, нам нужно исправить в описанном выше алгоритме небольшой недосмотр.

Когда мы рассматривали узлы, соседние с текущим, то игнорировали те, которые уже знаем, как достичь:

if adjacent not in reachable:
    adjacent.previous = node  # Remember how we got there.
    reachable.add(adjacent)

Это ошибка: что если мы только что обнаружили лучший способ добраться до него? В таком случае необходимо изменить ссылку previous узла, чтобы отразить этот более короткий путь.

Чтобы это сделать, нам нужно знать длину пути от начального узла до любого достижимого узла. Мы назовём это стоимостью (cost) пути. Пока примем, что перемещение из узла в один из соседних узлов имеет постоянную стоимость, равную 1.

Прежде чем начинать поиск, мы присвоим значению cost каждого узла значение infinity; благодаря этому любой путь будет короче этого. Также мы присвоим cost узла start_node значение 0.

Тогда вот как будет выглядеть код:

if adjacent not in reachable:
    reachable.add(adjacent)

# If this is a new path, or a shorter path than what we have, keep it.
if node.cost + 1 < adjacent.cost:
    adjacent.previous = node
    adjacent.cost = node.cost + 1

Одинаковая стоимость поиска

Давайте теперь рассмотрим метод choose_node. Если мы стремимся найти кратчайший возможный путь, то выбирать узел случайным образом — не самая лучшая идея.

Лучше выбирать узел, которого мы можем достичь из начального узла по кратчайшему пути; благодаря этому мы в общем случае будем предпочитать длинным путям более короткие. Это не значит, что более длинные пути не будут рассматриваться вовсе, это значит, что более короткие пути будут рассматриваться первыми. Так как алгоритм завершает работу сразу после нахождения подходящего пути, это должно позволить нам находить короткие пути.

Вот возможный пример функции choose_node:

function choose_node (reachable):
    best_node = None

    for node in reachable:
        if best_node == None or best_node.cost > node.cost:
            best_node = node
    
    return best_node

Интуитивно понятно, что поиск этого алгоритма расширяется «радиально» от начального узла, пока не достигнет конечного. Вот интерактивное демо такого поведения:

Заключение

Простое изменение в способе выбора рассматриваемого следующим узла позволило нам получить достаточно хороший алгоритм: он находит кратчайший путь от начального до конечного узла.

Но этот алгоритм всё равно в какой-то степени остаётся «глупым». Он продолжает искать повсюду, пока не наткнётся на конечный узел. Например, какой смысл в показанном выше примере выполнять поиск в направлении A, если очевидно, что мы отдаляемся от конечного узла?

Можно ли сделать choose_node умнее? Можем ли мы сделать так, чтобы он направлял поиск в сторону конечного узла, даже не зная заранее правильного пути?

Оказывается, что можем — в следующей части мы наконец-то дойдём до choose_node, позволяющей превратить общий алгоритм поиска пути в A*.

Часть 3. Снимаем завесу тайны с A*

Полученный в предыдущей части алгоритм достаточно хорош: он находит кратчайший путь от начального узла до конечного. Однако, он тратит силы впустую: рассматривает пути, которые человек очевидно назовёт ошибочными — они обычно удаляются от цели. Как же этого можно избежать?

Волшебный алгоритм

Представьте, что мы запускаем алгоритм поиска на особом компьютере с чипом, который может творить магию. Благодаря этому потрясающему чипу мы можем выразить choose_node очень простым способом, который гарантированно создаст кратчайший путь, не теряя времени на исследование частичных путей, которые никуда не ведут:

function choose_node (reachable):
    return magic(reachable, "любой узел, являющийся следующим на кратчайшем пути")

Звучит соблазнительно, но магическим чипам всё равно требуется какой-то низкоуровневый код. Вот какой может быть хорошая аппроксимация:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = magic(node, "кратчайший путь к цели")
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Это отличный способ выбора следующего узла: вы выбираем узел, дающий нам кратчайший путь от начального до конечного узла, что нам и нужно.

Также мы минимизировали количество используемой магии: мы точно знаем, какова стоимость перемещения от начального узла к каждому узлу (это node.cost), и используем магию только для предсказания стоимости перемещения от узла к конечному узлу.

Не магический, но довольно потрясающий A*

К сожалению, магические чипы — это новинка, а нам нужна поддержка и устаревшего оборудования. БОльшая часть кода нас устраивает, за исключением этой строки:

# Throws MuggleProcessorException
cost_node_to_goal = magic(node, "кратчайший путь к цели")

То есть мы не можем использовать магию, чтобы узнать стоимость ещё не исследованного пути. Ну ладно, тогда давайте сделаем прогноз. Будем оптимистичными и предположим, что между текущим и конечным узлами нет ничего, и мы можем просто двигаться напрямик:

cost_node_to_goal = distance(node, goal_node)

Заметьте, что кратчайший путь и минимальное расстояние разные: минимальное расстояние подразумевает, что между текущим и конечным узлами нет совершенно никаких препятствий.

Эту оценку получить достаточно просто. В наших примерах с сетками это расстояние городских кварталов между двумя узлами (то есть abs(Ax - Bx) + abs(Ay - By)). Если бы мы могли двигаться по диагонали, то значение было бы равно sqrt( (Ax - Bx)^2 + (Ay - By)^2 ), и так далее. Самое важное то, что мы никогда не получаем слишком высокую оценку стоимости.

Итак, вот немагическая версия choose_node:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = estimate_distance(node, goal_node)
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Функция, оценивающая расстояние от текущего до конечного узла, называется эвристикой, и этот алгоритм поиска, леди и джентльмены, называется … A*.

Интерактивное демо

Пока вы оправляетесь от шока, вызванного осознанием того, что загадочный A* на самом деле настолько прост, можете посмотреть на демо (или запустить его в оригинале статьи). Вы заметите, что в отличие от предыдущего примера, поиск тратит очень мало времени на движение в неверном направлении.

Заключение

Наконец-то мы дошли до алгоритма A*, который является не чем иным, как описанным в первой части статьи общим алгоритмом поиска с некоторыми усовершенствованиями, описанными во второй части, и использующим функцию choose_node, которая выбирает узел, который по нашей оценке приближает нас к конечному узлу. Вот и всё.

Вот вам для справки полный псевдокод основного метода:

function find_path (start_node, end_node):
    reachable = [start_node]
    explored = []

    while reachable is not empty:
        # Choose some node we know how to reach.
        node = choose_node(reachable)

        # If we just got to the goal node, build and return the path.
        if node == goal_node:
            return build_path(goal_node)

        # Don't repeat ourselves.
        reachable.remove(node)
        explored.add(node)

        # Where can we get from here that we haven't explored before?
        new_reachable = get_adjacent_nodes(node) - explored
        for adjacent in new_reachable:
            # First time we see this node?
            if adjacent not in reachable:
                reachable.add(adjacent)
        
            # If this is a new path, or a shorter path than what we have, keep it.
            if node.cost + 1 < adjacent.cost:
                adjacent.previous = node
                adjacent.cost = node.cost + 1

    # If we get here, no path was found :(
    return None

Метод build_path:

function build_path (to_node):
    path = []
    while to_node != None:
        path.add(to_node)
        to_node = to_node.previous
    return path

А вот метод choose_node, который превращает его в A*:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = estimate_distance(node, goal_node)
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Вот и всё.

А зачем же нужна часть 4?

Теперь, когда вы поняли, как работает A*, я хочу рассказать о некоторых потрясающих областях его применения, которые далеко не ограничиваются поиском путей в сетке ячеек.

Часть 4. A* на практике

Первые три части статьи начинаются с самых основ алгоритмов поиска путей и заканчиваются чётким описанием алгоритма A*. Всё это здорово в теории, но понимание того, как это применимо на практике — совершенно другая тема.

Например, что будет, если наш мир не является сеткой?

Что если персонаж не может мгновенно поворачиваться на 90 градусов?

Как построить граф, если мир бесконечен?

Что если нас не волнует длина пути, но мы зависим от солнечной энергии и нам как можно больше нужно находиться под солнечным светом?

Как найти кратчайший путь к любому из двух конечных узлов?

Функция стоимости

В первых примерах мы искали кратчайший путь между начальным и конечным узлами. Однако вместо того, чтобы хранить частичные длины путей в переменной length, мы назвали её cost. Почему?

Мы можем заставить A* искать не только кратчайший, но и лучший путь, причём определение «лучшего» можно выбирать, исходя из наших целей. Когда нам нужен кратчайший путь, стоимостью является длина пути, но если мы хотим минимизировать, например, потребление топлива, то нужно использовать в качестве стоимости именно его. Если мы хотим по максимуму увеличить «время, проводимое под солнцем», то затраты — это время, проведённое без солнца. И так далее.

В общем случае это означает, что с каждым ребром графа связаны соответствующие затраты. В показанных выше примерах стоимость задавалась неявно и считалась всегда равной 1, потому что мы считали шаги на пути. Но мы можем изменить стоимость ребра в соответствии с тем, что мы хотим минимизировать.

Функция критерия

Допустим, наш объект — это автомобиль, и ему нужно добраться до заправки. Нас устроит любая заправка. Требуется кратчайший путь до ближайшей АЗС.

Наивный подход будет заключаться в вычислении кратчайшего пути до каждой заправки по очереди и выборе самого короткого. Это сработает, но будет довольно затратным процессом.

Что если бы мы могли заменить один goal_node на метод, который по заданному узлу может сообщить, является ли тот конечным или нет. Благодаря этому мы сможем искать несколько целей одновременно. Также нам нужно изменить эвристику, чтобы она возвращала минимальную оцениваемую стоимость всех возможных конечных узлов.

В зависимости от специфики ситуации мы можем и не иметь возможности достичь цели идеально, или это будет слишком много стоить (если мы отправляем персонажа через половину огромной карты, так ли важна разница в один дюйм?), поэтому метод is_goal_node может возвращать true, когда мы находимся «достаточно близко».

Полная определённость не обязательна

Представление мира в виде дискретной сетки может быть недостаточным для многих игр. Возьмём, например, шутер от первого лица или гоночную игру. Мир дискретен, но его нельзя представить в виде сетки.

Но есть проблема и посерьёзней: что если мир бесконечен? В таком случае, даже если мы сможем представить его в виде сетки, то у нас просто не будет возможности построить соответствующий сетке граф, потому что он должен быть бесконечным.

Однако не всё потеряно. Разумеется, для алгоритма поиска по графам нам определённо нужен граф. Но никто не говорил, что граф должен быть исчерпывающим!

Если внимательно посмотреть на алгоритм, то можно заметить, что мы ничего не делаем с графом, как целым; мы исследуем граф локально, получая узлы, которых можем достичь из рассматриваемого узла. Как видно из демо A*, некоторые узлы графа вообще не исследуются.

Так почему бы нам просто не строить граф в процессе исследования?

Мы делаем текущую позицию персонажа начальным узлом. При вызове get_adjacent_nodes она может определять возможные способы, которыми персонаж способен переместиться из данного узла, и создавать соседние узлы на лету.

За пределами трёх измерений

Даже если ваш мир действительно является 2D-сеткой, нужно учитывать и другие аспекты. Например, что если персонаж не может мгновенно поворачиваться на 90 или 180 градусов, как это обычно и бывает?

Состояние, представляемое каждым узлом поиска, не обязательно должно быть только позицией; напротив, оно может включать в себя произвольно сложное множество значений. Например, если повороты на 90 градусов занимают столько же времени, сколько переход из одной ячейки в другую, то состояние персонажа может задаваться как [position, heading]. Каждый узел может представлять не только позицию персонажа, но и направление его взгляда; и новые рёбра графа (явные или косвенные) отражают это.

Если вернуться к исходной сетке 5×5, то начальной позицией поиска теперь может быть [A, East]. Соседними узлами теперь являются [B, East] и [A, South] — если мы хотим достичь F, то сначала нужно скорректировать направление, чтобы путь обрёл вид [A, East], [A, South], [F, South].

Шутер от первого лица? Как минимум четыре измерения: [X, Y, Z, Heading]. Возможно, даже [X, Y, Z, Heading, Health, Ammo].

Учтите, что чем сложнее состояние, тем более сложной должна быть эвристическая функция. Сам по себе A* прост; искусство часто возникает благодаря хорошей эвристике.

Заключение

Цель этой статьи — раз и навсегда развеять миф о том, что A* — это некий мистический, не поддающийся расшифровке алгоритм. Напротив, я показал, что в нём нет ничего загадочного, и на самом деле его можно довольно просто вывести, начав с самого нуля.

Дальнейшее чтение

У Амита Патела есть превосходное «Введение в алгоритм A*» [перевод на Хабре] (и другие его статьи на разные темы тоже великолепны!).

Когда вы пользуетесь навигатором, вы указываете точку А и точку Б, и дальше навигатор как-то сам строит маршрут. Сегодня посмотрим, что лежит в основе алгоритма, который это делает. Просто ради интереса. 

Графы и «задача коммивояжёра»

Ещё до появления навигаторов у людей была такая же проблема: как найти кратчайший путь из одного места в другое, если есть ограниченное количество промежуточных точек? Или как объехать ограниченное количество точек, затратив минимальные усилия. В общем виде это называется «задачей коммивояжёра», и мы уже рассказывали, в чём там идея:

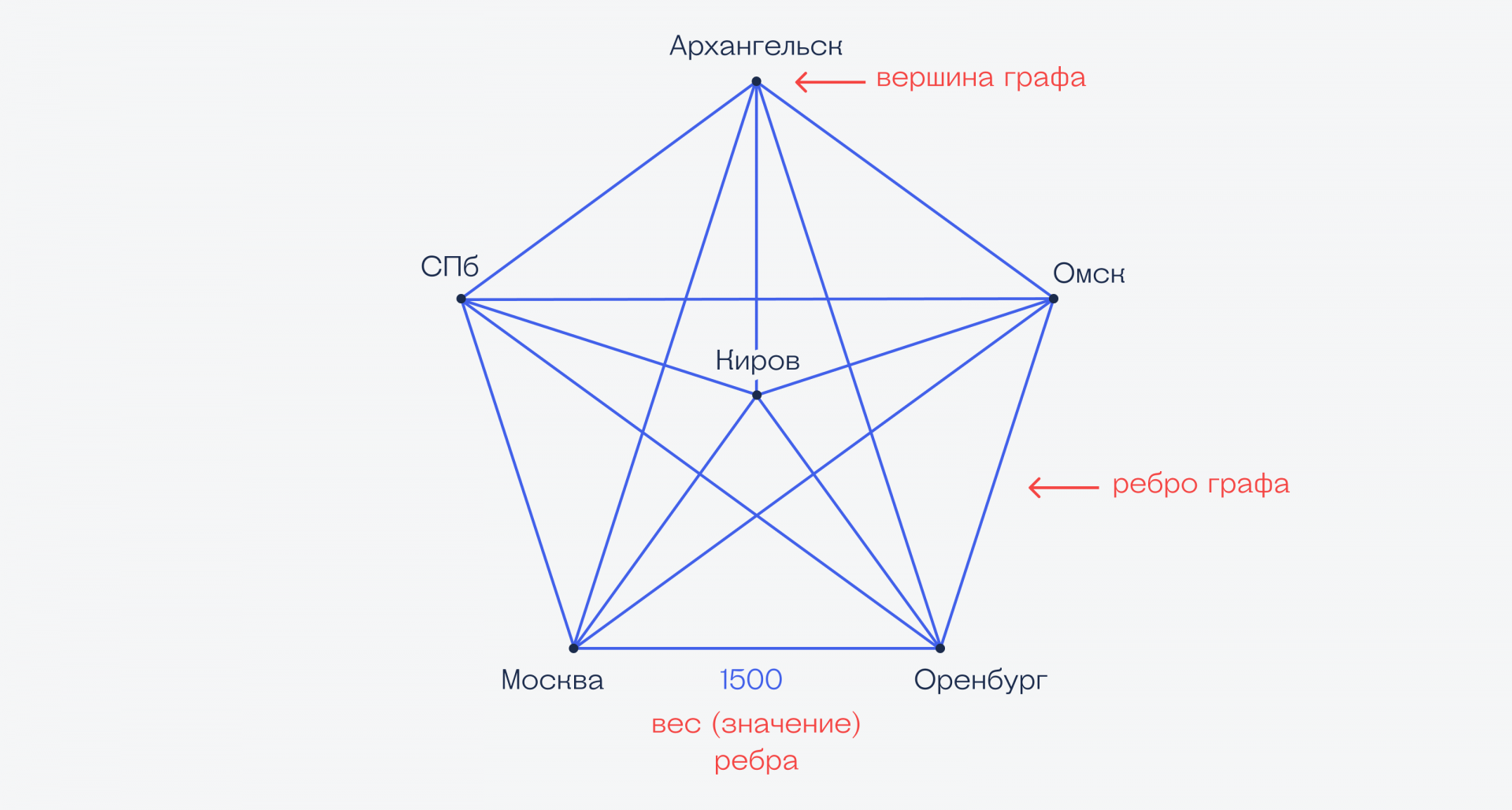
Если взять просто города и расстояния между ними, то с точки зрения математики это называется графом: города будут вершинами графа, а дороги между ними — рёбрами графа. Если мы знаем длину каждой дороги, то это будет значением (весом) рёбер графа. Этой теории нам уже хватит, чтобы понять, как работает навигатор в машине.

Алгоритм Дейкстры — ищем самый быстрый путь

Как только появилось решение полным перебором, математики стали искать другой подход, который работал бы гораздо быстрее и не требовал бы вычисления такого огромного объёма данных. В 1959 году Эдсгер Дейкстра придумал свой алгоритм, которым пользуются до сих пор. Идея его в том, чтобы не перебирать все варианты, а находить самый короткий путь только между соседними графами — и так, шаг за шагом, продвигаться к конечной точке.

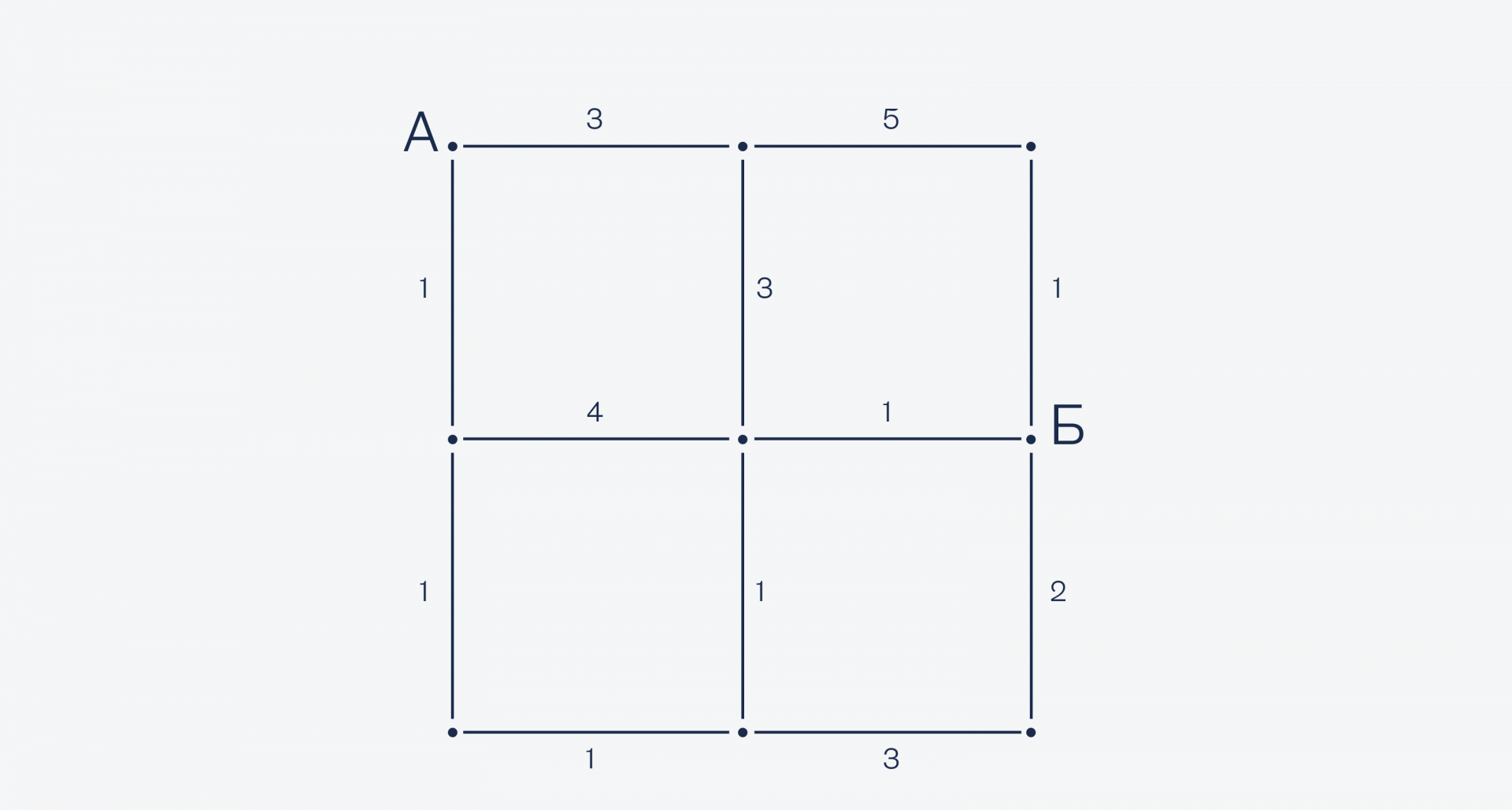
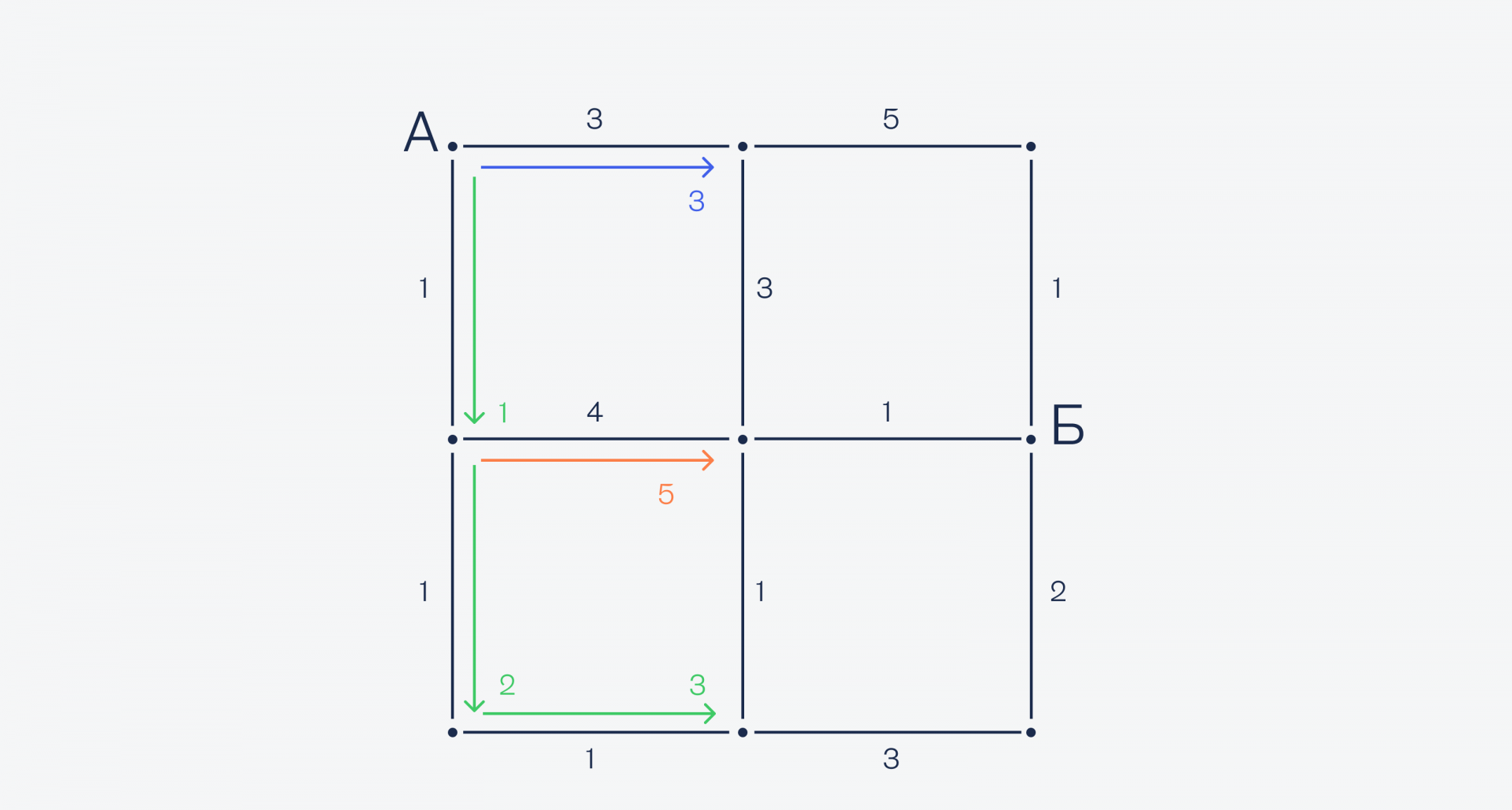
Допустим, у нас есть улицы, перекрёстки и мы знаем время пути между ними. Нарисуем это в виде графа, а чтобы было проще ориентироваться — сделаем визуально всё одинаковой длины:

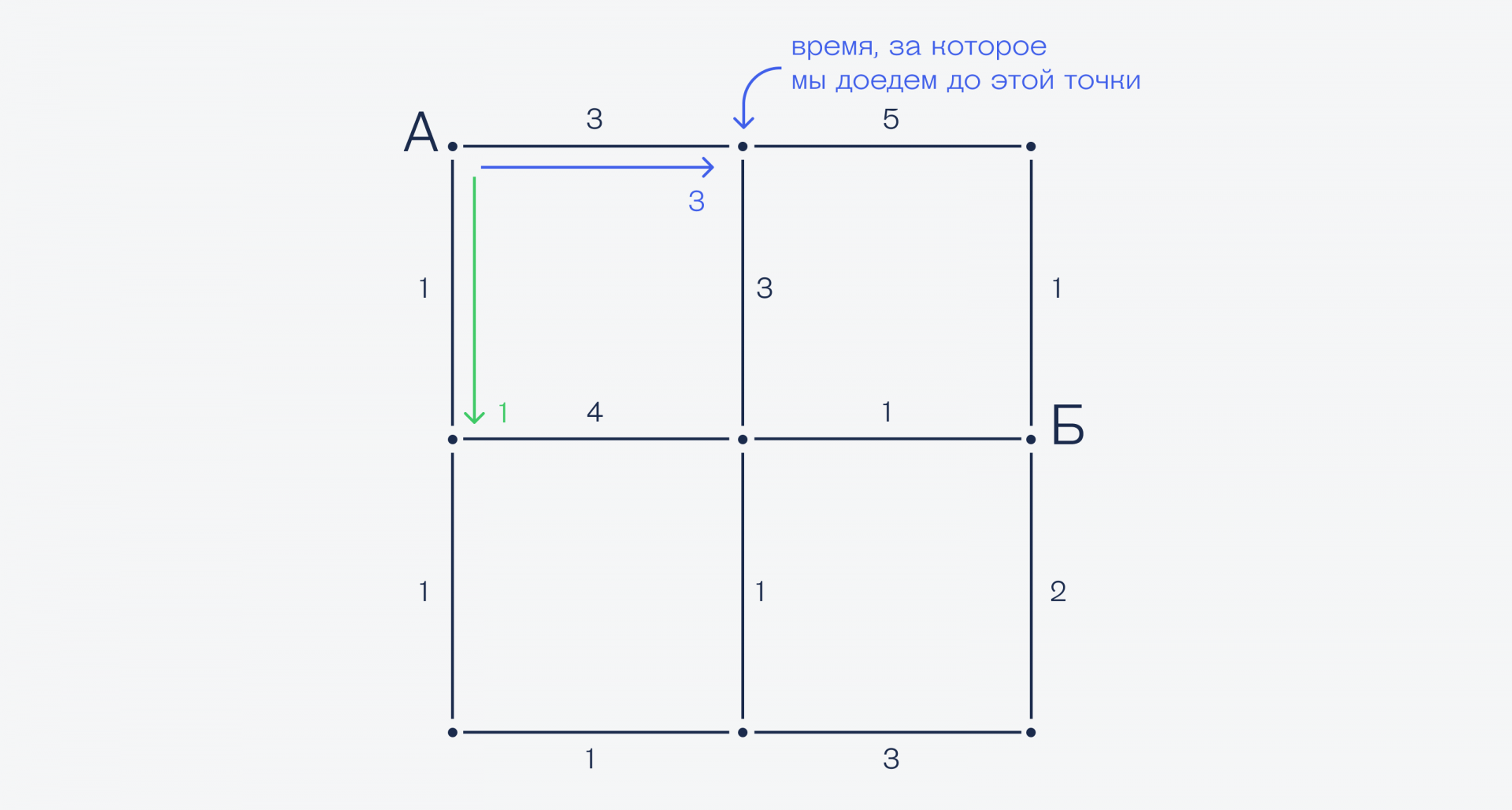
Чтобы найти самый быстрый путь из А в Б, мы смотрим сначала, какие пути у нас выходят из точки А. Видно, что поехать вниз будет быстрее, чем поехать направо:

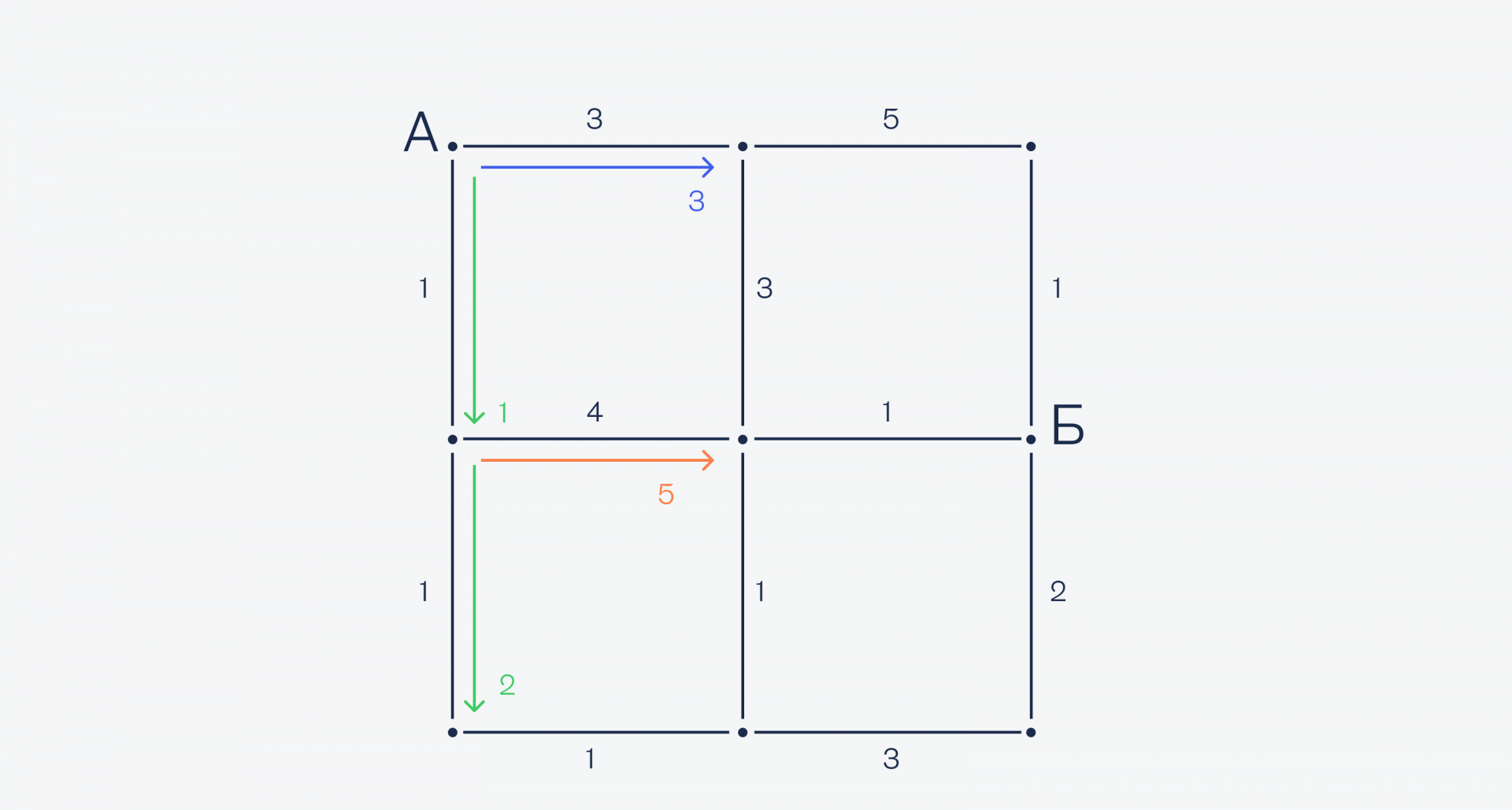
Значит, выбираем путь вниз. Теперь делаем то же самое для этой точки — смотрим, где быстрее: справа или внизу. Вниз быстрее (1 меньше, чем 4), поэтому едем по ней:

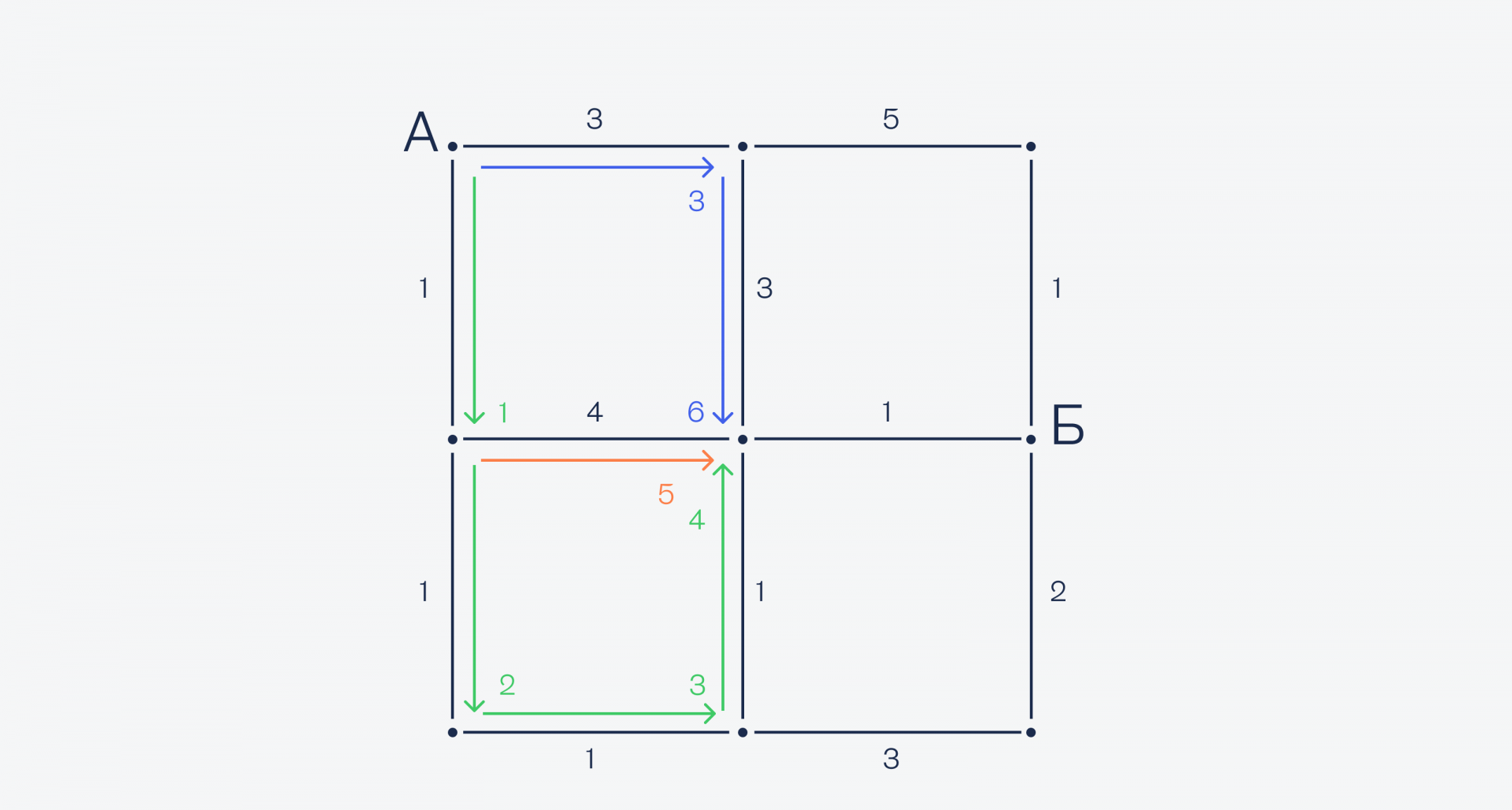
При этом мы не отбрасываем уже сделанные вычисления (всё равно уже посчитали), а запоминаем их на всякий случай. Из нижней точки есть только одна дорога — направо, поэтому едем по ней:

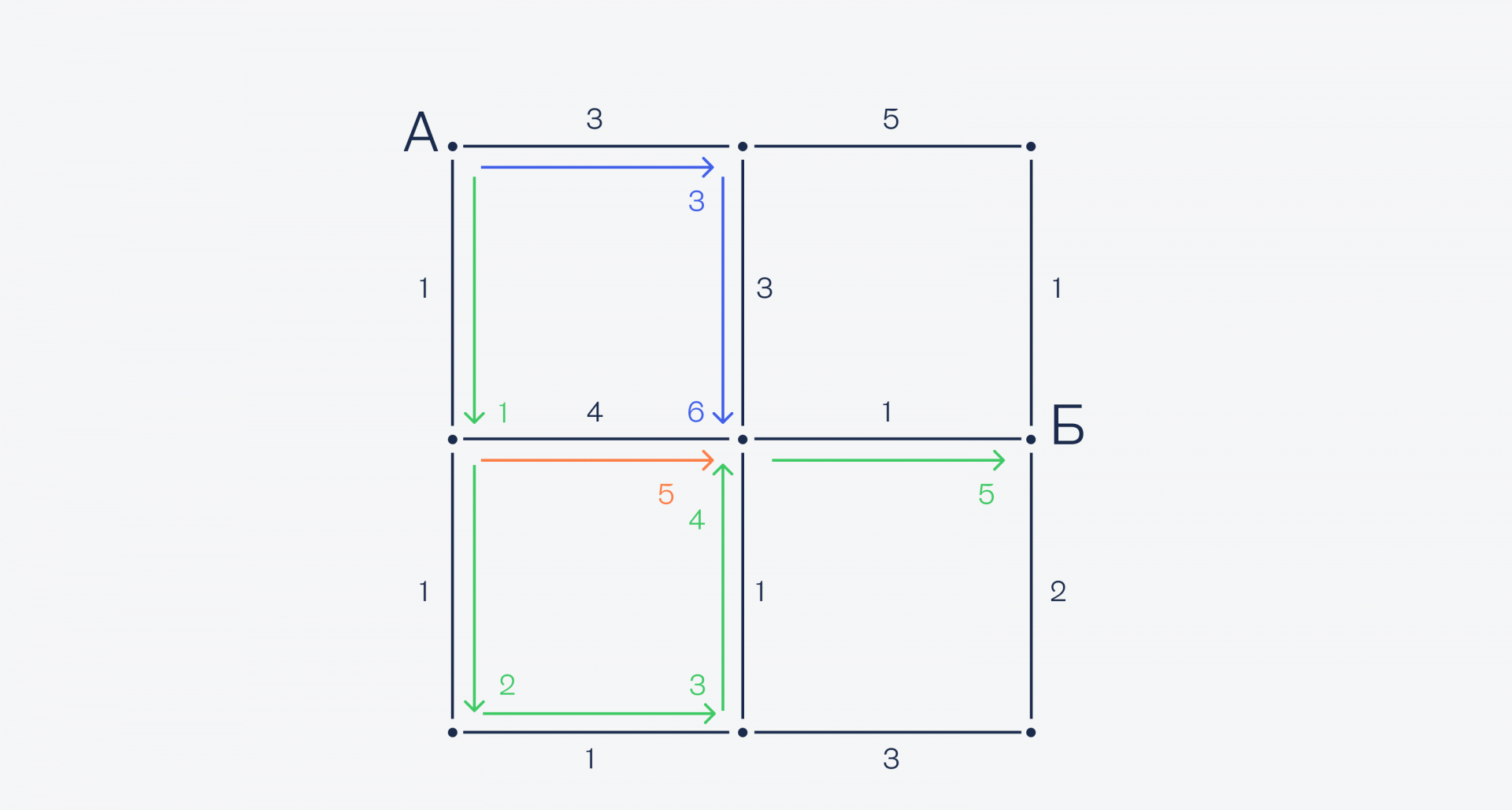
А теперь у нас получилась интересная ситуация: в центральную точку мы можем попасть как сверху, так и снизу, при этом и там, и там у нас одинаковое время — 3 минуты. Значит, посчитаем оба варианта — вдруг сверху будет быстрее и нам нужно будет перестроить маршрут заново:

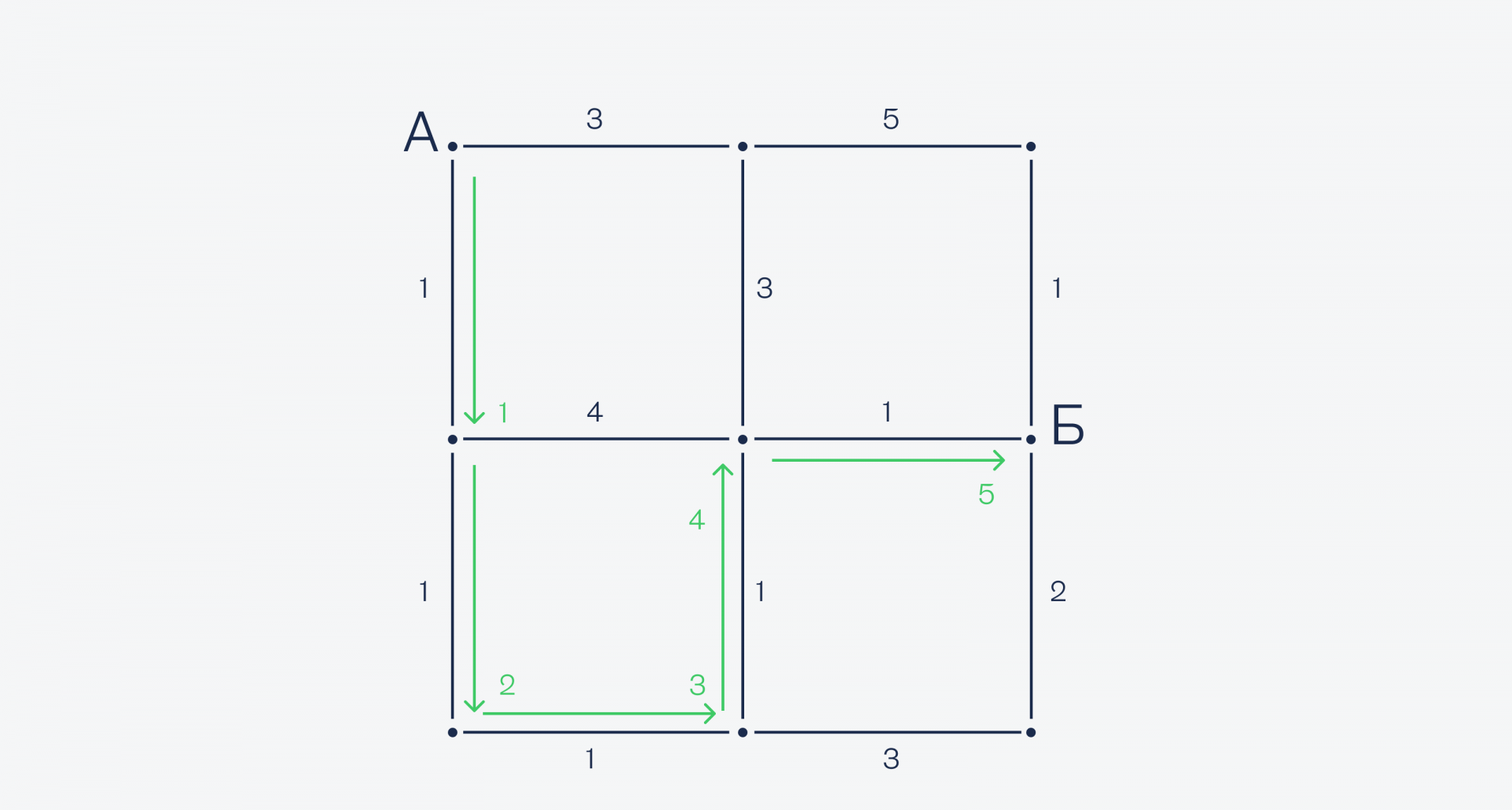
Оказывается, снизу ехать до центра быстрее, чем сверху — 4 минуты вместо 6, поэтому оставляем нижний маршрут. Наконец, из центральной точки до точки Б всего один путь — направо, поэтому выбираем его:

Как видите, нам не пришлось считать все варианты со всеми точками, а до некоторых мы просто не добрались. Это сильно сэкономило время и потребовало меньше ресурсов для вычисления.Такой алгоритм и лежит в основе автомобильных навигаторов — с вычислениями справится даже бюджетный смартфон.

Что ещё учитывает навигатор

Чтобы алгоритм оставался простым и работал только со временем, все остальные параметры дорог тоже привязывают ко времени. Покажем, как это работает, на паре примеров.

Комфорт. Если нам нужно построить не самый быстрый, а самый комфортный маршрут, то мы можем отдать предпочтение автомагистралям и дорогам с несколькими полосами — на них обычно и асфальт получше, и резких поворотов поменьше. Чтобы навигатор выбирал именно такие дороги, им можно присвоить коэффициент 0,8 — это виртуально сократит время на дорогу по ним на 20%, а навигатор всегда выберет то, что быстрее. 

С просёлочными и грунтовыми дорогами ситуация обратная. Они редко бывают комфортными, а значит, им можно дать коэффициент 1,3, чтобы они казались алгоритму более долгими и он старался их избегать. А лесным дорогам можно поставить коэффициент 5 — навигатор их выберет, только если это единственная дорога то точки назначения.

Сложность маршрута и реальное время. Маршрут из А в Б почти никогда не бывает прямым — на нём всегда есть повороты, развороты и съезды, которые отнимают время. Чтобы навигатор это учитывал, в графы добавляют время прохождения поворота — либо коэффициентом, либо отдельным параметром. Из-за этого алгоритм будет искать действительно быстрый маршрут с учётом геометрии дорог.

Пробки. Если есть интернет, то всё просто: навигатор получает данные о состоянии дорог и добавляет разные коэффициенты в зависимости от загруженности. Иногда навигатор ведёт дворами, когда трасса свободна — это не ошибка навигатора, а его прогноз на время поездки: если через 10 минут в этом месте обычно собираются пробки, то там лучше не ехать, а заранее поехать в объезд.

Если интернета нет, то алгоритм просто использует усреднённую модель пробок на этом участке. Эта модель скачивается заранее и постоянно обновляется в фоновом режиме.

Как построить маршрут по всей России

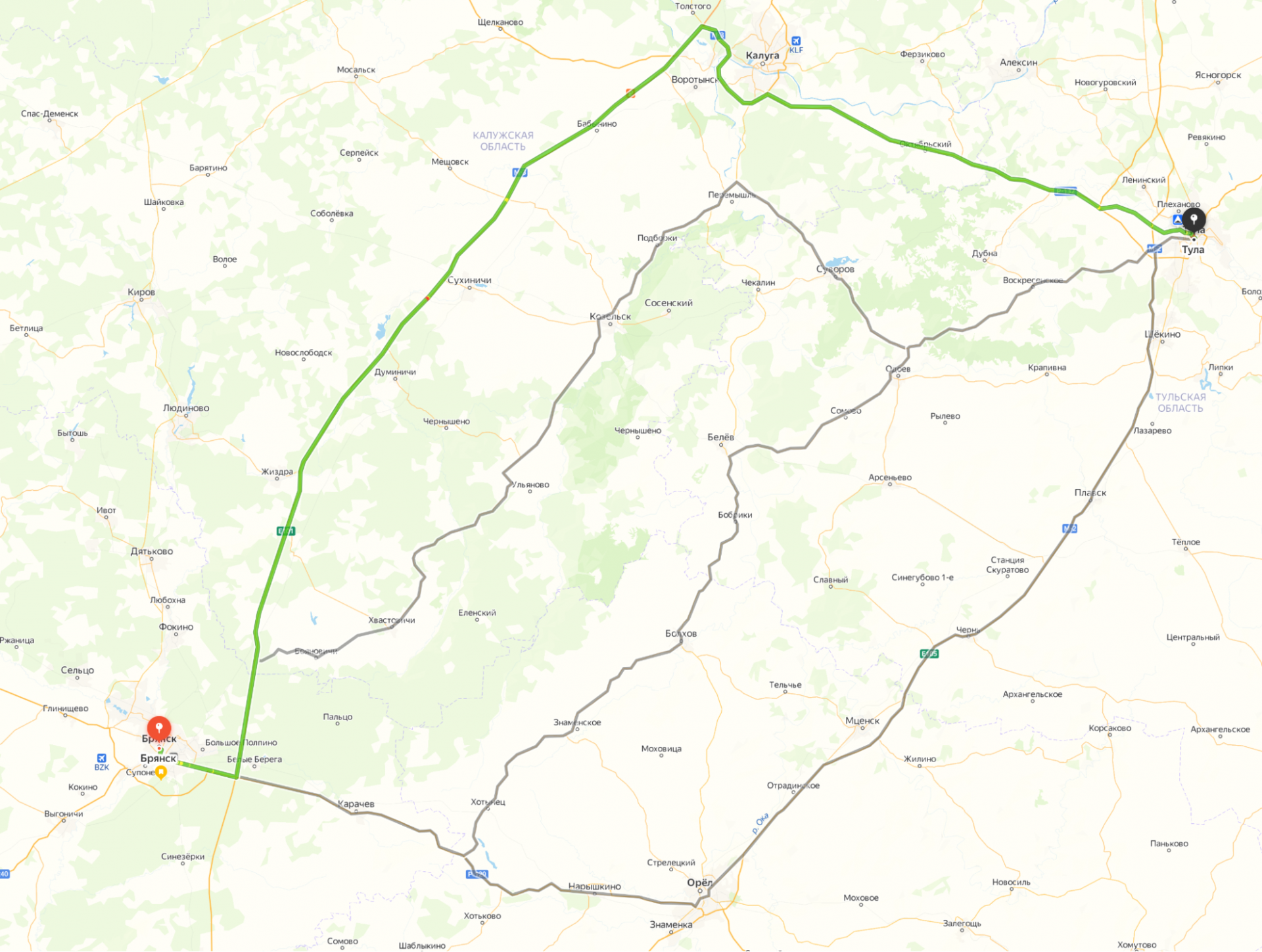
Если нам нужно построить маршрут из Брянска в Тулу, то с точки зрения компьютера это безумно сложная задача: ему нужно перебрать десятки тысяч улиц и миллионы перекрёстков, чтобы понять, какой путь выбрать. С этим плохо справляется даже обычный компьютер, не говоря уже о телефоне.

Если мы в Яндекс Картах построим такой маршрут, то навигатор нам предложит сразу 4 варианта:

Но мы не ждали полчаса, пока сервер на той стороне посчитает все перекрёстки, а получили результат через пару секунд. Хитрость в том, что алгоритм использует уже заранее просчитанные варианты маршрутов и подставляет их для ускорения.

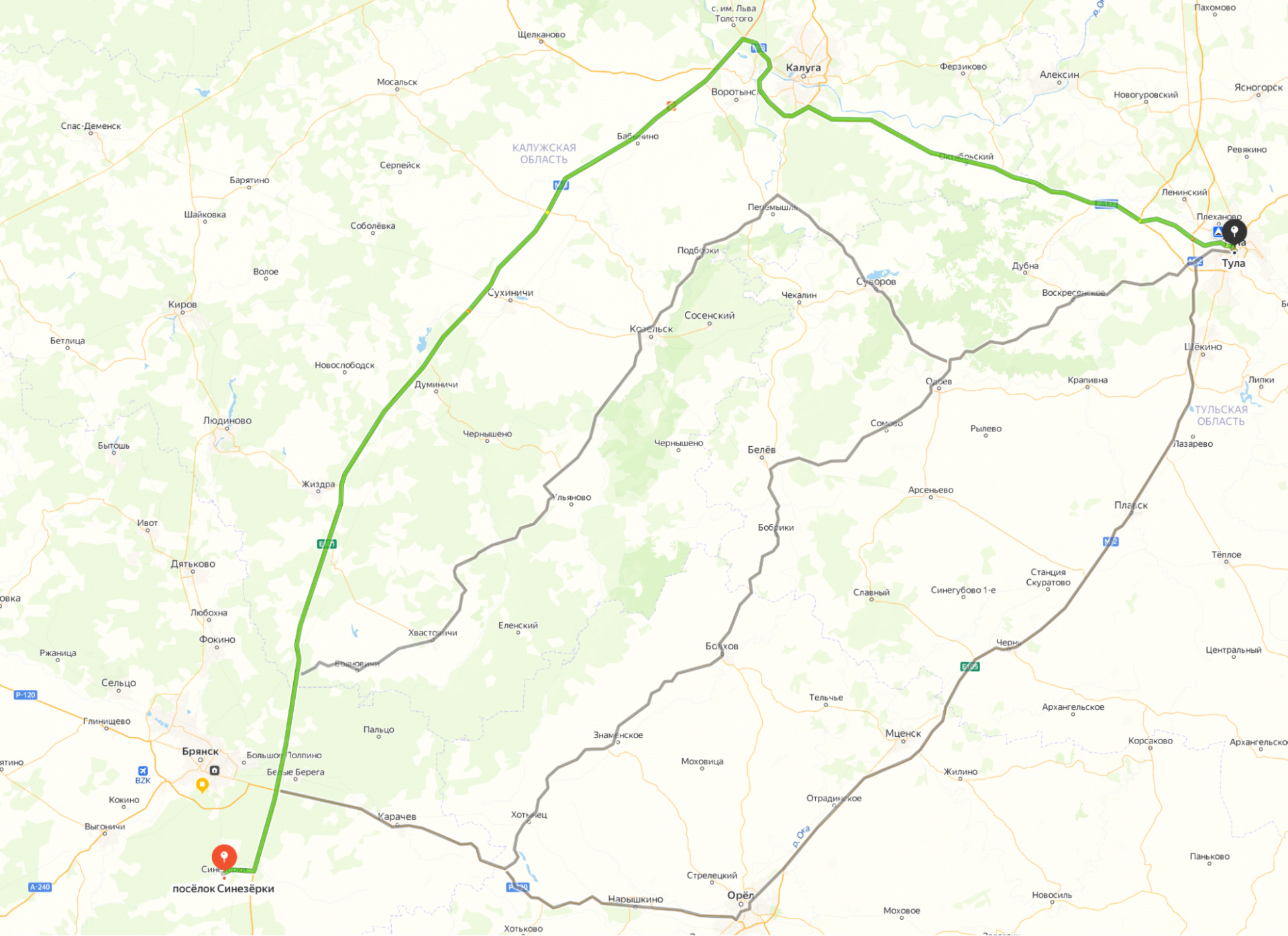
Например, если мы поедем в Тулу не из Брянска, а из Синезёрок, то поменяется только начальный маршрут по трассе М3, а всё остальное останется прежним:

Получается, что навигатору не нужно всё пересчитывать — он находит только ключевые точки пути, а маршрут между ними уже просчитан до этого. Этот приём работает и при перестроении маршрута во время движения: навигатор смотрит, как нужно поменять путь, чтобы вернуть вас на уже известную дорогу.

Что дальше

Следующий этап — напишем алгоритм Дейкстры сами и посмотрим, как он работает по шагам.

• Скачиваем с помощью “Play Market” и устанавливаем приложение “Яндекс Транспорт”;

  



• При первом запуске разрешаем программе использовать GPS;

Вы можете войти/создать аккаунт, однако этот пункт необязателен.

• Выбираем город, в котором вы живете;

Откроется карта и появится активная камера, на которой отображаются маршруты и положение транспорта в реальном времени.

Приложение позволяет отслеживать местоположение автобусов, троллейбусов и трамваев, остановок общественного транспорта (в том числе и метро), а также просматривать их расписание по выбранным остановкам.

Помимо всего на карте можно увидеть наименование улиц, объектов, которые на них находятся (например, название вашего любимого магазина Xistore).

С помощью программы можно мониторить аварии, а следовательно, заранее выбирать путь с учетом этих факторов.

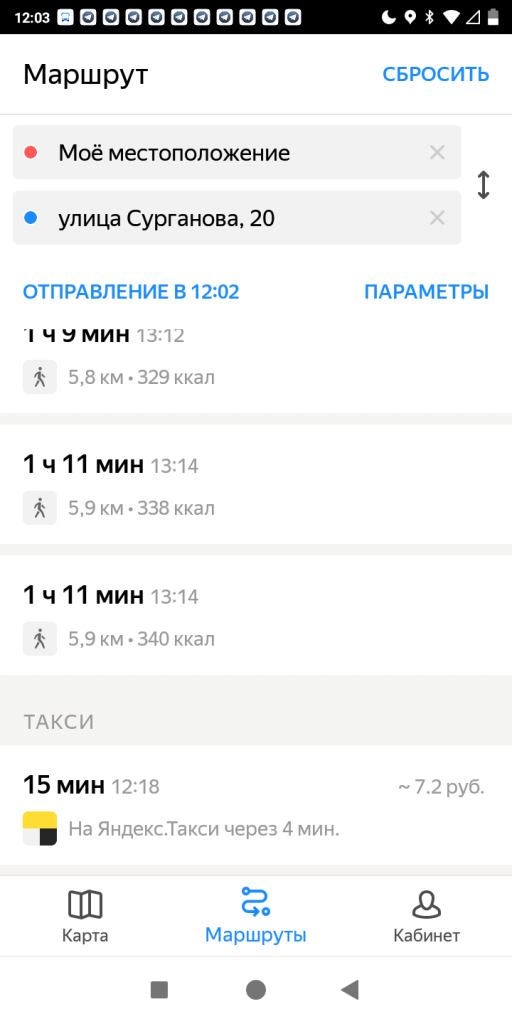
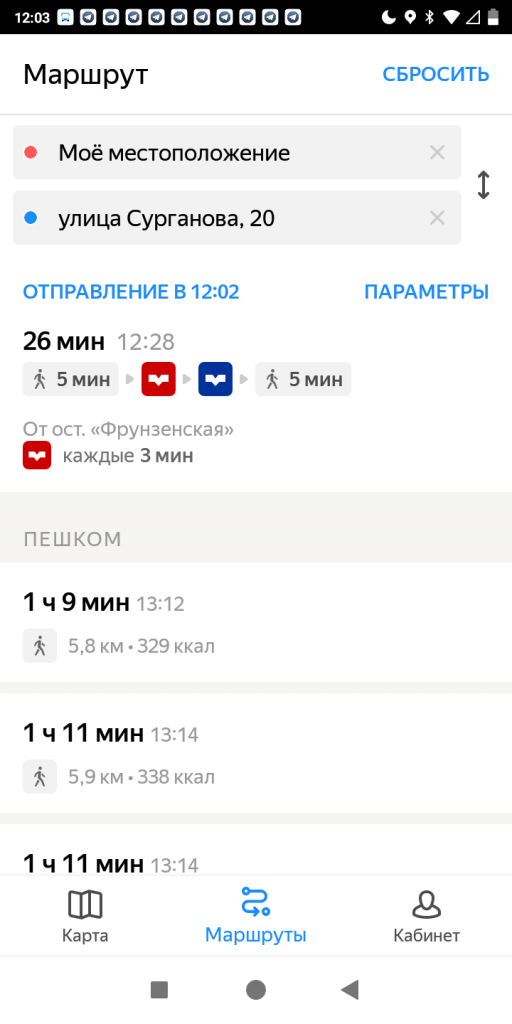
“Яндекс. Транспорт” умеет прорабатывать маршруты на общественном транспорте и подскажет не только способы передвижения, но и примерное время прибытия.

Также вы можете просматривать доступные автомобили через услугу “Яндекс.Такси” на новом смартфоне Redmi 5 Plus. 

Будьте мобильными вместе с Хistore!

Маршрутизация работает на сетевом уровне модель взаимодействия открытых систем OSI. Маршрутизация —  это поиск маршрута доставки пакета в крупной составной сети через транзитные узлы, которые называются маршрутизаторы.

Маршрутизация состоит из двух этапов:

1. На первом этапе происходит изучение сети, какие подсети есть в этой составной сети, какие маршрутизаторы и как эти маршрутизаторы объединены между собой.
2. Второй этап маршрутизации выполняется когда сеть уже изучена и на маршрутизатор поступил пакет, для этого пакета нужно определить куда именно его отправить. Иногда для второго этапа маршрутизации используется отдельный термин “продвижение” по-английски forwarding.

Варианты действий маршрутизатора

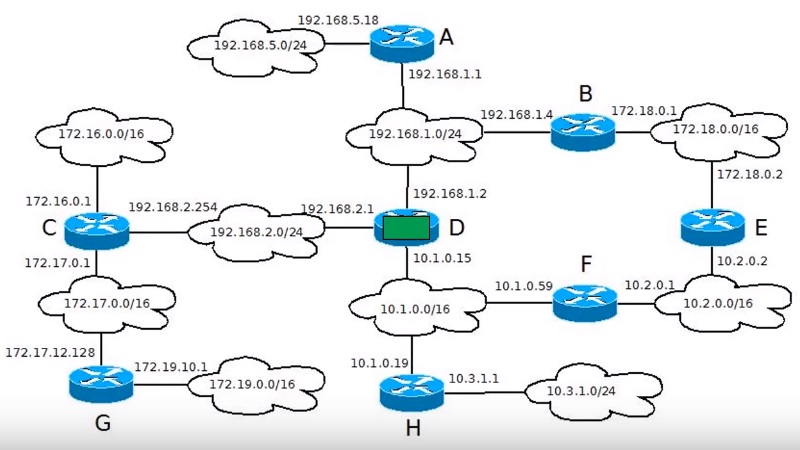
В качестве примера, рассмотрим схему составной сети, здесь показаны отдельные подсети, для каждой подсети есть ее адрес и маска, а также маршрутизаторы, которые объединяют эти сети.

Рассмотрим маршрутизатор D, на него пришел пакет, и маршрутизатор должен решить, что ему делать с этим пакетом. Начнем с того, какие вообще возможны варианты действий у маршрутизатора. Первый вариант, сеть которой предназначен пакет подключена непосредственно к маршрутизатору. У маршрутизатора D таких сетей 3, в этом случае маршрутизатор передает пакет непосредственно в эту сеть.

Второй вариант, нужная сеть подключена к другому маршрутизатору (А), и известно, какой маршрутизатор нужен. В этом случае, маршрутизатор D передает пакет на следующий маршрутизатор, который может передать пакет в нужную сеть, такой маршрутизатор называется шлюзом.

Третий вариант, пришел пакет для сети, маршрут которой не известен, в этом случае маршрутизатор отбрасывает пакет. В этом отличие работы маршрутизатора от коммутатора, коммутатор отправляет кадр который он не знает куда доставить на все порты, маршрутизатор так не делает. В противном случае составная сеть очень быстро может переполнится мусорными пакетами для которых не известен маршрут доставки.

Что нужно знать маршрутизатору для того чтобы решить куда отправить пакет?

• Во-первых у маршрутизатора есть несколько интерфейсов, к которым подключены сети. Нужно определить в какой из этих интерфейсов отправлять пакет.
• Затем нужно определить, что именно делать с этим пакетом. Есть 2 варианта, можно передать пакет в сеть (192.168.1.0/24), либо можно передать его на один из маршрутизаторов подключенные к этой сети. Если передавать пакет на маршрутизатор, то нужно знать, какой именно из маршрутизаторов подключенных к этой сети, выбрать для передачи пакета.

Таблица маршрутизации

Эту информацию маршрутизатор хранит в таблице маршрутизации. На картинке ниже показан ее упрощенный вид, в которой некоторые служебные столбцы удалены для простоты понимания.

Первые два столбца это адрес и маска подсети, вместе они задают адрес подсети. Затем столбцы шлюз, интерфейс и метрика. Столбец интерфейс говорит о том, через какой интерфейс маршрутизатора нам нужно отправить пакет.

Таблица маршрутизации Windows

Продолжим рассматривать маршрутизатор D, у него есть три интерфейса. Ниже на картинке представлен вид таблицы маршрутизации для windows, которые в качестве идентификатора интерфейса используют ip-адрес, который назначен этому интерфейсу. Таким образом в столбце интерфейс есть 3 ip-адреса, которые соответствуют трем интерфейсам маршрутизатора.

Столбец шлюз, говорит что делать с пакетом, который вышел через заданный интерфейс. Для сетей, которые подключены напрямую к маршрутизатору D, в столбце шлюз, указывается «подсоединен», которое говорит о том, что сеть подключена непосредственно к маршрутизатору и передавать пакет нужно напрямую в эту сеть.

Если же нам нужно передать пакет на следующий маршрутизатор то в поле шлюз указывается ip-адрес этого маршрутизатора.

Таблица маршрутизации Linux

В операционной системе linux таблица маршрутизации выглядит немного по-другому, основное отличие это идентификатор интерфейсов. В linux вместо ip-адресов используется название интерфейсов. Например, wlan название для беспроводного сетевого интерфейса, а eth0 название для проводного интерфейса по сети ethernet.

Также здесь некоторые столбцы удалены для сокращения (Flags, Ref и Use). В других операционных системах и в сетевом оборудовании вид таблицы маршрутизации может быть несколько другой, но всегда будут обязательны столбцы ip-адрес, маска подсети, шлюз, интерфейс и метрика.

Только следующий шаг!

Часто возникает вопрос, что делать, если сеть для который пришел пакет находится не за одним маршрутизатором? Чтобы в неё попасть, нужно пройти не через один, а через несколько маршрутизаторов, что в этом случае нужно вносить в таблицу маршрутизации.

В таблицу маршрутизации записываем только первый шаг, адрес следующего маршрутизатора, все что находится дальше нас не интересует.

Считаем, что следующий маршрутизатор должен знать правильный маршрут до нужной нам сети, он знает лучше следующий маршрутизатор, тот знает следующий шаг и так далее, пока не доберемся до нужные нам сети.

Метрика

Можно заметить, что в нашей схеме в одну и ту же сеть, например вот в эту (10.2.0.0/16) можно попасть двумя путями, первый путь проходят через один маршрутизатор F, а второй путь через два маршрутизатора B и E.

В этом отличие сетевого уровня от канального. На канальном уровне у нас всегда должно быть только одно соединение, а на сетевом уровне допускаются и даже поощряются для обеспечения надежности несколько путей к одной и той же сети.

Какой путь выбрать? Для этого используются поле метрика таблицы маршрутизации.

Метрика это некоторое число, которые характеризует расстояние от одной сети до другой. Если есть несколько маршрутов до одной и той же сети, то выбирается маршрут с меньшей метрикой.

Раньше, метрика измерялось в количестве маршрутизаторов, таким образом расстояние через маршрутизатор F было бы один, а через маршрутизаторы B и E два.

Однако сейчас метрика учитывает не только количество промежуточных маршрутизаторов, но и скорость каналов между сетями, потому что иногда бывает выгоднее пройти через два маршрутизатора, но по более скоростным каналам. Также может учитываться загрузка каналов, поэтому сейчас метрика — это число, которое учитывает все эти характеристики. Мы выбираем маршрут с минимальной метрикой в данном примере выше, будет выбран первый маршрут через маршрутизатор F.

Записи в таблице маршрутизации

Откуда появляются записей в таблице маршрутизации? Есть два варианта статическая маршрутизация и динамическая маршрутизация.

При статической маршрутизации, записи в таблице маршрутизации настраиваются вручную, это удобно делать если у вас сеть небольшая и изменяется редко, но если сеть крупная, то выгоднее использовать динамическую маршрутизацию, в которой маршруты настраиваются автоматически. В этом случае маршрутизаторы сами изучают сеть с помощью протоколов маршрутизации RIP, OSPF, BGP и других.

Преимущество динамической маршрутизации в том, что изменение в сети могут автоматически отмечаться в таблице маршрутизации. Например, если вышел из строя один из маршрутизаторов, то маршрутизаторы по протоколам маршрутизации об этом узнают, и уберут маршрут, который проходит через этот маршрутизатор. С другой стороны, если появился новый маршрутизатор, то это также отразится в таблице маршрутизации автоматически.

Маршрут по умолчанию

Если маршрутизатор не знает куда отправить пакет, то такой пакет отбрасывается. Таким образом получается, что маршрутизатор должен знать маршруты ко всем подсетям в составной сети. На практике для крупных сетей, например для интернета это невозможно, поэтому используются следующие решения.

В таблице маршрутизации назначается специальный маршрутизатор по умолчанию, на которой отправляются все пакеты для неизвестных сетей, как правило это маршрутизатор, который подключен к интернет.

Предполагается что этот маршрутизатор лучше знает структуру сети, и способен найти маршрут в составной сети. Для обозначения маршрута по умолчанию, в таблице маршрутизации используются четыре нуля в адресе подсети и четыре нуля в маске (0.0.0.0, маска 0.0.0.0), а иногда также пишут default.

Ниже пример маршрута по умолчанию в таблице маршрутизации в операционной системе linux.

Ip-адрес и маска равны нулю, в адрес и шлюз указываются ip-адрес маршрутизатора по умолчанию.

Длина маски подсети

Рассмотрим пример. Маршрутизатор принял пакет на ip-адрес (192.168.100.23), в таблице маршрутизации есть 2 записи (192.168.100.0/24 и 192.168.0.0/16) под который подходит этот ip-адрес, но у них разная длина маски. Какую из этих записей выбрать? Выбирается та запись, где маска длиннее, предполагается, что запись с более длинной маской содержит лучший маршрут интересующей нас сети.

Чтобы понять почему так происходит, давайте рассмотрим составную сеть гипотетического университета. Университет получил блок ip-адресов, разделил этот блок ip-адресов на две части, и каждую часть выделил отдельному кампусу.

На кампусе находятся свои маршрутизаторы, на которых сеть была дальше разделена на части предназначенные для отдельных факультетов. Разделение сетей производится с помощью увеличения длины маски, весь блок адресов имеет маску / 16, блоки кампусов имеют маску / 17, а блоки факультетов / 18.

Ниже показан фрагмент таблицы маршрутизации на маршрутизаторе первого кампуса. Он содержит путь до сети первого факультета, 2 факультета, до обще университетской сети, который проходит через университетский маршрутизатор, а также маршрут по умолчанию в интернет, который тоже проходит через обще университетский маршрутизатор.

Предположим, что у на этот маршрутизатор пришел пакет предназначенный для второго факультета, что может сделать маршрутизатор? Он может выбрать запись, которая соответствует второму факультету и отправить непосредственно в сеть этого факультета, либо может выбрать запись, которая соответствует всей университетской сети, тогда отправит на университетский маршрутизатор, что будет явно неправильным.

И так получается, что выбирается всегда маршрут с маской максимальной длины. Общие правила выбора маршрутов следующие.

• Самая длинная маска 32 — это маршрут конкретному хосту, если в таблице маршрутизации есть такой маршрут, то выбирается он.
• Затем выполняется поиск маршрута подсети с маской максимальной длины.
• И только после этого используется маршрут по умолчанию, где маска / 0 под которую подходят все ip-адреса.

Следует отметить, что таблица маршрутизации есть не только у сетевых устройств маршрутизаторов, но и у обычных компьютеров в сети. Хотя у них таблица маршрутизации гораздо меньше.

• Как правило такая таблица содержит описание присоединенной сети, который подключен данный компьютер.
• Адрес маршрутизатора по умолчанию (шлюз или gateway) через который, выполняется подключение к интернет, или к корпоративной сети предприятия.
• А также могут быть дополнительные маршруты к некоторым знакомым сетям, но это необязательно.

Для того чтобы просмотреть таблицу маршрутизации, можно использовать команды route или ip route (route print (Windows); route и ip route (Linux)).

Маршрутизация — поиск маршрута доставки пакета между сетями через транзитные узлы — маршрутизаторы.

Зачем нужен pathfinder и как его внедрить в игру так, чтобы игроки не считали врагов идиотами?

Поиск пути или pathfinder — определение компьютером самого оптимального маршрута между двумя точками. С ним часто можно столкнуться при разработке игр, например, если в них есть свободно передвигающиеся враги. В этой статье мы разберёмся, где и зачем поиск пути может пригодиться, и как подступиться к этой проблеме.

Почему возникает проблема поиска пути?

Компьютерным болванчикам нельзя просто сказать: «Эй ты, иди к башне!», — как людям. Им нужно прописать чёткий набор команд (иди один метр влево, потом метр вперёд и т.д.) или указать путь из промежуточных точек, чтобы они успешно добрались от точки A до точки B. Как раз нахождением этих промежуточных точек и занимается алгоритм поиска пути. Но этим его задачи не ограничиваются. Дополнительно он может определять расстояние до цели и то, возможно ли вообще добраться до какой-то точки.

Есть такой вид игр-головоломок — лабиринт Минотавра. Игрока помещают на сетчатое поле со стенками. Одна из клеток поля является выходом, а на другой стоит монстр. Задача игрока — добраться до выхода раньше, чем монстр доберётся до него. Игрок и монстр ходят по очереди на сколько-то клеток, но монстр всегда перемещается быстрее игрока.

Игрок бы постоянно проигрывал, но у монстра есть минус: он хоть и быстр, но туп. Он всегда пытается добраться до игрока кратчайшим способом и не обращает внимание на то, что в лабиринте есть стены. Если монстру на пути встречается стена, он просто стоит и грустно вздыхает перед ней, не пытаясь обойти.

В таких играх глупость врага оправдана, так как она является частью геймплея головоломки. В остальных играх пользователь ожидает, что враг начнёт искать пути обхода, а не будет застревать в камнях и деревьях.

Как найти путь?

Задача поиска пути состоит из двух этапов: адаптирование игрового мира в математическую модель и поиск в этой модели пути между двумя точками.

Адаптирование игрового мира

Компьютер не может просто посмотреть на камень и сказать, что это камень. Поэтому ему надо описать игровой мир в виде чисел и выбрать набор признаков, по которым будет определяться, что между двумя точками можно пройти.

Большая часть алгоритмов строится на графах — в математике так называется фигура, которая состоит из точек и соединяющих их линий (рёбер). Поэтому пути прохода по игровому миру превращают в графы. В качестве точек-кружочков обычно берут минимальную площадь мира, в которой передвижение от одного края до второго происходит мгновенно (или же за достаточно маленькое время, чтобы считать его мгновенным). Иначе говоря, в играх эти кружочки — это позиции персонажа. Рёбра же обозначают тот факт, что ты с первого куска мира можешь перейти на второй.

Одна из простых вариаций графа — игровая сетка, где кружочками являются клетки, а рёбра проводятся между любыми соседними клетками, свободными от препятствий. Проще всего разобраться в этом на примере пошаговых игр, у которых сетку видно невооружённым глазом, вроде Sneaky-Sneaky или Return of the Necrodancer.

Клетки, на которых стоят непреодолимые препятствия, обозначаются крестиком, а проходимые места — пустотой. Или, если говорить на языке программирования, клетки обозначаются 0 или 1, где 0 означает, что пройти нельзя, а 1 — что пройти можно. Более сложные игры вроде Heroes of Might and Magic III отличаются только тем, что их сетка рисуется более произвольно, а клетки, которые расположены на разных типах земли, отнимают разное количество шагов.

При работе с трёхмерными мирами можно использовать двухмерную карту проекции ландшафта с указанием высот в точках. В этом случае на каждой ячейке написана её высота, а проходимость определяется через разницу высот соседних клеток.

В Death Stranding упрощённую карту для поиска пути можно увидеть при сканировании местности. Крестиками показываются непроходимые места, жёлтым — проходимые с трудом, голубым — легко проходимые.

Зачастую адаптация игрового мира — это самая сложная часть, потому что алгоритмы поиска оптимальных маршрутов изобретены давно, можно даже найти готовый код для них. Поэтому разработчики внедряют один из алгоритмов и потом экспериментируют с разными моделями и вариациями сравнений двух путей, или комбинируют разные алгоритмы в попытках добиться наилучшего и наименее затратного результата.

Алгоритмы поиска пути

Как бы человек искал выход, если бы его внезапно высадили посреди лабиринта? Например, он мог бы воспользоваться правилом «одной руки», отмечать обследованные пути верёвкой или мелом, пока не найдёт выход. Большинство алгоритмов действуют по схожей схеме, за исключением того, что компьютер может размножаться и «ощупывать» одновременно несколько путей. Различаются же алгоритмы точностью и скоростью получения результата.

Поиск в ширину

Поиск в ширину начинает исследовать пути от начальной точки сразу во все стороны. Сначала ощупывает соседние со стартом точки, потом соседние с ними и так далее, пока не найдёт конечную точку или поле не закончится.

Работу алгоритма можно представить в виде монстра с щупальцами, которые могут раздваиваться. Это монстр сидит на стартовой клетке, тянет щупальца во все стороны и проверяет, можно ли здесь пройти. Если щупалец не хватает, он раздваивает одно из них, чтобы охватить все возможные дороги. Эта эпопея продолжается, пока одно из щупалец не нащупает конечную точку. Тогда путь щупальца от старта до конца и становится кратчайшим путём.

Если же описывать работу в виде алгоритма, то получатся такие шаги:

Такой алгоритм на каждом N цикле находит все точки, к которым можно дойти за N шагов. Чтобы получить путь, нужно запоминать не только проверенные точки, а ещё и последовательность точек до них. Или хотя бы предыдущую точку, с которой мы пришли на эту, чтобы по шагам восстановить маршрут.

Поиск в ширину хорошо работает, если переход между соседними точками всегда занимает одинаковое количество времени (или другого параметра, по которому мы стараемся минимизировать путь). Но если это не так, то он превращается в алгоритм Дейкстры.

Алгоритм Дейкстры

Алгоритм Дейкстры работает с моделями, в которых расстояния между точками могут быть разными. Например, в Heroes of Might and Magic III проход по снегу тратит на 50% больше очков перемещения, так что условно можно посчитать, что проход по снегу занимает 1.5 шага вместо 1 по обычной земле. В этом случае обход снега может быть быстрее, чем проход напрямую по нему, хоть визуально и будет пройдено большее расстояние.

От поиска в ширину алгоритм Дейкстры отличает пара моментов. Кроме сохранения уже проверенных точек, сохраняется ещё и количество шагов, потраченных на то, чтобы добраться до них. Точки исключаются из последующей проверки не тогда, когда были уже проверены, а только в случае, если предыдущий найденный путь до неё занимал меньшее количество «шагов». Точки в списке рассматриваются не по порядку, сначала выбираются те, до которых меньше идти.

Алгоритм:

Эвристический алгоритм

Минусом как поиска в ширину, так и алгоритма Дейкстры является то, что компьютер ищет путь во все стороны сразу и тратит время на очевидно бесперспективные пути, которые отдаляют от цели, а не приближают к ней.

Эвристический алгоритм помогает это исправить. Он работает точно так же, как и алгоритм Дейкстры, но с одним изменением. При выборе следующей точки на рассмотрение первой выбирается не та точка, которая ближе к началу пути, а та, что ближе к концу. Расстояние до конца рассчитывается приблизительно, например, просто как расстояние между двумя точками на карте.

Минус алгоритма в том, что найденный путь необязательно будет самым кратким. Зато его нахождение потребует меньше времени.

Алгоритм A*

Алгоритм А* пытается усидеть на обоих стульях сразу: найти кратчайшее расстояние, но сделать это за меньшее время, чем алгоритм Дейкстры. Поэтому следующая точка на рассмотрение выбирается по минимальной сумме расстояний до начала и до конца пути. Это единственное отличие от предыдущих алгоритмов.

Есть и другие алгоритмы, которые дают преимущества при разных условиях. Сами алгоритмы по поиску пути довольно просты, но они работают для сферических идеальных условий в вакууме. В реальных играх существует много нюансов, которые могут усложнить алгоритм. Например, может быть несколько вариантов перемещений, повороты, препятствия могут двигаться, могут быть узкие места, в которых врагам желательно не толпиться. Каждое такое условие делает движение более интересным, но и замедляет работу алгоритма. Из-за этого приходится что-то упрощать или выкручиваться по-другому для оптимизации работы игры.

Несколько интересных примеров можно прочитать в статьях про новый алгоритм поиска пути в Factorio и про устройство поведения полчищ крыс в A Plague Tale: Innocence.

Дополнительные материалы

Бонус: на этом сайте можно наглядно визуализировать работу разных алгоритмов, самостоятельно выстроив для них преграды.

Текст написала Алёна Киселёва, автор в Smirnov School. Мы готовим концепт-художников, левел-артистов и 3D-моделеров для игр и анимации. Если придёте к нам на курс, не забудьте спросить о скидке для читателей с DTF.