Как правильно найти сумму ряда - AvtoShod.ru - решение различных проблем

Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:

$$ frac{1}{(2n+1)(2n+3)} = frac{A}{2n+1} + frac{B}{2n+3} = frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$

Приравниваем числитель последней дроби к числителю первой дроби:

$$ A(2n+3)+B(2n+1) = 1 $$

Раскрываем скобки:

$$ 2An + 3A + 2Bn + B = 1 $$

Теперь определяем находим неизвестные коэффициенты:

$$ begin{cases} n^0: &2A+2B=0 \ n^1: &3A+B=1 end{cases}Rightarrow begin{cases} A=frac{1}{2} \ B=-frac{1}{2} end{cases} $$

После разложения общий член ряда записывается следующим образом:

$$ a_n =frac{1}{(2n+1)(2n+3)}=frac{1}{2} frac{1}{2n+1} — frac{1}{2} frac{1}{2n+3} $$

Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$

$$ a_1 = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) $$

$$ a_2 = frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) $$

$$ a_3 = frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) $$

$$ …………………………………. $$

$$ a_{n-1}=frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) $$

$$ a_n = frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) $$

Замечание

Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $.

Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок.

Итого, получаем:

$$ S_n = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) + frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) + frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) + … $$

$$ … + frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) + frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) = $$

Выносим дробь одну вторую $ frac{1}{2} $ за скобки:

$$ = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9} … + $$

$$ + … frac{1}{2n-1} — frac{1}{2n+1} + frac{1}{2n+1} — frac{1}{2n+3} bigg) = $$

Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:

$$ S_n = frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) $$

Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:

$$ S=lim_{ntoinfty} S_n = lim_{ntoinfty} frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = $$

$$ = frac{1}{2} lim_{ntoinfty} bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = frac{1}{2} cdot frac{1}{3} = frac{1}{6} $$

Источник

Вычисление
суммы сходящегося числового ряда.

Прежде чем приступить к решению задач
дадим основные определения.

Определение 1.Пусть—
последовательность действительных
чисел. Выражение вида:

называется числовым рядом.

Сумму
первых
слагаемых называют
-ой
частичной суммойряда и обозначают:

К примеру,

Частичные суммы ряда
образуют бесконечную числовую
последовательность.

Выражение само по себе определенного смысла не
имеет, потому что действие сложения
производится над конечным числом
слагаемых. Этот смысл выражению предстоит
приписать нам самим.

Введем понятие суммы ряда.

Определение 2.Суммойчислового
ряданазывается предел последовательности
частичных сумм ряда,
если этот предел существует и конечен:

Числовой ряд при этом называется
сходящимся.

В противном случае, т.е. если
равен бесконечности или не существует,
то

ряд называется расходящимся.

Определение 3.Пусть дан ряд.

Ряд
,
полученный из исходного отбрасываниемпервых членов называется
-м
остатком ряда.

Можно доказать, что если
,
то ряд сходится (существует конечная
сумма)
и наоборот: остатоксходящегося
ряда стремится к нулю с увеличением
номера.

Основной целью теории числовых
рядов является установление факта
сходимости или расходимости тех или
иных рядов и вычисление суммы сходящихся
рядов. При этом найти точное значение
суммы ряда удается далеко не всегда. В
этом случае используются методы
приближенного вычисления суммы
ряда.
Существует довольно много
приемов, позволяющих устанавливать
сходимость или расходимость рядов.
Такие приемы называются признаками
сходимости. К рассмотрению некоторых
из них мы и приступаем.

Теорема (необходимый признак
сходимости числового ряда).

Если ряд
сходится,
то его общий член стремиться к нулю,
т.е.

Из необходимого признака следует,
что если
-ый
член ряда не стремиться к нулю, то ряд
расходиться. Именно это утверждение
удобно использовать для решения задач.

Отметим, что необходимый признак
не является достаточным, т.е. если
,
то о сходимости ряда ничего сказать
нельзя: он может быть как сходящимся,
так и расходящимся.

Задача №1.Исследовать ряд на
сходимость.

Решение.

Используя необходимый признак сходимости,
делаем вывод о том, что ряд расходиться,
поскольку
-ый
член ряда не стремиться к нулю.

Ответ: ряд
расходится.

Задача №2.Исследовать ряд на
сходимость.

Решение.Общий член ряда

Следовательно, ряд расходиться по
необходимому признаку. Здесь для
вычислений использовали первый
замечательный предел:
.

Ответ: ряд расходится.

Задача №3.Исследовать ряд на
сходимость.

Решение.

не существует. Ряд расходится по
необходимому признаку.

Ответ: ряд расходится.

Приведем пример ряда, для которого
необходимый признак не дает ответа о
его сходимости:

Задача №4. Исследовать ряд на
сходимость.

Решение.

Необходимый признак для данного ряда
выполняется, поэтому он может быть или
сходящимся, или расходящимся. Докажем,
что этот ряд на самом деле расходится.
Оценим частичную сумму ряда
снизу:

Таким образом,

и.

Тогда по определению суммы ряда имеем:

Ответ: ряд расходится.

Задача №5.Исследовать ряд на
сходимость.

Решение.Воспользуемся необходимым
признаком и найдем предел-го
члена ряда:

Ответ: ряд расходится.

В предыдущих задачах нашей целью
было установить сам факт существования
суммы ряда. Рассмотрим задачи, в которых
удается вычислить точное значение суммы
ряда.

Пусть дан числовой ряд
,
составленный из членов геометрической
прогрессии. Здесь—
первый член прогрессии,—
знаменатель прогрессии. Если знаменатель
прогрессии удовлетворяет условию,
то прогрессия называется бесконечно
убывающей, а ряд, составленный из членов
такой прогрессии, сходится, причем
сумма ряда равна:

Задача №6.Найти сумму ряда.

Решение.

Этот ряд составлен из членов бесконечно
убывающей геометрической прогрессии,
.

Сумма ряда равна:

Ответ:
.

Задача №7. Найти сумму ряда.

Решение.

Здесь первый член геометрической
прогрессии
,
знаменатель.
Тогда.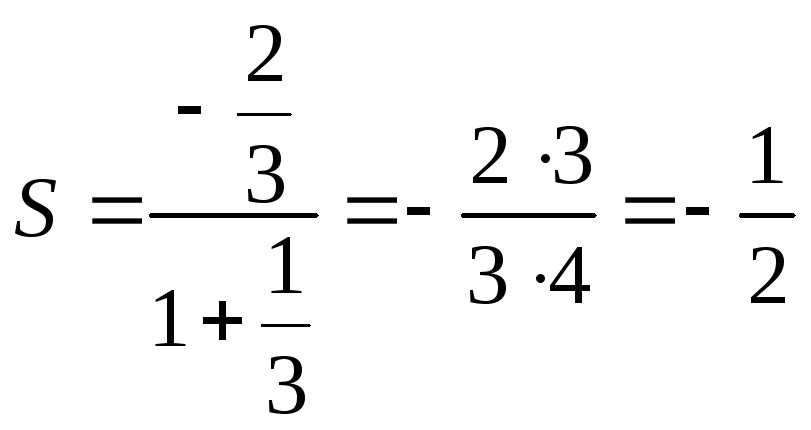

Ответ:
.

Задача №8.Найти сумму ряда.

Решение.

. Для этого ряда
.

Находим сумму:

Ответ:
.

Задача №9. Найти сумму ряда.

Решение.Для того чтобы найти сумму
этого ряда, представим общий член ряда
в виде суммы дробей:

Найдем неизвестные коэффициенты
следующим образом:

отсюда

При
из
последнего равенства получаем.

При
.

Таким образом

Найдем
-ую
частичную сумму ряда:

После сокращения противоположных
слагаемых получим

откуда

Ответ:
.

Соседние файлы в папке Ряды

Источник

Щебетун Виктор

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Пуская задано числовую последовательность $a_1, a_2,dots {,a}_n,dots ,$ тогда выражение:

$a_1+ a_2+dots {+a}_n+dots =sumlimits^{infty }_{n=1}{a_n}$называется числовым рядом.

Введем понятия частичных сумм ряда: $S_1= a_1, S_2=a_1+a_2, S_3=a_1+a_2+a_3,dots ,S_n=a_1+a_2+a_3+dots + a_n, dots .$ Эти частичные суммы образуют некоторую числовую последовательность $left(S_nright).$

Определение 1

Если последовательность частичных сумм $S_n$ ряда при неограниченном возрастании $n$, стремится к некоторому числу $S$, то есть:

${mathop{lim}_{nto infty } S_n= }S,$то этот ряд называется сходящимся, а число $S$ — его суммой.

В этом случае записывают:

[S=a_1+ a_2+dots {+a}_n+dots =sumlimits^{infty }_{n=1}{a_n}.]

В противоположном случае ряд называют расходящимся. Если

${mathop{lim}_{nto infty } S_n= }infty ,$то говорят, что расходящийся ряд имеет бесконечную сумму.

Определение 2

Последовательность $left{a_{n} right}$ называется ограниченной сверху, если существует такое число М, $Min $R, что $a_n

Определение 3

Последовательность $left{a_{n} right}$ называется ограниченной, если она ограничена как снизу, так и сверху, т.е. существует такое число М $ > 0$.

($Min $R), что $forall n:, , , left|a_{n} right|le M$.

Определение 4

Число а называется пределом последовательности $left{a_{n} right}$,если для любого сколь угодно малого положительного числа $varepsilon $найдётся такой номер $n_{0} in $N, зависящий от $varepsilon $, что для всех натуральных чисел $nge n_{0} $ выполняется неравенство $left|a_{n} -aright|

«Сумма ряда» 👇

Тогда $a=mathop{lim }limits_{nto infty } a_{n} , $означает, что $forall {rm varepsilon }>0, , , exists n{}_{0} =n_{0} ({rm varepsilon })in $N такое, что для всех $nge n_{0} ,, , nin $N: $left|a_{n} -aright|

Приведём некоторые свойства сходящихся последовательностей.

Если последовательность имеет предел, то он единственен.
Если последовательность имеет конечный предел, то эта последовательность ограничена.
Если последовательность возрастает (убывает) и ограничена сверху (снизу), то она имеет конечный предел.
Если последовательность возрастает (убывает) и не ограничена сверху (снизу), то она имеет бесконечный предел + $infty$ (- $infty$).

Основные свойства сходящихся рядов

Рассмотрим ряд

$a_1+ a_2+dots {+a}_n+dots $ (1)

и откинем от него $n$ первых членов:

$a_{n+1}+ a_{n+2}+dots {+a}_{n+k}+dots .$ (2)

Ряд (2) называют $n$-м остатком ряда (1).

Ряды (1) и (2) одновременно сходятся или расходятся, причем если ряд (1) сходится до $S$, то ряд (2) сходится к

[R_n=S-left(a_1+ a_2+dots {+a}_nright).]

Следствие 1

Присоединение или откидывание конечного числа первых членов не влияет на сходимость или расходимость ряда.

Следствие 2

Остаток ряда $R_nto 0,$ если $nto infty $.

Действительно, если в равенстве $R_n= S-S_n$ перейти в пределу при $nto infty $, то

[{mathop{lim}_{nto infty } R_n }=mathop{lim}_{nto infty }left(S-S_nright)=S-S=0.]

Теорема 2

Если ряд (1) сходится и его сумма $S$, то ряд

$sumlimits^{infty }_{n=1}{{ca}_n},$где $c=const$, также сходится и его сумма равняется $cS.$

Теорема 3

Сходящиеся ряды можно пожно почленно суммировати и отнимать, тоесть если ряды:

$sumlimits^{infty }_{n=1}{a_n,} sumlimits^{infty }_{n=1}{b_n,}$сходятся и имеют соответствующие суммы A, B, то сходятся также и ряды

$sumlimits^{infty }_{n=1}{{(a}_npm b_n)} $и суммы суммы их равняются $A pm B$.

Пример 1

Найти сумму ряда $sum limits _{n=1}^{infty }frac{1}{left(3n-2right)left(3n+1right)} $.

Решение. Подсчитаем $S_{n} $:

[begin{array}{c} {S_{n} =frac{1}{1cdot 4} +frac{1}{4cdot 7} +…+frac{1}{left(3n-2right)left(3n+1right)} =frac{1}{3} left(left(1-frac{1}{4} right)+left(frac{1}{4} -frac{1}{7} right)+…+left(frac{1}{left(3n-2right)} -frac{1}{left(3n+1right)} right)right)=} \ {=frac{1}{3} left(1-frac{1}{left(3n+1right)} right).} end{array}]

По определению $S=mathop{lim }limits_{nto infty } S_{n} =mathop{lim }limits_{nto infty } frac{1}{3} left(1-frac{1}{left(3n+1right)} right)=frac{1}{3} $.

Пример 2

Найти сумму ряда $sum limits _{n=1}^{infty }left(sqrt{n+2} -2sqrt{n+1} +sqrt{n} right) $.

Решение.

[begin{array}{c} {S_{n} =left(sqrt{3} -2sqrt{2} +1right)+left(sqrt{4} -2sqrt{3} +sqrt{2} right)+left(sqrt{5} -2sqrt{4} +sqrt{3} right)=} \ {=left(sqrt{n+1} -2sqrt{n} +sqrt{n-1} right)+left(sqrt{n+2} -2sqrt{n+1} +sqrt{n} right)=1-sqrt{2} +sqrt{n+2} -sqrt{n+1} .} end{array}]

Пользуясь определением суммы ряда и раскрывая неопределённость вида $left(infty -infty right)$, при вычислении предела, получим:

[begin{array}{c} {mathop{lim }limits_{nto infty } left(1-sqrt{2} +sqrt{n+2} -sqrt{n+1} right)=1-sqrt{2} +mathop{lim }limits_{nto infty } frac{n+2-n-1}{sqrt{n+2} +sqrt{n+1} } =} \ {=1-sqrt{2} +mathop{lim }limits_{nto infty } frac{1}{sqrt{n+2} +sqrt{n+1} } =1-sqrt{2} .} end{array}]

Пример 3

Исследовать на сходимость ряд

[sum limits _{n=1}^{infty }, frac{1}{n(n+1)} =frac{1}{2} +frac{1}{6} +frac{1}{12} +frac{1}{20} +…]

и найти его сумму.

Решение. Обозначим $frac{1}{n(n+1)} =a_{n} $ общий член ряда. Тогда частичная сумма ряда $S_{n} =a_{1} +a_{2} +…+a_{n} =frac{1}{2} +frac{1}{6} +, …, +frac{1}{n(n+1)} $. Так как $frac{1}{n(n+1)} =frac{1}{n} -frac{1}{n+1} $, то $S_{n} =left(1-frac{1}{2} right)+left(frac{1}{2} -frac{1}{3} right)+ldots +left(frac{1}{n} -frac{1}{n+1} right)=1-frac{1}{n+1} $. Тогда $mathop{lim }limits_{nto infty } S_{n} =mathop{lim }limits_{nto infty } left(1-frac{1}{n+1} right)=1, ,

Пример 4

Исследовать на сходимость ряд

[sum limits _{n=1}^{infty }, frac{4}{4n^{2} +4n-3} =frac{4}{5} +frac{4}{21} +frac{4}{45} +…]

и найти его сумму.

Решение. Обозначим $frac{4}{4n^{2} +4n-3} =a_{n} $ общий член ряда. Тогда,частичная сумма ряда $S_{n} =frac{4}{5} +frac{4}{21} +, …, +frac{4}{4n^{2} +4n-3} $. Так как

$frac{4}{4n^{2} +4n-3} =frac{1}{2n-1} -frac{1}{2n+3} $, то

$S_{n} =left(1-frac{1}{5} right)+left(frac{1}{3} -frac{1}{7} right)+left(frac{1}{5} -frac{1}{9} right)ldots +left(frac{1}{2n-3} -frac{1}{2n+1} right), +left(frac{1}{2n-1} -frac{1}{2n+3} right)=$$=1+frac{1}{3} -frac{1}{2n+1} -frac{1}{2n+3} =frac{4}{3} -frac{4n+4}{(2n+1)(2n+3)} $, тогда $mathop{lim }limits_{nto infty } S_{n} =mathop{lim }limits_{nto infty } left(frac{4}{3} -frac{4n+4}{(2n+1)(2n+3)} right)=frac{4}{3} , $, т.е. ряд сходится и его сумма $S=frac{4}{3} , $.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Содержание:

Понятие суммы ряда
Вычисление суммы ряда почленным интегрированием
Вычисление суммы ряда почленным дифференцированием

Понятие суммы ряда

Постановка задачи. Найти сумму ряда

где — целые числа.

План решения. Суммой ряда называется предел последовательности его частичных сумм , т.е.

где

1. По условию задачи

Если корни знаменателя различаются на целое число, т.е. где — натуральное число, то члены последовательности частичных сумм ряда легко найти, так как в выражении многие слагаемые взаимно уничтожаются.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

2. Разлагаем общий член ряда на элементарные дроби:

и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.

3. Находим -ю частичную сумму ряда:

сократив соответствующие слагаемые.

4. Вычисляем сумму ряда по формуле (1)

и записываем ответ.

Пример:

Найти сумму ряда

Решение:

1. Корни знаменателя и различаются на целое число, т.е. Следовательно, члены последовательности частичных сумм ряда легко найти, так как в выражении многие слагаемые взаимно уничтожаются.

2. Разлагаем общий член ряда на элементарные дроби

и выписываем несколько членов ряда:

3. Сокращая все слагаемые, какие возможно, находим -ю частичную сумму ряда:

4. Вычисляем сумму ряда по формуле (1):

Ответ:

Возможно вам будут полезны данные страницы:

Вычисление суммы ряда почленным интегрированием

Постановка задачи. Найти сумму функционального ряда вида

и указать область сходимости ряда к этой сумме.

План решения.

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

Если , ряд расходится. Если , ряд сходится условно (по признаку Лейбница). Следовательно, область сходимости определяется неравенствами

2. Делаем в исходном ряде замену , получим степенной ряд

с областью сходимости .

3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке , целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем

Заметим, что так как ряд (1) сходится в граничной точке , то сумма ряда непрерывна в этой точке (справа). Следовательно,

6. Вычисляем интеграл, делаем замену на и записываем ответ: сумму ряда и область его сходимости.

Замечание. Если ряд имеет вид

то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:

и вычисляем сумму каждого ряда почленным интегрированием.

Пример:

Найти сумму ряда

и указать область сходимости ряда к этой сумме.

Решение:

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

В граничных точках при ряд расходится, при ряд сходится условно.

Следовательно, данный ряд сходится при всех .

2. Сделаем замену Получим геометрический ряд (1) с областью сходимости

3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке , целиком принадлежащем интервалу сходимости, и используя формулу (4), получаем

Заметим, что так как ряд (1) сходится в граничной точке , то его сумма непрерывна в этой точке (справа). Следовательно, формула (5) справедлива при всех .

6. Заменяя на , получаем при

Ответ.

Вычисление суммы ряда почленным дифференцированием

Постановка задачи. Найти сумму функционального ряда вида

и указать область сходимости ряда к этой сумме.

План решения.

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

Если , ряд расходится (не выполнено необходимое условие сходимости). Следовательно, область сходимости определяется неравенствами .

2. Делаем в исходном ряде замену и записываем его в виде суммы двух рядов

Следовательно, достаточно найти суммы рядов

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем

6. Вычисляем производную и делаем замену на . Записываем ответ: сумму ряда и область его сходимости.

Замечание. Если ряд имеет вид

то вычисляем сумму трех рядов, причем при вычислении суммы ряда

применяем теорему о почленном дифференцировании степенного ряда дважды.

Пример:

Найти сумму ряда

и указать область сходимости ряда к этой сумме.

Решение:

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством . Отсюда . В граничных точках ряд расходится, так как не выполнено необходимое условие сходимости. Следовательно, ряд сходится в интервале .