Как правильно найти sin 2 - AvtoShod.ru - решение различных проблем

Синус двойного угла

ОПРЕДЕЛЕНИЕ

Формула синуса двойного угла имеет вид
(
sin 2 alpha=2 sin alpha cdot cos alpha
)

Эта формула легко получается из формулы синусоиды.
(
sin (alpha+beta)=sin alpha cdot cos beta+cos alpha cdot sin beta
)
вставляя его (
beta=alpha
)

В самом деле
(
sin 2 alpha=sin (alpha+alpha)=sin alpha cdot cos alpha+cos alpha cdot sin alpha=2 sin alpha cdot cos alpha
)

Синусоидальный угол может все еще выражаться через касательную и кокасательную:
(
sin 2 alpha=frac{2 operatorname{tg} alpha}{1+operatorname{tg}^{2} alpha}
), (
sin 2 alpha=frac{2 operatorname{ctg} alpha}{1+operatorname{ctg}^{2} alpha}
), (
sin 2 alpha=frac{2}{operatorname{tg} alpha+operatorname{ctg} alpha}
)

Примеры решения проблем

ПРИМЕР 1

Задание

Упростите выражение:
(
sin frac{alpha}{2} cdot cos frac{alpha}{2} cdot cos alpha
)

Решение

Выделите первые два фактора через синус двойного угла:
(
2 sin frac{alpha}{2} cdot cos frac{alpha}{2}=sin left(2 cdot frac{alpha}{2}right) sin frac{alpha}{2} cdot cos frac{alpha}{2}=frac{sin alpha}{2}
)

Тогда исходное выражение принимает вид
(
sin frac{alpha}{2} cdot cos frac{alpha}{2} cdot cos alpha=frac{sin alpha}{2} cdot cos alpha=frac{sin alpha cdot cos alpha}{2}
)

Умножьте числитель и знаменатель наклейки на 2:
(
sin frac{alpha}{2} cdot cos frac{alpha}{2} cdot cos alpha=frac{2 sin alpha cdot cos alpha}{2 cdot 2}
)
давайте применим к числителю формулу синуса двойного угла (
sin 2 alpha=2 sin alpha cdot cos alpha
) и, наконец, получим
(
sin frac{alpha}{2} cdot cos frac{alpha}{2} cdot cos alpha=frac{sin 2 alpha}{4}
)

Ответ

(
sin frac{alpha}{2} cdot cos frac{alpha}{2} cdot cos alpha=frac{sin 2 alpha}{4}
)

ПРИМЕР 2

Задание

Найти значение выражения
(
frac{operatorname{tg} 22^{circ} 30^{prime}}{1+operatorname{tg}^{2} 22^{circ} 30^{prime}}
)

Решение

Мы используем формулу с двойным углом синуса (
sin 2 alpha=frac{2 operatorname{tg} alpha}{1+operatorname{tg}^{2} alpha}
) , получаем
(
frac{operatorname{tg} 22^{circ} 30^{prime}}{1+operatorname{tg}^{2} 22^{circ} 30^{prime}}=sin left(2 cdot 22^{circ} 30^{prime}right)=sin 45^{circ}=frac{sqrt{2}}{2}
)

Ответ

(
frac{operatorname{tg} 22^{circ} 30^{prime}}{1+operatorname{tg}^{2} 22^{circ} 30^{prime}}=frac{sqrt{2}}{2}
)

ПРИМЕР 3

Задание

Упростить выражение
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}
)

Решение

Запишем в числителе и знаменателе синусов двойного угла, используя формулу (
sin 2 alpha=2 sin alpha cdot cos alpha
) , получим:
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=frac{(2 sin alpha cdot cos alpha)^{2}-4 sin ^{2} alpha}{(2 sin alpha cdot cos alpha)^{2}+4 sin ^{2} alpha-4}=frac{4 sin ^{2} alpha cdot cos ^{2} alpha-4 sin ^{2} alpha}{4 sin ^{2} alpha cdot cos ^{2} alpha+4 sin ^{2} alpha-4}
)

Мы выставляем скобки в числителе (
4 sin ^{2} alpha
) , а в знаменателе — 4:
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=frac{4 sin ^{2} alphaleft(cos ^{2} alpha-1right)}{4left(sin ^{2} alpha cdot cos ^{2} alpha+sin ^{2} alpha-1right)}=frac{sin ^{2} alphaleft(cos ^{2} alpha-1right)}{left(sin ^{2} alpha cdot cos ^{2} alpha+sin ^{2} alpha-1right)}
)

В полученном выражении мы используем основное тригонометрическое тождество и представляем единицу как (
1=sin ^{2} alpha+cos ^{2} alpha
), получаем
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=frac{sin ^{2} alphaleft(cos ^{2} alpha-left(sin ^{2} alpha+cos ^{2} alpharight)right)}{left(sin ^{2} alpha cdot cos ^{2} alpha+sin ^{2} alpha-left(sin ^{2} alpha+cos ^{2} alpharight)right)}==frac{sin ^{2} alphaleft(cos ^{2} alpha-sin ^{2} alpharight)}{left(sin ^{2} alpha cdot cos ^{2} alpha+sin ^{2} alpha-cos ^{2} alpharight)}=frac{sin ^{2} alphaleft(-sin ^{2} alpharight)}{left(sin ^{2} alpha cdot cos ^{2} alpha-cos ^{2} alpharight)}
)

Мы помещаем знаменатель(
cos ^{2} alpha
) для скобок
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=frac{sin ^{2} alphaleft(-sin ^{2} alpharight)}{left(sin ^{2} alpha cdot cos ^{2} alpha-cos ^{2} alpharight)}=frac{-sin ^{4} alpha}{cos ^{2} alphaleft(sin ^{2} alpha-1right)}
)

Снова в числителе записываем единицу, используя основное тригонометрическое тождество

(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=frac{-sin ^{4} alpha}{cos ^{2} alphaleft(sin ^{2} alpha-1right)}=frac{-sin ^{4} alpha}{cos ^{2} alphaleft(sin ^{2} alpha-left(sin ^{2} alpha+cos ^{2} alpharight)right)}=frac{-sin ^{4} alpha}{cos ^{2} alphaleft(sin ^{2} alpha-sin ^{2} alpha-cos ^{2} alpharight)}=frac{-sin ^{4} alpha}{cos ^{2} alphaleft(-cos ^{2} alpharight)}=frac{-sin ^{4} alpha}{-cos ^{4} alpha}=operatorname{tg}^{4} alpha
)

Ответ

(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=operatorname{tg}^{4} alpha
)

Источник

Единичная окружность помогает понять, чему равны sin 1, sin 2, sin 3, sin 4, sin 5, sin 6.

Итак, речь идет об углах в радианах. 1 радиан — это угол, длина дуги которого равна радиусу окружности. Соответственно, определяем приблизительное местонахождение на единичной окружности углов в 2, 3, 4, 5 и 6 радиан, отмечая каждую следующую точку через дугу, длина которой равна радиусу. Впрочем, если вспомнить, что п приближенно равно 3,14, задача существенно упростится.

Рисунок позволяет наглядно определять приблизительные значения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6, а также сравнивать их.

Поскольку синус — это ордината соответствующей точки на единичной окружности (как это легко запомнить — здес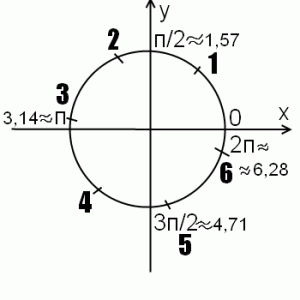ь), то для нахождения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6 достаточно определить значение y в точках 1, 2, 3, 4, 5 и 6 радиан.

Поскольку синус — это y, то вверху, над осью x, синус принимает положительные значения. Поэтому sin 1>0, sin 2>0, sin 3>0.

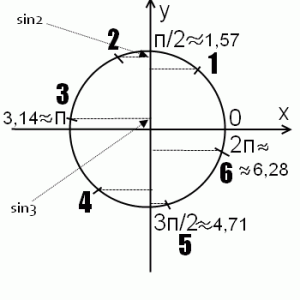
Соответственно внизу синус отрицателен: sin 4<0, sin 5<0, sin 6<o. Поэтому легко сравнить sin2 и sin4, например: sin2>sin4, ведь любое положительное число больше любого отрицательного.

Если требуется сравнить значения синуса одного знака, например, sin2 и sin3, то исходя из геометрических соображений, sin2>sin3.

Если нужно уточнить, чему равен 1 радиан, 2, 3, 4, 5 и 6 радиан в градусах, то приближенные значения таковы:

$[{1radian approx {{57}^0}17'}]$

$[{2rad approx {{115}^0}}]$

$[{3rad approx {{172}^0}}]$

$[{4rad approx {{229}^0}}]$

$[{5rad approx {{286}^0}}]$

$[{6rad approx {{343}^0}}]$

Приближенно чему равен синус 1, синус 2 и синус 3, можно узнать по таблицам Брадиса:

Используя геометрические соображения, можно найти и приблизительные значения углов, больших 6 радиан.

Источник

Синус двойного угла, формула

Данная формула позволяет найти синус двойного угла зная синус и косинус этого угла по отдельности:

[
sin(2α) = 2sin(α)cos(α)
]

Вычислить, найти синус двойного угла, по формуле (1)

α° (градусов)

α´ (минут)

α˝ (секунд)

Вычислить

нажмите кнопку для расчета

Синус двойного угла	стр. 215

Источник

Определение синуса угла

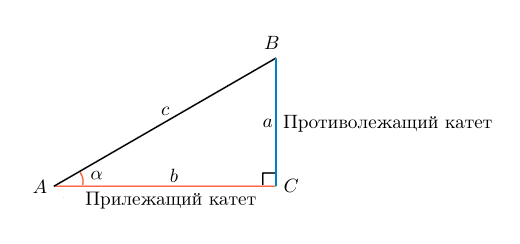
Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.

Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.

Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.

В случае с рисунком, описанным выше: sin⁡α=acsinalpha=frac{a}{c}

Задача 1

В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.

Решение

Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:

3⋅x=123cdot x=12

x=123=4x=frac{12}{3}=4

a=x=4a=x=4

По теореме Пифагора найдем гипотенузу:

a2+b2=c2a^2+b^2=c^2

42+32=c24^2+3^2=c^2

25=c225=c^2

c=5c=5

sin⁡α=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8

Ответ

0.80.8

Задача 2

Вычислите синус 45 градусов.

Решение

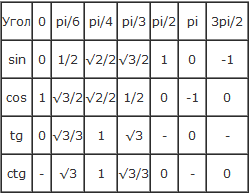
Для этого воспользуемся тригонометрической таблицей углов. Находим, что:

sin⁡45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785

Ответ

0.7850.785

Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:

Основное тригонометрическое тождество

sin⁡2α+cos⁡2α=1sin^2alpha+cos^2alpha=1

αalpha — любой угол.

Задача 3

Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.

Решение

Воспользуемся основным тригонометрическим тождеством:

sin⁡2α+cos⁡2α=1sin^2alpha+cos^2alpha=1

sin⁡2α+0.8=1sin^2alpha+0.8=1

sin⁡2α=0.2sin^2alpha=0.2

sin⁡α=0.2sinalpha=sqrt{0.2}

sin⁡α≈0.447sinalphaapprox0.447

Ответ

0.4470.447

Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!

Тест по теме «Вычисление синуса»

Источник

В данной таблице представлены значения синусов от 0° до 360°. Таблица синусов нужна, когда у вас под рукой нет калькулятора. Чтобы узнать, чему равен синус угла, просто найдите нужный градус в таблице. Для начала короткая версия таблицы.

https://uchim.org/matematika/tablica-sinusov — uchim.org

Таблица синусов для 0°-180°

sin(1°)	0.0175
sin(2°)	0.0349
sin(3°)	0.0523
sin(4°)	0.0698
sin(5°)	0.0872
sin(6°)	0.1045
sin(7°)	0.1219
sin(8°)	0.1392
sin(9°)	0.1564
sin(10°)	0.1736
sin(11°)	0.1908
sin(12°)	0.2079
sin(13°)	0.225
sin(14°)	0.2419
sin(15°)	0.2588
sin(16°)	0.2756
sin(17°)	0.2924
sin(18°)	0.309
sin(19°)	0.3256
sin(20°)	0.342
sin(21°)	0.3584
sin(22°)	0.3746
sin(23°)	0.3907
sin(24°)	0.4067
sin(25°)	0.4226
sin(26°)	0.4384
sin(27°)	0.454
sin(28°)	0.4695
sin(29°)	0.4848
sin(30°)	0.5
sin(31°)	0.515
sin(32°)	0.5299
sin(33°)	0.5446
sin(34°)	0.5592
sin(35°)	0.5736
sin(36°)	0.5878
sin(37°)	0.6018
sin(38°)	0.6157
sin(39°)	0.6293
sin(40°)	0.6428
sin(41°)	0.6561
sin(42°)	0.6691
sin(43°)	0.682
sin(44°)	0.6947
sin(45°)	0.7071

sin(46°)	0.7193
sin(47°)	0.7314
sin(48°)	0.7431
sin(49°)	0.7547
sin(50°)	0.766
sin(51°)	0.7771
sin(52°)	0.788
sin(53°)	0.7986
sin(54°)	0.809
sin(55°)	0.8192
sin(56°)	0.829
sin(57°)	0.8387
sin(58°)	0.848
sin(59°)	0.8572
sin(60°)	0.866
sin(61°)	0.8746
sin(62°)	0.8829
sin(63°)	0.891
sin(64°)	0.8988
sin(65°)	0.9063
sin(66°)	0.9135
sin(67°)	0.9205
sin(68°)	0.9272
sin(69°)	0.9336
sin(70°)	0.9397
sin(71°)	0.9455
sin(72°)	0.9511
sin(73°)	0.9563
sin(74°)	0.9613
sin(75°)	0.9659
sin(76°)	0.9703
sin(77°)	0.9744
sin(78°)	0.9781
sin(79°)	0.9816
sin(80°)	0.9848
sin(81°)	0.9877
sin(82°)	0.9903
sin(83°)	0.9925
sin(84°)	0.9945
sin(85°)	0.9962
sin(86°)	0.9976
sin(87°)	0.9986
sin(88°)	0.9994
sin(89°)	0.9998
sin(90°)	1

sin(91°)	0.9998
sin(92°)	0.9994
sin(93°)	0.9986
sin(94°)	0.9976
sin(95°)	0.9962
sin(96°)	0.9945
sin(97°)	0.9925
sin(98°)	0.9903
sin(99°)	0.9877
sin(100°)	0.9848
sin(101°)	0.9816
sin(102°)	0.9781
sin(103°)	0.9744
sin(104°)	0.9703
sin(105°)	0.9659
sin(106°)	0.9613
sin(107°)	0.9563
sin(108°)	0.9511
sin(109°)	0.9455
sin(110°)	0.9397
sin(111°)	0.9336
sin(112°)	0.9272
sin(113°)	0.9205
sin(114°)	0.9135
sin(115°)	0.9063
sin(116°)	0.8988
sin(117°)	0.891
sin(118°)	0.8829
sin(119°)	0.8746
sin(120°)	0.866
sin(121°)	0.8572
sin(122°)	0.848
sin(123°)	0.8387
sin(124°)	0.829
sin(125°)	0.8192
sin(126°)	0.809
sin(127°)	0.7986
sin(128°)	0.788
sin(129°)	0.7771
sin(130°)	0.766
sin(131°)	0.7547
sin(132°)	0.7431
sin(133°)	0.7314
sin(134°)	0.7193
sin(135°)	0.7071

sin(136°)	0.6947
sin(137°)	0.682
sin(138°)	0.6691
sin(139°)	0.6561
sin(140°)	0.6428
sin(141°)	0.6293
sin(142°)	0.6157
sin(143°)	0.6018
sin(144°)	0.5878
sin(145°)	0.5736
sin(146°)	0.5592
sin(147°)	0.5446
sin(148°)	0.5299
sin(149°)	0.515
sin(150°)	0.5
sin(151°)	0.4848
sin(152°)	0.4695
sin(153°)	0.454
sin(154°)	0.4384
sin(155°)	0.4226
sin(156°)	0.4067
sin(157°)	0.3907
sin(158°)	0.3746
sin(159°)	0.3584
sin(160°)	0.342
sin(161°)	0.3256
sin(162°)	0.309
sin(163°)	0.2924
sin(164°)	0.2756
sin(165°)	0.2588
sin(166°)	0.2419
sin(167°)	0.225
sin(168°)	0.2079
sin(169°)	0.1908
sin(170°)	0.1736
sin(171°)	0.1564
sin(172°)	0.1392
sin(173°)	0.1219
sin(174°)	0.1045
sin(175°)	0.0872
sin(176°)	0.0698
sin(177°)	0.0523
sin(178°)	0.0349
sin(179°)	0.0175
sin(180°)	0

Таблица синусов для 181°-360°

sin(181°)	-0.0175
sin(182°)	-0.0349
sin(183°)	-0.0523
sin(184°)	-0.0698
sin(185°)	-0.0872
sin(186°)	-0.1045
sin(187°)	-0.1219
sin(188°)	-0.1392
sin(189°)	-0.1564
sin(190°)	-0.1736
sin(191°)	-0.1908
sin(192°)	-0.2079
sin(193°)	-0.225
sin(194°)	-0.2419
sin(195°)	-0.2588
sin(196°)	-0.2756
sin(197°)	-0.2924
sin(198°)	-0.309
sin(199°)	-0.3256
sin(200°)	-0.342
sin(201°)	-0.3584
sin(202°)	-0.3746
sin(203°)	-0.3907
sin(204°)	-0.4067
sin(205°)	-0.4226
sin(206°)	-0.4384
sin(207°)	-0.454
sin(208°)	-0.4695
sin(209°)	-0.4848
sin(210°)	-0.5
sin(211°)	-0.515
sin(212°)	-0.5299
sin(213°)	-0.5446
sin(214°)	-0.5592
sin(215°)	-0.5736
sin(216°)	-0.5878
sin(217°)	-0.6018
sin(218°)	-0.6157
sin(219°)	-0.6293
sin(220°)	-0.6428
sin(221°)	-0.6561
sin(222°)	-0.6691
sin(223°)	-0.682
sin(224°)	-0.6947
sin(225°)	-0.7071

sin(226°)	-0.7193
sin(227°)	-0.7314
sin(228°)	-0.7431
sin(229°)	-0.7547
sin(230°)	-0.766
sin(231°)	-0.7771
sin(232°)	-0.788
sin(233°)	-0.7986
sin(234°)	-0.809
sin(235°)	-0.8192
sin(236°)	-0.829
sin(237°)	-0.8387
sin(238°)	-0.848
sin(239°)	-0.8572
sin(240°)	-0.866
sin(241°)	-0.8746
sin(242°)	-0.8829
sin(243°)	-0.891
sin(244°)	-0.8988
sin(245°)	-0.9063
sin(246°)	-0.9135
sin(247°)	-0.9205
sin(248°)	-0.9272
sin(249°)	-0.9336
sin(250°)	-0.9397
sin(251°)	-0.9455
sin(252°)	-0.9511
sin(253°)	-0.9563
sin(254°)	-0.9613
sin(255°)	-0.9659
sin(256°)	-0.9703
sin(257°)	-0.9744
sin(258°)	-0.9781
sin(259°)	-0.9816
sin(260°)	-0.9848
sin(261°)	-0.9877
sin(262°)	-0.9903
sin(263°)	-0.9925
sin(264°)	-0.9945
sin(265°)	-0.9962
sin(266°)	-0.9976
sin(267°)	-0.9986
sin(268°)	-0.9994
sin(269°)	-0.9998
sin(270°)	-1

sin(271°)	-0.9998
sin(272°)	-0.9994
sin(273°)	-0.9986
sin(274°)	-0.9976
sin(275°)	-0.9962
sin(276°)	-0.9945
sin(277°)	-0.9925
sin(278°)	-0.9903
sin(279°)	-0.9877
sin(280°)	-0.9848
sin(281°)	-0.9816
sin(282°)	-0.9781
sin(283°)	-0.9744
sin(284°)	-0.9703
sin(285°)	-0.9659
sin(286°)	-0.9613
sin(287°)	-0.9563
sin(288°)	-0.9511
sin(289°)	-0.9455
sin(290°)	-0.9397
sin(291°)	-0.9336
sin(292°)	-0.9272
sin(293°)	-0.9205
sin(294°)	-0.9135
sin(295°)	-0.9063
sin(296°)	-0.8988
sin(297°)	-0.891
sin(298°)	-0.8829
sin(299°)	-0.8746
sin(300°)	-0.866
sin(301°)	-0.8572
sin(302°)	-0.848
sin(303°)	-0.8387
sin(304°)	-0.829
sin(305°)	-0.8192
sin(306°)	-0.809
sin(307°)	-0.7986
sin(308°)	-0.788
sin(309°)	-0.7771
sin(310°)	-0.766
sin(311°)	-0.7547
sin(312°)	-0.7431
sin(313°)	-0.7314
sin(314°)	-0.7193
sin(315°)	-0.7071

sin(316°)	-0.6947
sin(317°)	-0.682
sin(318°)	-0.6691
sin(319°)	-0.6561
sin(320°)	-0.6428
sin(321°)	-0.6293
sin(322°)	-0.6157
sin(323°)	-0.6018
sin(324°)	-0.5878
sin(325°)	-0.5736
sin(326°)	-0.5592
sin(327°)	-0.5446
sin(328°)	-0.5299
sin(329°)	-0.515
sin(330°)	-0.5
sin(331°)	-0.4848
sin(332°)	-0.4695
sin(333°)	-0.454
sin(334°)	-0.4384
sin(335°)	-0.4226
sin(336°)	-0.4067
sin(337°)	-0.3907
sin(338°)	-0.3746
sin(339°)	-0.3584
sin(340°)	-0.342
sin(341°)	-0.3256
sin(342°)	-0.309
sin(343°)	-0.2924
sin(344°)	-0.2756
sin(345°)	-0.2588
sin(346°)	-0.2419
sin(347°)	-0.225
sin(348°)	-0.2079
sin(349°)	-0.1908
sin(350°)	-0.1736
sin(351°)	-0.1564
sin(352°)	-0.1392
sin(353°)	-0.1219
sin(354°)	-0.1045
sin(355°)	-0.0872
sin(356°)	-0.0698
sin(357°)	-0.0523
sin(358°)	-0.0349
sin(359°)	-0.0175
sin(360°)	-0

Существуют также следующие таблицы тригонометрических функций: таблица косинусов, таблица тангенсов и таблица котангенсов.

Как легко запомнить таблицу синусов (видео)

Таблицу важно всегда помнить на алгебре, чтобы найти синус.

Всё для учебы » Математика в школе » Таблица синусов углов (градусы, значения)

Источник

Синус двойного угла

Синус двойного угла, формула

Вычислить, найти синус двойного угла, по формуле (1)

Синус двойного угла

Тест по теме «Вычисление синуса»

Таблица синусов для 0°-180°

Таблица синусов для 181°-360°

Как легко запомнить таблицу синусов (видео)

Не пропустите также: