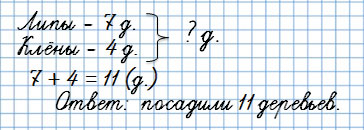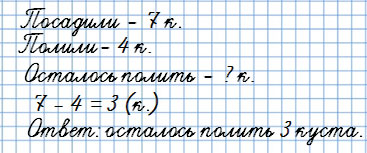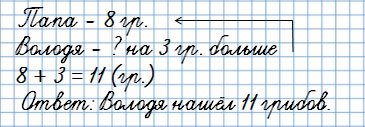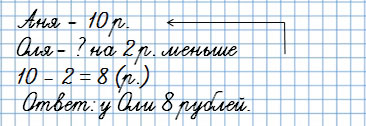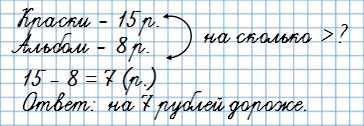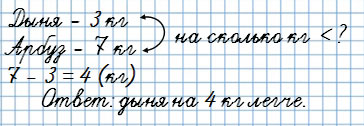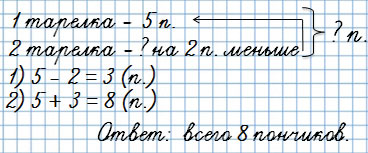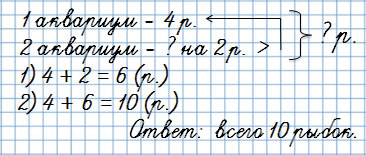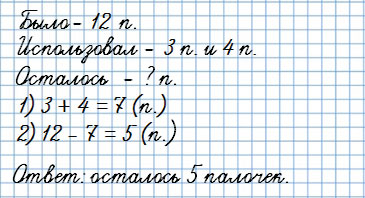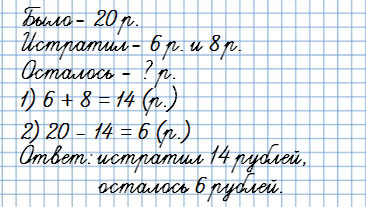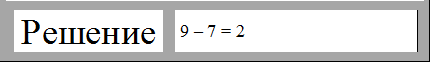- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Образцы оформления задачи
В разделе «Задачи» мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
1. Задачи на нахождение суммы
В вопросе задач такого типа всегда есть «Сколько всего?»
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
В вопросе «Сколько … осталось?»
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
3. Задачи на увеличение или уменьшение числа на несколько единиц
В условии «на … больше»
Папа с Володей собирали грибы. Папа нашёл 8 грибов, а Володя на 3 гриба больше.
Сколько грибов нашёл Володя?
В условии «на … меньше»
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
В вопросе «На сколько больше…?»
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
«На сколько меньше…?»
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии «Было…Стало…»
В вопросе «Сколько добавили?»
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии «Было… Осталось…»
В вопросе «Сколько уехало?»
«Сколько человек вышло?»
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии «Убрали… Осталось…»
В вопросе «Сколько было сначала?»
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Первый вид
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Второй вид
В классе два маленьких аквариума. В первом аквариуме 4 рыбки, а во втором — на 2 рыбки больше.
Сколько рыбок в двух аквариумах?
Третий вид
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
Четвёртый вид
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
или
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
II тип:
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
Задачи с составлением рисунка по условию:
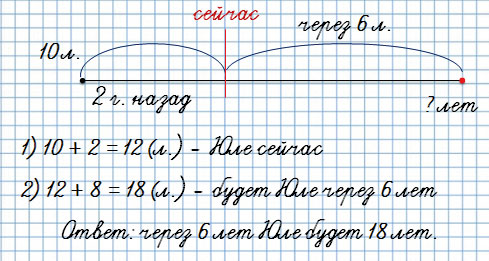
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Советуем посмотреть:
Обратные задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 15,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 23,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 24,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 27,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 30,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 31,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 5,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
2 класс
Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 63,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 68,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 52,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 57,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 110,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 52,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 76,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 10,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 13,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 13,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 73,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 12,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 4,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 21,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 102,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 418,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 81,
Мерзляк, Полонский, Якир, Учебник
Номер 105,
Мерзляк, Полонский, Якир, Учебник
Номер 165,
Мерзляк, Полонский, Якир, Учебник
Номер 366,
Мерзляк, Полонский, Якир, Учебник
Номер 383,
Мерзляк, Полонский, Якир, Учебник
Номер 478,
Мерзляк, Полонский, Якир, Учебник
Номер 481,
Мерзляк, Полонский, Якир, Учебник
Номер 498,
Мерзляк, Полонский, Якир, Учебник
Номер 5,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 361,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 419,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 420,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 424,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 428,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 429,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 432,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 437,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 443,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 449,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
План урока:
Понятие «задача». Составные части задачи
Задачи на нахождение целого
Задачи на увеличение числа на несколько единиц
Задачи на нахождение части
Задачи на уменьшение числа на несколько единиц
Задачи на разностное сравнение
Привет! По пути на наше занятие я встретила свою очень хорошую подружку. Ее зовут Даша – следопыт.
Она очень любознательная и стремиться находить ответы на все вопросы, даже самые сложные. Ей стало очень интересно, чем мы будем заниматься на сегодняшнем уроке. Я рассказала Даше, что тема у нас довольно непростая, мы будем разбираться в типах задач, искать способы их решения.
Даша подумала, что это будет очень увлекательно и попросила разрешить ей поприсутствовать у нас на уроке. Конечно же, я с радостью согласилась. Итак, сегодня наше занятие мы проведем втроем.
Понятие «задача». Составные части задачи
Послушай, какую историю рассказала мне Даша. Ее друг бычок Борька попросил помочь и провести расследование.
Утром у него на столе в вазочке лежало 9 шоколадных конфет.
А когда бычок вернулся с прогулки, то увидел в вазочке всего 6 конфет.
Борька обратился к Даше с просьбой разобраться с исчезновением конфет и узнать, куда они делись.
Даша определила, что конфет стало меньше. Она задумалась, почему это могло случиться. Например, конфеты могли выпасть из вазочки. Но конфет ни на столе, ни под столом не оказалось.
Тогда Даша решила, что конфеты кто-то забрал. Она внимательно присмотрелась к друзьям бычка, которые собрались в комнате, и заметила, что у лисенка Жулика щеки испачканы шоколадом.
Даша все поняла и нашла правильный ответ: это лисенок съел конфеты. И Жулик сразу же в этом сознался, а затем попросил прощение за свой поступок. Все были очень рады, что проблема решилась.
Я тоже очень обрадовалась, ведь история Даши поможет объяснить новый материал на сегодняшнем уроке. Давай по порядку проанализируем последовательность расследования.
- Бычок Борька рассказал, что произошло.
- Он задал вопрос и попросил найти ответ.
- Даша подумала, порассуждала и нашла правильное решение.
- Она дала ответ на вопрос бычка.
Это же и есть порядок работы над задачей! Вот определение понятия задача – это проблемная ситуация, которую нужно решить путем логических рассуждений, математических вычислений. В результате решения задачи нужно найти правильный ответ на поставленный вопрос.
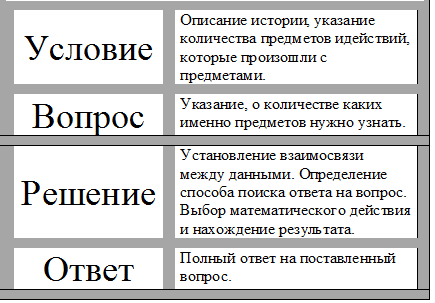
Вот составные части задачи.
Давай мы Дашину историю превратим в задачу и решим ее.
Итак, приступим. Сначала разберемся с условием.Для математической задачи важно иметь необходимые числовые данные.
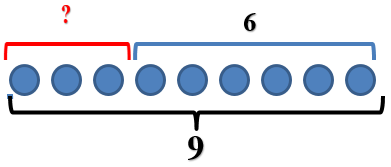
Чтобы лучше понять условие задачи, мы будем рисовать. Не обязательно рисовать именно конфеты. Можно их обозначить просто кружочками. Изобразим 9 кружочков–конфет.
Из этих конфет часть забрали и часть осталась. Мы знаем, что осталось 6 конфет. Отметим их.
Итак, мы проанализировали и изобразили условие нашей задачи. Идем дальше.
Теперь нам нужно определить вопрос задачи. Ее вопрос почти всегда включает слово «сколько».Даше нужно было узнать, куда исчезли конфеты. А мы узнаем, сколько исчезло конфет.
Для этого нам нужно определить количество конфет в той части, которую мы еще не выделили.
Пока все ясно? Тогда переходим к следующему этапу. Нам нужно понять, как найти решение задачи. Для этого давай подумаем. Нас интересуют конфеты в подмножестве, которое является частью множества из 9 конфет, лежавших в вазочке сначала. Мы с тобой выучили на прошлом уроке, что найти часть из целого можно с помощью действия вычитания. Осталось составить пример. Мы должны из общего количества конфет (число 9) вычесть количество конфет, которые остались (число 6). 9 минус 6 будет 3.
Ну вот, мы посчитали конфеты в подмножестве, которое забрали. Давай вспомним вопрос: «Сколько конфет исчезло?» Мы это только что установили, значит можно переходить к последнему этапу и дать ответ на вопрос.
Мы закончили работу над задачей.
- Разобрались с ее условием.
- Определили вопрос.
- Подумали над решением.
- И дали ответ.
Теперь ты сможешь решить любую задачу. Их очень много. Мы рассмотрим решение простых задач.
Задачи на нахождение целого
Вот наша первая задача. Ее составила для нас Даша.
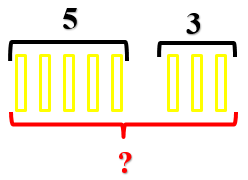
У обезьянки Башмачок было 5 бананов. А Даша принесла ей еще 3 банана.
Какой вопрос мы можем задать по условию этой задачи? Правильно, мы можем спросить, сколько всего бананов стало у обезьянки?
Итак, начнем работать. Сначала проанализируем первую составную часть задачи– условие.
О ком говорится в задаче? Правильно, об обезьянке. О том, что у нее было 5 бананов.
Что случилось потом? Верно, ей дали еще 3 банана. Запишем это в нашу таблицу
Теперь обозначим условие задачи схематически. Вместо бананов будем рисовать прямоугольники. Сначала нарисуем 5 бананов, которые были у обезьянки.
Поскольку обезьянке дали еще бананы, то нарисуем их рядом.
Вспомним вопрос задачи и запишем его в таблицу
Значит, нам нужно вместе посчитать бананы, которые были, и бананы, которые ей еще дали
Теперь приступим к решению задачи.
Получается, что теперь у обезьянки все бананы лежат вместе, т.е. подмножество бананов, которые были у нее раньше, объединилось с подмножеством бананов, которые она получила потом.
Давай вспомним материал прошлого урока. Какое математическое действие мы используем при объединении подмножеств в одно общее?
Правильно, это действие сложение. Значит, для решения нашей задачи мы должны составить выражение на сложение. К 5 бананам, которые были у обезьянки, прибавим 3 банана, которые ей дала Даша. Что получится?
Сумма чисел 5 и 3 равна 8. Вот мы и посчитали все бананы. Теперь у обезьянки всего стало 8 бананов.
Обрати внимание, мы нашли ответ на вопрос нашей задачи! Можно заканчивать
Вот мы и разобрались с нашей задачей.
С помощью какого действия мы нашли ответ? Да, это было действие сложение.
Почему мы использовали именно это действие? Совершенно точно, потому что по условию предметы добавлялись. Два подмножества предметов объединяются в одно целое. Такой тип задач называется задачи на нахождение целого.
Один из главных вопросов в задачах на нахождение целого «Сколько всего?» Потому что именно после объединения двух подмножеств надо пересчитать все предметы вместе.
В нашей задаче предметов прибавилось, потому что Даша дала еще бананы. Подумай, в каком еще случае предметов добавится?
Правильно, если:
- что-то подарят;
- что-то положат;
- сделают еще несколько предметов;
- кто-то придет или приедет;
- объединить две группы предметов (например, посчитать вместе мальчиков и девочек).
Во всех указанных случаях мы получим задачи на нахождение целого. Такие задачи нужно решать с помощью действия сложения.
Задачи на увеличение числа на несколько единиц
А вот другая задача. Она немного не похожа на предыдущие. Давай рассмотрим, в чем ее особенности.
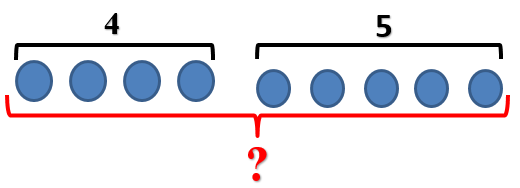
У Даши было 4 воздушных шарика, а у игуаны Иса – на 5 шариков больше. Сколько шариков было у игуаны?
Сначала проанализируем условия задачи. Что нам известно?
Правильно, мы знаем о Даше. У нее 4 шарика.
Но мы не знаем, сколько шариков у игуаны! Однако у нас есть подсказка о их количестве. В задаче сказано, что у игуаны на 5 шариков больше.
Запишем это условие и вопрос.
Попробуем изобразить. Вот 4 шарика Даши
А как показать шарики игуаны? У нее их на 5 больше, чем у Даши. Значит их столько же (т.е. 4) и еще 5. Покажем это.
Давай подумаем над решением этой задачи. Выбор действия подсказан в самом условии. Помнишь, в результате какого действия становится больше?
Правильно, это действие сложения. Значит, для решения задачи нам нужно составить пример на сложение
Мы посчитали, сколько шариков у игуаны, а это и есть вопрос нашей задачи. Ура! Мы нашли нужный ответ!
Задача решена!
Теперь давай разберемся, в чем ее особенность. В условии задачи содержалась подсказка, которая указала на выбор математического действия. Помнишь?
Было сказано, что у игуаны на несколько шариков больше. Больше становиться в результате действия сложения. Поэтому, чтобы посчитать шарики игуаны, нужно прибавлять.
Это задача на увеличение числа на несколько единиц. Их решать очень легко, если внимательно прочитать условие. Как только ты заметишь указание, что предметов, которые нужно посчитать, на несколько единиц больше, то сразу выбирай действие сложения.
Задачи на нахождение части
А сейчас еще одна задача.
На кусте росло 8 ягод. Лис жулик сорвал 2 ягоды. Сколько ягод осталось?
Довольно простое и понятное условие. Попробуй сам записать все, что нам известно.
Давай проверим. Мы знаем, сколько было ягод, и знаем, сколько ягод сорвал Жулик. Поэтому запись такая
Что нужно узнать? Запиши вопрос
Кажется, все понятно. Теперь давай порассуждаем. Из тех ягод, что были на кусте, часть ягод сорвали. Изобразим это на схеме
Подумай, что произойдет, если убрать часть предметов?
Правильно, их останется меньше.
А теперь вспомни, какое математическое действие используется при удалении из множества предметов одного его подмножества?
Конечно же, это действие вычитание. Значит нам нужно из числа 8, которое обозначает количество всех ягод вычесть число 2, которое обозначает количество сорванных ягод.
Запишем решение.
Мы узнали, что на кусте осталось 6 ягод. Можем записать ответ.
Вот как просто! Когда мы что-то убираем, то остается только часть от всего, что было. Это задачи на нахождение части. Они решаются с помощью действия вычитания.
Давай подумаем, в каких еще ситуациях будет оставаться только часть предметов.
Например:
- что-то съели;
- забрали;
- продали;
- ушли;
- увезли;
- отрезали;
- прочитали.
Можно еще продолжать, но главное, ты должен запомнить, что в результате таких действий часть предметов убирается и их остается меньше. Поэтому в задачах на нахождение части всегда используется действие вычитания.
Задачи на уменьшение числа на несколько единиц
Давай разбираться со следующей задачей. Ее придумала Даша.
Даша собралась в поход. Она положила себе в рюкзак 5 пар носков, а футболок взяла на 3 меньше.
Прочитай внимательно условие. Какие вещи взяла Даша? Что о них известно?
Правильно, мы знаем, что Даша взяла 5 пар носков.
А для каких вещей не указано точное количество?
Верно, мы не знаем точно, сколько Даша взяла футболок. Сказано, что их на 3 меньше, чем носков. Давай это запишем.
Можешь сказать, какой будет вопрос? Что нам нужно узнать?
Правильно, мы будем узнавать, сколько же футболок взяла с собой Даша
Это тоже задача с подсказкой. Мы можем даже не рисовать носки и футболки, чтобы понять, как ее решать. Ты уже догадался, что за подсказка?
Ну, конечно же, это указание, что футболок меньше! А мы уже знаем, какое математическое действие нужно применять, если предметов меньше. Это действие вычитание.
Все очень просто. Нам нужно из числа 5, которое обозначает количество носков, вычесть число 3, которое показывает, на сколько футболок меньше
Вот и все! Теперь нам известно, что Даша взяла в поход 2 футболки. Можем писать ответ
И задача решена!
Это мой любимый тип задачи. Он называется задачи на уменьшение числа на несколько единиц. При их решении невозможно ошибиться. Раз сказано, что предметов на несколько единиц меньше, значит, будем вычитать, и получим правильный ответ.
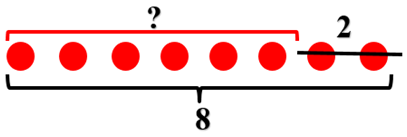
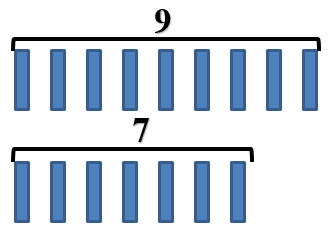
Задачи на разностное сравнение
А вот еще одна задача от Даши и о ее друге Паровозике.
В первый день Паровозик перевез 9 пассажиров, а во второй день – 7 пассажиров.
Очень простое и понятное условие. Все известно – и сколько в первый день перевез, и сколько во второй.
Можем это записать.
И нарисовать это можем. Пассажиров обозначим палочками. Сначала нарисуем пассажиров, которые ехал в первый день, а ниже тех, кто ехал во второй.
А вот вопрос Даша придумала очень необычный. Она решила, что мы слишком легко со всеми задачами справляемся и нужно немного усложнить. Вот вопрос.
Итак, нужно для начала определить в какой день он перевез пассажиров больше, а в какой меньше. Это довольно легко. Ты уже умеешь сравнивать числа. Скажи, что получиться?
Правильно, 9 > 7. Это можно прочитать, как «9 больше, чем 7» или «7 меньше, чем 9».
Но в задаче недостаточно только сравнить числа. Нужно узнать, какая между ними разница, т.е. выполнить разностное сравнение. Давай еще раз посмотрим на рисунок. Что ты заметил?
Видишь, в первый день изобразили палочек столько же, сколько и во второй день, и остались еще «лишние» палочки. Их можно отгородить. Для этого отделим одинаковое количество палочек. Во множестве с меньшим количеством элементов 7 палочек, значит, и во множестве с большим количеством элементов мы отсчитаем 7 палочек.
Чтобы найти ответ на вопрос задачи, нужно узнать количество «лишних» палочек.
То есть нам надо найти часть из множества, в котором 9 палочек.
А вот это уже просто! Вспомни, с помощью какого математического действия можно найти часть множества. Конечно же, это вычитание.
Получается, мы должны из большего числа вычесть меньшее число.
Мы провели не только сравнение чисел, но и нашли их разность. Это называется разностное сравнение чисел. Можно записывать ответ.
Вот мы и познакомились еще с одним типом задач – задачи на разностное сравнение. Их главная особенность в том, что вопрос начинается со слов «На сколько …?». Для решения этих задач нужно следовать такому алгоритму.
- Определить, какое число больше.
- Из большего числа вычесть меньшее.
Ты еще не устал? Мы выучили 5 разных типов задач:
- задачи на нахождение целого;
- задачи на увеличение числа на несколько единиц;
- задачи на нахождение части;
- задачи на уменьшение числа на несколько единиц;
- задачи на разностное сравнение.
Каждая из них имеет один единственно правильный вариант решения. Поэтому нужно очень хорошо подумать и разобраться. Всегда будь внимательным к вопросу задачи. Поиск правильного решения зависит именно от того, количество каких предметов нужно узнать.
Чтобы потренироваться в решении разных задач, попроси родителей приобрести сборник задач для 1 класса.
А сейчас давай проверим, как ты научился анализировать условие задачи и правильно определять ее тип. Выполни тестовые задания.
Для материалов урока взяты кадры из обучающего м/с «Даша-путешественница», 2004
Мы уже говорили о значимости понятного и реалистичного содержания задач в курсе арифметики в статьях «Какие задачи развивают ребёнка — лёгкие или трудные» и «Каким должно быть содержание задачи».
Второй важный фактор успешного обучения детей решению задач — сознательное усвоение ими условий задач. Ведь помимо образного представления реалий сюжета необходимо уловить числовые отношения, или математическую структуру задачи. Для этого классическая методика предлагает огромное количество форм работы. Давайте будем шаг за шагом осваивать эти приёмы.
1) Чтение, запись и повторение условия
В повседневной практике порой приходится наблюдать, как ребёнок слабо понимает текст условия из-за плохого чтения, особенно в первых двух классах. Процесс чтения условия задачи существенно отличается от чтения рассказов. Особые трудности для ребёнка представляет чередование в условии словесного текста с числами. Числа, как показывает опыт, читаются совсем иначе, чем слова. Объясняется это, главным образом, тем, что каждое число представляет собой особую комбинацию знаков — цифр, в то время как в словах знаки-буквы встречаются в своих специфических комбинациях. Вследствие этого ребёнок при чтении чисел делает больше фиксаций взгляда, а также больше регрессий (возвращений к просмотренному тексту), фиксации взгляда здесь более длительны, чем при чтении слова. При встрече числа в условии задачи ребёнок вынужден замедлять темп своего чтения.
Из сказанного видно, что чтение условия задач требует особых навыков. Поэтому нельзя полагаться на общие навыки чтения, которые приобретаются детьми на уроках словесности, а необходимо обучать их чтению текста математических задач как особому навыку.
Самый первый и простой приём, используемый учителем, — это чтение условия задачи не менее двух раз: при первом чтении ребёнок должен уловить общий смысл условия, а при вторичном — вникнуть в числовые данные.
Важный вопрос: кто должен читать условие — учитель или ученик? Наблюдения, а также исследования, которые проводились в данной области, показали, что дети лучше справляются с задачами, читаемыми учителем, чем с аналогичными задачами, условия которых они читают сами.
Следует ли из этого, что учитель должен всегда сам читать условие? Разумеется, нет. Конечная наша цель — развитие у детей умения самостоятельно, без посторонней помощи, решать задачи. Поэтому было бы вредно, если бы во всех случаях учитель сам читал условие. Вместо этого необходимо, начиная с I класса, приучать детей к чтению задач по учебнику.
Исходя из сказанного, наиболее правильным на первоначальных этапах обучения будет такой вариант: более сложные для понимания задачи правильнее читать учителю, причём более эффективно не читать, а рассказывать задачу наизусть, а на задачах более лёгких вырабатывать у детей навыки самостоятельного чтения и усвоения условия задачи.
2) Составление краткой записи
При работе над сложной задачей детям помогает запись её условия. Формы записи условия могут довольно разнообразными. Одна из них — краткая запись. Разберём её более подробно, так как краткая запись задачи — это настоящий бич современной начальной школы, сопоставимый по разрушительной силе со звуковыми транскрипциями и модулями-схемами.
Первый и самый важный момент: краткая запись не может и не должна быть самоцелью при обучении решению задач — это служебное подготовительное действие, которое нужно тогда и только тогда, когда задача настолько сложна, что ребёнок не может охватить её сюжет целиком. Краткая запись условия задачи должна способствовать пониманию, а не усложнять его; упрощать, а ни в коем случае не затруднять процесс решения задачи.
Итак, первоочередным условием использования краткой записи при усвоении условия задачи будем считать то, что задача настолько сложна, что ребёнок не может ухватить её сюжет целиком и нуждается в поэтапном (синтетическом) разборе задачи.
Выделение из текста условий числовых данных и их запись делает более ясным для учеников, что дано в задаче и что ищется. Такая запись помогает им лучше понять зависимость между величинами, о которых идёт речь в условии задачи.
Краткая запись условия может проводиться по-разному. Возьмём для примера задачу: «Конструктор, машинка и робот стоили 700 рублей. Конструктор стоил 130 рублей, машинка — в 2 раза больше, чем конструктор. Сколько стоил робот?»
Выписывая числовые данные из этого условия, можно расположить их в строчку, например:
3 игрушки — 700 руб.; конструктор — 130 руб., машинка — в 2 раза больше. Робот — ?
Можно расположить эти данные по-иному, схематически, примерно так:
Конструктор — 130 руб.
Машинка — в 2 раза больше.
3 игрушки — 700 руб.
Робот — ?
Легко видеть, что вторая форма записи делает условие более доходчивым для ребёнка, облегчает ему понимание зависимости между величинами. Целесообразно применять схематическую запись условия при решении трудных задач. Однако не нужно настаивать на каком-то однообразном, если не сказать однобоком, алгоритме краткой записи условия задачи. Подбирайте для каждой задачи наиболее понятную и удобную для целостного восприятия форму записи данных и искомых величин. Сделайте этот процесс творческим и интересным, а не «зубодробильным», как в современных методиках.
Очень полезно, чтобы учащиеся прибегали к краткой форме записи числовых данных при самостоятельном решении сложных задач, как в классе, так и дома. Пусть они выбирают свои приёмы записи, удобные для них. Это раскрепощает ребёнка перед задачей, побуждает его рассмотреть её с разных ракурсов, подталкивает мысль к нахождению путей решения, которых, как и форм краткой записи, может быть несколько. Чем свободнее и смелее ребёнок будет рассматривать и кратко записывать задачу по своему усмотрению, тем смелее и свободнее он решит её.
Однако следует ли всегда прибегать к схематической записи числовых данных задачи? Разумеется, нет, так как злоупотребление этой формой может привести к тому, что ученики не будут справляться с задачей при иной форме записи, в особенности же без записи условия.
А что делать, если ребёнок, только прочитав задачу, уже знает, как её решать? Ответ на этот вопрос однозначный — решай, моя умница!
3) Повторение, или пересказ условия
К сожалению, в современной общеобразовательной школе краткая запись стала единственной и безальтернативной формой работы с текстовыми задачами. Вводится она неоправданно рано и бесцельно усложняет решение простых и понятных ребёнку задач. Поэтому хочется обратить особое внимание наших читателей на другие формы работы над усвоением содержания задачи, в частности — на повторение, пересказ её условия.
Если вы начнёте практиковать пересказ задач, то убедитесь, что для формирования этого навыка также нужна практика. Обычно активно воспроизвести задачу могут немногие учащиеся, большая же часть детей воспринимает условие пассивно, на слух. Даже если вы дадите ребёнку прочитать задачу, которую он успешно решил несколько дней назад, и спросите его, может ли он её пересказать, скорее всего, он ответит утвердительно. Однако многие из тех детей, которые дают утвердительный ответ, всё же не могут повторить условие.
Здесь сказывается существенное различие между узнаванием и воспроизведением. Прочитав знакомое условие, ребёнок узнаёт его и чувствует уверенность, что может его повторить. При воспроизведении же оказывается, что он его не знает.
Наиболее часто дети затрудняются при пересказе середины и конца условия, в особенности же при пересказе главного вопроса. Иногда ученику требуется прочитать условие ранее решённой задачи несколько раз, пока он окажется в состоянии пересказать его.
Уметь пересказывать прочитанную задачу очень полезно, так как чаще всего бывает достаточно добиться хорошего пересказа условия, чтобы получить правильное решение задачи от ученика, который до этого не мог решить её.
Чтобы активизировать работу детей в процессе повторения задачи, можно рекомендовать им повторять условие прослушанной задачи сперва тихо или про себя и лишь после этого приступать к пересказу вслух. Таким образом, все учащиеся, а не только те, кого учитель вызывает для устного пересказа, будут повторять условие.
В том случае, когда дети сами читают условие, необходимо рекомендовать им читать задачу не менее двух раз, затем закрыть учебник и повторить условие тихо, про себя. При этом надо указать ученикам, что числовые данные можно не запоминать, главное — понять и усвоить содержание задачи. Следует предупреждать детей, что от них будет требоваться пересказ условия без книжки («Вы должны будете повторить задачу, не заглядывая в учебник. Числа запоминать не нужно»). По нашим наблюдениям, такие предупреждения заставляют детей читать условие внимательно и пересказывать его про себя, чтобы быть готовым к пересказу вслух.
Здесь уместно указать, что, как показали экспериментальные исследования, при чтении текста с необходимостью запомнить его читающий гораздо яснее представляет себе содержание читаемого. Вот что пишет по этому поводу проф. А. А. Смирнов:
«Под влиянием мнемонической направленности наглядные представления возникают чаще, чем в отсутствие её. Далее, при чтении в условиях мнемонической направленности образы чаще иллюстрируют само содержание текста, а не являются побочными, случайно связанными с тем, что говорится в тексте». «Пересказывая своими словами, — пишет в той же статье проф. Смирнов, — мы приспособляем воспринятое к самим себе, «ко всей системе нашей психической жизни», к нашему «образу мыслей». Мы действительно осваиваем текст».
Нередко дети приступают к решению заданной им задачи, не прочитав условия до конца, что оказывается причиной многих ошибочных решений. Внимательное чтение и пересказ условия могут способствовать заметному повышению правильности решений.
Следует рекомендовать детям, чтобы и при выполнении домашних заданий по арифметике они прочитывали условие заданной задачи не менее двух раз, повторяли его, не заглядывая в учебник, и лишь после правильного пересказа условия приступали к решению задачи.
Указанное требование не имеет ничего общего с требованием заучивать наизусть условие задаваемой задачи и знать его на память при проверке домашних задании на следующий день. Повторение условия про себя непосредственно перед решением задачи полезно, так как это способствует лучшему усвоению и пониманию детьми её содержания. Заучивание же условия задачи наизусть не имеет никакого смысла и зря обременяет память учащихся.
Особо следует остановиться на вопросе о том, как следует проводить повторение условия вслух.
Независимо от того, читает ли условие учитель или сами дети, нужно проверить, усвоили ли они условие (исключение должно допускаться лишь при вполне самостоятельном решении задач). В этих целях учитель может предложить вызываемым ученикам связно повторить условие либо ответить на отдельные частные вопросы, касающиеся содержания условия (повторение по вопросам учителя).
Как определить, какой способ уместнее в вашем конкретном случае? Здесь, как и всегда, опираемся на здравый смысл: когда решается новая, трудная задача, необходимость повторения условия и целиком, и по вопросам вполне оправдана; когда же решается сравнительно нетрудная задача, можно ограничиться тем, чтобы один-два ученика связно повторили условие, после чего можно переходить к её решению.
Однако и при такой форме работы возможен непродуктивный формальный подход, которого нужно стараться избегать. Порой при решении задачи обнаруживается, что ученик, правильно пересказавший условие, не представляет себе того, о чём он рассказывал. Очевидно, что при формальном усвоении словесного текста задачи ученик не всегда может правильно понять зависимость между величинами, о которых в ней идёт речь, и, как следствие, не может правильно решить задачу. Поэтому очень важно обращать внимание на то, чтобы дети ясно представляли себе содержание задачи, чтобы они видели в своём воображении то, о чём рассказывается в ней.
Д. Мартынов в своём пособии «Методика арифметики для начальной школы» говорит по этому поводу:
«Содержание задачи можно считать усвоенным лишь тогда, когда ученик достигнет до наглядного, как бы картинного представления между данными в задаче числами. Направить воображение ученика именно в эту сторону — дело учителя».
На значение отчётливого представления содержания задач указывает и проф. И. В. Арнольд, который пишет:
«Затруднения в использовании данных арифметических задач в большинстве случаев зависят от недостаточно отчётливого представления учащимися данных количественных взаимоотношений».
4) Понимание слов, входящих в состав условия
Прежде чем приступать к работе над задачей, учителю необходимо убедиться в том, что ребёнок понимает значение всех слов, входящих в состав условия. Тексты многих задач наших учебников содержат слова, недостаточно знакомые детям (а иногда и вовсе незнакомые им). Это затрудняет понимание смысла условия и, как следствие, понимание способа решения задачи.
Здесь внимание учителя должны привлекать не только особо трудные слова, с которыми дети редко встречаются, но и употребляемые более часто, которые, может быть, уже не раз встречались им, но о которых, как показывает целый ряд исследований, проведённых в этой области, у них нередко сформировываются неясные, а то и неверные представления.
Приведём для примера данные советского исследования этого вопроса.
Чтобы изучить доступность для учащихся III и IV классов словаря учебников по арифметике, из каждого сборника было выделено по 30 наиболее трудных слов.
Вот образцы слов, выделенных из учебника для III класса: «барка», «бетон», «домна», «ссыпной пункт», «кокс» и др. А вот образцы слов, выделенных из учебника для IV класса: «баржа», «зубчатое колесо», «зяблевая вспашка», «зольное удобрение», «мюльная машина», «шлюз» и др.
Перечисленные слова предложили соответственно учащимся третьих и четвёртых классов, при этом им дали задание — рядом с каждым словом написать, как они его понимают. Всего опросили 309 учащихся третьих классов и 438 учащихся четвёртых классов.
Полученные листки с ответами учащихся обработали так: по каждому слову был подсчитан процент полностью правильных, частично правильных, неправильных и отсутствующих ответов. Результаты обработки детских ответов показали, что многие из перечисленных выше слов малознакомы для школьников.
Приведём образцы детских ответов (правильных и неправильных) по отдельным словам.
Зяблевая вспашка:
«Вспашка, которую пашут под осень». «Это кто-нибудь вспашет и её замораживает». «Вспашка, у которой пахарь зябнет». «Зяблевая вспашка — это плохая работа». «Зяблевая вспашка называется вспашка бугристая, как будто озябший человек. Когда человек зябнет, то у него тело покрывается маленькими бугорками». «Это когда пашут и зябнут». «Зяблевая вспашка — это пашут зябликом». «Это он [видимо, зяблик] своим носом роет землю».
Чайная плантация:
«Поле, на котором возделывают чайные кусты». «Это большое поле, на котором растёт чай». «Это есть такая местность, где погружают чай». «Где прохожие пьют чай». «Посуда, из которой пьют чай». «Чайная плантация — небольшая лавочка». «Все чай пьют, все вместе». «Делают чайную посуду».
Более подробно результаты этого исследования изложены в статье «Изучение доступности словаря учебника» из журнала «Народный учитель» (1935).
Как видно из приведённых образцов, у некоторых учащихся превратные представления о словах, встречающихся в условиях задачи.
Оказывает ли наличие таких слов в условии влияние на правильность решения задачи? Чтобы проверить это, были составлены две пары задач, при этом задачи каждой пары были однородны по своей структуре, но различались между собой словарём: первая задача каждой пары содержала трудные слова, вторая задача была свободна от таких слов.
Вот первая пара задач:
1. «В районе 43 500 га посевной площади; 1/5 часть её — под яровыми. Средний урожай ярового поля — 1 700 кг с гектара. При переходе к зяблевой вспашке урожай яровых хлебов повысился на 170 кг с гектара. Сколько яровых хлебов собирает район при зяблевой вспашке?»
2. «В совхозе 23 400 га земли. 1/3 её засеяна пшеницей. Средний урожай пшеницы был 1 600 кг с гектара. На следующий год под пшеницу заняли столько же земли, как и раньше, но хорошо удобрили землю навозом, и урожай пшеницы повысился на 330 кг с гектара. Сколько пшеницы собрал совхоз с удобренной земли?»
А вот вторая пара задач:
1. «Два пассажирских поезда стоят один за другим. В одном — паровоз с тендером и 40 вагонов, в другом — паровоз с тендером и 45 вагонов. Длина вагона — 7 м, а паровоза с тендером — 23 м. Какой длины путь занимают оба поезда?»
2. «Два пассажирских поезда стоят один за другим. В одном — паровоз и 60 вагонов. В другом — паровоз и 76 вагонов. Длина вагона — 9 м, длина паровоза — 25 м. Какой длины путь занимают оба поезда?»
Опытная работа была проведена в трёх четвёртых классах. В каждом из этих классов сначала давались для самостоятельного решения две задачи в одной формулировке (вторая задача первой пары и первая задача второй пары), затем, ровно через шестидневку, в тот же час дня — две аналогичных задачи в другой формулировке (первая задача первой пары и вторая задача второй пары).
Из проведённого эксперимента стало очевидно, что наличие малопонятных слов в условии задачи оказывает отрицательное влияние на правильность её решения. Интересно, однако, отметить следующее: некоторые учащиеся из числа тех, которые обнаружили непонимание слов, входивших в состав контрольных задач, тем не менее, правильно решили их. Так, правильно решили задачу первой пары учащиеся, которые писали про зяблевую вспашку: «Это когда пашут и зябнут», «Это он своим носом роет землю» и др. Это значительно снижает ценность их работы, ибо образовательное значение решения задачи может в полной мере сказаться тогда, когда учащиеся правильно представляют себе, что такое посевная площадь, яровое поле, зяблевая вспашка. Лишь в этом случае они будут сознательно решать задачу и, кроме того, через посредство её решения уточнят свои знания о выгоде зяблевой вспашки, о которой идёт речь в условии.
Значит ли это, что сборники задач должны быть совершенно разгружены от трудных слов? Нет, ибо это могло бы привести к отрыву содержания задач от производственной и культурно-политической жизни взрослых. Тем самым решение задач потеряло бы в значительной мере своё воспитательно-образовательное значение. Речь должна идти не о разгрузке учебников от трудных слов, а лишь об исключении из них малоупотребительных слов с узко ограниченным применением в жизненной практике, при этом новые для учащихся слова должны вводиться в меру, с учётом уровня развития учащихся каждого класса. Нечего говорить о том, что значение каждого из таких слов должно подробно разъясняться детям.
Наши учебники в значительной части освобождены от слов, которые маловероятно встретятся в их жизни, однако нашей задачей было сохранить нравственный воспитательно-трудовой настрой учебника. В связи с этим у современных городских детей зачастую возникают трудности с пониманием некоторых слов задач. Обращайте на это особое внимание. Проводите краткие вводные беседы перед чтением текста задачи, содержащей понятия, малознакомые детям. Порой нам даже сложно предположить, что то или иное понятие (баржа, вагон пшеницы, экземпляр книги, железнодорожная ветка, лесной питомник, отрез ткани и т. п.) может вызвать затруднение у ребёнка.
5) Понимание жизненного смысла задачи
Когда мы убедились в том, что дети понимают значение отдельных слов, из которых состоит текст задачи, это ещё совершенно не означает того важного момента, что у ребёнка сложилось ясное представление о той жизненной среде (обстановке), из которой взята задача, что он понимает, кому и когда приходится решать такие задачи в жизни. Без этого трудно понять зависимость между величинами, о которых идёт речь в условии, и, как следствие, трудно правильно выбрать нужные действия.
При выборе тематики задач прежде всего следует соблюдать общедидактический принцип от близкого к далёкому, выбирая вначале задачи из близкого окружения детей и лишь постепенно переходя к менее знакомым для них областям жизни.
Для лучшего понимания условия, для активизации детского воображения возможно применять ещё целый ряд приёмов:
а) Вместо сжатой формулировки условия изложить его более полно — так, чтобы детям было легче представить себе жизненную обстановку, из которой взята задача, чтобы задача стала более понятной для них.
Приведём пример из школьной практики. Во II классе решали задачу:
«Чтобы оклеить комнату, достаточно иметь 6 кусков обоев по 14 м в каждом куске. Сколько кусков обоев пойдёт на эту комнату, если в каждом куске будет 12 м?»
При разборе задачи многие дети обнаружили непонимание способа её решения, непонимание зависимости между её величинами. Последнее, как это нетрудно было заметить, проистекало от непонимания ими жизненного смысла задачи.
Тогда учитель предложил ученикам условие задачи в новой редакции:
«Нужно оклеить комнату. Мастер велел купить 6 кусков обоев по 14 м в каждом. В магазине же оказались куски обоев длиною по 12 м каждый. Хозяйке нужно сосчитать, сколько таких кусков ей нужно купить?»
Далее учитель сказал: «Пусть каждый из вас представит себе, что он пошёл покупать обои для этой комнаты. Как бы вы стали решать задачу?»
И вот многие из тех учеников, которые до этого не знали, как решать задачу, стали более уверенно рассказывать её план и решение. Это явилось результатом того, что благодаря новой формулировке условия у детей возникло более ясное представление о жизненной обстановке, из которой взята задача, они поняли, зачем нужно было её решать (зачем нужно было узнавать количество кусков обоев по 12 м). Определённую роль здесь сыграло и то, что детей призвали поставить себя на место действующего лица — покупателя обоев, что сделало более активным их отношение к решаемой задаче.
Приведём ещё один пример. В IV классе решали задачу:
«Для осушения болота нужно вырыть канаву длиной в 1 080 м. Один землекоп может вырыть эту канаву за 40 дней, другой — за 60 дней. За сколько дней они выроют канаву, работая вместе?»
В беседе с учениками выяснили, для чего нужно было рыть канаву. Далее детям разъяснили содержание задачи примерно так:
«Для осушения болота нужно было вырыть канаву длиной в 1 080 м. Первый землекоп, которому предложили эту работу, был готов взяться за неё, но он сказал, что может вырыть канаву за 40 дней. Это оказалось слишком длинным сроком. Тогда обратились к другому землекопу. Но тот сказал, что он может вырыть канаву только за 60 дней. Этого срок был ещё длиннее. Чтобы канава была вырыта скорее, наняли обоих землекопов. В задаче спрашивается, за сколько дней оба землекопа выроют канаву, работая вместе».
Доведение до сознания учащихся жизненного смысла задачи помогло им лучше понять способ её решения.
При более полном изложении условия следует дополнять его лишь такими деталями, которые необходимы для лучшего понимания данных количественных отношений, так как излишние подробности могут отвлечь внимание детей от основной фабулы задачи и тем самым затруднить для них понимание зависимости между величинами.
Здесь уместно привести образцы задач из сборника Звягинцева и Бернашевского, в котором большинство задач изложено в форме рассказов:
«Костя помогает дедушке Савелию собирать в саду опавшие яблоки. Сегодня он собрал 22 спелых яблока и 13 зелёных. Сколько всего яблок собрал он?»
«Учительница рассказала ребятам, что ей пришлось однажды видеть в зверинце двух черепах: одну большую морскую весом 480 фунтов, а другую обыкновенную ручную весом 30 фунтов. Во сколько раз речная черепаха легче морской?»
В первой задаче, может быть, излишне указывать, как звали дедушку. Также можно было бы несколько короче изложить условие второй задачи. Но в целом введённые в эти задачи детали, не загромождая их основной фабулы, помогают детям легче представить содержание задачи, делают задачи более доходчивыми.
В то же время в этом сборнике много задач, условия которых чрезмерно загромождены излишними деталями. Приведём образцы таких задач:
«В жаркой стране Африке есть воробьи, которые целой стаей устраивают гнёздышки рядышком и выводят над ними общую крышу. Облюбовали эти воробьи большое высокое Дерево и устроили на нём под одной крышей 76 гнёзд. Потом прилетела к ним другая стайка, увеличила крышу и пристроила ещё 21 гнездо. Сколько всего гнёзд было под крышей?»
«Вывели воробьи птенцов и разлетелись. А когда настало время опять выводить птенцов, прилетели к тому же дереву сперва 38 пар воробьёв, потом — на 17 пар больше. Но поселились воробьи не в старых гнёздах, а свили и подвесили к ним новые гнёздышки, особое для каждой пары. Крыша же под гнёздами осталась прежняя. Сколько новых гнёзд устроили воробьи?»
Излишнее многословие, особенно во второй задаче, может затруднить детям решение, так как из-за обилия деталей они могут не понять данных количественных отношений.
Оживлению задач может способствовать введение в их условия прямой речи. Приведём образцы таких задач:
«Швее дали 15 м полотна и сказали: «Из 3 м сошьёте наволочки, а из остального полотна — 6 одинаковых простыней». Сколько метров полотна пошло на каждую простыню?»
«Мама выкопала в парнике 100 штук капустной рассады и говорит сыну: «На 4 маленьких грядках посадим по 10 штук, а остальные — на большой грядке». Сколько штук рассады мама хотела посадить на большой грядке?»
«Лиза рассказала своей подруге: «У меня было 70 см материи. Из 30 см я сшила своей кукле одеяльце, а из остальной материи — 2 одинаковых платьица». Сколько материи пошло на каждое платьице?»
Более полное изложение условий уместно, главным образом, в младших классах, особенно в первом, где умелое введение деталей в условие может способствовать усилению интереса детей к задаче, активизации их внимания.
б) Для того чтобы детям было легче понять, кому и при каких обстоятельствах приходится решать задачи, подобные данной, учитель после повторения условия проводит с детьми соответствующую беседу.
Приведём пример из школьной практики.
При решении в III классе задачи:
«Один каменщик укладывает 6 200 кирпичей за 5 дней, а другой — 7 350 кирпичей за 6 дней. Сколько кирпичей могут уложить оба каменщика за 25 дней?»
перед детьми поставили вопрос, кому из взрослых приходится решать такие задачи. Они ответили: инженерам, бригадирам. После этого был задан новый вопрос: зачем инженеру или бригадиру могло понадобиться вычислить, сколько кирпичей уложат оба каменщика за 25 дней. В беседе выяснили, что каменщики, возможно, были вновь приняты на работу, что каждого из них поставили на несколько дней на пробную кладку, чтобы выяснить, сколько кирпичей в среднем он может уложить за день. Затем их, может быть, поставили вместе работать, и нужно было сосчитать, сколько кирпичей они уложат за месяц вместе (за 25 рабочих дней).
в) В целях лучшего понимания детьми задачи иногда целесообразно проводить живое иллюстрирование условия, изображение его в лицах.
При решении в I классе задачи:
«2 мальчика пошли вместе на рыбалку и договорились делить пойманную рыбу поровну. Один мальчик поймал 7 рыб, а другой — 9. Сколько рыб досталось каждому мальчику?»
учитель после прочтения условия провёл с детьми беседу:
— Кто из вас когда-нибудь рыбачил (много мальчиков подняли руки)? Вот как много ребят удили рыбу! Двое из тех, кто удил рыбу, пойдут к доске. Вот вы двое встаньте у доски лицом к классу. Вы как бы будете теми мальчиками, о которых рассказывается в нашей задаче. Скажите, куда вы вместе пошли?
— Мы пошли на реку рыбачить.
— Сколько рыб ты поймал?
— Я поймал 7 рыб.
— А сколько рыб ты поймал?
— Я поймал 9 рыб.
— Как вы поделили между собою пойманную рыбу?
— Мы поделили её поровну.
— Что спрашивается в задаче?
— Сколько рыб получил каждый из нас.
В некоторых случаях полезно, чтобы дети, которые представляют действующих лиц задачи, изображали то, что делали последние. При решении задачи, в которой речь шла о собиравшей грибы девочке, вызванная ученица, держа в руках данную ей учительницей корзиночку, изображала в движениях то, о чём рассказывалось в задаче. Этот приём, как показывает опыт, активизирует внимание детей, помогает им более ясно представить содержание задачи.
Живое иллюстрирование условий применимо не только в первом, но иногда и в последующих классах. Приведём ещё пару примеров.
В III классе решали задачу:
«2 маляра вместе получили за свою работу 3 600 руб. Один из них работал 5 дней, а другой — 4 дня. Сколько рублей должен получить каждый маляр?»
При разборе задачи обнаружилось, что некоторые учащиеся не понимают способа её решения. Это выяснилось, когда дети стали предлагать неверный выбор действий для решения задачи (делить 3 600 на 5; 3 600 на 4 и т. п.). Тогда учитель в беседе с детьми выяснил, что маляры работали вместе, положим, вместе красили стены в школе. Один работал 5 дней, а другой — 4 дня. По окончании работы им выдали на двоих 3 600 руб., которые они должны были поделить между собой по количеству рабочих дней каждого. После этого учитель сказал учащимся: «Чтобы задача была вам понятнее, я вызову к доске двух учеников. Они как бы будут теми малярами, о которых рассказывается в задаче».
Затем вызванным ученикам были предложены следующие вопросы, на которые они отвечали:
— Сколько денег вы получили вместе за свою работу?
— Сколько дней ты работал?
— Сколько дней ты работал?
— Что вам нужно сосчитать?
Инсценирование условия оказалось в данном случае весьма эффективным и достаточным для осознанного решения задачи.
При решении в III классе задачи:
«Три парикмахера сообща купили 35 флаконов шампуня. Первый парикмахер дал на эту покупку 2 160 руб., второй — 1 620 руб., а третий — 2 520 руб. Сколько флаконов шампуня должен получить каждый парикмахер?»
в беседе выяснили, что парикмахеры, чтобы не ехать всем в магазин, могли послать туда одного человека закупить для них шампуни. Затем парикмахерам нужно было разделить между собой доставленные флаконы по количеству денег, которые каждый из них дал на эту покупку. После задача была инсценирована так же, как предыдущие.
Приведённые выше приёмы помогают детям яснее представить жизненное содержание задачи, обстоятельства, при которых приходится решать подобные вопросы в реальной жизни. Они содействуют активизации отношения учащихся к решению задач, как бы ставя их в положение действующих лиц, о которых рассказывается в задаче.
Само собой разумеется, эти приёмы уместны лишь тогда, когда дети без этого не понимают содержания задачи, её жизненного смысла, не могут самостоятельно решить задачу.
6) Применение наглядности
Лучшему усвоению условия задачи и, как следствие, лучшему пониманию способа её решения способствует применение наглядности. Здесь может быть использована как реальная наглядность, так и условная. Особенно уместно применение наглядности в младших классах. Применение наглядных пособий полезно при объяснении новых видов простых и составных задач и вообще во всех тех случаях, когда без этого детям трудно понять ход решения задачи.
Наглядные пособия должны подбираться с таким расчётом, чтобы они не освобождали ребёнка от мыслительной работы, а лишь облегчали ему процесс этой работы.
В качестве наглядных пособий при решении задач применим разного рода счётный материал, а также рисунки и чертежи.
Рисунки для иллюстрирования задач должны содержать, возможно, меньше деталей с тем, чтобы не отвлекать внимания от их математической стороны.
В наших учебниках встречаются следующие виды иллюстраций к задачам:
Когда вы даёте задачу для самостоятельного решения, очень полезно рекомендовать детям делать к ней рисунок или чертёж.
При частом применении наглядности во время классных и самостоятельных занятий дети, как показывает опыт, начинают прибегать к ней сами, без подсказки учителя. Этот навык чрезвычайно важен, особенно для решения нестандартных олимпиадных задач, так как они требуют хорошо развитого воображения и способности представить всю ситуацию, описанную в задаче.
Подробнее о методике обучения решению задач вы можете прочитать в пособии Г. Б. Поляка «Обучение решению задач в начальной школе».
Общая структура методики составления задач по математике
Математическое образование необходимо как часть общей культуры для всех учащихся, а поэтому изучение математики в колледже в группах, готовящих квалифицированных специалистов на базе основной школы с получением среднего образования и специальности, является необходимым. Уровень математического образования, обеспечиваемый введением новых программ, становится одним из важных элементов подготовки учащихся к общественно полезной деятельности. Задача для преподавателя математики в колледже непростая: в кратчайший срок, в отведенное по учебному плану время, а это в пределах 180 часов изучить программный материал в объеме математики 9 классов. И не только изучить, но и вооружить мобильными, ровными знаниями, которые при переходе на дальнейшую ступень учебы будут сразу востребованы.
Цель преподавания заключается в том, чтобы учащийся овладел математикой. Термин “овладел” очень растяжимый. Во-первых, учащийся должен нечто знать. Во-вторых, он должен на некоторую глубину понимать, т.е. под знанием подразумевается не только умение повторить формулировку, а мотивировать, почему так, а не иначе. В-третьих, учащийся должен уметь применять изученную им математику по профилю специальности.
Для достижения этих целей необходимо изучать теорию и решать задачи. Решая задачи, применяем теорию и тем самым познаем ее. Изучать математику, не решая задач, совершенно бесполезно. В этом вряд ли кто-то сомневается, но многие неправильно понимают роль задач. Обучение математике нельзя разделить на теорию и решение задач. Невозможно без решения задач усвоить теорию. Цель не в том, чтобы ученик решил задачу (т.е. получил ответ), а в том чтобы получил от этой задачи пользу, т.е. продвинулся на одну ступеньку по длинной лестнице овладения математикой. Цель не в ответе, а в процессе решения. Решая задачи учащийся приобретает новые знания и навыки, развивает в себе настойчивость, приобщается к математическому творчеству.
Наиболее эффективно и результативно развитие математического творчества проявляется при составлении математических задач преподавателем и учащимися, где отражается систематическое применение материалов по специальности, элементов производственного процесса. Математическое творчество прослеживается на всех этапах составления задач по математике. Целесообразно давать учащимся задания на составление задач, связанных с той или другой специальностью, чтобы при их решении нужно было использовать изучаемый на уроках материал. Например, предлагаются для групп по специальности “повар,кондитер” задачи на нахождение процентного содержания вещества, расчет наибольшего и наименьшего значения количества материала. Для групп по специальности “экономика и бухгалтерский учет” предлагаются задачи на определение величины дохода и возвращаемого займа, расчет прибыли, общей суммы дохода предприятия и т. д. После решения подобных задач учащиеся более подробно узнают об особенностях и значимости выбранной профессии, о трудностях в работе, об оплате.
Основным исходным положением, затрагивающим профессиональную направленность курса математики, является прикладная значимость знаний в практической деятельности. Прикладная направленность математических знаний означает осуществление реализации профессиональной подготовки. К основным направлениям этой работы в процессе обучения математике можно отнести следующие:
- усиление в аспекте прикладной ориентации взаимосвязи математики и других смежных дисциплин;
- сближение методов решения учебных задач с методами, применяемыми на практике;
- раскрытие своеобразия отражения математикой законов действительности;
- формирования у учащихся умений строить математические модели;
- изучение впечатлений учащихся, сложившихся в результате наблюдения трудового процесса, и учет обобщенных результатов при объяснении нового материала; превращение материалов наблюдения в средство повышения эффективности уроков математики;
- систематическое использование на уроках математики материала по специальности, элементов производительного процесса;
- ознакомление учащихся средствами математики с особенностями выбранной ими специальности;
Каждая решаемая задача имеет методическую цель. Поэтому преподаватель должен стремиться не к тому, чтобы задача была решена быстро и безошибочно или только на развитие тренировки, а к тому, чтобы она была решена творчески и чтобы из нее выжить как можно больше пользы для математического развития ученика.
Под составлением задачи по математике надо понимать не простую репродукцию задачи из сборника или учебного пособия, а самостоятельную постановку и решение проблемы учащимися, которая в общем случае решается с помощью логических умозаключений, математических действий на основе законов и методов математики.
Понимание взаимосвязи решения и составления задач позволит преподавателю добиться повышения эффективности и результативности составления и решения задач.
Последовательность операций в процессе составления задач сводится к следующим:
- обнаружение и наличие математической задачной ситуации;
- выявление и анализ элементов задачной ситуации (первичная модель задачи);
- краткая запись условия задачи с выполнением рисунка, чертежа, графика или схемы;
- вторичный анализ условия с выделением теории и законов, описывающих задачную ситуацию;
- упрощение условия, дополнение условия недостающими данными, постоянными;
- выбор методов, приемов, способов решения задачи;
- выделение звеньев (уравнений, выводов и т. д.);
- нахождение и осуществления решения в общем виде;
- анализ модели задачи, ее точная формулировка и корректирование;
- проверка и оценка условия задачи;
- исследование задачи, ее окончательная редакция, обсуждение, выделение и постановка новых задачных ситуаций;
Для составления и решения математических задач служат основой именно факты из практической деятельности человека для удовлетворения человеческих потребностей. Мировоззренческая направленность задачного подхода к математическому образованию требует:
- целостного видения предмета математики на каждом этапе с углублением картины математической реальности от этапа к этапу;
- “соразмерность” человеку, его потребностям, эмоциональной и интеллектуальной сферам;
- отражение мировоззренческих идей и выводов;
Можно выделить следующие виды заданий на составление задач:
- на установление аналогичных задач;
- на отыскание, составление подзадач;
- на дополнение данных по неполной ситуации;
- с другими численными данными;
- по схеме условия в общем виде;
- на отыскание, составление обратных задач;
- на отбор данных по избыточной ситуации;
- на постановку вопроса к условию;
- по схеме-решения в общем виде;
Предлагаемые учащимся преподавателем задания на составление по ситуациям в учебном материале:
- по рисункам учебника, пособия, задачника и т.д.;
- по тексту учебника, пособия;
- по материалам по профилю специальности;
- итоговое по теме, по материалам экзаменационных билетов;
- по графикам и схемам учебника, пособия задачника;
- по данной задачной ситуации;
В обучении и решении математических задач в среднем специальном заведении схемы “преподаватель-ученик”, “преподаватель-задача”, “ученик-задача” выступают в качестве составных взаимосвязанных и взаимообусловленных элементов современной концепции обучения математики: преподавания, учения и содержания изучаемого. Выделенные схемы включают в себя как прямые, так и обратные связи. Традиционное обучение решению математических задач в колледже предусматривает целенаправленное воздействие преподавателя на ученика непосредственно (“преподаватель-ученик”) или через задачу (“преподаватель–задача–ученик”). Составление математических задач позволяет осуществить эффективные и результативные обратные связи не только на уровне схемы, но и в рамках общей схемы “преподаватель-ученик-задача — преподаватель”. При этом по заданию преподавателя учащийся составляет задачу и предъявляет ее снова преподавателю. Так, в идеальном случае, ученик по требованию преподавателя составляет и решает задачу под его контролем. Но, самостоятельное, творческое составление математических задач достигается постепенным овладением всего процесса составления в ходе выполнения специальных заданий. Знания о задачах, приемах их постановки, формулировки и решения, актуализированными заданиями на составление задач, представляют собой содержание обучения составлению. Это содержание, вместе с преподаванием и учением, определяют структуру обучения составлению математических задач. Преподаватель ставит задание перед учащимися с требованием составить (полностью или частично) и решить задачу; ученик составляет и решает задачу, а саму задачу и ее решение предоставляет преподавателю для проверки с возможным последующим включением в учебно-воспитательный процесс по традиционной схеме.
В перспективе, при овладении учащимися достаточно высокого уровня в составлении математических задач, по требованию преподавателя ученик сам выбирает задачную ситуацию, составляет, решает ее, а преподаватель проверяет и осуществляет отбор для дальнейшего использования.
Математическое образование необходимо как
часть общей культуры для всех учащихся, а поэтому
изучение математики в колледже в группах,
готовящих квалифицированных бухгалтеров,
товароведов на базе основной школы с получением
среднего образования и специальности, является
необходимым. Уровень математического
образования, обеспечиваемый введением новых
программ, становится одним из важных элементов
подготовки учащихся, к общественно полезной
деятельности. Задача для преподавателя
математики в колледже непростая: в кратчайший
срок, за один год, в отведенное по учебному плану
время, а это в пределах 180 часов изучить
программный материал в объеме математики 10-11
классов. И не только изучить, но и вооружить
мобильными, ровными знаниями, которые при
переходе на дальнейшую ступень учебы будут сразу
востребованы при изучении высшей математики в
технологических и бухгалтерских группах.
Цель преподавания заключается в том, чтобы
учащийся овладел математикой. Термин “овладел”
очень растяжимый. Во-первых, учащийся должен
нечто знать. Во-вторых, он должен на некоторую
глубину понимать, т.е. под знанием
подразумевается не только умение повторить
формулировку, а мотивировать, почему так, а не
иначе. В-третьих, учащийся должен уметь применять
изученную им математику по профилю
специальности.
Для достижения этих целей необходимо изучать
теорию и решать задачи. Решая задачи, применяем
теорию и тем самым познаем ее. Изучать
математику, не решая задач, совершенно
бесполезно. В этом вряд ли кто-то сомневается, но
многие неправильно понимают роль задач. Обучение
математике нельзя разделить на теорию и решение
задач. Невозможно без решения задач усвоить
теорию. Цель не в том, чтобы ученик решил задачу
(т.е. получил ответ), а в том чтобы получил от этой
задачи пользу, т.е. продвинулся на одну ступеньку
по длинной лестнице овладения математикой. Цель
не в ответе, а в процессе решения. Решая задачи
учащийся приобретает новые знания и навыки,
развивает в себе настойчивость, приобщается к
математическому творчеству.
Наиболее эффективно и результативно развитие
математического творчества проявляется при
составлении математических задач
преподавателем и учащимися, где отражается
систематическое применение материалов по
специальности, элементов производственного
процесса. Математическое творчество
прослеживается на всех этапах составления задач
по математике. Целесообразно давать учащимся
задания на составление задач, связанных с той или
другой специальностью, чтобы при их решении
нужно было использовать изучаемый на уроках
материал. Например, предлагаются для групп по
специальности “товароведение” задачи на
нахождение процентного содержания вещества,
расчет наибольшего и наименьшего значения
количества материала. Для групп по специальности
“экономика и бухгалтерский учет” предлагаются
задачи на определение величины дохода и
возвращаемого займа, расчет прибыли, общей суммы
дохода предприятия и т. д. После решения подобных
задач учащиеся более подробно узнают об
особенностях и значимости выбранной профессии, о
трудностях в работе, об оплате.
Основным исходным положением, затрагивающим
профессиональную направленность курса
математики, является прикладная значимость
знаний в практической деятельности. Прикладная
направленность математических знаний означает
осуществление реализации профессиональной
подготовки. К основным направлениям этой работы
в процессе обучения математике можно отнести
следующие:
- усиление в аспекте прикладной ориентации
взаимосвязи математики и других смежных
дисциплин; - сближение методов решения учебных задач с
методами, применяемыми на практике; - раскрытие своеобразия отражения математикой
законов действительности; - формирования у учащихся умений строить
математические модели; - изучение впечатлений учащихся, сложившихся в
результате наблюдения трудового процесса, и учет
обобщенных результатов при объяснении нового
материала; превращение материалов наблюдения в
средство повышения эффективности уроков
математики; - систематическое использование на уроках
математики материала по специальности,
элементов производительного процесса; - ознакомление учащихся средствами математики с
особенностями выбранной ими специальности;
Каждая решаемая задача имеет методическую
цель. Поэтому преподаватель должен стремиться не
к тому, чтобы задача была решена быстро и
безошибочно или только на развитие тренировки, а
к тому, чтобы она была решена творчески и чтобы из
нее выжить как можно больше пользы для
математического развития ученика.
Под составлением задачи по математике надо
понимать не простую репродукцию задачи из
сборника или учебного пособия, а самостоятельную
постановку и решение проблемы учащимися, которая
в общем случае решается с помощью логических
умозаключений, математических действий на
основе законов и методов математики.
Понимание взаимосвязи решения и составления
задач позволит преподавателю добиться повышения
эффективности и результативности составления и
решения задач.
Последовательность операций в процессе
составления задач сводится к следующим:
- обнаружение и наличие математической задачной
ситуации; - выявление и анализ элементов задачной ситуации
(первичная модель задачи); - краткая запись условия задачи с выполнением
рисунка, чертежа, графика или схемы; - вторичный анализ условия с выделением теории и
законов, описывающих задачную ситуацию; - упрощение условия, дополнение условия
недостающими данными, постоянными; - выбор методов, приемов, способов решения задачи;
- выделение звеньев (уравнений, выводов и т. д.);
- нахождение и осуществления решения в общем
виде; - анализ модели задачи, ее точная формулировка и
корректирование; - проверка и оценка условия задачи;
- исследование задачи, ее окончательная редакция,
обсуждение, выделение и постановка новых
задачных ситуаций;
Для составления и решения математических задач
служат основой именно факты из практической
деятельности человека для удовлетворения
человеческих потребностей. Мировоззренческая
направленность задачного подхода к
математическому образованию требует:
- целостного видения предмета математики на
каждом этапе с углублением картины
математической реальности от этапа к этапу; - “соразмерность” человеку, его потребностям,
эмоциональной и интеллектуальной сферам; - отражение мировоззренческих идей и выводов;
Можно выделить следующие виды заданий на
составление задач:
- на установление аналогичных задач;
- на отыскание, составление подзадач;
- на дополнение данных по неполной ситуации;
- с другими численными данными;
- по схеме условия в общем виде;
- на отыскание, составление обратных задач;
- на отбор данных по избыточной ситуации;
- на постановку вопроса к условию;
- по схеме-решения в общем виде;
Предлагаемые учащимся преподавателем задания
на составление по ситуациям в учебном материале:
- по рисункам учебника, пособия, задачника и т.д.;
- по тексту учебника, пособия;
- по материалам по профилю специальности;
- итоговое по теме, по материалам экзаменационных
билетов; - по графикам и схемам учебника, пособия,
задачника; - по данной задачной ситуации;
В обучении и решении математических задач в
среднем специальном заведении схемы
“преподаватель-ученик”,
“преподаватель-задача”, “ученик-задача”
выступают в качестве составных взаимосвязанных
и взаимообусловленных элементов современной
концепции обучения математики: преподавания,
учения и содержания изучаемого. Выделенные схемы
включают в себя как прямые, так и обратные связи.
Традиционное обучение решению математических
задач в колледже предусматривает
целенаправленное воздействие преподавателя на
ученика непосредственно
(“преподаватель-ученик”) или через задачу
(“преподаватель–задача–ученик”). Составление
математических задач позволяет осуществить
эффективные и результативные обратные связи не
только на уровне схемы, но и в рамках общей схемы
“преподаватель-ученик-задача — преподаватель”.
При этом по заданию преподавателя учащийся
составляет задачу и предъявляет ее снова
преподавателю. Так, в идеальном случае, ученик по
требованию преподавателя составляет и решает
задачу под его контролем. Но, самостоятельное,
творческое составление математических задач
достигается постепенным овладением всего
процесса составления в ходе выполнения
специальных заданий. Знания о задачах, приемах их
постановки, формулировки и решения,
актуализированными заданиями на составление
задач, представляют собой содержание обучения
составлению. Это содержание, вместе с
преподаванием и учением, определяют структуру
обучения составлению математических задач.
Преподаватель ставит задание перед учащимися с
требованием составить (полностью или частично) и
решить задачу; ученик составляет и решает задачу,
а саму задачу и ее решение предоставляет
преподавателю для проверки с возможным
последующим включением в учебно-воспитательный
процесс по традиционной схеме.
В перспективе, при овладении учащимися
достаточно высокого уровня в составлении
математических задач, по требованию
преподавателя ученик сам выбирает задачную
ситуацию, составляет, решает ее, а преподаватель
проверяет и осуществляет отбор для дальнейшего
использования.