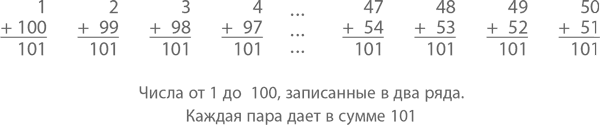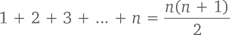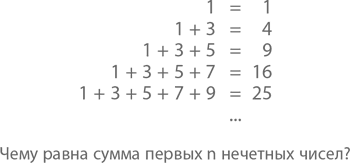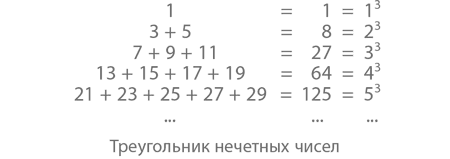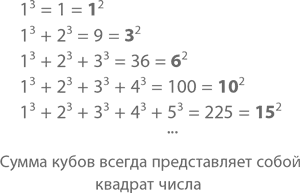Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом.
В чем смысл игры?
Игры такого рода развивают умение выделять закономерности в последовательном ряде элементов. Для этого сначала нужно внимательно рассмотреть задание: сравнить соседние объекты и попробовать определить правило закономерности.
Решить задачу можно с помощью простого счета, обобщения по какому-либо признаку или простого анализа рисунка, текста или схемы.
Как научить ребенка находить закономерности?
Маленьким детям, для решения задач на поиски закономерностей, понадобится только смекалка и воображение. Достаточно лишь объяснить, как можно установить закономерность между звеньями ряда. Если задачу решить не получается, то вместо прямых подсказок следует задать дополнительные вопросы, не раскрывая решение задачи полностью.
В любом случае, пользы будет больше, если ребенок решит, хотя бы одну задачу самостоятельно, нежели взрослый просто расскажет, как её решать.
Рассмотрим способы, которые помогут ребенку понять закономерности и последовательности в заданиях.
Инструкция по решению числовых последовательностей:
- Найти разницу между двумя рядом стоящими числами
- Определить алгоритм построения последовательности
- Применить алгоритм к следующей паре чисел
- Использовать алгоритм для определения следующего числа в ряду
Инструкция по нахождению закономерностей в заданиях с геометрическими фигурами:
- Рассмотреть фигуры и разделить их, на повторяющиеся группы
- Определить какой элемент изменился в группе
- Решить, какая именно фигура отсутствует или является лишней.
Задания для 1 класса
Задание 1
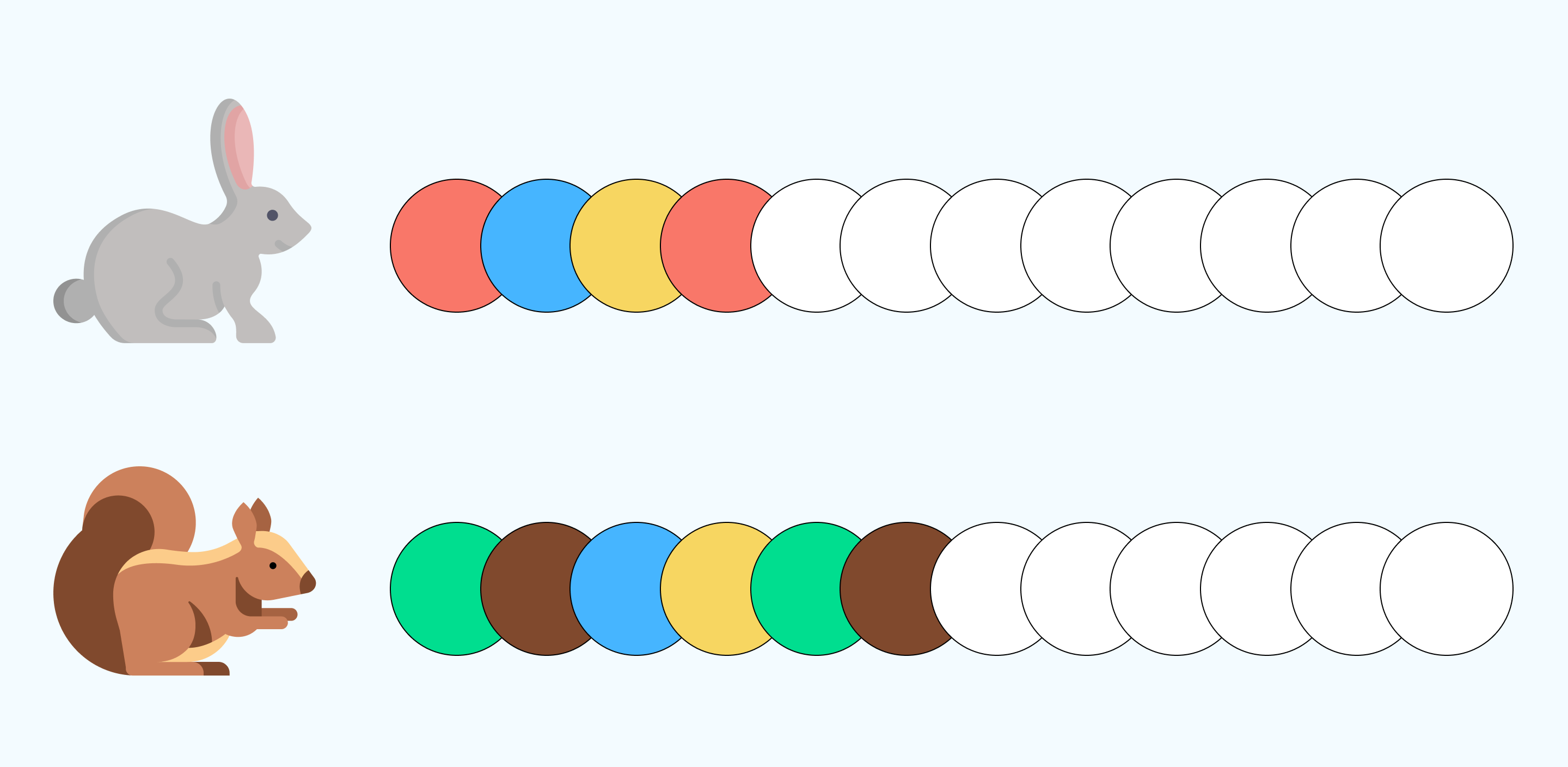
Раскрась дорожки для зайчика и белочки, сохраняя закономерность.
Решение: Белочка и зайчик бегут по разным дорожкам. У каждой дорожки есть своя закономерность. У зайчика повторяется 3 цвета на дорожке: красный, голубой, жёлтый, а у белочки 4: зеленый, коричневый, фиолетовый, жёлтый.
В этом задании можно обратить внимание на то, что обе дорожки состоят из 12 кругов. Но количество повторяющихся цветов разное.
Задание 2
Найди закономерность в ряду геометрических фигур.
Решение: В этом ряду нужно обратить внимание на размеры фигур, а не на цвет и форму. Сначала идет одна большая фигура, а за ней две маленькие, далее они повторяются.
Задание 3
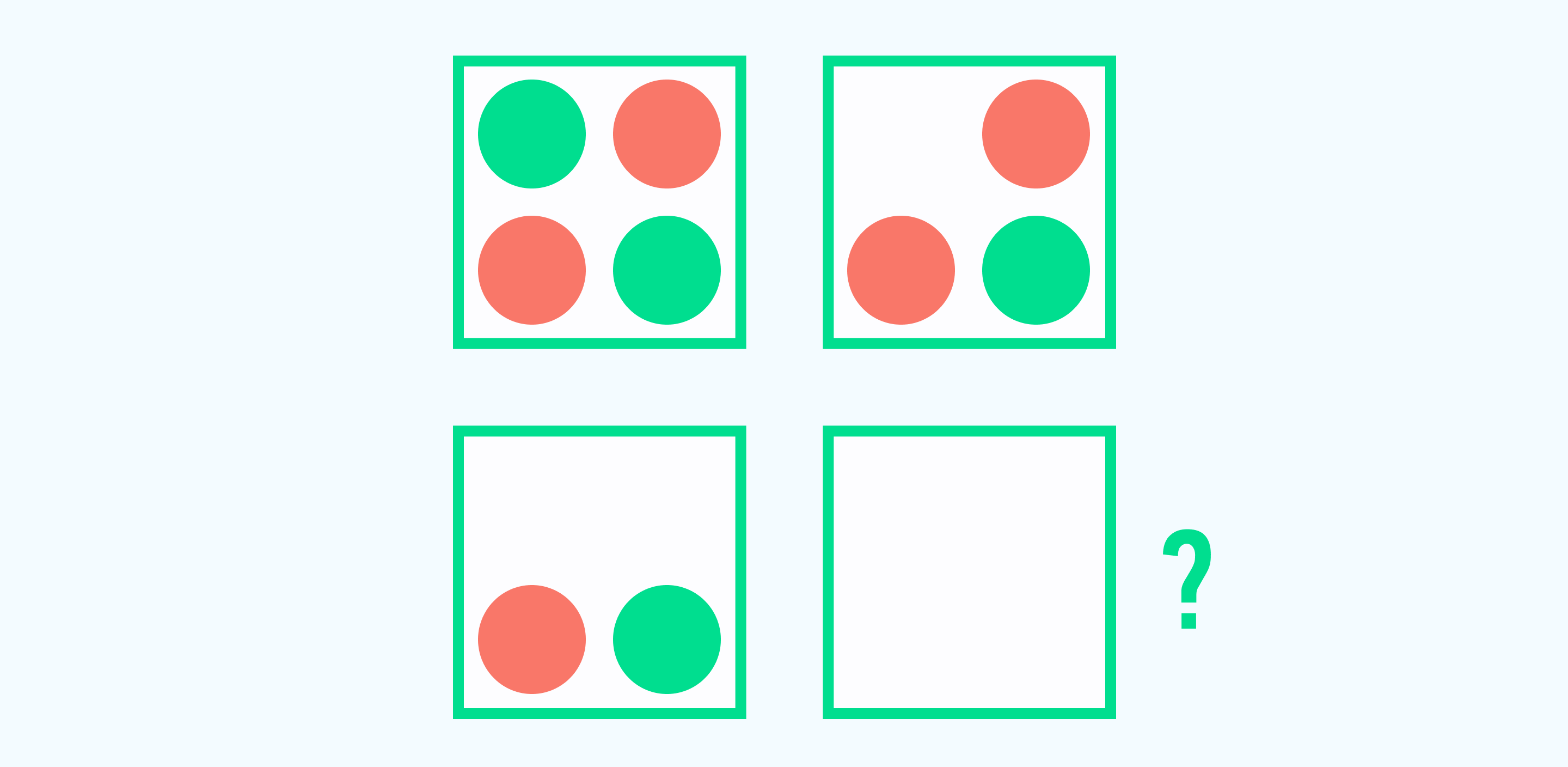
Нарисуйте в четвертом квадрате правильный ответ.
Решение: Рассмотрев внимательно рисунок, мы увидим, что круги в квадратах исчезают по одному, против часовой стрелки. В этой задаче имеет значение только расположение кругов квадрате. Таким образом, в последний квадрат мы должны нарисовать один синий круг в нижнем левом углу.
Задание 4
Соблюдая закономерность, продолжи ряд чисел до 10. Сформулируй правило, которое действует в этой закономерности. Используя это правило, придумай свою закономерность.
- 2, 4, 6,…
Решение: В этом ряду каждая цифра увеличивается на 2 относительно предыдущей – мы вычислили правило для данной закономерности. Значит, чтобы продолжить ряд, мы прибавим к каждой следующей цифре по 2. Ответ будет выглядеть так: 2,4,6,8,10.
Чтобы придумать подобную закономерность, нужно использовать сформулированное выше правило: например, 1,3,5,7,9.
Задания для 2 класса
Задание 1
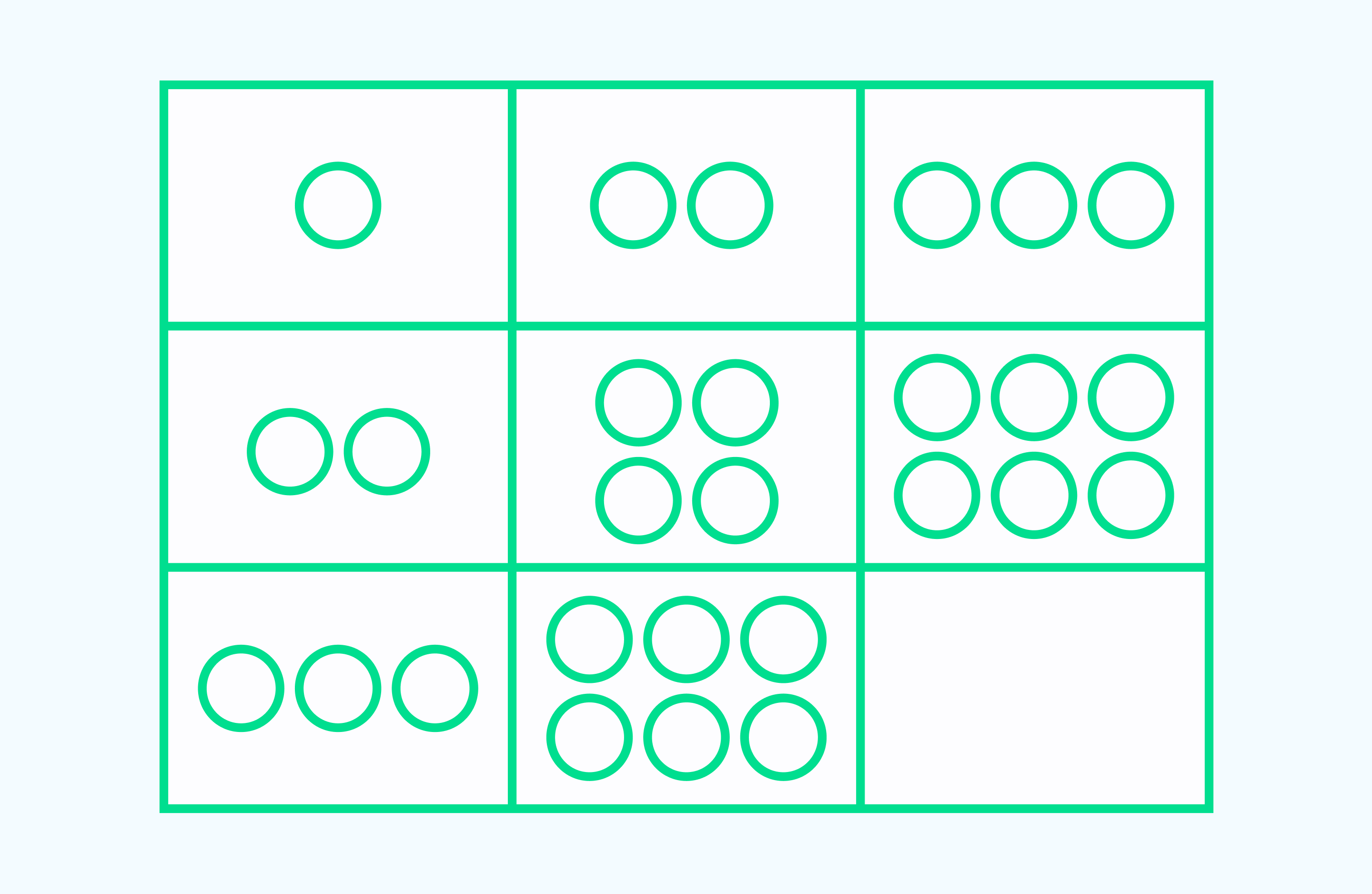
Найди закономерность и в пустом квадрате нарисуй нужное количество кругов.
Решение: В таблице в первом горизонтальном ряду количество кругов увеличивается на 1. Во втором ряду увеличивается на 2. Таким образом, можно предположить, что в третьем ряду количество кругов будет увеличиваться на 3 и ответ будет 9. Можно заметить, что и в вертикальных рядах эта закономерность повторяется.
Задание 2
В цепочке чисел найди закономерность и вставь пропущенные числа
- 95, 90, 85, 80, 75,_, 65,_, _,50
Решение: В цепочке чисел можно выделить пары: 95 -90, 85 – 80 и далее. Каждый раз, в паре, число уменьшается на 5. Значит, после 75 запишем 70, после 65 — 60, а затем 55 .
Задание 3
Найди закономерность и продолжи последовательность.
- 2, 3, 5, 8, …, …, …, …
Решение: В этой цепочке чисел к каждому последующему числу прибавляется предыдущее. 2+3=5+3=8+5=13+8=21+13=34 и далее.
Задание 4
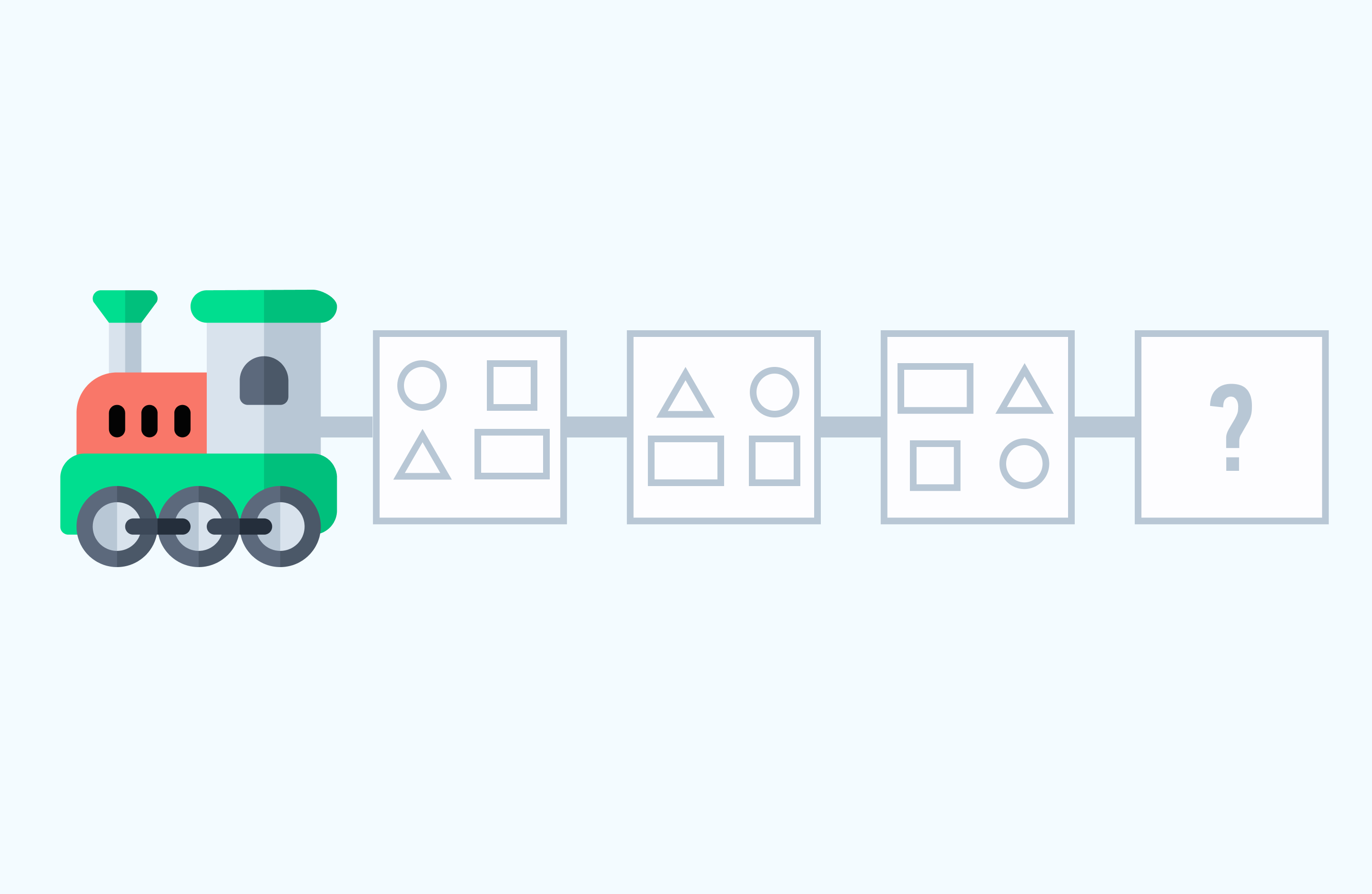
В поезде едут геометрические фигуры. Нарисуйте фигуры, в четвёртом вагоне, соблюдая закономерность их расположения.
Решение: В поезде едут геометрические фигуры: квадрат, треугольник, прямоугольник и круг. В трёх вагонах все места заняты фигурами, в определённом порядке. Расставим их и в четвертом вагоне: Круг в нём будет располагаться в нижнем левом углу, квадрат в верхнем левом, треугольник поедет в правом нижнем, а прямоугольник – в левом верхнем углу.
Задания для 3 класса
Задание 1
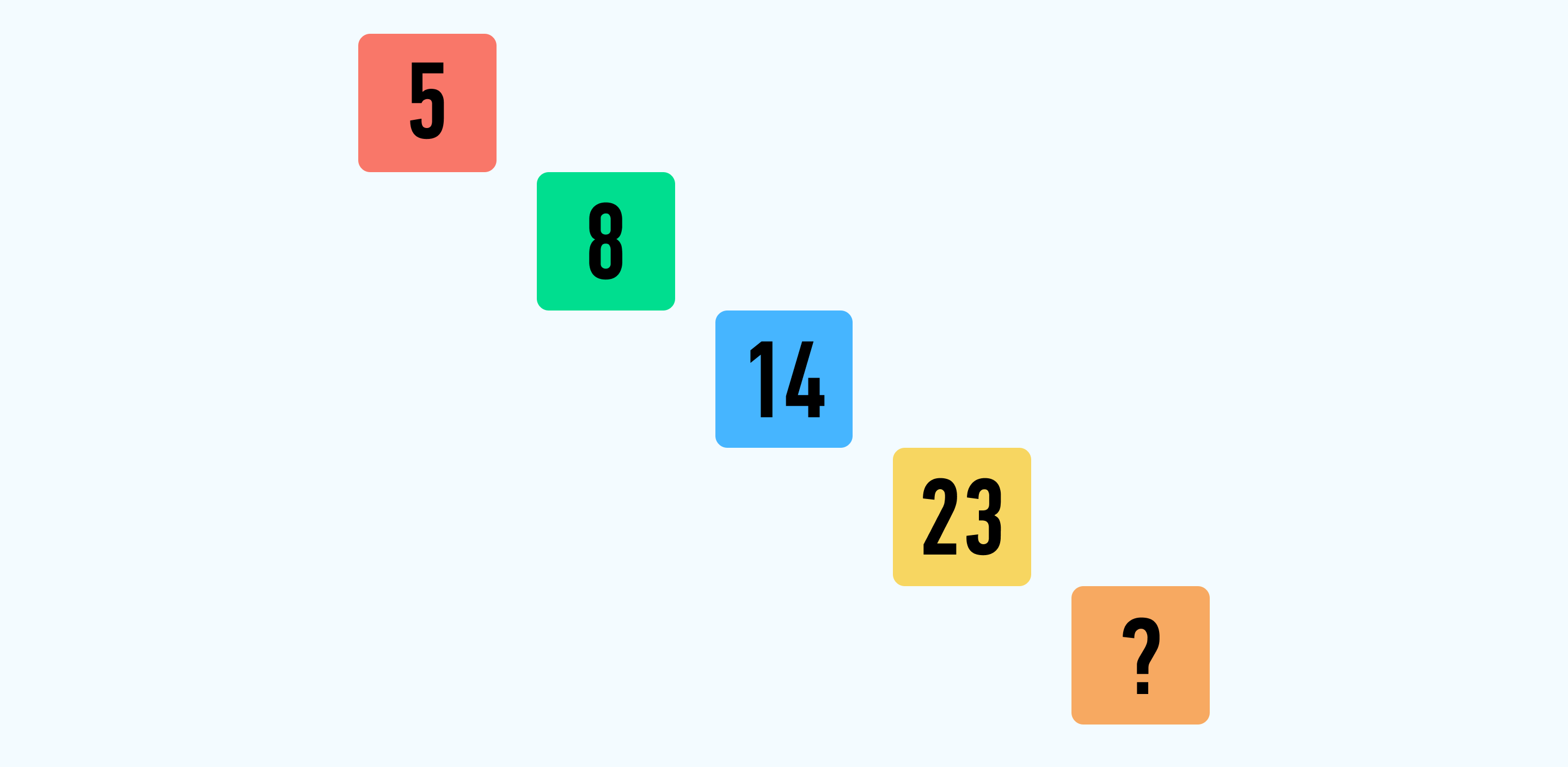
Рассмотрите картинку и найдите закономерность в задаче.
Решение: В таблице мы увидим такую закономерность:
8-5=3, то есть число увеличилось на 3; далее 14-8=6, соответственно, число увеличилось на 6. В последней связке 23-14=9 число увеличилось на 9. Мы делаем вывод, что каждое следующее число увеличивается на предыдущее значение+3. Таким образом, следующее число увеличивается на 9+3=12. 23 + 12 = 35. Ответ: 35.
Задание 2
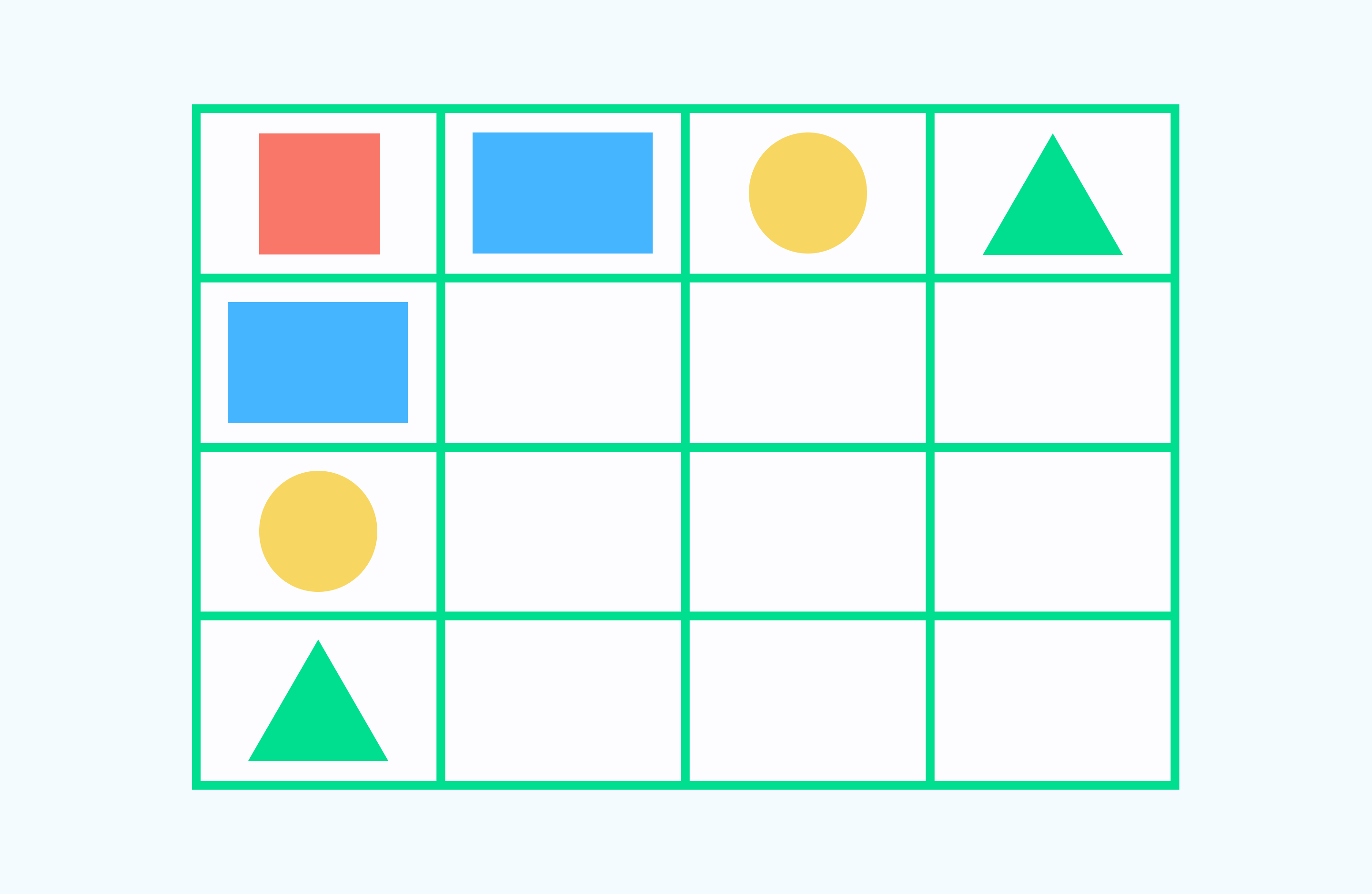
В пустые клетки вставьте геометрические фигуры, сохраняя закономерность.
Решение: Чтобы выполнить задание, нужно фигуры расставить по порядку, друг за другом, соблюдая последовательность. Значит, после прямоугольника стоит круг, треугольник и квадрат и т. д.
Задание 3
Найди закономерность и продолжи ряды:
- 12, 23, 34, 45, 56…
- 13, 24, 35, 46…
Решение: В этой задаче каждая последующая цифра увеличивается так: десятки на один десяток и единицы на одну единицу. 12=10+2, 23=20+3, 34=30+5 и т. д.
Задание 4
Продолжи ряд, сохраняя закономерность.
- 12, 36, 13, 39, 14, 42, 15,…
Решение: В числовой цепочке выделяем пары чисел. Первая пара:12 и 36. 12×3=36, далее по порядку: 13×3=39. Умножая каждый раз на 3, цифры, следующие по порядку (12,13,14,15…), мы продолжаем последовательный ряд. Ответ: 45.
Задания для 4 класса
Задание 1
Найди ошибку в бусах.
Решение: В первых бусах повторяются квадрат и круг, значит лишний шестой круг. Во вторых бусах, повторяется закономерность: круг, два треугольника, два круга, лишний – восьмой, по счету, круг.
Задание 2
Определите закономерность. Найдите лишнее число.
- 8, 16, 20, 24, 32, 40, 48, 56, 64, 72.
Решение: В этом числовом ряду таблица умножения на 8. Ответ: число 20 – лишнее.
Задание 3
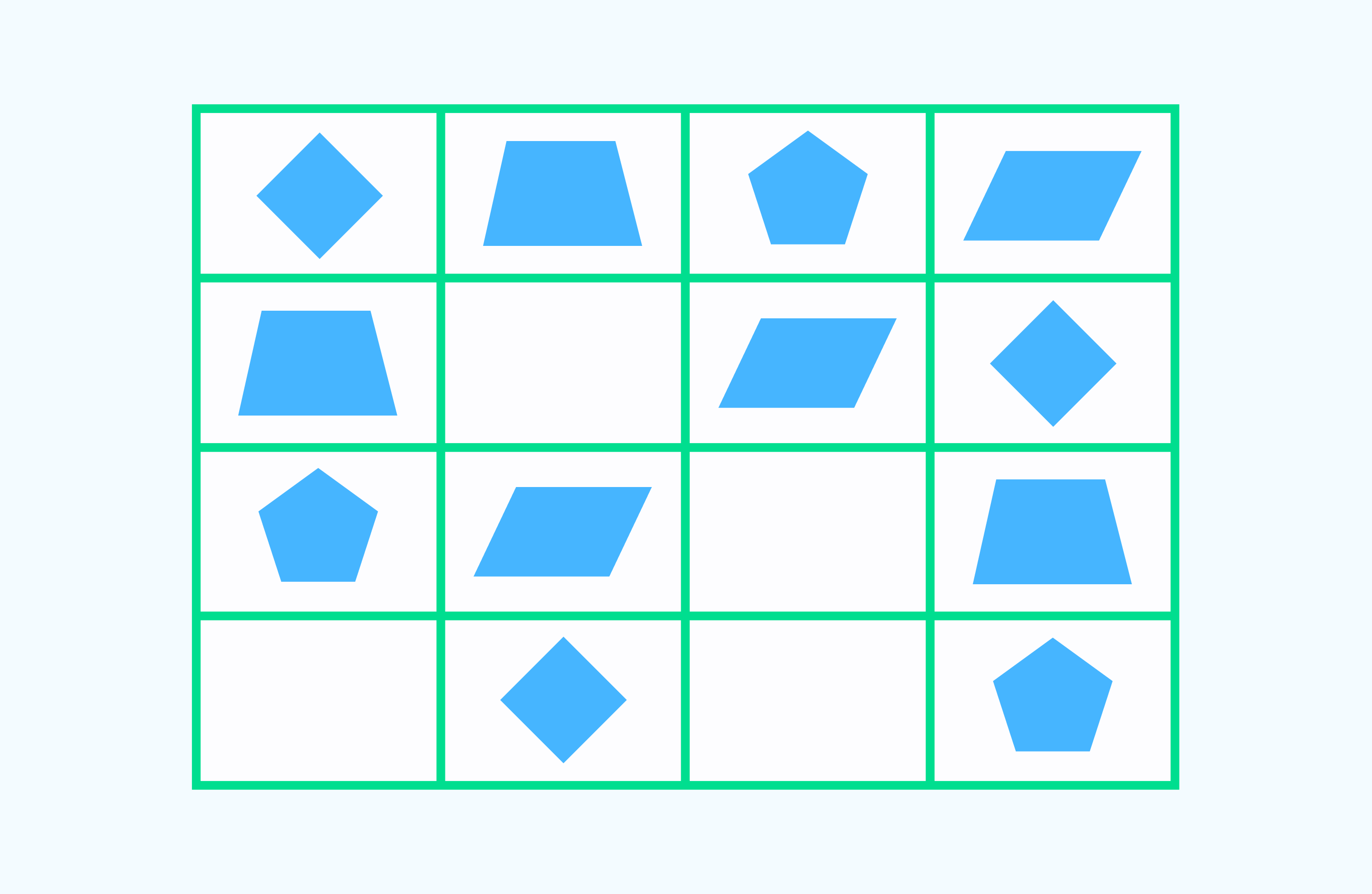
Каких геометрических фигур не хватает? Дорисуй их, соблюдая закономерность в таблице:
Решение: Определить, какой элемент изменился во втором и последующих рядах, можно, выделив последовательность: ромб, трапеция, шестиугольник и параллелограмм. Во втором ряду недостает шестиугольника, в третьем — ромба, в четвертом – параллелограмма и трапеции.


Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее

В одном из предыдущих уроков ты узнал о свойствах предметов и как они связаны с математикой. На этом уроке ты познакомишься с понятием — математическая закономерность.
Закономерность — постоянно повторяющаяся взаимосвязь явлений, действий или свойств предметов.
Закономерности, как и свойства предметов связаны с математикой и с логикой. Зная закономерность, ты точно можешь знать, что будет дальше. После четверга точно будет пятница, после 10 часов утра будет 11 часов утра. Последовательность действий, явлений, свойств или событий в закономерности всегда определена, то есть мы точно знаем что будет дальше.
Типы закономерностей
Существует несколько типов закономерностей: убывающие, возрастающие, циклические и сложные закономерности. Давайте познакомимся с каждой подробнее.
Возрастающая закономерность
Закономерность, у которой числовое свойство увеличивается согласно некоторому закону или формуле, называется возрастающей.
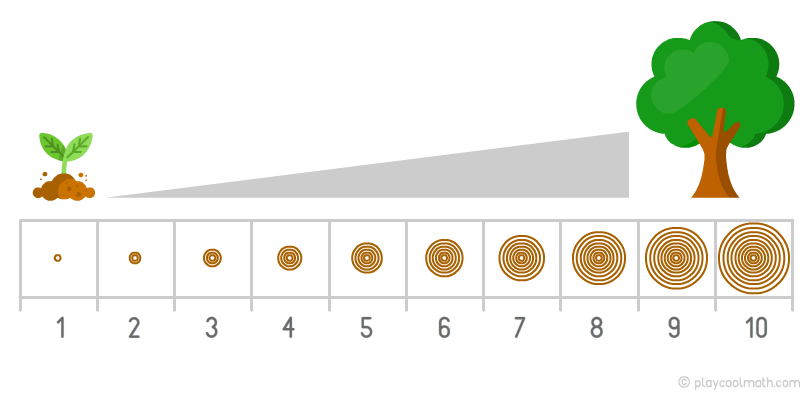
Например, дерево растет и на его стволе каждый год добавляется одно новое кольцо. Этот процесс называется простой возрастающей закономерностью. В этой закономерности легко вычислить, сколько колец будет через 2 года или через 10 лет. Количество колец в стволе соответствует возрасту дерева.
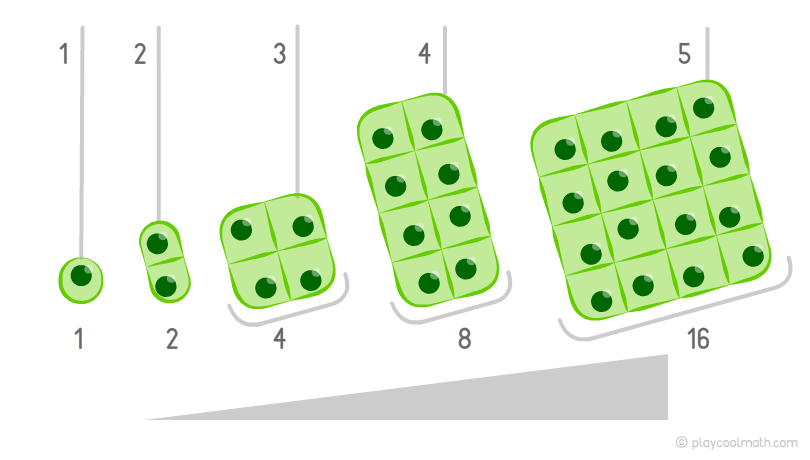
Приведем пример возрастающей закономерности, которая сложнее чем в примере с деревом. Представьте одноклеточный организм, который каждую минуту делится на две клетки. На картинке хорошо видно, что в первую минуту мы видим 1 клетку, во вторую — уже 2 клетки, а затем 4 клетки, 8, 16. Каждую минуту количество увеличивается в 2 раза. Зная предыдущее количество, можно узнать, сколько будет клеток в следующую минуту. Этот процесс называется тоже возрастающей закономерностью. Для настоящих математиков будет несложно установить формулу увеличения закономерности для этого примера. Эта задача для тебя еще сложная, так как ты только начали изучать математику. Главное сейчас чтобы ты понять, что такое закономерность.
Убывающая закономерность
Закономерность, у которой числовое свойство уменьшается согласно некоторому закону или формуле, называется убывающей.
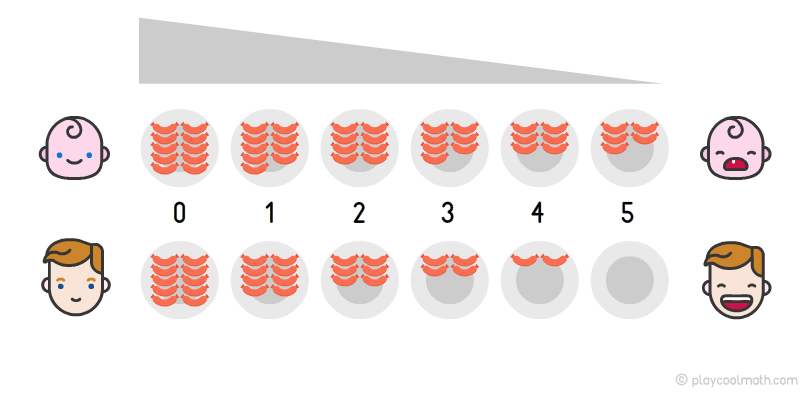
Представьте соревнования по поеданию сосисок на скорость, в которых участвуют два участника. У каждого по 10 сосисок на тарелке (это столько, сколько у тебя пальцев на руках). Первый съедает одну сосиску за минуту, а второй съедает 2 сосиски за минуту. Ясно, что второй участник соревнований победит, так как он съедает больше сосисок за минуту, чем первый участник. Но нам важно увидеть закономерность. На рисунке мы можем увидеть, как в каждой тарелке уменьшается количество сосисок. Этот процесс называется убывающей закономерностью. Второй участник съел всю тарелку сосисок за пять минут и победил!
Циклическая закономерность
Закономерность, которая повторяется каждый раз, называется циклической. Полный круг в циклической закономерности называется циклом закономерности.
Ты точно знаешь закономерность такого типа — это смена времен года. Весна-Лето-Осень-Зима и потом происходит повторение.
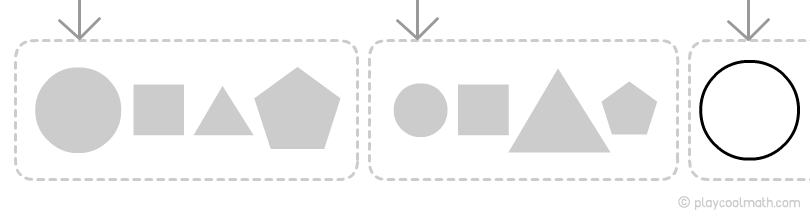
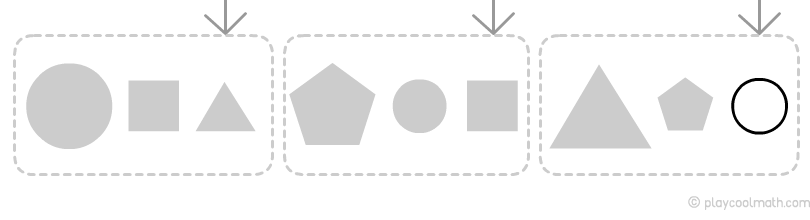
Рассмотрим пример с предметами разной формы. На рисунке ты видишь цепочку из разного количества предметов. Попробуй найти закономерность на рисунке ниже. Продолжи цепочку.
Предметы повторяются через каждые три ячейки. Зная закономерность, мы можем предположить, какие предметы будут дальше. За последним звеном будет треугольник, затем круг, далее квадрат.
Сложные закономерности
Закономерности, которые состоят из нескольких видов закономерностей или имеют несколько свойств, называются сложными.
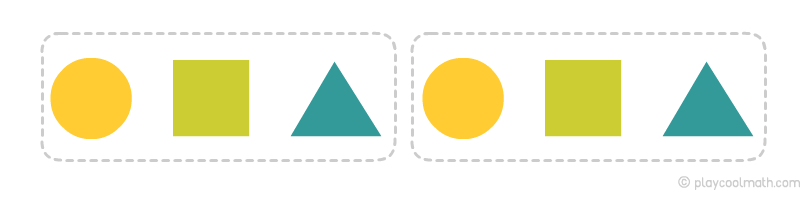
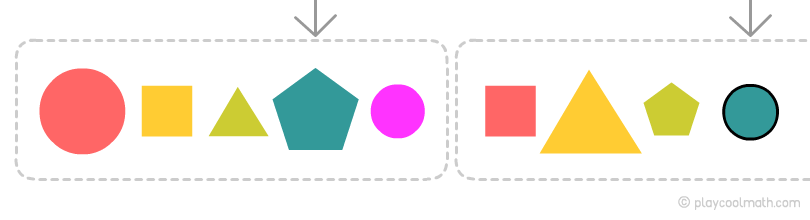
Рассмотрим пример закономерностей на одной и той же цепочке, но будем искать закономерности в зависимости от свойства звеньев. Попробуй найти следующее звено в примере ниже.
Закономерность по форме
Видим, как чередуются звенья цепочки. Точно знаем, что по форме следующим будет круг, обозначим его как большой круг
Закономерность по размеру
Видим, как чередуются звенья цепочки: большая и затем две маленькие фигуры, то есть следующей будет маленькая фигура.
Закономерность по цвету
Получилась самая длинная закономерность в цепочке, выделим ее и определим, какой будет следующий цвет.
Как видишь, закономерность зависит от свойств элементов цепочки. Для одной и той же цепочки мы нашли различные закономерности в зависимости от свойства. Объединим полученные результаты и узнаем, какое звено будут следующим.
Алгоритм поиска закономерностей
Давайте еще раз повторим все шаги для выявления закономерностей.
- Определяем количество свойств цепочки;
- Определяем закономерность для каждого свойства;
- Сопоставляем закономерности для определения всех свойств следующего звена в цепочке.
Поиск закономерностей — это очень хороший навык для юного математика. В будущем, когда ты будешь изучать цифры, тебе обязательно этот навык пригодится. Мы создали набор тестов, где ты сможешь потренироваться в поиске закономерностей. Попробуй пройти все тесты с хорошим результатом и двигайся дальше в изучении математики.
Числовые закономерности
Изучение математики всегда начинается с чисел. Сначала мы учимся выражать количество с помощью букв, цифр или самих предметов. А потом долгие и долгие годы складываем, вычитаем, умножаем, делим и решаем разные арифметические задачи. И за всей этой рутиной часто не видим магию чисел, способную развлечь и удивить любого, кто решится всего лишь заглянуть чуть глубже.
Вот, например, одна хитрость, с которой еще в детстве столкнулся немецкий математик Карл Фридрих Гаусс[2]. Как-то раз на уроке математики учитель попросил класс сложить между собой всей числа от 1 до 100. Вряд ли он хотел развлечь учеников – скорее, отвлечь: заставить заняться чем-нибудь нудным и требующим полного сосредоточения, а самому спокойно сделать другую работу. Представьте себе его удивление, когда через несколько секунд Гаусс вышел к доске и написал ответ – 5050. Хотите знать, как он это сделал? Он просто представил все эти числа в виде двух рядов: верхний – от 1 до 50, нижний – от 51 до 100, причем в нижнем ряду числа шли в обратном порядке, вот так:
Гаусс заметил, что сумма чисел в каждом из 50 столбцов одинаковая – 101, а значит, для того, чтобы получить искомый результат, нужно всего лишь умножить 101 на 50. Так у него и получилось 5050.
Собственно говоря, благодаря такой вот способности – не быстро считать в уме, но заставлять числа плясать под свою дудку – Гаусс и стал одним из величайших математиков XIX столетия. В этой главе мы как раз и поговорим об интересных числовых закономерностях и, конечно, увидим танец чисел. Одни из этих примеров полезны тем, что развивают способности умственного счета, другие – просто красивы.
Только что мы последовали путем гауссовой логики, чтобы получить сумму первой сотни простых чисел. Но что, если нам нужна сумма 17 из них? Или тысячи? Миллиона? Логика Гаусса позволяет подсчитывать сумму первых n чисел, где n – любое нужное вам количество! Некоторым людям легче разобраться с математическими абстракциями, если они могут их визуализировать. К примеру, числа 1, 3, 6, 10 и 15 иногда называют треугольными, потому что, заменив их соответствующим количеством кружков, можно легко сложить треугольники, вроде того, что изображен чуть ниже (конечно, один кружок треугольником можно назвать с очень большой натяжкой, но число 1, несмотря на это, все же считается треугольным). Согласно определению, треугольное число n равняется 1 + 2 + 3 +… + n.
Посмотрите, что произойдет, если мы расположим два треугольника основаниями друг к другу, вот так:
У нас получился прямоугольник из 5 рядов и 6 столбцов – всего 30 кружков. Значит, в каждом из двух наших треугольников была половина общего их количества, то есть по 15 кружков. Мы, это, разумеется, уже знаем, но давайте применим этот же принцип к двум прямоугольникам, количество рядов в которых равно n. Точно так же составим из них прямоугольник с n рядов и n + 1 столбцов. Кружков в нем будет n ? (n + 1) – ну или в более привычной записи – n(n + 1). В результате мы получим формулу, которая позволит нам подсчитывать сумму первых n чисел:
Видите, закономерность, которую мы использовали для сложения первой сотни чисел, вполне применима к любому подобному ряду, сколько бы членов в него ни входило. И если вдруг нам понадобится сложить между собой все числа от 1 до 1 000 000, сделать это можно будет всего за два шага: перемножив 1 000 000 и 1 000 001 и разделив результат пополам.
Разобравшись в одной формуле, вы с легкостью разберетесь и в остальных. Например, если мы удвоим обе части последнего уравнения, получится формула суммы первых n четных чисел:
2 + 4 + 6 +… + 2n = n(n + 1)
А как насчет суммы первых нечетных, спр?сите вы? Давайте посмотрим, что говорят нам числа.
То, что справа – квадраты целых чисел. 1 ? 1; 2 ? 2; 3 ? 3 и т. д. Сложно не заметить следующую закономерность: сумма первых n нечетных чисел равняется n ? n. Или n?. Но что, если это просто совпадение? Чуть позже, в главе 6, мы с вами увидим несколько путей развития этой формулы, но уже и сейчас понятно, что у такой простой закономерности должно быть не менее простое объяснение. Самое мое любимое – методом подсчета кружков: он наглядно показывает, почему числа вроде 25 называются квадратами. Но почему вдруг мы должны складывать первые 5 нечетных чисел с 5?? А просто посмотрите на квадрат размером 5 на 5:
Кружков в нем 5 ? 5 = 25, это очевидно. Но давайте подсчитаем иначе. Начнем с одинокого кружка в левом верхнем углу. Его окружают 3 кружка, потом 5, потом 7 и, наконец, 9. Следовательно,
1 + 3 + 5 + 7 + 9 = 25
И возьми мы квадрат со сторонами n на n, его можно будет легко разбить на n-ное количество L-образных секторов, в каждом из которых будет соответственно 1, 3, 5…., (2n – 1) кружков. Это и есть формула суммы первых n нечетных чисел
1 + 3 + 5 + … + (2n – 1) = n?
Отступление
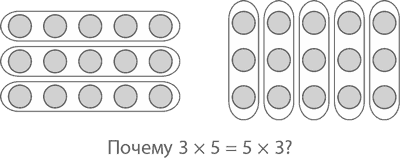
Чуть позже мы еще вернемся к методу подсчета кружков (как и к методу решения задачи двумя разными способами), и вы увидите, к каким интересным результатам он может привести в высшей математике. Но и для понимания основ он не менее полезен. Почему, например, 3 ? 5 = 5 ? 3? Уверен, вы никогда даже не задавались таким вопросом: просто однажды в детстве вам сказали, что порядок чисел при умножении абсолютно не важен (математики, кстати, называют это законом коммутативности). Но почему же три пакетика по пять жемчужин – это то же, что и пять пакетиков по три жемчужины? Самый простой способ объяснить этот закон – посчитать кружки в прямоугольнике размером 3 на 5. Считая ряд за рядом, мы видим 3 ряда, в каждом из них 5 кружков, то есть во всем прямоугольнике 3 ? 5 кружков. С другой стороны, мы можем подсчитать столбики, а не ряды: по 3 кружка в каждом из 5 рядов, значит, всего кружков 5 ? 3.
Эта закономерность может привести нас к другой, еще более красивой. Раз уж мы хотим заставить числа танцевать, почему бы не сделать это и с их квадратами?
Взгляните вот на такую пирамидку уравнений:
Какую закономерность вы видите? Подсчитать количество чисел в каждом ряду несложно: 3, 5, 7, 9, 11 и так далее. А дальше неожиданность: первое число каждого ряда – по крайней мере, первых 5 записанных здесь рядов – является квадратом числа. И правда: 1, 4, 9, 16, 25… Почему так получается? Возьмем пятый ряд. Сколько чисел ему предшествуют? Давайте сложим их количество: 3 + 5 + 7 + 9. Прибавим к ним еще единицу, и у нас получится первое число пятого ряда – сумма первых 5 нечетных чисел, которая, как мы уже знаем, равна 5?.
А теперь просчитаем пятое уравнение, ничего к нему не добавляя. Как бы это сделал Гаусс? Если пока не обращать внимания на начальное 25, слева у нас останется 5 чисел, каждое из которых будет ровно на 5 меньше, чем соответствующее ему число справа.
То есть сумма чисел справа будет ровно на 25 больше суммы чисел слева. Но это без учета 25, которые стоят в начале. А с ними у нас получается именно тот результат, который обещан нам знаком равенства. Следуя той же логике и призвав на помощь алгебру, мы докажем, что этот ряд можно продолжать бесконечно.
Отступление
А теперь – специально для тех, кто хотел немного алгебры. Ряду n предшествует количество чисел, равное 3 + 5 + 7 +… + (2n – 1) = n? – 1, поэтому левая сторона нашего уравнения должна начинаться с числа n?, за которым следует n последовательных чисел, от n? + 1 до n? + n. Справа – n последовательных чисел, начиная с n? + n + 1, заканчивая n? + 2n. Если мы временно «забудем» про число n? слева, то увидим, что каждое из n чисел справа на n больше, чем соответствующее ему последовательное число слева. Разница при этом составляет n ? n, то есть n?. Закономерность эта компенсируется начальным n? слева, поэтому-то левая и правая части и равны.
Перейдем к другой закономерности. Как мы уже видели, из нечетных чисел можно составлять квадраты. А теперь посмотрим, что произойдет, если собрать их в один большой треугольник – вроде того, что изображен чуть ниже.
Так отлично видно, что 3 + 5 = 8, а 7 + 9 + 11 = 27, а 13 + 15 + 17 + 19 = 64. Что общего у 1, 8, 27 и 64? Да это же полные кубы чисел! Например, если сложить между собой пять чисел пятого ряда, мы получим:
21 + 23 + 25 + 27 + 29 = 125 = 5 ? 5 ? 5 = 5?
Логика вроде бы подсказывает, что сумма чисел в ряду n будет равна n?. Но насколько верным будет этот вывод? Не простое ли это совпадение? Чтобы лучше понять эту закономерность, посмотрим на числа в середине 1, 3 и 5 рядов. Что мы видим? 1, 9 и 25. То есть квадраты. В середине 2 и 4 рядов чисел нет, но по сторонам центра 2 ряда видим числа 3 и 5, среднее арифметическое которых – 4, а по сторонам центра 4 ряда – 15 и 17 со средним арифметическим 16. Давайте подумаем, как эту закономерность можно использовать.
Снова возьмем 4 ряд. Что мы тут видим? А видим мы, что сумма всех чисел в нем есть 5? – и не нужно к ним ничего добавлять, чтобы заметить: все они симметрично расположены вокруг 25. Так как среднее арифметическое этих чисел – 5?, уравнение преобразуется в 5? + 5? + 5? + 5? + 5? = 5 ? 5?, то есть 5?. То же справедливо и в отношении 4 ряда: среднее арифметическое всех чисел в нем – 4?, их сумма – 4?. Чуть-чуть алгебры (к которой мы здесь не прибегаем), и вы легко сделаете вывод, что среднее арифметическое n чисел ряда n равно n?, а их сумма равна n?, что и требовалось доказать.
Кстати, если уж мы взялись оперировать квадратами и кубами, не могу удержаться, чтобы не указать вам на еще одну закономерность. Что получится, если сложить кубы чисел, начиная с 1??
Подсчитывая сумму кубов, мы получаем 1, 9, 36, 100, 225 и т. д. – числа, которые являются полными квадратами. Но это не любые квадраты, а квадраты 1, 3, 6, 10, 15 и т. д. – треугольных чисел! Мы уже знаем, что они по своей сути являются суммами простых чисел, а значит,
1? + 2? + 3? + 4? + 5? = 225 = 15? = (1 + 2 + 3 + 4 + 5)?
Другими словами, сумма кубов первых n чисел есть квадрат суммы этих самых первых n чисел. Подтвердить это мы пока не можем, но в главе 6 пару доказательств увидим.
Данный текст является ознакомительным фрагментом.
Сразу отметим, что единой универсальной методики для решения задач на числовые ряды нет. Закономерности, по которым числа следуют друг за другом, могут быть самыми разными, и научиться быстро решать такого рода задачи можно только путём практики — прорешав большое количество других задач на ряды.
Рассмотрим самые простые случаи.
Надо продолжить ряд
1) 2 4 6 8 …
В этом случае всё просто — каждое следующее число на 2 больше предыдущего (т.е. это ряд чётных чисел, или арифметическая прогрессия с шагом 2), поэтому следующее число будет 10
2) 4 8 16 32 …
Тут каждое следующее число в 2 раза больше предыдущего (геометрическая прогрессия), поэтому следующим будет число 64
3) 6 11 17 24 …
Этот случай уже чуть сложнее. В этом числовом ряду разница между соседними числами на 1 больше, чем разница между предыдущими
11 — 6 = 5
17 — 11 = 6
24 -17 = 7
Как видим, шаг (разница) между соседними числами каждый раз увеличивается на 1.
Соответственно, после 24 будет число, которое на 8 больше, то есть 32
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Пример 1
Ряд: 18 10 6 4 …
Взглянув на этот ряд, можно достаточно быстро понять, что разница между соседними числами с каждым шагом сокращается в 2 раза
18 – 10 = 8
10 — 6 = 4 (8:4 = 2)
6 – 4 = 2 (4:2 = 2)
Следовательно, следующий шаг — это 2:2 = 1, то есть число будет 4-1 = 3
Пример 2
Ряд: 7 15 31 63
Этот ряд противоположен предыдущему. Тут разница между соседними числами с каждым шагом увеличивается в 2 раза
15 – 7 = 8
31 – 15 = 16 (16:8 = 2)
63 – 31 = 32 (32:16 = 2)
Следующий шаг будет 32∙2 = 64, соответственно, следующее число будет 63 + 64 = 127
Ответ: 127
Пример 3
Ряд: 2 4 8 10 20 22 44 46 92 94
Взглянем на этот ряд подробнее.
4 – 2 = 2
8:4 = 2
10 – 8 =2
20:10 = 2
То есть одно число на 2 больше предыдущего, а следующее — в 2 раза больше предыдущего.
Далее опять — на 2 больше, и потом в два раза больше.
Следующие числа в этом ряду:
22 – 20 = 2
44:22 = 2
46 – 44 = 2
92:46 = 2
94 – 92 = 2
Соответственно, следующее число будет в 2 раза больше, чем 94. Т.е. это будет 94∙2 = 188
Ответ: 188
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример 4
Ряд: 1 2 3 5 7 11 13 17 19
В этом ряду бесполезно искать закономерности, насколько соседние числа отличаются друг от друга. Все числа в этом ряду — простые, то есть без остатка делятся только на 1 и на само себя. Соответственно, следующим в ряду будет следующее после 19 простое число, то есть 23.
После того, как вы поняли, что это ряд простых чисел, то вы поняли, почему иные закономерности в этом ряду искать бесполезно — ведь математики до сих пор не нашли закона, по которому распределяются простые числа, и как можно по формуле (а не путём перебора) найти следующее простое число, зная предыдущие.
Ответ: 23
Дата публикации
02.05.2020
Как понять найти закономерность
Всё в нашей жизни подчиняется каким-то правилам. Есть правила и в математике. Например, посмотрите на такой ряд чисел: 1, 2, 3. Числа стоят по порядку. Или такой ряд: 1, 3, 5: числа стоят через 1 число. 10, 20, 30: каждое следующее число больше предыдущего на 10. То есть при составлении какого-то последовательного ряда соблюдается какое-то правило. Это правило называется закономерность.
Закономерность – это правило, по которому что-то повторяется время от времени.
Повторяться могут изображения, буквы, числа и любые другие символы. Но обязательно в ряду должно быть не менее трёх чисел.
Например, 2, 3. Есть ли в этом ряду закономерность? Этого мы утверждать не можем. А если ряд 3, 6, 9, то какое число мы можем поставить дальше? Конечно. 12. Мы должны поставить это число по правилу данной закономерности (каждое число в ряду больше другого на 3).
В закономерности всегда не менее 3-х элементов!
На первых двух мы обычно предполагаем закономерность, а на третьем проверяем. Два элемента могут находиться рядом абсолютно случайно. А три – это уже правило.
Как находить закономерности?
1. Внимательно смотрим на ряд чисел, фигур или других картинок.
2. Если в этом ряду есть закономерность, то думаем, какая.
3. Проверяем, соблюдается ли это правило во всей последовательности чисел.
4. Вставляем числа (или фигуры), которые должны эту закономерность продолжить.

Как решать задания на закономерности, вы подробно можете посмотреть на сайте заочных школ на Методической страничке в пособии «Закономерности в цифрах и фигурах. Аналогичная закономерность». Скачайте и просмотрите. Там есть примеры аналогичных заданий.
Будьте очень внимательны при решении этих последовательностей!
КОНТРОЛЬНАЯ РАБОТА № 3 по предмету «Математическая мозаика» для 1 класса
Фамилия _______________________________ Имя __________________
Школа _______________ Класс ______________
Задание 1. Назовите следующее число в ряду:
Задание 2. Помогите коту Мурзику выбрать из предлагаемых вариантов геометрическую фигуру, которую нужно поместить в пустую клетку.
Задание 3. Машенька – ужасная модница. У нее два ящика с красивыми косынками. В первом ящике: красная косынка, синяя косынка в белый горошек, желтая косынка в мухоморчик, красная косынка в рыбку, зеленая косынка с птичкой, зеленая косынка в мороженку. Во втором ящике: синяя косынка в белочку, красная косынка в горошек, зеленая косынка в мухоморчик. Сколько различных по цвету косынок у Машеньки? Ответ: ________
Задание 4. Определи, какую картинку надо вставить в пустую клетку.

Задание 5. Найдите числа, которых не хватает каждой змейке. Впишите цифры в ответе.

Жёлтая змейка (верхняя) – ____
Зелёная змейка (средняя) – ______
Малиновая змейка (нижняя) – _____
Задание 6. Какая фигура лишняя?
3 4 5 Ответ: _______
Задание 7. Какой пример соответствует картинке?

Задачи на поиск закономерностей развивают логическое мышление ребёнка, учат сравнивать, рассуждать, классифицировать и делать выводы.
Выбирайте игру для старта
На платформе LogicLike.com дети с удовольствием развивают логику и способности к математике (смотреть отзывы). У нас 3500 занимательных заданий с ответами и пояснениями!
Что такое закономерность в математике?
Математическая закономерность – это определенное правило, по которому в числовом, фигурном или другом ряду элементов происходит повторение или изменение самих элементов или их свойств в соответствии с заданным правилом.
Из учебных материалов с картинками и видео, подготовленных опытными педагогами, ваш ребёнок узнает:
- что собой представляют закономерности, каких видов они бывают (циклические, возрастающие и убывающие);
- с чего начать решение задачи и как понять, в каких направлениях думать;
- как строятся умозаключения о том, какое число, буква или фигура должны продолжить предложенный ряд.
Очень часто в головоломках на закономерность встречаются буквы и цифры. Иногда могут встречаться и геометрические фигуры, и различные картинки, но это очень редко. Именно исходя из представленных букв и цифр, необходимо найти закономерность и додумать, какое же число или буква будет идти следующим. Очень часто в таких головоломках на закономерность буквы означают какие либо количественные признаки, а цифры – наоборот, зачастую обозначают буквы, или даже целые слова.
Последовательность букв
Однажды незнайка решая логические задачи, наткнулся на одну из них. И только сам Знайка смог отгадать эту загадку.
Нужно определить, какая буква скрывается под знаком вопроса?
И И А С О Н Д Я Ф М А ?
Показать Ответ
Автор получил 7 рублей за добавление этой Головоломки на сайт
Хочу так же
Сумма трёх последовательных чисел
Любопытная закономерность есть в натуральном числовом ряде, при сложении трёх последовательных чисел.
Есть бесконечный числовой ряд от 0 до бесконечности: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 и т. д.
Возьмём сумму трёх первых чисел:
0+1+2=3
Возьмём сумму следующих трёх чисел и сложим нумерически сумму и так далее:
3+4+5=12=1+2=[3]
6+7+8=21=2+1=[3]
9+10+11=30=3+0=[3]
12+13+14=39=3+9=12=1+2=[3]
15+16+17=48=4+8=12=1+2=[3]
18+19+20=57=5+7=12=1+2=[3]
21+22+23=66=6+6=12=1+2=[3]
24+25+26=75=7+5=12=1+2=[3]
27+28+29=84=8+4=12=1+2=[3]
30+31+32=93=9+3=12=1+2=[3]
. и т. д.
Вы уже поняли? Нумерически сумма трёх чисел в натуральном числовом ряду, взятая последовательно, всегда равна числу 3 (три).
Ещё удивительнее если мы возьмём первые три числа исключив первое число — ноль, например рассмотрим числовой ряд начинающий с числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33 и т. д.
Возьмём сумму трёх первых чисел:
1+2+3=6
Возьмём сумму следующих трёх чисел и сложим нумерически сумму и так далее:
4+5+6=15=1+5=[6]
7+8+9=24=2+4=[6]
10+11+12=33=3+3=[6]
13+14+15=42=4+2=[6]
16+17+18=51=5+1=[6]
19+20+21=60=6+0=[6]
22+23+24=69=6+9=15=1+5=[6]
25+26+27=78=7+8=15=1+5=[6]
28+29+30=87=8+7=15=1+5=[6]
31+32+33=96=9+6=15=1+5=[6]
. и т. д. бесконечно
Как видите в математике все закономерно, а если так предлагаю совершить следующий мозговой кульбит. Представим, что есть числовой ряд который начинается от числа 2.
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33 и т. д.
Возьмём сумму трёх первых чисел:
2+3+4=9
Возьмём сумму следующих трёх чисел и сложим нумерически сумму и так далее:
5+6+7=18=1+8=[9]
8+9+10=27=2+7=[9]
11+12+13=36=3+6=[9]
14+15+16=45=4+5=[9]
17+18+19=54=5+4=[9]
20+21+22=63=6+3=[9]
23+24+25=72=7+2=[9]
26+27+28=81=8+1=[9]
29+30+31=90=9+0=[9]
32+33+34=99=9+9=18=1+8=[9]
. и т. д. бесконечно
Продолжая отсчёт к числовому ряду начинающимся от числа три, мы возвращаемся к первому числовому ряду где: 3+4+5=12=1+2=[3]
Следовательно:
Любая сумма трёх последовательных чисел, нумерически равна либо числу 3, либо числу
6, либо числу 9.
PS от 11.11.2014 любопытная связь выявлена с треугольником чисел. 3, 6, 9 в миниатюре : http://www.proza.ru/2014/11/11/1029
PS от 7.09.2018 наткнулся в учебнике Арифметики за 1972 года «признак делимости числа на три : если сумма цифр числа делится без остатка на три, то это число делится на три» И знаете мне пришло в голову что миниатюра эта, является доказательством, что это не признак, а закон . делимости на три, а мои размышления это и есть доказательство признака. соответственно в закон, делимости на три.
Здравствуйте, Александр Альфабет!
Вчера случайно в сети наткнулась на Ваши работы в http://www.proza.ru/.
Получила большое удивление и удовольствие от прочитанного. Простота и красота нумерических сумм некоторых последовательностей простых чисел завораживает.
Я попыталась немного расширить количество суммируемых чисел натурального числового ряда, а так же суммировать четные и нечетные числа ряда. Получается очень интересно.
Если отбросить первое число ноль, которое фактически первым числом не является, то при суммировании трех последовательных чисел мы получим, как Вы показали в своей работе, числа 3, 6 или 9.
Если брать суммы не трех, а меньшего (2) или большего числа (4-9) чисел, то легко прослеживаются последовательности, дающие помимо чисел 3, 6 и 9, еще и число 1,5,7,8. Числа 2 и 4 нумерически при сложении последовательностей чисел не образуются. Но можно легко найти последовательности, при которых нумерически образуются числа 2 и 4 парами или тройками чисел, суммированием через 1,2 или более числа. При этом также видна последовательность, идущая от 1 до плюс бесконечности. Например, суммируя пары, тройки и т.д. (до сумм 9-ти чисел), можно сгруппировать их в ячейки, и разложить их на ряды, используя как идентификатор ряда его нумерическую сумму.
Я могу сейчас уже, через 1 час работы «с карандашем и бумагой» группировать последовательные или парные числа в любые комбинации с нумерической суммой 1,2,3,4,5,6,7,8,9. И это для каждого случая будет строгий закон, соблюдающийся на всем промежутке «от 1 до плюс бесконечности».
Все это прослеживается абсолютно легко, если работать не с цифрами, а с номерами ячеек, в которых они расположены. Более подробно я могу вам написать на Вашу электронную почту, если вы посчитаете это нужным.
Ваши работы помогли мне взглянуть на простые числа под другим углом зрения и «открыть» для себя нумерическую математику.
Большое Вам за это спасибо.
С уважением,
Майя
Майя, доброго времени суток.
Спасибо, за впечатления, которые вы изложили.
Моя электронная почта, открыта для всех на первой странице. Возможно только отвечаю с опозданиями.
Ещё раз за спасибо, за Ваш отзыв, от моих скромных работ.
Порекомендую Вам сайт «числонавтика», Алексея Алексеевича Корнеева.
Задайте в поиске , любой поисковой страницы слово — числонавтика.
В принципе во многом у истоков нумерической математике, стоял именно Корнеев А. А.. Видевшие в числах, не только количественные образы, но и качественные.
С уважением, АА.
Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.
Ежедневная аудитория портала Проза.ру – порядка 100 тысяч посетителей, которые в общей сумме просматривают более полумиллиона страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.
© Все права принадлежат авторам, 2000-2022. Портал работает под эгидой Российского союза писателей. 18+
«Многоликий девятиричный символ, о котором я так часто пишу, открыл одно из своих лиц Марко Родину (Marko Rodin), американцу с болгарскими корнями, когда тому было пятнадцать лет. Марко был последователем религии Бахаи, учение которой уходит корнями в мистические практики суфийских школ Персии, поэзию Аттара и Хафиза.
По словам Марко, он искал числовую формулу, выражающую величайшее из имен Бога. Согласно исламской Традиции, произносимыми являются лишь 99 Божественных Имен, тогда как сотое остается тайным. Посланник бахаистской веры, Бахаулла, возвестил, что величайшее Имя звучит БАХА. Все производные этого слова (например, АБХА) также рассматриваются как Величайшее Имя.
Марко использовал систему суфийской кодировки абджад, известную последователям Бахаи, для нахождения численных соответствий арабским буквам имени Бога АБХА. Согласно абджад, A=1, Б=2, Х=5 и А=1, что в сумме дает 9. (Девятиконечная звезда, кстати, является главным символом Бахаи).
Далее Марко нарисовал круг и поместил в его вершине цифру 9. Затем он обозначил цифры от 1 до 8 в направлении часовой стрелки на равном расстоянии друг от друга. Путем экспериментов, соединяя прямыми линиями точки на круге, Марко обнаружил следующую диаграмму, которую впоследствии назвал «математическим отпечатком пальцев Бога».
Последователи Марко, которых в последние десятилетия на Западе появилось немало, утверждают, что диаграмма Родина указывает на универсальный фактор, действующий на всех уровнях – от субатомного до космического, что с помощью древней математики, отражающей циклическую суть чисел, Марко приоткрыл завесу над источником энергии, заставляющей вращаться электроны, солнечные системы и галактики. (Хотя все знают, что электроны вращаются вокруг ядра атома, никто не знает источника энергии этого вращения).
Являются ли данные утверждения лишь громкими заявлениями, или в них есть хотя бы доля истины?
Итак, Марко начал эксперименты со своей девятиричной диаграммой, проведя линию от 1 до 2, затем от 2 до 4, и далее от 4 до 8.
. Интуитивно, он пошел по пути геометрической прогрессии или октавного удвоения вибраций. Г.И.Гурджиев, передавший Западу знание одного из вариантов эннеаграммы, говорил, что каждая нота октавы, символом которой является эннеаграмма, в свою очередь, содержит внутри себя целую октаву, и так далее. Марко сделал это очевидным, соединив линии внутри девятиричного символа в последовательности геометрической прогрессии.
Следующим в ряду удвоения должно было быть число 16, однако на диаграмме было лишь 9 делений. Марко пришла идея применить метод нумерологического сложения, с которым мы специально познакомились в прошлой заметке. Вычислив цифровой корень 16-ти, он нашел 7 (16=1+6=7).
То же самое он получил бы, конечно, просто вычтя 9 из 16. Здесь Родин вовсе не был новатором. Методы такого рода (сведение многозначных чисел до однозначных — извлечение цифрового корня путем вычета из изначального числа всех девяток) лежали в основе математики Вед, пифагорейской и каббалистической нумерологии. В наши дни они применяются в компьютерных науках, криптологии, теории чисел и т.д.
Итак, Марко провел линию от 8 к 7.
Затем он удвоил 16 и получил 32, цифровой корень которого был равен 5 (32=3+2+5), и соединил линией 7 и 5. Наконец, он удвоил 32, получив 64, и извлек из него цифровой корень (64=6+4=10=1+0=1). Так, последняя линия от 5 до 1 замнула полученный паттерн. и Марко получил символ бесконечности!
Продолжив бинарный ряд – 128, 256, 512, 1024, 2048. и так далее, заинтригованный Родин обнаружил, что, извлекая цифровой корень, вновь и вновь получает все ту же бесконечно повторяющуюся последовательность чисел — 1, 2, 4, 8, 7 и 5.
(Я проверяла, так и есть).
Точно такая же последовательность получалась и в обратном направлении — «вниз по октавной лестнице» при делении на 2:
Действительно, если разделить 1 на 2, получится 0,5. Марко провел линию от 1 к 5.
Далее, половина от 0,5 – 0,25, а 2+5=7. Он провел очередную линию — от 5 к 7.
Половиной от 0,25 будет 0,125 или 1+2+5=8. Значит, следующий шаг — от 7 к 8.
Затем, половина от 0,125 будет 0,0625, т.е. 0+6+2+5=13=1+3=4, линия от 8 к 4.
Половина от 0,0625 равна 0,03125 или 0+3+1+2+5=11=1+1=2. Проведя линию от 4 до 2, Марко обнаружил, что круг замкнулся.
Продолжая далее, он только подтвердил наличие той же самой последовательности чисел 1,2,4,8,7,5 не только при октавном умножении, но и при делении.
В сознании Марко возник образ вечно движущейся спирали, замкнутой на саму себя в виде тора. Точку, в которой кривая 124875 пересекает саму себя, Марко обозначил как 0, сердце тора, где встречаются два его вихревых потока – входящий и исходящий.
Мои уважаемые читатели давно заметили, наверное, что в моих сообщениях я вновь и вновь возвращаюсь к теме тора. Дело в том, что Природа опирается на единый универсальный паттерн для развития жизни на всех уровнях, и этот паттерн – тор. Он является единственной геометрической формой, полностью самодостаточной и способной поддерживать свою неизменность, находясь в непрерывном движении. Тороидальные поля формируют все физические тела – галактики, планеты, человека, растения, их клетки и атомы. Причина популярности в живой природе этой формы проста — благодаря ей создается вихрь или воронка, через которую происходит втяжение заряда жизненной силы. «Вихрь жизни» – не просто расхожий оборот речи.
Спустя годы работы с числами эннеаграммы, Марко Родин и его последователи, в частности, Рэнди Пауэл (Randy Powell), создали целую систему, названную ими «математикой вихря» (vortex-based math, VBM), в основе которой лежит принцип равновесия между силами расширения и втяжения, наиболее полно воплощенный в геометрии тора. Группа Родина утверждает, что на основе этой математики возможно создание энергосистем и машин без трения.
Я оставлю это утверждение без оценки, поскольку вдаваться в детали сложной математики тора или электротехнические подробности не является моей целью, и вернусь к предмету нашего интереса – девятиричной диаграмме.
. Итак, изучая повторяющуюся последовательность чисел 1,2,4,8,7,5, Марко заметил, что цифры 3, 6 и 9 были совершенно исключены из данного ряда. 3 и 6, однако, демонстрировали свой собственный, весьма интересный паттерн, и он тоже оказался цикличным:
*
3 при удвоении дает 6, а удвоенная 6 вновь превращается в 3 (12=1+2=3).
Удвоенное 12 опять обращается в 6 (24=2+4=6).
Далее, 24, помноженное на 2, снова равно 3 (48=4+8=12=1+2=3). и так далее, по кругу (я проверила).
Таким образом, 3 и 6 постоянно осциллируют в своей взаимной трансформации, «меняя пол», переходя друг в друга и оставаясь в стороне от 124875.
Только число 9 стоит особняком от всех метаморфоз, неизменно возвращаясь лишь к самому себе. Как бы мы ни делили и ни умножали девятку, цифровой корень результата всегда будет равен 9:
72+72=144=1+4+4=9. и так далее, в том же духе.
. Спустя годы работы со своей диаграммой, Марко пришел к выводу, что 3,6,9 представляют силы и энергии, лежащие за пределами материальной плоскости. Он сравнивал 3 и 6 с Инь и Ян древнекитайского полярного символа, где 9 представляло третью, уравновешивающую силу между ними, и одновременно источник, «родитель» этих противоположностей.
Гексанема 124875 находится в постоянном процессе интеграции и распада, сгущения и растворения, рождения и смерти, иначе говоря, перемен. Именно данная часть диаграммы – движущаяся. Древнекитайская «Книга Перемен» отражает цикл метаморфоз этих 6-и элементов в терминах 64-х гексаграмм.
124875 и по форме, и по сути являют из себя символ бесконечности, Уробороса, заглатывающего собственный хвост.
Когда какая-либо волна распространяется внутри единого поля по прямой, мы называем это «энергией», а когда та же самая волна «зацикливается на самой себе», подобно Уроборосу, мы называем это «материей».
124875 представляют мир, где мы находимся — мир материи. Чтобы создать материю, нужно заставить волну двигаться внутри себя.
124875 также представляют мир двойственности. Числа 1,2,4,8,16(7),32(5), 64(1) и т.д. являются не чем иным, как цифровыми корнями степеней двойки:
20 21 22 23 24 25 26
При каждом из шести шагов вибрации повышаются вдвое, а значит, каждый шаг есть октава. Кроме того, весь цикл от 1 до 8 – также большая октава, октава октав. В календаре майя число 64 не случайно является концом одного цикла бесконечности и началом следующего.
Как сказал Бог-Создатель устами Тота-Гермеса древнеегипетской Традиции (о чем нам напомнил уважаемый gray_swan): «Я —Один, который становится Двумя, который становится Четырьмя, который становится Восемью, а затем я вновь Один».
Действительно, пройдя октаву октав от 1 до 64, Создатель вновь становится единицей (6+4=10=1+0=1).
3,6,9 – неподвижная часть диаграммы.
3,6,9 лежат за пределами мира двойственности, но являются причиной его существования, источником его энергии. Отсюда знаменитое выражение Николы Теслы, о котором нам недавно напомнила уважаемая megera2012: «Если бы вы только знали все великолепие чисел 3,6,9, вы бы имели ключ ко Вселенной».
3 и 6 – посредники, позволяющие 9, нематериальному элементу, влиять на материальные элементы 124875.
3 и 6 – как движущиеся туда-сюда лапки «белки», крутящей колесо перемен, тогда как 9 – сама «белка». (Марко Родин действительно однажды сравнил 9 с «хомяком, вертящим колесо 124875»).
9 вызывает перемены, но не участвует в них. Она всегда замкнута на саму себя.
9 находится на уровень глубже, чем 124875.
Глубже этого уровня – только Ноль. 9 лежит между (нашей) реальностью ограниченных возможностей (124875) и реальностью неограниченных возможностей (0).
Как сказал Руми:
Свет, излучаемый оком [124875],
На деле — свет сердца [9].
Свет, наполняющий сердце [9],
На деле — свет Истинного [0],
Он чист и отделен от света разума и чувства [124875].
А что такое Ноль?
Здесь мы подходим к реальности, для описания которой не предназначен человеческий язык, поэтому закончим рассказ о Диаграмме строчкой Хафиза:
Ноль – вот где начинается Подлинная Игра!
А остального — слишком много считать. Quelle