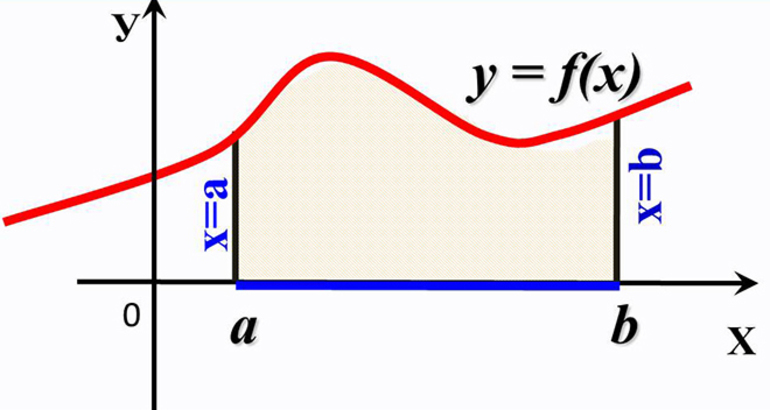
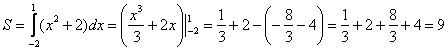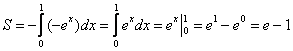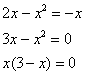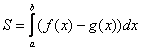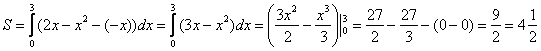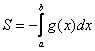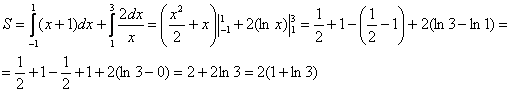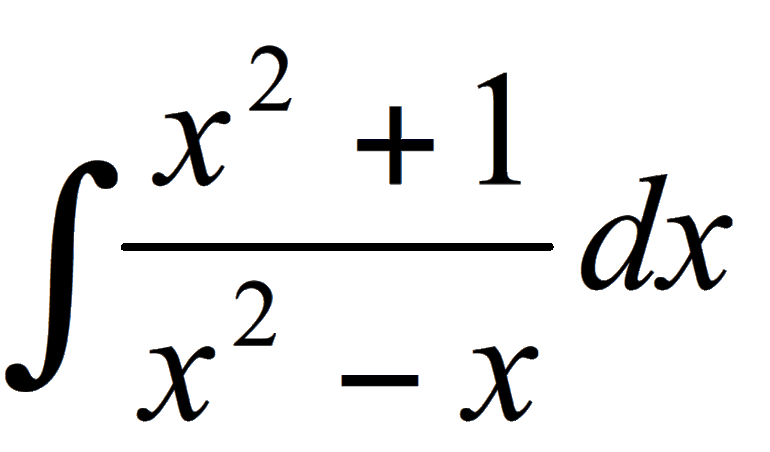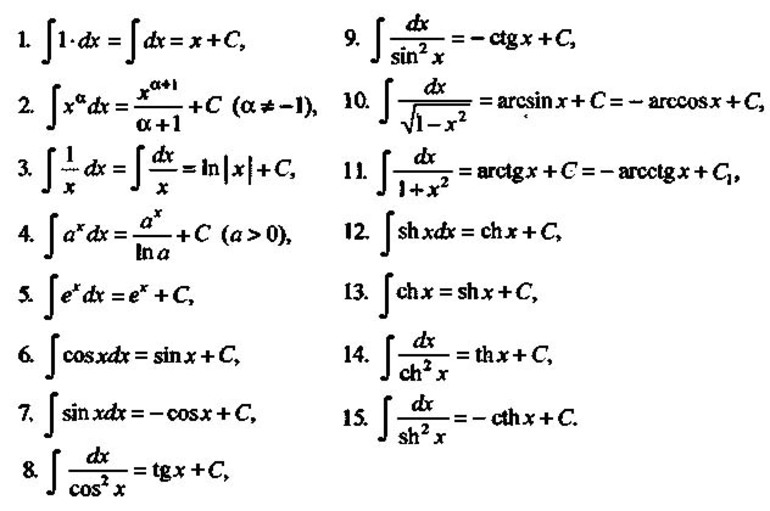Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:
Пример 10
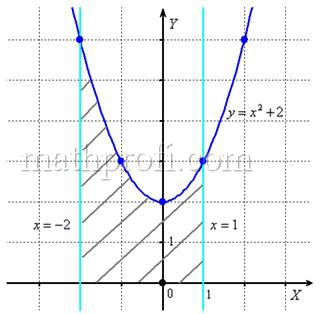
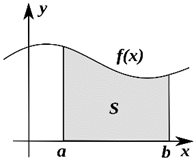
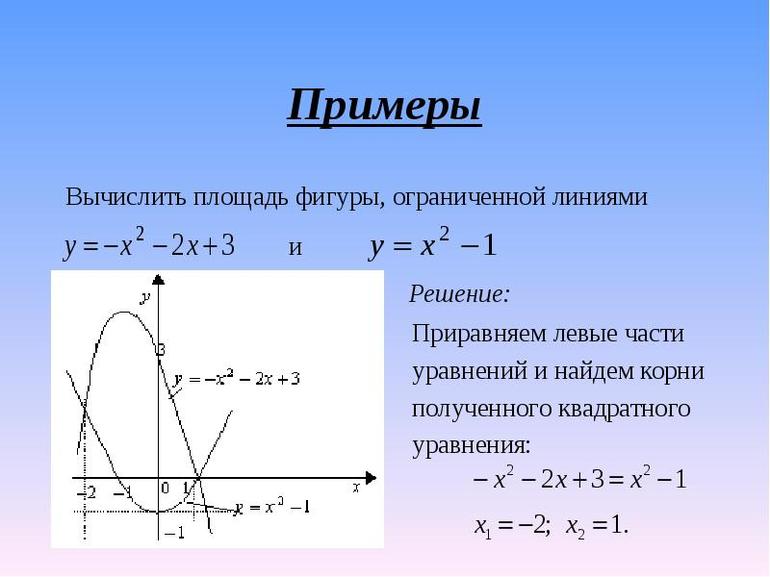
Вычислить площадь фигуры, ограниченной линиями .
И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.
В нашей задаче: прямая определяет ось
, прямые
параллельны оси
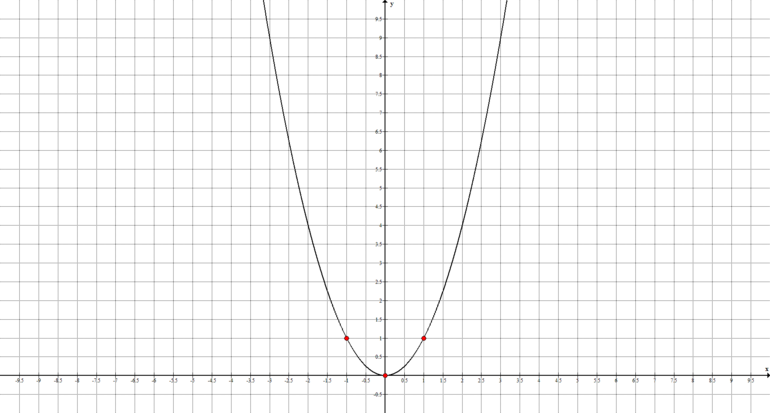
и парабола
симметрична относительно оси
, для неё находим несколько опорных точек:
Искомую фигуру желательно штриховать:
Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке график функции
расположен над осью
, поэтому искомая площадь:
Ответ:
После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.
И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.
Пример 11
Вычислить площадь фигуры, ограниченной линиями и осью
Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью :
Пример 12
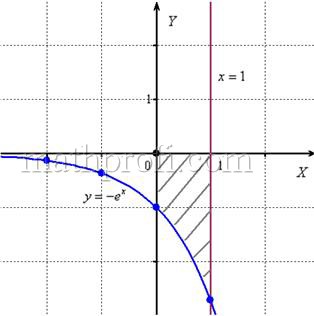
Вычислить площадь фигуры, ограниченной линиями ,
и координатными осями.
Решение: найдём несколько опорных точек для построения экспоненты:
и выполним чертёж, получая фигуру площадью около двух клеток:
Если криволинейная трапеция расположена не выше оси , то её площадь можно найти по формуле:
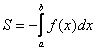
В данном случае:
Ответ: – ну что же, очень и очень похоже на правду.
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:
Пример 13
Найти площадь плоской фигуры, ограниченной линиями ,
.
Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы и прямой
, поскольку здесь будут находиться пределы интегрирования. Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:
таким образом:
Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».
С прямой всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
– именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:
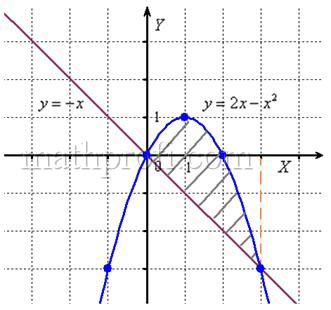
Выполним чертеж:
А теперь рабочая формула: если на отрезке некоторая непрерывная функция
больше либо равна непрерывной функции
, то площадь фигуры, ограниченной графиками этих функций и отрезками прямых
, можно найти по формуле:
Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.
В нашем примере очевидно, что на отрезке парабола располагается выше прямой, а поэтому из
нужно вычесть
Завершение решения может выглядеть так:
На отрезке :
, по соответствующей формуле:
Ответ:
Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы 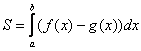
задаётся уравнением
, то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу
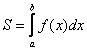
А сейчас пара типовых задач для самостоятельного решения
Пример 14
Найти площадь фигур, ограниченных линиями:
а) ,
.
б) ,
,
Решение с чертежами и краткими комментариями в конце книги
В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:
Пример 15
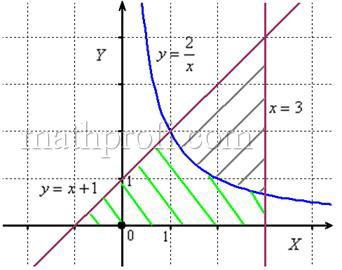
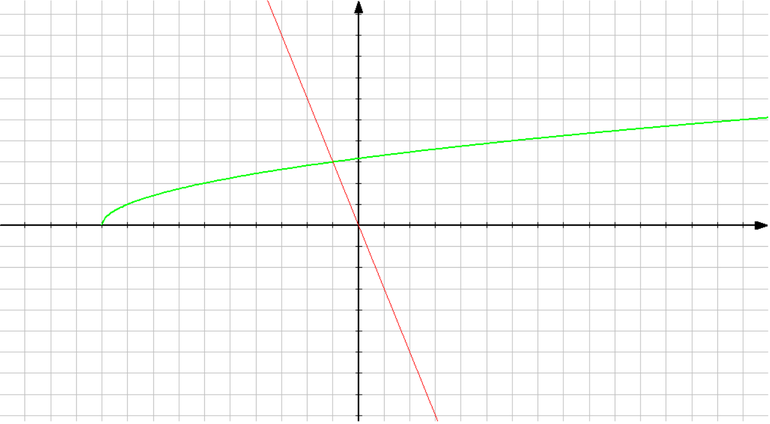
Вычислить площадь фигуры, ограниченной линиями
Решение: выполним бесхитростный чертёж,
хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую можно недочертить до оси
, и тогда мы вовсе не увидим нужную фигуру.
Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:
1) на отрезке над осью
расположен график прямой
;
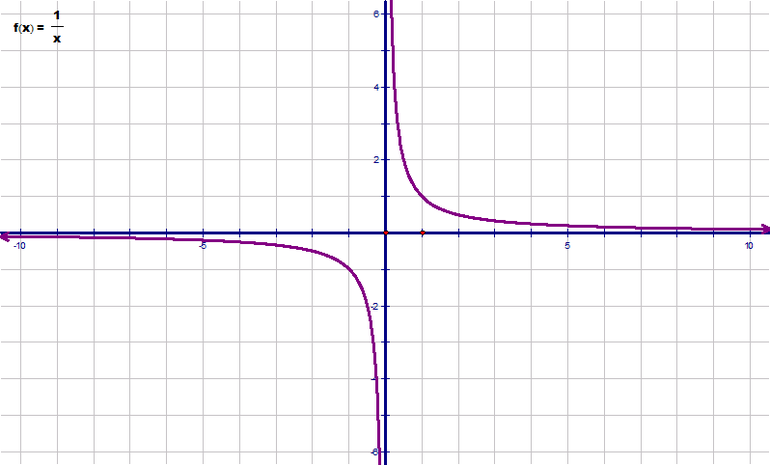
2) на отрезке над осью
расположен график гиперболы
.
Совершенно понятно, что площади можно (и нужно) сложить:
Ответ:
И познавательный пример для самостоятельного решения:
Пример 16
Вычислить площадь фигуры, ограниченной линиями ,
,
и координатными осями.
Итак, систематизируем важные моменты этой задачи:
На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.
Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.
Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой и прямой
, где из чертежа не понятна одна из точек их пересечения. В таких случаях следует использовать аналитический метод, составляем уравнение:
и находим его корни:
– нижний предел интегрирования,
– верхний предел.
Во-вторых, не всегда понятен «внешний вид» линии, и функция (Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html
После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.
Составляем определённый интеграл или несколько интегралов по формуле 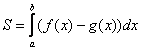
Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.
Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Конспект урока: Вычисление площадей с помощью интегралов
Интеграл
Вычисление площадей с помощью интегралов
План урока
- Вычисление площади криволинейной трапеции
- Вычисление площади фигуры, ограниченной графиками двух непрерывных функций
Цели урока
- Уметь изображать на схематическом рисунке фигуру, ограниченную заданными линиями
- Знать формулу для вычисления площади фигуры, ограниченной графиками двух непрерывных функций
- Уметь вычислять площадь криволинейной трапеции
Разминка
- Что такое криволинейная трапеция?
- Как связана площадь криволинейной трапеции с определённым интегралом
- Запишите формулу Ньютона-Лейбница
- Вычислите ∫-13x3dx
Вычисление площади криволинейной трапеции
Как показывалось ранее, площадь криволинейной трапеции можно вычислить по формуле S=∫abf(x)dx. Рассмотрим пример вычисления площади криволинейной трапеции.
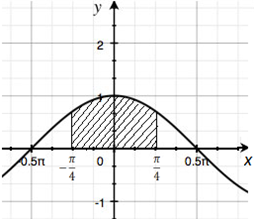
Вычислить площадь фигуры, ограниченной прямыми x=-π4, x=π4, осью Ox и графиком функции y=cos x.
Решение
Рис. 1.
Фигура, площадь которой надо найти, изображена на рисунке 1. Она представляет собой криволинейную трапецию. Поэтому воспользуемся формулой
S=∫abf(x)dx
S=∫-π4π4cos xdx=sin x-π4π4=sinπ4-sin -π4=22+22=2.
Ответ: 2.
Вычисление площади фигуры, ограниченной графиками двух непрерывных функций
Рис. 2.
С помощью интеграла можно вычислять площади не только криволинейных трапеций вида, представленного на рисунке 2, но и плоских фигур более сложного вида.
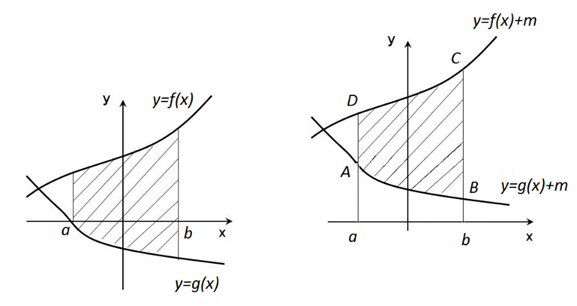
Рис. 3.
Рассмотрим фигуру, ограниченную прямыми x=a, x=b и графиками непрерывных функций y=f(x), y=g(x) такими, что на отрезке [a; b] выполняется условие g(x)≤f(x) (рис. 3а).
Выполним параллельный перенос данной фигуры на m единиц вверх
(m>0) так, чтобы данная фигура оказалась расположенной в координатной плоскости выше оси абсцисс (рис. 3б).
Теперь эта фигура ограничена сверху и снизу графиками функций y=f(x)+m и y=g(x)+m соответственно. При этом обе функции непрерывны и неотрицательны на отрезке [a; b]. Найдём площадь этой фигуры:
S=SABCD=SaDCb-SaABb=∫ab(f(x)+m)dx-∫ab(g(x)+m)dx=
=∫ab((f(x)+m)-(g(x)+m))dx=∫ab(f(x)-g(x))dx.
Таким образом, получили следующее правило: площадь S фигуры, ограниченной прямыми x=a, x=b и графиками функций y=f(x), y=g(x), непрерывных на отрезке [a; b] и таких, что для всех x из отрезка [a; b] выполняется неравенство g(x)≤f(x), вычисляется по формуле
S=∫ab(f(x)-g(x))dx.
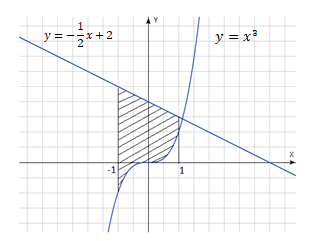
Вычислите площадь фигуры, ограниченной линиями x=-1, x=1, y=x3, y=-12x+2.
Решение
Рис. 4.
Построим данную фигуру (рис. 4).
Воспользуемся формулой
S=∫ab(f(x)-g(x))dx
S=∫-11-12x+2-x3dx=
=∫-11-x3-12x+2dx=-x44-x24+2x-11=
=-144-124+2·1—(-1)44-(-1)24+2·(-1)=
=-14-14+2+14+14+2=4.
Ответ: 4.
Вычислите площадь фигуры, ограниченной линиями y=x2+2x-3, y=-x2+2x+5.
Решение
Рис. 5.
Построим данную фигуру (рис. 5) и найдём точки пересечения графиков функции, решив уравнение
x2+2x-3=-x2+2x+5
2×2=8
x2=4
x1=-2; x2=2.
Воспользуемся формулой
S=∫ab(f(x)-g(x))dx
S=∫-22-x2+2x+5-x2+2x-3dx=∫-22-2×2+8dx=
=-2×33+8x-22=-2·233+8·2—2·(-2)33+8·(-2)=
=-163+16-163+16=643=2113.
Ответ: 2113.
1. Вычислите площадь фигуры, ограниченной прямыми x=-π2, x=π2 осью Ox и графиком функции y=1+12 cos x.
2. Вычислите площадь фигуры, ограниченной линиями x=-2, x=1, y=-x, y=3-x4.
Рис. 6.
3. Вычислите площадь фигуры, ограниченной линиями y=x2-4x+3, y=-x2+6x-5.
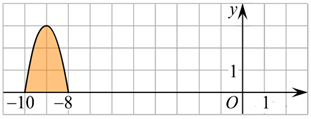
4. На рисунке 6 изображён график некоторой функции y = f(x). Функция F(x)=-x3-27×2-240x-8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Контрольные вопросы
- Запишите формулу площади криволинейной трапеции.
- Запишите формулу площади фигуры, ограниченной графиками двух непрерывных функций.
Предыдущий урок
Правила нахождения первообразных
Интеграл
Следующий урок
Вычисление интегралов
Интеграл
Общие сведения
Вычислить площадь фигуры на плоскости считается довольно простой операцией. Для ее выполнения необходимо знать только формулу. Существенно усложняет задачу фигура, ограниченная прямыми.
Одной из них считается криволинейная трапеция. Ее площадь можно определить только при нахождении значений определенного интеграла.
Операция интегрирования считается довольно сложной, поскольку необходимо знать основные правила. Перед нахождением площади криволинейной трапеции специалисты рекомендуют внимательно изучить и освоить правила интегрирования основных функций.
Разбирается неопределенный интеграл, а затем осуществляется переход к более сложным операциям.
Информация об интегралах
С понятием интеграла связано много направлений научных отраслей. Обозначается он символом «∫». С помощью интеграла открываются большие возможности по быстрому и эффективному нахождению значений следующих величин: площади криволинейной трапеции, объема тела вращения, поверхности, пути при неравномерном движении, массы неоднородного физического тела и так далее.
Упрощенный вариант представления и определения интеграла — сумма бесконечно малых слагаемых. Интеграл бывает нескольких типов: одинарный, двойной, тройной, криволинейный и так далее. Для любого элемента он может быть двух типов:
- Неопределенный.
- Определенный.
Операция нахождения первого типа значительно проще второго. Это объясняется тем, что во втором случае следует не только найти первообразную, но и выполнить правильную подстановку значений.
Неопределенным интегралом функции вида f(х) называется такая первообразная функция F(х), производная которой равна подинтегральному выражению. Записывается это таким образом: ∫(f(x)) = F(х) + С.
Последняя величина является константой, поскольку при выполнении операции нахождения производной константа равна 0.
Для нахождения первообразной используется специальная таблица интегралов:
Рисунок 1. Таблица интегралов и их первообразные.
В таблице приведены простые функции. Для нахождения площади фигуры, которая ограничена линиями, достаточно значений первообразных на рисунке 1. Вычисление определенного интеграла заключается в получении первообразной и подстановке начального и конечного значений. Следует отметить, что константа при этом не берется. Существует способ, чтобы найти определенный интеграл. Формула Ньютона-Лейбница позволяет быстро и эффективно вычислить площадь фигуры. Для этого нужно подставить значения ее границ (a и b) в первообразные: F(x)|(a;b) = F(b) — F(a).
Криволинейные фигуры
Криволинейная фигура (трапеция) — класс плоских фигур, которые ограничены графиком неотрицательной и непрерывной функции, а также осью ОУ и прямыми (х = а, х = b). Она изображена на рисунке 2. Для нахождения ее площади следует использовать определенный интеграл.
Рисунок 2. Фигуры с криволинейными сторонами.
Интегрирование разбивает фигуру на прямоугольные части. Длина каждой из них равна ординате y = f(х) через промежутки, которые очень малы, по оси декартовой системы координат (есть еще и полярная) ОХ на отрезке [a;b]. Ширина является бесконечно малым значением. При интегрировании находятся площади прямоугольников и складываются. Для того чтобы не путаться в графиках, геометрическую фигуру следует заштриховать.
Криволинейная трапеция — геометрическая фигура с неровными сторонами, которые образовались в результате пересечения графика непрерывной функции с осями абсцисс и ординат.
Применение обыкновенных методов нахождения площади этой фигуры невозможно, поскольку она обладает одной или несколькими неровными сторонами (кривыми линиями).
Способы вычисления и рекомендации
Для расчетов площади криволинейной трапеции используется несколько методов. Их условно можно разделить на следующие: автоматизированные и ручные. Первый из них выполняется при помощи специализированного программного обеспечения (ПО). Примером является онлайн-калькулятор, который не только находит площадь заданной фигуры, но и изображает ее в декартовой системе координат.
Существует и другое ПО, которое является более «мощным». К нему можно отнести наиболее популярные среды: Maple и Matlab. Однако существует множество программ, написанных на языке программирования Python. Программы нужны также при освоении темы интегрирования. Если необходимо рассчитать множество интегралов и площадей криволинейных фигур, то без них не обойтись.
Новичку для автоматизированных вычислений рекомендуется применять различные онлайн-калькуляторы. Однако следует выделить неплохую программу, которая обладает довольно неплохими функциональными возможностями.
Она называется Integral calculator и представляет собой очень удобное приложение для Android-устройств. Кроме того, можно скачать подобное ПО для Linux, Mac и Windows.
Программа — это калькулятор, который используется для нахождения интегралов и производных, а также его можно применять для решения уравнений интегрального и дифференциального типов. Integral calculator обладает такими функциональными возможностями:
- Вычисление производных.
- Нахождения первообразных для определенных и неопределенных интегралов.
- Решение систем уравнений.
- Выполнения операций над матрицами и определителями.
- Построение графиков заданных функций в 2D и 3D.
- Расчет точек перегиба.
- Вычисление рядов Фурье.
- Решение дифференциальных уравнений линейного типа первого и второго порядков.
Однако специалисты не рекомендуют использовать приложения такого типа, поскольку нужно уметь решать подобные задачи самостоятельно. Любые математические операции развивают мышление, а злоупотребление ПО приводит к значительной деградации. Решать какие-либо задачи рекомендуется также людям, которые не имеют отношения к математической сфере.
Основной алгоритм
При нахождении площади криволинейной трапеции рекомендуется следовать определенному алгоритму. Он поможет избежать ошибок, поскольку задача разбивается на несколько простых подзадач, решение которых довольно просто контролировать. Алгоритм имеет следующий вид:
- Нужно прочитать и понять условие задачи.
- Начертить декартовую систему координат.
- Построить график заданной функции.
- Изобразить линии, ограничивающие фигуру.
- После определения границ нужно аккуратно заштриховать фигуру.
- Вычислить неопределенный интеграл функции, которая дана в условии.
- Посчитать площадь, подставив значения ограничивающих прямых в первообразную.
- Проверить решение задачи при помощи программы.
Первый пункт — внимательное чтение условия задачи. Этап считается очень важным, поскольку формирует дальнейший алгоритм. Необходимо выписать все известные данные, а затем подумать над дальнейшим решением задачи. Следует обратить особое внимание на график функции, который при возможности нужно упростить. Далее следует выписать линии, которые будут ограничивать фигуру.
Следующий пункт считается наиболее простым, поскольку нужно начертить обыкновенную систему координат. В условии должен быть указан ее тип. Если обозначена полярная система, то следует ее начертить. Во всех остальных случаях изображается декартовая система координат.
Третий пункт алгоритма — правильное построение графика функции. В этом случае нет необходимости составлять таблицу зависимости значения функции от аргумента. График должен быть схематичным. Например, если это парабола, то нужно ее изобразить. В этом случае необходимо ознакомиться с основными базовыми функциями и их графиками.
Следующим шагом является правильное изображение прямых. Если ее уравнение имеет следующий вид «x = 5» или что-то подобное, то она будет проходить параллельно оси ОУ. Например, при y = 10 прямая проходит параллельно оси ОХ. В других случаях нужно составить таблицу зависимостей значений уравнения прямой от переменной. Следует брать всего два значения аргумента, поскольку их достаточно для проведения прямой.
После всех операций образуется фигура, которая ограничена линиями. Ее необходимо заштриховать. После этого вычисляется неопределенный интеграл заданной функции. Необходимо воспользоваться табличными значениями первообразных на рисунке 2. Однако здесь есть небольшой нюанс: константу записывать нет необходимости. Она «уничтожается» при подстановке в формулу Ньютона-Лейбница.
В полученное значение следует подставить значения границ. Кроме того, необходимо обратить особое внимание на знак формулы. При отрицательном значении границы формула принимает следующий вид: F(x)|(-a;b) = F(b) — F(-a) = F(b) + F(a). Проверка правильности решения выполняется с помощью ПО.
Примеры решения
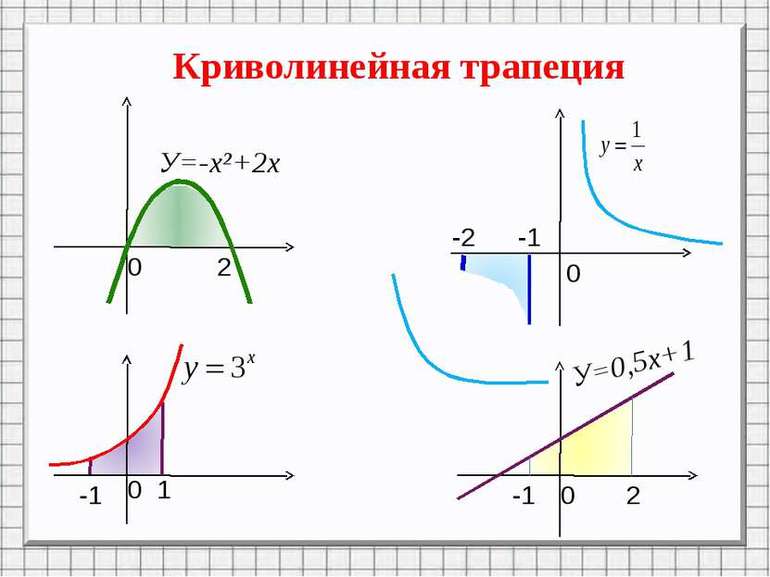
Для закрепления теоретического материала специалисты рекомендуют решить несколько задач. В качестве примера можно взять криволинейные трапеции, изображенные на рисунке 2.
Разновидность параболы
В первом примере функция вида y = -x^2 + 2x и ось ОХ образуют фигуру. Необходимо найти ее площадь. Из функции видно, что ветви параболы направлены вниз (отрицательный знак перед квадратом). Точки пересечения находятся следующим образом:
- Тело функции приравнивается к 0: -х^2 + 2x = 0.
- Выносится общий множитель: -x(x-2) = 0.
- Решаются обе части уравнения.
- Первый корень: -х1 = 0 или х1 = 0.
- Для нахождения второго нужно решить другую часть уравнения: х2-2 = 0. Отсюда, х2 = 2.
Ветви параболы проходят через координаты по ОХ: 0 и 2 соответственно. Координата «х» вершины точки параболы находится с помощью подстановки в формулу: x = -b/(2*a) = -2 / -2 = 1. В этом случае координата «у» вычисляется следующим образом: y = -(1^2) + 2 * 1 = -1 + 2 = 1. Точка с координатами (1;1) является вершиной параболы. Границы интегрирования — координаты по ОХ, через которые проходят ветви параболы.
После всех операций следует вычислить неопределенный интеграл функции, воспользовавшись таблицей на рисунке 1: ∫ (-х^2 + 2x) dx = — (x^3 / 3 + x^2) + C = x^2 — x^3 / 3 + C. После этого следует подставить начальное и конечное значения (константа убирается): S = x^2 — x^3 / 3 = (2^2 — 2^3 / 3) — (0^2 — 0^3 / 3) = 4 — 8/3 = 4 / 3 (кв. ед.). Последняя запись является единицей измерения площади. Она обозначается в условных единицах, так как в условии задачи размерность сторон фигуры не указана.
Гипербола, степенная и прямая
На следующем рисунке изображен график функции гиперболы (у = 1 / х). Прямые, которые ограничивают график, описываются следующими законами: у1 = -2 и у2 = -1. Для вычисления площади заданной фигуры следует взять интеграл: ∫(1/х) dx = ln (|x|) + С. Для окончательного решения необходимо подставить значения в натуральный логарифм: S = ln (2) — ln (1) = 0,6931 — 0 = 0,6931 (кв. ед.).
Фигура, которая ограничена прямыми y1 = -1 и y2 = 1, и представлена функцией вида y = 3^x. Площадь находится следующим образом: S = ∫ (3^x) dx = 3^x / (ln(|3|)) = [3^1 / (ln(3))] — [3^(-1) / (ln(3))] = (3 / 1,0986) — ((1/3) / 1,0986) = 2,7307 — 0,3034 = 2,4273 (кв. ед.).
Последняя фигура представлена графиком прямой y = 0,5х + 1, которую ограничивают прямые х1 = -1 и х2 = 2. Значение площади можно найти таким способом: S = ∫ (0,5х + 1) dx = (0,5 * х^2) / 2 + x = [((0,5 * 2^2) / 2) + 2] — [((0,5 * (-1)^2) / 2) + (-1)] = 3 — 0,75 = 2,25 (кв. ед.).
Для определения значения площади криволинейной фигуры (трапеции) необходимо использовать определенные интегралы. При решении нужно внимательно следить за знаками и первообразными из таблицы на рисунке 1.
Расчет площади фигуры является, пожалуй, одной из самых сложных задач теории площадей. В школьной геометрии учат находить области базовых геометрических фигур, таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т. д. Однако часто приходится иметь дело с вычислением площадей более сложных форм. Именно при решении таких задач очень удобно использовать интегральное исчисление.
Пример 1.
Найти площадьфигуры,офаниченной линиями 
Решение:
Найдем точки пересечения параболы и прямой. Приравняем правые части уравнений, задающих функции, и решим полученное уравнение
Фигура, площадь которой нужно найти, изображена на рисунке. Используя приведенную формулу, получим
Ответ: площадь фигуры равна 13,5 кв. ед.
Вычисление площадей плоских фигур в полярной системе координат
Пусть плоская фигура ограничена линией 



Если же фигура ограничена линиями 

По этой ссылке вы найдёте полный курс лекций по высшей математике:
Пример 2.
Найти площадь фигуры, ограниченной линией, заданной в полярной системе координат уравнением
Решение:
Ответ: площадь данной фигуры 9,5л кв. ед.
Пример З.
Найти площадь фигуры, ограниченной линиями, заданными в полярной системе координат
Решение:
Фигура, площадь которой требуется найти, показана на рисунке.
Найдем точки пересечения окружности и кардиоиды. Решая совместно данные уравнения, получим точки
По рисунку видно, что фигура симметрична. Вычислим площадь половины фигуры, учитывая, что она в свою очередь разделена на части 

Ответ: площадь фигуры
Возможно вам будут полезны данные страницы:
Пример 4.3.
Найти площадь фигуры, ограниченной линиями 
Решение:
Из чертежа (см. рис. 7)




получаем, что точка В пересечения прямой 

Тогда 

Данная задача может быть также решена другим способом. По определению определенного интеграла
Если 



криволинейной трапеции, ограниченной кривой 

Другими словами, в данном случае площадь вычисляется посредством проецирования криволинейной трапеции на ось ординат). Теперь возвращаясь к задаче нашего примера, можем записать: 
Если криволинейная трапеция ограничена кривой, заданной в параметрическими уравнениями
прямыми 







Пример 4.5.
1. Вычислить площадь фигуры, ограниченной линиями: 
Решение:
Решая систему уравнений, находим абсциссы точек пересечения эллипса и параболы 



Для вычисления первого интеграла применяем подстановку
Второй интеграл вычисляется непосредственно.
Ответ:
Пример 4.6
Вычислить площадь области, ограниченной эллипсом
Решение:
В силу симметричности эллипса относительно координатных осей вычислим часть области, лежащей в первой четверти, кода 

Пример 4.7
Вычислить площадь области, ограниченной лемнискатой

Решение:
Принимая во внимание симметрию линии относительно полярной оси, получаем:
Пример 4.8
Вычислить площадь фигуры, ограниченной прямыми 
Решение:
Так как максимум функции 




Пример 4.9
Вычислить площадь фигуры, лежащей в первом квадранте, ограниченной линиями 

Решение:
Функция 
составной график которой ограничивает трапецию сверху, является непрерывной на промежутке
Площадь криволинейной трапеции равна
Пример 5.0
Найти площадь астроиды
Решение:
Запишем уравнение астроиды в параметрическом виде 
Здесь удобнее вычислить сначала 
Лекции:
- Объем цилиндра
- Сходимость степенного ряда
- Матрица перехода
- Дифференциальные уравнения второго порядка
- Сюръекция, инъекция и биекция.
- Исследовать функцию на экстремум
- Нормальный закон распределения
- Что такое производная
- Криволинейный интеграл 1 рода
- Исследовать ряд на сходимость: пример решения
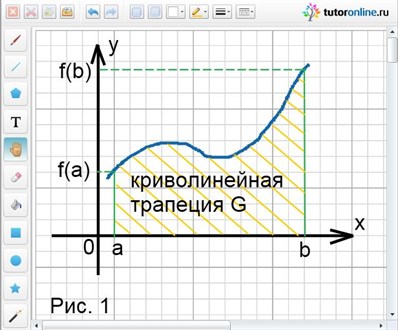
Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.
Определение.
Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).
Определенный интеграл ʃаb f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.
То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл ʃаb f(x)dx.
Таким образом, S(G) = ʃаb f(x)dx.
В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃаb f(x)dx.
Пример 1.
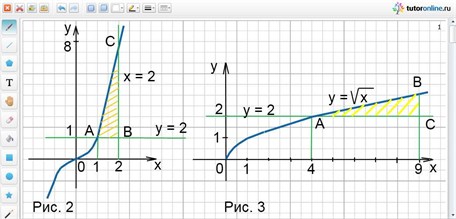
Вычислить площадь фигуры, ограниченной линиями у = х3; у = 1; х = 2.
Решение.
Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.
Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.
Используя формулу S = ʃаb f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:
{у = х3,
{у = 1.
Таким образом, имеем х1 = 1 – нижний предел и х = 2 – верхний предел.
Итак, S = SDACE – SDABE = ʃ12 x3 dx – 1 = x4/4|12 – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).
Ответ: 11/4 кв. ед.
Пример 2.
Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.
Решение.
Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции
у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.
Искомая площадь равна S = ʃаb(√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:
{у = √х,
{у = 2.
Таким образом, имеем, что х = 4 = а – это нижний предел.
Итак, S = ∫49 (√x – 2)dx = ∫49 √x dx –∫49 2dx = 2/3 x√х|49 – 2х|49 = (18 – 16/3) – (18 – 
Ответ: S = 2 2/3 кв. ед.
Пример 3.
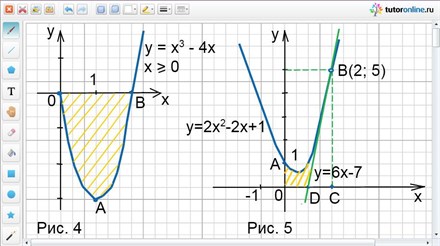
Вычислить площадь фигуры, ограниченной линиями у = х3 – 4х; у = 0; х ≥ 0.
Решение.
Построим график функции у = х3 – 4х при х ≥ 0. Для этого найдем производную у’:
y’ = 3x2 – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.
Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции уmin = -16/(3√3) ≈ -3.
Определим точки пересечения графика с осями координат:
если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;
если у = 0, то х3 – 4х = 0 или х(х2 – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х1 = 0, х2 = 2, х3 = -2 (не подходит, т.к. х ≥ 0).
Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.
Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.
Так как функция у = х3 – 4х принимает на (0; 2) отрицательное значение, то
S = |ʃ02 (x3 – 4x)dx|.
Имеем: ʃ02 (x3 – 4х)dx =(x4/4 – 4х2/2)|02= -4, откуда S = 4 кв. ед.
Ответ: S = 4 кв. ед.
Пример 4.
Найти площадь фигуры, ограниченной параболой у = 2х2 – 2х + 1, прямыми х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х0 = 2.
Решение.
Сначала составим уравнение касательной к параболе у = 2х2 – 2х + 1 в точке с абсциссой х₀ = 2.
Так как производная y’ = 4x – 2, то при х0 = 2 получим k = y’(2) = 6.
Найдем ординату точки касания: у0 = 2 · 22 – 2 · 2 + 1 = 5.
Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.
Построим фигуру, ограниченную линиями:
у = 2х2 – 2х + 1, у = 0, х = 0, у = 6х – 7.
Гу = 2х2 – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение 2х2 – 2х + 1 = 0 не имеет решений (D < 0). Найдем вершину параболы:
xb = -b/2a;
xb = 2/4 = 1/2;
yb = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).
Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.
Имеем: SОAВD = SOABC – SADBC.
Найдем координаты точки D из условия:
6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.
Площадь треугольника DBC найдем по формуле SADBC = 1/2 · DC · BC. Таким образом,
SADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.
Далее:
SOABC = ʃ02(2x2 – 2х + 1)dx = (2x3/3 – 2х2/2 + х)|02 = 10/3 (кв. ед.).
Окончательно получим: SОAВD = SOABC – SADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).
Ответ: S = 1 1/4 кв. ед.
Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями. Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.