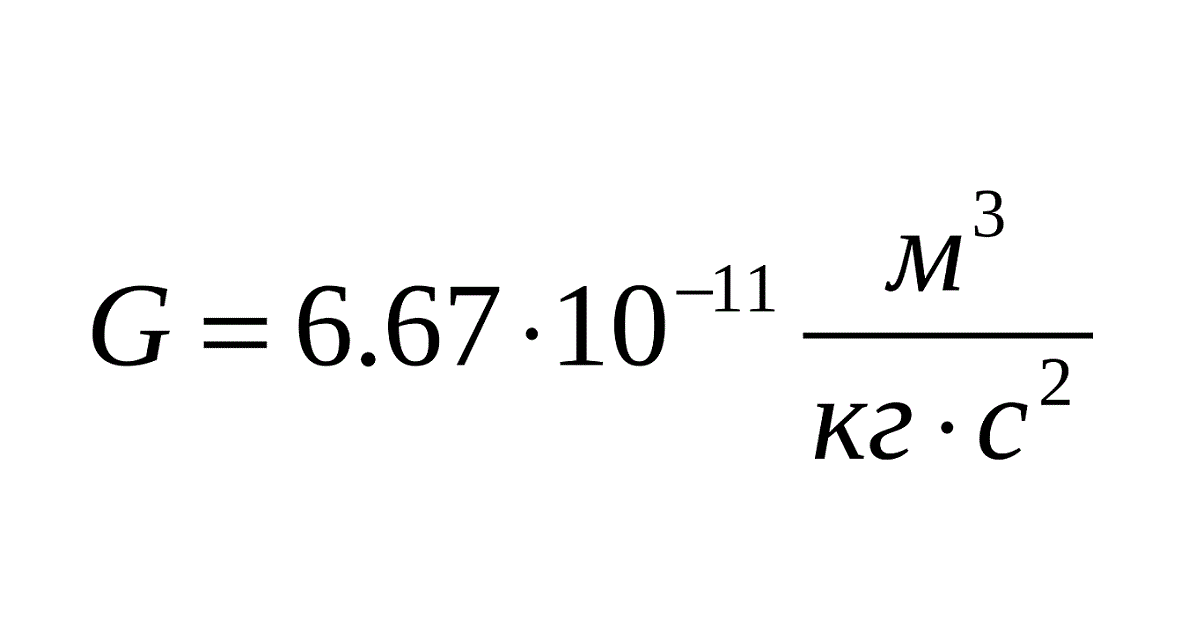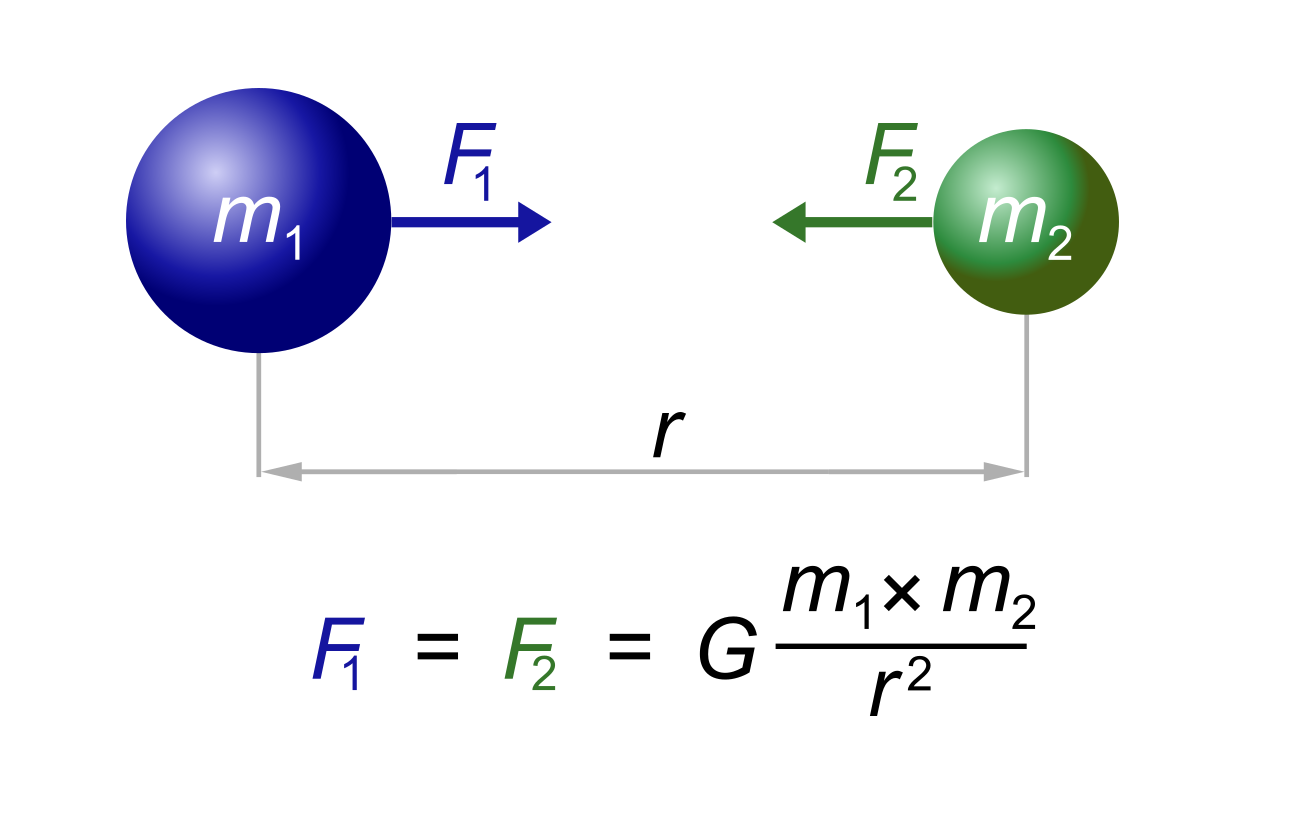В современной формулировке закона всемирного тяготения присутствует коэффициент , называющийся гравитационной постоянной и стоящий перед формулой особняком. Интересно, что Ньютон, открывший закон притяжения, не использовал явную форму константы, численно она была определена больше века спустя со дня смерти учёного.
Содержание
- Что такое и чему равна гравитационная постоянная
- В чём измеряется гравитационная постоянная
- Как найти гравитационную постоянную – история открытия
- Работы Ньютона
- Как была экспериментально определена гравитационная постоянная – эксперимент Кавендиша
- Измерение гравитационной постоянной
- Современная история изменений гравитационной постоянной
Что такое и чему равна гравитационная постоянная
Формула закона всемирного тяготения, известная по курсу школьной механики:
G – коэффициент пропорциональности или гравитационная постоянная;
m1, m2 – массы двух тел, испытывающих взаимное притяжение;
r – расстояние между ними.
Коэффициент пропорциональности G обозначает силу, с которой притягивается пара килограммовых объектов, расположенных друг от друга на метровом расстоянии. Значение константы обычно принимается равным:
Столь маленькое число объясняет, почему несмотря на постоянное действие гравитации люди, находящиеся рядом, не чувствуют силу тяготения – она проявляется на объектах огромных масс, имеющих высокие порядки, например, массе планет, Солнца, других звёзд.
В чём измеряется гравитационная постоянная
Несмотря на то, что гравитационная постоянная численно равна силе, её единицы измерения не ньютоны. Размерность коэффициента может показаться страшной –
, но её возникновение легко объясняется.
Согласно Международной системе единиц (системе интернациональной или СИ), сила измеряется в ньютонах, причём
то есть 1 ньютон – сила, изменяющая скорость килограммового объекта на 1 м/с за одну секунду.
После открытия закона тяготения определено: пара килограммовых тел притягивается друг к другу силой со значением, зависящим обратно пропорционально от квадрата расстояния между объектами.
То есть единица измерения гравитационной силы –
и размерность не совпадает с привычной . Требуется коэффициент, который должен уравнять единицы измерения привычной силы и силы гравитационного взаимодействия.
Проведём математические вычисления самостоятельно.
Нужно уравнять
и 
Для этого нужно разделить на 1с2 и 1кг, а также умножить на м3, получим:
Получилась требуемая размерность.
Следовательно, постоянная имеет размерность .
Как найти гравитационную постоянную – история открытия
Коэффициент G – универсальная константа, измерение которой осуществляется экспериментальным путём. Доподлинно неизвестно, кто открыл значение гравитационной постоянной, первое употребление в «Трактате по механике» Пуассона датируется 1811 годом.
Работы Ньютона
При публикации закона тяготения в трактате Ньютона отсутствовало явное обозначение константы, характеризующее гравитацию и её действие. Коэффициент не появлялся в работах по физике вплоть до конца восемнадцатого века, его точное значение не было вычислено.
Вместо известной сегодня постоянной присутствовал гравитационный параметр:
M – масса объекта, причём, масса планеты или звезды, так как гравитационный параметр нашёл широкое распространение в астрофизике.
Сегодня для объектов Солнечной системы значение параметра рассчитано точнее, чем гравитационная постоянная G и масса по отдельности, так как она не требует серьёзных экспериментов, вычисляется на основании астрономических наблюдений.
Например:
Подробнее о использовании закона всемирного тяготения в астрономии вы можете прочитать в нашей статье.
Как была экспериментально определена гравитационная постоянная – эксперимент Кавендиша
Естествоиспытатель Джон Митчел придумал эксперимент для определения массы Земли при помощи крутильных весов, однако не реализовал его. После его смерти идея опыта и аппаратура перешли к английскому физику и химику Генри Кавендишу, который, усовершенствовав прибор, провёл ряд экспериментов и осуществил задумку своего предшественника.
Главенствующая роль в опытах отводилась установке. На метровой нити из меди подвешивалось коромысло длиной 1,8 метра, на его концах устанавливалась пара свинцовых шариков диаметром 5 сантиметров, массой 775 грамм. Чуть выше крепилась поворотная ферма, причём тщательно соблюдалось требование совпадения оси вращения фермы с медной нитью. На концах поворотной штанги находилось по одному большому свинцовому шару диаметром 20 сантиметров, массой 49,5 килограмм. Чтобы избежать влияния конвекционных воздушных потоков, вся установка накрывалась плотным деревянным кожухом. Вследствие взаимодействия лёгкие шарики притягивались к тяжёлым, закручивая нить и отклоняя коромысло. Угол отклонения фиксировался двумя телескопами, а сила упругости нити приравнивалась гравитационному взаимодействию шаров.
Величина определённой силы притяжения составляла 0,17 микроньютона. Если сравнивать это значение с весом маленького шара, то оно меньше последнего примерно в 45 миллионов раз.
В результате своего эксперимента Генри Кавендиш рассчитал среднюю плотность Земли, причём его эксперимент был точным – погрешность измеренного значения в сравнении с современным значением составляет всего 0,7%. Именно Кавендишу приписывают открытие значения гравитационной постоянной, однако он никогда не задавался подобной целью при проведении своих опытов. Очевидно, величина константы определена на основании результатов его эксперимента, но кто сделал это первым, неизвестно.
Измерение гравитационной постоянной
Значение константы, полученное по измеренной Кавендишем плотности, по разным источникам разнится. Британская энциклопедия называет число, равное , с каковым некоторые современные физики. Леон Нил Купер утверждает, что экспериментально полученное число равно

.
Коэффициент пропорциональности определяли после Генри Кавендиша, причём зачастую его установку модернизировали новыми материалами. Например, в 1872 году Корню и Байль для измерения гравитационной постоянной использовали платиновые маленькие шарики и стеклянные, наполненные ртутью, большие. Результаты опыта показали значение

Современная история изменений гравитационной постоянной
Гравитационная постоянная – десятичная дробь, её значение постоянно уточняется, причём измерение коэффициента G происходит путём усовершенствования прибора Митчела и улучшения методов наблюдения. Например, в 2018 году учёные из России и Китая проводили опыты на установках разной конструкции. В первой группе применялся метод «time of swing» (TOS), где коэффициент пропорциональности зависит от колебательной частоты весов. Во второй – метод «angular acceleration feedback» (AAF), где угловое ускорение независимо вращающихся коромысел шаров измеряется системой управления с обратной связью, при этом нить поддерживается незакрученной.
По результатам команды первый метод продемонстрировал значение гравитационной постоянной , второй метод –
. Относительная погрешность составила 11,6*10-6
Комитет по данным для науки и техники (CODATA) рекомендовал на 2020 год значение коэффициента пропорциональности, равное:
Таким образом, гравитационная постоянная всё время уточняется, требуя новые, более точные способы измерения и вычисления.
На чтение 8 мин Просмотров 2.2к.
Наблюдая за перемещением небесных объектов, люди пытались найти объяснение происходящим на небе событиям. У древних людей преобладали версии мистического характера. Но в 17-м веке Исааком Ньютоном было предложено первое научное объяснение перемещению астрономических тел. Теория гравитации совершенствовалась еще несколько столетий, пока не приобрела современный вид.
Однако, несмотря на наблюдения и опыт, в современной астрофизике есть много пробелов и нестыковок, которые ученые затрудняются объяснить. Например, гравитационная константа, значение которой до сих пор не получается определить с достаточной степенью точности. А в последнее время появились предположения, что эта величина не совсем и константа. В этой статье мы и рассмотрим данный вопрос.
Содержание
- Что такое гравитационная постоянная
- Единица измерения гравитационной постоянной
- Как найти гравитационную постоянную, история открытия
- Работы Ньютона
- Экспериментальное определение гравитационной постоянной, эксперимент Кавендиша
- Измерение гравитационной постоянной
- Современная история изменений гравитационной постоянной
Что такое гравитационная постоянная
Гравитационной постоянной (постоянной Ньютона) называют коэффициент, входящий в формулу закона всемирного тяготения. Численное значение константы гравитации (G, GN или g) равно:
Постоянная Ньютона не зависит от характеристик взаимодействующих объектов и внешних критериев. Данный показатель активно используется практиками при вычислении орбит небесных объектов, в геолого-разведывательных процессах, в геодезии и геофизике.
Единица измерения гравитационной постоянной
Сила в физике сила измеряется в ньютонах:
Гравитационная постоянная численно равна силе, но при этом имеет другую размерность:
Данная единица измерения выводится при помощи несложных расчетов. Два тела весом по 1кг будут взаимно притягиваться с силой, обратно пропорциональной квадрату расстояния между ними:
Коэффициент, уравнивающий Н и единицу измерения гравитационной постоянной, вычисляется следующим образом:
Как найти гравитационную постоянную, история открытия
Открытию явления гравитации предшествовали труды многих исследователей. Еще в древней Греции были предложены гипотезы, которые пытались объяснить, почему материальные тела падают на землю, а не летят в произвольном направлении. История открытия гравитации представлена в таблице.
| Николай Коперник | Обосновал модель мира, в которой Солнце занимает центральное место, а остальные объекты вращаются вокруг него (гелиоцентрическая модель). |
| Уильям Гилберт | Высказал предположение, что наша планета и ее спутник являются магнитами друг для друга, при этом магнитная сила Земли больше из-за того, что больше ее масса. |
| Иоганн Кеплер | Сформулировал ряд законов, в том числе 3-й, который был использован при разработке теории гравитации: период обращения планет в квадрате соотносится как большие полуоси орбит в кубе. |
| Галилео Галилей | Обосновал, что если на тело не оказывать никаких воздействий, то оно будет оставаться в бездействии. Сформулировал закон, смысл которого заключался в том, что все тела, независимо от их тяжести, падают вниз с одинаковой скоростью, при этом пройденный путь пропорционален квадрату времени, за которое тело достигло поверхности Земли. |
| Роберт Гук | Сформулировал закон всемирного тяготения для некруговых орбит и предложил Ньютону обосновать его математически. Создал теорию об универсальной силе тяжести. |
| Эдмунд Галлей | Просчитал обратно пропорциональную зависимость силы тяжести и квадрата расстояния. |
| Исаак Ньютон | На основании работ предшественников вывел закон всемирного тяготения. |
| Генри Кавендиш | Собрал приспособление, с помощью которого можно определить величину константы гравитации. |
| Симеон Дени Пуассон | В его трудах впервые появляется понятие гравитационной константы. |
Ньютона интересовало выведение научных правил, а не чистота искомых значений. Экспериментаторы, которые применяли формулу Ньютона на практике, столкнулись с необходимостью введения поправочного коэффициента, который позже получил название ньютоновская константа. Возник вопрос, чему равна гравитационная постоянная. Последовавшие в данном направлении работы показали, что найти гравитационную постоянную можно только опытным путем.
Работы Ньютона
Научная почва для обоснования закона всемирного тяготения была основательно подготовлена предшественниками Ньютона. Большая часть расчетов базировалась на 3-м законе Кеплера. Сила, благодаря которой планеты удерживаются на орбитах, соизмерима с центростремительным ускорением, и должна быть обратно пропорциональна квадрату расстояния от центра планеты до центра Солнца. Сила, вызывающая падение предметов (пресловутого яблока) на землю, была сопоставлена ученым с силой, удерживающей Луну на ее орбите. Кроме того, физик установил центростремительное ускорение Луны относительно Земли.
Ранее опытным путем было установлено значение ускорения свободного падения объектов. Ученый применил удобные для вычислений цифры: дистанция от Луны до центра Земли в 60 раз больше, чем дистанция от объекта, находящегося на поверхности Земли. Если объект направить к центру Земли, то он за 1 секунду пролетит такой же путь, который пройдет Луна за 1 минуту. Эксперименты подтвердили точность теоретических выкладок с погрешностью около 1%. Это указывало на общность природы происхождения сил тяготения.
Из этого можно заключить, что сила обоюдного притяжения должна соответствовать каждой из масс. Также было подтверждено, что гравитация обратно пропорциональна квадрату расстояния между объектами. Исходя из вышесказанного, формула закона всемирного тяготения будет иметь следующий вид:
где F – сила гравитационного тяготения, g – гравитационная постоянная, m1 и m2 – массы объектов, R – расстояние между объектами.
Работы Ньютона внесли вклад в решение следующих вопросов:
- перемещения тел по космическим орбитам;
- ускорение свободного падения;
- приливы океанических вод;
- причины экваториальной выпуклости.
Эйнштейн использовал закон всемирного тяготения при разработке теории относительности. Постоянная гравитационная показывает соотношение между такими характеристиками уравнений поля, как геометрия пространства-времени и тензор энергии-импульса.
Вместо G Ньютон применял в расчетах «гравитационный параметр» µ. Практические наблюдения за космическими телами позволили определить для ряда небесных объектов значение µ с минимальной погрешностью. Рассчитывают µ по формуле:
µ=GM;
где G – константа гравитации, M – масса объекта
В трудах Кеплера также фигурирует гравитационный параметр. В физике с его помощью упрощают некоторые громоздкие формулы.
Экспериментальное определение гравитационной постоянной, эксперимент Кавендиша
Британец Джон Мичелл увековечил свое имя как создатель крутильных весов, с помощью которых впервые смогли определить величину g. Экспериментальное определение гравитационной постоянной не входило в планы исследователя. Он хотел «взвесить» нашу планету. Однако воплотить свои планы Мичелл не успел, и сконструированное им устройство после его кончины досталось Генри Кавендишу.
Кавендиш доработал установку. Конструкция включала шестифутовый стержень, закрепленный на медном волокне длиной 1 м. К плечам коромысла ученый прикрепил два шара из свинца по 775 грамм каждый, соорудив таким образом гантельку. Затем рядом с маленькими шариками он разместил крупные шары по 49,5 кг, что привело к возникновению явления гравитации между объектами. Стержень конструкции отклонился от первоначального положения, что дало возможность найти величину угла поворота гантельки. Опыт Кавендиша оказался успешным: увязав упругие свойства волокна, массу шаров, размер установки и значение угла, он определил массу Земли и ее среднюю плотность. Сегодня эксперимент Кавендиша по-прежнему актуален, исследователями разрабатываются инновационные модификации прибора.
Измерение гравитационной постоянной
С измерением степени точности гравитационной постоянной g сложилась парадоксальная ситуация. Последние многочисленные эксперименты определяют отклонение с точностью 10-4. Это хуже на несколько порядков по сравнению с точностью определения прочих базисных величин. Сравнительно аккуратные результаты можно получить в условиях лаборатории, измеряя силу гравитации между двумя телами с известной массой (модификации эксперимента Кавендиша). Новые атомно-интерферометрические устройства оказались непригодными в измерении гравитационной постоянной в связи с гораздо большей величиной погрешности, чем при эксперименте на механических устройствах.
Современная история изменений гравитационной постоянной
Неординарность ситуации с нахождением точного значения гравитационной константы привела к возникновению догадки, что G не является постоянной в классическом понимании и может с течением времени изменяться. В уравнениях общей теории относительности Эйнштейн увязал гравитационную постоянную и космологическую константу – параметр, который влияет на устойчивость Вселенной.
Хаббл и Фридман обосновали опытным путем модель расширяющейся Вселенной, что противоречило теории стационарной Вселенной Эйнштейна. На долгое время ученые прекратили учитывать при вычислениях космологическую постоянную. В конце 1990-х годов было выявлено и подтверждено ускорение расширения Вселенной. Вновь открытые результаты не вписывались в теорию Хаббла-Фридмана, концепцию пришлось пересматривать, и космологическая постоянная вернулась в физику.
Современная Лямбда-CDM модель Вселенной учитывает космологическую постоянную. Данная концепция объясняет наличие антигравитации, «темной материи», реликтового излучения, и является стандартом в астрофизике с 1998-го года.
Интересно, что Лямбда-CDM модель хорошо коррелирует с космологией черной дыры. Все больше ученых склонны отказываться от Теории большого взрыва, поскольку накопившиеся научные данные противоречат общепринятому взгляду на образование Вселенной. В гипотезу, что видимое нами пространство-время (и мы вместе с ним) бесконечно «падает» в гигантскую черную дыру, отлично вписывается явление ускорения расширения Вселенной, «странности» реликтового излучения, наличие темной материи.
Современная история изменений гравитационной постоянной привела к попыткам астрономов переосмыслить данный физический параметр. Так, Филипп Мангейм считает, что константа g в зависимости от условий ее измерения может менять свое значение. В условиях нашей планеты постоянная g будет иметь известную ученым величину, а вот в космосе значение G будет гораздо меньше.
Космологическая постоянная, описывающая скорость расширения Вселенной, имеет расчетное значение в 10120 раз превосходящее наблюдаемое. Если бы значение g было верным, то галактики не успели бы образоваться. По мнению Мангейма, в расчеты следует ввести новую величину, которая будет пропорциональна произведению космологической и гравитационной констант.
Такой подход позволит устранить существующие противоречия, но у него есть и свои недостатки: подвергаются сомнению основы теории относительности, не объясняется существование реликтового излучения и двойных пульсаров. Преимуществом идеи Мангейма является возможность синтеза теории гравитации и физики элементарных частиц в одну универсальную доктрину.
По вашему мнению, ньютоновская константа – это объективный параметр, или мы просто не все знаем о физических феноменах?
Значение гравитационной постоянной
Содержание:
- 1 Общие сведения
- 2 Работы Ньютона
- 3 Эксперимент Кавендиша
- 4 Измерение гравитационной постоянной
- 5 Материалы по теме
Общие сведения
Гравитационная постоянная или иначе – постоянная Ньютона – одна из основных констант, используемых в астрофизике. Фундаментальная физическая постоянная определяет силу гравитационного взаимодействия. Как известно, силу, с которой каждое из двух тел, взаимодействующих посредством гравитации, притягивается можно высчитать из современной формы записи закона всемирного тяготения Ньютона:
Гравитационное взаимодействие двух тел
Здесь:
- m1 и m2 — тела, взаимодействующие посредством гравитации
- F1 и F2 – векторы силы гравитационного притяжения, направленные к противоположному телу
- r – расстояние между телами
- G – гравитационная постоянная
Данный коэффициент пропорциональности равен модулю силы тяготения первого тела, которая действует на точечное второе тело единичной массы, при единичном расстоянии между этими телами.
G = 6,67408(31)·10−11 м3·с−2·кг−1, или Н·м²·кг−2.
Очевидно, что данная формула широко применима в области астрофизики и позволяет рассчитать гравитационное возмущение двух массивных космических тел, для определения дальнейшего их поведения.
Работы Ньютона
Примечательно, что в трудах Ньютона (1684—1686) гравитационная постоянная в явном виде отсутствовала, как и в записях других ученых аж до конца XVIII-го века.
Исаак Ньютон (1643 — 1727)
Ранее использовался так называемый гравитационный параметр, который равнялся произведению гравитационной постоянной на массу тела. Нахождение такого параметра в то время было более доступно, поэтому на сегодняшний день значение гравитационного параметра различных космических тел (в основном Солнечной системы) более точно известно, нежели порознь значение гравитационной постоянной и массы тела.
µ = GM
Здесь: µ — гравитационный параметр, G – гравитационная постоянная, а M — масса объекта.
Размерность гравитационного параметра — м3с−2.
Следует отметить тот факт, что значение гравитационной постоянной несколько варьируется даже до сегодняшнего дня, а чистое значение масс космических тел в то время было определить довольно сложно, поэтому гравитационный параметр нашел более широкое применение.
Эксперимент Кавендиша
Эксперимент по определению точного значения гравитационной постоянной впервые предложил английский естествоиспытатель Джон Мичелл, который сконструировал крутильные весы. Однако, не успев провести эксперимент, в 1793-м году Джон Мичелл умер, а его установка перешла в руки Генри Кавендишу – британскому физику. Генри Кавендиш улучшил полученное устройство и провел опыты, результаты которых были опубликованы в 1798-м году в научном журнале под названием «Философские труды Королевского общества».
Генри Кавендиш (1731 — 1810)
Установка для проведения эксперимента состояла из нескольких элементов. Прежде всего она включала 1,8-метровое коромысло, к концам которого крепились свинцовые шарики с массой 775 г и диаметром 5 см. Коромысло было подвешено на медной 1-метровой нити. Несколько выше крепления нити, ровно над ее осью вращения устанавливалась еще одна поворотная штанга, к концам которой жестко крепились два шара массой 49,5 кг и диаметром 20 см. Центры всех четырех шаров должны были лежать в одной плоскости. В результате гравитационного взаимодействия притяжение малых шаров к большим должно быть заметно. При таком притяжении нить коромысла закручивается до некоторого момента, и ее сила упругости должна равняться силе тяготения шаров. Генри Кавендиш измерял силу тяготения посредством измерения угла отклонения плеча коромысла.
Установка Генри Кавендиша
Более наглядное описание эксперимента доступно в видео ниже:
https://www.youtube.com/watch?v=iOgrSlzyFMA» frameborder=»0″ allowfullscreen>
Для получения точного значения константы Кавендишу пришлось прибегнуть к ряду мер, снижающих влияние сторонних физических факторов на точность эксперимента. В действительности Генри Кавендиша проводил эксперимент не для того, чтобы выяснить значение гравитационной постоянной, а для расчета средней плотности Земли. Для этого он сравнивал колебания тела, вызванные гравитационным возмущением шара известной массы, и колебания, вызванные тяготением Земли. Он достаточно точно вычислил значение плотности Земли – 5,47 г/см3 (сегодня более точные расчеты дают 5,52 г/см3). Согласно различным источникам, значение гравитационной постоянной, высчитанное из гравитационного параметра с учетом плотности Земли, полученной Кавердишем, составило G=6,754·10−11 м³/(кг·с²), G = 6,71·10−11м³/(кг·с²) или G = (6,6 ± 0,04)·10−11м³/(кг·с²). До сих пор неизвестно, кто впервые получил численное значение постоянной Ньютона из работ Генри Кавердиша.
Измерение гравитационной постоянной
Наиболее раннее упоминание гравитационной постоянной, как отдельной константы, определяющей гравитационное взаимодействие, найдено в «Трактате по механике», написанном в 1811-м году французским физиком и математиком — Симеоном Дени Пуассоном.
Материалы по теме
Измерение гравитационной постоянной проводится различными группами ученых и по сей день. При этом, несмотря на обилие доступных исследователям технологий, результаты экспериментов дают различные значения данной константы. Из этого можно было бы сделать вывод, что, возможно, гравитационная постоянная на самом деле непостоянная, а способна менять свое значение, с течением времени или от места к месту. Однако, если значения константы по результатам экспериментов разнятся, то неизменность этих значений в рамках этих экспериментов уже проверена с точностью до 10-17. Кроме того, согласно астрономическим данным постоянная G не изменилась в значительной степени за несколько последних сотен миллионов лет. Если постоянная Ньютона и способна меняться, то ее изменение не превысило б отклонение на число 10-11 – 10-12 в год.
Примечательно, что летом 2014-го года совместно группа итальянских и нидерландских физиков провели эксперимент по измерению гравитационной постоянной совсем иного вида. В эксперименте использовались атомные интерферометры, которые позволяют отследить влияние земной гравитации на атомы. Значение константы, полученное таким образом, имеет погрешность 0,015% и равняется G = 6.67191(99) × 10−11 м3·с−2·кг−1.
| Gravitational constant | |
|---|---|
|
Common symbols |
G |
| SI unit | m3⋅kg−1⋅s−2 |
| Dimension |  |
The gravitational constant (also known as the universal gravitational constant, the Newtonian constant of gravitation, or the Cavendish gravitational constant),[a] denoted by the capital letter G, is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton’s law of universal gravitation and in Albert Einstein’s theory of general relativity.
In Newton’s law, it is the proportionality constant connecting the gravitational force between two bodies with the product of their masses and the inverse square of their distance. In the Einstein field equations, it quantifies the relation between the geometry of spacetime and the energy–momentum tensor (also referred to as the stress–energy tensor).
The measured value of the constant is known with some certainty to four significant digits. In SI units, its value is approximately 6.674×10−11 m3⋅kg−1⋅s−2.[1]
The modern notation of Newton’s law involving G was introduced in the 1890s by C. V. Boys. The first implicit measurement with an accuracy within about 1% is attributed to Henry Cavendish in a 1798 experiment.[b]
Definition[edit]
According to Newton’s law of universal gravitation, the magnitude of the attractive force (F) between two point-like bodies is directly proportional to the product of their masses, m1 and m2, and inversely proportional to the square of the distance, r, directed along the line connecting their centers of mass:
The constant of proportionality, G, in this non-relativistic formulation is the gravitational constant. Colloquially, the gravitational constant is also called «Big G», distinct from «small g» (g), which is the local gravitational field of Earth (equivalent to the free-fall acceleration).[2][3] Where 

The gravitational constant appears in the Einstein field equations of general relativity,[4][5]
where Gμν is the Einstein tensor, Λ is the cosmological constant, gμν is the metric tensor, Tμν is the stress–energy tensor, and κ is the Einstein gravitational constant, a constant originally introduced by Einstein that is directly related to the Newtonian constant of gravitation:[5][6][c]
Value and uncertainty[edit]
| Value of G | Unit |
|---|---|
| 6.67430(15)×10−11[1] | N⋅m2⋅kg−2 |
| 6.67430(15)×10−8 | dyn⋅cm2⋅g−2 |
| 4.3009172706(3)×10−3 | pc⋅M⊙−1⋅(km/s)2 |
The gravitational constant is a physical constant that is difficult to measure with high accuracy.[7] This is because the gravitational force is an extremely weak force as compared to other fundamental forces at the laboratory scale.[d]
In SI units, the 2018 Committee on Data for Science and Technology (CODATA)-recommended value of the gravitational constant (with standard uncertainty in parentheses) is:[1][8]
This corresponds to a relative standard uncertainty of 2.2×10−5 (22 ppm).
Natural units[edit]
The gravitational constant is a defining constant in some systems of natural units, particularly geometrized unit systems, such as Planck units and Stoney units. When expressed in terms of such units, the value of the gravitational constant will generally have a numeric value of 1 or a value close to it. Due to the significant uncertainty in the measured value of G in terms of other known fundamental constants, a similar level of uncertainty will show up in the value of many quantities when expressed in such a unit system.
Orbital mechanics[edit]
In astrophysics, it is convenient to measure distances in parsecs (pc), velocities in kilometres per second (km/s) and masses in solar units M⊙. In these units, the gravitational constant is:
For situations where tides are important, the relevant length scales are solar radii rather than parsecs. In these units, the gravitational constant is:
In orbital mechanics, the period P of an object in circular orbit around a spherical object obeys
where V is the volume inside the radius of the orbit. It follows that
This way of expressing G shows the relationship between the average density of a planet and the period of a satellite orbiting just above its surface.
For elliptical orbits, applying Kepler’s 3rd law, expressed in units characteristic of Earth’s orbit:
where distance is measured in terms of the semi-major axis of Earth’s orbit (the astronomical unit, AU), time in years, and mass in the total mass of the orbiting system (M = M☉ + MEarth + M☾[e]).
The above equation is exact only within the approximation of the Earth’s orbit around the Sun as a two-body problem in Newtonian mechanics, the measured quantities contain corrections from the perturbations from other bodies in the solar system and from general relativity.
From 1964 until 2012, however, it was used as the definition of the astronomical unit and thus held by definition:
Since 2012, the AU is defined as 1.495978707×1011 m exactly, and the equation can no longer be taken as holding precisely.
The quantity GM—the product of the gravitational constant and the mass of a given astronomical body such as the Sun or Earth—is known as the standard gravitational parameter (also denoted μ). The standard gravitational parameter GM appears as above in Newton’s law of universal gravitation, as well as in formulas for the deflection of light caused by gravitational lensing, in Kepler’s laws of planetary motion, and in the formula for escape velocity.
This quantity gives a convenient simplification of various gravity-related formulas. The product GM is known much more accurately than either factor is.
Values for GM| Body | μ = GM | Value | Relative uncertainty |
|---|---|---|---|
| Sun | GM☉ | 1.32712440018(8)×1020 m3⋅s−2[9] | 6×10−11 |
| Earth | GMEarth | 3.986004418(8)×1014 m3⋅s−2[10] | 2×10−9 |
Calculations in celestial mechanics can also be carried out using the units of solar masses, mean solar days and astronomical units rather than standard SI units. For this purpose, the Gaussian gravitational constant was historically in widespread use, k = 0.01720209895, expressing the mean angular velocity of the Sun–Earth system measured in radians per day.[citation needed] The use of this constant, and the implied definition of the astronomical unit discussed above, has been deprecated by the IAU since 2012.[citation needed]
History of measurement[edit]
Early history[edit]
The existence of the constant is implied in Newton’s law of universal gravitation as published in the 1680s (although its notation as G dates to the 1890s),[11] but is not calculated in his Philosophiæ Naturalis Principia Mathematica where it postulates the inverse-square law of gravitation. In the Principia, Newton considered the possibility of measuring gravity’s strength by measuring the deflection of a pendulum in the vicinity of a large hill, but thought that the effect would be too small to be measurable.[12] Nevertheless, he had the opportunity to estimate the order of magnitude of the constant when he surmised that «the mean density of the earth might be five or six times as great as the density of water», which is equivalent to a gravitational constant of the order:[13]
- G ≈ (6.7±0.6)×10−11 m3⋅kg−1⋅s−2
A measurement was attempted in 1738 by Pierre Bouguer and Charles Marie de La Condamine in their «Peruvian expedition». Bouguer downplayed the significance of their results in 1740, suggesting that the experiment had at least proved that the Earth could not be a hollow shell, as some thinkers of the day, including Edmond Halley, had suggested.[14]
The Schiehallion experiment, proposed in 1772 and completed in 1776, was the first successful measurement of the mean density of the Earth, and thus indirectly of the gravitational constant. The result reported by Charles Hutton (1778) suggested a density of 4.5 g/cm3 (4+1/2 times the density of water), about 20% below the modern value.[15] This immediately led to estimates on the densities and masses of the Sun, Moon and planets, sent by Hutton to Jérôme Lalande for inclusion in his planetary tables. As discussed above, establishing the average density of Earth is equivalent to measuring the gravitational constant, given Earth’s mean radius and the mean gravitational acceleration at Earth’s surface, by setting[11]
Based on this, Hutton’s 1778 result is equivalent to G ≈ 8×10−11 m3⋅kg−1⋅s−2.
Diagram of torsion balance used in the Cavendish experiment performed by Henry Cavendish in 1798, to measure G, with the help of a pulley, large balls hung from a frame were rotated into position next to the small balls.
The first direct measurement of gravitational attraction between two bodies in the laboratory was performed in 1798, seventy-one years after Newton’s death, by Henry Cavendish.[16] He determined a value for G implicitly, using a torsion balance invented by the geologist Rev. John Michell (1753). He used a horizontal torsion beam with lead balls whose inertia (in relation to the torsion constant) he could tell by timing the beam’s oscillation. Their faint attraction to other balls placed alongside the beam was detectable by the deflection it caused. In spite of the experimental design being due to Michell, the experiment is now known as the Cavendish experiment for its first successful execution by Cavendish.
Cavendish’s stated aim was the «weighing of Earth», that is, determining the average density of Earth and the Earth’s mass. His result, ρ🜨 = 5.448(33) g·cm−3, corresponds to value of G = 6.74(4)×10−11 m3⋅kg−1⋅s−2. It is surprisingly accurate, about 1% above the modern value (comparable to the claimed standard uncertainty of 0.6%).[17]
19th century[edit]
The accuracy of the measured value of G has increased only modestly since the original Cavendish experiment.[18] G is quite difficult to measure because gravity is much weaker than other fundamental forces, and an experimental apparatus cannot be separated from the gravitational influence of other bodies.
Measurements with pendulums were made by Francesco Carlini (1821, 4.39 g/cm3), Edward Sabine (1827, 4.77 g/cm3), Carlo Ignazio Giulio (1841, 4.95 g/cm3) and George Biddell Airy (1854, 6.6 g/cm3).[19]
Cavendish’s experiment was first repeated by Ferdinand Reich (1838, 1842, 1853), who found a value of 5.5832(149) g·cm−3,[20] which is actually worse than Cavendish’s result, differing from the modern value by 1.5%. Cornu and Baille (1873), found 5.56 g·cm−3.[21]
Cavendish’s experiment proved to result in more reliable measurements than pendulum experiments of the «Schiehallion» (deflection) type or «Peruvian» (period as a function of altitude) type. Pendulum experiments still continued to be performed, by Robert von Sterneck (1883, results between 5.0 and 6.3 g/cm3) and Thomas Corwin Mendenhall (1880, 5.77 g/cm3).[22]
Cavendish’s result was first improved upon by John Henry Poynting (1891),[23] who published a value of 5.49(3) g·cm−3, differing from the modern value by 0.2%, but compatible with the modern value within the cited standard uncertainty of 0.55%. In addition to Poynting, measurements were made by C. V. Boys (1895)[24] and Carl Braun (1897),[25] with compatible results suggesting G = 6.66(1)×10−11 m3⋅kg−1⋅s−2. The modern notation involving the constant G was introduced by Boys in 1894[11] and becomes standard by the end of the 1890s, with values usually cited in the cgs system. Richarz and Krigar-Menzel (1898) attempted a repetition of the Cavendish experiment using 100,000 kg of lead for the attracting mass. The precision of their result of 6.683(11)×10−11 m3⋅kg−1⋅s−2 was, however, of the same order of magnitude as the other results at the time.[26]
Arthur Stanley Mackenzie in The Laws of Gravitation (1899) reviews the work done in the 19th century.[27] Poynting is the author of the article «Gravitation» in the Encyclopædia Britannica Eleventh Edition (1911). Here, he cites a value of G = 6.66×10−11 m3⋅kg−1⋅s−2 with an uncertainty of 0.2%.
Modern value[edit]
Paul R. Heyl (1930) published the value of 6.670(5)×10−11 m3⋅kg−1⋅s−2 (relative uncertainty 0.1%),[28] improved to 6.673(3)×10−11 m3⋅kg−1⋅s−2 (relative uncertainty 0.045% = 450 ppm) in 1942.[29]
Published values of G derived from high-precision measurements since the 1950s have remained compatible with Heyl (1930), but within the relative uncertainty of about 0.1% (or 1,000 ppm) have varied rather broadly, and it is not entirely clear if the uncertainty has been reduced at all since the 1942 measurement. Some measurements published in the 1980s to 2000s were, in fact, mutually exclusive.[7][30] Establishing a standard value for G with a standard uncertainty better than 0.1% has therefore remained rather speculative.
By 1969, the value recommended by the National Institute of Standards and Technology (NIST) was cited with a standard uncertainty of 0.046% (460 ppm), lowered to 0.012% (120 ppm) by 1986. But the continued publication of conflicting measurements led NIST to considerably increase the standard uncertainty in the 1998 recommended value, by a factor of 12, to a standard uncertainty of 0.15%, larger than the one given by Heyl (1930).
The uncertainty was again lowered in 2002 and 2006, but once again raised, by a more conservative 20%, in 2010, matching the standard uncertainty of 120 ppm published in 1986.[31] For the 2014 update, CODATA reduced the uncertainty to 46 ppm, less than half the 2010 value, and one order of magnitude below the 1969 recommendation.
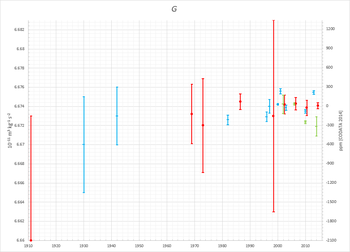
The following table shows the NIST recommended values published since 1969:
Timeline of measurements and recommended values for G since 1900: values recommended based on a literature review are shown in red, individual torsion balance experiments in blue, other types of experiments in green.
| Year | G (10−11·m3⋅kg−1⋅s−2) |
Standard uncertainty | Ref. |
|---|---|---|---|
| 1969 | 6.6732(31) | 460 ppm | [32] |
| 1973 | 6.6720(49) | 730 ppm | [33] |
| 1986 | 6.67449(81) | 120 ppm | [34] |
| 1998 | 6.673(10) | 1,500 ppm | [35] |
| 2002 | 6.6742(10) | 150 ppm | [36] |
| 2006 | 6.67428(67) | 100 ppm | [37] |
| 2010 | 6.67384(80) | 120 ppm | [38] |
| 2014 | 6.67408(31) | 46 ppm | [39] |
| 2018 | 6.67430(15) | 22 ppm | [40] |
In the January 2007 issue of Science, Fixler et al. described a measurement of the gravitational constant by a new technique, atom interferometry, reporting a value of G = 6.693(34)×10−11 m3⋅kg−1⋅s−2, 0.28% (2800 ppm) higher than the 2006 CODATA value.[41] An improved cold atom measurement by Rosi et al. was published in 2014 of G = 6.67191(99)×10−11 m3⋅kg−1⋅s−2.[42][43] Although much closer to the accepted value (suggesting that the Fixler et al. measurement was erroneous), this result was 325 ppm below the recommended 2014 CODATA value, with non-overlapping standard uncertainty intervals.
As of 2018, efforts to re-evaluate the conflicting results of measurements are underway, coordinated by NIST, notably a repetition of the experiments reported by Quinn et al. (2013).[44]
In August 2018, a Chinese research group announced new measurements based on torsion balances, 6.674184(78)×10−11 m3⋅kg−1⋅s−2 and 6.674484(78)×10−11 m3⋅kg−1⋅s−2 based on two different methods.[45] These are claimed as the most accurate measurements ever made, with a standard uncertainties cited as low as 12 ppm. The difference of 2.7σ between the two results suggests there could be sources of error unaccounted for.
Constancy[edit]
Analysis of observations of 580 type Ia supernovae shows that the gravitational constant has varied by less than one part in ten billion per year over the last nine billion years.[46]
See also[edit]
- Gravity of Earth
- Standard gravity
- Gaussian gravitational constant
- Orbital mechanics
- Escape velocity
- Gravitational potential
- Gravitational wave
- Strong gravity
- Dirac large numbers hypothesis
- Accelerating expansion of the universe
- Lunar Laser Ranging experiment
- Cosmological constant
References[edit]
Footnotes
- ^ «Newtonian constant of gravitation» is the name introduced for G by Boys (2000). Use of the term by T.E. Stern (1928) was misquoted as «Newton’s constant of gravitation» in Pure Science Reviewed for Profound and Unsophisticated Students (1930), in what is apparently the first use of that term. Use of «Newton’s constant» (without specifying «gravitation» or «gravity») is more recent, as «Newton’s constant» was also
used for the heat transfer coefficient in Newton’s law of cooling, but has by now become quite common, e.g.
Calmet et al, Quantum Black Holes (2013), p. 93; P. de Aquino, Beyond Standard Model Phenomenology at the LHC (2013), p. 3.The name «Cavendish gravitational constant», sometimes «Newton–Cavendish gravitational constant», appears to have been common in the 1970s to 1980s, especially in (translations from) Soviet-era Russian literature, e.g. Sagitov (1970 [1969]), Soviet Physics: Uspekhi 30 (1987), Issues 1–6, p. 342 [etc.].
«Cavendish constant» and «Cavendish gravitational constant» is also used in Charles W. Misner, Kip S. Thorne, John Archibald Wheeler, «Gravitation», (1973), 1126f.Colloquial use of «Big G», as opposed to «little g» for gravitational acceleration dates to the 1960s (R.W. Fairbridge, The encyclopedia of atmospheric sciences and astrogeology, 1967, p. 436; note use of «Big G’s» vs. «little g’s» as early as the 1940s of the Einstein tensor Gμν vs. the metric tensor gμν, Scientific, medical, and technical books published in the United States of America: a selected list of titles in print with annotations: supplement of books published 1945–1948, Committee on American Scientific and Technical Bibliography National Research Council, 1950, p. 26).
- ^ Cavendish determined the value of G indirectly, by reporting a value for the Earth’s mass, or the average density of Earth, as 5.448 g⋅cm−3.
- ^ Depending on the choice of definition of the Einstein tensor and of the stress–energy tensor it can alternatively be defined as κ = 8πG/c2 ≈ 1.866×10−26 m⋅kg−1
- ^ For example, the gravitational force between an electron and a proton 1 m apart is approximately 10−67 N, whereas the electromagnetic force between the same two particles is approximately 10−28 N. The electromagnetic force in this example is in the order of 1039 times greater than the force of gravity—roughly the same ratio as the mass of the Sun to a microgram.
- ^
M ≈ 1.000003040433 M☉, so that M = M☉ can be used for accuracies of five or fewer significant digits.
Citations
- ^ a b c «2018 CODATA Value: Newtonian constant of gravitation». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 20 May 2019.
- ^ Gundlach, Jens H.; Merkowitz, Stephen M. (23 December 2002). «University of Washington Big G Measurement». Astrophysics Science Division. Goddard Space Flight Center.
Since Cavendish first measured Newton’s Gravitational constant 200 years ago, ‘Big G’ remains one of the most elusive constants in physics
- ^ Halliday, David; Resnick, Robert; Walker, Jearl (September 2007). Fundamentals of Physics (8th ed.). p. 336. ISBN 978-0-470-04618-0.
- ^ Grøn, Øyvind; Hervik, Sigbjorn (2007). Einstein’s General Theory of Relativity: With Modern Applications in Cosmology (illustrated ed.). Springer Science & Business Media. p. 180. ISBN 978-0-387-69200-5.
- ^ a b Einstein, Albert (1916). «The Foundation of the General Theory of Relativity». Annalen der Physik. 354 (7): 769–822. Bibcode:1916AnP…354..769E. doi:10.1002/andp.19163540702. Archived from the original (PDF) on 6 February 2012.
- ^ Adler, Ronald; Bazin, Maurice; Schiffer, Menahem (1975). Introduction to General Relativity (2nd ed.). New York: McGraw-Hill. p. 345. ISBN 978-0-07-000423-8.
- ^ a b Gillies, George T. (1997). «The Newtonian gravitational constant: recent measurements and related studies». Reports on Progress in Physics. 60 (2): 151–225. Bibcode:1997RPPh…60..151G. doi:10.1088/0034-4885/60/2/001. S2CID 250810284.. A lengthy, detailed review. See Figure 1 and Table 2 in particular.
- ^ Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (21 July 2015). «CODATA Recommended Values of the Fundamental Physical Constants: 2014». Reviews of Modern Physics. 88 (3): 035009. arXiv:1507.07956. Bibcode:2016RvMP…88c5009M. doi:10.1103/RevModPhys.88.035009. S2CID 1115862.
- ^ «Astrodynamic Constants». NASA/JPL. 27 February 2009. Retrieved 27 July 2009.
- ^ «Geocentric gravitational constant». Numerical Standards for Fundamental Astronomy. IAU Division I Working Group on Numerical Standards for Fundamental Astronomy. Retrieved 24 June 2021 – via iau-a3.gitlab.io. Citing
- Ries JC, Eanes RJ, Shum CK, Watkins MM (20 March 1992). «Progress in the determination of the gravitational coefficient of the Earth». Geophysical Research Letters. 19 (6): 529–531. Bibcode:1992GeoRL..19..529R. doi:10.1029/92GL00259. S2CID 123322272.
- ^ a b c Boys 1894, p.330 In this lecture before the Royal Society, Boys introduces G and argues for its acceptance. See:
Poynting 1894, p. 4, MacKenzie 1900, p.vi - ^ Davies, R.D. (1985). «A Commemoration of Maskelyne at Schiehallion». Quarterly Journal of the Royal Astronomical Society. 26 (3): 289–294. Bibcode:1985QJRAS..26..289D.
- ^ «Sir Isaac Newton thought it probable, that the mean density of the earth might be five or six times as great as the density of water; and we have now found, by experiment, that it is very little less than what he had thought it to be: so much justness was even in the surmises of this wonderful man!» Hutton (1778), p. 783
- ^ Poynting, J.H. (1913). The Earth: its shape, size, weight and spin. Cambridge. pp. 50–56.
- ^ Hutton, C. (1778). «An Account of the Calculations Made from the Survey and Measures Taken at Schehallien». Philosophical Transactions of the Royal Society. 68: 689–788. doi:10.1098/rstl.1778.0034.
- ^ Published in Philosophical Transactions of the Royal Society (1798); reprint: Cavendish, Henry (1798). «Experiments to Determine the Density of the Earth». In MacKenzie, A. S., Scientific Memoirs Vol. 9: The Laws of Gravitation. American Book Co. (1900), pp. 59–105.
- ^ 2014 CODATA value 6.674×10−11 m3⋅kg−1⋅s−2.
- ^
Brush, Stephen G.; Holton, Gerald James (2001). Physics, the human adventure: from Copernicus to Einstein and beyond. New Brunswick, NJ: Rutgers University Press. pp. 137. ISBN 978-0-8135-2908-0.
Lee, Jennifer Lauren (16 November 2016). «Big G Redux: Solving the Mystery of a Perplexing Result». NIST. - ^ Poynting, John Henry (1894). The Mean Density of the Earth. London: Charles Griffin. pp. 22–24.
- ^ F. Reich, On the Repetition of the Cavendish Experiments for Determining the mean density of the Earth» Philosophical Magazine 12: 283–284.
- ^ Mackenzie (1899), p. 125.
- ^ A.S. Mackenzie , The Laws of Gravitation (1899), 127f.
- ^ Poynting, John Henry (1894). The mean density of the earth. Gerstein — University of Toronto. London.
- ^ Boys, C. V. (1 January 1895). «On the Newtonian Constant of Gravitation». Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. The Royal Society. 186: 1–72. Bibcode:1895RSPTA.186….1B. doi:10.1098/rsta.1895.0001. ISSN 1364-503X.
- ^ Carl Braun, Denkschriften der k. Akad. d. Wiss. (Wien), math. u. naturwiss. Classe, 64 (1897).
Braun (1897) quoted an optimistic standard uncertainty of 0.03%, 6.649(2)×10−11 m3⋅kg−1⋅s−2 but his result was significantly worse than the 0.2% feasible at the time. - ^ Sagitov, M. U., «Current Status of Determinations of the Gravitational Constant and the Mass of the Earth», Soviet Astronomy, Vol. 13 (1970), 712–718, translated from Astronomicheskii Zhurnal Vol. 46, No. 4 (July–August 1969), 907–915 (table of historical experiments p. 715).
- ^ Mackenzie, A. Stanley, The laws of gravitation; memoirs by Newton, Bouguer and Cavendish, together with abstracts of other important memoirs, American Book Company (1900 [1899]).
- ^ Heyl, P. R. (1930). «A redetermination of the constant of gravitation». Bureau of Standards Journal of Research. 5 (6): 1243–1290. doi:10.6028/jres.005.074.
- ^ P. R. Heyl and P. Chrzanowski (1942), cited after Sagitov (1969:715).
- ^ Mohr, Peter J.; Taylor, Barry N. (2012). «CODATA recommended values of the fundamental physical constants: 2002» (PDF). Reviews of Modern Physics. 77 (1): 1–107. arXiv:1203.5425. Bibcode:2005RvMP…77….1M. CiteSeerX 10.1.1.245.4554. doi:10.1103/RevModPhys.77.1. Archived from the original (PDF) on 6 March 2007. Retrieved 1 July 2006. Section Q (pp. 42–47) describes the mutually inconsistent measurement experiments from which the CODATA value for G was derived.
- ^ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (13 November 2012). «CODATA recommended values of the fundamental physical constants: 2010» (PDF). Reviews of Modern Physics. 84 (4): 1527–1605. arXiv:1203.5425. Bibcode:2012RvMP…84.1527M. CiteSeerX 10.1.1.150.3858. doi:10.1103/RevModPhys.84.1527. S2CID 103378639.
- ^ Taylor, B. N.; Parker, W. H.; Langenberg, D. N. (1 July 1969). «Determination of e/h, Using Macroscopic Quantum Phase Coherence in Superconductors: Implications for Quantum Electrodynamics and the Fundamental Physical Constants». Reviews of Modern Physics. American Physical Society (APS). 41 (3): 375–496. Bibcode:1969RvMP…41..375T. doi:10.1103/revmodphys.41.375. ISSN 0034-6861.
- ^ Cohen, E. Richard; Taylor, B. N. (1973). «The 1973 Least‐Squares Adjustment of the Fundamental Constants». Journal of Physical and Chemical Reference Data. AIP Publishing. 2 (4): 663–734. Bibcode:1973JPCRD…2..663C. doi:10.1063/1.3253130. hdl:2027/pst.000029951949. ISSN 0047-2689.
- ^ Cohen, E. Richard; Taylor, Barry N. (1 October 1987). «The 1986 adjustment of the fundamental physical constants». Reviews of Modern Physics. American Physical Society (APS). 59 (4): 1121–1148. Bibcode:1987RvMP…59.1121C. doi:10.1103/revmodphys.59.1121. ISSN 0034-6861.
- ^ Mohr, Peter J.; Taylor, Barry N. (2012). «CODATA recommended values of the fundamental physical constants: 1998». Reviews of Modern Physics. 72 (2): 351–495. arXiv:1203.5425. Bibcode:2000RvMP…72..351M. doi:10.1103/revmodphys.72.351. ISSN 0034-6861.
- ^ Mohr, Peter J.; Taylor, Barry N. (2012). «CODATA recommended values of the fundamental physical constants: 2002». Reviews of Modern Physics. 77 (1): 1–107. arXiv:1203.5425. Bibcode:2005RvMP…77….1M. doi:10.1103/revmodphys.77.1. ISSN 0034-6861.
- ^ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2012). «CODATA recommended values of the fundamental physical constants: 2006». Journal of Physical and Chemical Reference Data. 37 (3): 1187–1284. arXiv:1203.5425. Bibcode:2008JPCRD..37.1187M. doi:10.1063/1.2844785. ISSN 0047-2689.
- ^ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2012). «CODATA Recommended Values of the Fundamental Physical Constants: 2010». Journal of Physical and Chemical Reference Data. 41 (4): 1527–1605. arXiv:1203.5425. Bibcode:2012JPCRD..41d3109M. doi:10.1063/1.4724320. ISSN 0047-2689.
- ^ Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (2016). «CODATA Recommended Values of the Fundamental Physical Constants: 2014». Journal of Physical and Chemical Reference Data. 45 (4): 1527–1605. arXiv:1203.5425. Bibcode:2016JPCRD..45d3102M. doi:10.1063/1.4954402. ISSN 0047-2689.
- ^ Eite Tiesinga, Peter J. Mohr, David B. Newell, and Barry N. Taylor (2019), «The 2018 CODATA Recommended Values of the Fundamental Physical Constants» (Web Version 8.0). Database developed by J. Baker, M. Douma, and S. Kotochigova. National Institute of Standards and Technology, Gaithersburg, MD 20899.
- ^ Fixler, J. B.; Foster, G. T.; McGuirk, J. M.; Kasevich, M. A. (5 January 2007). «Atom Interferometer Measurement of the Newtonian Constant of Gravity». Science. 315 (5808): 74–77. Bibcode:2007Sci…315…74F. doi:10.1126/science.1135459. PMID 17204644. S2CID 6271411.
- ^ Rosi, G.; Sorrentino, F.; Cacciapuoti, L.; Prevedelli, M.; Tino, G. M. (26 June 2014). «Precision measurement of the Newtonian gravitational constant using cold atoms» (PDF). Nature. 510 (7506): 518–521. arXiv:1412.7954. Bibcode:2014Natur.510..518R. doi:10.1038/nature13433. PMID 24965653. S2CID 4469248. Archived (PDF) from the original on 9 October 2022.
- ^
Schlamminger, Stephan (18 June 2014). «Fundamental constants: A cool way to measure big G» (PDF). Nature. 510 (7506): 478–480. Bibcode:2014Natur.510..478S. doi:10.1038/nature13507. PMID 24965646. Archived (PDF) from the original on 9 October 2022. - ^ C. Rothleitner; S. Schlamminger (2017). «Invited Review Article: Measurements of the Newtonian constant of gravitation, G». Review of Scientific Instruments. 88 (11): 111101. Bibcode:2017RScI…88k1101R. doi:10.1063/1.4994619. PMC 8195032. PMID 29195410. 111101.
However, re-evaluating or repeating experiments that have already been performed may provide insights into hidden biases or dark uncertainty. NIST has the unique opportunity to repeat the experiment of Quinn et al. [2013] with an almost identical setup. By mid-2018, NIST researchers will publish their results and assign a number as well as an uncertainty to their value.
Referencing:- T. Quinn; H. Parks; C. Speake; R. Davis (2013). «Improved determination of G using two methods» (PDF). Phys. Rev. Lett. 111 (10): 101102. Bibcode:2013PhRvL.111j1102Q. doi:10.1103/PhysRevLett.111.101102. PMID 25166649. 101102. Archived from the original (PDF) on 4 December 2020. Retrieved 4 August 2019.
The 2018 experiment was described by C. Rothleitner. Newton’s Gravitational Constant ‘Big’ G – A proposed Free-fall Measurement (PDF). CODATA Fundamental Constants Meeting, Eltville – 5 February 2015. Archived (PDF) from the original on 9 October 2022.
- ^ Li, Qing; et al. (2018). «Measurements of the gravitational constant using two independent methods». Nature. 560 (7720): 582–588. Bibcode:2018Natur.560..582L. doi:10.1038/s41586-018-0431-5. PMID 30158607. S2CID 52121922..
See also: «Physicists just made the most precise measurement ever of Gravity’s strength». 31 August 2018. Retrieved 13 October 2018. - ^ Mould, J.; Uddin, S. A. (10 April 2014). «Constraining a Possible Variation of G with Type Ia Supernovae». Publications of the Astronomical Society of Australia. 31: e015. arXiv:1402.1534. Bibcode:2014PASA…31…15M. doi:10.1017/pasa.2014.9. S2CID 119292899.
Sources[edit]
- Standish., E. Myles (1995). «Report of the IAU WGAS Sub-group on Numerical Standards». In Appenzeller, I. (ed.). Highlights of Astronomy. Dordrecht: Kluwer Academic Publishers. (Complete report available online: PostScript; PDF. Tables from the report also available: Astrodynamic Constants and Parameters)
- Gundlach, Jens H.; Merkowitz, Stephen M. (2000). «Measurement of Newton’s Constant Using a Torsion Balance with Angular Acceleration Feedback». Physical Review Letters. 85 (14): 2869–2872. arXiv:gr-qc/0006043. Bibcode:2000PhRvL..85.2869G. doi:10.1103/PhysRevLett.85.2869. PMID 11005956. S2CID 15206636.
External links[edit]
- Newtonian constant of gravitation G at the National Institute of Standards and Technology References on Constants, Units, and Uncertainty
- The Controversy over Newton’s Gravitational Constant — additional commentary on measurement problems
Мы все учили в школе закон всемирного тяготения. Считается, что его придумал английский учёный Исаак Ньютон после удара яблоком по голове. Хотя это миф, и про яблоко, и про Ньютона.
Сэр Исаак Ньютон, величайший учёный прошлого (так нам говорят)
Согласно закону всемирного тяготения все тела притягиваются друг к другу. Формулу вы тоже наверняка помните. Что бы вычислить силу притяжения, надо умножить массы тел и поделить на квадрат расстояния между ними. Но в формуле присутствует ещё одна буква G. Которая обозначает гравитационную постоянную. Так же её называют постоянной Ньютона.
Формула закона всемирного тяготения
На русский язык переведен основной труд сэра Ньютона «Математические начала натуральной философии». Где он изложил свои фундаментальные законы — так пишут в околонаучных статьях и учебниках.
Титульный лист книги Исаака Ньютона «Математические начала натуральной философии»
Но если вы соизволите немного почитать эту жутко нудную работу по физике, то обнаружите, что никакой гравитационной постоянной там нет. Вообще. У Ньютона написано так:
Частица, находящаяся вне сферической поверхности, притягивается к центру сферы с силою, обратно пропорциональною квадрату её расстояния до центра сферы.
Всё. Можете сами проверять, никакой гравитационной постоянной вы у Ньютона не найдёте. Перечитайте хоть все «Начала». И в формулах на страницах книги она отсутствует.
Откуда же взялась гравитационная постоянная? Оказалось, её вычислили позднее экспериментальным путём. Пишут, что впервые это сделал английский физик Генри Кавендиш в конце 18-го века.
Кто-то решил, что это портрет Генри Кавендиша
Но кто подставил гравитационную постоянную в формулу всемирного тяготения — неизвестно. Кто записал эту формулу и сказал, что считать нужно именно так?
Удивительно, но наука об этом не имеет точных данных. Наука, которая запросто подсчитывает массы и скорости далёких планет, не в состоянии ответить на вопрос — кто и когда ввёл формулу, по которой вы считаете движения небесных объектов. Кто ввёл в расчёты гравитационную постоянную? Почему имя этого умного человека не написано на страницах учебников? Пусть даже это был не отдельный человек, а группа, например, учёный совет или команда обсерватории. Почему они недостойны войти в историю? Ответа нет, вместо него лишь неуверенное мычание, что кто-то где-то, возможно тот, возможно этот.
Получается, что всеведущая наука, которая рассказывает нам, что происходило во вселенной миллиарды лет назад, как зарождалась материя и пространство, не может объяснить, кто всего лишь столетием ранее придумал формулы? Которыми эта наука сама пользуется.
Как большой взрыв формировал вселенную. Процесс расписан посекундно.
Странновато это всё выглядит, уважаемые читатели. Закон, говорят, был давно, но его формула отличается от современной, по прошествию лет туда неизвестно кто воткнул гравитационную постоянную. Кто — до сих пор не выяснили. Тогда что вы нам рассказываете про спиральные рукава галактик и орбиты планет, если с таким простым вопросом разобраться не в состоянии? Ученые же пишут труды, книги, научные работы, диссертации очень давно. Ньютон написал книжку 350 лет назад, так её наука вдоль и поперёк знает. А кто первый приписал гравитационную постоянную в закон тяготения — неизвестно.
Знаете, почему произошла такая петрушка? Потому что наука физика переписана. Переделывать физику принялись в начале 20-го века. Что бы с виду правдоподобно объяснить движения планет, был придуман закон всемирного тяготения. Где тела крутятся вокруг друг друга, только исходя из массы и расстояния. На самом деле планеты движутся, исходя из других законов и других свойств пространства.
Всё летает согласно закону всемирного тяготения. С поправкой гравитационной постоянной. Понятно?
Но надо было убрать из физики некоторые части, поэтому придумали закон всемирного тяготения, а что бы косяки не слишком вылезали, его скруглили гравитационной постоянной. Получилось вроде правдоподобно. Для плебса хватает, а читать муторную книгу сэра Исаака никто из обычных людей читать от корки до корки не станет.
Конечно, вы в такое объяснение не поверите. Неужели большому количеству людей, в том числе учёных, можно задурить голову? Можно. И совсем не сложно. Примеров огромное количество, во всех областях науки.
Подписывайтесь на канал, в дальнейшем мы с вами разберём и другие неувязки в современной науке.
Автор: Артём Войтенков
Отсюда:https://zen.yandex.ru/media/id/5bebbfbb8a863900aa14ec0f/taina-gravitacionnoi-postoiannoi-5c5abf11f8b14900ae044278