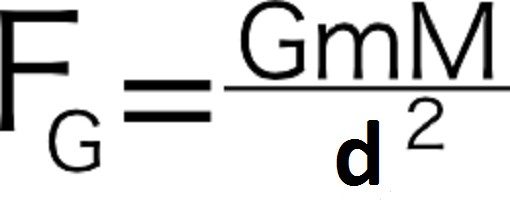Введение. Опыты Галилея по определению ускорения свободного падения
На предыдущем уроке мы обсудили вопрос, связанный с законом всемирного тяготения. Теперь перед нами стоит задача – рассмотреть, как этот закон связан с уже известным ускорением свободного падения. Ускорение свободного падения впервые определил итальянский ученый Галилео Галилей. Как вы помните, он измерял ускорение движения тел, которые двигались по наклонной плоскости, и ему удалось установить, что предельное ускорение таких тел (а это и есть ускорение свободного падения) составляет .
Вывод формулы для ускорения свободного падения на основании закона всемирного тяготения
Однако почему именно такое значение у этого ускорения, стало ясно только после открытия закона всемирного тяготения. Вспомним, что сила тяжести на Земле – это проявление действия закона всемирного тяготения для тел, которые находятся на поверхности Земли.
Рис. 1. Сила тяжести, действующая на тело на Земле
При этом вся масса Земли условно полагается сосредоточенной в ее центре. Радиус Земли – это расстояние между телами (рис. 1). Само тело, которое находится над поверхностью Земли, – то самое тело, которое притягивается. Запишем соответствующие формулы.
Сила тяжести на Земле:
, где
– масса тела, которое находится на поверхности Земли,
— ускорение свободного падения.
Закон всемирного тяготения в данном случае имеет вид:
Здесь – масса Земли,
– масса тела,
– радиус Земли,
– гравитационная постоянная. Если сравнить выражение для силы тяжести и для гравитационной силы, получим для ускорения свободного падения:
Обратите внимание: ускорение свободного падения зависит от массы Земли и от радиуса Земли. Если они будут изменяться, значит, будет изменяться и ускорение свободного падения.
Зависимость ускорения свободного падения от географической широты и других параметров. Искусственные спутники Земли
Как известно, Земля по форме не идеальный шар, а тело, которое немного сплюснуто с полюсов, поэтому полярный радиус несколько меньше, чем экваториальный (рис. 2). В этом случае надо понимать, что ускорение свободного падения на полюсе будет больше, а на экваторе – меньше. В общем случае ускорение свободного падения зависит от широты местности.
Рис. 2. Разность экваториального и полярного радиусов
Необходимо отметить еще вот что. Земля вращается, и вращательное движение Земли тоже влияет на ускорение свободного падения. Ускорение свободного падения на экваторе будет отличаться еще и по этой причине. Изменение ускорения свободного падения по всем вышеуказанным причинам достаточно незначительное, поэтому мы считаем, что ускорение свободного падения на Земле – величина постоянная и составляет .
Как видите, ускорение свободного падения зависит от радиуса Земли, значит, если увеличивать радиус, то ускорение свободного падения будет уменьшаться. Как такое может быть? Если мы поднимаем тело над поверхностью Земли (например, тот же спутник), то расстояние будет определяться суммой радиуса Земли и высоты над ее поверхностью (рис. 3).
Рис. 3. Тело, поднятое над поверхностью Земли.
В этом случае ускорение свободного падения тоже будет уменьшаться.
Ускорение свободного падения обратно пропорционально квадрату расстояния. Поэтому если высота будет равна радиусу Земли, то расстояние будет в 2 раза больше от центра Земли, чем для тела на поверхности. В этом случае ускорение свободного падения уменьшится в 4 раза.
Следует заметить, что многие спутники летают на небольшом расстоянии, приблизительно 200–300 км от поверхности Земли. На этом расстоянии ускорение свободного падения изменяется, но незначительно, поэтому мы будем считать, что в этом случае ускорение все-таки величина постоянная.
Обратите внимание на тот факт, что сила тяжести, как и ускорение свободного падения, с высотой будет убывать (по мере удаления от Земли сила тяжести будет убывать).
Как изменение  делает нас богаче
делает нас богаче
Дело в том, что измерение ускорения свободного падения в различных точках Земли является мощнейшим способом геологической разведки. Таким способом (без рытья шахт) можно определять наличие полезных ископаемых в толще земной коры. Первый способ: измерение при помощи пружинных весов (рис. 4). Они обладают феноменальной чувствительностью.
Рис. 4. Геологические весы
Второй способ: измерение при помощи математического маятника (груз, подвешенный на длинной нити). Оказывается, что период (время одного полного колебания) колебания такого маятника зависит от ускорения свободного падения.
Чем больше ускорение свободного падения, тем меньше период. То есть, измеряя период маятника в разных точках Земли, можно определить изменение ускорения свободного падения. Геологи используют очень точные маятники (рис. 5), которые позволяют измерять ускорение свободного падения с точностью до миллионных долей.
Рис. 5. Прибор с маятником для разведки полезных ископаемых
Что является нормой для величины ускорения свободного падения?
Как известно Земля имеет фору геоида (сплюснута у полюсов). Это значит, что значение ускорения свободного падания у полюсов больше чем на экваторе. Но на одной и той же географической широте ускорение свободного падения, при прочих равных условиях, должно быть одинаково. Измеряя в рамках одной широты ускорение свободного падения в разных точках, можно судит о наличии полезных ископаемых.
Представьте себе, что вы находитесь на широте Москвы. Допустим, норма ускорения свободного падения на этой широте равна . В рамках данной широты мы смещаемся западнее или севернее и замечаем, что
изменилось, теперь оно равно
.
Это означает, что мы наткнулись на место с залежами тяжелых ископаемых. Если же ускорение свободного падения уменьшилось, значит, там есть пустоты или залежи легких солей. Как правило, рядом с залежами легких солей находятся залежи нефти. Данный способ называется гравиметрической разведкой. Таким способом были обнаружены залежи нефти в Казахстане и Западной Сибири.
На рис. 6 изображены зоны, где ускорение свободного падения больше (красные области) или меньше (синие области).
Рис. 6. Области, где ускорение свободного падения отличается от
Залежи тяжелых веществ или наличие пустот оказывают влияние на направление ускорения свободного падения. Если вы проводите измерение вблизи большой горы, то это массивное тело будет оказывать влияние на направление
(рис. 7).
Рис. 7. Маятник в нормальных условиях и под воздействием массивного объекта
Ускорение свободного падения на других небесных телах на примере Луны
Теперь обсудим то, как определяется ускорение свободного падения на других телах.
Обратимся к уравнению, которое мы использовали для определения ускорения свободного падения на поверхности Земли: .
В этом уравнении вместо массы и радиуса Земли можно подставить массу и радиус любой другой планеты. Тогда мы получим ускорение свободного падения на любой из интересующих нас планет. В первую очередь нас интересует Луна. Ускорение свободного падения на Луне будет приблизительно равно: .
Как видно, ускорение свободного падения на Луне сильно отличается от ускорения свободного падения на Земле. Значит, если вдруг мы окажемся на Луне, мы почувствуем себя гораздо легче, чем на родной Земле. Например, у первых лунных космонавтов скафандр был массой .
Сила тяжести, действующая на скафандр на Земле:
Сила тяжести, действующая на скафандр на Луне:
Такую силу тяжести, как на Луне, на Земле бы имел скафандр массой :
 на разных небесных телах: сравнительная таблица
на разных небесных телах: сравнительная таблица
Значение величины ускорения свободного падения равное является самым комфортным для человека. Рассмотрим, какие значения принимает ускорение свободного падения на других небесных телах (Солнце, планеты, спутники).
Чем массивнее небесное тело, тем больше .
Рассмотрим таблицу для ускорения свободного падения для различных небесных тел.
|
Небесное тело |
|
|
Луна |
1,62 |
|
Солнце |
273,1 |
|
Меркурий |
3,72 |
|
Земля |
9,81 |
|
Уран |
8,86 |
|
Венера |
8,88 |
|
Сатурн |
10,44 |
Табл. 1. Ускорение свободного падения для различных небесных тел
Как видно, на Луне в 6 раз меньше, чем на Земле. Передвигаться на Луне гораздо легче, чем на Земле. На Солнце
в 30 раз больше, чем на Земле. Даже не учитывая больших температур, передвигаться на Солнце с учетом перегрузки в 30 раз невозможно. У Урана, Венеры и Сатурна более близкие значения
с Землей. На Уране и Сатурне достаточно холодно. А вот на Венере возможно существование каких-то форм жизни или возможно путешествие человека и организация базы для временного пребывания.
Зная ускорение свободного падения на небесных телах, можно посчитать и их среднюю плотность. Зная среднюю плотность, можно предсказывать то, из чего состоят небесные тела, и определять их строение.
Расчет массы Земли
При помощи полученной формулы мы можем определить массу тех планет и небесных объектов, которые нас интересуют. Посмотрим на формулу, которая позволяет это сделать. Рассмотрим это на примере Земли. Из формулы для ускорения свободного падения несложно получить: .
Эта формула позволяет определить массу Земли. Обычно всегда спрашивают, как удалось взвесить Землю?
Никто ее не взвешивал, а, воспользовавшись законом всемирного тяготения и, зная ускорение свободного падения на поверхности Земли, можно легко массу Земли вычислить.
Масса Земли все время уточняется. Все понимают, что эта величина является очень важной. Когда мы знаем массу Земли, то, пользуясь т. н. законами Кеплера, несложно определить массу других небесных тел. Если мы знаем расстояние между Землей и другой планетой, знаем, как они взаимодействуют друг с другом, мы можем легко определить массу других тел.
Поэтому в астрономии очень часто за единицу измерения принимают массу Земли, говорят, что масса Земли равна 1 единице, и все другие массы планет определяют уже в массах Земли.
Определение средней плотности Земли
Знание ускорения свободного падения на поверхности Земли и радиуса Земли дают возможность определить среднюю плотность вещества Земли.
Вспомним формулу для ускорения свободного падения:
Массу можно вычислить через плотность и объем тела:
Земля имеет форму шара, поэтому ее объем можно вычислить по формуле:
Из приведенных выше формул можно получить зависимость от плотности:
Выразим из данной формулы плотность и подставим все известные величины:
То есть кубик усредненного земного вещества размерами 1 см·1 см·1 см будет весить 5,5 грамм. Если взять вещество с поверхности Земли, то его плотность будет меньше усредненной (). Значит, внутри Земли (рис.

Рис.8 Строение Земли
По современным представлениям, в центре Земли находится раскаленное железное ядро. Считается, что Земля могла образоваться из метеоритов. Они сталкивались, постепенно образовывалось земное вещество, гравитационные силы стягивали наиболее тяжелые фракции к центру. В результате образовалось ядро. Более легкие фракции оказались на периферии.
Заключение
Закон всемирного тяготения и ускорение свободного падения имеют большое значение. В первую очередь для запуска искусственных спутников Земли.
Список дополнительной литературы
- Кикоин А. К. Вращение Земли и ускорение свободного падения //Квант. – 1984. – № 1. – С. 32–34.
- Кикоин И. К., Кикоин А. К. Физика: Учебник для 9 класса средней школы. – М.: Просвещение, 1992.
- Сивухин Д. В. Общий курс физики. – М.: Государственное издательство технико-теоретической литературы, 2005. – Т. 1. Механика. – С. 372.
- Смородинский Я. Закон всемирного тяготения //Квант. – 1990. – № 12. – С. 8–13; 51.
- Физика: Механика. 10 кл.: Учебник для углубленного изучения физики / под ред. Г. Я. Мякишева. – М.: Дрофа, 2002.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «class-fizika.narod.ru» (Источник)
- Интернет-портал «100ballov.kz» (Источник)
- Интернет-портал «eduspb.com» (Источник)
Домашнее задание
- Где на Земле ускорение свободного падения выше: на полюсах или на экваторе? Ответ обоснуйте.
- В чем заключались опыты Галилея по определению ускорения свободного падения?
- Определите, на какой высоте над Землей ускорение свободного падения в три раза меньше его значения на поверхности Земли.
- Известно, что Земля имеет определенную массу, но как удалось взвесить планету?
Опыт Галилея
Опыт Галилея
Хиви НАСА. Ещё довод:
— Но по фильму и получается, что астронавт в «безвоздушной среде» опускается на поверхность Луны быстрее, чем это делает песчинка. На них, что, по-разному действует закон свободного падения?
— Вы не можете по фильму замерить то время, за которое падает песчинка, во всяком случае, к научному рассмотрению такие короткие промежутки времени, замеренные секундомером, не принимаются. А ещё и по киноплёнке. А что, подкова и лошадь на Земле не падают с одинаковой скоростью? Если фильм — подделка, то, что, на астронавта и песчинку тоже по-разному действует закон свободного падения, хотя дело происходит на Земле? Как же они эту аномалию воспроизвели на Земле?
— А они и не воспроизводили. Это киномонтаж.
— Так что, они засняли отдельно песчинку с Луны и отдельно — космонавта???
— Такой эпизод в фильме. Олдрин с шутками и прибаутками спрыгивает с последней ступеньки лунного модуля на «Луну». Высота около 0,8 м, он руками придерживается за лестницу. Поскольку его вес в скафандре 27 кг, то есть в четыре раза легче, чем в одних трусах на Земле, то для его тренированных мускулов этот прыжок равносилен спрыгиванию на Земле с высоты 0,2 м, то есть с одной ступеньки. Попробуйте спрыгнуть с такой высоты (20 сантиметров!), даже придерживаясь за что-нибудь руками, и посмотрите на своё состояние. Олдрин при прыжке со ступеньки медленно опустился на поверхность, затем у него начали сгибаться колени и он согнулся в пояснице, то есть он так тяжело ударился при «прилунении», что его тренированные мускулы не удержали тело в скафандре в вертикальном положении.
— Ну, спрыгнул я с такой высоты. И тоже согнулся. А вы-то сами пробовали? А, теоретики… Не, ну, можно, конечно, так это нарочно прыгать «солдатиком», но зачем?
— Астронавты повторили на Луне опыт Галилея: кинули перо и молоток, чтобы они упали одновременно, чтобы доказать, что они на Луне. Но это доказывает только то, что там также действует закон свободного падения. Они, наверное, потом это перо в задницу засунули тому умнику, который придумал этот фокус. Время падения тела с высоты Н равно квадратному корню из 2h/a, где а — ускорение свободного падения. Астронавты кидают предметы с высоты примерно 1,4 метра, при лунном тяготении в 1,6 м/сек? они должны упасть на поверхность за 1,3 секунды. Я несколько раз прокрутил кусок фильма и замерил время падения секундомером. Среднее время падения получилось 0,83 сек. (Кстати, поясню оппонентам, что в технических экспериментах время замеряется секундомером, а не на глаз и не по ходикам с кукушкой.) Отсюда по формуле а = 2h / t? легко считается ускорение свободного падения. Оно составило 2 х 1,4 / 0,832 = 4,1 м/сек?. А на Луне эта величина должна составлять 1,6 м/сек?, значит, это не Луна! Доэкспериментировались, умники?!
— А правда, где же американцы снимали своё «лунное кино»? Если ускорение свободного падения равно 4 м/с?, то это — уж точно не Луна. На Луне оно действительно равно 1,6 м/с?, т. е. в два с половиной раза меньше. Но это — и не Земля: здесь оно равно 9,8 м/с?, в два с половиной раза больше тех 4 м/с?, что вы намерили по кинофильму. Из ближайших к Земле небесных тел подходит либо Меркурий, либо Марс: и там, и там ускорение свободного падения равно 3,7 м/с? — очень близко (с точностью 10%) к полученной вами величине.
Наверное, до Вас с Вашим секундомером ещё никому не удавалось так ловко вывести насовцев на чистую воду. На Луну слетать у них явно не получилось, вот и пришлось провернуть вариант попроще: втихаря махнуть на Марс и там «на натуре» быстренько сляпать свои фото — и кинофальшивки. (Домерился, умник?!)
Ю. И. МУХИН. Не надо про Марс, грусть моя, в Голливуде это снималось, в Голливуде! Бросил «Армстронг» вместе с молотком свинцовое «перо», а потом эту съёмку замедлили.
Хиви НАСА. Вообще-то по двумерному изображению невозможно точно определить высоту, с которой падали предметы. И, как уже говорилось, такое время секундомером не меряют. Если уж анализировать, то надо добыть кусок киноплёнки, на котором запечатлено падение, и смотреть, сколько кадров падают предметы, найти соответствующий этому количеству кадров интервал времени и т. д.
Такой покадровый анализ сейчас доступен любому, имеющему доступ в Интернет. На сайте NASA имеется видеоролик www.hq.nasa.gov/office/pao/History/alsj/a15/a15v1672206.]mpg(6mB), на котором изображён этот самый пресловутый опыт Галилея на Луне. Судя по его качеству, это, скорее всего, не киносъёмка, а видеозапись прямой телепередачи с Луны. Если изучить его с помощью какого-нибудь видеоредактора, то можно установить, что его частота кадров — 30 в секунду, а падение предметов на нём длится 36 кадров. Ниже приведены некоторые кадры из этого видеоролика (первый — начало процесса падения) (рис. 114).
Кадр 1, Кадр 5 , Кадр 18 , Кадр 31 , Кадр 34 , Кадр 36
Первый и пятый кадры отличаются очень мало, т. к. в начале падения скорость предметов незначительна, но при покадровом просмотре тот момент, когда астронавт разжимает руки, фиксируется достаточно чётко. Пёрышко при падении видно как радужное пятно — скорее всего, из-за несовершенства портативной цветной видеотехники конца 60-х годов прошлого века.
Время падения предметов, очевидно, равно 36 / 30 = 1,2 секунды. Отсюда, если принять, что высота падения составляла 1,4 метра, найдём ускорение: 2 х 1,4 / 1,22 = 1,9 м/с?. Это немного больше, чем 1,6 м/с? — истинное значение ускорения свободного падения на Луне. Однако вспомним, что хотя время падения мы определили более-менее точно, но высоту падения взяли «от фонаря», так что сравнительно небольшая (20%) ошибка не должна нас удивлять.
А перед тем, как включать секундомер, иногда полезно предварительно включить собственные мозги. У американцев наверняка была не профессиональная 35-миллиметровая камера (такие камеры слишком громоздкие и тяжёлые, чтобы тащить их на Луну, да и плёнки они съедают немерено), а 8— или 16-миллиметровая. Скорость съёмки у таких камер, как правило, 16 кадров в секунду. Если скопировать плёнку с такой камеры на 35-миллиметровую «кадр в кадр», а потом показать полученную 35-миллиметровую копию со стандартной для такой плёнки скоростью 24 кадра в секунду, то, как нетрудно сообразить, временные интервалы уменьшатся при таком показе в полтора раза. Скорости тел в полтора раза увеличатся. А ускорения при таком «сжатии времени» в полтора раза возрастут в 1,52=2,25 раза — это видно хотя бы из формулы для определения ускорения по высоте и времени падения с этой высоты а = 2h / t?: если время падения уменьшится в 1,5 раза, то полученная по этой формуле величина ускорения увеличится в 2,25 раза. Таким образом, если 16-миллиметровая плёнка в самом деле снималась там, где ускорение свободного падения составляет 1,6 м/с?, то по 35-миллиметровой копии исходного фильма мы найдём, что это ускорение составляло где-то около 1,6 x 2,25 = 3,6 м/с?. Вот как просто, оказывается, принять Луну за Марс — если не знать, с какой скоростью кино снимали и с какой показывали.
Впрочем, забудьте. Надо быть не американцем, а законченным дебилом, чтобы, снимая фальшивку, не суметь замедлить фильм в нужное количество раз. В данном случае «нужное количество» — квадратный корень из шести, т. е. примерно два с половиной. Замедлите фильм ровно в два с половиной раза — и ни один зритель не заподозрит подвоха, будь у него хоть дюжина секундомеров. Но, если перо и молоток падают с одинаковой скоростью, то это доказывает не только то, что в месте съёмки «также действует закон всемирного тяготения», но также и то, что дело происходит в вакууме (рис. 116). Чтобы снять этот эпизод с молотком и пёрышком на Земле, американцам пришлось бы соорудить герметичный съёмочный павильон и откачать оттуда воздух. Конструкция сама по себе не слабая (и очень не дешёвая): на каждый квадратный метр её стенок будет действовать сила давления атмосферы в 10 тонн. Да ещё и всю съёмочную группу пришлось бы одеть в настоящие космические скафандры — напомню, что такой скафандр с системой жизнеобеспечения весит на Земле несколько десятков килограммов. Стоил ли этот минутный эпизод таких усилий для его съёмки?
— Во-во! И я про то же! Они просто замедлили киноплёнку при показе! Почём я знаю, что они там кидали? Может, они это «перо» из свинца сделали и покрасили в белый цвет. Тогда понятно, почему оно одновременно с молотком упало.
Ю. И. МУХИН. Обращаю внимание читателей на то, что насовцы воздействуют на своих дебильных сторонников различными наукообразными словами и большим количеством разных подробностей, которые к делу никак не относятся.
Вот они начинают: «Вообще-то по двухмерному изображению невозможно точно определить высоту…» Ой как умно! Пространство имеет три меры: высоту, длину и ширину (глубину). Высота — это одна из мер, и она всегда одномерна. Как вы определяете высоту? Ставите рядом с измеряемым объектом линейку, а она-то одномерна. Причём тут «двухмерностъ изображений»? Глупость, но на идиота действует впечатляюще…
Ещё обратите внимание. Опыт Галилея был показан в прямой телепередаче «с Луны», т. е. это видеозапись. А насовцы рассусоливают про 35-мм киноплёнку, про 16-мм, про количество кадров. Кому это надо? Хиви советуют взять съёмку опыта Галилея на сайте НАСА в Интернете. Спасибо, но мне не требуются уже скорректированные подделки. Вы бы лучше пояснили другое. Разбирается текст моей статьи в «Дуэли» (дана в первой главе), но в ней я сделал три замера ускорения свободного падения: в опыте Галилея; камня, падающего из мешка на плече бегущего «астронавта»; и падения камня (или куска обшивки) при «старте лунного модуля с Луны». Но про два последних замера насовцы молчат, не приглашают на свой сайт посмотреть на них, не считают количество кадров. Почему?
В опыте Галилея «астронавт» стоял неподвижно, а на его фоне падали «перо» и молоток. В этом случае съёмку можно замедлить, сколько угодно, добиваясь, чтобы время падения молотка и «пера» соответствовали лунному. А в двух остальных эпизодах это невозможно: если замедлить падение камня, то замедлится и бег «астронавта», если замедлить падение обшивки, то нужно замедлить и её полёт вверх, иначе стартующая кабина в фильме неестественно «дёрнется». Пришлось им ограничиться пером, которое я рекомендовал насовцам засунуть автору эпизода с «опытом Галилея» в то место, которым он его придумал.
А с представленной фотографией пера насовцы меня просто умилили. Ведь снимали это перо наверняка уже в этом тысячелетии, снимали после того, как «полёты на Луну» были раскритикованы вдоль и поперёк. А ума — ни грамма! Сколько раз уже писалось, что «Аполлон-11», по легенде садился тогда, когда солнце над горизонтом стояло под углом 7,5°, т. е. тогда, когда тень от предмета почти в 8 раз превышает его высоту. А вы посмотрите на тень от этого пера «на Луне». Ну что тут скажешь — кретины! Я же им давал неплохой совет, что делать с этим пером, а они взялись его фотографировать.
Хиви НАСА. А нам опять говорят:
— При лунном-то притяжении пыль из-под колёс ихнего «луномобиля» должна лететь на метры вверх, а она летит совсем невысоко, как и положено на Земле.
— А вы попробуйте прокатиться на велосипеде по песку примерно с той же скоростью, что и американцы по Луне, километров 10 в час (По не очень толстому слою песка, конечно, и лучше на велосипеде с широкими шинами. Песчинки — достаточно тяжёлые, и сопротивление воздуха на их движении сильно не сказывается, а начальная их скорость будет примерно такой же, что и пыли, выброшенной колёсами «луномобиля». Высоко ли они подлетают? Не очень, прав да? На Луне при одной и той же начальной скорости песчинки и пылинки должны, конечно, подняться вшестеро выше, но «метров» всё равно не получается.
На рис. 116 приведён кадр из кинофильма, снятого астронавтами «Аполлона-16». Внимательно посмотрев на него, можно понять, что есть ещё одна очень существенная причина, почему пыль летит сравнительно невысоко. Точнее, даже не одна, а целых четыре: крылья. Отлетающие от колёс пылинки отрываются от нижней части шины: скорость таких пылинок невелика, т. к. скорость точек на поверхности шины в месте соприкосновения с лунной поверхностью вообще нулевая (разумеется, если колесо не проскальзывает), а вблизи этого места достаточно мала. Пылинки же, которые отрываются от шин на большей высоте от поверхности, имеют большую скорость и могли бы улететь достаточно высоко и далеко — если бы не крылья.
Главное тут в другом. Если бы это происходило в земной атмосфере, то мелкая пыль клубилась бы и долго висела в воздухе. А тут пыль вылетает из-под колёс и тут же падает вниз. Так что поездки на «луномобиле» явно снимали в вакууме.
Особенно хорошо это «странное» (для землян) поведение пыли видно на киноплёнке. Порой колёса «луномобиля», подпрыгивающего на ухабах, подкидывают пыль примерно на метр, но эта пыль падает вниз так же быстро, как и взлетает вверх. Фрагмент фильма, снятого астронавтами «Аполлона-16», можно посмотреть здесь: www.hq.nasa.gov/office/pao/ History/40thann/mpeg/ap16rover.mpg (2mB).
— А почему пыль, вылетающая из-под колёс «луномобиля», клубится, а не летит ровными струями? Наверно, всё-таки эти кадры снимали в атмосфере.
— А при чём тут атмосфера? Когда «луномобиль» подпрыгивает на ухабе, его колёса теряют сцепление с грунтом, прокручиваются и выбрасывают сгустки пыли с большой скоростью, и эти сгустки высоко взлетают. А в атмосфере поднятая пыль, во-первых, не подлетала бы так высоко, а во-вторых, не падала бы вниз так быстро, как на этих кинокадрах.
Ю. И. МУХИН. Для того чтобы смоделировать для Луны езду на велосипеде на Земле, нужно, соответственно, в шесть раз уменьшить вес велосипеда и велосипедиста. Вы, хиви, это сумели сделать, так почему же не порадовали нас фотографией этого эксперимента?
Этот наукообразный бред уже нужно разбирать. Повторюсь. Законы физики и на Луне законы. Частичка грунта при одинаковых условиях (скорость вращения колеса, его проскальзывание по отношению к грунту, форма протекторов и т. д.) и на Земле, и на Луне получит одинаковую кинетическую энергию. Эта энергия заставит частицу подлететь вверх до точки, у которой кинетическая энергия сравняется с потенциальной, равной произведению веса на высоту подъёма частицы. А поскольку вес частицы на Луне в шесть раз меньше, то и высота её подъёма будет в шесть раз больше и даже ещё больше, поскольку кинетическая энергия на Луне не гасится сопротивлением воздуха. И сколько ни болтай про крылья, которые и на Земле имеются у любого автомобиля, про нулевую скорость точек и «нижнюю часть шины», а на представленном хиви фото пыль от колёс «луномобиля» клубится точно так же, как на Земле. А следовательно, он и едет на Земле, а не на Луне. И то, что на Земле пыль не падает «вниз так быстро, как на этих кинокадрах» с «Луны», и есть подтверждение тому, что это Земля, а песок просто мокрый (обеспыленный), поскольку наоборот — это на Луне этот песок должен падать вниз в два с половиной раза медленнее, а вверх лететь значительно быстрее, чем на Земле. То есть это должна быть настолько непривычная для нас картина, что мы бы сразу поняли, что это Луна, а не Голливуд.
Читайте также
Расплата за опыт
Расплата за опыт
До 50-х годов XIV века к колдовству относились как к практическому элементу волшебства, необходимому для управления силами природы в чьих-либо интересах. Обычным делом было заклинание духов и использование чар для защиты людей и урожая, для обеспечения
Клюнийская реформа. Евангельская Галилея = Галлия = Франция. Евангельская Кана Галилейская = Канны во Франции
Клюнийская реформа. Евангельская Галилея = Галлия = Франция. Евангельская Кана Галилейская = Канны во Франции
В Западной Европе Первый крестовый поход 1096 г. начался из Южной Франции, из так называемых «клюнийских аббатств». Вообще, в истории XI века «клюнийские аббатства»
Опыт невозможного
Опыт невозможного
То, о чем мы расскажем дальше, уважаемые читатели, не является, конечно, точной реконструкцией замысла Сталина, исследованием замысла, воплотившегося в великой Красной империи, сверхдержавы ХХ века. Мы постараемся объективно и очень коротко рассказать
Опыт командования – I
Опыт командования – I
Из тех дней боев, которые были описаны выше, 17, 18 и 19 декабря имели некоторые особенности, которые в то время стали типичными для многих танковых дивизий: командир дивизии лично вел передовые силы мощной и мобильной штурмовой группы. Такой прием
Опыт командования – II
Опыт командования – II
Эти два примера использования боевых групп характерны для такого приема, когда бронетехника сосредоточена в обороне, но в нужный момент используется для наступления. Не очень знакомые с тактикой танковой войны командиры и те, кто имел дело только с
ОПЫТ КОМАНДОВАНИЯ – I
ОПЫТ КОМАНДОВАНИЯ – I
Из тех дней боев, которые были описаны выше, 17, 18 и 19 декабря имели некоторые особенности, которые в то время стали типичными для многих танковых дивизий: командир дивизии лично вел передовые силы мощной и мобильной штурмовой группы. Такой прием
ОПЫТ КОМАНДОВАНИЯ – II
ОПЫТ КОМАНДОВАНИЯ – II
Эти два примера использования боевых групп характерны для такого приема, когда бронетехника сосредоточена в обороне, но в нужный момент используется для наступления. Не очень знакомые с тактикой танковой войны командиры и те, кто имел дело только с
ИСТОРИЧЕСКИЙ ОПЫТ
ИСТОРИЧЕСКИЙ ОПЫТ
В России прекрасно знали, что собой представляет румынская армия и как союзник, и как противник. Первое знакомство состоялось в 1877–1878 годах, во время войны за освобождение Болгарии. Румынские офицеры до глубины души потрясли своих тогдашних российских
Опыт командования – II
Опыт командования – II
Эти два примера использования боевых групп характерны для такого приема, когда бронетехника сосредоточена в обороне, но в нужный момент используется для наступления. Не очень знакомые с тактикой танковой войны командиры и те, кто имел дело только с
Глава I Галилея и галилеяне
Глава I
Галилея и галилеяне
«Галилея Языческая» (неевреев) – так называл ее пророк Исаия[53], и такой она в действительности была. Вся она, на восток и на запад от Иордана – нееврейская по своей расе, хотя частично иудаистская по еврейскому культу, а в некоторых
Греческая Галилея
Греческая Галилея
Из всего нееврейского влияния в пределах и за пределами Галилеи греческое было самым всепроникающим и значительным. В Новом Завете можно было бы прочитать о Десятиградии, не задумываясь над степенью и полнотой его греческого духа. Эта область
1. Основные тенденции развития философии и психологии в XVII в Открытия Н. Коперника, Д. Бруно, Г. Галилея, У. Гарвея, Р. Декарта
1. Основные тенденции развития философии и психологии в XVII в
Открытия Н. Коперника, Д. Бруно, Г. Галилея, У. Гарвея, Р. Декарта
Интенсивное развитие капиталистических отношений в XVI–XVII вв. повлекло за собой бурный расцвет многих наук, прежде всего естествознания, особенно
От Коперника до Галилея и Ньютона
От Коперника до Галилея и Ньютона
В середине XVI в. Николай Коперник, польский астроном и одновременно, каноник собора во Фромборке (рыбачьем городке в устье Вислы), предложил отказаться от геоцентрической системы мира Птолемея в пользу гелиоцентрической системы,
Ускорение свободного падения – одно из множества открытий великого Ньютона, который не только суммировал опыт предшественников, но и дал строгое математическое объяснение огромному количеству фактов и экспериментальных данных.
Предпосылки открытия. Эксперименты Галилея
Один из многочисленных экспериментов Галилео Галилея был посвящен исследованию движения тел в полете. До этого в системе мировоззрения господствовало мнение, что более легкие тела падают медленнее, чем тяжелые. Бросая различные предметы с высоты Пизанской башни, Галилей установил, что ускорение свободного падения для тел с различной массой абсолютно одинаково.
Небольшие расхождения теории с экспериментальными данными Галилей справедливо отнес к влиянию сопротивления воздуха. Для доказательства своих рассуждений он предлагал повторить эксперимент в вакууме, но на тот момент техническая возможность для этого отсутствовала. Лишь через многие годы мысленный эксперимент Галилея провел Исаак Ньютон.
Теория Ньютона
Честь открытия закона всемирного тяготения принадлежит Ньютону, но сама идея уже около 200 лет витала в воздухе. Основной предпосылкой для формирования новых принципов небесной механики стали законы Кеплера, сформулированные им на основе многолетних наблюдений. Из океана допущений и домыслов Ньютон извлек предположение о силе притяжения Солнца и расширил свою теорию до понятия о всемирном тяготении. Он проверил свою гипотезу об обратной пропорциональности силы квадрату расстояния, рассмотрев орбиту Луны. Последующие проверки этой идеи осуществлялись при помощи исследования движения спутников Юпитера. Результаты наблюдений показали, что между спутниками планет и самими планетами действуют те же силы, что и при взаимодействии Солнца и планет.
Открытие гравитационной составляющей
Сила притяжения Земли к Солнцу подчинялась формуле:
Эксперименты показали, что множитель 1/d2 в этом соотношении был вполне применим и в случае рассмотрения других планет в Солнечной системе. Постоянная G являлась коэффициентом, приводившим значение пропорции к числовой величине.
Руководствуясь собственной теорией, Ньютон измерил соотношения масс различных небесных тел, например масса Юпитера / масса Солнца, масса Луны / масса Земли, но численный ответ на вопрос о том, сколько весит Земля, Ньютон дать не мог, так как постоянная G по-прежнему оставалась неизвестной.
Величина гравитационной постоянной была открыта лишь спустя полвека после смерти Ньютона. Оценки этой величины на основе гипотез, подобных предположениям Ньютона, показали, что данная величина является ничтожно малой, и в земных условиях вычислить ее значение практически невозможно. Обычная сила тяжести кажется огромной, поскольку все знакомые нам предметы невообразимо малы по сравнению с массой земного шара.
Конец 18 века. Измерение G
Первые попытки измерить G состоялись в конце 18 века. В качестве притягивающей силы они использовали гору огромных размеров. Оценка величины ускорения свободного падения производилась на основании отклонения от вертикали грузика маятника, расположенного в непосредственной близости от горы. С помощью геологических данных была произведена оценка массы горы и ее среднее расстояние от маятника. Так получили первое, довольно грубое измерение загадочной константы.
Измерения лорда Кавендиша
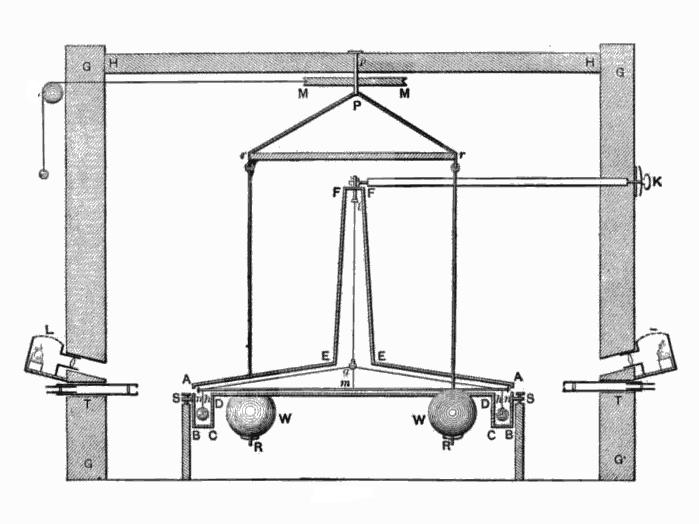
Лорд Кавендиш в своей лаборатории провел измерения гравитационного притяжения методом свободного взвешивания.
Для опытов был использован металлический шар и массивный кусок металла. Кавендиш прикреплял маленькие металлические шарики к тонкой планке и подносил к ним большие свинцовые шары. В результате воздействия планка закручивалась, пока эффект притяжения не компенсировал силы Гука. Эксперимент был настолько тонким, что даже малейшее дуновение ветерка могло свести на нет результаты исследований. Чтобы избежать конвекции, Кавендиш все измерительное оборудование разместил в большом коробе, затем поставил его в закрытой комнате, а наблюдения за экспериментом велись при помощи телескопа.
Вычислив силы закручивания нити, Кавендиш произвел оценку величины G, которая впоследствии была лишь немного откорректирована благодаря другим, более точным экспериментам. В современной системе единиц:
G =6.67384 × 10-11 м3 кг-1 с-2.
Данная величина является одной из немногочисленных физических констант. Ее значение неизменно в любой точке Вселенной.
Измерение ускорения Земли
Согласно третьему закону Ньютона сила притяжения двух тел зависит лишь от их массы и расстояния между ними. Таким образом, подставляя в правую часть уравнения множитель, известный из второго закона Ньютона, получаем:
ma= G(mM)/d2.
В нашем случае массу m можно сократить, а величина а и есть ускорение, с которым тело m притягивается к Земле. В настоящее время ускорение свободного падения принято обозначать буквой g. Получаем:
g = GM/d2.
В нашем случае d –радиус Земли, М – ее масса, а G –та самая неуловимая константа, которую на протяжении многих лет искали физики. Подставляя в уравнение известные данные, получим: g=9,8м/с2. Эта величина и составляет ускорение свободного падения на Земле.
Значения G для разных широт
Поскольку наша планета не имеет форму шара, а является геоидом, радиус ее не везде одинаков. Земля как бы сплюснута, поэтому на экваторе и на обоих полюсах ускорение свободного падения будет принимать различные значения. В целом разница в показаниях длины радиуса составляет около 43 км. Поэтому в физике для решения задач принимается то ускорение свободного падения, которое измерено на широте около 450 . Довольно часто для облегчения расчетов его принимают равным 10 м/с2.
Значение G для Луны
Наш спутник подчиняется тем же законам, что и остальные планеты Солнечной системы. Строго говоря, вычисляя ускорение на поверхности Луны, следует принимать во внимание и притяжение со стороны Солнца.
Но, как видно из формулы, с увеличением расстояния значение силы притяжения резко уменьшается. Поэтому, отбросив все второстепенные силы, используем ту же формулу:
GЛ = GM/d2.
Здесь М – масса Луны, а d – ее диаметр. Подставив известные величины, получим величину GЛ=1,622 м/с2. Эта величина и представляет собой ускорение свободного падения на Луне.
Именно такое малое значение GЛ является главной причиной того, что на Луне отсутствует атмосфера. По некоторым данным на заре времен наш спутник имел атмосферу, но из-за слабого притяжения Луна довольно быстро ее растеряла. Все планеты с большой массой обычно обладают собственной атмосферой. Ускорение свободного падения у них достаточно велико для того, чтобы не только не терять собственную атмосферу, но и прихватывать из космоса некоторое количество молекулярного газа.
Подведем некоторые итоги. Ускорение свободного падения — это величина, которой обладает каждое материальное тело. Как ни удивительно это звучит, но все, что обладает массой, притягивает к себе окружающие предметы. Просто это притяжение настолько мало, что в обычной жизни не играет никакой роли. Тем не менее ученые серьезно относятся даже к самым маленьким физическим константам, ведь влияние, которое они оказывают на окружающий мир, до конца еще нами не изучено.