Идеальные пропорции тела человека
Примерно в 1490 году великий итальянский ученый, художник, скульптор Леонардо да Винчи нарисовал свой знаменитый рисунок «Витрувианский человек». Этот рисунок часто используется как символ симметрии человеческого тела. На нем изображена фигура обнаженного мужчины в двух наложенных одна на другую позициях: с разведёнными в стороны руками и ногами, вписанная в окружность; с разведёнными руками и сведенными вместе ногами, вписанная в квадрат. Рисунок и пояснения к нему иногда называют каноническими пропорциями. Значение этого рисунка сложно переоценить. Ведь пропорции являются средством создания гармоничного образа не только для архитекторов, художников, проектировщиков, но и для модельеров одежды.
Тест на определение типа фигуры

Не знаете свой ТИП ФИГУРЫ?
Пройдите бесплатный ТЕСТ!
ПРОЙТИ ТЕСТ
Теория пропорционирования Леонардо да Винчи
Значение «Витрувианского человека» в том, что только идеальные пропорции тела человека позволяют позицию с разведенными руками и ногами вписать в круг, а с разведенными руками и сведенными ногами – в квадрат. Однако сама теория пропорционирования (Леонардо да Винчи лишь воплотил ее в рисунке) была создана другим римским ученым и архитектором – Марком Витрувием Поллионом. Позднее эта теория получила распространение в изобразительном искусстве и архитектуре.
Согласно этой теории следующие соотношения характерны для идеальных пропорций тела человека:
» длина от кончика самого длинного до самого низкого основания из четырех пальцев равна ладони
- » ступня равна четырем ладоням
- » локоть равен шести ладоням
- » высота человека составляет четыре локтя (и соответственно 24 кисти)
- » шаг равняется четырём локтям
- » размах человеческих рук равен его высоте
- » расстояние от линии волос до подбородка равняется 1/10 его высоты
- » расстояние от макушки до подбородка равняется 1/8 его высоты
- » расстояние от макушки до сосков составляет 1/4 его высоты
- » максимум ширины плеч составляет 1/4 его высоты
- » расстояние от локтя до кончика руки составляет 1/4 его высоты
- » расстояние от локтя до подмышки составляет 1/8 его высоты
- » длина руки составляет 2/5 его высоты
- » расстояние от подбородка до носа составляет 1/3 длины его лица
- » расстояние от линии волос до бровей 1/3 длины его лица
- » длина ушей 1/3 длины лица
- » Калькулятор пропорциональности
- » Калькулятор изящества
- » Индекс массы тела
- » Калькулятор физического состояния
Мастер-класс «Подбор гардероба по типу фигуры»

Теория золотого сечения
Однако теория пропорционирования Марка Витрувия Поллиона возникла намного позднее теории «золотого сечения» или «божественной пропорции». Принято считать, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные. Пирамида Хеопса в Египте, Парфенон в Афинах, Собор Нотредам де Пари, картины Леонардо да Винчи «Мона Лиза» и «Тайная вечеря», Ботичелли «Венера», Рафаеля «Афинская школа» и многие, многие другие объекты были созданы по принципу «золотого сечения».
- » Виды пропорций в одежде: подобная, гармоническая, контрастная
- » Норма роста, веса и длина ног
- » Как определить свои пропорции: нормативы
- » Какие бывают типы женских фигур?
- » Как определить тип фигуры? ТЕСТ.
Получите мои бесплатные рекомендации по стилю по электронной почте:

А ЧТО ВЫ ДУМАЕТЕ ПО ЭТОЙ ТЕМЕ?
«Золотое сечение» — это пропорциональное отношение частей друг к другу, примерно 62% к 38%, часто используемое в искусстве, фотографиях, картинах, изображении портретов, в архитектуре, а также в физических, технических и других науках, включая математику.
Золотое сечение — пропорция, которую можно увидеть в природе и природных явлениях. Человек — часть природы, и у него есть пропорции тела — в идеале, гармоничные, согласно золотого сечения.
Именно пропорции золотого сечения подсознательно радуют глаз и привлекают к себе, включая идеальные пропорции тела человека, женщины или мужчины.
Телосложение и пропорции тела человека тесно связаны с его психофизиологическими особенностями, высшей нервной деятельностью ЦНС — темпераментом, характером, психотипом и поведением.
Пропорции тела человека
Правильные пропорции тела человека — это показатель гармонии и красоты, поэтому великие художники и скульпторы использовали Золотое сечение в своих работах.
Женское тело отличается от мужского в пропорциях — у нее 8:5=1,6 у него 13:8=1,625 (идеал — Золотое сечение 1,62).
Нормальные пропорции новорожденного ребенка — 1:1
Золотое сечение — Идеальные пропорции тела человека использовал Леонардо да Винчи в своем «Витрувианском человеке».
Пропорции тела женщины
Идеальные пропорции тела (фигуры) женщины соответствуют Золотому сечению Леонардо да Винчи.
Размер головы (от подбородка до макушки) условно берется за единицу измерения пропорций всего тела женщины — в полном росте должно быть 7,5-8 «голов».
Золотое сечение пропорций женского тела по высоте (росту) и ширине
- От макушки до талии — три «головы»
- От талии до пяток — 5 «голов»
- Ширина (не объем) талии — 1 «голова»
- Ширина бедер — 1,5 «головы»
- Ширина каждого плеча — 1 «голова» (здесь берется ширина головы, а не высота, как у мужчин)
- От пяток до коленок — 2 «головы»
- Линия талии совпадает с линией локтя (от макушки до талии 3 «головы», от пяток до талии — 5 «голов»)
- От макушки до груди — 2 «головы»; от талии до груди — 1 «голова»
- Линия бедер, она же основание туловища — это половина всей длины тела женщины (ее роста).
Идеальные пропорции женского тела могут быть искажены, если женщина сутулится или перегибается, либо при приподнятых или опущенных плечах.
Недостаточный или лишний вес женского тела также нарушает пропорции золотого сечения.
Золотое сечение — пропорция тела женщин по объему (обхвату)
Всеми известный стандарт «идеальной» женской фигуры — 90-60-90 — не точно отражает золотую пропорцию женского тела (здесь все индивидуально).
Золотая пропорция талии к бедрам 62%, но не более 70% от объема последних (тоже самое талия и грудь).
Идеальная длина ног — половина или чуть больше общего роста женщины.
Идеальный объем груди (грудной клетки, а не бюста) — это половина роста девушки плюс 2,5 см. (а идеальный размер бюста — это размер груди плюс 8-10 см).
Отношение объема шеи к талии — 2:1 Длина шеи — 7% от роста.
Объем (обхват) запястья — равен 2-м объемам женской шеи.
Идеальный вес женщины (девушки) по возрасту — рассчитать на калькуляторе ИМТ онлайн
Таблица идеальных параметров женского тела
Существующие женские фигуры
- Песочные часы — сбалансированная, изящная и пропорциональная женская фигура с красивым бюстом, со стройными ногами и округлыми ягодицами.
- Треугольник, V-образная фигура — широкие плечи и большая грудь при узких бедрах, но стройных ногах.
- Прямоугольник — пропорции явно не золотого сечения, внешний вид как у мальчишки. Грудь, талия и бедра практически одинакового объема.
- Груша — фигура с широкими бедрами и не длинными ногами, при этом совсем непропорционально небольшие плечи и грудь.
- Яблоко — талия и живот у девушки с таким типом фигуры непропорционально больше объема груди и бедер, ягодицы зачастую плоские.
Золотые пропорции лица женщины
Формула пропорциональной фигуры:
П=Б:(Н+Р+Ш), где…
- П — пропорции тела женщины
- Б — обхват бедер под ягодичной складкой
- Р — окружность бедра
- Н — окружность голени
- Г — обхват груди
- Т — обхват талии
Идеал — 0,54 — 0,62
Пропорции тела мужчины
Золотые пропорции тела мужчин отличаются от женских (у него 13:8 у нее 8:5).
Каждый мужчина может определить для себя, есть ли у него золотое сечение в телесных пропорциях — рассчитывается также, как и у женщин (см. выше).
Длина головы берется за единицу измерения. Во всем теле (росте) должно быть 7,5 — 8 таких размеров («голов»)
Отличие измерений пропорций от женщин только в размере плеч (по высоте головы, а у женщин по ширине) и соотношениях талии, бедер и груди.
На рисунке ниже все схематично изображено.
Антропометрическая таблица для мужчин
Пропорции тела ребенка
Дети еще растут и развиваются, поэтому пропорции тела ребенка отличаются от взрослых.
Пропорции новорожденного 1:1 (у взрослого мужчины 13:8, женщины 8:5).
До подросткового возраста, лет до 10-13 (здесь все индивидуально, рост и развитие тела зависит от генетики и физиологических особенностей организма), размер головы ребенка составляет 1/5 (1/6) размера всего тела.
Т.е., если золотые пропорции тела взрослого человека составляют 7,5-8 «голов», то у ребенка 5,5 — 6.
Мальчики и девочки до пубертатного периода (начала полового созревания) практически имеют одинаковые пропорции тела (с одинаковой прической и со спины их не различить по полу).
У подростков, годам к 13-15, девочки обычно созревают раньше мальчиков, пропорции тела приобретают взрослые соотношения.
Далеко не у всех людей может быть золотое сечение — пропорция тела человека и тип телосложения обусловлены генетически.
Вы можете приблизится к идеальной пропорциональности, поддерживая свое психическое и физическое здоровье, ведя здоровый образ жизни, сбалансированно и полноценно питаясь, при этом не напрягая себя диетами и спортзалом, а главное — навязчивыми мыслями об идеальной фигуре.
Золотое сечение, Идеальные пропорции тела человека — далеко не главный критерий для счастья в жизни, гармоничных отношений и любви.
Читайте статью: Красивая и несчастная женщина
Подросткам, юношам, а особенно девушкам, не стоит мыслить дихотомически (по типу, все или ничего, черное или белое) и воспринимать мир по-максимуму, (отключаем «подростковый максимализм») — совершенства в мире не бывает.
Возможно вас заинтересует…
- Какие девушки нравятся парням?
- Как понять, нравишься ли ты мужчине?
- Тест нравлюсь ли я парню
- Как женщине стать женственной?
- Тест на чувство прекрасного
- Как стать желанной для мужчины?
- КАЛЬКУЛЯТОР ИДЕАЛЬНОЙ МАССЫ ТЕЛА (по полу и возрасту)
ВВЕДЕНИЕ
Эталонами красоты
человеческого тела, образцами гармонического телосложения издавна считаются великие
творения греческих скульпторов: Фидия, Поликтета, Мирона, Праксителя. Можно ли
выразить красоту человека с помощью формул и уравнений? Математика дает
утвердительный ответ. В создании своих творений греческие мастера использовали
принцип золотой пропорции. Золотое сечение является мерилом гармонии в природе
и в произведениях искусства на протяжении многих веков. Его изучением занимались
люди античности и эпохи Возрождения. В ХIХ и ХХ веке интерес к золотому сечению возродился с новой силой.
Соответствуют ли
современные люди тем идеальным пропорциям строения человеческого тела, которые дошли
до нас с античных времен? На этот вопрос мы постараемся ответить в
исследовательской работе «Золотое сечение в пропорциях тела человека».
Цель работы: изучение золотого сечения,
как идеальной пропорции строения человеческого тела.
Задачи:
1)
изучить
литературу по теме исследовательской работы;
2)
дать
определение золотому сечению, познакомиться с его построением, применением и
историей;
3)
узнать
математические закономерности в пропорциях тела человека;
4)
научиться
находить золотое сечение в пропорциях людей;
5)
определить
соответствие пропорций человеческого тела золотому сечению.
Гипотеза: пропорции каждого
человеческого тела соответствуют золотому сечению.
Объект
исследования:
человек.
Предмет
исследования:
золотое сечение в пропорциях человеческого тела.
Методы исследования: измерение роста и частей
тела человека, обработка полученных результатов математическими методами с
помощью программы Microsoft Office Excel 2007, сравнительный анализ полученных
измерений со значением золотого сечения.
Глава 1 Золотое сечение
1.1
Понятие
золотого сечения
Пифагор показал,
что отрезок единичной длины АВ (рисунок 1.1). можно разделить на две части так,
что отношение большей части (АС=х) к меньшей (СВ=1-х) будет равняться отношению
всего отрезка (АВ=1) к большей части(АС=х):
Рисунок
1.1 – Деление отрезка в крайнем и среднем отношении
По свойству
пропорции .. х2=1-х,
х2+х-1=0.
(1)
Положительным
корнем этого уравнения является , так что отношения в
приведенной пропорции равны: =
≈1,61803 каждое.
Такое деление
(точкой С) Пифагор называл золотым делением, или золотой пропорцией,
Евклид – делением в крайнем и среднем отношении, а Леонардо да Винчи –
общепринятым сейчас термином «золотое сечение».[7,с.18-19]
Золотое сечение — это
такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так
относится к большей части, как большая часть относится к меньшей; или другими
словами, меньший отрезок так относится к большему, как больший ко всему. [2,с.8]
Величину золотого
сечения принято обозначать буквой Ф. Это сделано в честь Фидия- творца
бессмертных скульптурных произведений. [1, с.141]
Ф=1,618033988749894.
Это значение золотого сечения с 15 знаками после запятой. Более точное значение
Ф можно увидеть в Приложении А.
Так как решение
уравнения (1) является отношением между длинами частей отрезка, оно не зависит
от длины самого отрезка. Другими словами, значение золотого сечения не зависит
от первоначальной длины. [4, с.24,25]
1.2 Построение и применение золотого сечения
Рассмотрим
геометрическое построение золотого сечения (рисунок 1.2) с помощью прямоугольного
треугольника АСВ, в котором стороны АВ и АС имеют следующие длины: АВ
= 1, АС
= 1/2. Проведем из центра окружности С дугу через точку А до пересечения с
отрезком СВ, получим точку D . Затем
проведем через точку D дугу с центром окружности В
до пересечения с отрезком АВ. Получили искомую точку Е, делящую отрезок АВ в
золотой пропорции. [5, с.12]
Рисунок
1.2 – Геометрическое построение золотого сечения
Еще Пифагор и пифагорейцы использовали золотое сечение для
построения некоторых правильных многогранников — тетраэдра, куба, октаэдра,
додекаэдра, икосаэдра.
Евклид
в III в. до н. э. использует вслед за пифагорейцами золотую пропорцию в своих
«Началах» для построения правильных (золотых) пятиугольников, диагонали которых
образуют пентаграмму. [7, с.19]
В пентаграмме на рисунке 1.3 точки пересечения диагоналей
делят их в золотом сечении, т. е. АВ/СВ = CB/DB = DB/CD .
Рисунок
1.3 — Пентаграмма
Арифметически
отрезки золотой пропорции выражаются бесконечной иррациональной дробью.
АС=0,618…, СВ=0,382…. В практике применяется округление: 0,62 и 0,38. Если
отрезок АВ принять за 100 частей (рисунок 1.4), то большая часть отрезка равна
62, а меньшая – 38 частям. [2, с.10]
Этот способ построения золотого сечения используют художники.
Если высоту или ширину картины разделить на 100 частей, то больший отрезок
золотой пропорции равен 62, а меньший – 38 частям. Эти три величины позволяют
нам построить ряд отрезков золотой пропорции. 100, 62, 38, 24, 14, 10 – это ряд
величин золотой пропорции, выраженных арифметически. [2, с.11]
Рисунок 1.4 — Линии золотого сечения
и диагонали на картине
Пропорции золотого сечения часто использовались художниками
не только при проведении линии горизонта, но и в соотношениях между другими
элементами картины.
Леонардо да Винчи и Альбрехт Дюрер находил золотое сечение в
пропорциях человеческого тела. Древнегреческий скульптор Фидий использовал его
не только в своих статуях, но и при оформлении храма Парфенона.[8, с.99-100]
Страдивари использовал это соотношение при изготовлении своих знаменитых
скрипок. [2, с.7]
Форма, организованная при помощи пропорций золотого сечения,
вызывает впечатление красоты, приятности, согласованности, соразмерности,
гармоничности. [2, с.6]
Учение о золотом сечении получило широкое применение в
математике, физике, химии, живописи, эстетике, биологии, музыке, технике.
1.3 История золотого сечения
Принято считать,
что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий
философ и математик (VI в. до н.э.). Однако еще
задолго до рождения Пифагора древние египтяне и вавилоняне использовали
принципы золотого сечения в архитектуре и искусстве. И действительно, пропорции
пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы
Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями
золотого деления при их создании.
Платон (427…347
гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен
математическим и эстетическим воззрениям школы Пифагора и, в частности,
вопросам золотого деления. [3, с17,18]
Античные скульпторы
и архитекторы широко использовали число 1,62 или близкие к нему числовые
соотношения в своих художественных произведениях. Например, в фасаде
древнегреческого храма Парфенона присутствуют золотые пропорции.
В дошедшей до нас
античной литературе золотая пропорция впервые упоминается в «Началах» Евклида
(325…265 гг. до н.э.) во второй книге, а в шестой книге дается определение и
построение деления отрезка в крайнем и среднем отношении. [4,с.148]
В эпоху итальянского Возрождения возникает новая волна
увлечения золотым сечением. Золотая пропорция возводится в ранг главного
эстетического принципа. Леонардо да Винчи именует ее «Sectio autea«,
откуда и происходит сам термин «золотое сечение» или «золотое
число». Лука Пачиоли в 1509 г. пишет первое сочинение о золотой пропорции,
озаглавленное «De divina
Proportioned«, что значит «О
божественной пропорции». Иоганн Кеплер, первым упоминающий о значении этой
пропорции в ботанике, говорит о ней, как о «бесценном сокровище, как об
одном из двух сокровищ геометрии» и называет ее «Sectio divina»
(божественное сечение). Нидерландский композитор Якоб Обрехт (1430—1505 гг.)
широко использует золотое сечение в своих музыкальных композициях, которые
уподобляют «кафедральному собору, созданному гениальным архитектором».
После эпохи Возрождения почти на два столетия золотое сечение
было предано забвению. В середине XIX в. немецкий ученый Цейзинг делает попытку
сформулировать всеобщий закон пропорциональности и при этом вновь открывает
золотое сечение. В своих «Эстетических исследованиях» (1855) он
показывает, что этот закон проявляется в пропорциях человеческого тела (рисунок
1.5) и в теле тех животных, формы которых отличаются изяществом. В теле
античных статуй и хорошо сложенных людей пуп является точкой деления высоты
тела в золотом сечении. [5,
c.4]
Рисунок 1.5 – Числовые
отношения в человеческом теле (по Цейзингу)[6,c.59]
Пропорциональные отношения, близкие к золотому сечению, Цейзинг
находит в некоторых храмах (в частности, в Парфеноне), в конфигурациях минералов,
растений, в звуковых аккордах музыки.
В конце XIX в. немецкий психолог Фехнер проводит ряд
психологических опытов для выяснения эстетического впечатления от
прямоугольников, имеющих различные отношения сторон. Опыты оказались
чрезвычайно благоприятными для золотого сечения.
В XX в. интерес к золотому сечению возрождается с новой
силой. В первой половине века композитор Л.Сабанеев формулирует общий закон
ритмического равновесия и при этом обосновывает золотое сечение в качестве некоторой
нормы творчества, нормы эстетической конструкции музыкального произведения. О
значении золотого сечения в природе и искусстве пишут Г. Е. Тимердинг, М. Гика ,
Г. Д. Гримм.
К «задаче о кроликах», с которой связано
возникновение чисел Фибоначчи, в своих истоках восходит математическая теория
биологических популяций. Закономерности, описываемые числами Фибоначчи и
золотой пропорцией, обнаруживают во многих явлениях физического и
биологического мира («магические» ядра в физике, ритмы мозга и др.).
Советский математик Ю. В. Матиясевич с использованием чисел
Фибоначчи решает 10-ю проблему Гильберта. Академик Г.В.Церетели обнаруживает
золотое сечение в поэме Шота Руставели «Витязь в тигровой шкуре».
Возникают изящные методы решения задач теории поиска и теории программирования,
основанные на числах Фибоначчи и золотой пропорции.
В последние
десятилетия числа Фибоначчи и золотая пропорция неожиданно проявили себя в
основании цифровой техники
Во второй половине XX века к числам Фибоначчи и золотому
сечению обращаются представители практически всех наук и искусств (математики,
физики, химии, ботаники, биологии, психологии, поэзии, архитектуры, живописи, музыки)
[5, с.4,5], потому что золотое сечение – ключ к пониманию секретов совершенства
в природе и искусстве.
Глава 2
Идеальные пропорции человеческого тела
Уже тысячелетия
пытаются люди найти математические закономерности в пропорциях тела человека,
прежде всего человека хорошо сложенного, гармоничного.
Древние греки,
считавшие золотое сечение проявлением гармонии в природе, создавали статуи
людей с соблюдением правила золотого сечения. В XIX веке профессор Цейзинг подтвердил это, измерив сохранившиеся
до наших дней древнегреческие статуи. Цейзинг даже выделил части тела человека,
которые, по его мнению, наиболее точно соответствуют золотому сечению. Если
разделить тело человека согласно правилу золотого сечения, то линия пройдет в
области пупка. Длина плеча относится к общей длине руки также согласно золотому
сечению. Соотношение частей лица, длины фаланг пальцев руки и многие другие
части тела подпадают под правило золотого сечения (рисунок 2.1). [3, с.24,25]
Рисунок 2.1 – Золотое сечение в строении тела человека
Золотая
пропорция занимает ведущее место в художественных канонах Леонардо да Винчи и
Дюрера. В соответствии с этими канонами золотая пропорция отвечает делению тела
на две неравные части линией талии.
Высота
лица (до корней волос) относится к вертикальному расстоянию между дугами бровей
и нижней частью подбородка, как расстояние между нижней частью носа и нижней
частью подбородка относится к расстоянию между углами губ и нижней частью
подбородка, это отношение равно золотой пропорции.
Пальцы
человека состоят из трех фаланг: основных, средних и ногтевых. Длина основных
фаланг всех пальцев, кроме большого, равна сумме длин двух остальных фаланг, а
длины всех фаланг каждого пальца соотносятся друг к другу по правилу золотой
пропорции. [1, с.144,145]
Леонардо
применил научные знания о пропорциях человеческого тела к теориям Пачоли и
Витрувия о красоте. На рисунке Леонардо «Витрувианский человек» мужская фигура,
вписанная в круг и квадрат (рисунок 2.2).
Рисунок 2.2 – «Витрувианский человек» Леонардо да
Винчи
Квадрат
и круг имеют разные центры. Гениталии человека являются центром квадрата, а
пупок – центром круга. Идеальные пропорции человеческого тела на таком
изображении соответствуют отношению между стороной квадрата и радиусом круга:
золотому сечению. [4,с.100,101]
«Витрувианский
человек» представляет собой приблизительные пропорции тела обычного взрослого
человека, которые со времен Древней Греции использовались в качестве
художественного канона для изображения человека. Пропорции сформулированы
следующим образом:
Рост человека = размаху рук (расстоянию между кончиками пальцев
разведенных в стороны рук) = 8 ладоням= 6 ступням= 8 лицам = 1,618 умноженному
на высоту пупка (расстояние от пупка до земли).[4,с.102]
Одним
из высших достижений классического греческого искусства может служить статуя
«Дорифор» («Копьеносец»), изваянная Поликтетом (рисунок 2.3).
Рисунок 2.3 – Статуя «Дорифор» греческого скульптора
Поликтета
Фигура
юноши выражает единство прекрасного и доблестного, лежащих в основе греческих
принципов искусства. Широкие плечи почти равны высоте туловища, половина высоты
тела приходится на лонное сращение, высота головы восемь раз укладывается в
высоте тела, а золотой пропорции отвечает положение пупка на теле атлета.[1,c.141,142]
В середине XIX века
немецкий ученый Цейзинг находил, что все тело человека в целом и каждый
отдельный его член связаны математически строгой системой пропорциональных
отношений, среди которых золотое сечение занимает важнейшее место. Измерив
тысячи человеческих тел, он установил, что золотая пропорция есть среднестатистическая
величина, характерная для всех хорошо развитых тел. Средняя пропорция мужского
тела близка к 13/8= 1,625, а женского — к 8/5=1,60, у новорожденного пропорция
равна 2, к 13 годам она равна 1,6, а к 21 году равняется мужской (рисунок 2.4).
[3, с.20]
Рисунок
2.4 – Сравнение пропорций головы и тела человека на различных этапах развития [4,c.126]
Бельгийский
математик Л.Кетле в XIX веке установил, что человек
идеален только при подсчете среднего арифметического. В 1871г. его исследования
пропорций тел жителей Европы полностью подтвердили идеальные пропорции.[4,с.102]
Золотую пропорцию
можно считать некоторой «константой гармонии», идеальным пределом, к которому
стремится тело человека в своем развитии.
Глава 3 Золотое сечение в
пропорциях тела человека. Исследование
Мы проверяли гипотезу
о том, что пропорции каждого человеческого тела соответствуют золотому сечению.
Для исследования
были привлечены учащиеся 1-х, 5-х, 9-х и 11-х классов и учителя разного возраста(от
25 до 53 лет).
В теле человека пуп является точкой деления высоты тела в
золотом сечении. Поэтому мы измеряли рост людей (a), высоту пупка (b) и расстояние от головы до пупка (c). Затем в программе Microsoft Office Excel 2007 находили отношения этих
величин (a/b, b/c) для каждого человека в
отдельности, cреднее значение для группы людей одного
возраста (a/b), сравнивали отношения с величиной
золотого сечения (1,618) и выбирали людей с золотой пропорцией (приложение Б).
Результаты
исследования мы представили в виде таблицы (таблица 3.1).
Таблица 3.1 – Соответствие пропорций
человеческого тела золотому сечению у людей разного возраста.
|
Класс |
Количество человек |
Полученное среднеарифметическое отношение |
Количество людей с золотой пропорцией |
|
1 |
11 |
1,701 |
0 |
|
5 |
14 |
1,652 |
0 |
|
9 |
19 |
1,640 |
2 |
|
11 |
8 |
1,622 |
1 |
|
Учителя |
10 |
1,630 |
2 |
|
11 класс и учителя |
62 |
1,626 |
3 |
Наглядно эти
данные можно представить в виде диаграмм (приложения В и Г).
По результатам проведенного
исследования можно сделать следующие выводы:
1)
с
возрастом у человека пропорции тела изменяются;
2)
пропорции
тела человека отличаются даже у людей одного возраста;
3)
у
взрослых людей пропорции тела приближаются к величине золотого сечения, но
редко соответствует ему;
4)
идеальные
пропорции золотого сечения не применимы ко всем людям.
Следовательно, золотое сечение в пропорциях тела человека — это
среднестатистическая величина, к которой приближаются пропорции тела взрослого
человека. Только у некоторых людей пропорции тела соответствуют золотому
сечению.
ЗАКЛЮЧЕНИЕ
Золотое сечение является мерилом гармонии в природе и в
произведениях искусства на протяжении многих веков. Учение о золотом сечении
получило широкое применение в математике, физике, химии, живописи, эстетике, биологии,
музыке, технике.
Целью
исследовательской работы было изучение золотого сечения, как идеальной
пропорции строения человеческого тела.
Для достижения
цели мы изучили литературу по теме исследовательской работы, познакомились с
золотым сечением, с его построением, применением и историей; узнали
математические закономерности в пропорциях тела человека; научились находить
золотое сечение в пропорциях людей (приложение Д).
В практической
части мы определяли соответствие пропорций человеческого тела золотому сечению,
проверяли следующую гипотезу: пропорции каждого человеческого тела
соответствуют золотому сечению.
Для проверки
гипотезы мы измеряли рост людей и некоторые части тела у учащихся 1, 5, 9, 11
классов и учителей разного возраста.. Затем в программе Microsoft Office Excel
2007 находили отношения величин для каждого человека в отдельности, cреднее значение для группы людей одного возраста,
сравнивали полученные отношения со значением золотого сечения и выбирали людей
с золотой пропорцией.
На основании результатов
проведенного исследования можно сделать следующие выводы:
1)
с
возрастом у человека пропорции тела изменяются;
2)
пропорции
тела человека отличаются даже у людей одного возраста;
3)
у
взрослых людей пропорции тела приближаются к величине золотого сечения, но
редко соответствует ему;
4)
идеальные
пропорции золотого сечения не применимы ко всем людям.
Следовательно, золотое сечение в пропорциях тела человека —
это среднестатистическая величина, к которой приближаются пропорции тела
взрослого человека. Только у некоторых людей пропорции тела соответствуют
золотому сечению. Наша гипотеза подтвердилась частично.
СПИСОК
ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1)
Васютинский,
Н.А. Золотая пропорция / Н.А.Васютинский – М.: Мол. гвардия, 1990. – 238 с.
2)
Ковалев,
Ф.В.Золотое сечение в живописи: учеб. пособие/ Ф.В. Ковалев. — К.:Выща школа.
Головное изд-во, 1989.—143 с.
3)
Лукашевич,
И.Г. Математика в природе /И.Г. Лукашевич. -Минск: Белорус. ассоц. «Конкурс», 2013.
— 48с.
4)
Мир
математики: в 40т. Т.1: ФернандоКорбалан. Золотое сечение. Математический язык
красоты /Пер.с англ. — М.:Де Агостини, 2014. — 160с.
5)
Стахов, А.П.
Коды золотой пропорции/А.П. Стахов. — М.: «Радио и связь»,1984. – 152с.
6)
Тимердинг,
Г.Е. Золотое сечение /Г.Е.Тимердинг; под ред. Г.М.Фихтенгольца; пер. с нем.-
Петроград: Научное книгоизд-во, 1924. – 86с.
7)
Урманцев,
Ю.А. Симметрия природы и природа симметрии /Ю.А.Урманцев. — М.,Мысль,1974. — 229с.

Я познаю
мир: Дет.энцикл: Математика /Авт.-сост. А.П.Савин и др.; худож.А.В.Кардашук и
др. — М.: АСТ: Астрель, 2002. — 475с.
ПРИЛОЖЕНИЕ А
ЗНАЧЕНИЕ ЗОЛОТОГО СЕЧЕНИЯ
Рисунок
А.1 – Более точное значение Ф
ПРИЛОЖЕНИЕ Б
СООТВЕТСТВИЕ
ПРОПОРЦИЙ ЧЕЛОВЕЧЕСКОГО ТЕЛА ЗОЛОТОМУ СЕЧЕНИЮ
Таблица Б.1-Результаты
измерения людей и вычисление среднеарифметических значений пропорций тела для
учащихся 1, 5, 9, 11 классов и учителей
|
Фамилия Имя |
Класс |
Рост (а) |
Высота линии пупка (b) |
Рассто-яние от пупка до головы (с) |
а/b |
b/c |
Среднее |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Золотое |
1,618 |
1,618 |
||||||
|
1 |
Андреев |
1а |
130 |
77 |
53 |
1,688 |
1,453 |
|
|
2 |
Грабцевич |
1а |
125 |
71 |
54 |
1,760 |
1,315 |
|
|
3 |
Ваванова |
1а |
127 |
74 |
53 |
1,716 |
1,396 |
|
|
4 |
Захаренко |
1а |
124 |
74 |
50 |
1,676 |
1,480 |
1класс |
|
5 |
Капориков |
1а |
133 |
79 |
54 |
1,684 |
1,463 |
1,701 |
|
6 |
Карсаков |
1а |
120 |
71 |
49 |
1,690 |
1,449 |
|
|
7 |
Лазовый |
1а |
128 |
75 |
53 |
1,707 |
1,415 |
|
|
8 |
Ласоцкая |
1а |
125 |
76 |
49 |
1,645 |
1,551 |
|
|
9 |
Моргунова |
1а |
116 |
66 |
50 |
1,758 |
1,320 |
|
|
10 |
Павлющенко |
1а |
129 |
77 |
52 |
1,675 |
1,481 |
|
|
11 |
Раковский |
1а |
128 |
75 |
53 |
1,707 |
1,415 |
|
|
12 |
Бахарева |
5а |
146 |
87 |
59 |
1,678 |
1,475 |
|
|
13 |
Бытковский |
5а |
145 |
85 |
60 |
1,706 |
1,417 |
|
|
14 |
Жданович |
5а |
146 |
86 |
60 |
1,698 |
1,433 |
5класс |
|
15 |
Климова |
5а |
155 |
95 |
60 |
1,632 |
1,583 |
1,652 |
|
16 |
Ларченко |
5а |
158 |
94 |
64 |
1,681 |
1,469 |
|
|
17 |
Листвягов |
5а |
143 |
87 |
56 |
1,644 |
1,554 |
|
|
18 |
Мухина |
5а |
144 |
88 |
56 |
1,636 |
1,571 |
|
|
19 |
Падерина |
5а |
151 |
91 |
60 |
1,659 |
1,517 |
|
|
20 |
Прочуханов |
5а |
151 |
92 |
59 |
1,641 |
1,559 |
|
|
21 |
Савкина |
5а |
140 |
87 |
53 |
1,609 |
1,642 |
|
|
22 |
Симакович |
5а |
137 |
84 |
53 |
1,631 |
1,585 |
|
|
23 |
Сурганова |
5а |
150 |
92 |
58 |
1,630 |
1,586 |
|
|
24 |
Смоляров |
5а |
142 |
86 |
56 |
1,651 |
1,536 |
|
|
25 |
Тихинский |
5а |
144 |
88 |
56 |
1,636 |
1,571 |
|
|
26 |
Аверков |
9а |
171 |
104 |
67 |
1,644 |
1,552 |
Продолжение таблицы
Б.1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
27 |
Власенко Анастасия |
9а |
162 |
99 |
63 |
1,636 |
1,571 |
|
|
28 |
Гелясов Евгений |
9а |
194 |
115 |
79 |
1,687 |
1,456 |
|
|
29 |
Герасимов Евгений |
9а |
177 |
108 |
69 |
1,638 |
1,565 |
9класс |
|
30 |
Дудкова Яна |
9а |
163 |
100 |
63 |
1,630 |
1,587 |
1,640 |
|
31 |
Кондратенко Андрей |
9а |
167 |
102 |
65 |
1,637 |
1,569 |
|
|
32 |
Лихачева Александра |
9а |
158 |
99 |
59 |
1,596 |
1,678 |
|
|
33 |
Мелашунас Дарья |
9а |
165 |
102 |
63 |
1,618 |
1,619 |
|
|
34 |
Романова Диана |
9а |
165 |
103 |
62 |
1,602 |
1,661 |
|
|
35 |
Савкина Александра |
9а |
171 |
104 |
67 |
1,644 |
1,552 |
|
|
36 |
Свищев Кирилл |
9а |
172 |
105 |
67 |
1,638 |
1,567 |
|
|
37 |
Свищева Анастасия |
9а |
162 |
99 |
63 |
1,636 |
1,571 |
|
|
38 |
Смирнова Татьяна |
9а |
160 |
98 |
62 |
1,633 |
1,581 |
|
|
39 |
Шкель Роман |
9а |
172 |
106 |
66 |
1,623 |
1,606 |
|
|
40 |
Алейников Егор |
9б |
184 |
110 |
74 |
1,673 |
1,486 |
|
|
41 |
Гегелева Ксения |
9б |
164 |
99 |
65 |
1,657 |
1,523 |
|
|
42 |
Димков Анатолий |
9б |
163 |
99 |
64 |
1,647 |
1,547 |
|
|
43 |
Рябцева Евгения |
9б |
170 |
103 |
67 |
1,651 |
1,537 |
|
|
44 |
Тарасенко Анатолий |
9б |
162 |
97 |
65 |
1,670 |
1,492 |
|
|
45 |
Дудов Роман |
11а |
165 |
101 |
64 |
1,634 |
1,578 |
|
|
46 |
Земцова Дарья |
11а |
161 |
101 |
60 |
1,594 |
1,683 |
11класс |
|
47 |
Ивлев Никита |
11а |
176 |
109 |
67 |
1,615 |
1,627 |
1,622 |
|
48 |
Розенберг Анастасия |
11а |
161 |
101 |
60 |
1,594 |
1,683 |
|
|
49 |
Цедрик Анна |
11а |
158 |
96 |
62 |
1,646 |
1,548 |
|
|
50 |
Шевченко Савелий |
11а |
182 |
111 |
71 |
1,640 |
1,563 |
|
|
51 |
Шевчуковская Елена |
11а |
164 |
102 |
62 |
1,608 |
1,645 |
|
|
52 |
Яковишин Никита |
11а |
179 |
109 |
70 |
1,642 |
1,557 |
|
|
53 |
Белогривцев В.В. |
учит. |
173 |
104 |
69 |
1,664 |
1,507 |
Учителя |
|
54 |
Булай Е.И. |
учит. |
163 |
101 |
62 |
1,614 |
1,629 |
1,630 |
|
55 |
Волкова О.В. |
учит. |
164 |
100 |
64 |
1,64 |
1,563 |
|
|
56 |
Гриневская Н.А. |
учит. |
166 |
101 |
65 |
1,644 |
1,554 |
|
|
57 |
Гринченко Е.Б. |
учит. |
162 |
99 |
63 |
1,636 |
1,571 |
|
|
58 |
Киреенко А.С. |
учит. |
175 |
108 |
67 |
1,620 |
1,612 |
|
|
59 |
Стукалов Д.М. |
учит. |
165 |
101 |
64 |
1,634 |
1,578 |
11класс и учителя |
|
60 |
Цедрик Н.Е. |
учит. |
158 |
96 |
62 |
1,646 |
1,548 |
|
|
61 |
Шкоркина Н.Н. |
учит. |
165 |
103 |
62 |
1,602 |
1,661 |
1,626 |
|
62 |
Яценко В.Н. |
учит. |
162 |
101 |
61 |
1,604 |
1,656 |
ПРИЛОЖЕНИЕ
В
РЕЗУЛЬТАТЫ
ВЫЧИСЛЕНИЯ ПРОПОРЦИЙ ТЕЛА У ЛЮДЕЙ РАЗНОГО ВОЗРАСТА
Рисунок В.1 – Результаты
вычисления пропорций тела у учащихся 1 класса
Рисунок В.2 – Результаты
вычисления пропорций тела у учащихся 5 класса
Рисунок В.3 – Результаты
вычисления пропорций тела у учащихся 9 класса
Рисунок В.4 – Результаты
вычисления пропорций тела у учащихся 11 класса
Рисунок В.5 – Результаты
вычисления пропорций тела у учителей
ПРИЛОЖЕНИЕ Г
СРАВНЕНИЕ
ПРОПОРЦИЙ ТЕЛА ЛЮДЕЙ РАЗНОГО ВОЗРАСТА
СО
ЗНАЧЕНИЕМ ЗОЛОТОГО СЕЧЕНИЯ
Рисунок Г.1 – Сравнение
средних пропорций тела людей разного возраста со значением золотого сечения
ПРИЛОЖЕНИЕ
Д
ЭТАПЫ
РАБОТЫ НАД ИССЛЕДОВАНИЕМ

а)
б) в)
Рисунок
Д.1 — Изучение литературы
 |
|||||
 |
|||||
 |
|||||
а)
б) в)
 |
|||
 |
|||
г)
д)
Рисунок
Д.2 — Проведение измерений учащихся и учителей
Рисунок
Д.3 – Ввод и обработка полученных данных
После предыдущей публикации про определение гармоничной длины платья с использованием золотого сечения, мне пришло несколько писем с вопросами от читательниц по определению длины с помощью золотого сечения.
Цитирую один из вопросов:
» Елена, добрый день! Формула золотого сечения подходит только для стройных и молодых. В 56 лет эту формулу не применить. А как для такого возраста найти правильную длину?». Светлана
Другие письма в целом со схожими вопросами — как определить нужную длину? как пользоваться золотым сечением? и т.п
Благодарю за вопросы! Раз они появились, значит тема может быть интересна широкому кругу читательниц.
Предлагаю рассмотреть применение золотого сечения подробнее, останавливаясь на разных вариантах.
Сразу оговорюсь, что рассмотренная схема нахождения длин, довольно относительна.
Для красивого, грамотного построения образа в целом, нужно учитывать разные нюансы — силуэт фигуры, осанку, рост, пропорцию, полноту, возраст , статус и предпочтения человека, выбирая комплексный подход.
ПРИМЕЧАНИЕ: Про силуэт читайте здесь , здесь и вот здесь;
Пропорции фигуры рассматриваются в этой публикации;
Типы телосложения тут;
Как определить осанку читайте на этой странице (кликайте по ссылкам, для перехода на нужную статью).
Но, для ориентирования при подборе длины и создания собственного образа, принцип золотого сечения будет хорошим дополнением и подспорьем особам сомневающимся и любителям точных цифр.
Не буду повторять данные из предыдущей статьи (её можно найти здесь), напомню лишь, что означает золотое сечение.
«Золотое сечение» — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, целая часть делится на две неравные так, чтобы меньшая её часть относилась к большей, как большая относится к целой части.
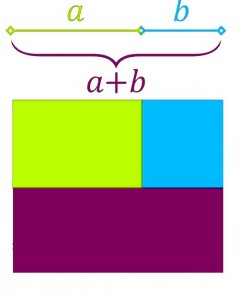
Если применить это утверждение к фигуре человека тогда выходит, что наиболее гармонично сложенная фигура будет иметь отношение верхней части ( от темени до талии) и нижней части (от талии до пола), как 3:5.
Почему именно такая пропорция?
Пропорции выступают в виде различных математических отношений. Самой гармоничной пропорцией считается «золотое сечение».
Напомню факт из прошлой публикации:
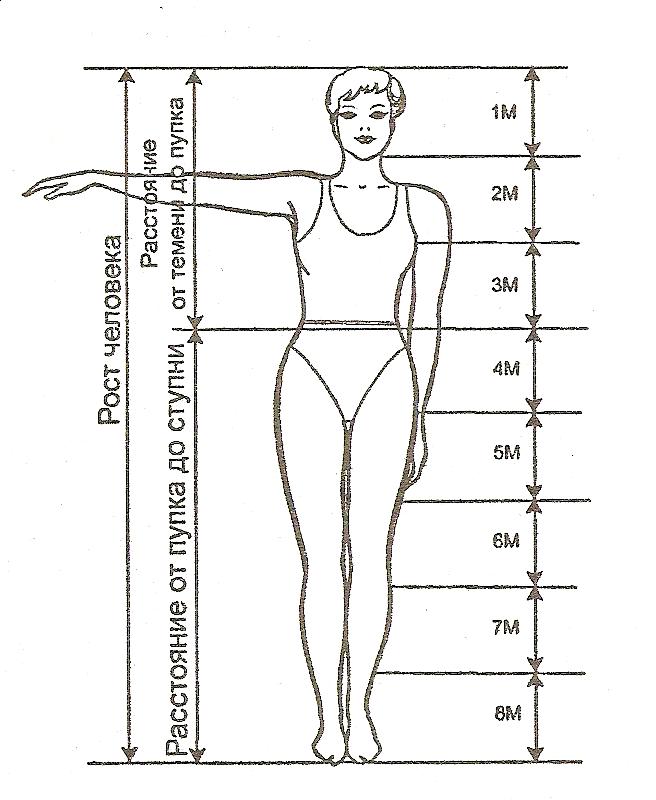
Профессор Цейзинг пришёл к выводу, что золотое сечение выражает средний статистический закон. Относительно этого закона, голова человека составляет 1/8 длины тела, а линия талии делит его как 5/8.
Соответственно, если брать за единицу модуль, длиной равной длине головы, получается та самая пропорция, а среднее значение пропорции выражается в соотношении 8 : 5 = 1,6.
Отсюда получаем нужный коэффициент для женской фигуры. Кстати, мужская фигура с пропорцией 13 : 8 = 1,625, несколько ближе подходят к золотому сечению…
Вернемся к гармонии и определению гармоничной длины при помощи золотого сечения…
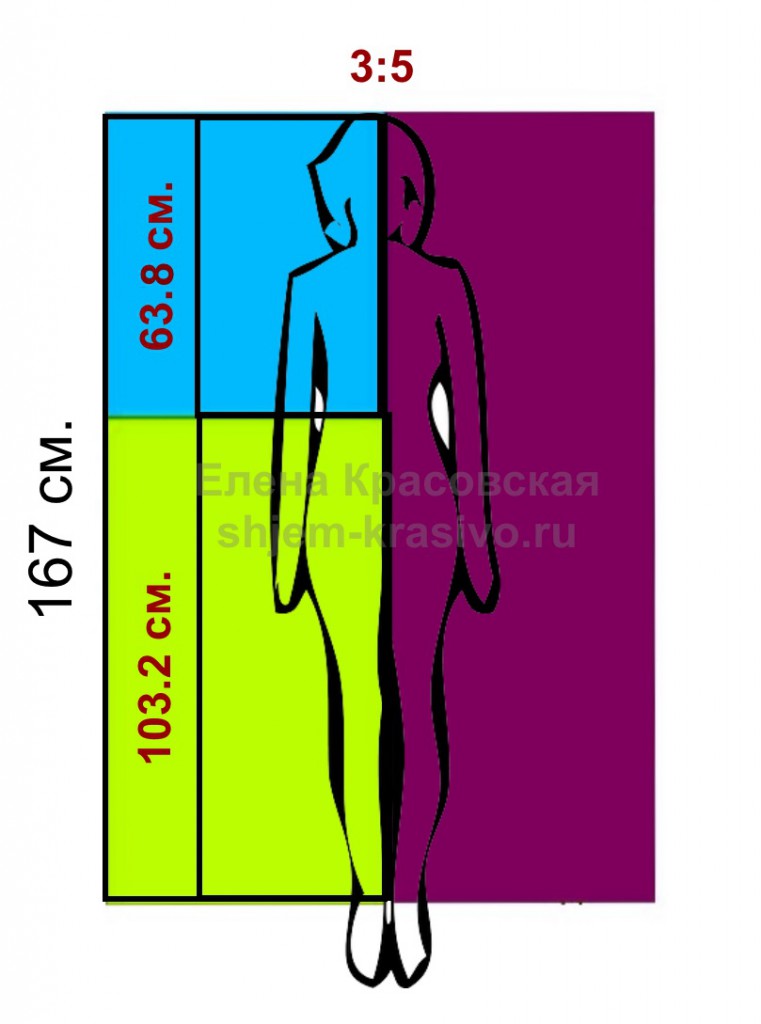
Возьмем, для примера, фигуру с ростом 167 см.
Применяя закон золотого сечения, делим 167 на 1.618 (коэффициент золотого сечения)
167 : 1.618 = 103.2 см.
Соответственно, наиболее гармоничное соотношение для данной фигуры, рассчитаем так:
167 — 103.2 = 63.8 см.
Таким образом пропорция 3:5 исполнена как 63.8 : 103.2 = длина от темени до талии : длина от талии до пола;
Для наглядности, приведу изображение:
Это идеальные пропорции для нашей «примерной» фигуры с ростом 167 см.. Вы можете измерить свой рост, рассчитать «идеальные» цифры, сравнить со своими и корректировать фигуру в соответствии с расчетами.
Например, если выяснится, что торс относительно ног удлинен, лучше выбирать одежду. зрительно удлиняющую ноги — завышенная линия талии юбок и брюк, платья в стиле ампир, широкие пояса и т.д .
Правда, удобный закон?
А теперь, давайте порассуждаем.
Зная закон золотого сечения (который не ограничивается данным утверждением, рассматриваемые в нем утверждения, гораздо шире — цель данной статьи не в этом…) можно определить нужную длину делением выбранного целого участка на коэффициент золотого сечения.
Продолжу на примере для фигуры с ростом 167 см.
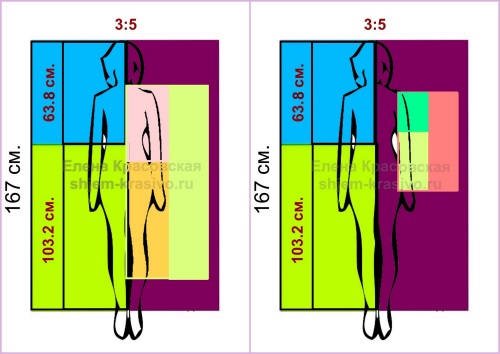
Итак, нужно определить оптимальную длину юбки, для этого:
- Измеряем длину от талии до пола сбоку (не забудьте повязать резинку/поясок на талию);
- Делим получившееся значение на 1.618.
Допустим, длина от талии до пола равна 103.5 см.,
103.5 см. : 1.618 = 63.96 ( примерно 64 см.)
Это значит, наиболее гармонично на фигуре с длиной нижней части тела 103.5 см., будет смотреться юбка длиной 64 см.
Также можно рассчитать любое гармоничное сочетание длин — длину рукава, длину блузы, платья, жакета и т.д. — нужно взять целую часть за исходную и разделить на 1.618.
Помните? Целая часть делится на две неравные так, чтобы меньшая её часть относилась к большей, как большая относится к целой части.
Если упростить, тогда получится, что от целой части нужно найти примерно 2/3 — это и будет гармоничная пропорция.
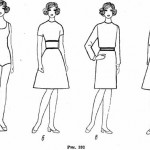
Кстати, есть определенные таблицы пропорций соотношения длин одежды, можете воспользоваться ими.
Эстетически целесообразные варианты пропорциональных отношений одежды по высоте разработаны Т.А.Кравцовой (таблички увеличиваются по клику):
Исходным параметром для расчета является проекционное расстояние между точкой основания шеи и уровнем высоты талии.
ВАЖНО! Тема пропорций фигуры человека достаточно обширна, именно поэтому, при определении длины с помощью коэффициента золотого сечения, не нужно слепо доверять цифрам.
Оценивайте весь образ в целом, с учетом пропорций, силуэтных линий, полноты и возраста, доверяя своему вкусу.
А метод определения гармоничной длины при помощи золотого сечения, оставьте в своей швейно-рукодельной копилке для проверки ваших сомнений и предположений.
С пожеланиями удачи и верой в Ваш успех, Елена Красовская
Идеальные пропорции мужского тела
На чтение 4 мин Просмотров 1к. Опубликовано 26.06.2021 Обновлено 14.07.2021
Онлайн калькулятор для расчета идеальных пропорций тела бодибилдера/бодибилдерши или спортсмена на основании его роста. Для произведения вычислений достаточно измерить свой рост и ввести его значение в поле ниже, после чего нажать кнопку «Рассчитать».
Калькулятор расчета пропорций тела бодибилдера по росту
Идеальными пропорциями мужского тела считается высокий рост, V-образный торс и соблюдение определенных параметров, которые могут отличаться у мужчин разного возраста. Национальность и род деятельности тоже наносят некоторый отпечаток на эталон красоты. При этом спортивная фигура, широкие плечи и грудь, рельефные мышцы в сочетании с узкими бедрами всегда приковывали к себе внимание прекрасной половины человечества.
Измерение параметров тела
Путь к идеальному телу начинается с его измерения. То есть, прежде чем что-то в себе менять, нужно определить, какая часть тела требует доработки.
Для более правильного результата замеров их следует проводить в утреннее время, так как после пробуждения, то есть в тот период, когда отдохнувшие мышцы расслаблены, показатели организма будут максимально точными. В течение дня различные нагрузки способны сильно исказить данные. Игнорировать это правило могут только те, у кого по каким-либо причинам по утрам наблюдается отечность.
Основные измеряемые места мужского тела
Для измерения вполне подойдет обычный швейный сантиметр или рулетка. Если же ничего из перечисленного нет под рукой, сгодится нитка и линейка: ниткой обхватить, линейкой замерить.
Ниже приведены основные правила, которых стоит придерживаться при замерах:
Золотое сечение в пропорциях мужского тела
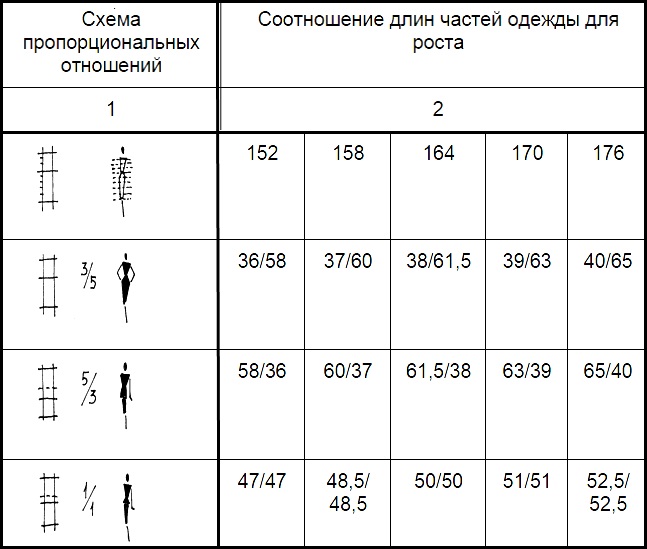
Пифагор одним из первых всерьез заинтересовался соотношением пропорций тела человека, к которому применил свое знаменитое правило «Золотого сечения». Согласно ему, идеальными параметрами можно считать следующие соотношения:
- Оптимальная ширина плеч – это ¼ роста.
- Талия должна составлять две окружности шеи.
- Окружность шеи должна быть равна двум окружностям запястья.
- Промежуток от темени до талии в идеале должен составлять 1/3 часть от роста.
- Длина стопы должна равняться длине предплечья.
Человеческий скелет выдержан в пропорциях, очень близких к золотому сечению. Чем ближе телосложение к подобному соотношению, тем более правильным, соответствующим идеалу красоты оно считается.
Скульптуру Поликлета «Копьеносец» («Дорифор») принято считать эталоном красоты мужского тела времен Древней Греции. Могучий торс, массивные плечи и грудные мышцы, рельефный пресс служат образцом совершенной пропорциональности на протяжении многих веков.
Идеальные пропорции атлетов
У мужчин, занимающихся бодибилдингом, есть несколько разных схем, по которым рассчитываются идеальные параметры. Каждый выбирает для себя ту схему, автор которой кажется ему более авторитетным.
Ниже приведены таблицы, в которых собраны сведения о пропорциях мужского тела. Они составлены на основании наблюдения за спортсменами в течение многих лет.
Значение таблицы Марселя Руэ наиболее близки к античным пропорциям.
При росте 165-175 см идеальными считаются следующие параметры:
В свой черед, для роста 176-185 см будут подходить такие измерения:
Джо Уайдер, известный бодибилдер и тренер, который в свое время тренировал многих известных культуристов, составил собственную таблицу идеальных параметров:
Эталон красоты для мужчины-модели
Чтобы мужчина мог построить карьеру в модельном бизнесе, он должен обладать несколько другими параметрами. Его рост должен быть 182-188 см. Он должен иметь красивое атлетическое телосложение, но не слишком сильно развитую мускулатуру, быть немного худощавым, но при этом выглядеть мужественно. Наиболее востребованные модели имеют 46-48 размер одежды.
Статистика показывает, что практически любой здоровый мужчина способен стать обладателем привлекательного, почти совершенного телосложения. Все зависит только от желания и прилагаемых усилий.

Дипломированный специалист по раннему развитию детей, высшее образование по специальности «Учитель начальных классов», заботливая мама троих детей. Я буду рада помочь вам в развитии Вашего ребенка на всем жизненном пути: от его нахождения в животике до половозрелого состояния!