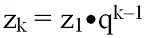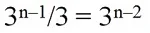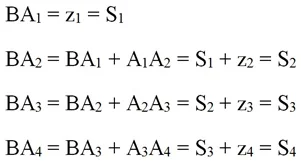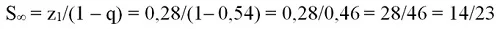Как найти знаменатель геометрической прогрессии с дробями

Геометрическая прогрессия

Понятие геометрической прогрессии
Формула n-го члена геометрической прогрессии
Свойства геометрической прогрессии
Сумма первых n членов геометрической прогрессии
Примеры

п.1. Понятие геометрической прогрессии

Геометрической прогрессией называют числовую последовательность, каждый член которой b_n, начиная со второго, равен произведению предыдущего члена b_n-1 и некоторого постоянного числа q: $$ mathrm{ b_n=b_{n-1}q, ninmathbb{N}, n ge 2, qne 0, qne 1, b_1ne 0 } $$ Число q называют знаменателем геометрической прогрессии.

Например:
1. Последовательность 1, 3, 9, 27, … является геометрической прогрессией с b₁ = 1, q = 3.

2. Последовательность (mathrm{9, -3, 1, -frac13, frac19,…}) является геометрической прогрессией с b₁ = 9, (mathrm{q=-frac13}).

п.2. Формула n-го члена геометрической прогрессии

По определению геометрической прогрессии мы получаем рекуррентную формулу для n-го члена: b_n = b_n-1q. Из неё можно вывести аналитическую формулу:

b₂ = b₁q, b₃ = b₂q = (b₁q)q = b₁q², b₄ = b₃q = (b₁q²)q = b₁q³,…

Получаем:

b_n = b₁q^n-1

Например:
Найдём b₅, если известно, что (mathrm{b_1=frac12, q=2}).
По формуле n-го члена получаем: (mathrm{b_5=b_1q^4=frac12cdot 2^4=2^3=8})

п.3. Свойства геометрической прогрессии

Свойство 1. Экспоненциальный рост/падение

Геометрическая прогрессия с положительными первым членом и знаменателем b₁ > 0, q > 0 является показательной функцией вида f(n) = kqⁿ: $$ mathrm{ b_n=frac{b_1}{q}q^n } $$

При b₁ > 0, q > 1 прогрессия экпоненциально растёт

При b₁ > 0, 0 < q < 1 прогрессия экпоненциально падает

Свойство 2. Признак геометрической прогрессии

Для того чтобы числовая последовательность была геометрической прогрессией необходимо и достаточно, чтобы каждый её член, начиная со второго, был средним геометрическим предыдущего и последующего членов: $$ mathrm{ left{b_nright} — text{геометрическая прогрессия} Leftrightarrow b_n=sqrt{b_{n-1}b_{n+1}}, ninmathbb{N}, n geq 2 } $$ Следствие: аждый член прогрессии является средним геометрическим двух равноудалённых от него членов: $$ mathrm{ b_n=sqrt{b_{n-k}b_{n+k}}, ninmathbb{N}, kinmathbb{N}, n geq k+1 } $$

Например:
Найдём b₉, если известно, что (mathrm{b_7=frac{1}{16}, b_{11}=4})
По следствию из признака геометрической прогрессии: (mathrm{b_9=sqrt{b_7b_{11}}=sqrt{frac{1}{16}cdot 4}=frac12})

Свойство 3. Равенство сумм индексов

Если {b_n} – геометрическая прогрессия, то из равенства сумм индексов следует равенство произведений членов: $$ mathrm{ m+k=p+q Rightarrow b_mb_k=b_pb_q } $$ Следствие: произведение членов, равноудалённых от концов прогрессии, является постоянной величиной: $$ mathrm{ b_1b_n = b_2b_{n-1}=b_3b_{n-2}=… } $$

Например:
Найдём b₆, если известно, что b₂ = 5, b₄ = 10, b₈ = 40
По равенству сумм индексов b₂b₈ = b₄b₆
Откуда (mathrm{b_6=frac{b_2b_8}{b_4}=frac{5cdot 40}{10}=20})

п.4. Сумма первых n членов геометрической прогрессии

Сумма первых n членов геометрической прогрессии равна $$mathrm{ S_n=frac{b_nq-b_1}{q-1}, qne 1} $$

Если учесть, что b_n = b₁q^n-1, получаем ещё одну формулу для суммы: $$mathrm{ S_n=b_1frac{q^n-1}{q-1}, qne 1} $$

Например:
Найдём сумму первых 10 степеней двойки: 2 + 2² + 2³ + … + 2¹⁰
В этом случае b₁ = 2, q = 2, n = 10
Получаем: (mathrm{ S_{10}=2cdot frac{2^{10}-1}{2-1}=2cdot (1024-1)=2046})

п.5. Примеры

Пример 1. Найдите знаменатель геометрической прогрессии и сумму первых 10 членов, если:
а) b₅ = 9, b₈ = 243
Найдём отношение $$ mathrm{ frac{b_8}{b_5}=frac{b_1cdot q^7}{b_1cdot q^4}=q^3, frac{b_8}{b_5}=frac{243}{9}=27=3^3, q^3=3^3Rightarrow q = 3 } $$ Найдём 1-й член: $$ mathrm{ b_1=frac{b_5}{q^4}=frac{9}{3^4}=frac{3^2}{3^4}=frac{1}{3^2}=frac19 } $$ Сумма: $$ mathrm{ S_{10}=b_1frac{q^{10}-1}{q-1}=frac{3^{10}-1}{9cdot 2}=frac{29524}{9}=3280frac49 } $$ Ответ: q = 3, S₁₀ = (mathrm{3280frac49})

б) b₁ = 3, b_n = 96, S_n = 189
По формуле суммы: $$ mathrm{ S_{n}=frac{b_nq-b_1}{q-1}Rightarrow 189 =frac{96q-3}{q-1}Rightarrow 189(q-1)=96q-3Rightarrow 93q=186Rightarrow q = 2 } $$ Сумма: $$ mathrm{ S_{10}=b_1frac{q^{10}-1}{q-1}=3cdot frac{2^{10}-1}{2-1}=3cdot 1023=3069 } $$ Ответ: q = 2, S₁₀ = 3069

Пример 2. Между числами (mathrm{40frac12 text{и} 5frac13}) вставьте такие четыре числа, чтобы они вместе с данными числами образовали геометрическую прогрессию.
По условию (mathrm{b_1=40frac12, b_6=5frac13}) $$ mathrm{ frac{b_6}{b_1}=q^5, frac{b_6}{b_1}=5frac13 : 40frac12=frac{16}{3} : frac{81}{2}=frac{16}{3} cdot frac{2}{81}=frac{32}{243}=frac{2^5}{3^5}=left(frac23right)^5 } $$ Знаменатель (mathrm{q=frac23})
Находим промежуточные члены прогрессии: begin{gather*} mathrm{ b_2=b_1q=40frac12cdotfrac23=frac{81}{2}cdot frac23=27, b_3=b_2q=27cdotfrac23=18, }\ mathrm{ b_4=b_3q=18cdotfrac23=12, b_5=b_4q=12cdotfrac23=8 } end{gather*} Ответ: 27, 18, 12 и 8

Пример 3. Найдите первый и последний члены геометрической прогрессии, если: $$ left{ begin{array}{ l } mathrm{b_4-b_2=0,6} & \ mathrm{b_5-b_3=1,2} & \ mathrm{S_n=12,7} & end{array}right. $$ Заметим, что b₄=b₂q², b₅=b₃q². Для первых двух уравнений получаем: $$ left{ begin{array}{ l } mathrm{b_2q^2-b_2=0,6} & \ mathrm{b_3q^2-b-3=1,2} & end{array}right. Rightarrow left{ begin{array}{ l } mathrm{b_2(q^2-1)=0,6} & \ mathrm{b_3(q^2-1)=1,2} & end{array}right. $$ Делим второе уравнение на первое: $$ mathrm{ frac{b_3(q^2-1)}{b_2(q^2-1)}=frac{1,2}{0,6}Rightarrowfrac{b_3}{b_2}=q=2 } $$ Подставляем найденное значение знаменателя прогрессии в первое уравнение: $$ mathrm{ b_2(2^2-1)=0,6 Rightarrow b_2=frac{0,6}{3}=0,2 Rightarrow b_1=frac{b_2}{q}=frac{0,2}{2}=0,1 } $$ Для третьего уравнения можем записать: begin{gather*} mathrm{ S_n=b_1frac{q^n-1}{q-1}=0,1cdotfrac{2^n-1}{2-1}=frac{2^n-1}{10}=12,7 Rightarrow 2^n-1=127 Rightarrow }\ mathrm{ Rightarrow 2^n=128=2^7 Rightarrow n=7 } end{gather*} 7-й член b₇ = b₁q⁶ = 0,1 · 2⁶ = 6,4
Ответ: b₁ = 0,1; b₇ = 6,4

Пример 4. В геометрической прогрессии, все члены которой положительны, сумма первого и второго членов равна 48, а сумма третьего и четвёртого членов равна 12. Найдите значение n, при котором S_n = 63. $$ text{По условию} left{ begin{array}{ l } mathrm{b_1+b_2=48} & \ mathrm{b_3+b_4=12} & \ mathrm{S_n=63} & end{array}right. $$ Заметим, что b₃ = b₁q², b_4=b_2q². Второе уравнение можно переписать в виде: $$ mathrm{ b_3+b_4=b_1q^2+b2q^2=underbrace{(b_1+b_2)}_{=48} q^2=12 Rightarrow q^2=frac{12}{48}=frac14 Rightarrow q=frac12 } $$ Берём положительное значение q, т.к. по условию все члены положительны.
Из первого уравнения $$ mathrm{ b_1+b_2=b_1(1+q)=48 Rightarrow b_1=frac{48}{1+frac12}=48cdotfrac23=32 } $$ Для третьего уравнения можем записать: begin{gather*} mathrm{ S_n=b_1frac{q^n-1}{q-1}=b_1frac{1-q^n}{1-q}=32cdotfrac{1-frac{1}{2^n}}{1-frac12}=64left(1-frac{1}{2^n}right)=63 }\ mathrm{ 64-frac{64}{2^n}=63 Rightarrow 1=frac{2^6}{2^n} Rightarrow n=6 } end{gather*} Ответ: 6

Пример 5. Бактерия, попав в организм, делится надвое каждые 20 мин. Сколько бактерий будет в организме через сутки?
Сутки – это 24 · 60 = 1440 мин, или n = 1440 : 20 = 72 цикла деления.
По условию необходимо найти

N = N₀ · 2ⁿ, где N₀ = 1
N = 2⁷² = 4 722 366 482 869 645 213 696 ≈ 4,7 · 10²¹

Ответ: 4,7 · 10²¹ бактерий

Источник

16
Июл 2013

Категория: Справочные материалы

Геометрическая прогрессия

2013-07-16
2021-06-28

А вы знаете удивительную легенду о зернах на шахматной доске? + показать

Определение

Геометрическая прогрессия — последовательность чисел (членов прогрессии) , в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии):

, где

Например, последовательность 1, 2, 4, 8, 16, … – геометрическая ()

Геометрическая прогрессия

Знаменатель геометрической прогрессии

$q=frac{b_{k+1}}{b_k}$ ,

Характеристическое свойство геометрической прогрессии

$b_n^2=b_{n-1}cdot b_{n+1}$ для

Последовательность является геометрической тогда и только тогда, когда для любого n > 1 выполняется указанное выше соотношение.

В частности, для геометрической прогрессии с положительными членами, верно: $b_n=sqrt{b_{n-1}cdot b_{n+1}}$

Формула n-го члена геометрической прогрессии

$b_n=b_1cdot q^{n-1}$

Сумма n первых членов геометрической прогрессии

$S_n=frac{b_1(q^n-1)}{q-1}$ , где

(если же , то )

Бесконечно убывающая геометрическая прогрессия

При , геометрическая прогрессия называется бесконечно убывающей. Суммой бесконечно убывающей геометрической прогрессии называется число $S=lim_{nto infty}S_n$ и $S=frac{b_1}{1-q}$

Посмотри это видео

Примеры

Пример 1. Последовательность {} –геометрическая прогрессия.

Найдите , если $b_6=-frac{1}{81}$ , $q=-frac{1}{9}.$

Решение: + показать

Приметр 2. Найдите знаменатель геометрической прогрессии {}, в которой $b_8=172,;b_{11}=2frac{11}{16}.$

Решение: + показать

Пример 3. Найдите девятый член геометрической прогрессии, если ее десятый член равен , а одиннадцатый член равен

Решение: + показать

Пример 4. Найдите сумму первых шести членов геометрической прогрессии

Решение: + показать

Пример 5. Найдите сумму первых пяти членов геометрической прогрессии {}, в которой $b_3=frac{1}{2},;b_5=2,;q>0.$

Решение: + показать

Пример 6. Представьте в виде обыкновенной дроби число

Решение: + показать

Пример 7. Найдите , если известно, что числа являются последовательными членами геометрической прогрессии (в указанном порядке).

Решение: + показать

Пример 8. Найдите знаменатель геометрической прогрессии, отношение суммы первых четырех членов которой, к сумме первых двух членов равно $frac{82}{81}.$

Решение: + показать

Пример 9. Между числами и вставьте три числа так, чтобы получилась геометрическая прогрессия

Решение: + показать

Вы можете пройти тест по теме «Геометрическая прогрессия»

Автор: egeMax |

комментариев 5

Печать страницы

Источник

запиши периодическую дробь (0,(8)) обыкновенной дробью.

Решение.

Достаточно очевидно, что (0,(8)=0,8+0,08+0,008+…) Слагаемые в правой части равенства образуют бесконечно убывающую геометрическую прогрессию, первый член которой равен (0,8), знаменатель равен (0,1). Найдём сумму по формуле:

S=b11−q=0,81−0,1

Осталось выполнить нужные действия с десятичными дробями:

0,81−0,1=0,80,9=89

Таким образом, бесконечная периодическая десятичная дробь (0,(8)) обращается в обыкновенную дробь (8/9).

Ответ: (0,(8)=8/9).

Источник

Что такое геометрическая прогрессия?
Формулы и свойства геометрической прогрессии
Калькуляторы геометрической прогрессии
Примеры решения заданий с геометрической прогрессией

Ученикам может показаться, что изучение геометрической прогрессии – это нечто абстрактное и оторванное от жизни. На самом деле множество экономических процессов построены именно на основе геометрической прогрессии.

Например, если вы положите деньги на банковский депозит и захотите посчитать сколько процентов заработаете за три года, самым удобным способом провести вычисления будет именно через формулу геометрической прогрессии. Этот инструмент также применяется в проектировании, архитектуре и строительстве.

В этом тексте вы сможете узнать базовую информацию о формулах и свойства геометрической прогрессии, а также понять принцип, по которому она действует.

Что такое геометрическая прогрессия?

3, 12, 48, 192, 768, 3072 – это пример геометрической прогрессии. Все эти объединенные единым общим множителем. В теории геометрической прогрессии он называется знаменателем и обозначается как q. В этом случае q = 4. Чтобы создать геометрическую прогрессию, нам нужно сначала три умножить на четыре, затем 12 – снова на 4, потом 48 на 4 и так далее.

Читайте также: Плюсы и минусы образования за рубежом

Определение геометрической прогрессии

Геометрическая прогрессия – это прежде всего последовательность чисел. Каждый пункт этой последовательности, начиная со второго, равен предыдущему числу, умноженному на одинаковый множитель.

Устойчивое число множитель, которое собственно и образует последовательность под названием геометрическая прогрессия, называется знаменателем прогрессии и обозначается, как мы уже отметили выше, буквой q.

Члены прогрессии обозначаются как , где под индикатором n имеется в виду порядковый номер члена в прогрессии. Соответственно, первый член прогрессии (в нашем первом примере равен 3 – это b1, а второй (12) – это b2.

Предполагается, что ни первый член, ни знаменатель прогрессии не равен нулю.

Свойства геометрической прогрессии

Геометрическая прогрессия становится удобным инструментом вычислений, когда вы понимаете, что с помощью ее свойств и связанных с ней формул можно легко вычислить, чему равно

И действительно – если попробуем вручную умножать каждое число ряда на 4, в конце концов восьмым числом этой геометрической прогрессии станет 49152.

После усвоения главного принципа, лежащего в основе геометрической прогрессии, можем закрепить знания, проверив на практике первый пример с банковским депозитом.

Допустим, вы кладете на свой счет $ 100 под 6% годовых, и хотите узнать, какую сумму получите за 3 года. В таком случае вы будете использовать в своих расчетах геометрическую прогрессию, ведь ежегодно вы будете умножать все большую сумму на один и тот же множитель (в данном примере он равен 6%, то есть – 1,06)

Чтобы вычислить сумму вклада в момент завершения действия депозита, используем уже знакомую формулу для нахождения значения любого члена прогрессии:

В чем разница между геометрической и арифметической прогрессией?

В геометрической прогрессии члены прогрессии умножаются на постоянное число, тогда как арифметическая прогрессия воплощает последовательность чисел, в которой к каждому предыдущему члена добавляется одно и то же постоянное число.

Представим это на примерах.

Предположим, что знаменатель (q) в случае геометрической прогрессии составит 3 и так же в арифметической прогрессии устойчивое слагаемое будет равно 3. И стартовый член прогрессии в обоих случаях также составит одно и то же число – 4.

Арифметическая прогрессия тогда будет выглядеть как последовательность 4, 7 (= 4 + 3), 10 (= 7 + 3) .., 13 .., 16 .., 19 …

А геометрическая прогрессия – как последовательность 4, 12 (= 4 * 3), 36 (= 12 * 3), 108 .., 324 …

Формулы и свойства геометрической прогрессии

Свойства членов геометрической прогрессии – это формулы, упрощающие расчеты. Вот некоторые из них:

Чтобы найти знаменатель геометрической прогрессии, следует использовать следующую формулу:

Произведение членов, равноудаленных от краев геометрической прогрессии, то есть, соседних, всегда является постоянной величиной, то есть:

С формулой расчета любого члена геометрической прогрессии мы уже знакомы. Она выглядит так:

А формула нахождения суммы п первых членов геометрической прогрессии выглядит так:

Любой член геометрической прогрессии, начиная со второго, будет равняться среднему арифметическому соседних с ним членов, то есть при ,

Калькуляторы геометрической прогрессии

В сети есть множество калькуляторов как арифметической, так и геометрической прогрессии. Некоторые из них могут не только посчитать сумму прогрессии или найти знаменатель, но и отразить пошаговое решение того или иного примера. Пользуясь ими вы не только найдете ответ, но и сможете понять принцип действий и запомнить некоторые из формул.

Однако если вы переживаете сложности с пониманием геометрической прогрессии, эффективным решением может быть работа с репетитором по алгебре. На сайте БУКИ вы можете найти репетитора по любому предмету.

Что касается онлайн-калькуляторов прогрессии, то в Keisan Online Calculator вы можете вычислить или сумму геометрической прогрессии, а также значение любого ее члена с пошаговым решением вашего примера. А в Geometric Sequence Calculator вы сможете вычислить любой составляющая прогрессии: и знаменатель геометрической прогрессии (q), и сумму бесконечный прогрессии (Sn), и сумму первых членов (Sn).

Примеры решения заданий с геометрической прогрессией

Вычислим знаменатель геометрической прогрессии, если b1=5,5; b2=11.

Решение:

Вычислим знаменатель прогрессии, поделив друг на друга соседние члены:

q = b2/b1 = 11/5,5 = 2.

Ответ:

Знаменатель прогрессии (q) равен 2.

Вычислим знаменатель геометрической прогрессии, если b1=0,3; b2= -30.

Решение:

Вычислим знаментель прогрессии, поделив друг на друга соседние члены:

q = b2/b1= -30/0,3= -100.

Ответ:

Знаменатель прогрессии (q) равен -100.

Читайте также: Самые популярные специальности в мире: выбор студентов 2021

Источник

План урока:

Геометрическая прогрессия

Сумма первых n членов геометрической прогрессии

Сумма бесконечно убывающей геометрической прогрессии

Геометрическая прогрессия

Изучим послед-ть

1, 2, 4, 8, 16, 32, 64, 128…

Здесь каждый следующее число больше предыдущего в 2 раза:

1jhgjty

Подобные послед-ти именуют геометрическими прогрессиями. Они постоянно встречаются в реальной жизни в банковской сфере (при начислении процентов на вклад), при изучении демографических процессов и в ряде других дисциплин.

2gfyu

Из этого определения следует рекуррентная формула, которая задает геом. прог-сию:

3gfhf

где q – это какое-то постоянное число, которое называют знаменателем геометрической прогрессии. Так, в прог-сии

1, 2, 4, 8, 16, 32, 64, 128…

знаменатель равен 2. Чтобы найти его, достаточно поделить какой-нибудь член геометрической прогрессии на предыдущий, например:

4gfj

или

5jhkf

Если q= 0, то и все числа послед-ти, начиная со второго, получатся равными нулю:

6hfgh

Такая послед-ть не представляет интерес для математиков, поэтому считается, что знаменатель q не должен равняться нулю.

Пример. Первое число геом. прог-сии z₁ равно 10, а знаменатель q равен 3. Запишите первые пять чисел прог-сии.

Решение. Будем использовать рекуррентную формулу:

7hgfh

Итак, получаем послед-ть:

10, 30, 90, 270, 810…

Ответ: 10, 30, 90, 270, 810

Пример. Про геом. прог-сию известно, что v₁ = 16, q = 0,5. Определите семь первых чисел прог-сии.

Решение: Снова используем рекуррентную формулу:

8gfddd

Пример. Геом. прог-сия начинается с числа 27, а знаменатель q = – 1. Запишите 4 первых числа прог-сии.

Решение. Используя рекуррентную формулу, можно записать:

9hgrt

Получили послед-ть:

27, -27, 27, -27

Ответ: 27, -27, 27, -27

Попытаемся вывести формулу n-ого члена геом. прог-сии. Пусть нам известны z₁и q. Тогда можно записать:

9hgrt

Легко заметить, что числа прог-сии вычисляются по формуле:

10gdfg

Докажем ее. Для этого необходимо использовать метод индукции. Очевидно, что формула справедлива для n = 1:

11fdsfs

Здесь мы использовали тот факт, что любое число в нулевой степени равно единице, то есть q⁰ = 1.

Итак, мы доказали базис индукции. Теперь докажем ее шаг. Предположим, что формула работает для какого-то произвольного n = k:

12gfdgd

Необходимо доказать, что (n + 1)-ый член вычисляется по формуле:

13ghdh

И действительно, используя рекуррентную формулу, можно получить:

14gfdgd

Тем самым мы подтвердили справедливость формулы

15gfdgs

16ytrur

Пример. Первое число послед-ти равно 5, а каждое следующее вдвое больше. Определите 15-тый член этой послед-ти.

Решение. Описанная послед-ть является геометрической, у которой z₁ = 5, q = 2. Найдем ее 15 член:

17gfdss

Ответ: 81920.

Пример. Известно, что геом. прогрессия начинается с числа 6, а третий член – это число 216. Каким может быть второй этой прог-сии?

Решение. Сначала попробуем найти знаменатель прог-сии. Мы знаем, что z₁ = 6, z₃ = 216. Запишем формулу 2-его члена прогр-сии:

18gfdsa

Получили квадратное уравнение. Решая его можем найти возможные значений q:

19fdsa

Получили два возможных значения знаменателя. Для каждого случая определим второй член прогр-сии:

при q = – 6 получаем z₂ = z₁•q = 6•(– 6) = – 36;

при q = 6 получаем z₂ = z₁•q = 6•6 = 36.

Ответ: – 6 или 6.

Пример. Вася решил положить 1 млн рублей на банковский вклад на 1 год. В банке «Золотой гном» ему предлагают доход в 25%, который выплатят в конце года. В банке «Слон» ему предлагают выплачивать каждый месяц по 2%. Какой из вариантов выгоднее для Васи?

Решение. Напомним, что получение дохода в 25% означает увеличение суммы вклада в 1 + 25/100 = 1,25 раза. Получение 2%-ого дохода означает увеличение суммы в 1 + 2/100 = 1,02 раза.

Посчитаем, сколько у Васи будет денег через год, если он выберет банк «Золотой гном»:

20fdaa

Во втором случае сумма будет увеличиваться в 1,02 раза каждый месяц. Если выписывать суммы, лежащие на вкладе в «Слоне», то получится геом. прог-сия, у которой знаменатель равен 1,02, а первый член – миллиону

23fdssa

Тогда сумма, лежащая на вкладе через 12 месяцев, составит

24gfasd

(Примечание.Величину 1,02¹² можно посчитать на калькуляторе или компьютере.)

Получается, что второй вариант выгоднее, ведь он принесет Васе большую сумму денег.

Ответ: Лучше выбрать банк «Слон».

Пример. Дана геом. прог-сия, у которой z₁ = 5, d = 3. Может ли в этой прог-сии находиться числа: 324; 405; 406?Также проверьте числа 123456789 и 5555555555.

Решение. Первый способ (простой, но требующий большого числа расчетов). Так как каждое следующее число в прог-сии больше предыдущего в 3 раза, то мы имеем дело с возрастающей последовательностью. Будем вычислять ее члены, пока не сможем получить число, большее 406:

Получили, что число 405 входит в прог-сию (z₅ = 405), а числа 324 и 406 не входят в число первых 6 членов прог-сии. Однако, так как z₆ = 1215 больше этих двух чисел, а каждый следующий член прог-сии ещё больше, то ясно, что 324 и 406 уже не встретятся в ней. Однако проверить таким способом длинные числа довольно тяжело.

Второй способ. Каждый член последовательности можно записать в виде

26hghjd

Напомним, что если один из множителей произведения делится нацело на какое-то число, то и всё произведение делится на это же число. Множитель 3^n–1 делится на 3 (при n ≥2):

27gfdg

Число 5 делится само на себя. Следовательно, числа, входящие в эту геом. послед-ть, должны делится и на 3, и на 5.

Теперь проанализируем числа 1234546789 и 5555555555, используя признаки делимости на 3 и 5. Первое из них НЕ делится нацело на 5, так как заканчивается на 9. Число 5555555555 НЕ делится на 3, так как сумма его цифр не делится нацело на 3:

28gfsg

Значит, они не могут входить в геом. прог-сию.

Ответ: число 405 входит в прог-сию, а остальные – нет.

Сумма первых n членов геометрической прогрессии

Попытаемся вычислить сумму первых членов геом. прог-сии. Обозначим её как S_n:

29gfsdg

Умножим обе части рав-ва на знаменатель прог-сии q:

30gfdfg

Вспомним рекуррентную формулу:

31fdsg

Из нее следует, что

Тогда ур-ние (2) можно переписать так:

33gfdhg

Теперь вычтем из (3) рав-во (1)

34fhdfh

Обратите внимание – справа слагаемые z₂, z₃, z₄… z_n сначала идут со знаком «плюс», а потом – со знаком «минус». Это значит, что их можно сократить! Тогда справа останется разница z_n₊₁– z₁. Это связано с тем, что для слагаемых z_n₊₁и z₁ не нашлось противоположного числа, чтобы сократиться. Можно записать:

Далее произведем замену z_n₊₁ = z₁•qⁿ:

36gffg

Если q– 1 ≠ 0, то можно поделить обе части рав-ва и получить окончательную формулу:

37gfsdf

Отдельно рассмотрим случай, когда q– 1 = 0. Тогда полученная формула будет некорректной (будет получаться деление на ноль). Если q– 1 = 0, то q = 1. Это значит, что все члены прог-сии равны друг другу:

Тогда сумма n первых членов будет равна z₁•n:

39hgfhd

Пример. Найдите сумму первых шести членов геом. прог-сии, у которой z₁ = 3, q = 2.

Решение. Используем формулу:

41gfdfh

Ответ: 189.

Пример. Определите сумму первых пяти членов геом. послед-ти, у которой z₁ =1 и q = 1/2.

Решение. Здесь в степень придется возводить дробь 1/2:

Ответ: 31/16

Сумма бесконечно убывающей геометрической прогрессии

Легко заметить, что если знаменателем геом. прог-сии – это положительное число, которое больше единицы, то прог-сия является убывающей послед-тью. Такие последовательности называют бесконечно убывающими геометрическими прогрессиями.

В качестве примера приведем послед-ть, у которой z₁ = 1, q = 1/2:

Каждый ее член может быть рассчитан по формуле

Очевидно, что чем больше n, тем меньше z_n, причем значение z_nкак бы стремится к нулю. Например, на компьютере можно посчитать, что

То, что величина (1/2)^n–1 при больших n стремится к нулю, в математике записывается так:

46gfdf

Запись «lim» означает «предел», а символ «∞» означает бесконечность. Выражение читается так: «предел (1/2)^n–1 при n, стремящемся к бесконечности, равен нулю». Мы не будем давать строгое определение понятия «предел», так как эта задача выходит за рамки элементарной математики и относится уже к математике высшей. Грубо говоря, предел – это то число, к которому выражение приближается как угодно близко, но не может его достигнуть. Так при – 1 <q< 1 выражение qⁿстремится к нулю, если n стремится к бесконечности:

47gfdfg

Отобразим сумму первых n членов послед-ти

48hggh

с помощью координатной прямой. Пусть в точке с координатой 0 находится точка B. Отложим от нее вправо точку А₁ так, чтобы ВА₁ =z₁ = 1. Далее от точки А₁ также вправо будем откладывать точку А₂, но длина отрезка А₁А₂ будет уже вдвое меньше, то есть она составит 1/2. Будем и далее откладывать точки А₃, А₄… до какой то точки А_n:

49gfdfg

С одной стороны, длина каждого следующего отрезка будет равна члену геом. прог-сии:

C другой стороны, длина отрезков BA₁, BA₂, BA₃… будет равна сумме нескольких первых членов геом. прог-сии:

51gfdfg

Отметим, что при таком построении с увеличением n точка А_nвсё ближе приближается к числу 2, однако так и не доходит до нее. Действительно, каждая следующая точка делит оставшееся расстояние надвое, поэтому она всегда остается левее точки 2, но приближается к ней. Получается, что сумма первых n членов прог-сии c ростом n приближается к двойке. В математике говорят, что число 2 является пределом послед-ти S_n. Запишем это:

На рисунке мы рассмотрели поведение послед-ти, у которой q = 1/2. Однако оказывается, что и любая другая бесконечная убывающая геометрическая прогрессия ведет себя похожим образом. Для каждой такой послед-ти существует предел суммы ее членов. Покажем, как его найти.

Запишем формулу суммы n членов геом. прог-сии в более удобном дробном виде:

53gfdfg

Умножим и числитель, и знаменатель одновременно на (– 1), при этом можно будет поменять местами уменьшаемое и вычитаемое:

54gdfgd

Далее выделим целую часть:

55gfdgs

Проанализируем полученное выражение. Уменьшаемое z₁/(1 – q) не содержит переменной n, а потому не зависит от этой переменной. А вот вычитаемое содержит множитель qⁿ. Можно доказать, что если выполняется условие–1 <q< 1, то с ростом n этот множитель стремится к нулю:

Значит, и всё вычитаемое также стремится к нулю:

57gfdfg

Получается, что при, бесконечно большом значении n сумма S_∞может быть вычислена так:

58gfdfh

Итак, удалось получить формулу S_∞ = z₁/(1 – q). Ещё раз отметим, что по-настоящему строгое доказательство требует использование понятие предела из высшей математики, а потому не рассматривается здесь.

59hgfh

60gfdgd

Зачем вообще находить сумму бесконечной геометрической прогрессии? Оказывается, что такая задача встает при изучении ряда других разделов математики, а также при расчете вероятностей некоторых событий.

Пример. Найдите сумму S_∞ для прог-сии, у которой z₁ = 0,1, q = 0,1.

Решение. Запишем первые несколько членов прог-сии:

61gfdgf

Теперь будем записывать суммы S_n этой прог-сии:

62gfdgd

Очевидно, что при бесконечном n получается бесконечная периодическая дробь:

63gfdfg

Подробнее о бесконечных периодических дробях можно узнать из этого урока.

Теперь найдем сумму S_∞, используя формулу S_∞ = z₁/(1 – q):

64hgfgh

Получили дробь 1/9. Получается, что обыкновенная дробь 1/9 и бесконечная периодическая дробь 0,(1) – это одно и то же число! И действительно, если на калькуляторе поделить 1 на 9, то он покажет 0,111111111…:

Пример. Какая дробь при разложении ее в бесконечную десятичную дробь дает число 0,010101010101 = 0,(01)?

Решение: По аналогии с предыдущей задачей можно записать:

0,(01) = 0,01010101… = 0,01 + 0,0001 + 0,000001 + 0,00000001…

Получили слева сумму бесконечной прог-сии

в которой z₁ = 0,01, а знаменатель q = 0,01. Ее сумма может быть рассчитана по формуле:

67gfdfg

Получили дробь 1/99. То есть

68hgfgh

Проверим себя с помощью калькулятора:

69gfdgh

Пример. В квадрат со стороной 1 вписали другой квадрат, причем его вершины располагаются на серединах описанного квадрата. По тому же принципу в полученный квадрат вписали следующий квадрат, в него ещё один и т. д. Чему равна общая площадь всех полученных квадратов и каков их общий периметр?

70gfdg

Решение. Сторона первого квадрата равна 1. Найдем сторону вписанного треугольника:

71gfdgd

Изучим треугольник АВС. В нем АВ = ВС = 1/2 (ведь они составляют половину от сторон DB и BF, который по условию равны 1). Угол АВС – прямой, а потому можно воспользоваться теоремой Пифагора:

Получили, что сторона вписанного квадрата в √2 раз меньше, чем сторона исходного квадрата. Аналогично можно показать, что и у следующего квадрата сторона будет ещё в √2 раз меньше и т. д. Соответственно и периметры квадратов будут уменьшаться в √2 раз, при этом периметр первого квадрата равен 4•1 = 4.

Получаем, что периметры квадратов образуют убывающую геом. прог-сию, в которой

73gfhgh

Найдем сумму S_∞для этой прог-сии:

74gfdgd

Итак, общий периметр найден. Теперь найдем сумму площадей. Площадь исходного квадрата равна 1•1 = 1. Площадь вписанного квадрата составляет:

75hfdgh

Получили, что площадь вписанного квадрата вдвое меньше площади исходного. Тогда площади квадратов образуют геом. прог-сию, в которой

Найдем и для этой прог-сии сумму:

Итак, суммарная площадь всех квадратов равна двум.

Наконец, рассмотрим задачу, имеющую практическое содержание.

Пример. Два спортсмена, Вася и Петя, играют в настольный теннис. Счет в их партии равен 10:10, и поэтому у них действует правило «баланса». Согласно нему, игроки при равном счете должны разыграть два очка, причем в первом розыгрыше подавать будет Вася, а во втором – Петя. Если одному игроку удастся выиграть оба очка, то он выиграет всю партию. Если каждый из игроков выиграет по одному розыгрышу, то счет в их партии становится равным, и тогда им снова надо разыгрывать ещё два очка. Проще говоря, партия не закончится, пока разница в счете не составит два очка.

Известно, что при подаче Васи вероятность его победы в розыгрыше составляет 0,7. При подаче Пети шансы подающего на выигрыш очка равны 0,6. Каковы шансы Васи и Пети на победу в партии?

Решение. По условию начальный счет равен 10:10. Будем считать, что первое число в счете – это очки Васи,а второе – очки Пети. Игра закончится победой одного из игроков, когда его преимущество в счете достигнет 2 очков. Тогда возможные варианты развития событий можно изобразить с помощью схемы:

79gfdgf

Обратим внимание, что в игре возможно бесконечное количество вариантов развития событий. Так, окончательный счет может быть равен даже 102:100 или 100002:100000 (хотя это и крайне маловероятно). Пусть вероятность, что игра закончится, например, со счетом 15:13, будет обозначаться как Р_15:13. Тогда, чтобы найти вероятность победы Васи, надо сложить бесконечное число вероятностей:

80gfdgf

Первую подачу при счете «ровно» Вася выиграет с вероятностью 0,7, поэтому шансы Пети забрать 1-ое очко себе равны 1 – 0,7 = 0,3.

На второй подаче Петя выиграет с вероятностью 0,6, а шансы Васи составят 1 – 0,6 = 0,4.

Тогда вероятность, что Вася выиграет оба очка, составит

81fsdf

Для Пети вероятность забрать себе оба очка равна

82gfdfg

Есть и третий вариант развития событий – после двух розыгрышей счет останется равным (каждый выиграет один мяч), и снова возникает «баланс». Вероятность такого исхода равна

83gdfg

Следовательно, можно записать:

84gdfg

Счета 13:11, 12:12 и 11:13 могут наступить только в том случае, если сначала был достигнут счет 11:11. «Переход» из счета 11:11 к счету 13:11 произойдет, если Вася выиграет два очка подряд, а вероятность такого исхода мы уже считали: Р_в = 0,7•0,4 = 0,28. Поэтому можно записать

85gdfgd