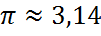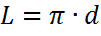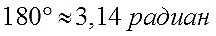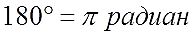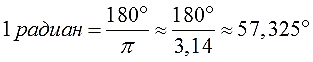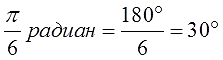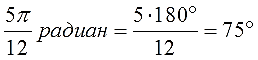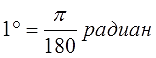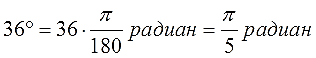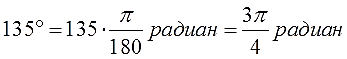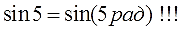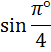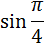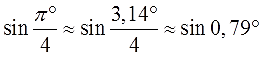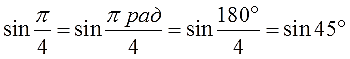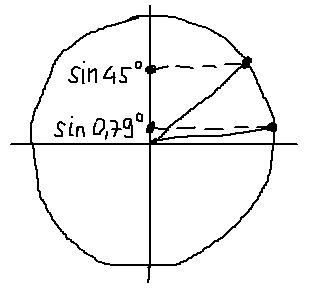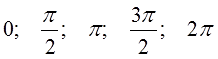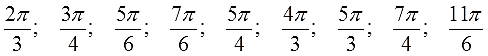Как найти знак радиана

Перевод градусов в радианы и обратно: формулы, примеры

Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.

Связь между градусами и радианами

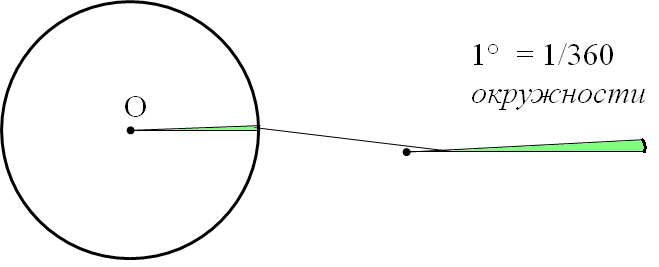
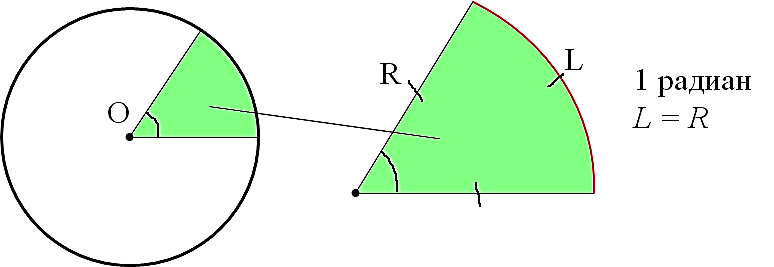
Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π · r . Разделим длину дуги на радиус и получим радианную меру угла: π · r r = π рад.

Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.

Связь градусов с радианами

Связь между радианами и градусами выражается формулой

Формулы перевода радианов в градусы и наоборот

Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.

Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.

1 р а д = 180 π ° — градусная мера угла в 1 радиан равна 180 π .

Также можно выразить один градус в радианах.

1 ° = π 180 р а д

Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.

1 р а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °

Значит, в одном радиане примерно 57 градусов

1 ° = π 180 р а д = 3 , 1416 180 р а д = 0 , 0175 р а д

Один градус содержит 0,0175 радиана.

Формула перевода радианов в градусы

x р а д = х · 180 π °

Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.

Примеры перевода градусов в радианы и радианов в градусы

Пример 1. Перевод из радианов в градусы

Пусть α = 3 , 2 рад. Нужно узнать градусную меру этого угла.

Применим формулу перехода от радианов к градусам и получим:

3 , 2 р а д = 3 , 2 · 180 π ° ≈ 3 , 2 · 180 3 , 14 ° ≈ 576 3 , 14 ° ≈ 183 , 4 °

Аналогично можно получить формулу перевода из градусов в радианы.

Формула перевода из градусов в радианы

y ° = y · π 180 р а д

Переведем 47 градусов в радианы.

Согласно формуле, умножим 47 на пи и разделим на 180.

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.

Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .

И синус, и косинус принимают значения от до .

Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.

Знаки синуса, косинуса, тангенса и котангенса.

Синус — функция нечётная, косинус — чётная.

Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .

А теперь подробно о тригонометрическом круге:

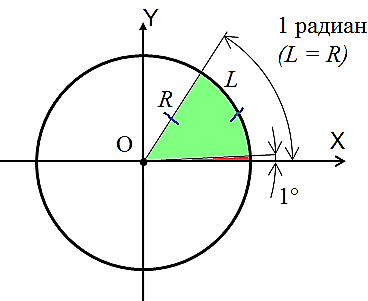
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

Единичная окружность

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Единичная окружность в тригонометрии

Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.

Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.

В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.

Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.

Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.

Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:

Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.

Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.

Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.

Число радиан для полной окружности — 360 градусов.

Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.

Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.

Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:

2π радиан = 360°
1 радиан = (360/2π) градусов
1 радиан = (180/π) градусов
360° = 2π радиан
1° = (2π/360) радиан
1° = (π/180) радиан

Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.

Уравнение единичной окружности

При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

источники:

http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/

http://skysmart.ru/articles/mathematic/edinichnaya-okruzhnost

Источник

Radian
An arc of a circle with the same length as the radius of that circle subtends an angle of 1 radian. The circumference subtends an angle of 2π radians.
General information
Unit system	SI
Unit of	angle
Symbol	rad
Conversions
1 rad in …	… is equal to …
milliradians	1000 mrad
turns	1/2π turn
degrees	180/π° ≈ 57.296°
gradians	200/π grad ≈ 63.662^g

The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at the centre of a circle by an arc that is equal in length to the radius.^[1] The unit was formerly an SI supplementary unit and is currently an SI derived unit, expressed in terms of the SI base unit metre (m) as rad=m/m.^[1] Thus, the radian is defined in the SI as being a derived dimensionless unit,^[1] with 1 rad = 1.^[2] Its symbol is accordingly often omitted, especially in mathematical writing.

Definition

One radian is defined as the angle subtended from the center of a circle which intercepts an arc equal in length to the radius of the circle.^[3] More generally, the magnitude in radians of a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, ${displaystyle theta ={frac {s}{r}}}$ , where θ is the subtended angle in radians, s is arc length, and r is radius. A right angle is exactly ${frac {pi }{2}}$ radians.^[4]

The rotation angle (360°) corresponding to one complete revolution is the length of the circumference divided by the radius, which is ${displaystyle {frac {2pi r}{r}}}$ , or 2π. Thus, 2π radians is equal to 360 degrees.

The relation 2π rad = 360° can be derived using the formula for arc length, ${textstyle ell _{text{arc}}=2pi rleft({tfrac {theta }{360^{circ }}}right)}$ . Since radian is the measure of an angle that is subtended by an arc of a length equal to the radius of the circle, ${textstyle 1=2pi left({tfrac {1{text{ rad}}}{360^{circ }}}right)}$ . This can be further simplified to ${textstyle 1={tfrac {2pi {text{ rad}}}{360^{circ }}}}$ . Multiplying both sides by 360° gives 360° = 2π rad.

Unit symbol

The International Bureau of Weights and Measures^[4] and International Organization for Standardization^[5] specify rad as the symbol for the radian. Alternative symbols that were in use in 1909 are ^c (the superscript letter c, for «circular measure»), the letter r, or a superscript ^R,^[6] but these variants are infrequently used, as they may be mistaken for a degree symbol (°) or a radius (r). Hence an angle of 1.2 radians would be written today as 1.2 rad; archaic notations could include 1.2 r, 1.2^rad, 1.2^c, or 1.2^R.

In mathematical writing, the symbol «rad» is often omitted. When quantifying an angle in the absence of any symbol, radians are assumed, and when degrees are meant, the degree sign ° is used.

Dimensional analysis

Plane angle is defined as θ = s/r, where θ is the subtended angle in radians, s is arc length, and r is radius. One radian corresponds to the angle for which s = r, hence 1 radian = 1 m/m.^[7] However, rad is only to be used to express angles, not to express ratios of lengths in general.^[4] A similar calculation using the area of a circular sector θ = 2A/r² gives 1 radian as 1 m²/m².^[8] The key fact is that the radian is a dimensionless unit equal to 1. In SI 2019, the radian is defined accordingly as 1 rad = 1.^[9] It is a long-established practice in mathematics and across all areas of science to make use of rad = 1.^[10]^[11] In 1993 the American Association of Physics Teachers Metric Committee specified that the radian should explicitly appear in quantities only when different numerical values would be obtained when other angle measures were used, such as in the quantities of angle measure (rad), angular speed (rad/s), angular acceleration (rad/s²), and torsional stiffness (N⋅m/rad), and not in the quantities of torque (N⋅m) and angular momentum (kg⋅m²/s).^[12]

Giacomo Prando says «the current state of affairs leads inevitably to ghostly appearances and disappearances of the radian in the dimensional analysis of physical equations».^[13] For example, an object hanging by a string from a pulley will rise or drop by y = rθ centimeters, where r is the radius of the pulley in centimeters and θ is the angle the pulley turns in radians. When multiplying r by θ the unit of radians disappears from the result. Similarly in the formula for the angular velocity of a rolling wheel, ω = v/r, radians appear in the units of ω but not on the right hand side.^[14] Anthony French calls this phenomenon «a perennial problem in the teaching of mechanics».^[15] Oberhofer says that the typical advice of ignoring radians during dimensional analysis and adding or removing radians in units according to convention and contextual knowledge is «pedagogically unsatisfying».^[16]

At least a dozen scientists between 1936 and 2022 have made proposals to treat the radian as a base unit of measure defining its own dimension of «angle».^[17]^[18]^[19] Quincey’s review of proposals outlines two classes of proposal. The first option changes the unit of a radius to meters per radian, but this is incompatible with dimensional analysis for the area of a circle, πr². The other option is to introduce a dimensional constant. According to Quincey this approach is «logically rigorous» compared to SI, but requires «the modification of many familiar mathematical and physical equations».^[20]

In particular, Quincey identifies Torrens’ proposal to introduce a constant η equal to 1 inverse radian (1 rad⁻¹) in a fashion similar to the introduction of the constant ε₀.^[20]^[a] With this change the formula for the angle subtended at the center of a circle, s = rθ, is modified to become s = ηrθ, and the Taylor series for the sine of an angle θ becomes:^[19]^[21]

${displaystyle operatorname {Sin} theta =sin _{text{rad}}(eta theta )=eta theta -{frac {(eta theta )^{3}}{3!}}+{frac {(eta theta )^{5}}{5!}}-{frac {(eta theta )^{7}}{7!}}+cdots .}$

The capitalized function Sin is the «complete» function that takes an argument with a dimension of angle and is independent of the units expressed,^[21] while sin_rad is the traditional function on pure numbers which assumes its argument is in radians.^[22] can be denoted sin if it is clear that the complete form is meant.^[19]^[23]

SI can be considered relative to this framework as a natural unit system where the equation η = 1 is assumed to hold, or similarly, 1 rad = 1. This radian convention allows the omission of η in mathematical formulas.^[24]

A dimensional constant for angle is «rather strange» and the difficulty of modifying equations to add the dimensional constant is likely to preclude widespread use.^[19] Defining radian as a base unit may be useful for software, where the disadvantage of longer equations is minimal.^[25] For example, the Boost units library defines angle units with a plane_angle dimension,^[26] and Mathematica’s unit system similarly considers angles to have an angle dimension.^[27]^[28]

Conversions

Conversion of common angles

Turns	Radians	Degrees	Gradians
0 turn	0 rad	0°	0^g
1/72 turn	π/36 rad	5°	5+5/9^g
1/24 turn	π/12 rad	15°	16+2/3^g
1/16 turn	π/8 rad	22.5°	25^g
1/12 turn	π/6 rad	30°	33+1/3^g
1/10 turn	π/5 rad	36°	40^g
1/8 turn	π/4 rad	45°	50^g
1/2π turn	1 rad	c. 57.3°	c. 63.7^g
1/6 turn	π/3 rad	60°	66+2/3^g
1/5 turn	2π/5 rad	72°	80^g
1/4 turn	π/2 rad	90°	100^g
1/3 turn	2π/3 rad	120°	133+1/3^g
2/5 turn	4π/5 rad	144°	160^g
1/2 turn	π rad	180°	200^g
3/4 turn	3π/2 rad	270°	300^g
1 turn	2π rad	360°	400^g

Between degrees

As stated, one radian is equal to ${displaystyle {180^{circ }}/{pi }}$ . Thus, to convert from radians to degrees, multiply by ${displaystyle {180^{circ }}/{pi }}$ .

${text{angle in degrees}}={text{angle in radians}}cdot {frac {180^{circ }}{pi }}$

For example:

$1{text{ rad}}=1cdot {frac {180^{circ }}{pi }}approx 57.2958^{circ }$

$2.5{text{ rad}}=2.5cdot {frac {180^{circ }}{pi }}approx 143.2394^{circ }$

${frac {pi }{3}}{text{ rad}}={frac {pi }{3}}cdot {frac {180^{circ }}{pi }}=60^{circ }$

Conversely, to convert from degrees to radians, multiply by ${displaystyle {pi }/{180^{circ }}}$ .

${text{angle in radians}}={text{angle in degrees}}cdot {frac {pi }{180^{circ }}}$

For example:

${displaystyle 1^{circ }=1^{circ }cdot {frac {pi }{180^{circ }}}approx 0.0175{text{ rad}}}$

${displaystyle 23^{circ }=23^{circ }cdot {frac {pi }{180^{circ }}}approx 0.4014{text{ rad}}}$

Radians can be converted to turns (one turn is the angle corresponding to a revolution) by dividing the number of radians by 2π.

Between gradians

2pi radians equals one turn, which is by definition 400 gradians (400 gons or 400^g). To convert from radians to gradians multiply by ${displaystyle 200^{text{g}}/pi }$ , and to convert from gradians to radians multiply by ${displaystyle pi /200^{text{g}}}$ . For example,

$1.2{text{ rad}}=1.2cdot {frac {200^{text{g}}}{pi }}approx 76.3944^{text{g}}$

${displaystyle 50^{text{g}}=50^{text{g}}cdot {frac {pi }{200^{text{g}}}}approx 0.7854{text{ rad}}}$

Usage

Mathematics

Some common angles, measured in radians. All the large polygons in this diagram are regular polygons.

In calculus and most other branches of mathematics beyond practical geometry, angles are measured in radians. This is because radians have a mathematical naturalness that leads to a more elegant formulation of some important results.

Results in analysis involving trigonometric functions can be elegantly stated when the functions’ arguments are expressed in radians. For example, the use of radians leads to the simple limit formula

$lim _{hrightarrow 0}{frac {sin h}{h}}=1,$

which is the basis of many other identities in mathematics, including

${frac {d}{dx}}sin x=cos x$

${frac {d^{2}}{dx^{2}}}sin x=-sin x.$

Because of these and other properties, the trigonometric functions appear in solutions to mathematical problems that are not obviously related to the functions’ geometrical meanings (for example, the solutions to the differential equation ${displaystyle {tfrac {d^{2}y}{dx^{2}}}=-y}$ , the evaluation of the integral ${displaystyle textstyle int {frac {dx}{1+x^{2}}},}$ and so on). In all such cases, it is found that the arguments to the functions are most naturally written in the form that corresponds, in geometrical contexts, to the radian measurement of angles.

The trigonometric functions also have simple and elegant series expansions when radians are used. For example, when x is in radians, the Taylor series for sin x becomes:

$sin x=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-{frac {x^{7}}{7!}}+cdots .$

If x were expressed in degrees, then the series would contain messy factors involving powers of π/180: if x is the number of degrees, the number of radians is y = πx / 180, so

$sin x_{mathrm {deg} }=sin y_{mathrm {rad} }={frac {pi }{180}}x-left({frac {pi }{180}}right)^{3} {frac {x^{3}}{3!}}+left({frac {pi }{180}}right)^{5} {frac {x^{5}}{5!}}-left({frac {pi }{180}}right)^{7} {frac {x^{7}}{7!}}+cdots .$

In a similar spirit, mathematically important relationships between the sine and cosine functions and the exponential function (see, for example, Euler’s formula) can be elegantly stated, when the functions’ arguments are in radians (and messy otherwise).

Physics

The radian is widely used in physics when angular measurements are required. For example, angular velocity is typically expressed in the unit radian per second (rad/s). One revolution per second corresponds to 2π radians per second.

Similarly, the unit used for angular acceleration is often radian per second per second (rad/s²).

For the purpose of dimensional analysis, the units of angular velocity and angular acceleration are s⁻¹ and s⁻² respectively.

Likewise, the phase difference of two waves can also be expressed using the radian as the unit. For example, if the phase difference of two waves is (n⋅2π) radians with n is an integer, they are considered to be in phase, whilst if the phase difference of two waves is (n⋅2π + π) with n an integer, they are considered to be in antiphase.

Prefixes and variants

Metric prefixes for submultiples are used with radians. A milliradian (mrad) is a thousandth of a radian (0.001 rad), i.e. 1 rad = 10³ mrad. There are 2π × 1000 milliradians (≈ 6283.185 mrad) in a circle. So a milliradian is just under 1/6283 of the angle subtended by a full circle. This unit of angular measurement of a circle is in common use by telescopic sight manufacturers using (stadiametric) rangefinding in reticles. The divergence of laser beams is also usually measured in milliradians.

The angular mil is an approximation of the milliradian used by NATO and other military organizations in gunnery and targeting. Each angular mil represents 1/6400 of a circle and is 15/8% or 1.875% smaller than the milliradian. For the small angles typically found in targeting work, the convenience of using the number 6400 in calculation outweighs the small mathematical errors it introduces. In the past, other gunnery systems have used different approximations to 1/2000π; for example Sweden used the 1/6300 streck and the USSR used 1/6000. Being based on the milliradian, the NATO mil subtends roughly 1 m at a range of 1000 m (at such small angles, the curvature is negligible).

Prefixes smaller than milli- are useful in measuring extremely small angles. Microradians (μrad, 10⁻⁶ rad) and nanoradians (nrad, 10⁻⁹ rad) are used in astronomy, and can also be used to measure the beam quality of lasers with ultra-low divergence. More common is the arc second, which is π/648,000 rad (around 4.8481 microradians).

History

Pre-20th century

The idea of measuring angles by the length of the arc was in use by mathematicians quite early. For example, al-Kashi (c. 1400) used so-called diameter parts as units, where one diameter part was 1/60 radian. They also used sexagesimal subunits of the diameter part.^[29] Newton in 1672 spoke of «the angular quantity of a body’s circular motion», but used it only as a relative measure to develop an astronomical algorithm.^[30]

The concept of the radian measure is normally credited to Roger Cotes, who died in 1716. By 1722, his cousin Robert Smith had collected and published Cotes’ mathematical writings in a book, Harmonia mensurarum.^[31] In a chapter of editorial comments, Smith gave what is probably the first published calculation of one radian in degrees, citing a note of Cotes that has not survived. Smith described the radian in everything but name – «Now this number is equal to 180 degrees as the radius of a circle to the semicircumference, this is as 1 to 3.141592653589» –, and recognized its naturalness as a unit of angular measure.^[32]^[33]

In 1765, Leonhard Euler implicitly adopted the radian as a unit of angle.^[30] Specifically, Euler defined angular velocity as «The angular speed in rotational motion is the speed of that point, the distance of which from the axis of gyration is expressed by one.»^[34] Euler was probably the first to adopt this convention, referred to as the radian convention, which gives the simple formula for angular velocity ω = v/r. As discussed in § Dimensional analysis, the radian convention has been widely adopted, and other conventions have the drawback of requiring a dimensional constant, for example ω = v/(ηr).^[24]

Prior to the term radian becoming widespread, the unit was commonly called circular measure of an angle.^[35] The term radian first appeared in print on 5 June 1873, in examination questions set by James Thomson (brother of Lord Kelvin) at Queen’s College, Belfast. He had used the term as early as 1871, while in 1869, Thomas Muir, then of the University of St Andrews, vacillated between the terms rad, radial, and radian. In 1874, after a consultation with James Thomson, Muir adopted radian.^[36]^[37]^[38] The name radian was not universally adopted for some time after this. Longmans’ School Trigonometry still called the radian circular measure when published in 1890.^[39]

As a SI unit

As Paul Quincey et al. writes, «the status of angles within the International System of Units (SI) has long been a source of controversy and confusion.»^[40] In 1960, the CGPM established the SI and the radian was classified as a «supplementary unit» along with the steradian. This special class was officially regarded «either as base units or as derived units», as the CGPM could not reach a decision on whether the radian was a base unit or a derived unit.^[41] Richard Nelson writes «This ambiguity [in the classification of the supplemental units] prompted a spirited discussion over their proper interpretation.»^[42] In May 1980 the Consultative Committee for Units (CCU) considered a proposal for making radians an SI base unit, using a constant α₀ = 1 rad,^[43]^[24] but turned it down to avoid an upheaval to current practice.^[24]

In October 1980 the CGPM decided that supplementary units were dimensionless derived units for which the CGPM allowed the freedom of using them or not using them in expressions for SI derived units,^[42] on the basis that «[no formalism] exists which is at the same time coherent and convenient and in which the quantities plane angle and solid angle might be considered as base quantities» and that «[the possibility of treating the radian and steradian as SI base units] compromises the internal coherence of the SI based on only seven base units».^[44] In 1995 the CGPM eliminated the class of supplementary units and defined the radian and the steradian as «dimensionless derived units, the names and symbols of which may, but need not, be used in expressions for other SI derived units, as is convenient».^[45] Mikhail Kalinin writing in 2019 has criticized the 1980 CGPM decision as «unfounded» and says that the 1995 CGPM decision used inconsistent arguments and introduced «numerous discrepancies, inconsistencies, and contradictions in the wordings of the SI».^[46]

At the 2013 meeting of the CCU, Peter Mohr gave a presentation on alleged inconsistencies arising from defining the radian as a dimensionless unit rather than a base unit. CCU President Ian M. Mills declared this to be a «formidable problem» and the CCU Working Group on Angles and Dimensionless Quantities in the SI was established.^[47] The CCU met most recently in 2021, but did not reach a consensus. A small number of members argued strongly that the radian should be a base unit, but the majority felt the status quo was acceptable or that the change would cause more problems than it would solve. A task group was established to «review the historical use of SI supplementary units and consider whether reintroduction would be of benefit», among other activities.^[48]^[49]

Notes

References

^ ^a ^b ^c International Bureau of Weights and Measures 2019, p. 151: «The CGPM decided to interpret the supplementary units in the SI, namely the radian and the steradian, as dimensionless derived units.»
^ International Bureau of Weights and Measures 2019, p. 151: «One radian corresponds to the angle for which s = r, thus 1 rad = 1.»
^ Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, p. APP-4, LCCN 76087042
^ ^a ^b ^c International Bureau of Weights and Measures 2019, p. 151.
^ «ISO 80000-3:2006 Quantities and Units — Space and Time».
^ Hall, Arthur Graham; Frink, Fred Goodrich (January 1909). «Chapter VII. The General Angle [55] Signs and Limitations in Value. Exercise XV.». Written at Ann Arbor, Michigan, USA. Trigonometry. Vol. Part I: Plane Trigonometry. New York, USA: Henry Holt and Company / Norwood Press / J. S. Cushing Co. — Berwick & Smith Co., Norwood, Massachusetts, USA. p. 73. Retrieved 2017-08-12.
^ International Bureau of Weights and Measures 2019, p. 151: «One radian corresponds to the angle for which s = r«
^ Quincey 2016, p. 844: «Also, as alluded to in Mohr & Phillips 2015, the radian can be defined in terms of the area A of a sector (A = 1/2 θ r²), in which case it has the units m²⋅m⁻².»
^ International Bureau of Weights and Measures 2019, p. 151: «One radian corresponds to the angle for which s = r, thus 1 rad = 1.»
^ International Bureau of Weights and Measures 2019, p. 137.
^ Bridgman, Percy Williams (1922). Dimensional analysis. New Haven : Yale University Press. Angular amplitude of swing […] No dimensions.
^ Aubrecht, Gordon J.; French, Anthony P.; Iona, Mario; Welch, Daniel W. (February 1993). «The radian—That troublesome unit». The Physics Teacher. 31 (2): 84–87. Bibcode:1993PhTea..31…84A. doi:10.1119/1.2343667.
^ Prando, Giacomo (August 2020). «A spectral unit». Nature Physics. 16 (8): 888. Bibcode:2020NatPh..16..888P. doi:10.1038/s41567-020-0997-3. S2CID 225445454.
^ Leonard, William J. (1999). Minds-on Physics: Advanced topics in mechanics. Kendall Hunt. p. 262. ISBN 978-0-7872-5412-4.
^ French, Anthony P. (May 1992). «What happens to the ‘radians’? (comment)». The Physics Teacher. 30 (5): 260–261. doi:10.1119/1.2343535.
^ Oberhofer, E. S. (March 1992). «What happens to the ‘radians’?». The Physics Teacher. 30 (3): 170–171. Bibcode:1992PhTea..30..170O. doi:10.1119/1.2343500.
^ Brinsmade 1936; Romain 1962; Eder 1982; Torrens 1986; Brownstein 1997; Lévy-Leblond 1998; Foster 2010; Mills 2016; Quincey 2021; Leonard 2021; Mohr et al. 2022
^ Mohr & Phillips 2015.
^ ^a ^b ^c ^d Quincey, Paul; Brown, Richard J C (1 June 2016). «Implications of adopting plane angle as a base quantity in the SI». Metrologia. 53 (3): 998–1002. arXiv:1604.02373. Bibcode:2016Metro..53..998Q. doi:10.1088/0026-1394/53/3/998. S2CID 119294905.
^ ^a ^b Quincey 2016.
^ ^a ^b Torrens 1986.
^ Mohr et al. 2022, p. 6.
^ Mohr et al. 2022, pp. 8–9.
^ ^a ^b ^c ^d Quincey 2021.
^ Quincey, Paul; Brown, Richard J C (1 August 2017). «A clearer approach for defining unit systems». Metrologia. 54 (4): 454–460. arXiv:1705.03765. Bibcode:2017Metro..54..454Q. doi:10.1088/1681-7575/aa7160. S2CID 119418270.
^ Schabel, Matthias C.; Watanabe, Steven. «Boost.Units FAQ – 1.79.0». www.boost.org. Retrieved 5 May 2022. Angles are treated as units
^ Mohr et al. 2022, p. 3.
^ «UnityDimensions—Wolfram Language Documentation». reference.wolfram.com. Retrieved 1 July 2022.
^ Luckey, Paul (1953) [Translation of 1424 book]. Siggel, A. (ed.). Der Lehrbrief über den kreisumfang von Gamshid b. Mas’ud al-Kasi [Treatise on the Circumference of al-Kashi]. Berlin: Akademie Verlag. p. 40.
^ ^a ^b Roche, John J. (21 December 1998). The Mathematics of Measurement: A Critical History. Springer Science & Business Media. p. 134. ISBN 978-0-387-91581-4.
^ O’Connor, J. J.; Robertson, E. F. (February 2005). «Biography of Roger Cotes». The MacTutor History of Mathematics. Archived from the original on 2012-10-19. Retrieved 2006-04-21.
^ Cotes, Roger (1722). «Editoris notæ ad Harmoniam mensurarum». In Smith, Robert (ed.). Harmonia mensurarum (in Latin). Cambridge, England. pp. 94–95. In Canone Logarithmico exhibetur Systema quoddam menfurarum numeralium, quæ Logarithmi dicuntur: atque hujus systematis Modulus is est Logarithmus, qui metitur Rationem Modularem in Corol. 6. definitam. Similiter in Canone Trigonometrico finuum & tangentium, exhibetur Systema quoddam menfurarum numeralium, quæ Gradus appellantur: atque hujus systematis Modulus is est Numerus Graduum, qui metitur Angulum Modularem modo definitun, hoc est, qui continetur in arcu Radio æquali. Eft autem hic Numerus ad Gradus 180 ut Circuli Radius ad Semicircuinferentiam, hoc eft ut 1 ad 3.141592653589 &c. Unde Modulus Canonis Trigonometrici prodibit 57.2957795130 &c. Cujus Reciprocus eft 0.0174532925 &c. Hujus moduli subsidio (quem in chartula quadam Auctoris manu descriptum inveni) commodissime computabis mensuras angulares, queinadmodum oftendam in Nota III. [In the Logarithmic Canon there is presented a certain system of numerical measures called Logarithms: and the Modulus of this system is the Logarithm, which measures the Modular Ratio as defined in Corollary 6. Similarly, in the Trigonometrical Canon of sines and tangents, there is presented a certain system of numerical measures called Degrees: and the Modulus of this system is the Number of Degrees which measures the Modular Angle defined in the manner defined, that is, which is contained in an equal Radius arc. Now this Number is equal to 180 Degrees as the Radius of a Circle to the Semicircumference, this is as 1 to 3.141592653589 &c. Hence the Modulus of the Trigonometric Canon will be 57.2957795130 &c. Whose Reciprocal is 0.0174532925 &c. With the help of this modulus (which I found described in a note in the hand of the Author) you will most conveniently calculate the angular measures, as mentioned in Note III.]
^ Gowing, Ronald (27 June 2002). Roger Cotes — Natural Philosopher. Cambridge University Press. ISBN 978-0-521-52649-4.
^ Euler, Leonhard. Theoria Motus Corporum Solidorum seu Rigidorum [Theory of the motion of solid or rigid bodies] (PDF) (in Latin). Translated by Bruce, Ian. Definition 6, paragraph 316.
^ Isaac Todhunter, Plane Trigonometry: For the Use of Colleges and Schools, p. 10, Cambridge and London: MacMillan, 1864 OCLC 500022958
^ Cajori, Florian (1929). History of Mathematical Notations. Vol. 2. Dover Publications. pp. 147–148. ISBN 0-486-67766-4.
^
- Muir, Thos. (1910). «The Term «Radian» in Trigonometry». Nature. 83 (2110): 156. Bibcode:1910Natur..83..156M. doi:10.1038/083156a0. S2CID 3958702.
- Thomson, James (1910). «The Term «Radian» in Trigonometry». Nature. 83 (2112): 217. Bibcode:1910Natur..83..217T. doi:10.1038/083217c0. S2CID 3980250.
- Muir, Thos. (1910). «The Term «Radian» in Trigonometry». Nature. 83 (2120): 459–460. Bibcode:1910Natur..83..459M. doi:10.1038/083459d0. S2CID 3971449.
^ Miller, Jeff (Nov 23, 2009). «Earliest Known Uses of Some of the Words of Mathematics». Retrieved Sep 30, 2011.
^ Frederick Sparks, Longmans’ School Trigonometry, p. 6, London: Longmans, Green, and Co., 1890 OCLC 877238863 (1891 edition)
^ Quincey, Paul; Mohr, Peter J; Phillips, William D (1 August 2019). «Angles are inherently neither length ratios nor dimensionless». Metrologia. 56 (4): 043001. arXiv:1909.08389. Bibcode:2019Metro..56d3001Q. doi:10.1088/1681-7575/ab27d7. S2CID 198428043.
^ Le Système international d’unités (PDF) (in French), 1970, p. 12, Pour quelques unités du Système International, la Conférence Générale n’a pas ou n’a pas encore décidé s’il s’agit d’unités de base ou bien d’unités dérivées. [For some units of the SI, the CGPM still hasn’t yet decided whether they are base units or derived units.]
^ ^a ^b Nelson, Robert A. (March 1984). «The supplementary units». The Physics Teacher. 22 (3): 188–193. Bibcode:1984PhTea..22..188N. doi:10.1119/1.2341516.
^ Report of the 7th meeting (PDF) (in French), Consultative Committee for Units, May 1980, pp. 6–7
^ International Bureau of Weights and Measures 2019, pp. 174–175.
^ International Bureau of Weights and Measures 2019, p. 179.
^ Kalinin, Mikhail I (1 December 2019). «On the status of plane and solid angles in the International System of Units (SI)». Metrologia. 56 (6): 065009. arXiv:1810.12057. Bibcode:2019Metro..56f5009K. doi:10.1088/1681-7575/ab3fbf. S2CID 53627142.
^ Consultative Committee for Units (11–12 June 2013). Report of the 21st meeting to the International Committee for Weights and Measures (Report). pp. 18–20.
^ Consultative Committee for Units (21–23 September 2021). Report of the 25th meeting to the International Committee for Weights and Measures (Report). pp. 16–17.
^ «CCU Task Group on angle and dimensionless quantities in the SI Brochure (CCU-TG-ADQSIB)». BIPM. Retrieved 26 June 2022.

International Bureau of Weights and Measures (20 May 2019), The International System of Units (SI) (PDF) (9th ed.), ISBN 978-92-822-2272-0, archived (PDF) from the original on 8 May 2021
Brinsmade, J. B. (December 1936). «Plane and Solid Angles. Their Pedagogic Value When Introduced Explicitly». American Journal of Physics. 4 (4): 175–179. Bibcode:1936AmJPh…4..175B. doi:10.1119/1.1999110.
Romain, Jacques E. (July 1962). «Angle as a fourth fundamental quantity». Journal of Research of the National Bureau of Standards Section B. 66B (3): 97. doi:10.6028/jres.066B.012.
Eder, W E (January 1982). «A Viewpoint on the Quantity «Plane Angle»«. Metrologia. 18 (1): 1–12. Bibcode:1982Metro..18….1E. doi:10.1088/0026-1394/18/1/002. S2CID 250750831.
Torrens, A B (1 January 1986). «On Angles and Angular Quantities». Metrologia. 22 (1): 1–7. Bibcode:1986Metro..22….1T. doi:10.1088/0026-1394/22/1/002. S2CID 250801509.
Brownstein, K. R. (July 1997). «Angles—Let’s treat them squarely». American Journal of Physics. 65 (7): 605–614. Bibcode:1997AmJPh..65..605B. doi:10.1119/1.18616.
Lévy-Leblond, Jean-Marc (September 1998). «Dimensional angles and universal constants». American Journal of Physics. 66 (9): 814–815. Bibcode:1998AmJPh..66..814L. doi:10.1119/1.18964.
Foster, Marcus P (1 December 2010). «The next 50 years of the SI: a review of the opportunities for the e-Science age». Metrologia. 47 (6): R41–R51. doi:10.1088/0026-1394/47/6/R01. S2CID 117711734.
Mohr, Peter J; Phillips, William D (1 February 2015). «Dimensionless units in the SI». Metrologia. 52 (1): 40–47. arXiv:1409.2794. Bibcode:2015Metro..52…40M. doi:10.1088/0026-1394/52/1/40.
Quincey, Paul (1 April 2016). «The range of options for handling plane angle and solid angle within a system of units». Metrologia. 53 (2): 840–845. Bibcode:2016Metro..53..840Q. doi:10.1088/0026-1394/53/2/840. S2CID 125438811.
Mills, Ian (1 June 2016). «On the units radian and cycle for the quantity plane angle». Metrologia. 53 (3): 991–997. Bibcode:2016Metro..53..991M. doi:10.1088/0026-1394/53/3/991. S2CID 126032642.
Quincey, Paul (1 October 2021). «Angles in the SI: a detailed proposal for solving the problem». Metrologia. 58 (5): 053002. arXiv:2108.05704. Bibcode:2021Metro..58e3002Q. doi:10.1088/1681-7575/ac023f. S2CID 236547235.
Leonard, B P (1 October 2021). «Proposal for the dimensionally consistent treatment of angle and solid angle by the International System of Units (SI)». Metrologia. 58 (5): 052001. Bibcode:2021Metro..58e2001L. doi:10.1088/1681-7575/abe0fc. S2CID 234036217.
Mohr, Peter J; Shirley, Eric L; Phillips, William D; Trott, Michael (23 June 2022). «On the dimension of angles and their units». Metrologia. 59 (5): 053001. arXiv:2203.12392. Bibcode:2022Metro..59e3001M. doi:10.1088/1681-7575/ac7bc2.

External links

Look up radian in Wiktionary, the free dictionary.

Media related to Radian at Wikimedia Commons

Источник

Угол может измеряться следующими величинами:

Градусами (и соответствующими ему величинами: угловыми минутами и секундами);
Радианами.

Градусная мера угла

Если взять развернутый угол (это два прямых угла) и поделить его на 180 частей, то одна такая часть будет называться одним градусом. Для того, чтобы измерить градусную меру угла, необходимо посчитать, сколько раз 1 градус входит в данный угол. Полученное число и будет ответом.

Если угол таков, что его нельзя измерить целым числом, либо же он меньше единичного угла, то используют такие меры измерения как угловые минуты и секунды.

Если градус поделить на 60 частей, то одной такой частью будет минута. В свою же очередь, если минуту разделить на те же 60 частей, то полученным числом будет 1 секунда.

Радианная мера угла

Радианом называют угол, образованный дугой окружности длинной равной радиусу этой окружности.

Длина окружности равна:

l=2⋅π⋅rl=2cdotpicdot r,

где rr — радиус этой окружности.

Тогда, разделив на радиус, получаем, что полный угол в радианах равен:

lr=2⋅π⋅rr=2⋅π радианfrac{l}{r}=frac{2cdotpicdot r}{r}=2cdotpitext{ радиан}

В градусах этот же угол равен, как известно, 360∘360^{circ}.

Отсюда находим связь между радианами и градусами:

2⋅π радиан=360∘2cdotpitext{ радиан}=360^{circ}

Это та главная формула, которая нужна, чтобы переводить градусы в радианы и наоборот.

Один радиан равен:

1 радиан=360∘2⋅π≈57.3∘1text{ радиан}=frac{360^{circ}}{2cdotpi}approx57.3^{circ}

Один радиан в минутах:

1 радиан=360∘2⋅π⋅60≈3438′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60approx3438′

Один радиан в секундах:

1 радиан=360∘2⋅π⋅60⋅60≈206280′′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60cdot60approx206280»

Перевод градусов в радианы

Если по условию известна градусная мера угла, то чтобы перевести ее в радианную, нужно сделать следующие действия: умножить ее на πpi и разделить на 180.

Перевод градусов в радианы

y радиан=π180⋅xytext{ радиан}=frac{pi}{180}cdot x

xx — значение угла в градусах;
yy — значение того же угла в радианах.

Пример 1

Переведите 45 градусов в радианную меру измерения. Ответ округлите до десятой доли.

Решение

45∘=π180⋅45 радиан≈0.8 радиан45^{circ}=frac{pi}{180}cdot 45text{ радиан}approx0.8text{ радиан}

Ответ

0.8 радиан0.8text{ радиан}

Задача

Земля совершила треть от половины оборота вокруг Солнца. На какой угол в радианах она повернулась?

Решение

Найдем сначала этот угол в градусах. Полный угол составляет 360∘360^circ. Половина от полного оборота это 180∘180^{circ}. Нам же нужна треть этого угла, то есть:

180∘3=60∘frac{180^circ}{3}=60^circ

Земля отклонилась на угол 60∘60^circ от своего начального положения. Переведем теперь этот угол в радианы:

60∘=π180⋅60 радиан≈1 радиан60^circ=frac{pi}{180}cdot 60text{ радиан}approx1text{ радиан}

Решение

1 радиан1text{ радиан}

Перевод радиан в градусы

Чтобы перевести радианы в градусы, нужно умножить угол в радианах на 180 и разделить на πpi.

Перевод радиан в градусы

y∘=180π⋅xy^{circ}=frac{180}{pi}cdot x

xx — значение угла в радианах;
yy — значение того же угла в градусах.

Пример 2

Переведите 3 радиана в градусную меру угла.

Решение

3 радиана=180π⋅3≈172∘3text{ радиана}=frac{180}{pi}cdot3approx172^circ

Ответ

172∘172^circ

Ищете, где можно заказать задачу по математике недорого? Обратитесь к нашим экспертам в данной области!

Тест по теме «Перевод градусов в радианы и наоборот»

Источник

В прошлый раз мы с вами ответили на первый вопрос, касаемый работы с углами. А именно — как отсчитываются углы. Рассмотрели положительные и отрицательные углы, а также углы, большие 360 градусов. И на круге углы порисовали.)

В этом же уроке настал черёд ответить на второй вопрос, связанный с измерением углов. Здесь мы разберёмся с загадочными радианами и особенно — с пресловутым числом «пи», которое будет мозолить нам глаза на протяжении всего дальнейшего изучения тригонометрии. Поймём, что это за число, откуда оно берётся и как с ним работать. И задания порешаем, само собой. Стандартные и не очень…)

Разберёмся? Ну сколько же можно бояться числа «пи», в конце-то концов!)

Итак, в чём же измеряются углы в математике? Начнём с привычного и знакомого. С градусов.

Что такое один градус? Градусная мера угла.

К градусам вы уже попривыкли. Геометрию изучаете, да и в жизни постоянно сталкиваетесь. Например, «повернул на 90 градусов».) Короче, градус — штука простая и понятная.

Вы и вправду так думаете? Тогда сможете сказать мне, что такое градус? Нет, гуглить и потрошить Википедию не надо. Ну как, слабо с ходу? Вот так-то…

Начнём издалека. С древнейших времён. А именно — с двух очагов древних цивилизаций Вавилона и Египта.)

Градус — это 1/360 часть окружности. И всё!

Смотрим картинку:

Придумали градусы в Древнем Вавилоне.) Как? Очень просто! Просто взяли да разбили окружность на 360 равных кусочков. Почему именно на 360? А не на 100 или на 1000? Вроде бы, число 100 поровнее, чем 360… Вопрос хороший.

Основная версия — астрономическая. Ведь число 360 очень близко к числу дней в году! А для наблюдений за Солнцем, Луной и звёздами это было оч-чень удобно.)

Кроме того, в астрономии (а также строительстве, землемерии и прочих смежных областях) очень удобно делить окружность на равные части. А теперь давайте прикинем чисто математически, на какие числа делится нацело 100 и на какие — 360? И в каком из вариантов этих делителей нацело больше? А людям такое деление очень удобно, да…)

Что такое число «пи»? Как оно возникло?

А теперь переместимся из Древнего Вавилона в Древний Египет. Примерно в то же самое время там разгадывали другую загадку. Не менее интересную, чем вопрос, на сколько частей бить окружность. А именно — во сколько раз длина окружности больше её диаметра? Или по-другому: чему равна длина окружности с диаметром, равным единице?

И так измеряли и сяк… Каждый раз получалось чуть-чуть больше трёх. Но как-то коряво получалось, неровно…

Но они, египтяне, ни в чём не виноваты. После них математики всех мастей продолжали мучиться аж до 18 века! Пока в 1767 году окончательно не доказали, что, как бы мелко ни нарезать окружность на равные кусочки, из таких кусочков сложить точно длину диаметра нельзя. Принципиально нельзя. Только лишь примерно.

Нет, конечно же, во сколько раз длина окружности больше её диаметра установили давным-давно. Но, опять же, примерно… В 3,141592653… раза.

Это число — и есть число «пи» собственной персоной.) Да уж… Корявое так корявое… После запятой — бесконечное число цифр безо всякого порядка, безо всякой логики. В математике такие числа называются иррациональными. И на сегодняшний день доказательство факта иррациональности числа «пи» занимает аж десять (!) лекций на 4-м курсе мехмата МГУ… Этот факт, кстати, и означает, что из одинаковых кусочков окружности её диаметр точно не сложить. Никак. И никогда…

Конечно, рациональные приближения числа «пи» известны людям ещё со времён Архимеда. Например:

22/7 = 3,14285714…

377/120 = 3,14166667…

355/113 = 3,14159292…

Сейчас, в век суперкомпьютеров, погоня за десятичными знаками числа «пи» не стихает, и на сегодняшний день человечеству известно уже два квадриллиона (!) знаков этого числа…

Но нам для практического применения такая сверхточность совершенно не требуется. Чаще всего достаточно запомнить всего лишь две цифры после запятой.

Запоминаем:

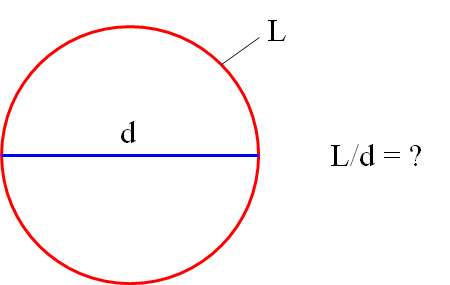
Вот и всё. Раз уж нам ясно, что длина окружности больше её диаметра в «пи» раз, то можно записать (и запомнить) точную формулу для длины окружности:

Здесь L — длина окружности, а d — её диаметр.

В геометрии всяко пригодится.)

Для общего развития скажу, что число «пи» сидит не только в геометрии или тригонометрии. Оно возникает в самых различных разделах высшей математики. В интегралах, например. Или в теории вероятностей. Или в теории комплексных чисел, а также рядов. Само по себе возникает, хотим мы того или нет… Поступите в ВУЗ — убедитесь лично.)

Ну а теперь снова вернёмся к старым добрым градусам. Как мы помним, один градус — это 1/360 часть окружности. С исторической и практической точек зрения людям такое деление на 360 равных частей оказалось очень даже удобно, но…

Как выяснилось гораздо позже Древнего Вавилона, градусы удобны далеко не всем. Например, высшей математике они ой как неудобны! Высшая математика — дама серьёзная. По законам природы устроена. И она справедливо заявляет: «Сегодня вы на 360 частей круг разбили, завтра — на 100 разобьёте, послезавтра — на 250… А мне что делать? Каждый раз под ваши хотелки подстраиваться?»

Против природы не попрёшь… Пришлось прислушаться и уступить. И ввести новую меру угла, не зависящую от наших хотелок. )

Итак, знакомьтесь — радиан!

Что такое один радиан? Радианная мера угла.

В основе определения радиана — та же самая окружность. Угол в 1 радиан — это угол, который отсекает от окружности дугу, длина которой (L) равна радиусу окружности (R). И всё!

Смотрим картинку:

Причём величина угла в один радиан не зависит от радиуса окружности! Никак. Можно нарисовать очень большую окружность, можно очень маленькую. Но угол, отсекающий от окружности дугу, равную радиусу, никогда не изменит своей величины и будет составлять ровно один радиан. Всегда. Это важно.)

Запоминаем:

Угол в один радиан — это угол, вырезающий из окружности дугу, равную радиусу окружности. Величина угла в 1 радиан не зависит от радиуса окружности.

Кстати говоря, градусная мера угла тоже не зависит от радиуса окружности. Большая окружность, маленькая — углу в один градус без разницы. Но градус — это величина, искусственно придуманная людьми для их личного удобства! Древними вавилонянами, если мы помним.) 1/360 часть окружности. Так уж сложилось чисто исторически. А если бы по каким-то причинам договорились на 100 частей разбить окружность? Или на 200? Кто знает, что тогда называлось бы градусом сегодня… Вот на сколько частей разобьём окружность, такой «градус» и получим. А вот радиан — штука универсальная!) К способу разбиения окружности никак не привязан. Строго дуга, равная радиусу! И чем больше радиус, тем больше (по длине) будет и соответствующая вырезаемая дуга. И наоборот. Но сама величина угла в один радиан не меняется. И разбиение окружности (любой!) радианами — всегда одинаковое. И сейчас мы в этом лично убедимся.)

Как переводить радианы в градусы и обратно?

К этому моменту вам уже должно быть интуитивно понятно, что один радиан существенно больше одного градуса. Всё-таки непонятно? Тогда смотрим снова на картинку:

Будем считать, что малюсенький красный угол имеет величину примерно один градус. Совсем крохотный уголок, почти и нет его… А большой зелёный угол — примерно один радиан! Чувствуете разницу?) Конечно же, один радиан сильно больше одного градуса…

А вот теперь начинается самое интересное! Вопрос: а во сколько раз один радиан больше одного градуса? Или сколько градусов в одном радиане? Сейчас выясним!)

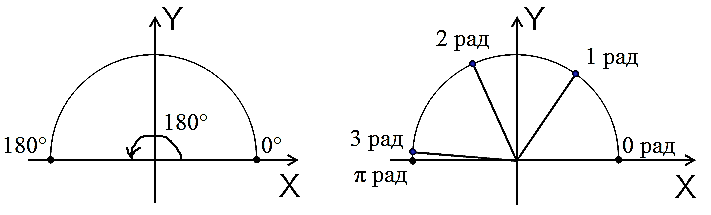
Смотрим на очередные картинки:

На картинке слева изображён полукруг. Обычный развёрнутый угол величиной 180°. А вот на картинке справа — тот же самый полукруг, но нарезанный радианами! Видно, что в 180° помещается примерно три с хвостиком радиана.

Вопрос на засыпку: как вы думаете, чему равен этот хвостик?)

Да! Он равен 0,141592653… Привет, число «пи», вот мы про тебя и вспомнили!)

Стало быть, в 180° укладывается 3,141592653… радиан. Понятное дело, что каждый раз писать такое длинное число неудобно, поэтому пишут приближённо:

Или точно:

Вот и всё. Вот и весь секрет тотального присутствия числа «пи» в тригонометрии. Эту простую формулку надо знать железно. Уловили?)

Так сколько же градусов в одном радиане? Не вопрос! Если в «пи» радианах содержится 180 градусов, то сколько же тогда градусов сидит в одном радиане? Правильно, в «пи» раз меньше! То есть меньше примерно в 3,14 раза.

Вот и делим обе части нашего соотношения на «пи» и получаем один радиан в градусах:

Это приближённое равенство также очень полезно запомнить. В одном радиане примерно 60 градусов. Такой грубой оценки бывает вполне достаточно для ответа на очень многие каверзные вопросы, связанные с углами. Бывает и недостаточно, конечно. В своё время мы такие хитрые задачки рассмотрим.)

Но это не самое главное применение этой формулы!) А самое главное — перевод радианов в градусы и обратно.

Переводим радианы в градусы!

Чаще всего углы в тригонометрии заданы в радианах с числом «пи». Это — самая стандартная ситуация. Если угол задан в радианах с числом «пи», то всё очень просто. Мы знаем, что «пи» радиан — это 180 градусов. Вот и подставляем вместо «пи» радиан — число 180. Сокращаем всё что сокращается и получаем угол в градусах.

Например:

Или более мудрёный угол:

Просто, правда?)

Переводим градусы в радианы!

Обратный перевод градусов в радианы чуть сложнее, но ненамного. Если угол задан в градусах, то сначала нам надо узнать, сколько составляет один градус в радианах. И умножить это значение на количество градусов.) И чему же равен 1° в радианах?

Снова смотрим на нашу формулу и соображаем. Если 180° — это «пи» радиан, то 1° в 180 раз меньше. Вот и делим обе части формулы на 180! Получаем, что 1° в радианах равен:

Вот и все дела. Умножаем дробь π/180 на количество градусов, сокращаем что сокращается и получаем угол в радианах. Например:

Или аналогично:

Вот и всё. Заменять «пи» на примерно 3,14 никакой необходимости нет: его всегда буквой пишут. Что правда, то правда: нас же в заданиях обычно точный ответ интересует! А не приближённый.) Кстати, кому интересен приближённый ответ, посчитайте на калькуляторе. Получите примерно 0,628 и 2,356 радиана соответственно.

Итак, в непринуждённой беседе с лирическими отступлениями мы узнали, что радианы — это очень даже просто, не больно и не страшно.) Да и перевод туда-обратно несложен. И «пи» — не кусается… Так откуда же проблемы?

Что ж, вскрою тайну. Всё дело в том, что в тригонометрии значок градусов — пишется. Всегда и везде. Например, cos30° — это косинус 30 градусов! А вот значок радианов («рад») — не пишется! Он — подразумевается. В чём причина — неизвестно. Может, обленились математики, может ещё что… Но договорились не писать. Например, sin5 — это синус пяти радианов!

Это и приводит к казусам. Человек смотрит на пример, видит «пи» и автоматически считает, что это 180°. Везде и всюду. Кстати, это срабатывает. До поры до времени, пока примеры — типовые. Но любое отклонение примера от шаблона — тут же валит наповал! Почему?

Потому, что само по себе «пи» — это число! А никакие не градусы! Это «пи» радиан = 180°!

Ещё раз запоминаем:

Просто «пи» — это число! «Пи» РАДИАН — это 180°!

Это заклинание надо понимать железно. Причём не просто механически зазубрить, а именно понимать каждое слово и каждый значок! И особенно — слово «радиан». Я не шучу. Ибо, если на вопрос, «Что такое «пи» в тригонометрии?», вы, блистая знаниями, радостно заявляете:

«Пи — это 180 градусов!!!» ,

то это говорит о том, что вы не понимаете до конца смысла этой зелёной фразы. И все дальнейшие беседы уже бессмысленны, да…

Ещё раз: «пи» — это число! Примерно равное 3,14. Точного значения этого числа не знает никто: оно бесконечно длинное, корявое, иррациональное. Но — число! Такое же, как 2 или 7. Можно пройти примерно «пи» километров. Три километра и ещё около 140 метров. Можно купить «пи» килограммов картошки. Если продавец образованный встретится.) Можно выпить «пи» литров кока-колы. Если здоровье не жалко… И так далее…

Всё равно непонятна зелёная запись? Хорошо, вот вам простые житейские фразы:

1 километр — это 1000 метров;

3 часа — это 180 минут;

2 года — это 730 дней;

И тому подобное. Точно так же и с градусами/радианами:

«Пи» радиан — это 180 градусов!

Уяснили, что «пи» — это просто число? Или я уже достал вас этой заезженной фразой? Ну ладно, убедили. Тогда вот вам парочка нестандартных вопросов:

1. Что больше?

или

2. Что меньше?

cos5°

или

cos5

Если у вас случился ступор, не беда. Вспоминаем нашу мантру: «Пи» — это число! В первом синусе нам чётко сказано, что угол — в градусах! Следовательно, машинально заменять «пи» на 180° — нельзя. «Пи» градусов — это примерно 3,14°. Вот и пишем:

Во втором синусе никаких значков нет. Значит, там — радианы. И вот тут замена «пи» на 180° — вполне законна.) Переводим радианы в градусы и получаем:

А теперь сравниваем эти два синуса. Как? По кругу, разумеется! Рисовать углы мы с вами уже умеем, что такое синус угла на круге — тоже знаем. Вперёд! Рисуем круг, углы примерно 0,79° и 45° и смотрим какие синусы у этих углов. Даже на самом корявом круге будет видно, что sin45° гораздо больше, чем sin0,79°.

С косинусами — всё то же самое. Рисуем на круге в правильных четвертях углы примерно 5 градусов и 5 радианов (помним, чему примерно равен один радиан в градусах?). Круг нам всё и подскажет. А именно, что cos5 меньше, чем cos5°.

Вообще, задачки с углами в радианах без «пи» (типа определить знак выражения sin10∙cos20) относятся к разряду нестандартных. В следующем уроке разберём парочку таких.)

Ну что, потренируемся с переводом углов?) Решаем несложные задания.

1. Переведите следующие углы из градусной меры в радианную:

180°; 0°; 360°; 90°; 270°.

Ответы (по возрастанию):

Как вы думаете, что это были за углы? Да! Это углы, которые попадают на координатные оси! Эти опорные значения надо держать в голове надёжно. До автоматизма! Как в градусах, так и в радианах. Зачем? Да всё за тем же! Для правильного распределения любых углов по четвертям.) Это полезное умение — залог успеха в любом задании по тригонометрии. Любом! От примитивных примеров до вполне себе солидных ЕГЭшных задачек части 2 (уравнения с отбором корней, тригонометрические неравенства и прочие хитрые штучки).

Продолжаем развлекаться.

2. Переведите углы в радианную меру:

30°; 45°; 60°.

Ответы (в беспорядке):

Получилось? Рад за вас. Почему я выделил именно эти три угла? По той же самой причине. Эти углы — особые личности в тригонометрии. Потому что именно про эти углы вы обязаны знать всё! И где они находятся и весь комплект их тригонометрических функций. Скажем, значение sin20° вы знать не обязаны. А вот sin30° — уж будьте так добры! Это обязательные значения, без которых во всей остальной тригонометрии делать вообще нечего. Но об этом — в отдельном уроке.)

Продолжим тренировку.

Переведите следующие углы из радианной меры в градусную:

Ответы (в беспорядке):

300°; 225°; 120°; 330°; 240°; 135°; 210°; 315°; 150°.

А это что за углы? Правильно! Это углы, в пределах одного оборота, кратные предыдущим трём! Но не попадающие на оси координат. Такие углы вы также обязаны уметь просчитывать! И более того, все углы, кратные 30, 45 или 60 градусам, вы обязаны уметь просчитывать! Как в пределах одного оборота, так и за его пределами. Как положительные, так и отрицательные… В соответствующем уроке мы научимся с вами проделывать такие полезные вещи.

Если и это получилось, то тогда можно считать, что перевод радианов в градусы и обратно — уже не ваша проблема. Но перевод углов из одной размерности в другую — это лишь ещё один шаг вперёд к успешному постижению тригонометрии. Шаг мощный, но недостаточный. Ведь, чаще всего, с углами надо потом ещё и что-то делать.) Рисовать на круге, например. Или синус/косинус считать. Да и тангенс/котангенс тоже…

Второй серьёзный шаг — это умение правильно определять положение любого угла на тригонометрическом круге. Любого! Как в градусах, так и в радианах. С градусами на круге мы уже плотно поработали в предыдущем уроке. Теперь настал черёд набивать руку в работе с радианами.

Об этом — в следующей теме.

Источник

Основное понятие градуса и радиана и их взаимосвязь

В математике, такое определение, как угол принято измерять градусами и радианами.

Эти два измерения угла имеют взаимосвязь и необходимо четко понимать в чем она заключается.

В данном материале, мы постараемся разобраться и вывести

основную формулу для вычисления градусов в значение радиан, и соответственно в обратном порядке.

Определение

Радиан — это угол, который образуется окружной дугой, ее длина, следовательно, равняется радиусу данной окружности.

Радианная мера — угловое значение,где за единицу берется угол в 1 радиан. А именно, вышеупомянутая мера любого угла — это соотношение принятого угла к радиану. Из этого следует, что величина полного значения угла равняется [2 cdot pi] радиан.

Определяем длину окружности, по стандартной формуле:

[ l=2 cdot pi cdot r ]

Чтобы определить полный угол в радианах проводим следующие действие: [frac{l}{r}=frac{2 cdot pi cdot r}{r}=2 cdot pi] , соответственно в градусах значение будет равно 360. Отсюда следует [2 cdot pi=360^{circ}].

Какова связь между градусами и радианами?

Угол имеет градусную и радианную меру. Зная ее, можно установить связь между градусом и радианом.

Например, возьмем для примера центральный угол, который примыкает к диаметру окружности радиуса R.

Нам необходимо вычислить значение радианной меры угла. Для решения этой задачи, длину самой дуги поделить на длину радиуса окружности.

Заданный угол равен [pi] радиан. Данный угол 180 градусов и по законам математики, является развернутым. Отсюда следует, что 180 градусов эквивалентно [pi] радиан.

Данную связь можно выразить через формулу.

[text { п рад }=180 text { град. }]

Перевод радианов в градусы и соответственно в обратном порядке

Для перевода радиан в градусы и наоборот необходимо знать и применять на практике следующие формулы:

Один радиан равен: [frac{360^{circ}}{2 cdot pi} approx 57^{circ}];

Один радиан в минутах: [frac{360^{circ}}{2 cdot pi} cdot 60 approx 3438];

Один радиан в секундах: [frac{360^{circ}}{2 cdot pi} cdot 3600 approx 206280].

[ 1 text { радиан }=left(frac{180}{pi}right) text { градусов. } ]

[ 1 text { градус }=left(frac{pi}{180}right) text { рад. } ]

Рассмотрим на конкретном примере:

[1 text { радиан }=left(frac{180}{pi}right)=left(frac{180}{3,14}right)=57,324] следовательно в 1 радиане 57 градусов.

[1 text { градус }=left(frac{pi}{180}right) text { радиан }=left(frac{3,14}{180}right)=0,017] радиан (сокращенно рад.).

[text { х радиан }=left(frac{chi cdot 180}{pi}right)], дословно будет звучать как: 180 * умножить на числовое значение угла и раздели.

Соответствие градусов и радиан принято, для удобства решения сводить в таблицу.

Пример, приведен в таблице 1.

Таблица 1. Соотношение значений.

Числовые значения в градусах	Соответствующие данные радиан
1°	0,018
2°	0,035

Как мы видим изученная тема не очень сложная. Достаточно знать основные формулы и в расчетах, и проблем не должно возникать.

Для более лучшего закрепления разберемся и решим несколько задач по вычислении градусов и радианов углов.

Нет времени решать самому?

Наши эксперты помогут!

Задача №1

Переведите 35 градусов в радианы.

[ 35^{circ}=left(frac{pi}{180}right) cdot 35 text { радиан }=0,6 text { рад } ]

Ответ: 35°=0,6 рад.

Задача №2

Переведите 55 градусов в радианы.

[55^{circ}=left(frac{pi}{180}right) cdot 55 text { радиан}=0,9 text { paд }]

Ответ: 55°=0,9 рад.

Задача №3

Необходимо вычислить значение третьей половины полного угла.

Для начала определяем угол в градусах.

Нужно определить третью часть угла. Следовательно полный угол равняется 360 градусов, половина 180, а треть [frac{180}{3}=60] градусов.

Пользуясь формулой из задач №1 и 2, определяем значение в радианах.

[ 60^{circ}=left(frac{pi}{180}right) cdot 60 text { радиан }=1 text { рад } ]

Ответ: 1 рад.

Источник

Перевод градусов в радианы и обратно: формулы, примеры

Связь между градусами и радианами

Формулы перевода радианов в градусы и наоборот

Примеры перевода градусов в радианы и радианов в градусы

Тригонометрический круг: вся тригонометрия на одном рисунке

А теперь подробно о тригонометрическом круге:

Единичная окружность

Единичная окружность в тригонометрии

Definition

Unit symbol

Dimensional analysis

Conversions

Between degrees

Between gradians

Usage

Mathematics

Physics

Prefixes and variants

History

Pre-20th century

As a SI unit

See also

Notes

References

External links

Градусная мера угла

Радианная мера угла

Перевод градусов в радианы

Перевод радиан в градусы

Тест по теме «Перевод градусов в радианы и наоборот»

Основное понятие градуса и радиана и их взаимосвязь

Какова связь между градусами и радианами?

Перевод радианов в градусы и соответственно в обратном порядке

Не пропустите также: