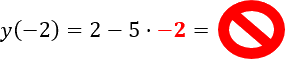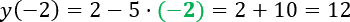Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».
После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание.
Функция задана формулой «y = 2x − 1»
- Вычислить «y» при «x = 15»
- Найти значение «x», при котором
значение «y» равно «−19».
Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.
Запись решения выглядит следующим образом.
y(15) = 2 · 15 − 1 = 30 − 1 = 29
Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.
То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .
−19 = 2x − 1
Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.
Запомните!
Не забывайте про правило переноса в уравнениях.
При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.
−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.
−2x = 18 | · (−1)
2x = −18
Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .
2x = −18 | (: 2)
x = −9
Как проверить верно ли равенство для функции
Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».
Верно ли равенство
«f(−2) = −18»?
Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.
Важно!
Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.
Не забывайте использовать
правило знаков.
Неправильно
Правильно
С помощью расчетов мы получили
«f(−2) = 12».
Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию «y = x2 −5x + 6»
Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).
Для этой задачи нет необходимости, строить график заданной функции.
Запомните!
Чтобы определить, принадлежит ли точка функции,
достаточно подставить её координаты в функцию (координату по оси
«Ox» вместо
«x» и координату по оси «Oy»
вместо «y»).
Если получится верное равенство, значит, точка принадлежит функции.
Вернемся к нашему заданию. Подставим в функцию «y = x2 − 5x + 6»
координаты точки (1; 2).
Вместо «x» подставим «1».
Вместо «y» подставим «2».
2 = 12 − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)
У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.
Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x2 − 5x + 6»?
Вместо «x» подставим «0».
Вместо «y» подставим «1».
1 = 02 − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)
В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x2 − 5x + 6»
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.
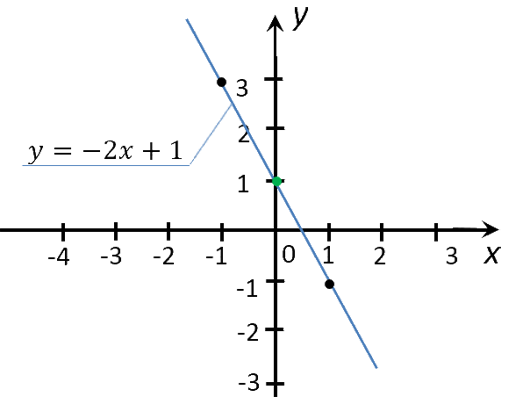
Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.
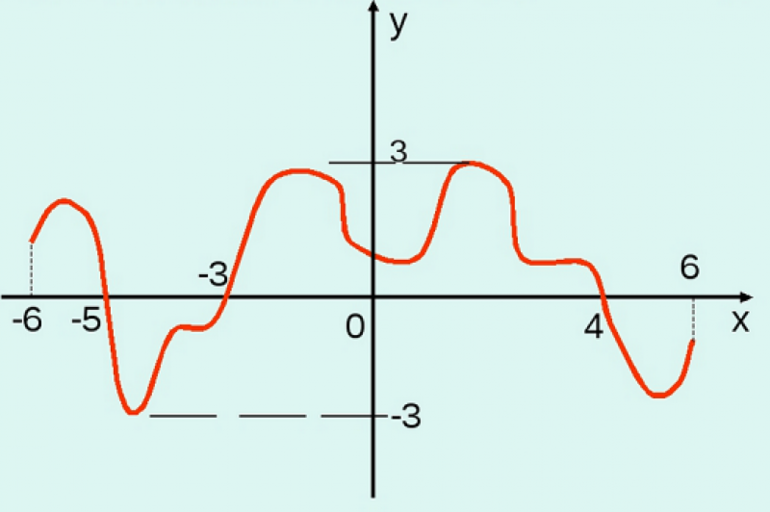
Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.
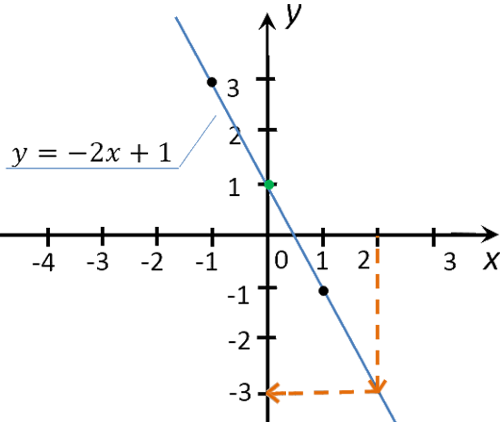
Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».
Полученное значение «−3» на оси «Oy» и будет искомым значением «y».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».
Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.
y(2) = −2 · 2 + 1 = −4 + 1 = −3
При расчетах мы также получили y = −3.
Значит, мы правильно получили координаты с графика функции.
Важно!
Все полученные координаты точки с графика функции обязательно проверяйте
подстановкой значений «x» в функцию.
При подстановке числового значения «x» в функцию в результате должно получиться
то же значение «y», которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
11 ноября 2018 в 15:46
Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Функция y=f(x) является нечётной и при x ⩽0 задаётся формулой y= — x² — 8x.Найдите значение фун. в т. минимума (y min).
0
Спасибо
Ответить
12 ноября 2018 в 3:25
Ответ для Веточка Сакуры
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
ymin = y(4) = -16.
0
Спасибо
Ответить
17 сентября 2018 в 13:28
Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Добрый день помогите пожалуйста с задачкой
f(x2-3x)=3x2+5x-4
f(3)=?
0
Спасибо
Ответить
17 сентября 2018 в 23:01
Ответ для Alesger Mammedov
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
f(3) = 26 ± 7√21
0
Спасибо
Ответить
13 ноября 2016 в 6:43
Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
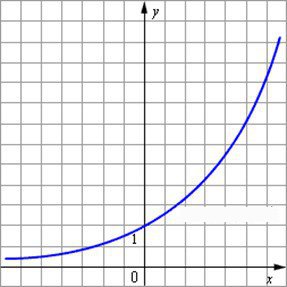
0
Спасибо
Ответить
14 ноября 2016 в 17:30
Ответ для Роман Безбородов
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
y = ax; a > 1.
0
Спасибо
Ответить
7 сентября 2016 в 22:08
Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
у=Х2+2Х-3 найдите значение функции, если значение аргумента равно -2
у=3х-5 при каком значении аргумента значение функции раво 10
0
Спасибо
Ответить
8 сентября 2016 в 15:26
Ответ для Иван Баранов
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
аргумент это х значит у=(-2)2+2 · (-2)-3=4-4-3=-3
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5
0
Спасибо
Ответить
Загрузить PDF
Загрузить PDF
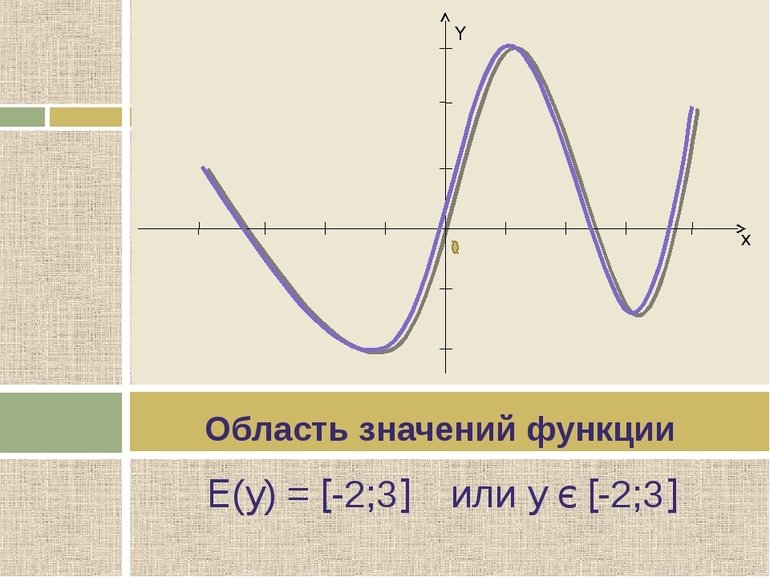
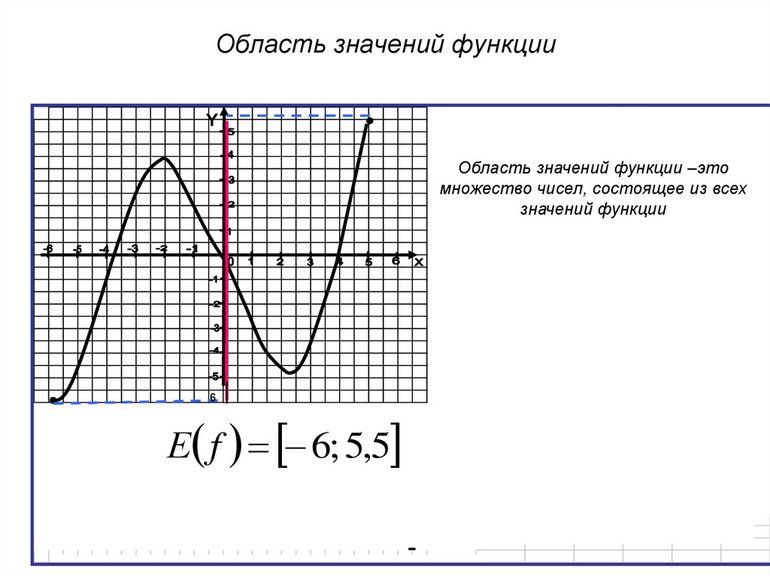
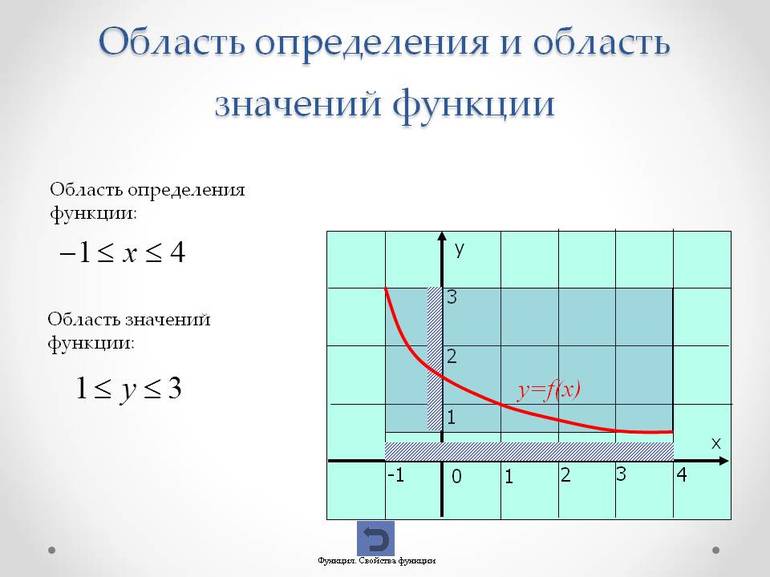
Множество значений (область значений) функции — все значения, которые принимает функция в ее области определения. Другими словами, это те значения у, которые вы получаете при подстановке всех возможных значений х. Все возможные значения х и называются областью определения функции. Выполните следующие действия для нахождения множества значений функции.
-
1
Запишите функцию. Например: f(x) = 3x2 + 6x -2. Подставив x в уравнение, мы сможем найти значение y. Эта квадратичная функция, и ее график — парабола.
-
2
Найдите вершину параболы. Если вам дана линейная функция или любая другая с переменной в нечетной степени, например, f(x) = 6x3+2x + 7, пропустите этот шаг. Но если вам дана квадратичная функция или любая другая с переменной х в четной степени, нужно найти вершину графика этой функции. Для этого используйте формулу х=-b/2a. В функции 3x2 + 6x -2 a = 3, b = 6, c = -2. Вычисляем: х = -6/(2*3)= -1.
- Теперь подставьте х= -1 в функцию, чтобы найти у. f(-1) = 3*(-1)2 + 6*(-1) -2 = 3 — 6 -2 = -5.
- Координаты вершины параболы (-1,-5). Нанесите ее на координатную плоскость. Точка лежит в третьем квадранте координатной плоскости.
-
3
Найдите еще несколько точек на графике. Для этого подставьте в функцию несколько других значений х. Так как член x2 положительный, то парабола будет направлена вверх. Для подстраховки подставим в функцию несколько значений x, чтобы узнать, какие значения y они дают.
- f(-2) = 3(-2)2 + 6(-2) -2 = -2. первая точка на параболе (-2, -2)
- f(0) = 3(0)2 + 6(0) -2 = -2. Вторая точка на параболе (0,-2)
- f(1) = 3(1)2 + 6(1) -2 = 7. Третья точка на параболе (1, 7).
-
4
Найдите множество значений функции на графике. Найдите наименьшее значение у на графике. Эта вершина параболы, где у=-5. Так как парабола лежит выше вершины, то множество значений функции y ≥ -5.
Реклама
-
1
Найдите минимум функции. Вычислите наименьшее значение у. Допустим, минимум функции у=-3. Это значение может становиться все меньше и меньше, вплоть до бесконечности, так что минимум функции не имеет заданной минимальной точки.
-
2
Найдите максимум функции. Допустим, максимум функции у= 10. Как и в случае с минимумом, максимум функции не имеет заданной максимальной точки.
-
3
Запишите множество значений. Таким образом, множество значений функции лежит в диапазоне от -3 до +10. Запишите множество значений функции как: -3 ≤ f(x) ≤ 10
- Но, допустим, минимум функции у=-3, а ее максимум — бесконечность (график функции уходит бесконечно вверх). Тогда множество значений функции: f(x) ≥ -3.
- С другой стороны, если максимум функции у=10, а минимум — бесконечность (график функции уходит бесконечно вниз), то множество значений функции: f(x) ≤ 10.
Реклама
-
1
Запишите множество координат. Из множества координат можно определить его область значения и область определения. Допустим, дано множество координат: {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)}.[1]
-
2
Перечислите значения у. Чтобы найти область значений множества, просто запишите все значения у: {-3, 6, -1, 6, 3}.[2]
-
3
Удалите все повторяющиеся значения у. В нашем примере удалите «6»: {-3, -1, 6, 3}.[3]
-
4
Запишите область значений в порядке возрастания. Областью значений множества координат {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} будет {-3, -1, 3, 6}.[4]
-
5
Убедитесь, что множество координат дано для функции. Чтобы это было так, каждому одному значению х должно соответствовать одно значение у. Например, множество координат {(2, 3) (2, 4) (6, 9)} дано не для функции, потому что одному значению х=2 соответствуют два разных значения у: у=3 и у=4.[5]
Реклама
-
1
Прочитайте задачу. «Ольга продает билеты в театр по 500 рублей за билет. Общая вырученная сумма за проданные билеты является функцией от количества проданных билетов. Какова область значений этой функции?»
-
2
Запишите задачу как функцию. В этом случае М — общая вырученная сумма за проданные билеты, а t — количество проданных билетов. Так как один билет стоит 500 рублей, надо умножить количество проданных билетов на 500, чтобы найти вырученную сумму. Таким образом, функция может быть записана в виде M(t) = 500t.
- Например, если она продаст 2 билета, нужно умножить 2 на 500 — в итоге получим 1000 рублей, вырученных за проданные билеты.
-
3
Найдите область определения. Для нахождения области значений вы должны сначала найти область определения. Это все возможные значения t. В нашем примере Ольга может продать 0 или больше билетов, — она не может продать отрицательное число билетов. Поскольку мы не знаем количество мест в театре, можно предположить, что теоретически она может продать бесконечное число билетов. И она может продавать только целые билеты (она не может продать, например, 1/2 билета). Таким образом, область определения функции t = любое неотрицательное целое число.
-
4
Найдите область значений. Это возможное количество денег, которые Ольга выручит от продажи билетов. Если вы знаете, что область определения функции — любое неотрицательное целое число, а функция имеет вид: М(t) = 5t, то вы можете найти вырученную сумму, подставив в функцию любое неотрицательное целое число (вместо t). Например, если она продаст 5 билетов, то М(5) = 5*500 = 2500 рублей. Если она продаст 100 билетов, то М(100) = 500 х 100 = 50000 рублей. Таким образом, область значений функции — любые неотрицательные целые числа, кратные пятистам.
- Это означает, что любое неотрицательное целое число, которое делится на 500, является значением у (вырученная сумма) нашей функции.
Реклама
Советы
- В более сложных случаях лучше сначала чертить график, используя область определения, и только потом находить область значений.
- Посмотрите, можете ли вы найти обратную функцию. Область определения обратной функции равна области значений исходной функции.
- Проверьте, повторяется ли функция. Любая функция, которая повторяется вдоль оси x, будет иметь ту же область значений для всей функции. Например, область значений для f(x) = sin(x) будет составлять от -1 до 1.
Реклама
Об этой статье
Эту страницу просматривали 455 114 раз.
Была ли эта статья полезной?
Как найти значение функции
Под понятием функции в математике понимают связь между элементами множеств. Если говорить более точно, это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Вам понадобится
- Знания в области алгебры и математического анализа.
Инструкция
Значения функции это некая область, значения из которой может принимать функция. Например область значения функции f(x)=|x| от 0 до бесконечности. Чтобы найти значение функции в конкретной точке необходимо подставить вместо аргумента функции его числовой эквивалент, полученное число и будет значением функции. Пусть дана функция f(x)=|x| — 10 + 4x. Найдем значение функции в точке x=-2. Подставим вместо x число -2: f(-2)=|-2| — 10 + 4*(-2) = 2 — 10 — 8 = -16. То есть значение функции в точке -2 равно -16.
Обратите внимание
Прежде чем искать значение функции в точке — убедитесь, что она входит в область определения функции.
Полезный совет
Аналогичным способом можно найти значение функции нескольких аргументов. Отличие в том, что вместо одного числа необходимо будет подставить несколько — по числу аргументов функции.
Общая информация
У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.
Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.
В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.
Основные понятия
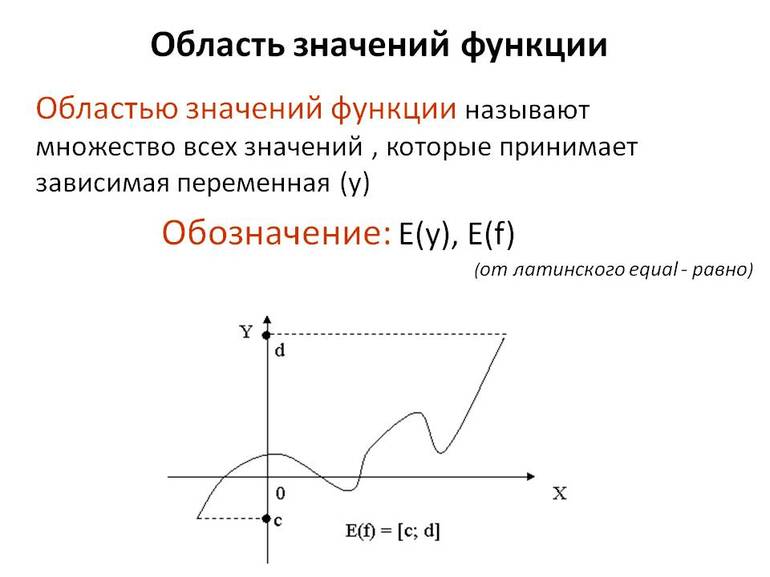
Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».
Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.
Например, нужно найти область значений квадратичной функции y = 3x 2 — 2x — 1. Следует записать уравнение 3x 2 — 2x — 1 = 0. Ордината вычисляется таким образом: y0 = -D / 4a = -[b 2 — 4ac] / 4a = -[(-2)^2 — 4 * 3 * (-1)] / (4 * 3) = -16 / 12 = -4/3. Если коэффициент а>0, то ветви параболы направлены вверх. Следовательно, E (y) = (-4/3;+бесконечность).
Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.
Типы функций
Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:
- (-бесконечность;+бесконечность): y =kx + b, y = x^(2n+1), y = x^(1/(2n+1)), y = log (x) с основанием а, y = tg (x) и y = ctg (x).
- [0;+бесконечность): y = x^(2n), y = x^(1/(2n)) и y = a^x.
- (-бесконечность;0] U [0;+бесконечность) только для y = k / x (гипербола).
- [-1;1]: y = sin (x) и y = cos (x).
- [0;Pi]: y = arccos (x) и arcsin (x).
- [-Pi/2;Pi/2]: y = arctg (x) и arcsin (x).
Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.
Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.
Важные свойства
Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:
- В случае, когда функция f (x) является непрерывной, и наблюдается ее возрастание или убывание на отрезке [a;b], то множество значений — интервал [f (a);f (b)].
- Если y = f (x) обладает непрерывностью на промежутке [a;b], и существует некоторое минимальное m и максимальное М ее значения, то множеством ее значений является интервал [m;M].
- При непрерывности и дифференцируемости функции на промежутке [a;b], она имеет минимальное и максимальное значения на данном промежутке.
Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.
Методы нахождения
Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:
- Отдельное нахождение значений элементов сложной функции.
- Оценочный.
- Учет непрерывности и монотонности.
- Взятие производной.
- Использование max и min функции.
Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.
Для каждого элемента
Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:
- Выполнить необходимые преобразования — упростить выражение.
- Разбить выражение на элементы.
- Выполнить поиск E (f) для каждого элемента.
- Произвести замену.
- Анализ.
- Результат решения.
Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:
- Упростить (выделить квадрат): y = log0.5 (4 — 2 * 3^x — 9^x) = log0.5 [5 — (1 — 2 * 3^x — 9^x)] = log0.5 [5 — (3^x + 1)].
- Разбить на элементарные функции: y = 3^x, y = 3^x + 1, y = [-(3^x + 1)]^2 и y = [5 — (3^x + 1)]^2.
- Определить для каждого элемента E (f): E (3^x) = (0;+бесконечность), E (3^x + 1) = (1;+бесконечность), E ([-(3^x + 1)]^2) = (-бесконечность;-1) и E ([5 — (3^x + 1)]^2) = (-бесконечность;4).
- Произвести замену: t = 5 — (3^x + 1)]^2 (-бесконечность <= t <=4).
- Анализ: поскольку E (f) на луче (-бесконечность;4) совпадает с интервалом (0;4), то функция непрерывна и убывает. Необходимо отметить, что интервал (0;4) получен при пересечении луча (-бесконечность;4) с областью определения функции логарифмического типа (0;+бесконечность). На интервале (0;4) эта функция непрерывна и убывает. Если t>0, то она стремится к бесконечности. Когда t = 4, ее значение равно -2.
- Результат решения — искомый интервал: E (f) = (-2;+бесконечность).
Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.
Оценочный способ
Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:
- Доказать непрерывность.
- Составить неравенство или неравенства для нескольких функций.
- Узнать оценку.
- Записать интервал.
Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:
- Функция вида y = cos (x) является непрерывной.
- Неравенства: -1<=cos (7x)?1 и -5<=5 * cos (x)?5.
- Оценка получает при объединении неравенств: -6<=y?6. При значениях независимой переменной x = Pi и x = 0 функция принимает значения -6 и 6 соответственно (нижняя и верхняя границы). Функция состоит из двух элементов, следовательно, она является линейной и непрерывной.
- Интервал: E (y) = [-6;6].
Метод позволяет найти решение без использования дополнительных вычислений. Но при его использовании легко ошибиться.
Учет непрерывности и монотонности
Одним из простых способов решения, который специалисты рекомендуют новичкам, является метод учета непрерывности и монотонности. Для этого существует специальный алгоритм:
- Упростить выражение.
- Выполнить замену при необходимости.
- Найти вершину графика.
- Определить промежуток.
- Вычислить максимальное и минимальное значения.
- Записать E (f).
Например, существует некоторая функция y = cos (2x) + 2cos (x). Необходимо найти ее E. Искать следует по алгоритму решения методом учета монотонности и непрерывности:
- Упростить (по формуле двойного угла): y = 2 * (cos (x))^2 + 2cosx — 1.
- Замена t = cos (x): y = 2 * t 2 + 2 * t — 1 = 2 * (t + 0,5)^2 — 1,5.
- Показательная функция является параболой. Она монотонна, непрерывна и имеет вершину по оси ОУ -1,5. Промежуток, который рассматривается — [-1;1], поскольку E (cos (x)) = [-1;1].
- Минимальное значение равно -1,5, так как ветви направлены вверх. Максимальное на промежутке [-1;1] — MAX (y) = 3. Для его нахождения нужно построить график параболы y = 2 * (t + 0,5)^2 — 1,5.
- Искомый интервал — E (cos (2x) + 2cos (x)) = [-1,5;3].
Чтобы построить график параболы, нужно найти ее вершину и точки пересечения с осью абсцисс. Последние находятся при решении уравнения 2 * (t + 0,5)^2 — 1,5 = 0. Однако существует способ намного проще. Для этого следует привести выражение к виду 2 * (t + 0,5)^2 = 1,5. Отсюда t = — 0,5. Следовательно, координаты вершины — (-0,5;-1,5). Корни уравнения при его решении: t1 = -[(1 + (3)^0.5)] / 2 и t2 = -[(1 — (3)^0.5)] / 2.
Производная, min и max
Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:
- Найти производную.
- Анализ.
- Указать MAX (f) и MIN (f).
- Запись интервала в формате (MIN (f);MAX (f)).
Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:
- Производная: y’ = [arcsin (x)]’ = 1 / [(1 — x 2 )^0.5].
- Функция возрастает на интервале (-1;1).
- Минимум и максимум на отрезке (-1;1): MIN (arcsin (-1)) = -Pi/2 MAX (arcsin (1)) = Pi/2.
- Интервал: E (arcsin (x)) = [-Pi/2;Pi/2].
В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:
- Производная: y’ = [sin (x)]’ = cos (x).
- Период функции равен 2Pi. Следует взять отрезок [0;2Pi]. Для нахождения множества значений на нем нужно приравнять производную функции к 0, т. е. cos (x) = 0. Найти х = Pi/2 + Pi * к, где «к» принадлежит Z. Точки экстремума равны Pi/2 и 3Pi/2.
- Минимум и максимум на отрезке [0;2Pi): MIN ([sin (3Pi/2)]) = -1 и MAX ([sin (3Pi/2)]) = 1.
- E (sin (x)) = [-1;1].
Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.
Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.