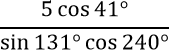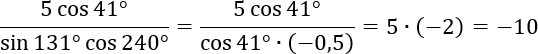При изучении геометрии вы установили, что
если
Свойство периодичности тригонометрических функций позволяет свести вычисление значений синуса, косинуса, тангенса и котангенса произвольного угла к вычислению значений этих функций при значениях аргумента, принадлежащих промежутку 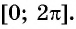
На практике принято сводить значения тригонометрических функций произвольного угла к вычислению значений этих функций для угла, принадлежащего промежутку 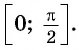
Это можно делать с помощью формул приведения.
Рассмотрим промежуток 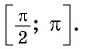
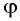
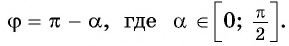
Например,
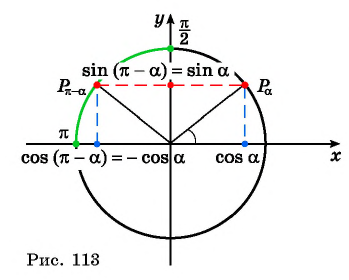
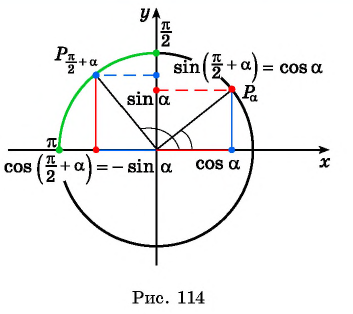
Поскольку ординаты точек 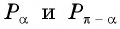
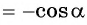
Тогда для 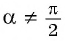
А для 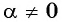
Вместе с тем любое число 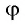
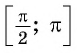
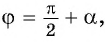
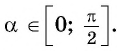
Так как ордината точки 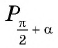
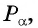
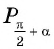
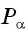
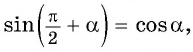
Для 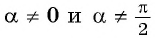
Так как любое число 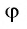
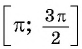
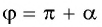
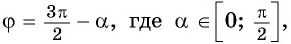
Поскольку любое число 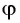
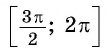
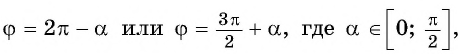
Проанализировав полученные формулы, можно заметить закономерности, позволяющие сформулировать правило, с помощью которого можно применять формулы приведения, не заучивая их:
В правой части формулы приведения ставится тот знак, который имеет в соответствующей четверти исходная функция, если считать, что угол 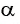
Если в формуле приведения аргумент имеет вид:
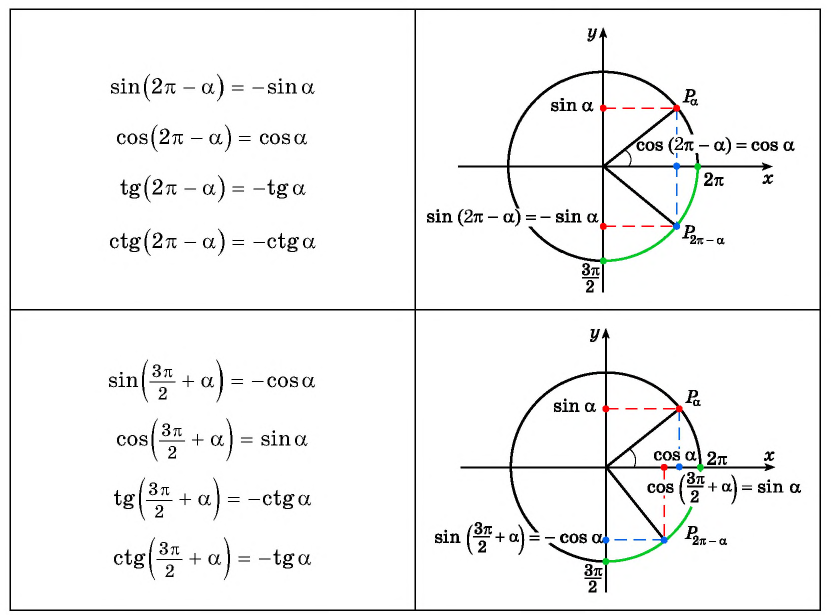
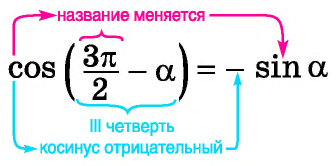
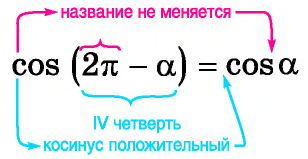
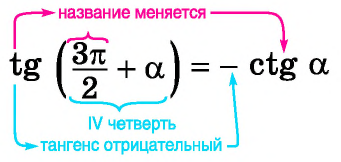
Например, применим полученное правило для выражения
- Если считать, что угол
— острый, то —
— угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».
- Поскольку аргумент имеет вид
то название функции «косинус» нужно поменять на «синус». Таким образом, получим:
Пример:
Приведите выражение к тригонометрической функции числа 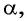
Решение:
Применим правило:
а) 1. Так как 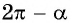
2. Поскольку аргумент имеет вид 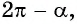
б) 1. Так как 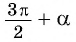
2.Поскольку аргумент имеет вид 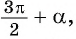
в) 1. Так как 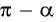
2. Поскольку аргумент имеет вид 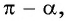
Пример:
Используйте формулы приведения и найдите значение выражения:
Решение:
Первый способ:
- Так как
угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».
- Поскольку аргумент имеет вид
то название функции «синус» не меняется. Значит,
Второй способ:
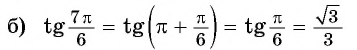
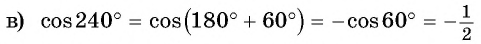
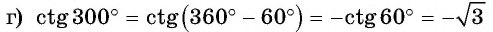
- Заказать решение задач по высшей математике
Пример:
Вычислите, используя формулы приведения:
Решение:
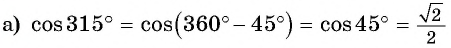
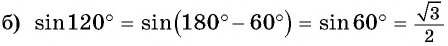

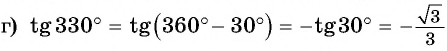
Пример:
Найдите значение выражения:
Решение:
а) Так как синус — нечетная функция, то
Применим формулы приведения:
б) Воспользуемся свойством четности косинуса и получим:
По формулам приведения:
в) Воспользуемся свойством периодичности тангенса и получим:
Применим формулы приведения:
г) Поскольку котангенс — нечетная функция, то
Используем свойство периодичности котангенса и получим:
Пример:
По формулам приведения:
Приведите к тригонометрической функции угла
Решение:
а) Используем свойство периодичности косинуса и получим:
По формулам приведения:
б) Воспользуемся свойством периодичности котангенса:
Применим формулы приведения:
в) Так как тангенс — нечетная функция, то 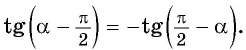
г) Поскольку синус — нечетная функция, то
Воспользуемся свойством периодичности синуса и получим:
По формулам приведения:
Пример:
Приведите к тригонометрической функции угла 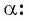
Решение:
Пример:
Вычислите:
Решение:
Пример:
Упростите выражение:
Решение:
а) Применим формулы приведения:
б)Воспользуемся периодичностью косинуса и формулами приведения и получим:
в)Применим формулы приведения:
г) Используем периодичность тангенса, нечетность котангенса и формулы приведения:
Пример:
Решите уравнение:
Решение:
Применим формулы приведения и получим:
Ответ:
- Синус, косинус, тангенс суммы и разности
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
Алгебра и начала математического анализа, 10 класс
Урок №37. Формулы приведения.
Перечень вопросов, рассматриваемых в теме:
- формулы приведения;
- мнемоническое правило для формул приведения;
- преобразование тригонометрических выражений на основе использования формул приведения;
- вычисление значений тригонометрических выражений на основе формул приведения;
- доказательство тригонометрические тождества на основе формул приведения;
- решение уравнения с использованием формул приведения.
Глоссарий по теме
Формулы приведения – это формулы, которые позволяют синус, косинус, тангенс и котангенс различных углов приводить к острым углам.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.
Теоретический материал для самостоятельного изучения
Для вычисления углов больше 90
Пример: Вычислить 

Представим число 
Рассмотрим точку А(1;0) на единичной окружности. При повороте вокруг начала координат на угол 





А так как 

Количество полных оборотов по 360





Справедливы равенства:



Пусть точка А(1;0) переместилась в точку В1 при повороте на угол 

Рисунок 2 – точки А, В, В1 на единичной окружности
Запишем 

Поэтому 

А так как 


Помним, что 


Докажем, что для всех углов 


Воспользуемся формулой синуса и косинуса разности:




Аналогично доказываются формулы:










Эти формулы называются формулами приведения для синуса и косинуса.
Пример: вычислите 


Выведем формулы для тангенса, используя его определение

Найдём 


Получаем формулы для тангенса и котангенса:








Пример: вычислите 
Преобразуем выражение в скобке

Обратите внимание, что все эти формулы связывают синусы с синусами или косинусами, а тангенсы с тангенсами или котангенсами. В одних случаях синус меняется на косинус и наоборот, в других – нет. Так, например, в формулах 1,2,3,8 и 13, где в левой части присутствуют 
В остальных формулах, где в левой части присутствуют 

Формул приведений много и их не обязательно каждый раз выводить и запоминать.
Для этого придумали мнемоническое правило.
- Если в левой части присутствуют
и т.д. синусы, косинусы и тангенсы не меняются.
Если в левой части присутствуют 

- Знак в правой части ставим тот же, который имело исходное число в левой части, при условии
.
Существует легенда про рассеянного математика, который всё время забывал менять или не менять синус на косинус и наоборот. Он смотрел на свою сообразительную лошадь и она кивала головой вдоль той оси, где стояли числа 


Рисунок 3 – «правило лошади»
Если аргумент содержал 


Так же помните: чётные числа вида 

Если в выражении перед 
Примеры и разбор решения заданий тренировочного модуля
Пример 1: упростите выражение 


Рисунок 4 – перемещение точки по единичной окружности
Значит 

Пример 2: вычислите
Преобразуем выражение в скобке: 

$$ctg(pi-alpha)=-ctg(alpha);$$
Давайте вместо угла (alpha) возьмем какой-нибудь реальный угол. Суть от этого не изменится. Чтобы усложнить задачу, я не буду рисовать рисунок. Нарисуйте окружность сами и по пунктам сделайте пример.
Пример 7
$$cos(3pi+frac{pi}{6})=?;$$
- Угол ((3pi+frac{pi}{6})) лежит в третьей четверти. Действительно, (3pi=2pi+pi) можно представить как полный круг плюс еще половина;
- В третьей четверти косинус отрицательный. Знак минус;
- (3pi) лежит на горизонтальной оси в точке (C). Значит косинус не меняется на синус;
$$cos(3pi+frac{pi}{6})=-cos(frac{pi}{6})=-frac{sqrt{3}}{2};$$
До этого мы рассматривали примеры, когда угол (alpha) был острым. А что, если он больше (90^o)?
В этом случае нам придется сделать из него острый угол. Рассмотрим пример:
Пример 8
$$tg(frac{pi}{2}-frac{5pi}{6})=?;$$
Угол (frac{5pi}{6}) — тупой угол. Для того, чтобы воспользоваться формулой приведения, можно представить:
$$frac{5pi}{6}=pi-frac{pi}{6};$$
Подставим в исходный пример
$$tg(frac{pi}{2}-frac{5pi}{6})=tg(frac{pi}{2}-pi+frac{pi}{6})=tg(frac{pi}{6}-frac{pi}{2});$$
Угол (frac{pi}{6}) острый и теперь можно воспользоваться правилом лошади.
- ((frac{pi}{6}-frac{pi}{2})) лежит в четвертой четверти. Отмечаем (frac{pi}{6}) и по часовой стрелке вычитаем из него (frac{pi}{2});
- В четвертой четверти тангенс отрицательный;
- (frac{pi}{2}) лежит на вертикальной оси, тангенс меняется на котангенс;
$$tg(frac{pi}{2}-frac{5pi}{6})=tg(frac{pi}{6}-frac{pi}{2})=-ctg(frac{pi}{6})=-sqrt{3};$$
У любопытного читателя может возникнуть вопрос: а почему данный алгоритм называется правилом лошади? При чем тут, казалось бы, лошадь?
Лошадь, действительно, не при чем. Но дело в том, что когда вы определяете в третьем пункте, меняется ли наша тригонометрическая функция на противоположную или нет, то в случае, если дополнительный угол к (alpha) лежит на вертикальной оси, мы как бы смотрим вверх-вниз, киваем головой, как лошадь, говоря себе: «Да, меняем». Или если угол лежит на горизонтальной оси, то мы киваем влево вправо вдоль горизонтальной оси, как бы говоря: «Нет, не меняем». Такое вот странное название у правила.
26 декабря 2013
Задача. Найдите значение выражения:

И еще одна задача B11 на ту же тему — из реального ЕГЭ по математике.
Задача. Найдите значение выражения:

В этом коротком видеоуроке мы узнаем, как применять формулы приведения для решения реальных задач B11 из ЕГЭ по математике. Как вы видите, перед нами — два тригонометрических выражения, каждое из которых содержит синусы и косинусы, а также довольно зверские числовые аргументы.
Прежде чем решать эти задачи, давайте вспомним, что такое формулы приведения. Итак, если у нас есть выражения вида:
То мы можем избавиться от первого слагаемого (вида k · π/2) по специальным правилам. Начертим тригонометрическую окружность, отметим на ней основные точки: 0, π/2; π; 3π/2 и 2π. Затем смотрим на первое слагаемое под знаком тригонометрической функции. Имеем:
- Если интересующее нас слагаемое лежит на вертикальной оси тригонометрического круга (например: 3π/2; π/2 и т.д.), то исходная функция заменяется на ко-функцию: синус заменяется косинусом, а косинус — наоборот, синусом.
- Если же наше слагаемое лежит на горизонтальной оси, то исходная функция не меняется. Просто убираем первое слагаемое в выражении — и все.
Таким образом, мы получим тригонометрическую функцию, не содержащую слагаемых вида k · π/2. Однако на этом работа с формулами приведения не заканчивается. Дело в том, что перед нашей новой функцией, полученной после «отбрасывания» первого слагаемого, может стоять знак плюс или минус. Как определить этот знак? Вот сейчас и узнаем.
Представим, что угол α, оставшийся внутри тригонометрической функции после преобразований, имеет очень малую градусную меру. Но что значит «малая мера»? Допустим, α ∈ (0; 30°) — этого вполне достаточно. Рассмотрим для примера функцию:
Тогда, следуя нашим предположениям, что α ∈ (0; 30°), заключаем, что угол 3π/2 − α лежит в третьей координатной четверти, т.е. 3π/2 − α ∈ (π; 3π/2). Вспоминаем знак исходной функции, т.е. y = sin x на этом интервале. Очевидно, что синус в третьей координатной четверти отрицателен, поскольку по определению синус — это ордината конца подвижного радиуса (короче синус — это координата y). Ну, а координата y в нижней полуплоскости всегда принимает отрицательные значения. Значит, и в третьей четверти y тоже отрицателен.
На основании этих размышлений мы можем записать окончательное выражение:
Задача B11 — 1 вариант
Вот эти же самые приемы вполне подходят для решения задачи B11 из ЕГЭ по математике. Разница лишь в том, что во многих реальных задачах B11 вместо радианной меры (т.е. чисел π, π/2, 2π и т.д.) используется градусная мера (т.е. 90°, 180°, 270° и т.д.). Давайте посмотрим на первую задачу:
Сначала разберемся с числителем. cos 41° — это нетабличное значение, поэтому мы ничего не можем сделать с ним. Пока так и оставим.
Теперь смотрим на знаменатель:
sin 131° = sin (90° + 41°) = cos 41°
Очевидно, что перед нами формула приведения, поэтому синус заменился на косинус. Кроме того, угол 41° лежит на отрезке (0°; 90°), т.е. в первой координатной четверти — именно так, как требуется для применения формул приведения. Но тогда 90° + 41° — это вторая координатная четверть. Исходная функция y = sin x там положительна, поэтому мы и поставили перед косинусом на последнем шаге знак «плюс» (другими словами не поставили ничего).
Осталось разобраться с последним элементом:
cos 240° = cos (180° + 60°) = −cos 60° = −0,5
Здесь мы видим, что 180° — это горизонтальная ось. Следовательно, сама функция не поменяется: был косинус — и останется тоже косинус. Но вновь возникает вопрос: плюс или минус будет стоять перед полученным выражением cos 60°? Заметим, что 180° — это третья координатная четверть. Косинус там отрицательный, следовательно, перед косинусом в итоге будет стоять знак «минус». Итого, получаем конструкцию −cos 60° = −0,5 — это табличное значение, поэтому все легко считается.
Теперь подставляем полученные числа в исходную формулу и получаем:
Как видим, число cos 41° в числителе и знаменателе дроби легко сокращается, и остается обычное выражение, которое равно −10. При этом минус можно либо вынести и поставить перед знаком дроби, либо «держать» рядом со вторым множителем до самого последнего шага вычислений. Ответ в любом случае получится −10. Все, задача B11 решена!
Задача B14 — 2 вариант
Переходим ко второй задаче. Перед нами снова дробь:
Ну, 27° у нас лежит в первой координатной четверти, поэтому здесь ничего менять не будем. А вот sin 117° надо расписать (пока без всякого квадрата):
sin 117° = sin (90° + 27°) = cos 27°
Очевидно, перед нами снова формула приведения: 90° — это вертикальная ось, следовательно, синус поменяется на косинус. Кроме того, угол α = 117° = 90° + 27° лежит во второй координатной четверти. Исходная функция y = sin x там положительна, следовательно, перед косинусом после всех преобразований все равно остается знак «плюс». Другими словами, там ничего не добавляется — так и оставляем: cos 27°.
Возвращаемся к исходному выражению, которое требуется вычислить:
Как видим, в знаменателе после преобразований возникло основное тригонометрическое тождество: sin2 27° + cos2 27° = 1. Итого −4 : 1 = −4 — вот мы и нашли ответ ко второй задаче B11.
Как видите, с помощью формул приведения такие задачи из ЕГЭ по математике решаются буквально в пару строчек. Никаких синусов суммы и косинусов разности. Все, что нам нужно помнить — это только тригонометрический круг.
Смотрите также:
- Основное тригонометрическое тождество
- Тест к уроку «Знаки тригонометрических функций» (1 вариант)
- Схема Бернулли. Примеры решения задач
- Метод коэффициентов, часть 2
- Тест по задачам B14: средний уровень, 1 вариант
- Трубы и резервуары: разный объем
9. Преобразование числовых и буквенных выражений
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Числовые тригонометрические выражения
(blacktriangleright) Алгоритм применения формул приведения:
Шаг 1: определить, меняется ли функция на кофункцию: [sin
longleftrightarrow cos] [mathrm{tg} longleftrightarrow mathrm{ctg}]
Шаг 2: определить знак, который имеет изначальная функция, поняв, в какой четверти тригонометрической окружности находится изначальный угол (предполагая, что (alpha) – острый)
(blacktriangleright) Если угол можно представить в виде ((pi npm
alpha)), где (n) – натуральное, то функция на кофункцию не меняется.
Пример: (sin (pi npm alpha)=bigodot sin alpha), где на месте (bigodot) должен стоять знак синуса для угла ((pi npm alpha))
(blacktriangleright) Если угол можно представить в виде (left(dfrac{pi}2npm alpharight)), где (n) – нечетное число, то функция на кофункцию меняется
Пример: (sin left(dfrac{pi}2npm alpharight)=bigodot cos
alpha), где на месте (bigodot) должен стоять знак синуса для угла (left(dfrac{pi}2npm alpharight))
(blacktriangleright) Основные формулы:
[begin{array}{|ccc|}
hline sin^2 alpha+cos^2 alpha =1&& mathrm{tg} alpha cdot
mathrm{ctg}alpha
=1\ &&\
mathrm{tg} alpha=dfrac{sin alpha}{cos alpha}&&mathrm{ctg}
alpha
=dfrac{cos alpha}{sin alpha}\&&\
cos {2alpha}=cos^2 alpha — sin^2 alpha&&cos
{2alpha}=1-2sin^2
alpha\&&\
cos {2alpha}=2cos^2alpha -1&&sin {2alpha}=2sin alpha cos
alpha\
hline
end{array}]
Задание
1
#573
Уровень задания: Легче ЕГЭ
Найдите значение выражения (2sin^2 30^circ + cos^2 30^circ).
Используя основное тригонометрическое тождество, исходное выражение можно преобразовать следующим образом: [2sin^2 30^circ + cos^2 30^circ = sin^2 30^circ + (sin^2 30^circ + cos^2 30^circ) = sin^2 30^circ + 1.] Так как (sin 30^circ = 0,5), то значение исходного выражения равно (0,5^2 + 1 = 1,25).
Ответ: 1,25
Задание
2
#2958
Уровень задания: Равен ЕГЭ
Найдите значение выражения [dfrac{24}{sin^2127^circ+1+sin^2217^circ}]
Заметим, что (217^circ=90^circ+127^circ). Так как по формуле приведения (sin(90^circ+alpha)=cos alpha), то [sin
217^circ=sin (90^circ+127^circ)=cos 127^circ] Следовательно, выражение можно переписать в виде: [dfrac{24}{sin^2127^circ+cos^2127^circ+1}=dfrac{24}{1+1}=12,] так как по основному тригонометрическому тождеству (sin^2alpha+cos^2alpha=1) для любого угла (alpha).
Ответ: 12
Задание
3
#2626
Уровень задания: Равен ЕГЭ
Найдите значение выражения
[sqrt{48}-sqrt{192}sin^2dfrac{19pi}{12}]
(Задача от подписчиков.)
Заметим, что (192=48cdot 4), следовательно, (sqrt{192}=2sqrt{48}). Таким образом, выражение примет вид (по формуле косинуса двойного угла (cos2x=1-2sin^2x)):
[sqrt{48}left(1-2sin^2dfrac{19pi}{12}right)=
sqrt{48}cdot cosdfrac{19pi}6]
Т.к. (dfrac{19pi}6=dfrac{18pi+pi}6=3pi+dfrac{pi}6), то по формуле приведения:
[sqrt{48}cosleft(3pi+dfrac{pi}6right)=
sqrt{48}cdot left(-cosdfrac{pi}6right)=-sqrt{48}cdot
dfrac{sqrt3}2=-4sqrt3cdot dfrac{sqrt3}2=-6.]
Ответ: -6
Задание
4
#2434
Уровень задания: Равен ЕГЭ
Найдите значение выражения
[8left(sindfrac{pi}{12}cosdfrac{pi}{12}-1right)]
По формуле синуса двойного угла (sin2alpha=2sinalphacosalpha) имеем: (sinalphacosalpha=frac12sin2alpha). Следовательно,
[8left(dfrac12sin2cdotdfrac{pi}{12}-1right)=8left(dfrac12sindfrac{pi}6-1right)=
8left(dfrac12cdot dfrac12-1right)=-6.]
Ответ: -6
Задание
5
#2625
Уровень задания: Равен ЕГЭ
Найдите значение выражения
[dfrac{32}{sinleft(-dfrac{35pi}4right)cdot cos dfrac{25pi}4}]
(Задача от подписчиков.)
Т.к. синус — нечетная функция, то есть (sin (-alpha)=-sin
alpha), то (sinleft(-frac{35pi}4right)=-sin frac{35pi}4).
Заметим, что :
(dfrac{35pi}4=dfrac{36pi
-pi}4=9pi-dfrac{pi}4);
(dfrac{25pi}4=dfrac{24pi+pi}4=6pi+dfrac{pi}4).
Таким образом, по формулам приведения:
(sin
dfrac{35pi}4=sinleft(9pi-dfrac{pi}4right)=sindfrac{pi}4);
(cos
dfrac{25pi}4=cosleft(6pi+dfrac{pi}4right)=cosdfrac{pi}4).
Следовательно, выражение принимает вид:
[dfrac{32}{-sindfrac{pi}4cosdfrac{pi}4}=
-dfrac{32}{dfrac{sqrt2}2cdot dfrac{sqrt2}2}=-64.]
Ответ: -64
Задание
6
#581
Уровень задания: Равен ЕГЭ
Найдите значение выражения (dfrac{7sin{11^circ}}{cos{79^circ}}).
Используя формулу приведения (sin(90^circ pm alpha) = cos alpha), исходное выражение можно преобразовать следующим образом: [dfrac{7sin{11^circ}}{cos{79^circ}} = dfrac{7sin{(90^circ — 79^circ)}}{cos{79^circ}} = dfrac{7cos{79^circ}}{cos{79^circ}} = 7.]
Ответ: 7
Задание
7
#1841
Уровень задания: Равен ЕГЭ
Найдите значение выражения (dfrac{15}{sin{(-frac{20pi}{3})}
cdot cos{(-frac{43pi}{6})}}).
Используя формулы приведения, а также четность косинуса и нечетность синуса, исходное выражение можно преобразовать следующим образом: [dfrac{15}{-sin{left(6pi + frac{2pi}{3}right)} cdot
cos{left(7pi + frac{pi}{6}right)}} =
dfrac{15}{-sin{left(frac{2pi}{3}right)} cdot
(-cos{left(frac{pi}{6}right)})} =
dfrac{15}{-frac{sqrt{3}}{2} cdot ({-frac{sqrt{3}}{2})}} = 20.]
Ответ: 20

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

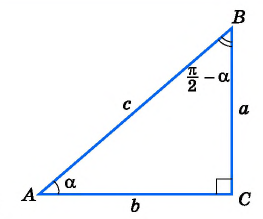
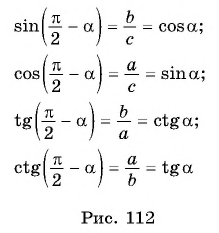
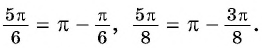
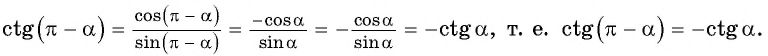
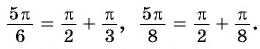
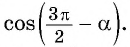
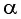 — острый, то —
— острый, то — 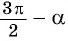 — угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».
— угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».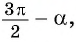 то название функции «косинус» нужно поменять на «синус». Таким образом, получим:
то название функции «косинус» нужно поменять на «синус». Таким образом, получим: 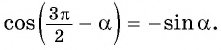
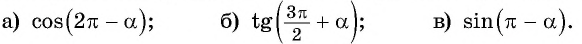
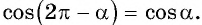
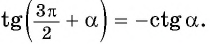

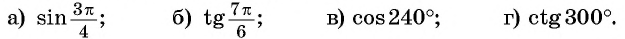
 угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».
угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».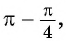 то название функции «синус» не меняется. Значит,
то название функции «синус» не меняется. Значит, 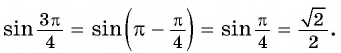


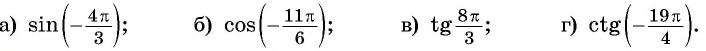
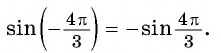
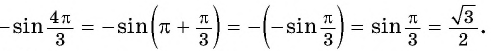
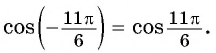
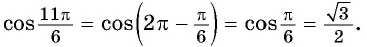
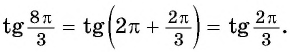
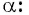
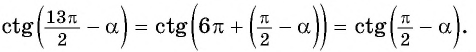
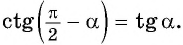
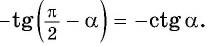
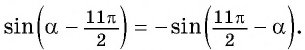
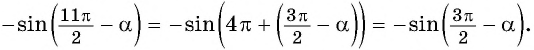
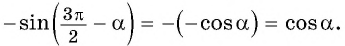

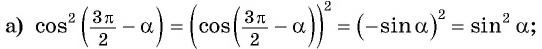
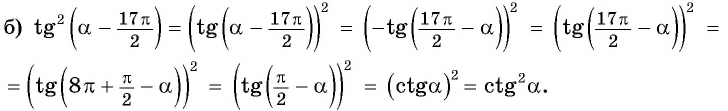

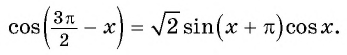
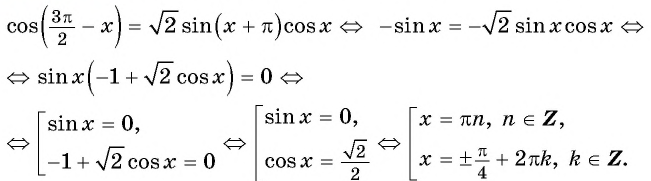
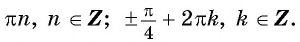







 и т.д. синусы, косинусы и тангенсы не меняются.
и т.д. синусы, косинусы и тангенсы не меняются.  .
.