Урок
математики
3 класс
Тема: «Площадь
прямоугольника».
Тип урока: урок открытия нового знания
Форма
урока: урок – исследование.
Цель
урока: посредством
формирования умения вычислять площадь прямоугольника с использованием формулы
развивать у учащихся навыки решения простых задач на вычисление площади
геометрической фигуры.
Планируемые
образовательные результаты учащихся
Личностные:
• способность к
милосердию (желанию помочь ближнему);
• опыт
самодисциплины и самоорганизации;
• интерес к
интеллектуальному творчеству.
Метапредметные:
• сотрудничество с
одноклассниками в решении учебных задач;
• освоение
метапредметных понятий «вычисление», «величина»;
• опыт
осуществления логических операций анализа, синтеза, сравнения.
Предметные:
• умение
вычислять площадь прямоугольника новым способом с использованием формулы;
• расширение опыта
решения простых задач на нахождение площади геометрической фигуры.
Используемые
технологии:
—
проблемно – поисковый метод;
— интерактивные
технологии (работа в группе, в паре);
— ИКТ.
Ход урока:
1.
Организационный
момент.
Учитель: — Добрый день, ребята! Проверьте все ли у вас готово, чтобы начать урок
математики!
2. Мотивация (самоопределение)
к учебной деятельности.
Учитель: Сегодня мы
с вами отправимся в лес… на охоту. Удивились? Да, да! Не волнуйтесь, мы никого
обижать не будем. Мы отправимся на «охоту за пятерками», а попадать в цель нам
помогут наши знания.
Ø Обсуждаем правила
работы на уроке.
Учитель: — Друзья,
чтобы охота прошла удачно, предлагаю выработать «Правила охотника за
пятерками». Эти правила помогут нам в работе на уроке.
|
Поднимать руку на уроке выше. |
|
|
Приходить на помощь другу. |
|
|
Узнать, |
|
|
На |
|
|
Внимательно |
|
|
Ходить |
|
|
Уважать |
|
|
Вешать всегда портфель на крючок. |
Задание: Прочитайте список
правил. Выберите из этого списка те правила, которые важны для успешной
работы на уроке.
Лист «Мои действия
на уроке»
Учитель: Какие
правила выбрали?
— Ребята! Не
забывайте эти правила и тогда пятерки точно будут в ваших тетрадочках.
Учитель:
—
Ну, а теперь самое время выдать вам «Билеты охотника за пятерками».
(Учащимся
выдаются «листы самооценки», которые они заполняют по ходу работы на
уроке).
Я желаю вам сегодня попадать только в цель. Итак, в путь!
3.Актуализация знаний и фиксирование
индивидуального затруднения в пробном действии (7 минут)
Учитель: — А
начнем нашу «охоту» с разминки. Как мы уже сказали, в сегодняшней охоте
нам помогут знания. Давайте определим, знания по какой теме нам сегодня
пригодятся?
Ø
Индивидуальная
работа.
Задание 1: Найти
значения выражений. Выберите из ответов только чётные числа. Расположите их в
порядке возрастания и составьте ключевое слово.
|
9 • 4 = Ь |
7 • 2 = О |
|
6 • 4 = Д |
3 • 9 = Е |
|
32 : 4 = Л |
7 • 3 = М |
|
2 • 9 = А |
16 : 8 = П |
|
15 : 5 = Р |
4 • 4 = Щ |
36,
24, 8, 18, 14, 2, 16.
2,8,14,16,18,24,36.
Ключевое слово
урока: ПЛОЩАДЬ
Учитель: —
Верно, сегодня мы вновь будем работать по теме «Площадь».
Учитель: — Что мы
уже узнали на уроках математики про площадь?
— Это величина, которая
указывает, сколько места занимает фигура на плоскости.
— Ее можно
измерять, сравнивать.
— Единицы
измерения площади: кв.см., кв. дм., кв. м)
На доске учащиеся составляют
кластер «Площадь».
Учитель:
—
В «Билете охотника» отметьте, как поразили вы цель на разминке
(листы самооценки)
Учитель:
— А вот мы уже с вами в лесу, здесь и будет настоящая «охота за пятерками». Как я
сказала, никого обижать мы не будем, а вот в помощи не откажем. На нашем пути
повстречалась Баба Яга.
Ø
Проблемная ситуация.
Задание 2.
Задача: Место,
где стояла избушка Бабы Яги затопило. Баба Яга
обнаружила два участка земли для нового места жительства. Она хотела бы
выбрать участок с большей площадью. Какой же участок больше?
Учитель.
– Ну, что ж «охотники» пора браться за работу. У вас на столе
«макеты» этих земельных участков.
Работа
в парах. У учащихся по 2 прямоугольника.
Синий прямоугольник – 4
см • 8 см
Зеленый прямоугольник –
3 см • 9 см
Учитель: — Что можете
сказать про фигуры? Определите сходство.
(Это
прямоугольники, они имеют четыре стороны, 4 прямых угла, стороны
противоположные равны).
Учитель:
— Назовите различия. ( У них разная длина, ширина, площадь)
Учитель:
— Как
узнать, какой прямоугольник больше? (Надо сравнить их площади)
Учитель:
— Давайте уточним тему урока. («Площадь прямоугольника»).
5. Построение проекта выхода из затруднения.
Учитель:
— Сравните площади прямоугольников на глаз. Площадь, какого прямоугольника
больше, какого — меньше? (Нереально
сравнить на глаз, при наложении фигуры не совпадают ни по длине, ни по ширине)
Учитель:
Как же узнать, площадь какого прямоугольника больше? (Надо найти их
площадь). Каким способом воспользуемся? (Разбить
прямоугольник на квадраты со стороной 1 см, подсчитать их количество и сравнить
площади).
Ø Практическая
работа. Работа в парах.
Задание
3. Учащиеся должны с помощью мерки (кв.см), разбить прямоугольник
зеленого цвета на квадраты и сосчитать их.
Вывод: Что
можете сказать? (Требуется много
времени, чтобы разделить прямоугольник на квадраты и пересчитать их).
Какие возникают
вопросы?
1) Как
быстрее найти площадь прямоугольника?
2) Как узнать
площадь прямоугольника, не разбивая на квадратики фигуру?
Учитель: — Какую
ставим мы сегодня цель?
Цель: Научиться
находить площадь прямоугольника новым способом.
5.Реализация построенного проекта. Совместное открытие
новых знаний.
Учитель:
— Ребята, предлагаю найти способ вычисления площади прямоугольника, который
позволил бы выполнить эту работу быстрее. Возьмем зеленый прямоугольник.
—
Уважаемые «охотники», кто самый наблюдательный? Что интересного
заметили?
1) Пересчитаем
квадраты, расположенные в первом ряду по длине прямоугольника. (их 9) Если
сторона квадрата 1 см, значит длина прямоугольника 9 см. Возьмем линейку
и проверим.
2) Определим
сколько таких рядов. (их 3) Значит, ширина прямоугольника 3 см.
Выполним проверку с помощью линейки.
3) Мы
по 9 взяли 3 раза. Надо 9 умножить на 3. Значит, длину умножили на ширину.
Площадь равна 27 кв.см.
Вывод:
Длина прямоугольника показывает, сколько кв. см помещается в строке, а ширина — в
столбце.
Знакомство
с правилом: «Чтобы найти площадь прямоугольника, надо длину умножить на
ширину».
Учитель:
Обозначим площадь буквой S, длину буквой a, ширину
– буквой в и запишем правило в виде формулы
6. Применение
знаний с проговариванием во внешней речи.
Задание 4. —
Вычислите площадь синего прямоугольника по формуле. Чем воспользуетесь
при нахождении площади? (Линейкой)
(Учащиеся
вычисляют площадь прямоугольника самостоятельно. Желающие записывают решение на
доске. Затем объясняют, как решали задачу.)
Решение: а = 8
см, в = 4 см 8 • 4 = 32 кв.см.
Учитель: — Так
какой участок лучше выбрать Яге? (Площадью 32 кв. см)
Итог. — Какое
открытие мы сделали на этом этапе урока?
— Мы узнали, новый
способ нахождения площади прямоугольника.
— Мы открыли
формулу нахождения площади прямоугольника.
Учитель:
— Предлагаю дополнить наш кластер. (Дети добавляют в кластер табличку с
формулой площади)
Учитель:
—
В «Билете охотника» отметьте, знаете ли вы, как найти площадь прямоугольника с
помощью формулы. (Листы самооценки)
Ø Физминутка.
«Мы чертёжники».
Начертите
глазами луч (на стене найдите точку и отправьте луч далеко сквозь окно),
кончиком носа — окружность, правой рукой — прямой угол, а левой — острый!
Чертите аккуратно! Левой ногой — квадрат, а правой прямоугольник.
Ø Составление
алгоритма нахождения площади прямоугольника.
Учитель – Ребята!
Предлагаю для всех жителей леса составить памятку «Как найти
площадь прямоугольника»
Задание 5. (в
группах) Составьте план своих действий. Для этого выберите
только необходимые действия и расставьте их по порядку.
|
1 |
Измерить длину прямоугольника |
|
Надо разбить прямоугольник на квадратики |
|
|
2 |
Измерить ширину прямоугольника |
|
Надо нарезать мерки – квадратики |
|
|
Надо найти сумму длин сторон прямоугольника |
|
|
3 |
Надо длину умножить на ширину. |
Учитель: — Ребята, а
зачем надо уметь находить площадь прямоугольника? (поклеить
обои, покрасить пол, поклеить потолок).— В «Билете
охотника» отметьте, знаете ли вы, алгоритм нахождения площади прямоугольника. (Листы
самооценки)
7. Включение
в систему знаний и повторение.
Учитель: — Что ж продолжим нашу «охоту за пятерками». На нашем пути лесные
жители: Гномы. Им тоже нужна помощь «охотников за пятерками». Прочитайте
задание и подумайте, кому вам по силам помочь справиться с трудностями.
Задание . Лесным гномам выделили под строительство домов одинаковые
участки. Помоги гномам найти участки с одинаковой площадью. Раскрась их
красным цветом. (Проведи необходимые измерения и вычисли площадь фигур,
воспользовавшись формулой).
 |
|||
 |

номерами 1 и 5. Решение: 3 2= 6 кв. см.
Учитель: Молодцы, ребята! Правильно выбрали участки!
—
Скажите, а людям каких профессий нужно хорошо знать математику,
производить расчёты, находить площадь фигур? (архитектору, конструктору,
инженеру, строителю)
Предлагаю
вам побыть в роли строителей. Постройте дом для Гномов, пользуясь
математическими знаниями. (Дети из цветного
картона строят у доски дом, работа в группах по карточкам)
1.
Кто знает, с чего начинается
строительство дома? (Со строительства
фундамента – 1 группа)
Задача.
Длина
прямоугольника 8см, а ширина в 2 раза меньше. Чему равна площадь
прямоугольника? (32 см2).
2.
Следующий этап в строительстве дома.
(Возведение стен – 2 группа)
—
Выразить в указанных единицах измерения
2
дм 4 см = …см 78 см = …дм …см
5
см 6мм = … мм 39 дм = …м …дм
3.
Следующий этап в строительстве дома.
(Возведение крыши – 3 группа)
—
Какой формы крыша? (Треугольной)
—
Найти периметр треугольника — крыши.
4.
В доме должны быть окна. (Окна – 4 группа)
—
Какую форму имеет окно (квадратную)
—
Найдите площадь окна, если сторона квадрата 2 см.
Доп-но:
— Почему вы площадь квадрата нашли таким же способом? (Квадрат – это
прямоугольник с равными сторонами)
—Какая
должна быть формула? (S = а ∙ а)
—
Что вы скажите о множителях? (одинаковые)
5.
Возведем печь. (Печь – 5 группа)
—
Какую форму имеет печная труба? (прямоугольную)
—
Найдите площадь печной трубы, если ширина 3 см, а длина 1 см.
6.
Сделаем ворота.
–
Увеличить в 7 раз
4,
3 ,6, 10, 9.
Дом
построен! Легко ли быть строителем? Пригодятся ли математические знания
строителям? У кого из вас возникло желание быть строителем?
Учитель: — В
«Билете охотника» отметьте, умеете ли вы решать задачи на вычисление площади
прямоугольника, работать в парах, группах. (Листы самооценки)
8. Рефлексия учебной деятельности на уроке.
Самооценка.
Учитель:
— Ребята! Пора заканчивать «охоту за пятерками».
— Какие новые
знания вам помогли сегодня выйти из леса?
Где мы сможем применить эти знания и умения?
Закончите
предложения:
Я знаю… Я
могу… Я умею…
Учитель: —
Посмотрите в свои «Билеты настоящего охотника». Выполняя, какие задания вам
удалось попасть точно в цель? Как вы думаете, кто сегодня получит за урок
«пятерку»? (Ребята, которые сегодня попадали точно в цель во время всей
охоты). Поздравляем настоящих «охотников за пятерками»!
Домашнее
задание.
Творческое задание. Придумать задачу на нахождение площади прямоугольника для
своего друга.
Обновлено: 26.05.2023
Памятка поможет запомнить формулы периметра, площади фигур.
| Вложение | Размер |
|---|---|
| perimetr_i_ploshchad.docx | 13.16 КБ |
Предварительный просмотр:
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Периметр – сумма длин всех сторон фигуры.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
По теме: методические разработки, презентации и конспекты
Цели:развивать логическое мышление, пространственное воображение средствами изучения симметричных фигур и решение текстовых задач.Совершенствовать навыки табличного умножения на 8, на 9.Задачи: — сфор.
Урок математики во 2кл. «Площадь фигур. Единицы площади»
Урок по программе «Начальная школа 21 века» во 2 классе.
Конспект урока по математике 2 класс на тему «Площадь фигур. Сравнение площадей.»
Урок разработан по программе «Школа 2100», первый при изущении темы: «Площадь фигур».
Тип урока: ознакомление с новым материалом. Цель: познакомить с новой величиной – площадью фигуры.
Площадь фигуры. Сравнение площадей фигур.
Открытый урок математики в з классе по программе «Школа России» (ФГОС) с использованием ИКТ. Материал содержит конспект урока и приложения к уроку.
Памятка по математике.4 класс.Алгоритм нахождения площади фигуры с помощью палетки.
Памятка по математике.4 класс.Алгоритм нахождения площади фигуры с помощью палетки.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
ПЕРИМЕТР ПРЯМОУГОЛЬНИКА И КВАДРАТА.
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра прямоугольника
а = 3 см
в = 5 см
Р= ?
Р = 2 ∙ (а +в)
Ответ: периметр равен 16 см
Нахождение периметра квадрата
а = 3 см
Р = а ∙ 4
Ответ: периметр равен 12 см
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА И КВАДРАТА.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади прямоугольника и квадрата
Прямоугольник
S = а · b
S = 6 ∙ 2 = 12 см 2
Ответ: площадь равна 12 см2
S = а · а
S = 4 ∙ 4 = 16 см 2
Ответ: площадь равна 16 см2
ПЕРИМЕТР ПРЯМОУГОЛЬНИКА И КВАДРАТА.
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра прямоугольника
а = 3 см
в = 5 см
Р= ?
Р = 2 ∙ (а +в)
Ответ: периметр равен 16 см
Нахождение периметра квадрата
а = 3 см
Р = а ∙ 4
Ответ: периметр равен 12 см
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА И КВАДРАТА.
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади прямоугольника и квадрата
Прямоугольник
S = а · b
S = 6 ∙ 2 = 12 см 2
Ответ: площадь равна 12 см2
S = а · а
S = 4 ∙ 4 = 16 см 2
Ответ: площадь равна 16 см2
- подготовка к ЕГЭ/ОГЭ и ВПР
- по всем предметам 1-11 классов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- ЗП до 91 000 руб.
- Гибкий график
- Удаленная работа
Дистанционные курсы для педагогов
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 591 272 материала в базе
Материал подходит для УМК
Площадь. Единицы площади
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
Свидетельство и скидка на обучение каждому участнику
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
- 25.11.2021 760
- DOCX 36.9 кбайт
- 55 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Карачева Марина Васильевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
40%
- Подготовка к ЕГЭ/ОГЭ и ВПР
- Для учеников 1-11 классов
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В приграничных пунктах Брянской области на день приостановили занятия в школах
Время чтения: 0 минут
Студенты российских вузов смогут получить 1 млн рублей на создание стартапов
Время чтения: 3 минуты
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Время чтения: 0 минут
Курские власти перевели на дистант школьников в районах на границе с Украиной
Время чтения: 1 минута
Университет им. Герцена и РАО создадут портрет современного школьника
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Вся фигура состоит из 8 квадратов со стороной 1 см каждый.
Площадь одного такого квадрата называют квадратным сантиметром и записывают: 1 см 2 .
Площадь всей фигуры 8 см 2 .
Запомните!
Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.
В математике для нахождения площади геометрических фигур используют специальные формулы, в которых площадь обозначается заглавной латинской буквой S.
Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.
Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата, равна 1 м, то его площадь равна 1 квадратному метру (1 м 2 ); если длина его стороны равна 1 см, то его площадь равна 1 квадратному сантиметру (1 см 2 ).
Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.
Как перевести квадратные единицы
Рассмотрим квадрат со стороной 1 см.
Его площадь равна:
S = 1 см · 1 см = 1 см 2 .
Рассмотрим квадрат со стороной 1 м.
Его площадь равна:
S = 1 м · 1 м = 1 м 2 .
Известно, что: 1 м = 100 см.
1 м 2 = 1 м · 1 м = 100 см · 100 см = 10 000 см 2 .
Увеличим сторону квадрата равную 1 м в 10 раз. Получим квадрат со стороной 10 м.
Площадь такого квадрата называют ар или сотка.
S = 10 м · 10 м = 100 м 2 .
В одном аре — сто квадратных метров.
1 ар (сотка) = 100 м 2 .
Чтобы выразить ар в cм 2 , вспомним, что 1 м 2 = 10 000 см 2 .
Значит: 1 ар (сотка) = 100 м 2 = 100 · 10 000 см 2 = 1 000 000 см 2
Увеличим сторону квадрата равную 10 м в 10 раз. Получим квадрат со
стороной 100 м.
Площадь такого квадрата называют гектар. Сокращенно га. Но при произношении вслух наименование проговаривается полностью.
Выразим гектар в квадратных метрах.
1 га = 100 м · 100 м = 10 000 м 2
Теперь определим, сколько в одном гектаре аров.
Значит: 10 000 м 2 : 100 м 2 = 100 (ар)
Для измерения больших площадей, например, территорий государств, материков используютквадратный километр. То есть квадрат со стороной 1 км и площадью 1 км 2 .
1 км 2 = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м 2 .
Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.
Таблица переводов квадратных единиц
Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.

З адачи на кратное сравнение чисел.
Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее.
8:2=4 (раза)
8 больше, чем 2 в 4 раза
2 меньше, чем 8 в 4 раза
Порядок действий.
В выражениях без скобок сначала выполняется умножение и деление, а затем сложение и вычитание.
Умножение и деление, а также сложение и вычитание между собой выполняются по порядку, так как это действия одной ступени:
94 — 2 . 2 + 3 – 25 : 5 = 94 – 4 + 3 – 5 = 88
В выражениях со скобками сначала выполняются все действия в скобках, затем действия умножения и деления и только после этого остальные действия по порядку:
22 — (15 + 3) : 6 + 7 . (11- 7) + 5 = 22 – 18 : 3 + 7 . 3 + 25 = 22 – 6 + 21 + 5 = 42
Если в выражениях одни скобки находятся внутри других, сначала выполняют действия во внутренних скобках.
Периметр геометрической фигуры – это сумма длин всех сторон фигуры.
Единицы периметра: мм, см, дм, м
I способ: (4 + 3) . 2 = 7 . 2 = 14 см (Сложить длину и ширину прямоугольника и взять эту сумму 2 раза)
II способ: 4 . 2 + 3 . 2 = 8 + 6 = 14 см (Длину взять 2 раза, ширину взять 2 раза, полученные суммы сложить.)
П ериметр квадрата
У квадрата длина равна ширине: 3см + 3 см + 3 см + 3 см = 3 см х 4 = 12 см
Найти периметр квадрата, значит, его длину умножить на 4. 3 . 4=12 см
Единицы площади: мм 2 , см 2 , дм 2 , м 2
1 см 2 — это квадрат, длина стороны которого равна 1 см.
1 дм 2 – это квадрат, длина стороны которого равна 1 дм.
1 м 2 – это квадрат, длина стороны которого равна 1 м.
Площадь прямоугольника.
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину или наоборот. 4 . 3 = 3 . 4 = 12 см 2
Площадь квадрата.
3 . 3 = 9 см 2
1 м 2 = 100 дм 2 = 10000 см 2
1дм 2 = 100 см 2 = 10000 мм 2
1см 2 = 100 мм 2
на 2 больше
надо + 2
на 2 меньше
надо – 2
в 2 раза больше
надо . на 2
в 2 раза меньше
надо : на 2
Единицы массы
1 т = 10 ц = 1000 кг
1 ц = 100 кг
1 кг = 1000 г
Деление с остатком: 28:3.
Надо 28 разделить на 3. Самое большое число, которое делится на 3 без остатка и близкое к 28 – это 27. Делим 27 на 3, получаем 9. Мы разделили 27 на 3, а надо разделить 28. Узнаем, сколько единиц не разделили. Для этого из 28 вычтем 27, получится 1. Значит, 28 : 3=9 (ост.1).
Делаем проверку: 9 . 3 + 1=28. Остаток должен быть меньше делителя. Остаток 1 меньше делителя 3. 28 : 3 = 9 (ост.1)
Окружность – линия, которая является границей круга.
Центр окружности – точка, вокруг которой чертят окружность.
Отрезки АМ и АС – радиусы окружности.
Если вершиной угла является центр окружности, угол называется центральным углом.
Угол МАС или САМ– центральный угол.
Сторонами центрального угла являются радиусы окружности.
Радиусы одной окружности равны между собой: АМ = АС.
Градус – мерка для измерения углов.
Угол величиной в один градус записывают так: 1 0 .
Если угол разделить на 360 равных углов, то получится угол в 1 градус.
Транспортир – прибор для измерения углов.
Распределительное свойство умножения относительно сложения: при умножении суммы на число значение выражения не изменится, если умножить на него каждое слагаемое и полученные результаты сложить.
Умножение суммы на число: (4+3) . 2.
(4 + 3) . 2 = 7 . 2 = 14
(4 + 3) . 2 = 4 . 2 + 3 . 2 = 8 + 6 = 14
Пользуясь этими способами умножения суммы на число, находим значения следующих выражений:
23 . 2 = (20 + 3) . 2 = 20 . 2 + 3 . 2 = 40 + 6 = 46
17 . 3 = (10 + 7) . 3 = 10 . 3 + 7 . 3 = 30 + 21 = 51
Умножение числа на сумму: 7 . (6 + 2).
7 . (6 + 2) = 7 . 8 = 56
7 . (6 + 2) = 7 . 6 + 7 . 2 = 42 + 14 = 56
Пользуясь этими способами умножения числа на сумму, находим значения следующих выражений:
4 . 15 = 4 . (10 + 5) = 4 . 10 + 4 . 5 = 40 + 20 = 60
3 . 28 = 3 . (20 + 
Деление суммы на число: (6+4) : 2.
(6 + 4) : 2 = 10 : 2 = 5
(6 + 4) : 2 = 6 : 2 + 4 : 2 = 3 + 2 = 5
При делении суммы на число значение выражения не изменится, если разделить на него каждое слагаемое и полученные результаты сложить.
Пользуясь этими способами деления суммы на число, находим значения следующих выражений:
28 : 2 = (20 + 
3 6 : 2 = (20 + 16) : 2 = 20 : 2 + 16 : 2 = 10 + 8 = 18
Чтобы найти общие решения двух неравенств их объединяют фигурной скобкой и называют системой неравенств.
система неравенств
Можно записать одно сложное (двойное) неравенство: 17 a
1 м = 10 дм = 100 см
1 дм = 10 см = 100 мм
Единица вместимости – литр (л)
Масса 1 л воды равна 1 кг
1 ч = 60 мин = 3600 с
1 неделя = 7 дней
1 месяц = 28 (29), 30, 31 день
1 год = 365 (366) дней
Цена. Количество. Стоимость.
Цена = стоимость : на количество (ц = с : к)
Количество = стоимость : на цену (к = с : ц)
Стоимость = цену . на количество (с = ц . к)
Скорость. Время. Расстояние.
Расстояние = скорость . на время (s = v . t)
Время = расстояние : на скорость (t = s : v)
Скорость = расстояние : на время (v = s : t)
Единицы измерения расстояния: км, м
Единицы измерения времени: ч, мин, с
Единицы измерения скорости: км/ч, м/мин, м/с, км/ч
2м/с – читаем как 2 метра в секунду.
Числовой луч – наглядное изменение расположения чисел относительно друг друга. Он напоминает линейку с одинаковыми мерками.
Мерку, которую выбирают для построения числового луча, называют единичным отрезком.
Координата – число, которое соответствует точке числового луча.
Координату точки на числовом луче записывают так: М (3, Е (6), У (5)…
Числовой луч чаще называют координатным лучом.
Дробные числа
Вместо слова половина часто говорят одна вторая. Одна вторая – это дробное число или дробь: ½.
Знаменатель – (число под чертой) показывает, на сколько частей разделили.
Числитель – (число над чертой) показывает, сколько таких частей взяли.
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
Если истинные размеры изменены, то изображение выполнено в масштабе.
1:3 –в масштабе один к трём (размеры уменьшены в 3 раза).
Класс единиц и класс тысяч
10 сотен образуют новую единицу счёта – тысячу: 1000
Класс единиц – единицы (единицы 1 разряда), десятки (единицы второго разряда), сотни (единицы третьего разряда).
Класс тысяч – тысячи (единицы четвёртого разряда), десятки тысяч (единицы пятого разряда), сотни тысяч (единицы шестого разряда).
Памятка в помощь ученикам начальной школы для вычисления площади и периметра для прямоугольника и квадрата. Лист с формулами и чертежами нужно распечатать и дать ребёнку.
Всего 14 карточек по этой теме. Они позволят проверить полученные знания на вычисление площадей прямоугольника, используя разные единицы площади.
Итоговый тест по математике проводится в 3 классе в конце учебного года с целью проверки знаний.
Карточки с разными примерами на знание таблицы умножения на 9.
Восемь карточек на проверку знания таблицы умножения и деление на число 8.
Карточки с примерами на умножение и деление чисел на 7 для учеников 3 класса позволят проверить как ученики знают таблицу умножения.
Читайте также:
- Сценка про папу который пришел в детский сад
- Не хожу на родительские собрания в школе форум
- Тени на мосту айои краткое содержание
- Справка итоги 1 полугодия в школе
- Беседа трех святителей краткое содержание
Тип урока: урок закрепления изученных знаний, урок знакомства с новой темой и мультимедиа-ресурсом.
Вид урока: проблемный урок с элементами исследования, с элементами игровой деятельности.
Используемые педагогические технологии:
- проблемное обучение;
- личностно-ориентированное обучение;
- традиционная педагогическая технология с элементами развивающей;
- информационно-коммуникационная технология;
- элементы технологии организации исследовательской деятельности обучающихся и элементы дифференцированного подхода к обучению;
Методы обучения: проектно-исследовательский метод, методы наблюдения, конструирования, беседы, тестирования, контроля и самоконтроля. Метод стимулирования и авансирования, эмоционального воздействия, наглядности.
Материалы и оборудование: Учебник для общеобразовательных учреждений (в двух частях) под редакцией М.И. Моро, М.А. Бантовой, Г.В. Бельтюковой, С.И. Волковой, С.В. Степановой «Математика», 3 класс, серия «Школа России». Издательство «Просвещение», 2010, С. 55. Рабочие тетради; детские ноутбуки; медиапроектор, компьютер, экран; тесты, карточки с формулами нахождения периметра и площади прямоугольника, индивидуальные геометрические фигуры и картинка с «Карандашом», палетки.
Продолжительность: урок 45 минут.
Авторский медиапродукт: презентация к уроку (25 минут).
Цель урока: Создание условий для становления и развития психических функций, способностей, мотивационных установок, творческого исследовательского мышления через вовлечение учащихся в активную учебно-исследовательскую деятельность на уроке математики.
Задачи урока:
- Продолжить формирование у детей УУД.
- Развивать и совершенствовать критическое мышление учащихся, морально-волевые качества, коммуникативные умения, умения контролировать свое поведение в учебных ситуациях.
- Воспитывать толерантное отношение друг к другу.
Межпредметные связи: урок окружающего мира, урок русского языка и технологии.
Обучающиеся по итогам урока должны:
- Иметь представления о площади, способах измерения и сравнения площадей фигур: визуально, наложением, с использованием мерок, палетки.
- Знать правило нахождения площади прямоугольника и формулу её нахождения, единицы измерения площади фигур (см²).
- Уметь сравнивать фигуры на глаз, наложением, с использованием палетки. Уметь решать задачи на нахождение площади прямоугольника, пользоваться формулой S=a•b
Этапы урока:
- организационный.
- устный счёт (повторение таблицы умножения на 8 и 9);.
- постановка проблемы: так какая тема сегодняшнего урока;
- актуализация знаний и входная диагностика;
- сообщение темы и целей урока;
- знакомство с различными значениями слова «площадь»;
- способы измерения и сравнения площади фигур;
- физ. минутка (релаксация для глаз);
- единицы измерения площади (по гиперссылке вернуться к слайду 18, затем по гиперссылке возвратиться к слайду 22);
- постановка проблемы: есть ли такие единицы измерения площади, как 1мм², 1дм², 1м², и зачем они нужны;
- постановка проблемы: площадь какой фигуры больше;
- работа в парах (индивидуальные геометрические фигуры);
- знакомство с палеткой;
- нахождение площади прямоугольника;
- знакомство с формулой нахождения площади прямоугольника;
- закрепление изученного материала;
- физ. минутка (релаксация для глаз);
- работа с учебником (взаимопроверка);
- итоговая диагностика (работа с детскими ноутбуками);
- подведение итогов;
- рефлексия.
Ход урока
 |
Слайд 1 Орг. момент Учитель читает стихи про карандаш. |
 |
Слайды 2-6 Устный счёт «Собери букет», «Испеки пирог». (таблица умножения на 8, 9) |
 |
Слайд 7 – Ребята, какая я невнимательная, забыла написать тему сегодняшнего урока. Как быть? Слайд 8 |
 |
– Прочитайте задание на слайде. – Открываем тетрадь. Прочитайте внимательно задания теста. – Выполните все задания теста. Время – 5минут! – Так какая тема сегодняшнего урока? |
 |
Слайд 9 – Совершенно верно, тема сегодняшнего урока: «Площадь прямоугольника». – Перед нами стоят такие задачи: 1) Выяснить значения слова площадь; 2) Повторить способы сравнения площади фигур и познакомиться с новым способом; 3) Сформулировать правило нахождения площади прямоугольника и вывести формулу; 4) Уметь решать задачи на нахождение площади прямоугольника. |
 |
Слайд 10 – Какие ассоциации у вас возникают при слове «площадь»? Что сразу приходит на ум? – Пожалуйста, поделитесь своими мыслями. Учитель заслушивает все варианты ответа. (площадь в центре города, строительная площадка, площадка во дворе для игр, спортивная площадка, лестничная площадка, площадь обоев, площадь стола, площадь футбольного поля, площадь поля, засеянного какими-либо культурами и др.) |
 |
Слайд 11 – Посмотрите, что изображено на слайде? – Да, это Красная площадь – центральная площадь Москвы. Возникновение Красной площади относится к концу 15 века, когда по приказу царя Ивана III были снесены деревянные постройки вокруг Кремля, угрожавшие постоянными пожарами. На их месте была организована площадь для мелкой торговли. Первоначально она так и называлась – Торговая. Красной площадь стали называть только в 17 веке. – А это что за площадь? Это одна из центральных площадей города Санкт-Петербурга. Она называется Сенатская площадь. Сенатская площадь была названа так после размещения на ней правительственного учреждения Сената. Сенатская площадь является одной из самых старых площадей Санкт-Петербурга. – Все узнали центральную площадь нашего города. Кто знает, как она называется? Совершенно верно, это площадь Ленинского комсомола. – Почему её так назвали? В каком году была построена площадь? Какие важные здания находятся на этой площади? – Обратитесь за помощью к родителям, бабушкам и дедушкам, справочной литературе, сети Интернет, чтобы найти ответы на эти вопросы. А на ближайшем уроке окружающего мира мы вернёмся к этой теме. |
 |
Слайд 12 – Давайте прочитаем значения слова «площадь». Два ученика по слайду зачитывают по просьбе учителя. |
 |
Слайд 13 – Заглянем в толковый словарь русского языка В.И. Даля. – Внимательно прочитайте значение слова «площадь». Вдумайтесь в смысл! |
 |
Слайд 14 – Какие способы измерения площади фигур вам известны? Учитель заслушивает все варианты ответа. |
 |
Слайд 15 – Действительно, существует несколько способов: визуально, т.е. на глаз, способ наложения фигур и с использованием мерок. |
 |
Слайд 16 – Сравните на глаз площади треугольников. Что вы можете о них сказать? – Какова площадь круга: больше или меньше? |
 |
Слайд 17 – Что можете сказать о площади квадратов? – Почему площадь зелёного квадрата меньше? (полностью помещается в розовом квадрате) – Можно ли утверждать, что площадь треугольника больше площади самого маленького квадрата? – Почему? |
 |
Слайд 18 – Ещё один способ: подсчёт количества мерок, уложившихся в той или иной фигуре. – Сколько мерок уложилось в жёлтом прямоугольнике? – Площадь какого прямоугольника больше? – Что получится, если я буду использовать разные мерки для сравнения площадей этих прямоугольников: квадраты, круги, треугольники, овалы и т.д.? |
 |
Слайд 19 – Прочитаем вывод хором! Учитель говорит о том, что пришло время отдохнуть, напоминает о взаимной вежливости. |
 |
Слайд 20 Физ.минутка |
 |
Слайд 21 Учитель зачитывает по слайду. Гиперссылка = нажать на слово «единицы». – Если данная мерка – это один квадратный сантиметр, то чему тогда равна площадь каждого прямоугольника? (ответы детей)Гиперссылка = нажать на слово «мерка». |
 |
Слайд 22 – Есть ли такие единицы измерения площади, как квадратный дециметр, квадратный метр?Учитель заслушивает все варианты ответов. – Об этом мы узнаем на ближайших уроках математики. |
 |
Слайд 23 лежат конверты. Откройте их, достаньте геометрические фигуры. – Прочитайте задание на слайде. – Работа в парах: нужно сравнить площади этих фигур. – Как это сделать? Время для работы – одна минута! |
 |
– Ребята, вы молодцы! – Есть такое приспособление в математике!Слайд 24 Учитель зачитывает по слайду, раздаёт всем палетки. – Измерьте при помощи палетки площади данных фигур. – Что вы заметили? |
 |
Слайд 25 Дети сравнивают свои ответы с данным. – Молодцы! |
 |
Слайд 26 – Прочитайте вывод. |
 |
Слайд 27 – Как найти площадь прямоугольника? |
 |
Слайд 28 – Сначала нужно измерить стороны прямоугольника, т.е. узнать длину и ширину. – Потом перемножить полученные числа. |
 |
Слайд 29 – Прочитайте «про себя» правило нахождения площади прямоугольника. – Постарайтесь запомнить его, а дома выучить наизусть. |
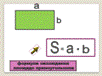 |
Слайд 30 – Постарайтесь запомнить эту формулу. – Эта формула будет находиться здесь, на стенде.– На уроках мы будем постоянно к ней обращаться. |
| Слайды 31 – 34 Применение формулы – устные задания. Закрепление изученного материала. |
|
 |
Слайд 35 – Пришло время отдохнуть! |
 |
Слайд 36 Дети работают по учебнику самостоятельно, используя формулы на слайде. – Ребята, у вас 3 минуты! – Поменяйтесь тетрадями (взаимопроверка). |
 |
Слайд 37 – Проверьте, пожалуйста! |
 |
Слайд 38 Работа с ноутбуками – Тестовая работа с вариантами ответа «да», «нет». – У вас 3-5минут. Приступайте! Дети отсылают результаты теста учителю, выходят из программы, отключают ноутбуки. |
 |
Слайд 39 Подведение итогов. Рефлексия (на доске три плаката: «я отлично понял тему», «я хорошо усвоил изученный материал», «у меня встречаются трудности при решении задач на нахождение площади прямоугольника»). Дети приклеивают картинки с «Карандашом». |
Аннотированный список используемых ресурсов:
Картинки:
- 0lik.ru/uploads/posts/2007-12/1198423906_0lik.ru_prew.jpg – шапка
- www.sumka.su/products_pictures/varezki2_resize.JPG – варежки
Музыка:
- www.parkov3.narod.ru/veter.htm
- detkam.e-papa.ru/mp/6/13.html
- karaoke.yarsk.info/
Источники:
- www.sefon.ru/mp3/
- www.lenagold.ru/fon/clipart/k/klo2.html
- mywap.artemka.ru/mp3.pwml?view=abc&litera=72&isp=864
- yandex.ru/yandsearch
- www.rusedu.ru/
- 02
Янв 18
Числа от 1 до 100 (продолжение)
Внетабличное умножение и деление
19. 1) Для детского сада купили 6 красных шаров и 3 синих, по цене 5 р. за каждый. Сколько денег заплатили за все эти шары?
Реши задачу двумя способами, составляя выражения.
1-й способ 2-й способ
6 • 5 + 3 • 5 = 45 (р.) (6 + 3) • 5 = 45 (р.)
О т в е т: заплатили 45 р. О т в е т: заплатили 45 р.
2) Запиши и объясни, как можно найти площадь прямоугольника ABCD, умножая сумму на число, и как можно найти его площадь другим способом.
Сторона BC состоит из отрезков BK и KC. Аналогично, сторона AD состоит из отрезков AM и MD. Причём, BK = AM = 4 см, а KC = MD = 2 см. AB = MK = DC = 2 см. Тогда, площадь прямоугольника ABCD равна: (BK + KC) • AB = (4 + 2) • 2 = 12 см2.
Можно представить площадь прямоугольника ABCD в виде суммы площадей прямоугольника ABKM и квадрата MKCD: 4 • 2 + 2 • 2 = 12 см2.
3) Вычисли значения выражений любым способом.
(3 + 6) • 4 = 9 • 4 = 36
(5 + 
3 • (7 + 2) = 3 • 9 = 27
ГДЗ по математике. Рабочая тетрадь. 3 класс. Часть 2. Моро М. И., Волкова С. И.
Математика. 3 класс
3 класс. Рабочая тетрадь №2. Ответы к стр. 10
4 (80.93%) от 410 голосующих
Задачи на нахождение площади и периметра.
1. Стороны прямоугольника равны 4см и 5см. Найдите площадь и периметр данного прямоугольника.
2. Длина прямоугольника 3дм, ширина равна 2дм. Чему равны площадь и периметр этого прямоугольника?
3. Найдите площадь и периметр квадрата со стороной 6см.
4. Длина прямоугольника 8см, а ширина в 2 раза короче. Чему равна площадь данного прямоугольника?
5. Ширина прямоугольника 5см, а длина в 2 раза длиннее. Найдите площадь и периметр данного прямоугольника?
6. Ширина прямоугольника 4см, длина равна асм. Найдите площадь данного прямоугольника.
7. Площадь прямоугольника 42см², ширина его равна 6см. Чему равна длина прямоугольника?
8. Периметр прямоугольника 20см, ширина его равна 4см. Найдите площадь этого прямоугольника.
9. Периметр квадрата 20см. Найдите площадь этого квадрата.
10. Периметр квадрата 24дм. Какова будет площадь этого квадрата, если его сторону увеличить на 2 дм?
11. Площадь прямоугольника 36см², длина этого прямоугольника 9см. Чему будет равна площадь прямоугольника если длину уменьшить на 2см.
12. Длина клумбы прямоугольной формы 10м, ширина в 2 раза меньше. Найдите площадь клумбы.
13.Часть участка прямоугольной формы площадью 60м² засажена картофелем, другая часть квадратной формы отведена под лук. Длина участка отведенного под лук 4 метра. Чему равна площадь участка занятая картофелем?
14. Четвёртая часть участка длиной 10м, шириной 8 метров, отведена под землянику, а остальная часть — под цветник. Какая площадь занята цветником?
15. Под цветы отведено 2 клумбы. Длина прямоугольной клумбы 10м, ширина 5 метров. Сторона квадратной клумбы 6 метров. Площадь какой клумбы больше и на сколько?
16. Ширина участка 6м, а периметр равен 28 метров. Найдите площадь этого участка.