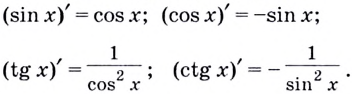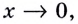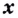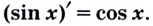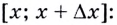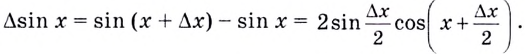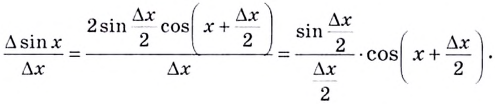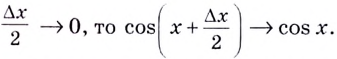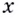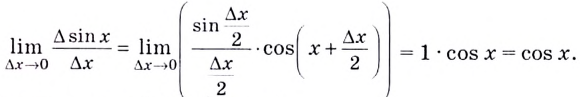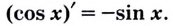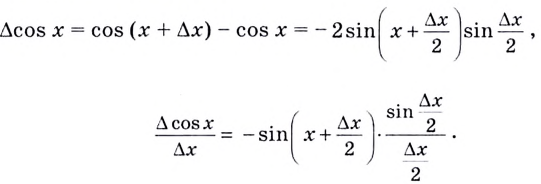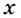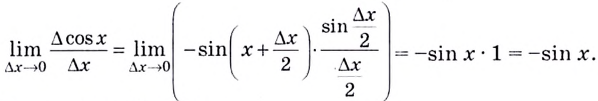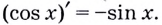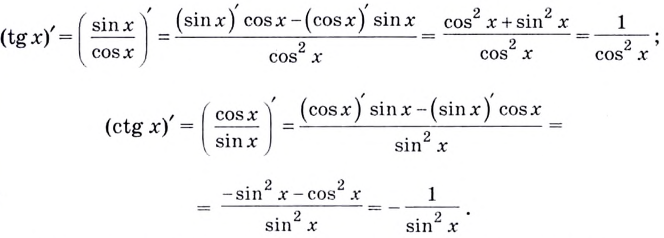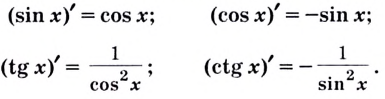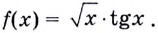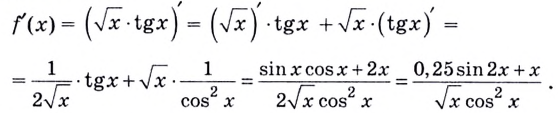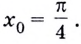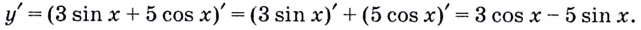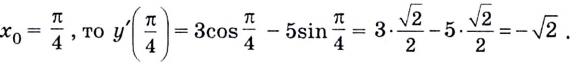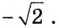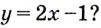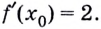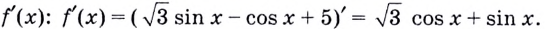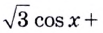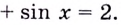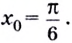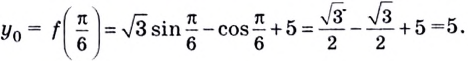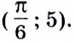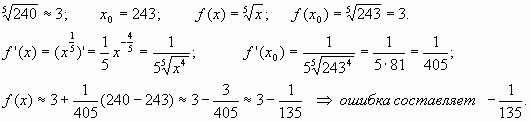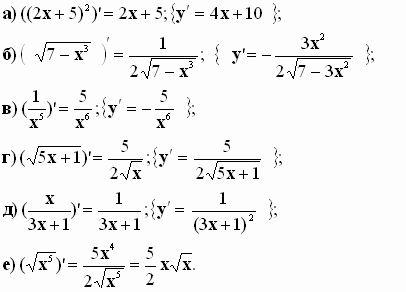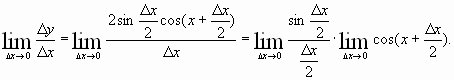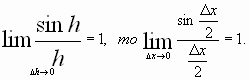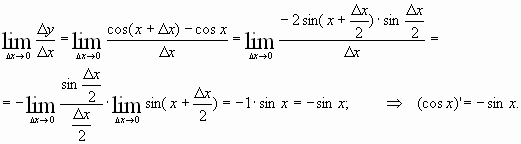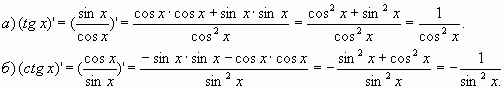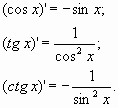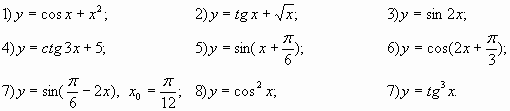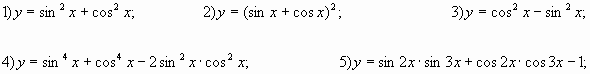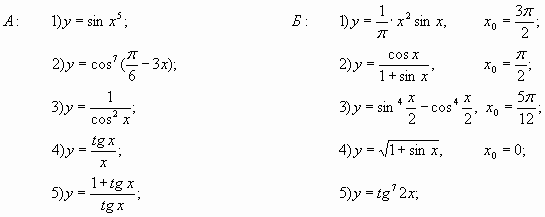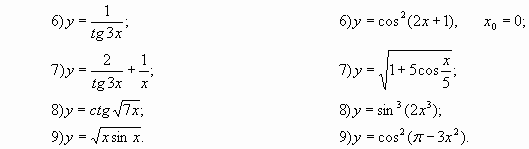Простое объяснение принципов решения производных тригонометрических функций и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения производных тригонометрических функций
Для нахождения производных основных тригонометрических функций, используется таблица производных элементарных функций. Решаются, как обычные производные.
При решении задач на поиск производных тригонометрических функций следует пользоваться следующей таблицей:
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Примеры решений производных тригонометрических функций
Задача
Найти производную функции
Решение
Функция является сложной, поэтому процесс нахождения производной будет происходить в два этапа.
Обозначим . Исходная функция примет следующий вид:
Найдём её производную по таблице основных тригонометрических функций:
Далее найдём производную :
Производная сложной функции будет равна произведению и
:
Ответ
Задача
Найти производную функции .
Решение
Функция является сложной, поэтому процесс нахождения производной будет происходить в два этапа.
Обозначим . Исходная функция примет следующий вид:
Найдём её производную по таблице основных тригонометрических функций:
Далее найдём производную :
Производная сложной функции будет равна произведению и
:
Ответ
Задача
Найти производную функции
Решение
Функция является сложной, поэтому процесс нахождения производной будет происходить в два этапа, однако в этом раз найдём производную без введения промежуточной переменной.
Вначале найдём производную
По таблице производных определяем, что
Т.к. аргумент косинуса сам является функцией от , то необходимо найти его производную по
:
Окончательно, производная будет равна произведению
и числа
:
Ответ
Задача
Найти производную функции
Решение
Данная функция является сложной, т.к. подкоренным выражением является функция синус.
Найдём производную данной функции, как произведение производных корня и синуса:
Производные тригонометрических функций
- Производная синуса
- Производная косинуса
- Производная тангенса и котангенса
- Примеры
п.1. Производная синуса
Найдем производную функции (f(x)=sinx) по общему алгоритму.
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=sin(x+triangle x)-sinx=\ =2sinfrac{x+triangle x-x}{2}cosfrac{x+triangle x+x}{2}=2sinfrac{triangle x}{2}cosfrac{2x+triangle x}{2} end{gather*} Используем первый замечательный предел (см. §39 данного справочника): begin{gather*} lim_{xrightarrow 0}frac{sinx}{x}=1 end{gather*} Ищем производную: begin{gather*} f'(x)=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{2sinfrac{triangle x}{2}cosfrac{2x+triangle x}{2}}{triangle x}=underbrace{left(lim_{triangle xrightarrow 0}frac{sinfrac{triangle x}{2}}{frac{triangle x}{2}}right)}_{=1}cdot lim_{triangle xrightarrow 0}cosfrac{2x+triangle x}{2}=\ =1cdot cosfrac{2x+0}{2}=cos x end{gather*} Или: ((sinx)’=cos x)
Для любого действительного x: $$ (sinx)’=cos x $$
Например:
((x^2sinx)’=(x^2)’cdot sinx+x^2cdot (sinx)’=2xsinx+x^2cosx)
п.2. Производная косинуса
Найдем производную функции (f(x)=cosx) по общему алгоритму.
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=cos(x+triangle x)-cosx=\ =-2sinfrac{x+triangle x-x}{2}sin{x+triangle x+x}{2}=-2sinfrac{triangle x}{2}sinfrac{2x+triangle x}{2} end{gather*} Как и для производной синуса, используем первый замечательный предел. Ищем производную: begin{gather*} f'(x)=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{-2sinfrac{triangle x}{2}sinfrac{2x+triangle x}{2}}{triangle x}=underbrace{-left(lim_{triangle xrightarrow 0}frac{sinfrac{triangle x}{2}}{frac{triangle x}{2}}right)}_{=1}cdot lim_{triangle xrightarrow 0}sinfrac{2x+triangle x}{2}=\ =-1cdot sinfrac{2x+0}{2}=-sinx end{gather*} Или: ((cosx)’=-sinx)
Для любого действительного x: $$ (cosx)’=-sinx $$
Например:
((sqrt{x}cosx)’=(sqrt{x})’cdot cosx+sqrt{x}cdot (cosx)’=frac{1}{2sqrt{x}}cosx-sqrt{x}sinx )
п.3. Производная тангенса и котангенса
Производные от тангенса и котангенса найдем с помощью формулы производной частного двух функций (см. §43 данного справочника). begin{gather*} (tgx)’=left(frac{sinx}{cosx}right)’=frac{(sinx)’cosx-sinx(cosx)’}{cos^2x}=\ =frac{cosxcosx-sinx(-sinx)}{cos^2x}=frac{cos^2x+sin^2x}{cos^2x}=frac{1}{cos^2x} end{gather*} Аналогично: begin{gather*} (ctgx)’=left(frac{cosx}{sinx}right)’=frac{(cosx)’sinx-cosx(sinx)’}{sin^2x}=\ =frac{sinx(-sinx)-cosxcosx}{sin^2x}=frac{-sin^2x-cos^2x}{sin^2x}=-frac{sin^2x+cos^2x}{sin^2x}=-frac{1}{sin^2x} end{gather*}
Как видно из результатов, производные тангенса и котангенса имеют те же ограничения по ОДЗ, что и сами функции.
begin{gather*} (tgx)’=frac{1}{cos^2x}, xnefracpi 2+pi k\ (ctgx)’=-frac{1}{sin^2x}, xnepi k end{gather*}
Например:
( left(frac{tgx}{x}right)’=frac{(tgx)’cdot x-tgxcdot(x)’}{x^2}=frac{frac{x}{cos^2x}-tgx}{x^2}=frac{x-tgxcdot cos^2x}{x^2cos^2x}=frac{x-sinxcosx}{x^2cos^2x} )
п.4. Примеры
Пример 1. Найдите производную:
a) ( f(x)=2sinx-5x ) begin{gather*} f'(x)=2cdot sin’x-5cdot x’=2cosx-5 end{gather*}
б) ( f(x)=3sqrt{x}ctgx ) begin{gather*} f'(x)=3left((sqrt{x})’cdot ctgx+sqrt{x}(ctgx)’right)=3left(frac{ctgx}{2sqrt{x}}-frac{sqrt{x}}{sin^2x}right) end{gather*}
в) ( f(x)=9cosx-3tgx ) begin{gather*} f'(x)=9cdot cos’x-3cdot tg’x=-9sinx-frac{3}{cos^2x} end{gather*}
г) ( f(x)=frac{2x}{sinx} ) begin{gather*} f'(x)=2frac{(x)’cdot sinx-xcdot sin’x}{sin^2x}=frac{2(sinx-xcosx)}{sin^2x} end{gather*}
Пример 2. Найдите значение производной в данной точке:
a) ( f(x)=sinx+cosx, x_0=fracpi 4 ) begin{gather*} f'(x)=sin’x+cos’x=cosx-sinx\ f'(fracpi 4)=cosfracpi 4-sinfracpi 4=frac{sqrt{2}}{2}-frac{sqrt{2}}{2}=0 end{gather*}
б) ( f(x)=tgx-5cosx, x_0=pi ) begin{gather*} f'(x)=tg’x-5cos’x=frac{1}{cos^2x}+5sinx\ f'(pi)=frac{1}{cos^2pi}+5sinpi=1+0=1 end{gather*}
в) ( f(x)=sinxcosx, x_0=frac{pi}{12} ) begin{gather*} f'(x)=sin’xcosx+sinxcos’x=cos^2x-sin^2x=cos2x\ f’left(frac{pi}{12}right)=cosleft(2cdotfrac{pi}{12}right)=cosfracpi 6=frac{sqrt{3}}{2} end{gather*}
г) ( f(x)=frac{x}{cosx}, x_0=pi ) begin{gather*} f'(x)=frac{x’cdot cosx-xcos’x}{cos^2x}=frac{cosx+xsinx}{cos^2x}\ f'(pi)=frac{cospi+pi sinpi}{cos^2pi}=frac{-1+picdot 0}{(-1)^2}=-1 end{gather*}
Пример 3. Решите уравнение:
a) ( y’cdot y+y^2=0), если (y=3cosx)
(y’=3cdot cos’x=-3sinx)
Подставляем: begin{gather*} -3sinxcdot 3cosx+(3cosx)^2=0\ -9sincosx+9cos^2x=0\ 9cosx(cosx-sinx)=0 end{gather*} Уравнение: begin{gather*} left[ begin{array}{l} cosx=0\ cosx-sinx=0 |:cosx end{array} right. Rightarrow left[ begin{array}{l} x=fracpi 2+pi k\ 1-tgx=0 end{array} right. Rightarrow left[ begin{array}{l} x=fracpi 2+pi k\ tgx=1 end{array} right. Rightarrow left[ begin{array}{l} x=fracpi 2+pi k\ x=fracpi 4+pi k end{array} right. end{gather*} Ответ: (left{fracpi 2+pi k; x=fracpi 4+pi kright})
б) ( (y’)^2+y^2=1), если (y=1-cosx)
(y’=1′-cos’x=0+sinx=sinx)
Подставляем: begin{gather*} sin^2x+(1-cosx)^2=1\ sin^2x+1-2cosx+cos^2x=1\ 1-2cosx=0\ cosx=frac12\ x=pmfracpi 3+2pi k end{gather*} Ответ: (left{pmfracpi 3+2pi kright})
Рейтинг пользователей
Преподаватель который помогает студентам и школьникам в учёбе.
Производные тригонометрических функции с примерами решения
Производные тригонометрических функции
Рассмотрим производные тригонометрических функций. Правильны следующие формулы:
Для доказательства двух первых формул вспомним первый замечательный предел (см. с. 106), а именно: когда
Теорема (о производной синуса). Для каждого действительного
Доказательство. Найдём приращение функции 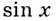
Поэтому
Если 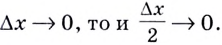
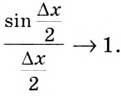
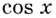
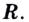
Следовательно, для произвольного
То есть, всегда
Теорема (о производной косинуса). Для каждого действительного
Доказательство.
Если 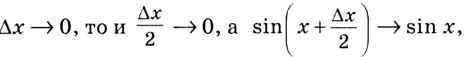
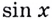
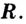
To есть
Формулы производных тангенса и котангенса можно доказать, используя теорему о производной частного:
Итак, в каждой точке 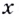
Пример №536
Найдите производную функции
Решение:
Воспользуемся теоремой о производной произведения:
- Заказать решение задач по высшей математике
Пример №537
Вычислите значение производной функции 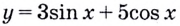
Решение:
Воспользуемся теоремой о производной суммы:
Если
Ответ.
Пример №538
В какой точке касательная, проведённая к графику функции
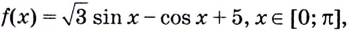
Решение:
В искомой точке угловой коэффициент 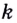
Кроме этого, угловой коэффициент 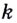
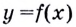
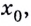
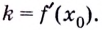
Найдём
Абсциссу искомой точки найдём, решив уравнение
Имеем: 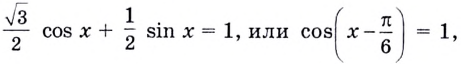
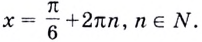
Промежутку 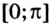
Тогда
Ответ.
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Тригонометрические функции
Цель:
- Формирование у учащихся представления о
производной. Применение производной в физике, в
геометрии и к приближенным вычислениям. - Отработка навыков представления сложных
функций в виде композиции более простых функций. - Вывод формул производных тригонометрических
функций и отработка навыков их вычислений.
Ход урока
I. Обзор пройденного материала.
1) Что такое производная?
2) Механический смысл производной.
Задача 1. Точка движется прямолинейно
по закону Найдите среднюю скорость точки на
промежутке [1;4]. Найдите скорость лодки в момент
времени t = 3 с.
Задача 2. Точка движется прямолинейно по закону В
какой момент времени скорость точки окажется
равной нулю.
в
конце 2 секунды.
3) Найти ошибку приближенного вычисления.
4) Проверить правильно ли найдена производная
функцию.
5) Вычислить
значение производной данной функции в точке .
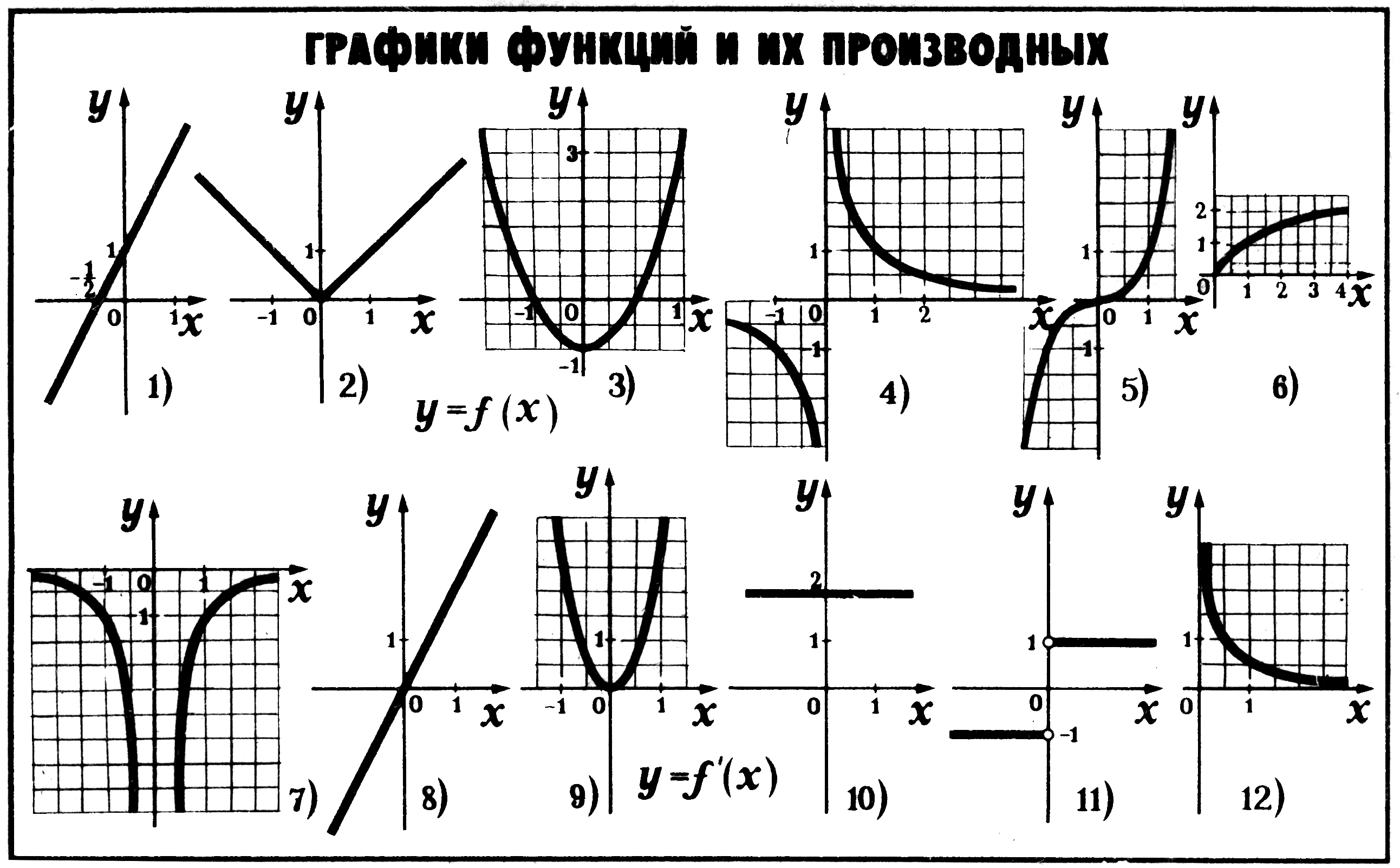
6) Объедините графики функций в пары.
1 – 10; 2 – 11; 3 – 8; 4 – 7; 5 – 9; 6 – 12.
Производные тригонометрических функций.
1) Найдем производную функции
Дадим x приращение , тогда
Воспользовавшись формулой преобразования
разности синусов в произведение получим:
Разделим обе части этого равенства на и перейдем к
пределу при?
Так как
Так как функция непрерывна в любой точке x, то
В итоге получаем
Таким образом
Аналогично выводится формула
2) Доказать, что Самостоятельно.
3) Как, зная формулу производной синуса и
формулы приведения вывести формулу производной
косинуса?
4) Воспользовавшись формулой – производная
частного двух функций, найдите производные
функций
В итоге получаем
Закрепление:
Задайте формулой хотя бы одну из функций f,
если:
Домашнее задание:
Производные тригонометрических функций.
Найдите производную функции:
Найдите производную функции:
Найти производную функции: