Как найти значение по графику функции огэ

Для того, чтобы решать задания с графиками функций, необходимо иметь представление о том, что такое функция, и какие основные виды функций бывают

1. Введение

2. Результаты выполнения учащимися школы заданий на
ОГЭ по теме «Функция и графики»

3. Требования к содержанию и уровню подготовки
обучающихся для проведения ОГЭ по математике.

4. Теоретическая часть.

4.1.
Линейная функция.

4.2.
Обратная
пропорциональность.

4.3.
Функция
y =

Пусть n (n≥2) –
натуральное число. Каждому неотрицательному числу x поставим в
соответствие число y, равное
арифметическому корню степени n из x. Иными словами,
на множестве неотрицательных чисел зададим функцию y =

4.4.
Квадратичная функция и ее
график

4.5.
График функции y =

5. Разбор типовых заданий

22. Задания для самостоятельного решения.

23. Некоторые полезные советы учащимся для
успешной подготовки к ОГЭ по математике

24. Заключение.

25. Используемая литература

Разбор решения задания 11 ОГЭ по математике

Для того, чтобы решать задания с графиками функций, необходимо иметь представление о том, что такое функция, и какие основные виды функций бывают

1. Введение

2. Результаты выполнения учащимися школы заданий на
ОГЭ по теме «Функция и графики»

3. Требования к содержанию и уровню подготовки
обучающихся для проведения ОГЭ по математике.

4. Теоретическая часть.

4.1.
Линейная функция.

4.2.
Обратная
пропорциональность.

4.3.
Функция
y =

4.4.
Квадратичная функция и ее
график

4.5.
График функции y =

5. Разбор типовых заданий

22. Задания для самостоятельного решения.

23. Некоторые полезные советы учащимся для
успешной подготовки к ОГЭ по математике

24. Заключение.

25. Используемая литература

Разбор решения задания 11 ОГЭ по математике

Для того, чтобы решать задания с графиками функций, необходимо иметь представление о том, что такое функция, и какие основные виды функций бывают

1. Введение

2. Результаты выполнения учащимися школы заданий на ОГЭ по теме «Функция и графики»

3. Требования к содержанию и уровню подготовки обучающихся для проведения ОГЭ по математике.

4. Теоретическая часть.

4.1. Линейная функция.

4.2. Обратная пропорциональность.

4.3. Функция y = <img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" width="25" height="24" src="https://documents.infourok.ru/6e793035-69e8-418a-b432-48ca9147f7fa/0/image022.png" />

4.4. Квадратичная функция и ее график

4.5. График функции y = <img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" width="18" height="27" src="https://documents.infourok.ru/6e793035-69e8-418a-b432-48ca9147f7fa/0/image033.png" />

5. Разбор типовых заданий

22. Задания для самостоятельного решения.

23. Некоторые полезные советы учащимся для успешной подготовки к ОГЭ по математике

24. Заключение.

25. Используемая литература

Разбор решения задания 11 ОГЭ по математике

2. Результаты выполнения учащимися школы заданий на
ОГЭ по теме «Функция и графики»

3. Требования к содержанию и уровню подготовки
обучающихся для проведения ОГЭ по математике.

4.1.
Линейная функция.

4.2.
Обратная
пропорциональность.

4.3.
Функция
y =

4.4.
Квадратичная функция и ее
график

4.5.
График функции y =

23. Некоторые полезные советы учащимся для
успешной подготовки к ОГЭ по математике

График квадратичной функции.

График квадратичной функции.

РЕКОМЕНДУЕМЫЕ ТОВАРЫ

Не пропустите также:

График квадратичной функции.

РЕКОМЕНДУЕМЫЕ ТОВАРЫ

Не пропустите также:

Каталог заданий.
Чтение графиков функций

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Найдите значение a по графику функции изображенному на рисунке.

Найдите значение b по графику функции изображенному на рисунке.

Найдите значение c по графику функции изображенному на рисунке.

Найдите значение k по графику функции изображенному на рисунке.

На рисунке изображён график функции  Какие из утверждений относительно этой функции неверны? Укажите их номера.

1)  функция возрастает на промежутке 

4)  прямая  y=2   пересекает график в точках   и 

Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)

Пройти тестирование по этим заданиям

Источник

Функция – это такая вещь, которая связывает две (или более) переменных между собой. Другими словами, функция помогает найти одну переменную, если мы знаем значение второй переменной. Например, если у нас в кармане есть 100 рублей, а шоколадка стоит 50 рублей, то мы можем купить 2 шоколадки. Если у нас в кармане есть 200 рублей, то мы можем купить 4 шоколадки. В этом случае первая переменная – это сумма, которая есть в кармане, а вторая переменная – количество шоколадок, которые мы можем купить. Стоимость шоколадки составляет 50 рублей, она не зависит от того сколько у нас денег, поэтому эта величина является постоянной.

Можно составить функцию для этого случая: у = 50 • х, где у – деньги в кармане, х – количество шоколадок.

Естественно функции бывают более сложными. Но для решения заданий ОГЭ по математике достаточно знать как выглядят графики основных функций.

1. Функция вида y = kx + b (прямая линия)

В этой функции k и b это числа. Функция может быть записана в разном виде: y = x, y = 2x, y = 3x – 4, y = -9x +44, y = $displaystyle frac{3x}{4} + 7$ и т д. Главным признаком является присутствие икса (х) в первой степени (то есть все случаи, когда мы не делим на х).
Число k в этом случае отвечает за то, в какую сторону наклонена линия. Если k > 0, то функция возрастает вправо. Если k < 0, то функция возрастает влево.

Число b – это точка пересечения графика с осью y. Если b >0, то график пересекает ось y выше начала координат, если b < 0 – ниже.

2. Функция вида y = ax² + bx +c (парабола)

В этой функции a, b, c – числа. Функция может быть записана в разном виде: y = x^2, y = 3x² + 8, y = 2x² -4x + 10, y = -x² – 9x +1, y = $displaystyle frac{x^2}{3}$ – 7 и т. д. Главным признаком является наличие икса в квадрате (x²).

Число а отвечает за то, в какую сторону (вверх или вниз) направлены ветви параболы (я еще называю веселый смайлик и грустный смайлик). Если a > 0, то веселый смайлик, если a < 0 – грустный.

Число b отвечает за то в какую сторону (вправо или влево) смещена точка начала параболы (точка перегиба) относительно оси y. Если b > 0, то график смещен влево, если b < 0 – вправо.

Число c – это точка пересечения графика с осью y. Если c >0, то график пересекает ось y выше начала координат, если c < 0 – ниже.

3. Функция вида y = k/x + b (гипербола)

Эта функция по виду напоминает функцию прямой, за тем исключением, что х находится в знаменателе. Это как раз и является ее отличительной особенностью. Число k отвечает за расположение функции по четвертям, если k > 0, то ветви гиперболы располагаются в первой и третьей четвертях, если k < 0, то ветви располагаются во второй и четвертой четвертях.

Число а отвечает за сдвиг всей функции вниз (а < 0) или вверх (a > 0).

4. Функция вида y = a (прямая)

В этом случае функция выглядит как прямая, параллельная оси х. Например у = 2, это прямая линия, которая проходит параллельно оси х и пересекает ось у в точке 2.

5. Функция вида y = √x

Этот вид встречается в заданиях редко, однако лучше запомнить. Это практически парабола, но повернутая по часовой стрелке на 90⁰, а также в ней отсутствует ее нижняя половина. Если не понятно, то просто смотрите на рисунок:

Источник

ФУНКЦИИ,
ИХ ГРАФИКИ И СВОЙСТВА

(Методическое
пособие для учащихся и учителей)

Шепова В.М.

Учитель математики

С. СЕМИОЗЁРКА

2016/17 УЧЕБНЫЙ ГОД

Оглавление

1. Введение

2. Результаты
выполнения учащимися школы заданий на ОГЭ по теме «Функция и графики»

3. Требования к
содержанию и уровню подготовки обучающихся для проведения ОГЭ по
математике.

4. Теоретическая часть.

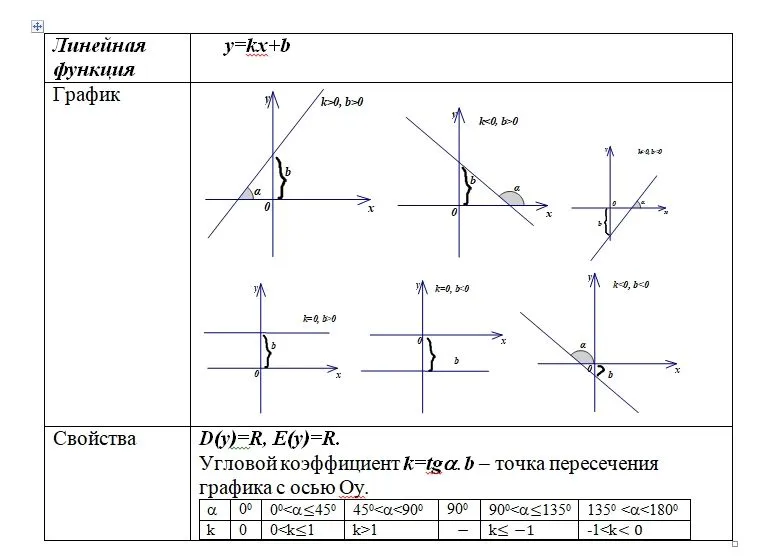
4.1. Линейная функция.

4.2. Обратная
пропорциональность.

4.3. Функция y =

4.4. Квадратичная функция и
ее график

4.5. График функции y =

5. Разбор типовых
заданий

6.
Задания для самостоятельного решения.

7. Некоторые полезные
советы учащимся для успешной подготовки к ОГЭ по математике

8. Заключение.

9. Используемая
литература

Целью данного
пособия является оказание практической помощи выпускникам 9 класса в приобретении,
освоении и закреплении знаний как теоретического, так и практического характера
по теме «Функция» на ОГЭ и ГВЭ, а так же с целью повышения уровня
самоподготовки к ОГЭ по математике.

Тема «Функции, их
свойства и графики» является одной из важных тем курса алгебры основной
школы. Она отражена в заданиях 1-й (базового уровня) и 2-й (повышенного и высокого
уровня) частях экзаменационной работы.

Готовясь к итоговому
экзамену учащимся необходимо ориентироваться на задания и более высокой
сложности и тогда можно рассчитывать на положительный результат. Учащиеся
выпускного класса должны иметь более высокий уровень теоретических знаний и
умений правильно применять их.

По моему опыту, тема
«Функции и графики» очень важная и серьезная, но которой дети не уделяют
достойного внимания. В своей работе я даю рекомендацию по выполнению заданий по
этой теме. Так же надеюсь, что пособие поможет не только экзаменуемым, но и
учителям, которые будут повторять эту тему при подготовке к ОГЭ. Я хочу найти
самые рациональные методы решения.

№ задания	уровень сложности	основные проверяемые требования к математической подготовке	% выполнения
2014	2015	2016
5	Б	Уметь строить и читать графики функций.	75%	44%	20%
15	Б	Описание с помощью функций различные реальные зависимости между величинами, интерпретация	75%	56%	20%
18	Б	Анализировать реальные числовые данные, представленные в таблицах, на диаграммах, графиках.	73%	11%	40%
Итого базовый уровень сложности	74%	37%	27%
23	В	Строить и читать графики функций, строить и исследовать простейшие математические модели.	0	0%	0%
Итого высокий уровень сложности:	0%	0%	0%

По
результатам ОГЭ за три последних года по этой теме процент выполнения заданий учащимися
школы базового уровня снизился с 74% в 2014 году до 27% в 2016 году. К решению
заданий высокого уровня учащиеся не приступали.

С
каждым годом уменьшается количество учащихся 9 класса от 15 в 2014 году до
семи в 2016 году. Вместе с тем увеличивается количество учащихся с ОВЗ,
обучающихся по АООП ЗПР.

№ задания	Основные проверяемые требования к математической подготовке	Коды проверяемых элементов содержания	коды разделов элементов требований	уровень сложности	максимальный балл за выполнение задания
Часть 1
Модуль «Алгебра»
5	Уметь строить и читать графики	5	4	Б	1
Модуль «Реальная математика»
15	Описывать с помощью функций различные реальные зависимости между величинами, интерпретировать графики реальных зависимостей.	5	7	Б	1
18	Анализировать реальные числовые данные, представленные в таблицах, н а диаграммах, графиках	8	7	Б	1
Часть 2.
Модуль «Алгебра»
23	Уметь строить и читать графики функций, строить и исследовать простейшие математические модели	4,5	4,2	В	2

Код раздела	код контролируемого умения	Требования (умения), проверяемые заданиями экзаменационной работы
4		уметь строить и читать графики функций
	4.1	Определять координаты точки плоскости, строить точки с заданными координатами.
4.2	Определять значение функции по значению аргумента при различных способах задания функции, решать обратные задачи.
4.3.	Определять свойства функции по её графику (промежутки возрастания, убывания, промежутки знакопостоянства, наибольшее и наименьшее значение функции)
4.4	Строить графики изученных функций, описывать их свойства
7	7.4	Описывать с помощью функций различные реальные зависимости между величинами, интерпретировать графики реальных зависимостей
	7.6	Анализировать реальные числовые данные, представленные в таблицах, на диаграммах, графиках

код раздела	код контролируемого элемента	Элементы содержания, проверяемые заданиями экзаменационной работы
5		Функция
5.1		Числовые функции
	5.1.1	Понятие функции. Область определения функции. Способы задания функции.
	5.1.2	График функции, возрастание и убывание функции, наибольшее и наименьшее значение функции, нули функции, промежутки знакопостоянства, чтение графиков функции.
	5.1.3	примеры графических зависимостей, отражающие реальные процессы
	5.1.4	Функция, описывающая прямую пропорциональную зависимость, её график
	5.1.5	Линейная функция. Её график, геометрический смысл коэффициентов
	5.1.6	Функция, описывающая обратную пропорциональную зависимость, её график. Гипербола.
	5.1.7	Квадратичная функция, её график. Парабола. Координаты вершины параболы, ось симметрии.
	5.1.8	График функции
	5.1.9	График функции у =
	5.1.10	График функции у =
8		Статистика и теория вероятности
8.1		Описательная статистика
	8.1.1	Представление данных в виде таблиц, диаграмм, графиков

Как видно из обобщенного
плана варианта КИМ 2017 года   задания на чтение графиков функции, описание с
помощью функций различных реальных процессов между величинами, интерпретация
графиков реальных зависимостей, анализ реальных числовых данных, представленных
на графиках,   входят в три задания базового уровня (№ 5,15,18) первой части
и задание № 23 высокого уровня сложности   модуля «Алгебра» части 2.

В пятом задании идет работа с графиками функций. В большинстве
случаев требуется установить соответствие между графиком функции и
математическим выражением (формулой). В задании сопоставляется различная
информация о функциях. Необходимо находить и использовать в выполнении
задания область определения функции, ее промежутки возрастания и убывания,
промежутки знакопостоянства, нули функции, уметь читать графики функций.
Работать надо с функциями, описывающими прямую и обратную пропорциональные зависимости,
линейными функциями, квадратичными функциями.

Зависимость одной переменной от
другой называют функциональной зависимостью или функцией.
Зависимость каждому значению независимой переменной соответствует единственное
значение зависимой переменной.

Независимую переменную иначе
называют аргументом, а о зависимой переменной говорят, что она является
функцией от этого аргумента.

Значение зависимой переменной
называют значениями функции.

Все значения, которые принимает
независимая переменная, образуют область определения функции.

Определение. Линейной функцией называется функция, которую можно задать
формулой y=kx+b, где x-независимая
переменная, k и b – некоторые числа.

График функции y=kx+b, где k≠0, есть прямая, параллельная прямой y=kx. Если b>0 – график
поднимается вверх. Если b<0 – то график опускается вниз.

Формула y=kx+b при k=0 принимает вид y=b. В этом случае графиком функции y=kx+b является прямая, параллельная оси x при b≠0 или сама ось xпри b=0.

На рисунке построен график функции y=3. Таким Образом, график линейной функции
является прямая.

Для построения графика линейной функции достаточно найти
координаты двух точек графика, отметить эти точки на координатной плоскости и
провести через них прямую.

Определение. Прямой пропорциональностью называется функция, которую можно
задать формулой вида y= kx, где x-независимая переменная, k — не равное нулю число.

Число k в формуле y=kx называется коэффициентом прямой пропорциональности.

1. Если k>0 функция
возрастает.

2. Если k<0 функция
убывает.

График прямой пропорциональности представляет собой прямую,
проходящую через начало координат.

Определение. Обратную
пропорциональностью называется функция, которую можно задавать формулой вида y = , где x – независимая переменная и k – не равное нулю
число.

Областью определения
функции является множество всех чисел, отличных от нуля. Это следует из того,
что выражение y = имеет смысл при всех x≠0.

Свойства функции:

1.
Если x>0, то y>0; если x<0, то y<0.

2.
На промежутке (-∞; 0) функция убывает, на промежутке (0; +∞)
функция также убывает.

3.
Если положительное x стремится к 0, то y = cтремится к 0. Если отрицательное x стремится к 0, то y = , стремится к -∞; если x стремится к -∞, то y = стремится к 0.

4.
Функция y = нечетная функция.
Поэтому ее график симметричен относительно начала координат.

5.
Функция непрерывна на каждом из промежутков (-∞; 0) и (0; +∞).

График функции y = (k>0) можно получить из графика функции y = растяжением его в k раз вдоль оси Oy, если k>1, и сжатием его
в k раз вдоль оси Oy, если 0<k<1.

График функции y = при k≠0 также называют гиперболой.

При k>0 точки гипербол находятся в 1 и 3 четвертях, а при k<0 – во 2 и 4
четвертях. Говорят, при k>0 ветви гиперболы находятся в 1 и 3 четвертях, а при k<0 – во 2 и 4
четвертях.

Чтобы построить график функции y = надо построить график функции y = , затем сначала сдвинуть построенный
график на│x₀│единиц вправо , если x₀>0, и влево, если y₀<0, и вниз, если y₀<0.

Чтобы построить график функции y = надо
сдвинуть построенный график на 1 единицу вправо и на 2 единицы вверх.

Таким
образом, областью определения функции является множество неотрицательных чисел:
x≥0.

Отметим
следующие свойства функции.

1)
Если
x=0, то y=0.

2)
Если
x>0, то y>0.

3)
Функция
возрастает.

4)
Если
x→+∞, то y→+∞/

5)
Функция
непрерывна.

Легко
видеть, что график функции отражает свойства 1-5 функции.

Действительно,
график функции проходит через начало координат – свойство 1; график функции
расположен выше оси Ox для x>0
– свойство 2; график изображает возрастающую функцию – свойство 3; при x→+∞ ординаты соответствующих точек
графика функции неограниченно возрастают – свойство 4; график функции есть
непрерывная кривая – свойство 5.

Приведем
еще некоторые свойства арифметических корней.

1)
Если
x>1, то >1

2)
Если
0<x<1, то 0<<1

Функция y=ax², ее график и свойства.

Определение. Квадратичной
функцией называется функция, которую можно задать формулой вида

y=ax²+bx+c,

где x— независимая
переменная, a, b и c–некоторые числа, причем a≠0.

Областью определения
квадратичной функции является множество всех чисел.

График функции y=ax², где a≠0, как и график
функции y=x², называется параболой.

Сформулируем свойства
функции y=ax² при a>0.

1.
Если x=0, то y=0. График функции проходит через начало координат.

2.
Если x≠0, то y>0. График функции расположен в верхней полуплоскости.

3.
Противоположным значениям аргумента соответствуют равные значения
функции. График функции симметричен относительно оси y.

4.
Функция убывает в промежутке (-∞; 0] и возрастает в промежутке [0;
+∞).

5.
Наименьшее значение, равное нулю, функция принимает при x=0, наибольшего
значения функция не имеет. Областью
значений функции является промежуток [0; +∞).

Теперь сформулируем свойства
функции y=ax²при a<0.

1. Если x=0, то y=0. График функции проходит через
начало координат.

2.
Если
x≠0, то y<0. График функции расположен в нижней
полуплоскости.

3.
Противоположным
значениям аргумента соответствуют равным значения функции. График функции симметричен
относительно оси y.

4.
Функция
возрастает в промежутке (-∞; 0] и убывает в промежутке [0; +∞).

5.
Наибольшее
значение, равное нулю, функция принимает при x=0, наименьшего значения функция не
имеет. Областью значений функции является промежуток (-∞; 0].

График функции y=a(x—m)² является
параболой, которую можно получить из графика функции y=ax²с помощью
параллельного переноса вдоль оси xна m единиц вправо, если m>0, или на –m единиц влево, если m<0.

1)
На рисунках изображены графики функций вида y = ax² + bx + c. Установите
соответствие между знаками коэффициентов a и c и графиками функций.

Коэффициенты:

А) a > 0, c
> 0 Б) a < 0, c > 0 В) a >
0, c < 0

Графики:

Решение:

Мы вспоминаем,
за что отвечают коэффициенты a и b при построении графиков функции вида

y = ax² + bx + c. Коэффициент a определяет направление ветвей параболы:
если a > 0, то ветви направлены вверх, а если a < 0,
то ветви направлены вниз.

Таким образом,
мы видим, что только у второй параболы ветви направлены вниз, а значит a
< 0.

У первой и третьей
ветви направлены вверх, то есть a > 0. Далее мы смотрим, на что влияет
коэффициент c.
Коэффициент c отвечает
за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а
именно:

если c
> 0, то вершина параболы расположена выше оси х

если c
< 0, то вершина параболы расположена ниже оси x

Так, у первой
параболы c < 0, у второй и третьей c > 0.

Из всего
вышеперечисленного можно найти ответ: 321.

2)
Установите соответствие между функциями и их графиками.

Функции:

A) y = -3/x Б) y
= 3/x В) y = 1/(3x)

Графики:

Решение: В данной
ситуации можно воспользоваться двумя подходами — можно руководствоваться
общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую
решать задачу общими соображениями, а проверять подстановкой.

Общие правила:

—
если уравнение гиперболы
положительное (то есть не стоит знак -, как во втором и третьем случае), то
график функции лежит в первой и третьей координатной четверти

—
если перед уравнением
гиперболы стоит знак — (как в первом случае), то график лежит во второй и
четвертой четвертях

Таким образом
можно сразу определить, что первое уравнение соответствует графику под номером
2.

Второе правило,
которым я пользуюсь, звучит так:

—
чем больше число в
знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям
координатной плоскости

—
и наоборот:

—
чем больше число в
числителе уравнения гиперболы, тем слабее и медленнее график функции
прижимается к осям

Следовательно,
функция Б слабее прижимается к осям и ей соответствует график 3, а функции В
соответствует график 1, так как она сильнее прижимается к осям.

Ответ: 231.

3)
Установите соответствие между функциями и их графиками.

Функции:

A) y = 3x Б) y = -3x В) y = (1/3)x

Графики:

Решение: Функция
представляет собой линейную зависимость, а именно уравнение первого порядка вида
y = kx + b

График данной
функции зависит от k и b.

—
если k < 0, то функция убывает, то есть линия идет сверху
вниз, как на третьем рисунке

—
если k > 0, то функция возрастает, то есть линия идет снизу
вверх, как на первых двух рисунках

—
коэффициент b определяет сдвиг по оси y, если b < 0, то прямая
пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в
точке y = b

—
если k >1, то прямая идет круче, чем обычная y = x (как на
первом и втором графике), если k <1 , то на рисунка №3

Следовательно,
графику y =
3x соответствует рисунок 2, так как прямая идет снизу вверх и
она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.

Графику 3
соответствует функция y = -3x так как k = -3 < 0, и график идет
сверху вниз.

Ответ: 231.

3. Выявить влияние
коэффициентов а, b и с на расположение графика функции у
= ах² + +bх + с.

Решение: Учащиеся обладают
достаточными знаниями, чтобы выполнить это задание самостоятельно. Следует
предложить им все полученные выводы занести в тетрадь, при этом выделив
«основную» роль каждого из коэффициентов.

1) Коэффициент а влияет на
направление ветвей параболы: при а > 0 – ветви направлены вверх, при а
< 0 – вниз.

2) Коэффициент b влияет
на расположение вершины параболы. При b = 0 вершина лежит на оси ОY.

3) Коэффициент с показывает
точку пересечения параболы с осью ОУ.

После этого можно привести пример,
показывающий, что можно сказать о коэффициентах а, b и с
по графику функции.

Значение с можно назвать
точно: поскольку график пересекает ось ОУ в точке (0; 1), то с =
1.

Коэффициент а можно сравнить
с нулем: так как ветви параболы направлены вниз, то а < 0.

Знак коэффициента b можно
узнать из формулы, определяющей абсциссу вершины параболы: , m= — так
как а < 0 и т = 1, то b > 0.

4. Определите, график какой
функции изображен на рисунке, опираясь на значение коэффициентов а, b
и с.

1) у = –х²
+ 2х;

2) у = х²
+ 2х + 2;

3) у = 2х²
– 3х – 2;

4) у = х² –
2.

Решение.

По изображенному графику делаем
следующие выводы о коэффициентах а, b и с:

а > 0, так как ветви параболы
направлены вверх;

b ≠ 0, так как вершина параболы не
лежит на оси ОУ;

с = –2, так как парабола пересекает
ось ординат в точке (0; –2).

Всем этим условиям удовлетворяет
только функция у = 2х² – 3х – 2. Ответ: 3.

5. Определите, график какой
функции изображен на рисунке, опираясь на значение коэффициентов а, b
и с.

1) у = х² –
2х;

2) у = –2х²
+ х + 3;

3) у = –3х²
– х – 1;

4) у = –2,7х²
– 2х.

Решение.

По изображенному графику делаем
следующие выводы о коэффициентах а, b и с:

а < 0, так как ветви параболы
направлены вниз;

b ≠ 0, так как вершина параболы не
лежит на оси ОУ;

с = 0, так как парабола пересекает
ось ОУ в точке (0; 0).

Всем этим условиям удовлетворяет
только функция у = –2,7х² – 2х. Ответ: 4.

6. По графику функции у
= ах² + bх + с определите знаки коэффициентов а,
b и с:

а)
б)

Решение.

а) Ветви параболы направлены вверх,
поэтому а > 0.

Парабола пересекает ось ординат
в нижней полуплоскости, поэтому с < 0. Чтобы узнать знак
коэффициента b воспользуемся формулой для нахождения абсциссы вершины
параболы: m= — . По графику видно, что т
< 0, и мы определим, что а > 0. Поэтому b > 0.

б) Аналогично определяем знаки
коэффициентов а, b и с: а < 0, с > 0, b
< 0.

6.
Для
каждого графика укажите соответствующую ему формулу.

7.
Установите
соответствие между графиками функций и формулами, которые их задают.

8.
Установите
соответствие между графиками функций и формулами, которые их задают.

ГРАФИКИ

9.
Установите
соответствие между графиками функций и формулами, которые их задают.

10.
Установите
соответствие между графиками функций и формулами, которые их задают.

11.
Установите
соответствие между графиками функций и формулами, которые их задают.

12. На рисунке изображен
график функции y=ax²+bx+c. Найдите значение b.

13.
Найдите
значение k по графику y = ,
изображенному на рисунке.

14.

15.

16.
Найдите
значение по графику функции .

Если у нас график квадратичной
функции на рисунке пересекает ось ординат, то достаточно вместо x подставить 0. Получим y = c
— это и будет искомое значение. Если график на рисунке не
пересекает ось ординат то:

1. Найти значение a по графику функции y=ax²+ bx+c. Уравнение параболы y=a+bx+c запишем в другом виде: y=a(x—m)²+n, где (m;n)-
координаты вершины параболы

Поиск:

а)
(m;n) = (-4; 1) — вершина

б)
(x; y) = (-3; 0) — точка параболы

а)
a(-3+4)²+1=0

а
= -1

2.Найти значение b по графику функции y=a+bx+c. Уравнение параболы y= аx²+bx+c запишем в другом виде: y=a(x—m)²+ n, где (m—n)
— вершина параболы/ Формула абсциссы параболы: m=
, b=-2am, b=-2*(-1)*(-4)
= — 8, b = — 8.

3.Чтобы найти значение с, подставим в формулу функции y=ax²+bx+c
значение коэффициента а = -1, значение коэффициента b = -8, значение (x; y)
= (-3;0) — координат точки параболы.

0=
-1*(-3)²+(-8)*(-3)+с

0=
-9+24+с, с=-15.

Ответ:
-15.

17.
Найти
значение a по графику функции y=ax²+bx+c

Уравнение параболы y=a+bx+c запишем в другом виде: y = a(x—m)²+ n, где (m;n)
— координаты вершины параболы.

Поиск:

а)
(m;n) = (-4; 1)-вершина

б)
(x; y) = (-3; 0)-точка параболы

а*(-3+4)²+1=0

а
= -1

Ответ:
-1.

18.
График
какой из приведенных ниже функций изображен на рисунке?

1) y=-2) y=; 3) y= — ;
4) y=

Поиск:

1.
K<0 (ветви гиперболы в 2
и 4 четвертях). Тогда рассматриваем 1) и 3) функции;

2.
Выберем
на графике произвольную точку, например: A( 1; -2)

3.
Подставим
координаты точки А в 1) и 3) уравнение:

1)-2=-(верно)
3) -2= —(неверно)

Ответ: 1

19.
Укажите
номер рисунка, на котором изображён график функции y=-2x+3.

1)
                               2)
3)                                   4)

Поиск:

1.a>0 (ветви параболы — вверх),
тогда рассматриваем 1) и 2) рисунки;

2.Выберем на графиках
произвольную точку: 1) А(1; 2) 2) В(-1; 2)

3.Подставим координаты
точек А и В в уравнение:

1) 2=1²-2*1+3(верно)

2) 2=(-1)²-2(-1)+3(неверно)

Ответ:1.

20.
Укажите
номер рисунка на котором изображен график функции y=-

1) 2)
3) 4)

Поиск:

1.k=-2 (ветви гиперболы – во 2 и 4
четвертях)

2.Рассматриваем
3) и 4) рисунки.

3.Выберем
на графиках произвольные точки: 3) А(1; -0,5) и 4)В(1; -2)

4.Подставим
координаты точек А и В в уравнение:

3)
1*(-0,5)=-2(неверно)

4)1*(-2)=-2(верно)

Ответ:
4.

21.
Укажите
номер рисунка, на котором изображена гипербола.

Чтобы выполнить задание этой группы необходимо хорошо знать, как выглядят
графики каждой функции.

№1. График гипербола, k>0ветви гиперболы находятся в I и III
четвертях.

№2. Функция квадратичная, график
парабола, а<0 ветви направлены вниз.

№3. Функция линейная, график
прямая, k<0 функция убывающая.

№4.График функции

Ответ:1.

22.
Укажите
номер рисунка — график функции .

Функция
y=x²+2x-3 квадратичная, графиком является
парабола, а>0 ветви направлены вверх.

Ответ:
4.

23.
На
рисунке изображены графики функций вида y=
kx+b.Установите соответствие между
знаками коэффициентов k и b и графиками.

Графики

Коэффициенты

А)
k >0, b < 0;

Б)
k > 0; b > 0;

В)
k < 0; b < 0.

Решение.

Графиком функции вида y = kx + b является прямая, направление которой определяется знаками
коэффициентов k и b.

Используя данную таблицу, определяем по графику знаки
коэффициентов и .

1		2		3		4
	k<0 b <0		k > 0 b < 0		k > 0 b > 0		k < 0 b > 0

Ответ:
231.

24. Для каждой
функции, заданной формулой, укажите ее график.

Формулы

A)      y = -3x
Б)   y = —                             В)
y =

Графики

Решение.

Графиком функции вида y = kx является прямая, которая проходит через точку
(0;0) направлена в соответствии со знаком коэффициента .

Используя таблицу, определяем по графику знаки коэффициента .

1)		2)		3)
	k < 0 k < 0 имееют две формулы A) y = — 3x и Б) y = —. Для определения значения коэффициента выберем произвольную точку графика, например (1;-3) и подставим в формулу общего вида y = kx, получаем -3 = =k*1, k = — 3. Значит данному графику соответствует формула A) y = -3x		k > 0 k > 0 имеет формула В) y =		k < 0 k < 0 имееют две формулы A) y = -3x и Б) y = — . Для определения значения коэффициента выберем произвольную точку графика, например (3;-1) и подставим в формулу общего вида y = kx. Получаем *-1 =* k*3. . Значит данному графику соответствует формула Б) y = —
	Вывод:	А	Б	В
	1	3	2

Ответ:
132.

25.
Установите соответствие между графиками функций и формулами,
которые их задают.

Формулы

А) y = Б) y = В) y = —

Графики

Решение.

Графиком функции y = является гипербола,
расположение которой определяется знаком коэффициента k.

k > 0	k < 0

Используя таблицу, определяем по графику знаки коэффициента .

По
графикам 1 и 2 определяем , что k < 0, что соответствует формуле В) y = — . Для
определения соответствующего графика подставим координаты произвольной
точки каждого графика в формулу.

По
графикам 3 и 4 определяем , что k > 0, что соответствует формулам А) y = и Б) y = . Для определения
соответствующего графика подставим координаты произвольной точки
каждого графика в формулу.

Выберем
произвольную точку графика, например x = 1 и подставим в формулу В) y = — .
Получаем — = — 9.
что не соответствует графику.

Выберем
произвольную точку графика, например (3;-3) и подставим в формулу В) y = — .
Получаем –
3 = ,

т.
е. -3 = -3.

Вывод: B

Выберем
произвольную точку графика, например (3;3) и подставим:

Выберем произвольную
точку графика, например x = 1 и подставим

в оставшуюся формулу А) y = . Получаем

y = = , что соответствует
графику( при
значение ).

Вывод: А

в формулу

А) y
=

Получаем

3
.

в
формулу Б)
y =

Получаем
3=3.

Вывод:

Б
.

Анализируя все
рассуждения получаем

Ответ: 432.

26. Установите соответствие
между графиками функций и формулами, которые их задают.

Формулы

1) y = x² — 2           2)   y = x²          3) y = 2x
     4)   y = —

Графики

А)

Б)

В)

Решение.

А)		Б)		В)
Графиком является парабола, соответствующая формуле 1) y = x² — 2 (функция вида y = x², сдвинута на 2 единицы вниз).	Графиком является гипербола, соответствующая формуле 4) y = — .	Графиком является прямая, соответствующая формуле 3)

Ответ: 143.

27. На рисунке
изображены функции вида y
= ax² + bx
+ c. Установите соответствие между графиками и
знаками коэффициентов a и c.

Графики

Коэффициенты

1) a < 0, c >
0,

2) a < 0, c < 0,

3)
a > 0, c < 0,

4) a > 0, c > 0.

Решение.

Для определения знака коэффициента замечаем, что

a < 0 — ветви параболы направлены
вниз;

a > 0 — ветви параболы направлены
вверх.

Для
определения знака коэффициента c находим координату точки
пересечения параболы с осью Oy, это значение равно
коэффициенту c.

А		Б		В
a > 0, c > 0	a > 0, c > 0	a < 0, c > 0
Вывод:	А	Б	В
4	3	1

Ответ: 431.

28. На рисунке
изображены функции вида y = ax²
+ bx + c. Для каждого графика
укажите соответствующее ему значения коэффициента a
и дискриминанта D.

Графики

Знаки чисел

1) a > 0, D > 0

2) a
> 0, D < 0,

3) a
< 0, D > 0,

4)
a < 0, D < 0.

Решение.

Графиком функции вида y = ax²
+ bx + c является парабола.

При
этом возможны следующие случаи:

*a > 0*	*a < 0*
1. Парабола пересекает ось (т.е. уравнение ax² + bx + c = 0 имеет два корня, D > 0 ).

2. Парабола не пересекает ось (т.е. уравнение ax² + bx + c = 0 не имеет корней, D < 0).

3. Парабола пересекает ось в одной точке (т.е. уравнение ax² + bx + c = имеет один корень, D = 0).

Используя таблицу, определяем по графику знаки значения
коэффициента a и дискриминанта D.

a >
0, D > 0,

a <
0, D < 0

a >
0, D < 0

a < 0, D < 0

Вывод:

Ответ:
1423.

29.
Установите соответствие между графиками функций и формулами,
которые их задают.

Графики

Формулы

1) y
= 2x² + 6x + 3

2 y = 2x² — 6x + 3

3) y
= -2x² — 6x — 3

4) y = -2x² + 6x — 3

Решение.

А)		Б)		В)
По графику можно определить, что , , но этому условию соответствует две функции : 3) y = -2x² — 6x — 3 4) y = -2x² + 6x — 3 Для дальнейшего определения найдём абсциссу вершины параболы x_{0 =}	По графику можно определить, что a > 0, c = 3, но этому условию соответствует две функции : 1) y = 2x² + 6x + 3 2) y = 2x² — 6x + 3 Для дальнейшего определения найдём абсциссу вершины параболы x_{0 =}	По графику можно определить, что , a < 0, c = — 3, но этому условию соответствует две функции : 3) y = -2x² — 6x — 3 4) y = -2x² + 6x — 3 Для дальнейшего определения найдём абсциссу вершины параболы. x_{0 =}
3)y = -2x²— 6x — 3 x₀== -1,5Вывод: 3	4)y =-2x² +6x -3 x₀== 1,5 *— не соответствует графику.*	1) y = 2x² + 6x + 3 x₀== -1,5 Вывод: Б	2) y=2x²-6x+3 x₀= — не соответствует графику.	3)y = -2x²-6x -3 x₀= — не соответствует графику.	4)y = -2x²+6x— 3 x₀= Вывод: B

Анализируя все рассуждения, получаем:	А	Б	В
3	1	4

Ответ: 314.

30.
На
рисунке изображены графики функций вида y
= ax²
+ bx + c.
Установите
соответствие между утверждениями и промежутками, на которых эти утверждения
удовлетворяются.

Утверждения

А) Функция возрастает на
промежутке

Б) Функция убывает на
промежутке

Промежутки

Решение.

Ответ: 23.

31.
На
рисунке изображён график квадратичной функции y = f (x)

Какие
из следующих утверждений о данной функции являются верными? Запишите их номера.

1)
f (x) > 0 при x > 2.

2)
Функция убывает на промежутке

3) f (0) < f (5)

Решение.

1) f (x) > 0 при x > 2	2) Функция убывает на промежутке	3) f (0) < f (5)

Вывод: утверждение не верно.	Вывод: утверждение верно.	Вывод: утверждение не верно.

Ответ:
2.

1.
Установите соответствие между графиками функций и формулами,
которые их задают. Впишите в приведённую в ответе таблицу под каждой буквой
соответствующую цифру.

Графики функций

Формулы

1) y = x
+3 2) y = — 3x 3) y = 3 4) y = 3

2.
На
рисунке изображены графики функций вида. y = kx + b. Установите соответствие
между знаками коэффициентов k и b и графиками.

Графики

Коэффициенты

А)
k < 0, b < 0.

Б)
k < 0, b > 0

В)
k > 0, b < 0.

3.
Установите соответствие между графиками функций и формулами,
которые их задают.

Графики

А)

Б)

В)

Формулы

1) y = 2) y = 3)
y = — 4) y =

4. Установите
соответствие между графиками функций и формулами, которые их задают.

Формулы

1) y
= x²+ 2 2) y = — 3) y = 2x
4) y =

Графики

А)

Б)

В)

5. На рисунке
изображены функции вида . y
= ax²
+ bx + c.
Установите соответствие между графиками и знаками коэффициентов и .

Графики

Коэффициенты

1) a > 0, c <
0.

2) a < 0, c < 0

3) a > 0, c > 0

4) a < 0, c > 0

6. На рисунке
изображены функции вида y = ax²
+ bx + c.
Для каждого графика укажите соответствующее ему значения коэффициента и дискриминанта .

Графики

Знаки чисел

1) a > 0, D > 0

2) a
> 0, D < 0

3) a
< 0, D > 0

4)
a < 0, D < 0

7.
Установите соответствие между графиками функций и формулами, которые их задают.

Графики

Формулы

1) y = x²+7x + 16

2) y = — x²— 7x — 16

3) y = — x²+ 7x – 16

4) y = x²— 7x + 16

32.
На
рисунке изображён график квадратичной функции y = f (x)

Какие
из следующих утверждений о данной функции являются неверными? Запишите
их номера.

1) f (x) < 0 при x < 1

2)
Наибольшее значение функции равно 3;

3) f (x) > f (4)

33.
На
рисунке изображены графики функций вида y
= ax²
+ bx + c.
Установите соответствие
между утверждениями и промежутками, на которых эти утверждения удовлетворяются.

Утверждения

А) Функция возрастает на
промежутке

Б) Функция убывает на промежутке

Промежутки

2) [

3) [-3;-1]

4) [-2; 2]

10.

11.

1) Не секрет, что
успешнее сдает экзамен тот, кто в полном объеме владеет материалом, хорошо
знаком с процедурой проведения экзамена, психологически готов к экзамену и
адекватно реагирует на нестандартные ситуации.

2) Хорошо знать
документы, регламентирующие проведение экзамена по математике:

—
«Кодификатор требований к уровню подготовки обучающихся для
проведения основного государственного экзамена по математике»

—
«Кодификатор элементов содержания для проведения основного
государственного экзамена по математике»;

—
«Спецификация контрольных измерительных материалов для проведения
основного государственного экзамена по математике»;

—
«Демонстрационный вариант контрольных измерительных материалов для
проведения основного государственного экзамена по математике»;

—
Литературу для подготовки к ОГЭ.

—
Список сайтов, содержащих демоверсии и позволяющие
онлайн-тестироваться.

3) На основании
школьного плана подготовки к экзамену, составить личный план, включив в него
консультации, которые проводит учитель, расписание «пробных» ОГЭ.

4) Тщательно
анализировать пробные ОГЭ. По итогам пробных ОГЭ корректировать
самостоятельную подготовку к экзамену.

5) Собирать свой
портфолио-папку со всеми выполненными пробниками. Вести мониторинг выполнения
всех заданий пробных экзаменов.

6) Серьезное
внимание уделять устному счету, который проводит учитель на уроках. Эти
упражнения активизируют мыслительную деятельность, требуют осознанного усвоения
учебного материала. При их выполнении развивается память, речь, внимание,
быстрота реакции. Устные упражнения позволяют корректировать знания, умения и
навыки учащихся, а также автоматизировать навыки простейших вычислений и
преобразований.

7)
Научиться
«читать» условие задачи до начала решения и после ее решения для того, чтобы
верно ответить на поставленный вопрос (что нужно было найти?).

Математика – это
набор инструментов, который необходим в познании окружающего мира. И этим
инструментом необходимо владеть в совершенстве, чтобы познавать, развивать и
изменять нашу жизнь.

Все изученные в
школе функции относятся к классу элементарных функций, и строить графики этих
функций интересно и просто. А график является портретом функции, поэтому выполнять
задания следует после того, как изучен весь теоретический материал по теме.

В своей работе я
обобщила знания о функции, о их графиках и свойствах. Изучила и
систематизировала прототипы заданий ОГЭ, привела алгоритмы их решения. В
процессе этой работы наглядно видно, что задания по теме «Функции», представленные
в разных вариантах, имеют не одинаковый уровень сложности. Это подтверждает и
изучение результатов экзаменов 2013/14, 2014/15, 2015/17 учебных годов.

1)
3000 задач с ответами по математике. Задачник. ч.1._Ященко_2017 — 480с

2)
Учебное пособие «ОГЭ
2017. Математика. 9 класс. Основной государственный экзамен. Тематические
тестовые задания: Три модуля: алгебра, геометрия, реальная математика»
Минаевой С.С.

3)
ОГЭ-2017. Математика. Новый сборник заданий. Лаппо, Попов, 2017 -160 с

4)
https://infourok.ru/metodicheskoe-posobie-dlya-podgotovki-k-oge-po-teme-funkcii-i-grafiki-funkciy-1142155.html

5)
http://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2015/04/07/funktsii-i-grafiki-na-oge-po-matematike

6)
http://85.142.162.119/os11/xmodules/qprint/index.php?theme_guid=3a79f6089541e311b960001fc68344c9&proj_guid=AC437B34557F88EA4115D2F374B0A07B

7)
https://math-oge.sdamgia.ru/test?id=6473675&nt=True&pub=False

http://spadilo.ru/oge-po-matematike/

9)
https://www.youtube.com/watch?v=p9hegRGXD-4

10)
http://www.uchportal.ru/video/vic/ogeh_gia_po_matematike/zadacha_5

Источник

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции y=x^2 имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции y=x^2 , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент a=1 , то график квадратичной функции имеет ровно такую же форму, как график функции y=x^2 при любых значениях остальных коэффициентов.

График функции y=-x^2 имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции y=-x^2 симметричен графику функции y=x^2 относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) — это точки пересечения графика функции y=f(x) с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

Теперь внимание!

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если D<0 ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если a>0 ,то график функции выглядит как-то так:

2. Если D=0 ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если a>0 ,то график функции выглядит примерно так:

3. Если D>0 ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

$x_1={-b+sqrt{D}}/{2a}$ , $x_2={-b-sqrt{D}}/{2a}$

Если a>0 ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

$x_0=-{b/{2a}}$

$y_0=-{D/{4a}}=y(x_0)$

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как a=2>0 ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

$x_1={-3+7}/4=1$ , $x_1={-3-7}/4=-2,5$

3. Координаты вершины параболы:

$x_0=-{b/{2a}}=-3/4 =-0,75$

$y_0=-{D/{4a}}=-49/8=-6,125$

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

$x_0=-{b/{2a}}=-3/4 =-0,75$

$y_0=-{D/{4a}}=-49/8=-6,125$

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2. Уравнение квадратичной функции имеет вид — в этом уравнении x_0;y_0 — координаты вершины параболы

или в уравнении квадратичной функции a=1 , и второй коэффициент — четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

сначала построить график функции ,
затем одинаты всех точек графика умножить на 2,
затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции . В уравнении этой функции a=1 , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

2. Координаты вершины параболы: $x_0={x_1+x_2}/2={2-1}/2=1/2$

$y_0=y(-1)=({1/2}-2)({1/2}+1)=-9/4=-2,25$

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,

— сдвига графика функции вдоль оси от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

Скачать таблицу квадратичная функция

И.В. Фельдман, репетитор по математике.

Источник

Вы успешно справитесь с заданием 11 ОГЭ по математике в 2023 году при условии, что

Владеете понятием функция и связанными с ним основными понятиями, такими как область определения функции и область значений функции.
Знаете уравнения, свойства и графики
функций, которые изучали в курсе алгебры.
Умеете читать графики известных функций: по виду графика определять свойства функции.

Функция — это соответствие f (зависимость, правило) между двумя множествами X и Y, при котором каждому элементу множества X соответствует единственный элемент множества Y.

На рисунке изображены три соответствия: f , h и g
. Определим, какое из них является функцией, а какое – нет.

Соответствие f – функция. Обозначают f: X илиy=f( x).

X
– область определения функции, обозначают D (f).

Y
– область значений функции, обозначают E(f ).

Соответствие h не является функцией, так как не каждому элементу множества X соответствует элемент множества Y.

Соответствие g не является функцией так как элементу a
множества X соответствует два элемента (не единственный!) множества Y.

Рассмотрим несколько примеров того, как решать 11 задания ОГЭ по математике 2023.

Пример 1.
Найдите область определения и область значений функции y=

Решение. Дробь имеет смысл, когда её знаменатель не равен нулю, значит при этом подкоренное выражение может быть только положительным, то естьx-2>0. Итак, область определения функции (2; + . При x>2 y>0, значит область значений — (0; +

Напомним свойства функций, которые применяются в задании 11.

Пример 2.

На рисунках изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций. В таблице под каждой буквой запишите соответствующий номер.

Решение. На каждом из трёх рисунков обозначим угол a, который прямая составляет с положительным направлением оси Ox, а также точку пересечения прямой с осью Oy (см. рис.__). Рисунку 1 соответствует А (k<0, b<0), рисунку 2 — В (k<0,b>0), рисунку 3 – Б (k>0, b<0).

Заполняем таблицу

Ответ. 132.

Пример 3. Установите соответствие между графиками функций и формулами, которые их задают.

ГРАФИКИ

ФОРМУЛЫ

1) y= – x²– 2x+1 2) y= x²+2x– 1 3) y=x²– 2x– 1

Решение. Из трёх формул 1) — 3) только в формуле 3 старший коэффициент отрицательный, а из графиков только у графика В ветви параболы направлены вниз, значит В соответствует 1. В формуле 2 а в формуле 3 значит А соответствует 3, а Б – 2.

Ответ. 321

ГРАФИКИ

Решение. Графиком квадратичной функции А является парабола, значит А соответствует 3. График обратной пропорциональности Б гипербола 1, а графиком линейной функции В является прямая 2.

Ответ. 312

Вывод: функция на данном
промежутке не монотонна.

Вывод: функция на данном
промежутке возрастает, т.е. А

Вывод: функция на данном
промежутке убывает, т.е. Б

Вывод: функция на данном
промежутке не монотонна.

Анализируя все
рассуждения получаем