Как найти значение линейного коэффициента корреляции - AvtoShod.ru

Загрузить PDF

Коэффициент корреляции (или линейный коэффициент корреляции) обозначается как «r» (в редких случаях как «ρ») и характеризует линейную корреляцию (то есть взаимосвязь, которая задается некоторым значением и направлением) двух или более переменных. Значение коэффициента лежит между -1 и +1, то есть корреляция бывает как положительной, так и отрицательной. Если коэффициент корреляции равен -1, имеет место идеальная отрицательная корреляция; если коэффициент корреляции равен +1, имеет место идеальная положительная корреляция. В остальных случаях между двумя переменными наблюдается положительная корреляция, отрицательная корреляция или отсутствие корреляции. Коэффициент корреляции можно вычислить вручную, с помощью бесплатных онлайн-калькуляторов или с помощью хорошего графического калькулятора.

1
Соберите данные. Перед тем как приступить к вычислению коэффициента корреляции, изучите данные пары чисел. Лучше записать их в таблицу, которую можно расположить вертикально или горизонтально. Каждую строку или столбец обозначьте как «х» и «у».^[1]
- Например, даны четыре пары значений (чисел) переменных «х» и «у». Можно создать следующую таблицу:
  - x || y
  - 1 || 1
  - 2 || 3
  - 4 || 5
  - 5 || 7
2

Вычислите среднее арифметическое «х». Для этого сложите все значения «х», а затем полученный результат разделите на количество значений.^[2]
3

Найдите среднее арифметическое «у». Для этого выполните аналогичные действия, то есть сложите все значения «у», а затем сумму разделите на количество значений.^[3]
4

Вычислите стандартное отклонение «х». Вычислив средние значения «х» и «у», найдите стандартные отклонения этих переменных. Стандартное отклонение вычисляется по следующей формуле:^[4]
5

Вычислите стандартное отклонение «у». Выполните действия, которые описаны в предыдущем шаге. Воспользуйтесь той же формулой, но подставьте в нее значения «у».^[5]
6
Запишите основную формулу для вычисления коэффициента корреляции. В эту формулу входят средние значения, стандартные отклонения и количество (n) пар чисел обеих переменных. Коэффициент корреляции обозначается как «r» (в редких случаях как «ρ»). В этой статье используется формула для вычисления коэффициента корреляции Пирсона.^[6]
- $rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}}}right)*left({frac {y-mu _{y}}{sigma _{y}}}right)$
- Здесь и в других источниках величины могут обозначаться по-разному. Например, в некоторых формулах присутствуют «ρ» и «σ», а в других «r» и «s». В некоторых учебниках приводятся другие формулы, но они являются математическими аналогами приведенной выше формулы.
7

Вычислите коэффициент корреляции. Вы вычислили средние значения и стандартные отклонения обеих переменных, поэтому можно воспользоваться формулой для вычисления коэффициента корреляции. Напомним, что «n» – это количество пар значений обеих переменных. Значение других величин были вычислены ранее.^[7]
8
Проанализируйте полученный результат. В нашем примере коэффициент корреляции равен 0,988. Это значение некоторым образом характеризует данный набор пар чисел. Обратите внимание на знак и величину значения.^[8]
- Так как значение коэффициента корреляции положительно, между переменными «х» и «у» имеет место положительная корреляция. То есть при увеличении значения «х», значение «у» тоже увеличивается.
- Так как значение коэффициента корреляции очень близко к +1, значения переменных «х» и «у» сильно взаимосвязаны. Если нанести точки на координатную плоскость, они расположатся близко к некоторой прямой.
Реклама

1

В интернете найдите калькулятор для вычисления коэффициента корреляции. Этот коэффициент довольно часто вычисляется в статистике. Если пар чисел много, вычислить коэффициент корреляции вручную практически невозможно. Поэтому существуют онлайн-калькуляторы для вычисления коэффициента корреляции. В поисковике введите «коэффициент корреляции калькулятор» (без кавычек).
2
Введите данные. Ознакомьтесь с инструкциями на сайте, чтобы правильно ввести данные (пары чисел). Крайне важно вводить соответствующие пары чисел; в противном случае вы получите неверный результат. Помните, что на разных веб-сайтах различные форматы ввода данных.
- Например, на сайте http://ncalculators.com/statistics/correlation-coefficient-calculator.htm значения переменных «х» и «у» вводятся в двух горизонтальных строках. Значения разделяются запятыми. То есть в нашем примере значения «х» вводятся так: 1,2,4,5, а значения «у» так: 1,3,5,7.
- На другом сайте, http://www.alcula.com/calculators/statistics/correlation-coefficient/, данные вводятся по вертикали; в этом случае не перепутайте соответствующие пары чисел.
3

Вычислите коэффициент корреляции. Введя данные, просто нажмите на кнопку «Calculate», «Вычислить» или аналогичную, чтобы получить результат.

Реклама

1
Введите данные. Возьмите графический калькулятор, перейдите в режим статистических вычислений и выберите команду «Edit» (Редактировать).^[9]
- На разных калькуляторах нужно нажимать различные клавиши. В этой статье рассматривается калькулятор Texas Instruments TI-86.
- Чтобы перейти в режим статистических вычислений, нажмите [2nd] – Stat (над клавишей «+»). Затем нажмите F2 – Edit (Редактировать).
2
Удалите предыдущие сохраненные данные. В большинстве калькуляторов введенные статистические данные хранятся до тех пор, пока вы не сотрете их. Чтобы не спутать старые данные с новыми, сначала удалите любую сохраненную информацию.^[10]
- С помощью клавиш со стрелками переместите курсор и выделите заголовок «xStat». Затем нажмите Clear (Очистить) и Enter (Ввести), чтобы удалить все значения, введенные в столбец xStat.
- С помощью клавиш со стрелками выделите заголовок «yStat». Затем нажмите Clear (Очистить) и Enter (Ввести), чтобы удалить все значения, введенные в столбец уStat.
3
Введите исходные данные. С помощью клавиш со стрелками переместите курсор в первую ячейку под заголовком «xStat». Введите первое значение и нажмите Enter. В нижней части экрана отобразится «xStat (1) = __», где вместо пробела будет стоять введенное значение. После того как вы нажмете Enter, введенное значение появится в таблице, а курсор переместится на следующую строку; при этом в нижней части экрана отобразится «xStat (2) = __».^[11]
- Введите все значения переменной «х».
- Введя все значения переменной «х», с помощью клавиш со стрелками перейдите в столбец yStat и введите значения переменной «у».
- После ввода всех пар чисел нажмите Exit (Выйти), чтобы очистить экран и выйти из режима статистических вычислений.
4
Вычислите коэффициент корреляции. Он характеризует, насколько близко данные расположены к некоторой прямой. Графический калькулятор может быстро определить подходящую прямую и вычислить коэффициент корреляции.^[12]
- Нажмите Stat (Статистика) – Calc (Вычисления). На TI-86 нужно нажать [2nd] – [Stat] – [F1].
- Выберите функцию «Linear Regression» (Линейная регрессия). На TI-86 нажмите [F3], которая обозначена как «LinR». На экране отобразится строка «LinR _» с мигающим курсором.
- Теперь введите имена двух переменных: xStat и yStat.
  - На TI-86 откройте список имен; для этого нажмите [2nd] – [List] – [F3].
  - В нижней строке экрана отобразятся доступные переменные. Выберите [xStat] (для этого, скорее всего, нужно нажать F1 или F2), введите запятую, а затем выберите [yStat].
  - Нажмите Enter, чтобы обработать введенные данные.
5

Проанализируйте полученные результаты. Нажав Enter, на экране отобразится следующая информация:^[13]

Реклама

1
Разберитесь с понятием корреляции. Корреляция – это статистическая взаимосвязь двух величин. Коэффициент корреляции – это числовое значение, которое можно вычислить для любых двух наборов данных. Значение коэффициента корреляции всегда лежит в диапазоне от -1 до +1 и характеризует степень взаимосвязи двух переменных.^[14]
- Например, даны рост и возраст детей (около 12 лет). Скорее всего, здесь будет наблюдаться сильная положительная корреляция, потому что с возрастом дети становятся выше.
- Пример отрицательной корреляции: штрафные секунды и время, проведенное на тренировках по биатлону, то есть чем больше спортсмен тренируется, тем меньше штрафных секунд будет начислено.
- Наконец, иногда имеет место очень слабая корреляция (положительная или отрицательная), например, между размером обуви и оценками по математике.
2
Запомните, как вычислить среднее арифметическое. Чтобы вычислить среднее арифметическое (или среднее значение), нужно найти сумму всех данных значений, а затем разделить ее на количество значений. Помните, что среднее арифметическое необходимо для вычисления коэффициента корреляции.^[15]
- Среднее значение переменной обозначается буквой с горизонтальной чертой над ней. Например, в случае переменных «х» и «у» их средние значения обозначаются так: x̅ и y̅. Иногда среднее значение обозначается греческой буквой «μ» (мю). Чтобы записать арифметическое среднее значений переменной «х», используйте обозначение μ_x или μ(x).
- Например, даны следующие значения переменной «х»: 1,2,5,6,9,10. Среднее арифметическое этих значений вычисляется так:
3
Обратите внимание на важность стандартного отклонения. В статистике стандартное отклонение характеризует степень разброса чисел по отношению к их среднему значению. Если стандартное отклонение мало, числа расположены близко к среднему значению; если стандартное отклонение велико, числа расположены далеко от среднего значения.^[16]
- Стандартное отклонение обозначается буквой «s» или греческой буквой «σ» (сигма). Таким образом, стандартное отклонение значений переменной «х» обозначается так: s_x или σ_x.
4
Запомните символ, обозначающий операцию суммирования. Символ суммирования является одним из наиболее распространенных символов в математике и указывает на сумму значений. Этот символ представляет собой греческую букву «Σ» (прописная сигма).^[17]
- Например, если даны следующие значения переменной «х»: 1,2,5,6,9,10, то Σx означает:
  - 1 + 2 + 5 + 6 + 9 + 10 = 33.
Реклама

Советы

Коэффициент корреляции иногда называют «коэффициентом корреляции Пирсона» в честь его разработчика Карла Пирсона.
В большинстве случаев, когда коэффициент корреляции больше 0,8 (положительный или отрицательный), имеет место сильная корреляция; если же коэффициент корреляции меньше 0,5 (положительный или отрицательный), наблюдается слабая корреляция.

Предупреждения

Корреляция характеризует взаимосвязь значений двух переменных. Но помните, что корреляция не имеет ничего общего с причинно-следственной связью. Например, если сравнить рост и размер обуви людей, вы, вероятно, обнаружите сильную положительную корреляцию. Как правило, чем выше человек, тем больше размер обуви. Но это не означает, что увеличение роста приводит к автоматическому увеличению размера обуви, или что большие ноги приведут к ускоренному росту. Эти величины просто взаимосвязаны.

Об этой статье

Эту страницу просматривали 79 138 раз.

Была ли эта статья полезной?

Источник

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

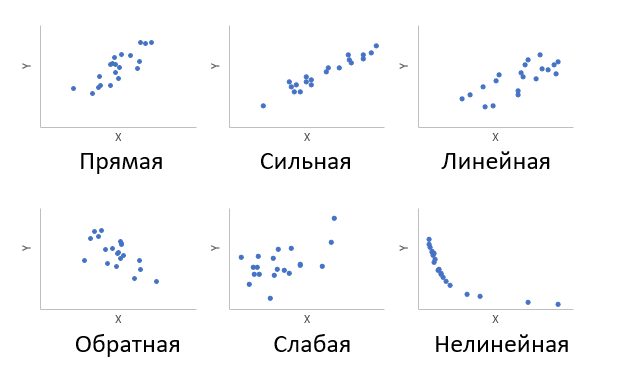
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

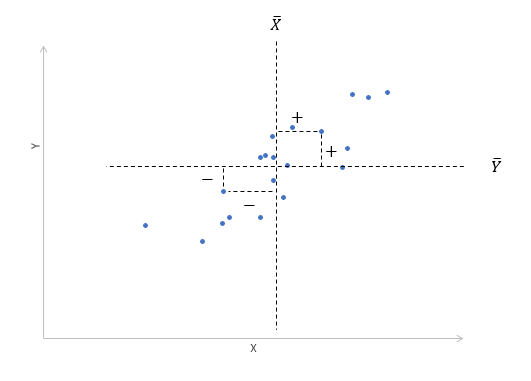
Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.

Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.

Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.

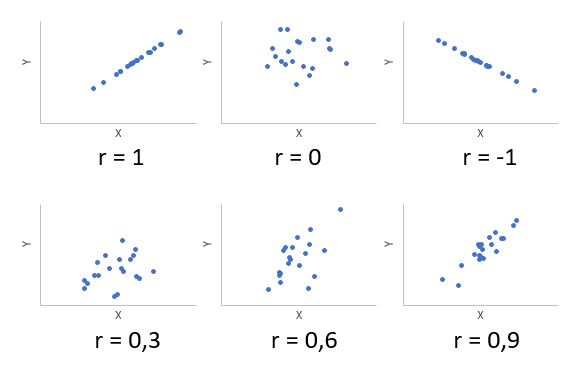
Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.

Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.

Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r², который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.

Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r² = 0,01 или 1%, при r = 0,5 r² = 0,25 или 25%.

Выборочный коэффициент корреляции

Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.

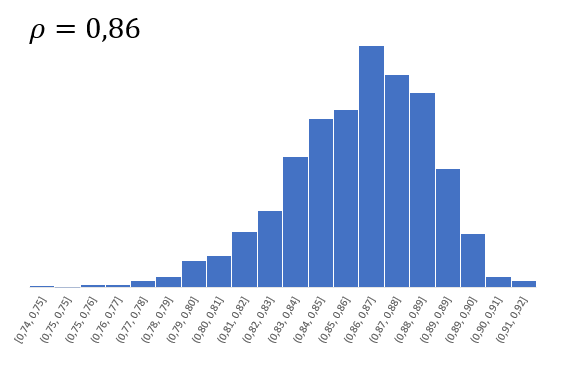
Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.

Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.

В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:

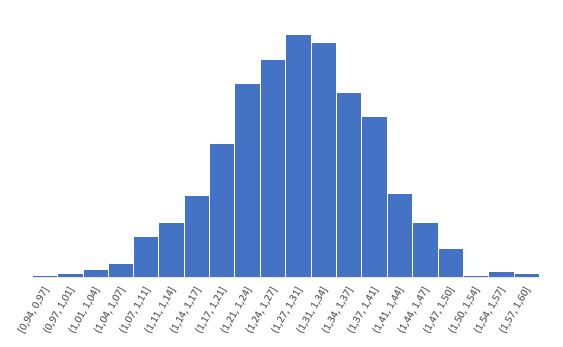
Распределение z для тех же r имеет следующий вид.

Намного ближе к нормальному. Стандартная ошибка z равна:

Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.

c_γ – квантиль стандартного нормального распределения;
N^-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.

Нижняя граница z:

Верхняя граница z:

Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:

Верхняя граница r:

Это была теоретическая часть. Переходим к практике расчетов.

Как посчитать коэффициент корреляции в Excel

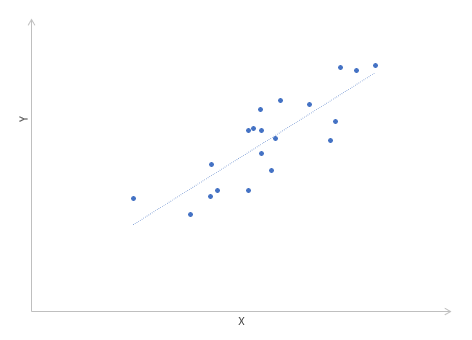
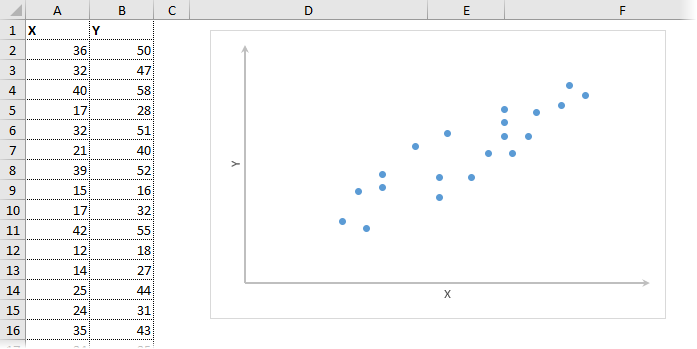
Корреляционный анализ в Excel лучше начинать с визуализации.

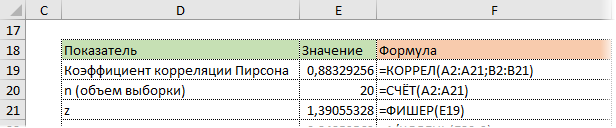
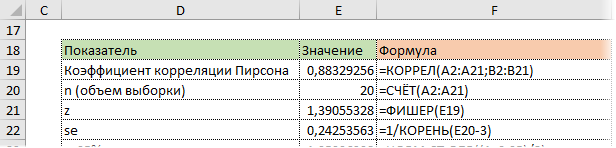
На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.

Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.

Расчет доверительного интервала для коэффициента корреляции в Excel

В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:

— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.

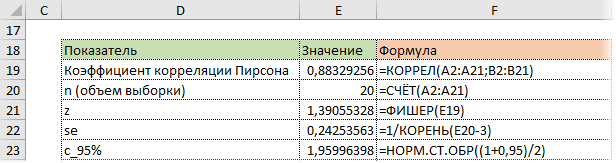
Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.

Стандартная ошибка z легко подсчитывается с помощью формулы.

Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.

Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.

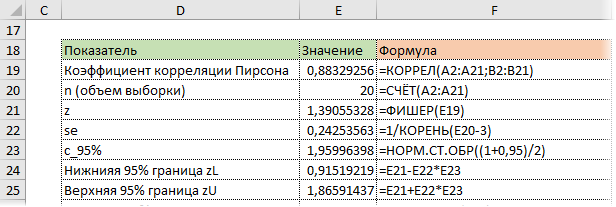
Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.

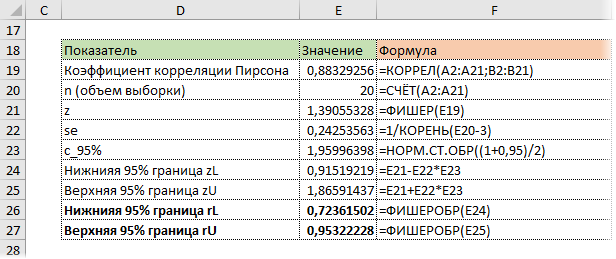
Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.

Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.

Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.

Несколько важных замечаний

1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).

2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.

3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.

В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.

↓ Скачать файл с примером ↓

Поделиться в социальных сетях:

Источник

Линейный коэффициент корреляции

Краткая теория

Под теснотой связи между
двумя величинами понимают степень сопряженности между ними, которая
обнаруживается с изменением изучаемых величин. Если каждому заданному
значению

соответствуют
близкие друг другу значения

, то связь считается тесной (сильной); если
же значения

сильно
разбросаны, то связь считается менее тесной.

Рассмотрим наиболее важный
для практики и теории случай линейной зависимости вида:

При тесной корреляционной
связи корреляционное поле представляет собой более или менее сжатый эллипс. Две
корреляционные зависимости переменной

от

приведены на рисунке.

Очевидно, что в случае (а)
зависимость между переменными менее тесная, чем в случае (б), так как точки
корреляционного поля (а) дальше отстоят от линии регрессии, чем точки поля (б).

Перейдем к оценке тесноты
линейной корреляционной зависимости. Для показателя тесноты связи нужная такая
стандартная система единиц измерения, в которой данные по различным
характеристикам оказались бы сравнимы между собой. Статистика знает такую
систему единиц. Эта система использует в качестве единицы измерения переменной
ее среднее квадратическое отклонение

Учтем, что

и запишем
уравнение парной линейной зависимости

в эквивалентном виде:

В этой системе величина:

показывает, на сколько
величин

изменится
в среднем

, когда

увеличится
на одно

Величина

является
показателем тесноты связи и называется линейным коэффициентом корреляции. Коэффициент
корреляции, определяемый по выборочным данным, называется выборочным коэффициентом корреляции.

Если

, то корреляционная связь между переменными
называется прямой, если

– обратной.

Приведем другие модификации
формулы для расчета линейного коэффициента корреляции:

или

Наиболее часто для расчета
используют формулу, получаемую простыми преобразованиями:

По этой формуле

находится
непосредственно из данных наблюдений и на значении

не
скажутся округления данных, связанных с расчетом средних и дисперсий.

Линейный выборочный
коэффициент корреляции

(при
достаточно большом объеме выборки

) обладает следующими свойствами:

, т.е.

. При этом, чем ближе по модулю

к
единице – тем теснее связь.
При

корреляционная
связь представляет собой линейную функциональную зависимость. При этом все
наблюдаемые значения располагаются на прямой линии.
При

линейная
корреляционная связь отсутствует. При этом линия регрессии параллельна оси

Расчет линейного коэффициента корреляции предполагает, что
переменные

распределены нормально. В других случаях
(когда распределения

отклоняются от нормальных) линейный
коэффициент корреляции не следует рассматривать как строгую меру взаимосвязи
переменных.

Пример решения задачи

Задача

Компания,
занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон
определенной модели цену, дифференцированную по регионам. Следующие данные
показывают цены на видеомагнитофон в 10 различных регионах о соответствующее им
число продаж:

Число продаж, шт.	420	380	350	400	440	380	450	425	430	480
Цена, тыс.руб.	5.6	6.0	6.5	6.0	5.0	6.4	4.5	5.0	5.7	4.4

Рассчитайте
выборочный коэффициент линейной корреляции и проверьте его значимость
при

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Составим
расчетную таблицу:

Вычислим
линейный коэффициент корреляции:

Вывод

Связь
между числом продаж и ценой очень тесная, обратная – с уменьшением цены
увеличивается объем продаж.

Проверим
значимость коэффициента корреляции:

По таблице критических точек t-критерия Стьюдента (по уровню значимости

и числу степеней свободы

) находим:

— коэффициент корреляции значим.

Кроме этой задачи на другой странице сайта есть еще

задача на расчет коэффициента корреляции, коэффициента детерминации, построение линии линейной регрессии и корреляционного поля.

Источник

Линейный коэффициент корреляции, обозначаемый буквой r – это мера линейной корреляции (отношение, учитывающее как интенсивность, так и направление) между двумя переменными. Оно находится в интервале от -1 до +1, причем знаки плюс и минус используются для представления положительной и отрицательной корреляции. Если линейный коэффициент корреляции равен -1, то отношение между двумя переменными – это идеальная отрицательная аппроксимация; если же он равен +1, то соотношение представляет собой идеальную положительную аппроксимацию. В других случаях, две переменные могут характеризоваться положительной корреляцией, отрицательной корреляцией или отсутствием корреляции. Если вам нужно найти коэффициент линейной корреляции, то начинайте читать шаг 1.

Часть 1 из 2: Основы

Усвойте концепцию корреляции. Корреляцией называется статистическое отношение между двумя величинами. Специалисты в области статистики часто используют корреляцию для того, чтобы определить взаимосвязь двух или более переменных.
Знайте, как найти среднее. Среднее арифметическое, или просто “среднее”, подборки данных вычисляется сложением всех значений и делением результата на количество значений.
- Среднее значение обозначается как символ переменной с горизонтальной чертой над ним.
Обратите внимание на важность среднеквадратического отклонения. В статистике среднеквадратическое отклонение является мерой варьирования и отражает то, как данные рассеяны по отношению к среднему значению.
- Математически среднеквадратическое отклонение обозначается как Sx, Sy, и так далее (что означает “среднеквадратическое отклонение x,” “ среднеквадратическое отклонение y,” и т.д.).
Разберитесь в записи суммы. Оператор суммы – один из самых распространенных в математике и означает сумму значений. Он обозначается заглавной греческой буквой сигма, или ∑.
Изучите простейшую формулу для расчета линейного коэффициента корреляции. Формула расчета линейного коэффициента корреляции использует средние значения, среднеквадратические отклонение и количество пар в группе данных (обозначаемых n). Она выглядит следующим образом:

Часть 2 из 2: Нахождение линейного коэффициента корреляции

Соберите все ваши данные. Чтобы рассчитать линейный коэффициент корреляции, сначала взгляните на ваши пары данных. Полезно записать их в виде таблицы.
- Допустим, например, что у вас есть пары данных x и y. Таблица будет выглядеть следующим образом:
Вычислите среднее значение x-ов. Чтобы вычислить среднее значение, вам нужно будет сложить все значения x, а затем разделить получившуюся сумму на количество значений, используя следующую формулу:
- В нашем примере у нас есть четыре значения для x. Чтобы вычислить среднее, сложите все значения x, а затем разделите их на 4. Ваши расчеты будут выглядеть так:
Найдите среднее значение y-ов. Чтобы найти среднее значение y-ов, придерживайтесь таких же шагов, сложив все значения y, а затем разделив их на количество значений:
- В нашем примере есть четыре значения y. Сложите все эти значения, а затем разделите ответ на 4. Ваши расчеты будут выглядеть так:
Определите среднеквадратическое отклонение x. Как только вы получите ваши средние значения, вы можете вычислить среднеквадратическое отклонение. Для этого воспользуйтесь следующей формулой:
- Для приведенного выше примера ваши расчеты должны выглядеть следующим образом:
- Обратите внимание, что часть уравнения, содержащая xi – среднее значение x, вычисляется вычитанием среднего из каждого значения x в вашей таблице.
Вычислите среднеквадратическое отклонение y. Используя такие же шаги, найдите среднеквадратическое отклонение y. Используйте следующую формулу:
- В нашем примере ваши расчеты будут иметь следующий вид:
- И снова, обратите внимание, что часть уравнения, содержащая yi – среднее значение y вычисляется вычитанием среднего из каждого значения y в вашей таблице.
Найдите линейный коэффициент корреляции. Теперь у вас есть средние значения и среднеквадратические отклонения ваших переменных, следовательно, вы можете переходить к к использованию формулы линейной корреляции. Помните, что n представляет собой число имеющихся у вас переменных. Другая информация относительно данной формулы была рассмотрена выше.
- В нашем примере вы должны вводить данные в формулу линейного коэффициента корреляции и производить вычисления следующим образом: Таким образом, коэффициент линейной корреляции будет равен 0,989949. Обратите внимание, что это число очень близко к +1, поэтому эти значения характеризуются сильной положительной корреляцией.

Советы

Линейный коэффициент корреляции иногда называют “коэффициентом корреляции Пирсона”, в честь предложившего его ученого, Карла Пирсона.
В общем, коэффициент линейной корреляции больше 0,8 (как положительный, так и отрицательный) отражает сильную корреляцию, коэффициент линейной корреляции менее 0,5 (опять же, как положительный, так и отрицательный) отражает слабую корреляцию.

Источник

Различные
экономические явления как на микро-,
так и на макроуровне не являются
независимыми, а связаны между собой
(цена товара и спрос на него, объём
производства и прибыль фирмы и.т.д.).

Эта
зависимость может быть строго
функциональной (детермированной) и
статистической.

Зависимость
между
иназываетсяфункциональной,
когда
каждому значению одного признака
соответствует одно единственное значение
другого признака. (Примером такой
однозначной зависимости может служить
зависимость площади круга от радиуса).

В
реальной действительности чаще
встречается иная связь между явлениями,
когда каждому значению одного признака
могут соответствовать несколько значений
другого (например, связь между возрастом
детей и их ростом).

Форма
связи, при которой один или несколько
взаимосвязанных показателей (факторов)
оказывают влияние на другой показатель
(результат) не однозначно, а с определенной
долей вероятности, называется
статистической.
В частности, если при изменении одной
из величин изменяется среднее значение
другой, то в этом случае статистическую
зависимость называют корреляционной.

В
зависимости от числа факторов, включаемых
в модель, различают парную
корреляцию
(связь двух переменных) и множественную
(зависимость результата от нескольких
факторов).

Корреляционный
анализ
состоит в определении направления,
формы и степени
связи (тесноты) между двумя (несколькими)
случайными признаками
и.

По
направлению
корреляция
бывает положительной
(прямой),
если при увеличении значений одной
переменной увеличивается значение
другой, и отрицательной
(обратной),
если при увеличении значений одной
переменной, уменьшается значение другой.

По
форме
корреляционная связь может быть линейной
(прямолинейной),
когда изменение значений одного признака
приводит к равномерному изменению
другого (математически описывается
уравнением прямой
),
икриволинейной,
когда изменение значений одного признака
приводит к неодинаковым изменениям
другого (математически она описывается
уравнениями кривых линий, например
гиперболы
,
параболыи т.д.).

Простейшей формой
зависимости между переменными является
линейная зависимость. И проверка наличия
такой зависимости, оценивание её
индикаторов и параметров является одним
из важнейших направлений эконометрики.

Существуют
специальные статистические методы и,
соответственно, показатели, значения
которых определённым образом
свидетельствуют о наличии или отсутствии
линейной связи между переменными.

3.1. Коэффициент линейной корреляции

Наиболее
простым, приближенным способом выявления
корреляционной связи является графический.

При
небольшом объеме выборки экспериментальные
данные представляют в виде двух рядов
связанных между собой значений
и.
Если каждую парупредставить точкой на плоскости,
то получится так называемоекорреляционное
поле (рис.1).

Если корреляционное
поле представляет собой эллипс, ось
которого расположена слева направо и
снизу вверх (рис.1в), то можно полагать,
что между признаками существует линейная
положительная связь.

Если корреляционное
поле вытянуто вдоль оси слева направо
и сверху вниз (рис.1г), то можно полагать
наличие линейной отрицательной связи.

В
случае же если точки наблюдений
располагаются на плоскости хаотично,
т.е корреляционное поле образует круг
(рис.1а), то это свидетельствует об
отсутствии связи между признаками.

На рис.1б представлена
строгая линейная функциональная связь.

Под
теснотой
связи между двумя величинами понимают
степень сопряженности между ними,
которая обнаруживается с изменением
изучаемых величин. Если каждому заданному
значению
соответствуют близкие друг другу
значения,
то связь считается тесной (сильной);
если же значениясильно разбросаны, то связь считается
менее тесной. При тесной корреляционной
связи корреляционное поле представляет
собой более или менее сжатый эллипс.

Количественным
критерием направления и тесноты линейной
связи является коэффициент
линейной корреляции.

Коэффициент
корреляции, определяемый по выборочным
данным, называется выборочным
коэффициентом корреляции. Он
вычисляется
по формуле:

где
,
текущие значения признаков
и;и
средние арифметические значения
признаков;
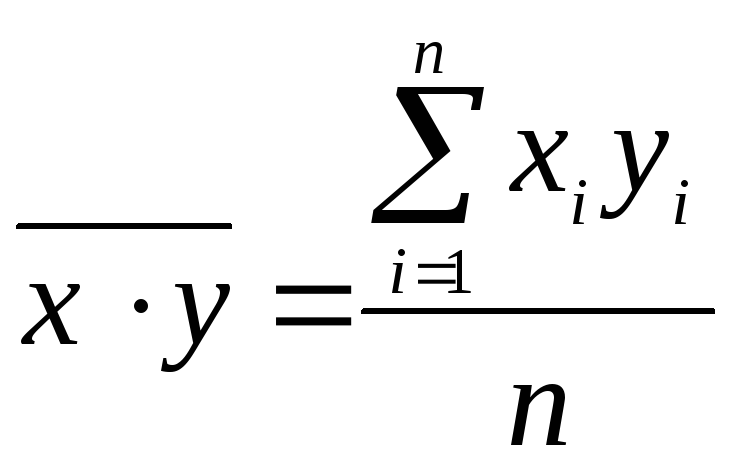
— среднее арифметическое произведений
вариант,и
средние квадратические отклонения этих
признаков;

объём выборки.

Для
вычисления коэффициента корреляции
достаточно принять предположение о
линейной связи между случайными
признаками. Тогда вычисленный коэффициент
корреляции и будет мерой этой линейной
связи.

Коэффициент
линейной корреляции принимает значения
от −1 в случае строгой линейной
отрицательной связи, до +1 в случае
строгой линейной положительной связи
(т.е.
).
Близость коэффициента корреляции к 0
свидетельствует об отсутствиилинейной
связи между признаками, но не об отсутствии
связи между ними вообще.

Коэффициенту
корреляции можно дать наглядную
графическую интерпретацию.

Если
,
то между признаками существует линейная
функциональная зависимость вида,
что означаетполную
корреляцию
признаков. При
,
прямая имеет положительный наклон по
отношению к оси,
при
отрицательный (рис. 1б).

Если
,
точкинаходятся в области ограниченной линией,
напоминающей эллипс. Чем ближе коэффициент
корреляции к,
тем уже эллипс и тем теснее точки
сосредоточены вблизи прямой линии. Приговорят оположительной
корреляции.
В этом случае значения
имеют тенденцию к возрастанию с
увеличением(рис.1в). Приговорят оботрицательной
корреляции;
значения
имеют тенденцию к уменьшению с ростом(рис.1г).

Если
,
то точкирасполагаются в области, ограниченной
окружностью. Это означает, что между
случайными признакамииотсутствует корреляция, и такие признаки
называютсянекоррелированными
(рис.1а).

Также
коэффициент линейной корреляции может
быть близок (равен) нулю, когда между
признаками есть связь, но она нелинейная
(рис.2).

При оценке тесноты
связи можно использовать следующую
условную таблицу:

Теснота связи	Величина коэффициента корреляции при наличии
прямой связи (+)	обратной связи (−)
Связь отсутствует
Связь слабая
Связь умеренная
Связь сильная
Полная функциональная

Заметим,
что в числителе формулы для выборочного
коэффициента линейной корреляции
величин
ис
тоит ихпоказатель
ковариации:

Этот
показатель, как и коэффициент корреляции
характеризует степень линейной связи
величин
и.
Если он больше нуля, то связь между
величинами положительная, если меньше
нуля, то связь – отрицательная, равен
нулю – линейная связь отсутствует.

В
отличие от коэффициента корреляции
показатель ковариации нормирован – он
имеет размерность, и его величина зависит
от единиц измерения
и.
В статистическом анализе показатель
ковариации обычно используется, как
промежуточный элемент расчёта коэффициента
линейной корреляции. Т.о. формула расчёта
выборочного коэффициента корреляции
приобретает вид: