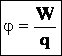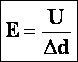Электрический потенциал — это скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.
Если вы хотите расширить свои знания об электрическом потенциале или сначала узнать, что такое электрический потенциал, то вы пришли по адресу.
Простое объяснение
В классической механике рассмотрение проблемы с точки зрения энергии может значительно упростить ситуацию по сравнению с рассмотрением ее с точки зрения сил, действующих на систему. В частности, в этом контексте существенную роль играет тот факт, что энергия является сохраняющейся переменной.
Также в классической электродинамике рассмотрение на энергетическом уровне оказывается очень полезным. Поэтому электрический потенциал φ (также называемый электростатическим потенциалом) определяется как отношение потенциальной энергии Eпот пробного электрического заряда и его величины электрического заряда q: φ = Eпот / q .
Возможность определения такого электрического потенциала обусловлена тем, что электрическое поле E распределения заряда и результирующая электростатическая сила Fc на пробном электрическом заряде является консервативной силой, подобной гравитационной силе.
Электрический потенциал имеет единицу измерения вольт В или также джоуль на кулон Дж / Кл .
Формулы
В этом разделе мы познакомим вас с двумя важными формулами для электрического потенциала определенных распределений электрических зарядов. Мы также кратко обсудим аналогию между электрическим потенциалом и гравитацией.
Пластинчатый конденсатор
Мы рассматриваем ситуацию, когда две плоские пластины расположены параллельно на расстоянии d друг от друга. Кроме того, пусть одна из двух пластин заряжена положительно, а другая — отрицательно. Такая комбинация также называется пластинчатым конденсатором. Обозначим точку на положительной пластине через A, а точку на отрицательной пластине через B. Тогда для разности потенциалов между этими двумя точками получим:
φВ — φA = — E * d .
Здесь E — величина электрического поля между двумя пластинами, которое предполагается однородным. Такая разность потенциалов также называется электрическим напряжением, которое существует между этими двумя точками.
Из этого уравнения видно, что электрический потенциал на положительно заряженной пластине (пластина A) выше, чем потенциал на отрицательно заряженной пластине (пластина B). Поэтому положительный заряд в пластинчатом конденсаторе перемещается к отрицательной пластине. В общем случае электрическое поле — а значит, и направление движения положительного заряда — направлено в ту сторону, в которой электрический потенциал убывает быстрее всего.
Аналогия с гравитационным полем
Если умножить уравнение (приведенное выше в статье) на величину электрического заряда q пробного электрического заряда и предположить, что отрицательно заряженная пластина имеет электрический потенциал, равный нулю, то электрическая потенциальная энергия на расстоянии h от пластины равна:
Eпот. эл = q * φ = q * E * h
Здесь φ обозначает электрический потенциал в точке пробного электрического заряда.
Сравним это уравнение с потенциальной энергией в однородном гравитационном поле:
Eпот. гр = m * g * h .
Мы определяем, что количество заряда электрического q играет роль массы m, а величина электрического поля E играет роль гравитационного ускорения g. Масса, находящаяся на высоте h над землей, ускоряется по направлению к земле под действием земного притяжения.
Таким образом, масса движется в том направлении, в котором уменьшается ее потенциальная энергия. Аналогично, положительный электрический заряд движется в направлении, в котором его электрическая потенциальная энергия будет уменьшаться. Поскольку электрическая потенциальная энергия и электрический потенциал линейно связаны, это наблюдение аналогично тому, что положительно заряженная частица движется в направлении уменьшения электрического потенциала.
Подобно потенциальной энергии, только разность потенциалов имеет физический смысл, поскольку при определении электрического потенциала необходимо произвольно определить точку отсчета, от которой затем можно обозначить другие точки в пространстве. В этом смысле электрический потенциал сам по себе не имеет реального физического смысла, поскольку для данной точки в пространстве его значение можно изменить, выбрав другую точку отсчета. Таким образом, электрический потенциал ведет себя подобно высоте, потому что вы не можете говорить о высоте, пока у вас нет точки отсчета.
На топографической карте — пути, вдоль которых высота не меняется, называются изолиниями. Аналогично, пути, вдоль которых электрический потенциал постоянен, называются эквипотенциальными линиями.
Заряженные частицы
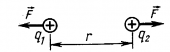
Предположим, что частица с зарядом q находится в начале выбранной нами системы координат. Пусть положение другой точки равно r и пусть r — расстояние между двумя точками. Для электрического потенциала в точке r действует следующее соотношение:
φ (r) = q / 4 * π * ε0 * r ,
здесь ε0 — электрическая постоянная.
В этом уравнении предполагается, что под действием электрического поля положительный пробный электрический заряд переносится из бесконечности в положение r.
Примеры задач
Наконец, давайте вместе рассчитаем небольшой пример. Предположим, что электрон ускоряется от отрицательно заряженной пластины к положительно заряженной через разность потенциалов 2000 В. Как изменяется потенциальная энергия электрона?
Для разности электрических потенциалов между двумя пластинами: φB — φA = ΔEпот / q , преобразованной в искомое изменение потенциальной энергии, получаем:
ΔEпот = q * ( φB — φA ) .
Величина электрического заряда электрона равна qe = e = — 1,6 * 10-19 Кл и поэтому получаем:
ΔEпот = e * ( φB — φA ) = — 1,6 * 10-19 Кл * 2000 В = -3,2 * 10-19 Дж.
Обратите внимание, что [ В ] = Дж / Кл. Кроме того, мы предположили, что пластина с точкой B заряжена положительно, поэтому перед 2000 В нет знака минус. Расчет показывает, что потенциальная энергия электрона уменьшается.
Список использованной литературы
- Соколович Ю. А., Богданова Г. С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Мякишев Г. Я., Буховцев Б. Б., Сотский Н. Н. Физика: Учеб. для общеобразоват. учреждений. Базовый и профильный уровни. 19-е издание – М.: Просвещение, 2010.
Потенциал. Эквипотенциальные поверхности.
В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W1 — W2 на заряд q, получим
Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.
Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:
Единица потенциала — вольт:
Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.
С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде
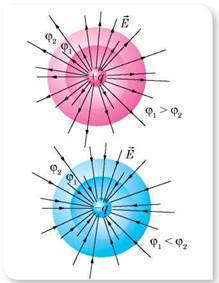
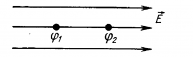
Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ1 — φ2 )> 0, то потенциал φ1 больше чем потенциал φ2 . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.
Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ∞ ). Поскольку φ∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,
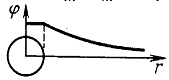
Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле
По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.
Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.
Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.
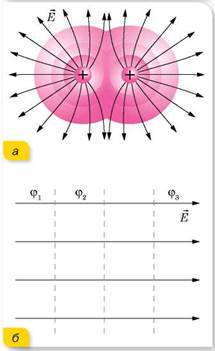
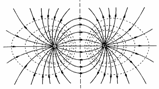
В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ1 + φ2 + φ3 . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.
Разность потенциалов
Практическое значение имеет не сам потенциал в точке, а изменение (разница) потенциала φ1 — φ2 , которое не зависит от выбора нулевого уровня отсчета потенциала. Разность потенциалов φ1 — φ2 еще называют напряжением и обозначают латинской буквой U. Тогда формула для работы по перемещению заряда приобретает вид
Напряжение U — это физическая величина, определяемая работой электрического поля по перемещению единичного положительного заряда между двумя точками поля,
Единица разности потенциалов (напряжения), как и потенциала, — вольт,
Поскольку работа сил поля по перемещению заряда зависит только от разности потенциалов, то в случае перемещения заряда с первой эквипотенциальной поверхности на другую (потенциалы которых соответственно φ1 и φ2 ) выполненная полем работа не зависит от траектории этого движения.
Связь напряженности электрического поля с напряжением
Из формул A = Eqd и A = qU можно установить связь между напряженностью и напряжением электрического поля: Ed = U. С этой формулы следует:
- чем меньше меняется потенциал на расстоянии d, тем меньше есть напряженность электрического поля;
- если потенциал не меняется, то напряженность равна нулю;
- напряженность электрического поля направлена в сторону уменьшения потенциала.
Поскольку
то именно из этой формулы и выводится еще одна единица напряженности — вольт на метр,
|
Потенциал. Разность потенциалов. Напряжение. |
|
|
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: — энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. |
|
|
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. |
|
|
— следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически). |
|
|
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах: |
|
|
Разность потенциалов |
|
|
|
|
|
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! |
|
|
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
|
|
Связь между напряженностью и напряжением. |
|
|
Из доказанного выше: напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). |
|
|
Из этого соотношения видно:
|
|
|
Эквипотенциальные поверхности. ЭПП — поверхности равного потенциала. Свойства ЭПП: — работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; — вектор напряженности перпендикулярен к ЭПП в каждой ее точке. |
|
|
|
|
|
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. |
|
|
Потенциальная энергия взаимодействия зарядов. |
|
|
|
|
|
Потенциал поля точечного заряда |
|
|
|
|
|
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. |
|
|
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. |
Содержание
- Разность электрических потенциалов
- Знаки и значения разности потенциалов
- Как рассчитать электрический потенциал?
- Электрический потенциал для дискретных распределений заряда
- Электрический потенциал при непрерывном распределении нагрузки
- Примеры электрического потенциала
- Аккумуляторы и батарейки
- Выход
- Напряжение между заряженными облаками и землей
- Генератор Ван дер Граффа
- Электрокардиограмма и электроэнцефалограмма
- Упражнение решено
- Решение для
- Решение б
- Решение c
- Решение d
- Решение e
- Решение f
- Ссылки
В электрический потенциал он определяется в любой точке, где существует электрическое поле, как потенциальная энергия этого поля на единицу заряда. Точечные заряды и точечные или непрерывные распределения зарядов создают электрическое поле и, следовательно, имеют связанный потенциал.
В Международной системе единиц (СИ) электрический потенциал измеряется в вольтах (В) и обозначается буквой V. Математически он выражается как:
V = U / qили
Где U — потенциальная энергия, связанная с зарядом или распределением, а qили это положительный тестовый заряд. Поскольку U — скаляр, значит и потенциал.
Согласно определению, 1 вольт — это просто 1 джоуль / кулон (Дж / Кл), где джоуль — это единица измерения энергии в системе СИ, а кулон (Кл) — это единица измерения электрического заряда.
Предположим, что точечный заряд q. Мы можем проверить природу поля, создаваемого этим зарядом, используя небольшой положительный тестовый заряд, называемый qили, используется как зонд.
Работа W, необходимая для перемещения этого небольшого груза из точки к до точки б, является отрицательной величиной разности потенциальная энергия ΔU между этими точками:
Wа → б = -ΔU = — (Uб — ИЛИк)
Делим все между qили:
Wа → б / qили= — ΔU / qили = — (Uб — ИЛИк) / qили = — (Vб — Vк) = -ΔV
Здесь Vб — потенциал в точке b и Vк это точка а. Разность потенциалов Vк — Vб потенциал о б и называется Vab. Порядок нижних индексов важен, если бы он был изменен, он представлял бы потенциал b относительно a.
Разность электрических потенциалов
Из вышеизложенного следует, что:
-ΔV = Wа → б / qили
Таким образом:
ΔV = -Wа → б / qили
Теперь работа рассчитывается как интеграл от скалярного произведения между электрическими силами F между q и qили а вектор смещения dℓ между точками а и б. Поскольку электрическое поле — это сила на единицу заряда:
А ТАКЖЕ = F/ qили
Работа по переносу испытательной нагрузки от a до b:
Это уравнение предлагает способ напрямую вычислить разность потенциалов, если электрическое поле заряда или его порождающее распределение известно ранее.
Также отмечается, что разность потенциалов — это скалярная величина, в отличие от электрического поля, которое является вектором.
Знаки и значения разности потенциалов
Из предыдущего определения мы видим, что если А ТАКЖЕ и гℓ перпендикулярны, разность потенциалов ΔV равна нулю. Это не означает, что потенциал в таких точках равен нулю, а просто то, что Vк = Vб, то есть потенциал постоянен.
Линии и поверхности, на которых это происходит, называются эквипотенциальный. Например, эквипотенциальные линии поля точечного заряда представляют собой окружности, концентрические заряду. А эквипотенциальные поверхности представляют собой концентрические сферы.
Если потенциал создается положительным зарядом, электрическое поле которого состоит из радиальных линий, проецирующих заряд, по мере удаления от поля потенциал будет становиться все меньше и меньше. В качестве тестовой нагрузки qили положительный, он чувствует меньшее электростатическое отталкивание, чем дальше от q.
Напротив, если нагрузка какие отрицательный, пробный заряд qили (положительный) будет иметь более низкий потенциал по мере приближения к q.
Как рассчитать электрический потенциал?
Приведенный выше интеграл служит для нахождения разности потенциалов и, следовательно, потенциала в данной точке б, если опорный потенциал известен в другой точке к.
Например, в случае точечной нагрузки какие, вектор электрического поля которого в точке, находящейся на расстоянии р нагрузки составляет:
А ТАКЖЕ = kq / r2р
Где k — электростатическая постоянная, значение которой в единицах Международной системы составляет:
к = 9 х 10 9 Нм2 / C2.
И векторр— единичный вектор вдоль линии, соединяющей какие с точкой P.
Он заменяется в определенииΔV:
Выбирая эту точку б быть на расстоянии р заряда и что при a → ∞ потенциал равен 0, то Vк = 0, а предыдущее уравнение выглядит так:
V = kq / r
Выберите Vк = 0, когда a → ∞ имеет смысл, потому что в точке, очень далекой от нагрузки, трудно понять, что она существует.
Электрический потенциал для дискретных распределений заряда
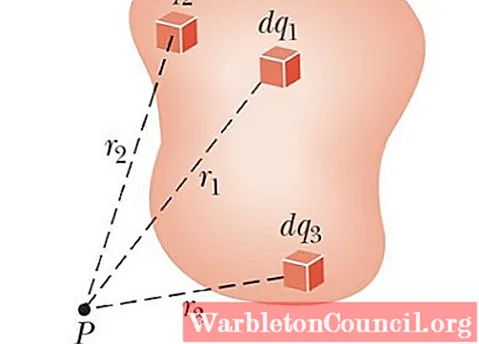
Когда в области распределено много точечных зарядов, электрический потенциал, который они создают в любой точке P в пространстве, вычисляется путем сложения индивидуальных потенциалов, которые производит каждый из них. Так:
V = V1 + V2 + V3 +… VN = ∑ Vя
Суммирование простирается от i = до N, и потенциал каждого заряда рассчитывается с использованием уравнения, приведенного в предыдущем разделе.
Электрический потенциал при непрерывном распределении нагрузки
Исходя из потенциала точечного заряда, потенциал, создаваемый заряженным объектом измеримого размера, можно найти в любой точке P.
Для этого тело делится на множество мелких бесконечно малых зарядов. dq. Каждый вносит свой вклад в полный потенциал dV бесконечно малый.
Затем все эти вклады складываются через интеграл, и таким образом получается полный потенциал:
Примеры электрического потенциала
В различных устройствах, благодаря которым можно получать электроэнергию, есть электрический потенциал, например, аккумуляторы, автомобильные аккумуляторы и электрические розетки. Электрические потенциалы также возникают в природе во время грозы.
Аккумуляторы и батарейки
В элементах и батареях электрическая энергия сохраняется за счет химических реакций внутри них. Это происходит, когда цепь замыкается, позволяя протекать постоянному току и зажигать лампочку или запускать стартер автомобиля.
Они бывают разного напряжения: 1,5 В, 3 В, 9 В и 12 В являются наиболее распространенными.
Выход
Бытовые приборы и устройства, работающие от сети переменного тока, подключаются к встроенной розетке. В зависимости от местоположения напряжение может составлять 120 В или 240 В.
Напряжение между заряженными облаками и землей
Это тот, который возникает во время грозы из-за движения электрического заряда в атмосфере. Может быть порядка 108 В.
Генератор Ван дер Граффа
Благодаря резиновой конвейерной ленте образуется заряд трения, который накапливается на токопроводящей сфере, помещенной на изолирующий цилиндр. Это создает разность потенциалов, которая может составлять несколько миллионов вольт.
Электрокардиограмма и электроэнцефалограмма
В сердце есть специализированные клетки, которые поляризуются и деполяризуются, вызывая разность потенциалов. Их можно измерить как функцию времени с помощью электрокардиограммы.
Этот простой тест проводится путем размещения на груди человека электродов, способных измерять слабые сигналы.
Поскольку они имеют очень низкое напряжение, вам нужно удобно их усилить, а затем записать на бумажную ленту или просмотреть через компьютер. Врач анализирует пульс на предмет отклонений и таким образом обнаруживает проблемы с сердцем.
Электрическую активность головного мозга также можно записать с помощью аналогичной процедуры, называемой электроэнцефалограммой.
Упражнение решено
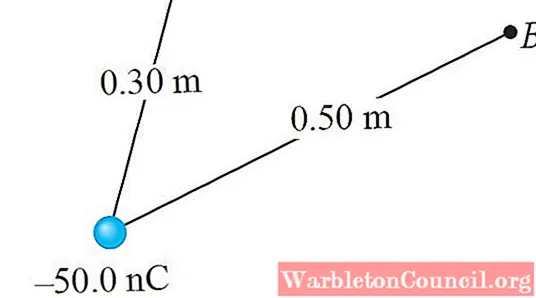
Нагрузка Q = — 50,0 нКл находится на расстоянии 0,30 м от точки К и 0,50 м от точки B, как показано на следующем рисунке. Ответьте на следующие вопросы:
а) Каков потенциал в А, создаваемый этим зарядом?
б) А каков потенциал у B?
c) Если заряд q перемещается от A к B, через какую разность потенциалов он перемещается?
г) Согласно предыдущему ответу, его потенциал увеличивается или уменьшается?
д) Если q = — 1,0 нКл, каково изменение его электростатической потенциальной энергии при перемещении от A к B?
е) Какую работу совершает электрическое поле, создаваемое Q, при перемещении испытательного заряда от А к В?
Решение для
Q — точечный заряд, поэтому его электрический потенциал в A рассчитывается по формуле:
VК = kQ / rК = 9 х 109 х (-50 х 10-9) / 0,3 В = -1500 В
Решение б
Точно так же
VB = kQ / rB = 9 х 109 х (-50 х 10-9) / 0,5 В = -900 В
Решение c
ΔV = Vб — Vк = -900 — (-1500) В = + 600 В
Решение d
Если заряд q положительный, его потенциал увеличивается, но если он отрицательный, его потенциал уменьшается.
Решение e
ΔV = ΔU / qили → ΔU = qили ΔV = -1,0 х 10-9 х 600 Дж = -6,0 х 10-7 Дж.
Отрицательный знак вΔU указывает на то, что потенциальная энергия в B меньше, чем у A.
Решение f
Поскольку W = -ΔU, поле реализует+6,0 х 10-7 J работы.
Ссылки
- Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 5. Электростатика. Отредактировал Дуглас Фигероа (USB).
- Джамбаттиста, А. 2010. Физика. 2-й. Эд. Макгроу Хилл.
- Резник, Р. (1999). Физический. Том 2. 3-е изд. На испанском языке. Compañía Editor Continental S.A. de C.V.
- Типлер П. (2006) Физика для науки и техники. 5-е изд., Том 2. От редакции Reverté.
- Сервей, Р. Физика для науки и техники. Том 2. 7-е. Под ред. Cengage Learning.
Как определить потенциал
Потенциал является энергетической характеристикой электрического поля. Для того чтобы найти его значение, нужно потенциальную энергию заряда в данной точке электрического поля поделить на сам заряд. Для различных типов полей используются разные формулы расчета потенциала.
Вам понадобится
- — линейка.
Инструкция
Если известна потенциальная энергия заряда тела в данной точке электрического поля (условно, это работа по перемещению заряда в бесконечность), то найдите потенциал, поделив эту потенциальную энергию в Джоулях на величину заряда в Кулонах: φ=Wp/q,где: φ — величина искомого потенциала,Wp — потенциальная энергия заряда тела,q — величина заряда.Потенциал измеряется в вольтах.
Если электрическое поле образовано точечным зарядом, то для определения потенциала его поля в любой точке, найдите расстояние от этой точки до заряда. Тогда потенциал поля в данной точке будет равен произведению коэффициента 9•10^9 на значение заряда поделенному на расстояние до заряда в метрах: φ=9•10^9•q/r,где:r — расстояние до заряда.
В том случае, когда поле образуется сферой, то рассматривайте два случая. Потенциал поля в точке, которая находится внутри сферы или на ее поверхности равен произведению коэффициента 9•10^9 на заряд сферы, поделенный на ее радиус:φ=9•10^9•Q/R, где:Q — заряд сферы,R — радиус сферы. Данная формула применяется независимо от того, в каком месте сферы находится точка пространства.
Если точка пространства находится вне сферы, то рассчитайте потенциал поля как произведение коэффициента 9•10^9 на значение заряда сферы поделенного на расстояние от точки пространства до центра сферы:φ=9•10^9•Q/R,в данном случае, R — расстояние от точки до центра сферы.
Для того чтобы определить потенциал поля, образованного другими заряженными поверхностями, с помощью теоремы Гаусса определите напряженность поля, образованного этими поверхностями. После этого найдите расстояние от поверхности до точки пространства, в которой определяется потенциал. Для этого из точки опустите перпендикуляр к поверхности. Чтобы найти потенциал, умножьте значение напряженности электрического поля в данной точке на измеренное расстояние:φ=Е•d, где:Е — значение напряженности электрического поля,d — расстояние от поверхности до точки.
Если между источником электрического поля находится некоторое вещество, то все результаты, которые получаются при расчете, нужно поделить на значение диэлектрической проницаемости среды, которая находится между точкой поля и его источником.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.