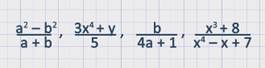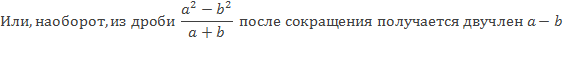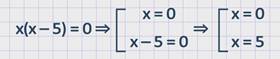- Учебники
- 8 класс
- Алгебра 👍
- Макарычев
- №4
авторы: Макарычев, Миндюк, Нешков, Суворова.
издательство: «Просвещение» 2013 г
Раздел:
- ГЛАВА I. РАЦИОНАЛЬНЫЕ ДРОБИ
- §1. РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ СВОЙСТВА
- 1. Рациональные выражения
ГДЗ учебник по алгебре 8 класс Макарычев. 1. Рациональные выражения. Номер №4
- Предыдущее
- Следующее
Найдите значение дроби:
а)
a
−
8
2
a
+
5
при a = −2;
б)
b
2
+
6
2
b
при b = 3.
reshalka.com
ГДЗ учебник по алгебре 8 класс Макарычев. 1. Рациональные выражения. Номер №4
Решение а
a
−
8
2
a
+
5
=
−
2
−
8
2
∗
(
−
2
)
+
5
=
−
10
−
4
+
5
=
−
10
1
=
−
10
Решение б
b
2
+
6
2
b
=
3
2
+
6
2
∗
3
=
9
+
6
6
=
15
6
=
5
2
=
2
,
5
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
ГДЗ и решебники
вип уровня
- ГДЗ
- 8 класс
- Алгебра
- Макарычев
- Задание 4
Условие
Найдите значение дроби:
а) a-8/2a+5 при а = -2; б) b^2+6/2b при b = 3.
Решение 1
Другие задачи из этого учебника
Популярные решебники
Сложение ⭐ и вычитание дробей с одинаковыми знаменателями: правила, примеры задач
Понятие дроби и ее основные свойства
Понятие «дроби» используют, когда характеризуют доли.
Определение 1
Доли — равные части целого.
Пример 1
Например, если разделить шоколадку на равные части, то каждая часть станет долей.
Предположим, шоколадку разделили на 10 равных частей. По одному кусочку раздали десяти ребятам. Тогда каждый получил «одну десятую долю шоколадки» или «одну десятую шоколадки». Пишут: 110 шоколадки.
Примечание 1
Существуют специальные наименования для некоторых долей:
- 12— одну вторую предмета или объекта — называют половиной;
- 13— одну третью предмета или объекта — третью;
- 14— одну четвертую предмета или объекта — четвертью.
Пример 2
Пиццу разрезали на 7 долей. Даша съела 3 доли. Осталось 4 доли пиццы. Оставшиеся четыре доли обозначают 47.
Записи числа вида 47 называют обыкновенными дробями. Их используют для описания количества долей. Число 4 — числитель, 5 — знаменатель. Черта, которая разделяет эти два числа, называется дробной чертой.
Дробную черту можно заменить знаком деления.
Иногда вместо горизонтальной черты используют наклонную.
Определение 2
Числитель — число, которое показывает, сколько долей предмета взято или используется. Пишут над чертой или слева от наклонной черты.
Определение 3
Знаменатель показывает, на сколько долей разделили предмет. Указывают под чертой или справа от наклонной черты.
С помощью обыкновенных дробей записывают результат деления двух натуральных чисел.
Пример 3
Например, 8 апельсинов разделили на 11 человек. Результат деления записывают: 711. У каждого человека оказалось семь одиннадцатых долей.
Определение 4
Обыкновенной дробью называется запись числа, которую можно свести к буквенному видуmn.
В этом буквенном выражении m и n подразумевают натуральными числами.
Примечание 2
Натуральные числа — такие количественные значения, которые используют для подсчета объектов и предметов.
Правила чтения дробей:
- числитель дроби — количественное числительное женского рода;
- знаменатель — порядковое числительное.
Читают: 47 — четыре седьмых; 110 — одна десятая; 35 — три пятых; 2745 — двадцать семь сорок пятых.
Если знаменатель обыкновенной дроби равен единице, то рассматриваемый предмет целый. Он неделим. Значит, такая дробь имеет смысл натурального числа.
Любое натуральное число можно представить в виде обыкновенной дроби, в которой:
- в знаменателе находится единица;
- в числителе — само число.
Виды обыкновенных дробей:
- Правильные — числитель меньше знаменателя — 23; 413; 45199.
- Неправильные — числитель больше знаменателя —143; 2413; 1145199.
Правильные дроби всегда меньше единицы. Неправильные дроби — больше единицы.
Когда числитель обыкновенной дроби равен знаменателю дроби, то преобразуют выражение в единицу:
aa=1 — знаменатель дроби равен числителю. Значит, дробь дает единицу.
Пояснение: aa=a:a=1 — дробная черта подразумевает знак деления. Когда делим одинаковые числа друг на друга, по правилу получаем единицу.
Сложение дробей с одинаковыми знаменателями
Пример 4
Пиццу разделили на 6 равные частей — долей. Вначале на тарелку положили 3 доли, потом еще 2 доли. На тарелке оказалось 5 долей, то есть 56 пиццы:
36+26=56.
Правило 1
Если нужно сложить две дроби с одинаковыми знаменателями, то к числителю первой дроби прибавляют числитель второй дроби, а знаменатель оставляют неизменным.
Пример 5
1316+216=13+216=1516.
Этот пример можно прочитать по тем же правилам, которые используются при прочтении выражений с натуральными числами.
1316+216 — сумма тринадцати шестнадцатых и двух шестнадцатых;
1316+216 — к тринадцати шестнадцатым прибавить две шестнадцатых.
Формула 1
Общая формула сложения дробей с одинаковыми знаменателями с использованием букв записывается так:
ac+bc=a+bc.
Вычитание дробей с одинаковыми знаменателями
Пример 6
Пиццу разделили на шесть долей. Мише отложили 5 долей, и он съел 4 доли. Осталось 1 доля, то есть 16 пиццы:56-46=16.
Правило 2
Чтобы вычесть дроби с одинаковыми знаменателями, нужно от числителя первой дроби отнять числитель второй дроби, а знаменатель оставить тем же.
Пример 7
2536-1436=25-1436=1136.
Пример читается по тем же правилам, что и соответствующие выражения с натуральными числами:
2536-1436 — разность двадцати пяти тридцать шестых и четырнадцати тридцать шестых.
2536-1436 — от двадцати пяти тридцать шестых отнять четырнадцать тридцать шестых.
2536-1436 — из двадцати пяти тридцать шестых вычесть четырнадцать тридцать шестых.
Формула 2
Общая формула вычитания дробей с одинаковыми знаменателями с помощью букв записывается так:
ac-bc=a-bc.
Задания для самостоятельной работы
Задача 1
Выполните действие:37+47.
Решение.
Перед нами сумма двух обыкновенных дробей. Для выполнения сложения воспользуемся правилом: чтобы сложить две дроби с одинаковыми знаменателями, складываем числители дробей, а знаменатель оставляем без изменений.
Получаем:
37+47=3+47=77.
Когда числитель дроби равен знаменателю, выражение можно упростить. Получаем просто единицу: 77=1.
Ответ: 1.
Задача 2
Самостоятельно выполните сложение: 213+413.
Решение.
В примере представлена сумма обыкновенных дробей с одинаковыми знаменателями. Для решения используем правило сложения дробей: числители складываем, знаменатель оставляем без изменений.
Получаем: 213+413=2+413=613.
Ответ: 613.
Задача 3
Выполните действие: 521-421.
Решение.
В примере представлена разность двух обыкновенных дробей с одинаковыми знаменателями. Для нахождения значения выражения, воспользуемся правилом: чтобы из одной обыкновенной дроби вычесть другую, нужно от числителя первой дроби отнять числитель второй дроби, а знаменатель оставить тем же.
Получим: 521-421=5-421=121.
Ответ: 121.
Задача 4
Найдите значение выражения: 2649-1749.
Решение.
Чтобы найти разность двух обыкновенных дробей, воспользуемся правилом: из числителя первой дроби вычитаем числитель второй дроби, знаменатель оставляем без изменений.
Получаем: 2649-1749=26-1749=949.
Ответ:949.
Задача 5
Вычислите: 1421345-361345.
Решение.
В примере представлена разность двух дробей с одинаковыми знаменателями. Для вычисления воспользуемся правилом: чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, знаменатель оставить без изменений.
Получаем: 1421345-361345=142-361345=1061345.
Краткий ответ: 1061345.
Задача 6
Найти значения выражения: 425+225-325.
Решение.
В этом выражении нужно выполнить два действия: сложение и вычитание. Определяем порядок действий: знаки равнозначные, скобок нет, значит, действия выполняем по порядку.
Первое действие — сложение. Чтобы сложить две дроби с одинаковыми знаменателями, складываем числители, знаменатель оставляем.
Получаем: 425+225=4+225=625.
Второе действие — вычитание. Чтобы найти разность обыкновенных дробей с одинаковыми знаменателями, от числителя первой дроби отнимаем числитель второй дроби. Знаменатель оставляем без изменений.
Из результата первого действия вычитаем дробь 325.
Получаем:625-325=325.
Упрощенная запись решения: 425+225-325=4+2-325=6-325=325.
Ответ: 325.
Задача 7
Вычислите: 1547-347+547.
Решение.
В примере два действия: вычитание и сложение.
Чтобы найти значение выражения, определим порядок действий. В этом примере есть скобки, значит, первое действие будет в скобках.
Первое действие — сложение. Складываем дроби с одинаковыми знаменателями по правилу: числители суммируем, знаменатель оставляем тем же.
Получим: 347+547=3+547=847.
Второе действие — вычитание. От дроби 1547 отнимаем результат первого действия.
Получим: 1547-847=15-847=747.
Запись решения в одну строку: 1547-347+547=1547-3+547=1547-847=15-847=747.
Ответ: 747.
Задача 8
В первый день квеста Ваня прошел игры. Во второй день — 315игры. Какую часть квеста прошел Ваня за два дня?
Решение.
Запишем краткое условие задачи.
| День | Решено |
| 1 | 415квеста |
| 2 | 315 квеста |
Чтобы найти, какую часть квеста прошел Ваня за два дня, нужно к результату первого дня прибавить итог второго дня.
Получим: 415+315=4+315=715.
Ответ: за два дня Ваня прошел 715 квеста.
Задача 9
Утром Даша съела 39 банки варенья. Вечером — на 19 банки больше. Сколько варенья съела Даша за день?
Решение.
Запишем краткое условие задачи
| Время суток | Съедено |
| Утро | 39 банки |
| Вечер | на 19 банки больше — ? |
Всего — ?
Если Даша вечером съела больше варенья на 19 банки, то, чтобы узнать, сколько же она съела за вечер, нужно к 39 прибавить 19.
Получим: 39+19=3+19=49.
Значит, за вечер Даша съела 49.
Осталось узнать, какую часть варенья она съела за день. Для этого сложим съеденные части за утро и вечер.
Получим: 39+49=3+49=79.
Ответ: за день Даша съела 79 банки варенья.
8 класс Алгебра Рациональные выражения Урок 1 и 2 | Презентация урока для интерактивной доски по алгебре (8 класс) на тему:
Слайд 1
МсСВУ ФГКОУ Московское суворовское военное училище 06.10.2013 Рациональные выражения Урок 1-2 Преподаватель математики Каримова С.Р.
Слайд 2
Работа над ошибками
Слайд 3
Алгебраическим выражением называется выражение, составленное из чисел и переменных с помощью действий сложения, вычитания, умножения, деления, возведения в степень и с помощью скобок . Целые выражения составлены из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число , отличное от нуля. Дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными
Слайд 4
ВЫРАЖЕНИЯ целые дробные рациональные выражения Рациональными называются целые и дробные выражения.
Слайд 5
Переместите выражения в соответствующие столбцы Дробные выражения Целые выражения
Слайд 6
Параметры / Изделия БМП-2, боевая машина пехоты Масса, кг 14300 Электропитание, В 3 Расчет, чел. 7 (десант) Пушка, тип 30 -мм 2А42 Пулемет 7.62 -мм ПКТ (ПКТМ) Боекомплект, шт: 30 -мм х 500, 7,62 -мм х 2000 Двигатель УТД-20, мощность 300 л.с . по шоссе до 65 на плаву до 7 Запас хода по шоссе, км 600 Параметры / Изделия БМП-3, гусеничная плавающая боевая машина пехоты Масса, кг 18700 Электропитание, В 3 Расчет, чел. 7 Пушка, тип 1х 100 -мм 2А70, 1х 30 -мм 2А72 Пулемет 3х 7,62 -мм ПКТ Боекомплект, шт: 30 х100-мм, в т.ч . 8 УР; 500х 30 -мм; 6000х 7,62 -мм Двигатель УТД-29, дизель по шоссе 70 на плаву 10 Запас хода по шоссе, км 600 Во сколько раз масса БМП-3 больше массы БМП-2? Составить целое выражение.
Слайд 7
Упражнения О б р а з е ц о ф о р м л е н и я: № 5 (а). ; а = –3, b = –1. 1,5. 1) Учебник № 3, № 4, № 5 (а)
Слайд 8
Упражнения Учебник 2) № 7 (а), № 8 3) № 9, № 16.
Слайд 9
Устно: – Какое выражение называется целым? дробным? – Как называются целые и дробные выражения? – Что такое рациональная дробь? – Всякая ли рациональная дробь является дробным выражением? Приведите примеры. – Как найти значение рациональной дроби при заданных значениях входящих в неё переменных?
Слайд 10
Допустимые значения переменных, входящих в дробное выражение Подставьте вместо * какое-нибудь число и назовите полученную дробь: а) ; б) ; в ) ; г) ; д ) ; е) ; ж) ; з) . Устно:
Слайд 11
– Какую дробь называют рациональной? – Всякая ли дробь является дробным выражением? – Как найти значение рациональной дроби при заданных значениях входящих в неё переменных? Устно: З а д а н и е. Найдите значение дроби при указанных значениях переменной: при х = 4; 0; 1.
Слайд 12
при х = 1 невозможно найти значение дроби. Это позволяет сделать следующий вывод : в рациональную дробь нельзя подставлять числа , которые обращают её знаменатель в нуль.
Слайд 13
Как находить допустимые значения переменных? 1) Если выражение является целым, то все значения входящих в него переменных будут допустимыми. 2) Чтобы найти допустимые значения переменных дробного выражения, нужно проверить, при каких значениях знаменатель обращается в нуль. Найденные числа не будут являться допустимыми значениями.
Слайд 14
Упражнения: О б р а з е ц о ф о р м л е н и я : № 11. г) 4 х ( х + 1) = 0 4 х = 0 или х + 1 = 0 х = 0 х = –1 О т в е т: х ≠ 0 и х ≠ 1 (или все числа, кроме 0 и –1). 1. № 10, № 11.
Слайд 15
Упражнения: 2. № 13. 3. № 14 (а, в), № 15 . 4 . № 17 .
Слайд 16
Решение: № 15. г) х ( х + 3) = 0 2 х + 6 ≠ 0 х = 0 или х = –3 х ≠ –3 О т в е т: х = 0.
Слайд 17
Дополнительно*: № 18 и № 20
Слайд 18
Решение: а ) . Из всех дробей с одинаковым положительным числителем большей будет та, у которой знаменатель является наименьшим.
Слайд 19
Решение: № 20. Дробь будет принимать наибольшее значение, если выражение (2 х + у ) 2 + 9 принимает наименьшее значение. Поскольку (2 х + у ) 2 не может принимать отрицательные значения, то наименьшее значение выражения (2 х + у ) 2 + 9 равно 9. Тогда значение исходной дроби равно = 2.
Слайд 20
Итог урока: – Какие значения называются допустимыми значениями переменных, входящих в выражение? – Каковы допустимые значения переменных целого выражения? – Как найти допустимые значения переменных дробного выражения? – Существуют ли рациональные дроби, для которых все значения переменных являются допустимыми? Приведите примеры таких дробей.
Слайд 21
№ 2, № 5 (б), № 6, № 7 (б ). № 12, № 14 (б, г), № 212. Д о п о л н и т е л ь н о: № 19. Задание на самоподготовку:
Слайд 22
Алгебpа . 8 класс. Учебник. ФГОС. Ю.Н. Макарычев, Н.Г. Миндюк , К.И. Нешков , С.Б. Суворова. Под ред. С.А.Теляковского . 2013г . Алгебра, 8 класс, Поурочные планы, Дюмина Т.Ю., Махонина А.А., 2012: CD; http://www.arms-expo.ru/049049052052124049051054055.html http://s4.goodfon.ru/wallpaper/previews-middle/219776.jp Литература и Интернет–ресурсы :
учебных-ассоциаций,-llc-урок-6-умножить-и-разделить-рациональные-числа — Google подобные
AlleBilderVideosNewsMapsShoppingBücher
suchoptionen
[PDF] Multiply and Dividecas0 9m.10093
3
3 in.us › cms › lib › Centricity › Домен › Урок 6 cw
В Уроке 4 вы узнали правила умножения и деления целых чисел. Взгляните на эту проблему. Вере дают три дроби.
[PDF] Умножение и деление рациональных чисел — изображения
images.
Урок 6 Умножение и деление рациональных чисел. Название: Урок 6. Умножение рациональных чисел. Изучите пример задачи, показывающий, как умножать рациональные числа …
Урок 6. Умножение и деление рациональных чисел – Сайты Google
Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если …
Es fehlt: tutorial- Associates,- llc-
[PDF] На предыдущих уроках вы выполняли операции с целыми числами. Теперь…
iblog.dearbornschools.org › wp-content › uploads › site › 2018/10
На предыдущих уроках вы выполняли операции с целыми числами. Теперь вы узнаете о выполнении операций с другими типами рациональных чисел.
Учебный план Associates, ООО Урок 6 Умножение и деление рационального …
macchineolearieumbria.it › Учебный план Associates,-ll.
3Эти лабиринты на умножение и деление рациональных чисел состоят из 2 версий, в которых учащиеся должны решить задачу на умножение или деление положительных и …
www.scribd.com › документ › урок-6-работа ученика…
Bewertung 5,0
(1)
числа, которые нужно умножить, выполняя вместе следующее задание. ©Curriculum Associates, LLC Копирование запрещено. Урок 6 Умножение на 3, 4 и 6 125
[PDF] Учебный план по математике — Школьный округ U-46
www.u-46.org › cms › lib › Centricity › Domain
Уроки 8–9: Применение свойств операций для сложения и вычитания рациональных чисел ………….. 87. Тема B: Умножение и деление целых чисел …
Ähnliche Fragen
По какому правилу умножаются и делятся рациональные числа?
Как научить умножать рациональные числа?
[PDF] Урок 15: Умножение и деление рациональных чисел
opencurriculum.
29.10.2013 · Учащиеся в течение двух минут работают с партнерами по обучению или группой, чтобы составить текстовую задачу на умножение целых чисел. Учащиеся могут использовать …
МАТЕМАТИКА G7: Умножение и деление рациональных чисел
уроки.unbounded.org › математика › тема-b › урок-15
Учащиеся понимают, что правила умножения и деления целых чисел применимы к рациональное число. Скачать Урок. Связанные ресурсы …
Ähnlichesuchanfragen
Калькулятор умножения и деления рациональных чисел
Уровни успеваемости по математике NAEP по классам
4 класс
8 класс
12 класс
12 класс (1990—2003)
Конкретные определения
НАЭП Базовый ,
NAEP Proficient и
NAEP Продвинутые уровни успеваемости для 4, 8 и 12 классов представлены в таблицах ниже. Из-за
изменения, внесенные в математическую структуру NAEP в 2005 г.
точки среза, указанные ниже для класса 12, были обновлены. Чтобы сохранить тенденцию, результаты для 4-го и 8-го классов представлены по шкале от 0 до 500, а результаты для 12-го класса, начиная с оценки 2005 года, представлены по шкале от 0 до 300.
Просмотрите описания уровней достижений NAEP для 12 класса и сокращенные баллы, использовавшиеся до 2005 года.
Уровни достижений NAEP суммируются; Поэтому студенты, выступающие на
NAEP Профессиональный уровень
также демонстрируют компетенции, связанные с NAEP Базовый уровень , а учащиеся NAEP Продвинутый уровень также демонстрируют навыки и знания, связанные с
NAEP Basic и
NAEP Профессиональный уровень . В скобках указана оценка сокращения, указывающая нижний предел диапазона оценок для каждого уровня.
Найдите общую информацию об уровнях достижений NAEP и подробные описания других предметов NAEP.
4 класс
|
НАЭП Базовый (214) |
Студенты, выступающие в
Студенты выступают на
|
|---|---|
|
NAEP Proficient (249) |
Студенты, выступающие в
Студенты, выступающие в
Студенты, выступающие в
3 Учащиеся выступление на
|
|
НАЭП Продвинутый (282) |
Студенты, выступающие в
NAEP Advanced уровень достижения, вероятно, может
Студенты, выступающие на
Студенты, выступающие на
Студенты, выступающие на
|
|
рамки. |
Топ
8 класс
|
НАЭП Базовый (262) |
Студенты, выступающие в
Студенты, выступающие на
Студенты, выступающие в Уровень достижений NAEP Basic , вероятно, может Студенты, выступающие в
|
|---|---|
|
NAEP Proficient (299) |
Студенты, выступающие в
|
|
NAEP Advanced (333) |
Студенты, выступающие в
Студенты, выступающие в
Студенты, выступающие в
Студенты, выступающие в
Уровень достижений NAEP Advanced , вероятно, может
|
|
Примечание. Описания содержимого, представленные в отчетах ALD, предназначены для отражения содержимого, определенного в структуре. |
Топ
12 класс
|
НАЭП Базовый (141) |
Студенты, выступающие в
Учащиеся
|
|---|---|
|
NAEP Proficient (176) |
Студенты, выступающие на
Студенты, выступающие в
Студенты выступают на
Студенты, выступающие в
|
|
NAEP Advanced (216) |
Студенты, выступающие в
Студенты, выступающие в
Студенты выступают на
NAEP Advanced Уровень достижения, вероятно, может
|
|
Примечание. |
Топ
Уровни успеваемости по математике NAEP для 12 класса, 1990–2003 гг.
|
НАЭП Базовый (288) |
Учащиеся двенадцатого класса выступают на Выступление двенадцатиклассников в Они должны уметь применять статистические рассуждения при организации и отображении данных, а также при чтении таблиц и графиков. Они также должны уметь обобщать закономерности и примеры из области алгебры, геометрии и статистики. На этом уровне они должны использовать правильный математический язык и символы для передачи математических отношений и процессов рассуждения, а также должным образом использовать калькуляторы для решения задач. |
|---|---|
|
Уровень владения NAEP (336) |
Учащиеся двенадцатого класса выступают на Выступление двенадцатиклассников на |
|
NAEP Advanced (367) |
Учащиеся двенадцатого класса выступают на Выступление двенадцатиклассников в No related posts. |
Содержание:
- § 1 Понятие алгебраической дроби
- § 2 Допустимые значения переменных алгебраической дроби
§ 1 Понятие алгебраической дроби
Алгебраической дробью называют выражение
где Р и Q —многочлены; Р — числитель алгебраической дроби, Q — знаменатель алгебраической дроби.
Вот примеры алгебраических дробей:
Любой многочлен – это частный случай алгебраической дроби, потому что любой многочлен можно записать в виде
Например:
Значение алгебраической дроби зависит от значения переменных.
Например, вычислим значение дроби
1)
2)
В первом случае получаем:
Заметим, данную дробь можно сократить:
Таким образом, вычисление значения алгебраической дроби упрощается. Воспользуемся этим.
Во втором случае получим:
Как видно, с изменением значений переменных изменилось значение алгебраической дроби.
§ 2 Допустимые значения переменных алгебраической дроби
Рассмотрим алгебраическую дробь
Значение x = –1 является недопустимым для данной дроби, т.к. знаменатель дроби при таком значении х обращается в нуль. При этом значении переменной алгебраическая дробь не имеет смысла.
Таким образом, допустимыми значениями переменных алгебраической дроби являются такие значения переменных, при которых знаменатель дроби не обращается в нуль.
Решим несколько примеров.
Пример 1:
При каких значениях переменной не имеет смысла алгебраическая дробь:
Решение:
Для нахождения недопустимых значений переменных знаменатель дроби приравнивается к нулю, и находятся корни соответствующего уравнения.
Ответ:
Пример 2:
При каких значениях переменной равна нулю алгебраическая дробь:
Решение:
Дробь равна нулю, если числитель равен нулю. Приравняем к нулю числитель нашей дроби и найдем корни получившегося уравнения:
Далее следует найти недопустимые значения переменной х. Действуем как в предыдущем примере, приравниваем к нулю знаменатель алгебраической дроби и решаем получившееся уравнение:
Таким образом, при x = 0 и x= 3 данная алгебраическая дробь не имеет смысла, а значит, мы должны исключить эти значения переменной из ответа.
Ответ:
Итак, на этом уроке Вы изучили основные понятия алгебраической дроби: числитель и знаменатель дроби, а также допустимые значения переменных алгебраической дроби.
Список использованной литературы:
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч.1 Учебник для общеобразовательных учреждений / А.Г. Мордкович. – 9-е изд., перераб. – М.: Мнемозина, 2007. – 215 с.: ил.
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч.2 Задачник для общеобразовательных учреждений / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. – 8-е изд., – М.: Мнемозина, 2006 – 239с.
- Алгебра. 8 класс. Контрольные работы для учащихся образовательных учреждений Л.А. Александрова под ред. А.Г. Мордковича 2-е изд., стер. — М.: Мнемозина 2009. — 40с.
- Алгебра. 8 класс. Самостоятельные работы для учащихся образовательных учреждений: к учебнику А.Г. Мордковича, Л.А. Александрова под ред. А.Г. Мордковича. 9-е изд., стер. — М.: Мнемозина 2013. — 112с.
Конспект
Целые выражения – это такие выражения, которые состоят из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на число, отличное от нуля.
Дробные выражения – это выражения, которые помимо действий сложения, вычитания, умножения и деления на число, отличное от нуля, содержат деление на выражение с переменными.
Целые и дробные выражения вместе называют рациональными выражениями.
Дробь – это выражение вида .
Целое выражение имеет смысл при любых значениях входящих в него переменных, потому что действия для нахождения значения целого выражения, всегда возможны.
Дробное выражение при некоторых значениях переменной может не иметь смысла.
Примеры
Дробные выражения имеют смысл при любых значениях входящих в них переменных, кроме тех, что обращают знаменатель в нуль.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями.
Рациональная дробь – это дробь, числитель и знаменатель которой многочлены.
Примеры
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Чтобы найти допустимые значения переменных в дроби, необходимо:
-
• Приравнять знаменатель, содержащий переменные, к нулю.
• Решить полученное уравнение. Корни этого уравнения будут являться теми значениями переменных, которые обращают знаменатель в нуль.
• Исключить эти значения из всех действительных чисел.
Пример 1.
Найти допустимые значения переменной в дроби 
1) x(x + 1) = 0
2) x = 0 или x + 1 = 0
x = 0 или x = –1.
Корни уравнения 0 и – 1.
3) Допустимыми значениями x являются все числа, кроме 0 и –1.
Пример 2.
Найти значения x, при которых дробь 

1) x2 – 1 = 0
2) (x – 1)(x + 1) = 0
x = ±1
3) x + 1 ≠ 0
x ≠ –1.

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.





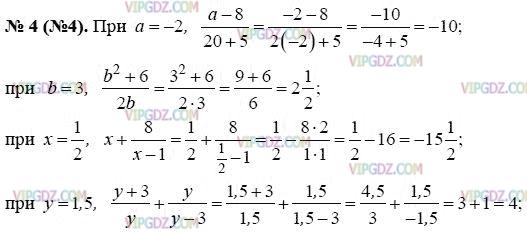



 концепции
концепции 
 д.) диаграмм, основанных на перпендикулярных или параллельных прямых
д.) диаграмм, основанных на перпендикулярных или параллельных прямых  Описания содержимого, представленные в отчетах ALD, предназначены для отражения содержимого, определенного в структуре.
Описания содержимого, представленные в отчетах ALD, предназначены для отражения содержимого, определенного в структуре. 
 Они должны уметь выполнять алгебраические операции с многочленами, обосновывать геометрические отношения, а также оценивать и защищать разумность ответов применительно к реальным ситуациям. Эти студенты должны уметь анализировать и интерпретировать данные в табличной и графической форме; понимать и использовать элементы концепции функции в символьной, графической и табличной форме; делать предположения, защищать идеи и приводить подтверждающие примеры.
Они должны уметь выполнять алгебраические операции с многочленами, обосновывать геометрические отношения, а также оценивать и защищать разумность ответов применительно к реальным ситуациям. Эти студенты должны уметь анализировать и интерпретировать данные в табличной и графической форме; понимать и использовать элементы концепции функции в символьной, графической и табличной форме; делать предположения, защищать идеи и приводить подтверждающие примеры.