Как найти заряд конденсатора до разрядки - AvtoShod.ru

Конденсаторы часто применяются в электрических схемах, помогая трансформировать электросигнал под определенные характеристики. Используя их основное свойство — накапливать электрический заряд, можно регулировать прохождение тока по цепи, убирать нежелательные пульсации напряжения или повысить энергоэффективность сети. При решении подобных задач в расчет берутся конкретные параметры того или иного электронакопителя, а также общие процессы, связанные с зарядом и разрядом конденсаторов.

Заряд конденсатора
Процессы зарядки и разрядки конденсаторов
Емкость и энергия конденсатора
Как зарядить конденсатор
Время, необходимое для зарядки конденсатора
Заряд конденсатора: формула
Время разряда конденсатора

Заряд конденсатора

Устройство обычного конденсатора состоит из двух пластин (обкладок), подключаемых к выходам цепи, и диэлектрика между ними. При этом величина заряда, накаливаемого конденсатором, зависит от его емкостной характеристики основных параметров: площади обкладок, толщины и диэлектрических свойств прокладочного материала.

Емкость конденсатора определяется по формуле:

C = S • ε • ε0 / d,

где S – площадь обкладок, ε — диэлектрическая проницаемость прокладки, ε0 — диэлектрическая постоянная (8,85•10-12 Ф/м), d – расстояние между пластинами.

Конденсируемый же заряд равняется произведению емкости конденсатора на напряжение в цепи: q = С × U.

Процессы зарядки и разрядки конденсаторов

При включении конденсатора в цепь через него начинает проходить ток. С движением электронов по проводнику на одной обкладке устройства скапливается отрицательный заряд, а на другой (при недостатке электронов) — положительный. Между пластинами образуется индуктивное поле, создающее разность потенциалов определенного значения. В проводниках постоянного тока накопление заряда идет до тех пор, пока уровень напряжения на обкладках не сравняется с номинальным напряжением элемента питания, после чего течение электротока останавливается.

Когда цепь размыкается и на конденсатор не подается напряжение, он может сохранять заряд на протяжение определенного времени, а затем с исчезновением электрического поля между пластинами заряд начнет перетекать в проводник. Процесс разряда конденсатора характеризуется переходом электронов с одной обкладки на другую. Конденсатор разряжается полностью, когда количество свободных электронов на обеих пластинах сравнивается. При этом все электродинамические процессы в цепи прекращаются.

Емкость и энергия конденсатора

Конденсатор, как и всякий объект, получающий электрический заряд, обладает энергией. Для его зарядки требуется определенная работа, которая идет на разделение заряженных частиц — именно она считается энергией конденсаторного устройства. Ее можно увидеть, если заряженный конденсатор присоединить, например, к светодиоду. Накопитель отдаст заряд лампочке, и она на некоторое время загорится, тем самым энергия перейдет в свет и тепло.

Для определения энергии конденсатора в расчет берут количество заряда, толщину диэлектрика и напряженность электрического поля. Последняя является векторной величиной и представляет собой силу, действующую на точечный заряд.

Поскольку заряды на обкладках равны между собой по модулю, во внимание принимается только значение напряженности одной из них, а значит, эта величина делится пополам — Е/2. Общая же энергия определяется по формуле:

Wp = qEd/2.

Произведение напряженности на расстояние между пластинами само себе представляет разность потенциалов или напряжение — U = E × d. Таким образом, энергию можно выразить через заряд и напряжение на конденсаторе. Формула будет иметь следующий вид:

Wp = qU/2.

Учитывая, что заряд и напряжение находятся в зависимости от емкости конденсатора, можно вывести еще пару формул энергии:

Wp = q2/2C

Wp = CU2/2

Как зарядить конденсатор

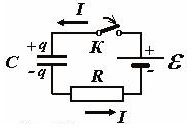
Для зарядки конденсатора требуется генератор электротока. Возникающие при этом процессы удобнее разобрать на примере простой цепи, включающей в себя конденсатор (С) и резистор (R).

Зарядка конденсатора от источника постоянной ЭДС

В соответствии с законом Ома разность потенциалов, возникающая на резисторе и конденсаторе, суммарно равна электродвижущей силе генератора тока. Математически это можно представить следующими формулами:

UC = q/C – напряжение конденсатора;

UR = IR – напряжение резистора;

ε = UC + UR – ЭДС источника.

Для пояснения зарядного процесса определим равенство

IR = ε – q / C.

Эта формула представляет динамические изменения заряда силы тока. Более конкретно это может быть выражено уравнением:

I = dq / dt.

Изменение заряда во времени можно подставить к сопротивлению. Соответственно, получаем

R • dq / dt = ε – q / C.

В строгом смысле это уравнение предписывает бесконечное время зарядки конденсаторного устройства. Однако этим можно пренебречь, если учесть, что заряд фактически дискретен и может быть подвержен случайным изменением и флуктуациям. Таким образом, в данном выражении имеются в виду усредненная динамика зарядного процесса. На его основании можно записать изменение ЭДС и составляющих напряжений обоих элементов цепи:

dε = d(IR) + d(q/C).

Фактически ЭДС генератора не меняется во времени, а значит, dε = 0, а емкость конденсатора и сопротивление обладают постоянными значениями, поэтому их можно обозначить без d:

R • dI = — 1/C • dq.

Поделив данное уравнение на временной период, за который заряжается конденсатор, можно вывести выражение, учитывающее корреляцию между динамикой заряда и силой тока:

dI / dt = –I/RC.

Это уравнение означает отношение скорости, с которой уменьшается сила тока к ее фактическому значению.

В начале процесса заряда конденсатора значение q равняется нулю. В этот момент при наибольшей разнице напряжений источника питания и электронакопителя сила тока имеет максимальное значение. По мере увеличения заряда значение I постепенно падает. Когда конденсатор заряжается полностью, его напряжение сравнивается с ЭДС генератора, а сила тока принимает значение 0. Соответственно, электродинамический процесс прекращается.

Дополнительно можно рассмотреть, как в процессе зарядки трансформируется энергия. Вполне очевидно, что генератор тока является причиной возникновения электротока в цепи и, следовательно, заряда электронакопителя.

В этом усматривается некое противоречие: когда конденсатор получает от генератора тока заряд q, это значит, что ЭДС выполнила работу равную заряду (А = qe), однако энергия самого накопителя определяется по формуле W = q2 / 2C = qε / 2, что составляет только половину от работы, произведенной источником питания. Этот парадокс объясняется самим фактом прохождения тока по электроцепи, которое сопровождается выделением тепловой энергии на резисторе, то есть определенное количество энергопотери приходится на тепло.

Дифференциальные расчеты для малых отрезков времени процесса зарядки показывают, что энергия от генератора, действительно, разделяется на электрическую, идущую на заряд конденсаторного устройства, и тепловую. При этом сопротивление цепи само по себе никак не влияет на количество выделяемой теплоты, которое равняется энергии конденсатора.

Заряд конденсатора, ток

При подключении конденсатора к источнику тока в начале зарядки заряд на пластинах практически отсутствует. Максимальное значение I в этой ситуации объясняется минимальным сопротивлением. С увеличением заряженных частиц, возрастает сопротивление индуктивного поля, которое препятствует прохождению тока по проводнику.

Период времени, за начальную точку которого берут момент наибольшей силы тока, а за конечную полное прекращение движения заряженных частиц, носит название переходного периода зарядки конденсатора.

Начальный момент зарядки конденсатора характеризуется нулевым напряжением между его пластинами. Показатель U начинает возрастать с появлением на обкладках разноименно заряженных частиц. Большая сила тока в начале процесса обусловливает большую скорость увеличения напряжения. По мере ее падения рост напряжения замедляется, достигнув максимального значения при полной зарядке электронакопителя.

График увеличения напряжения имеет вид параболы, будучи противоположным графику снижения силы тока.

Математически динамическую взаимозависимость тока, напряжения и емкости конденсатора можно выразить следующим образом:

I = С • dV / dt.

Время, необходимое для зарядки конденсатора

Время зарядки конденсатора определяется его емкостью, электродвижущей силой генератора тока, напряжением и сопротивлением в цепи.

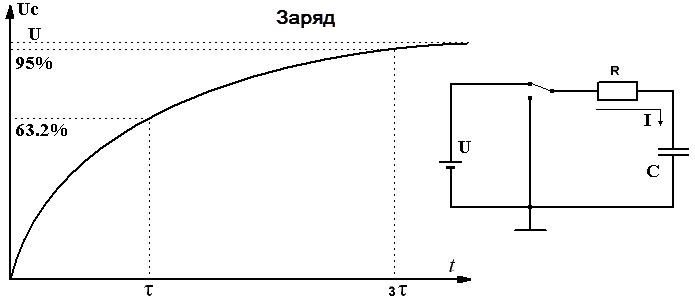
Заряд конденсатора описывается как экспоненциальный процесс. Чтобы оценить его время, принимается, что значение заряда увеличивается равномерно, при этом скорость заряда приравнивается к силе тока в начале процесса. Отсюда следует уравнение постоянной времени:

τ = q / I0 = RC.

Зависимость динамики напряжения от длительности зарядки определяется по следующей формуле:

U(t) = UC • (1 – e-t/τ).

Значение высчитывается с привлечением основания натурального логарифма (е), которое относится к функции экспоненты и равняется приблизительно 2,718. При этом UC обозначает напряжение ЭДС источника.

Процент заряда по постоянной времени τ определяется в соответствии с формулой:

(1 — 1/еτ) • 100%.

Таким образом, конденсатор достигает почти полной зарядки за 5 τ.

• 1 τ — 63,2%;

• 2 τ — 86,5%

• 3 τ — 95,1%

• 4 τ — 98,2%

• 5 τ — 99,3%

Учитывая экспоненциальный характер увеличения напряжения конденсатора, можно сказать, что время его зарядки до уровня ЭДС генератора длится бесконечно долго.

Заряд конденсатора: формула

Конденсатор заряжается довольно быстро. Обычно для этого достаточно нескольких миллисекунд. Равенство напряжения электродвижущей силы источника питания и электронакопителя определяет максимальный заряд конденсатора. Формула заряда может быть определена с учетом общих параметров конденсатора:

q = Uεε0S/d.

Также можно принять во внимание конструкционные особенности конденсатора. Так, для цилиндрического накопителя заряд равняется:

q = U2πεε0l/ln(r2/r1),

где l – высота цилиндров, r2 – радиус наружной пластины, r1 — радиус внутренней пластины.

Время разряда конденсатора

Если конденсатор переключить на нагрузку резистора, он сам станет источником питания и будет отдавать заряд в цепь. Движение тока при этом начинается от пластины с отрицательным зарядом на положительно заряженную пластину и далее по контуру. Напряжение в начальный момент будет такое же как и после полной зарядки накопителя. В соответствии с законом Ома можно определить и первоначальную силу тока:

IC = UC / R.

Отдавая заряд, конденсатор будет терять напряжение. Соответственно будет уменьшаться и сила тока. Снижение обоих показателей идет по экспоненциальной кривой с замедлением скорости падения. Это значит, что динамику разрядки конденсатора можно описать, как и в случае зарядки, при помощи постоянной времени τ.

Изменение основных электрических показателей при заряде и разряде конденсатора играют ключевую роль в электротехнике и радиоэлектронике. Эта функциональность в полной мере проявляется в цепях переменного тока, где оба процесса сменяют друг друга с определенной периодичностью. На частотно-зависимых качествах электронакопителей основан принцип действия таких электроустановок, как колебательные контуры, реле времени, цепи обратной связи, частотные фильтры и другие.

Понравилась статья? Расскажите друзьям:

Оцените статью, для нас это очень важно:

Проголосовавших: 3 чел.
Средний рейтинг: 5 из 5.

Источник

Значение диэлектрика

Кроме общего размера обкладок и расстояния между ними, существует ещё один параметр, влияющий на ёмкость — используемый тип изолятора. Фактор, по которому определяется способность диэлектрика повышать ёмкость конденсатора в сравнении с вакуумом, называется диэлектрической проницаемостью и описывается для разных материалов постоянной величиной от 1 и до бесконечности (теоретически):

вакуум: 1,0000;
воздух: 1,0006;
бумага: 2,5—3,5;
стекло: 3—10;
оксиды металлов 6—20;
электротехническая керамика: до 80.

Кроме конденсаторов с твёрдым диэлектриком (керамических, бумажных, плёночных) существуют также электролитические. В последних используют алюминиевые или танталовые пластины с оксидным изолирующим слоем в качестве одного электрода и раствор электролита в качестве другого.

Энергия, которую способны накопить большинство конденсаторов, обычно невелика — не больше сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому конденсаторы не могут заменить, например, аккумуляторные батареи в качестве источника питания. И хотя они способны эффективно выполнять только одну работу (сохранение заряда), их применение весьма многообразно в электрических цепях. Конденсаторы используются как фильтры, для сглаживания сетевого напряжения, в качестве устройств синхронизации и для других целей.

Синтаксис

Для пользователей XMPP клиентов, используется команда

fiz ключи

где ключи это известные параметры, параметра=значение, разделенные точкой с запятой

Обязателен ключ key=razryad при расчете разаряда конденсатора

и zaryad при расчете заряда

Так как при других параметрах ключах будут рассчитываться совершенно другие формулы. Например баллистического движения или давления над уровнем моря.

Заметьте, чем данный калькулятор отличается от других:

Во первых: данные можно вводить не переводя из наноФарад в Фарады, а килоОмы в Омы. Если уж заданы параметры в единицах измерения то так и пишите. Если не напишите то считается что данные заданы в основным единицах СИ ( то есть метр, Фарад, Ом)

Во вторых: Расчет ведётся по тем параметрым которые можно рассчитать зная исходные.Это очень удобно, когда нужно рассчитать любой из параметров в формуле, когда известны все остальные. Другие известные калькуляторы могут рассчитывать только по определенному алгоритму и только в одну сторону.

Разряд конденсатора

После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания. Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.

В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.

Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.

Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки ( ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.

Продукт RC (сопротивление, умноженное на емкость) формирует временную константу ? (тау). За один ? конденсатор заряжается или разряжается на 63%. За пять ? конденсатор заряжается или разряжается полностью.

Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:

Заряд конденсатора. Ток

По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.

Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов. Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.

В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.

Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют переходным периодом заряда конденсатора.

Формула

Нахождение тока конденсаторного заряда происходит по формуле, представленной ниже. Измеряется он в фарадах, что равно кулону или вольту.

Формула нахождения заряда конденсатора

В целомэто элемент электросети, накапливающий и сохраняющий напряжение в ней. Бывает разного типа и размера, к примеру, электролитическим, керамическим и танталовым. Состоит, в основном, из нескольких токопроводящих обкладок с диэлектриком. Его емкость зависит от размеров диэлектрика и заполнителя между обкладками. Заряжается благодаря электричеству. Определить ток конденсаторного заряда можно измерительными приборами и формулой.

Устройство и принцип работы

В простейшем варианте конструкция состоит из двух электродов в форме проводящих пластин (называемых обкладками), разделённых диэлектриком, толщина которого ничтожно мала по сравнению с размерами обкладок. Практически применяемые радиоэлектронные компоненты содержат много слоёв диэлектрика и электродов. В качестве обозначения конденсатора на схеме используются два параллельных отрезка с пространством между ними. Они символизируют металлические пластины обкладок физического прибора, электрически разделённые между собой.

Многие считают Майкла Фарадея автором изобретения, но на самом деле это не так. Но он сделал главное — продемонстрировал первые практические примеры и способы использования этого прибора для хранения электрического заряда в своих экспериментах. Благодаря Фарадею человечество получило способ измерять возможность накапливать заряд. Эта величина называется ёмкостью и измеряется в Фарадах.

https://youtube.com/watch?v=tuVEW69oXuw

Работу конденсатора можно проиллюстрировать на примере событий, проходящих во вспышке цифровой фотокамеры за отрезок времени между нажатием кнопки и тем моментом, когда вспышка погаснет. Основой электронной схемы этого осветительного устройства является конденсатор, в котором происходит следующее:

Зарядка. После нажатия кнопки поток электронов приходит в конденсатор и останавливается на одной из его пластин благодаря диэлектрику. Этот поток называется зарядным током.
Накопление. Поскольку под действием электродвижущей силы всё больше и больше электронов будут поступать на обкладку и распределяться по ней, отрицательный заряд обкладки может расти до момента, пока накопленный потенциал не будет отталкивать поступающий избыточный поток электронов. Вторая пластина из-за дефицита электронов приобретает положительный заряд, по модулю равный отрицательному на первой. Зарядный ток будет протекать до тех пор, пока напряжение на обеих пластинах не сравняется с приложенным. Сила или скорость тока зарядки будет находиться на максимальном уровне в момент, когда пластины полностью разряжены, и приблизится к нулю в момент, когда напряжение на обкладках и источнике будут равны.
Сохранение. Поскольку обкладки заряжены противоположно, ионы и электроны будут притягиваться друг к другу, но не смогут соединиться из-за диэлектрической прослойки, создавая электростатическое поле. Благодаря этому полю конденсатор удерживает и сохраняет заряд.
Разряд. Если в цепи появляется возможность для электронов протечь другим путём, то напряжение, накопленное между положительными и отрицательными зарядами обкладок, мгновенно реализуется в электрический ток, импульс которого в лампе вспышки преобразуется в световую энергию.

Определение заряда

Определить, заряжен ли проводник, можно специальным измерительным прибором. К примеру, сделать это можно при помощи индикаторной отвертки. При разряде избыточные виды электронов, имеющих левую пластину, будут перемещены через некоторое время по проводам к правой части пластины, то есть они будут смещены к местам, где их недостаточно.

Обратите внимание! Когда число электронов будет одинаковым, то разряд прекратится и проводная энергия вместе с сопротивлением исчезнет. Использование измерительного оборудования для определения конденсаторного заряда

Использование измерительного оборудования для определения конденсаторного заряда

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.

Как видите, здесь нет ничего сложного

Относительная диэлектрическая проницаемость

Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.

Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.

Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.

Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.

Воздух – 1.0005

Бумага – от 2.5 до 3.5

Стекло – от 3 до 10

Слюда – от 5 до 7

Порошки оксидов металлов – от 6 до 20

Плоский конденсатор.

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

E = frac{sigma}{2varepsilon_0thinspacevarepsilon}

Здесь sigma– это поверхностная плотность заряда: sigma = frac{q}{S}, а varepsilon – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

E_+ = E_- = frac{q}{2varepsilon_0thinspacevarepsilon S}

Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

E = E_+ + E_- = frac{q}{2varepsilon_0thinspacevarepsilon S} + frac{q}{2varepsilon_0thinspacevarepsilon S} = frac{q}{varepsilon_0thinspacevarepsilon S}

А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0

От чего зависит емкость

Емкость это свойство накопления и удержания электрозаряда. Чем она больше, тем больше заряд, увеличивающий вместимость сосуда с газовым баллоном. Она зависит от того, какова форма и размер электродов. Также зависит от того, какое расположение и свойство имеет диэлектрик, разделяющий электрод. Есть плоский конденсаторный источник с параллельной и цилиндрической пластиной.

Имеет не только специально предусмотренное устройство, но и несколько проводников, которые разделены при помощи диэлектрика. Емкость существенно влияет на электротехнические установки переменного тока. К примеру, источник с определенной емкостью имеется электрический провод с живым электрическим кабелем, жилой и металлической кабельной оболочкой.

От чего зависит емкость

Емкость и энергия конденсатора.

Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда конденсатора q одного из проводников к разности потенциалов между проводниками:

C = frac{q}{Deltavarphi} = frac{q}{U}

Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:

U = Ed = frac{qd}{varepsilon_0thinspacevarepsilon S}

Здесь у нас d – это расстояние между пластинами конденсатора, а q – заряд конденсатора. Подставим эту формулу в выражение для емкости:

C = frac{qvarepsilon_0thinspacevarepsilon S}{qd} = frac{varepsilon_0thinspacevarepsilon S}{d}

Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить varepsilon = 1.

Для запасенной энергии конденсатора справедливы следующие выражения:

W = frac{CU^2}{2} = frac{qU}{2} = frac{q^2}{2C}

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

Итак, мы сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики! Так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку. Не пропустите!

Помогла ли вам статья?

Задать вопрос

Пишите ваши рекомендации и задавайте вопросы в комментариях

Источник

Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление. Формулы, по которым идет расчет, приведены под калькуляторами.

Заряд конденсатора от источника постоянной ЭДС

Время зарядки, миллисекунд

Точность вычисления

Знаков после запятой: 2

Постоянная времени RC-цепи, миллисекунд

Время зарядки конденсатора до 99.2%, миллисекунд

Максимальная рассеиваемая мощность, Ватт

Напряжение на конденсаторе, Вольт

Заряд на конденсаторе, микроКулон

Энергия конденсатора, миллиДжоуль

Работа, совершенная источником, миллиДжоуль

Разряд конденсатора через сопротивление

Начальное напряжение на конденсаторе, Вольт

Время разрядки, миллисекунд

Точность вычисления

Знаков после запятой: 2

Начальная энергия конденсатора, миллиДжоуль

Начальный заряд конденсатора, микроКулон

Постоянная времени RC-цепи, миллисекунд

Максимальная рассеиваемая мощность, Ватт

Конечный заряд конденсатора, микроКулон

Конечная энергия конденсатора, миллиДжоуль

Конечное напряжение конденсатора, Вольт

Понять приводимые ниже формулы поможет картинка, изображающая электрическую схему заряда конденсатора от источника постоянной ЭДС (батареи):

Итак, при замыкании ключа К в цепи пойдет электрический ток, который будет приводить к заряду конденсатора.
По закону Ома сумма напряжений на конденсаторе и резисторе равна ЭДС источника, таким образом:
$epsilon=IR+frac{q}{C}$
При этом заряд и сила тока зависят от времени. В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.
$I=frac{epsilon}{R}, P=I^2R$
Во время зарядки конденсатора, напряжение на нем изменяется по закону
$V(t)=epsilon(1-e^{-frac{t}{RC}})$
где величину
tau=RC
называют постоянной времени RC-цепи или временем зарядки конденсатора.
Вообще говоря, согласно уравнению выше, заряд конденсатора бесконечно долго стремится к величине ЭДС, поэтому для оценки времени заряда конденсатора используют величину
5tau — это время, за которое напряжение на конденсаторе достигнет значения 99,2% ЭДС.
Заряд на конденсаторе:
Q=CV
Энергия, запасенная в конденсаторе:
$W=frac{Q^2}{2C}$
Работа, выполненная источником ЭДС:

Источник

Значение диэлектрика

вакуум: 1,0000;
воздух: 1,0006;
бумага: 2,5—3,5;
стекло: 3—10;
оксиды металлов 6—20;
электротехническая керамика: до 80.

Синтаксис

Для пользователей XMPP клиентов, используется команда

fiz ключи

где ключи это известные параметры, параметра=значение, разделенные точкой с запятой

Обязателен ключ key=razryad при расчете разаряда конденсатора

и zaryad при расчете заряда

Заметьте, чем данный калькулятор отличается от других:

Разряд конденсатора

Продукт RC (сопротивление, умноженное на емкость) формирует временную константу ?

(тау). За один
?
конденсатор заряжается или разряжается на 63%. За пять
?
конденсатор заряжается или разряжается полностью.

Электроника для всех

Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.

О многочисленных способах применения которой я сегодня и решил рассказать. Но вначале про каждый элемент в отдельности:

Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Ток через резистор определяется законом ома — I=U/R

, где U напряжение на выводах резистора, R — его сопротивление.

Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику. Получается интересная зависимость — есть ток, нет напряжения, есть напряжение — нет тока.

Чтобы визуализировать себе этот процесс, представь ган… эмм.. воздушный шарик который наполняется водой. Поток воды — это ток. Давление воды на упругие стенки — эквивалент напряжения. Теперь смотри, когда шарик пуст — вода втекает свободно, большой ток, а давления еще почти нет — напряжение мало. Потом, когда шарик наполнится и начнет сопротивляться давлению, за счет упругости стенок, то скорость потока замедлится, а потом и вовсе остановится — силы сравнялись, конденсатор зарядился. Есть напряжение натянутых стенок, но нет тока!

Теперь, если снять или уменьшить внешнее давление, убрать источник питания, то вода под действием упругости хлынет обратно. Также и ток из конденсатора потечет обратно если цепь будет замкнута, а напряжение источника ниже чем напряжение в конденсаторе.

Емкость конденсатора. Что это? Теоретически, в любой идеальный конденсатор можно закачать заряд бесконечного размера. Просто наш шарик сильней растянется и стенки создадут большее давление, бесконечно большое давление. А что же тогда насчет Фарад, что пишут на боку конденсатора в качестве показателя емкости? А это всего лишь зависимость напряжения от заряда (q = CU). У конденсатора малой емкости рост напряжения от заряда будет выше.

Представь два стакана с бесконечно высокими стенками. Один узкий, как пробирка, другой широкий, как тазик. Уровень воды в них — это напряжение. Площадь дна — емкость. И в тот и в другой можно набузолить один и тот же литр воды — равный заряд. Но в пробирке уровень подскочит на несколько метров, А в тазике будет плескаться у самого дна. Также и в конденсаторах с малой и большой емкостью. Залить то можно сколько угодно, но напряжение будет разным.

Плюс в реале у конденсаторов есть пробивное напряжение, после которого он перестает быть конденсатором, а превращается в годный проводник

А как быстро заряжается конденсатор?

В идеальных условиях, когда у нас бесконечно мощный источник напряжения с нулевым внутренним сопротивлением, идеальные сверхпроводящие провода и абсолютно безупречный конденсатор — этот процесс будет происходить мгновенно, с временем равным 0, равно как и разряд.

Но в реальности всегда существуют сопротивления, явные — вроде банального резистора или неявные, такие как сопротивление проводов или внутреннее сопротивление источника напряжения. В этом случае скорость заряда конденсатора будет зависить от сопротивлений в цепи и емкости кондера, а сам заряд будет идти по экспоненциальному закону

А у этого закона есть пара характерных величин:

Т — постоянная времени
, это время при котором величина достигнет 63% от своего максимума. 63% тут взялись не случайно, тут прямая завязка на такую формулу VALUET=max—1/e*max.
3T — а при троекратной постоянной значение достигнет 95% своего максимума.

Постоянная времени для RC цепи Т=R*C

Чем меньше сопротивление и меньше емкость, тем быстрей конденсатор заряжается. Если сопротивление равно нулю, то и время заряда равно нулю.

Рассчитаем за сколько зарядится на 95% конденсатор емкостью 1uF через резистор в 1кОм:

T= C*R = 10-6 * 103 = 0.001c 3T = 0.003c через такое время напряжение на конденсаторе достигнет 95% от напряжения источника.

Разряд пойдет по тому же закону, только вверх ногами. Т.е. через Твремени в на конденсаторе остаенется всего лишь 100% — 63% = 37% от первоначального напряжения, а через 3T и того меньше — жалкие 5%.

Ну с подачей и снятием напряжения все ясно. А если напряжение подали, а потом еще ступенчато подняли, а разряжали также ступеньками? Ситуация тут практически не изменится — поднялось напряжение, конденсатор дозарядился до него по тому же закону, с той же постоянной времени — через время 3Т его напряжение будет на 95% от нового максимума. Чуть понизилось — подразрядился и через время 3Т напряжение на нем будет на 5% выше нового минимума. Да что я тебе говорю, лучше показать. Сварганил тут в мультисиме хитровыдрюченный генератор ступечнатого сигнала и подал на интегрирующую RC цепочку:

Видишь как колбасится Обрати внимание, что и заряд и разряд, вне зависимости от высоты ступеньки, всегда одной длительности!!!

А до какой величины конденсатор можно зарядить? В теории до бесконечности, этакий шарик с бесконечно тянущимися стенками. В реале же шарик рано или поздно лопнет, а конденсатор пробьет и закоротит. Вот поэтому у всех конденсаторов есть важный параметр — предельное напряжение

. На электролитах его часто пишут сбоку, а на керамических его надо смотреть в справочниках. Но там оно обычно от 50 вольт. В общем, выбирая кондер надо следить, чтобы его предельное напряжение было не ниже того которое в цепи. Добавлю что при расчете конденсатора на переменное напряжение следует выбирать предельное напряжение в 1.4 раза выше. Т.к. на переменном напряжении указывают действующее значение, а мгновенное значение в своем максимуме превышает его в 1.4 раза.

Что следует из вышеперечисленного? А то что если на конденсатор подать постоянное напряжение, то он просто зарядится и все. На этом веселье закончится.

А если подать переменное? То очевидно, что он будет то заряжаться, то разряжаться, а в цепи будет туда и обратно гулять ток. Движуха! Ток есть!

Выходит, несмотря на физический обрыв цепи между обкладками, через конденсатор легко протекает переменный ток, а вот постоянному слабо.

Что нам это дает? А то что конденсатор может служить своего рода сепаратором, для разделения переменного тока и постоянного на соответствующие составляющие.

Любой изменяющийся во времени сигнал можно представить как сумму двух составляющих — переменной и постоянной.

Например, у классической синусоиды есть только переменная часть, а постоянная равна нулю. У постоянного же тока наоборот. А если у нас сдвинутая синусоида? Или постоянная с помехами?

Переменная и постоянная составляющие сигнала легко разделяются! Чуть выше я тебе показал как конденсатор дозаряжается и подразряжается при изменениях напряжения. Так что переменная составляющая сквозь кондер пройдет на ура, т.к. только она заставляет конденсатор активно менять свой заряд. Постоянная же как была так и останется и застрянет на конденсаторе.

Но чтобы конденсатор эффективно разделял переменную составляющую от постоянной частота переменной составляющей должна быть не ниже чем 1/T

Возможны два вида включения RC цепочки: Интегрирующая и дифференцирующая

. Они же фильтр низких частот и фильтр высоких частот.

Фильтр низких частот без изменений пропускает постоянную составляющую (т.к. ее частота равна нулю, ниже некуда) и подавляет все что выше чем 1/T. Постоянная составляющая проходит напрямую, а переменная составляющая через конденсатор гасится на землю. Такой фильтр еще называют интегрирующей цепочкой потому, что сигнал на выходе как бы интегрируется. Помнишь что такое интеграл? Площадь под кривой! Вот тут она и получается на выходе.

Как здесь вычисляется постоянная составляющая? А с виду и не скажешь, но надо помнить, что любой периодически сигнал раскладывается в ряд Фурье

, превращаясь в сумму из постоянной составляющей и пачки синусоид разной частоты и амплитуды.

Фильтр высоких частот работает наоборот. Он не пускает постоянную составляющую (т.к. ее частота слишком низка — 0) — ведь конденсатор для нее равносилен обрыву, а вот переменная пролазит через кондер без проблем.

А дифференцирующей цепью ее называют потому, что на выходе у нас получается дифференциал входной функции, который есть не что иное как скорость изменения этой функции.

На участке 1 происходит заряд конденсатора, а значит через него идет ток и на резисторе будет падение напряжения.
На участке 2 происходит резкое увеличение скорости заряда, а значит и ток резко возрастет, а за ним и падение напряжения на резисторе.
На участке 3 конденсатор просто удерживает уже имеющийся потенциал. Ток через него не идет, а значит на резисторе напряжение тоже равно нулю.
Ну и на 4м участке конденсатор начал разряжаться, т.к. входной сигнал стал ниже чем его напряжение. Ток пошел в обратную сторону и на резисторе уже отрицательное падение напряжения.

А если подать на вход прямоугольнй импульс, с очень крутыми фронтами и сделать емкость конденсатора помельче, то увидим вот такие иголки:

Вверху идет осциллограма того что на входе, внизу то что на выходе дифференциальной цепи. Как видишь, тут мощные всплески на фронтах. Оно и понятно, в этом месте функция меняется резко, а значит производная (скорость изменения) этой функции велика, на пологих участках сигнал константа и его производная, скорость изменения, равна нулю — на графике ноль.

А если загнать в дифференциатор пилу, то на выходе получим…

прямоугольник. Ну, а чо? Правильно — производная от линейной функции есть константа, наклон этой функции определяет знак константы.

Короче, если у тебя сейчас идет курс матана, то можешь забить на богомерзкий Mathcad, отвратный Maple, выбросить из головы матричную ересь Матлаба и, достав из загашников горсть аналоговой рассыпухи, спаять себе истинно ТРУЪ аналоговый компьютер Препод будет в шоке

Правда на одних только резисторах кондерах интеграторы и диффернциаторы обычно не делают, тут юзают операционные усилители. Можешь пока погуглить на предмет этих штуковин, любопытная вещь

А вот тут я подал обычный приямоугольный сигнал на два фильтра высоких и низких частот. А выходы с них на осциллограф:

И вот что получилось на осциллографе:

Вот, чуть покрупней один участок:

Как видишь, на одном срезало постоянную составляющую, на другом переменную.

Ладно, что то мы отвлеклись от темы.

Как еще можно применить RC цепь?

Да способов много. Часто ее используют не только в качестве фильтров, но и как формирователи импульсов. Например, на сбросе контроллера AVR, если надо чтобы МК стартанул не сразу после включения питания, а с некоторой выдержкой:

При старте кондер разряжен, ток через него вваливат на полную, а напряжение на нем мизерное — на входе RESET сигнал сброса. Но вскоре конденсатор зарядится и через время Т его напряжение будет уже на уровне логической единицы и на RESET перестанет подаваться сигнал сброса — МК стартанет. А для AT89C51

надо с точностью наоборот RESET организовать — вначале подать единицу, а потом ноль. Тут ситуация обратная — пока кондер не заряжен, то ток через него течет большой, Uc — падение напряжения на нем мизерное Uc=0. А значит на RESET подается напряжение немногим меньше напряжения питания Uпит-Uc=Uпит. Но когда кондер зарядится и напряжение на нем достигнет напряжения питания (Uпит=Uс), то на выводе RESET уже будет Uпит-Uc=0

Аналоговые измерения

Но фиг сними с цепочками сброса, куда прикольней использовать возможность RC цепи для замера аналоговых величин микроконтроллерами в которых нет АЦП. Тут используется тот факт, что напряжение на конденсаторе растет строго по одному и тому же закону — экспоненте. В зависимости от кондера, резистора и питающего напряжения. А значит его можно использовать как опорное напряжение с заранее известными параметрами.

Работает просто, мы подаем напряжение с конденсатора на аналоговый компаратор, а на второй вход компаратора заводим измеряемое напряжение. И когда хотим замерить напряжение, то просто вначале дергаем вывод вниз, чтобы разрядить конденсатор. Потом возвращем его в режим Hi-Z, cбрасываем и запускаем таймер. А дальше кондер начинает заряжаться через резистор и как только компаратор доложит, что напряжение с RC догнало измеряемое, то останавливаем таймер.

Зная по какому закону от времени идет возрастание опорного напряжения RC цепи, а также зная сколько натикал таймер, мы можем довольно точно узнать чему было равно измеряемое напряжение на момент сработки компаратора. Причем, тут не обязательно считать экспоненты. На начальном этапе зарядки кондера можно предположить, что зависимость там линейная. Или, если хочется большей точности, аппроксимировать экспоненту кусочно линейными функциями, а по русски — отрисовать ее примерную форму несколькими прямыми или сварганить таблицу зависимости величины от времени, короче, способов вагон просто.

Если надо заиметь аналоговую крутилку, а АЦП нету, то можно даже компаратор не юзать. Дрыгать ножкой на которой висит конденсатор и давать ему заряжаться через перменный резистор.

По изменению Т, которая, напомню T=R*C и зная что у нас С = const, можно вычислить значение R. Причем, опять же необязательно подключать тут математический аппарат, в большинстве случаев достаточно сделать замер в каких-нибудь условных попугаях, вроде тиков таймера. А можно пойти другим путем, не менять резистор, а менять емкость, например, подсоединяя к ней емкость своего тела… что получится? Правильно — сенсорные кнопки!

Если что то непонятно, то не парься скоро напишу статью про то как прикрутить к микроконтроллеру аналоговую фиговину не используя АЦП. Там подробно все разжую.

Теперь, думаю, ты понял за что я так люблю RC цепочки и почему на моей отладочной плате PinBoard

их несколько и с разными параметрами

Заряд конденсатора. Ток

Советы и предупреждения

После того как процесс разряда завершен можно обернуть его выводы фольгой, чтобы эта радиодеталь оставалась разряженной.
Все конденсаторы со временем могут разрядиться сами через несколько дней, при условии, что они не подключены к внешним источникам питания. Но всегда лучше считать, что они находятся в заряженном состоянии и контрольная разрядка будет совсем не лишней.
Необходимо постоянно помнить, что крупные радиодетали, коммутирующие электроэнергию, очень опасны. Для работы с такими радиодеталями требуются профессиональные навыки.
При работе с электрическими устройствами всегда необходимо соблюдать меры предосторожности.

Формула

Определение результирующего сопротивления конденсатора

Результирующее сопротивление конденсатора нельзя находить суммируя величины его активного и емкостного сопротивлений. Это делается по формуле

Tweet Нравится

Предыдущая запись: Мощность переменного тока
Следующая запись: Проверка радиодеталей

Устройство и принцип работы

https://youtube.com/watch?v=tuVEW69oXuw

Зарядка. После нажатия кнопки поток электронов приходит в конденсатор и останавливается на одной из его пластин благодаря диэлектрику. Этот поток называется зарядным током.
Накопление. Поскольку под действием электродвижущей силы всё больше и больше электронов будут поступать на обкладку и распределяться по ней, отрицательный заряд обкладки может расти до момента, пока накопленный потенциал не будет отталкивать поступающий избыточный поток электронов. Вторая пластина из-за дефицита электронов приобретает положительный заряд, по модулю равный отрицательному на первой. Зарядный ток будет протекать до тех пор, пока напряжение на обеих пластинах не сравняется с приложенным. Сила или скорость тока зарядки будет находиться на максимальном уровне в момент, когда пластины полностью разряжены, и приблизится к нулю в момент, когда напряжение на обкладках и источнике будут равны.
Сохранение. Поскольку обкладки заряжены противоположно, ионы и электроны будут притягиваться друг к другу, но не смогут соединиться из-за диэлектрической прослойки, создавая электростатическое поле. Благодаря этому полю конденсатор удерживает и сохраняет заряд.
Разряд. Если в цепи появляется возможность для электронов протечь другим путём, то напряжение, накопленное между положительными и отрицательными зарядами обкладок, мгновенно реализуется в электрический ток, импульс которого в лампе вспышки преобразуется в световую энергию.

Разрядное устройство своими руками

Перед тем как измерить емкость, проверить кондёры на пробой или утечку, или если нужна замена несправного элемента необходимо его разрядить. Особенно актуально сделать правильный разряд у высоковольтных радиодеталей большой емкости. Накопленная энергия может сохраняться длительное время и неправильный демонтаж или хранение может нести угрозу для жизни.

Для безопасной разрядки высоковольтных конденсаторов можно собрать недорогое, простое в реализации электронное устройство. Оно разряжает вполне эффективно и безопасно.

Посмотрим на его принципиальную схему:

Напряжение с высоковольтного конденсатора поступает на гасящий резистор R1 и далее уходит на диодный ограничитель напряжения двустороннего типа.

Сам диодный ограничитель из двух параллельных цепочек диодов D1-D3 и D4-D6. Это сделано для того чтобы от любого диода в цепи снять напряжение порядка 2 вольт для работы светодиодных индикаторов D7, D8. Поступающий ток на светодиоды ограничивается резистором R2.

Светодиод запускает процесс разряда высоковольтного конденсатора до безопасного напряжения порядка двух вольт.

На процесс разряда может потребоваться некоторое время от 10 сек. и больше. Время разряда зависит от емкости подключенного кондёра и, какое остаточное напряжение в нем оставалось.

Как только светодиод потухнет можно провести окончательный разряд, с помощью отвертки закоротив выводы радиодетали.

Схема вполне работоспособна.

Всю плату можно собрать самостоятельно и поместить в пластиковый корпус.

Определение заряда

Процессы зарядки и разрядки конденсаторов.

Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?

Как видите, здесь нет ничего сложного

Относительная диэлектрическая проницаемость

Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость

. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме
.
Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации

– смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.

Воздух – 1.0005

Бумага – от 2.5 до 3.5

Стекло – от 3 до 10

Слюда – от 5 до 7

Порошки оксидов металлов – от 6 до 20

Как разряжать правильно

Для того чтобы узнать, как правильно разрядить конденсатор надо иметь ввиду все те параметры, которые присуще конкретному элементу, а именно

Номинальную емкость;
Допуски по емкости;
Допустимое переменное напряжение;
Потери в диэлектрике;
Температурный коэффициент;
Разрешенная импульсная нагрузка;
Номинальная мощность;
Частота.

Самый главный параметр, для безопасной разрядки этого электронного элемента — емкость.

Плоский конденсатор.

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

E = frac{sigma}{2varepsilon_0thinspacevarepsilon}

E_+ = E_- = frac{q}{2varepsilon_0thinspacevarepsilon S}

E = E_+ + E_- = frac{q}{2varepsilon_0thinspacevarepsilon S} + frac{q}{2varepsilon_0thinspacevarepsilon S} = frac{q}{varepsilon_0thinspacevarepsilon S}

От чего зависит емкость

Виды и области применения

Существует много способов классификации современных конденсаторов, которые позволяют группировать их в зависимости от типа конструкции, рабочего напряжения, видов поляризации и назначения, изменению емкости, а также разновидности диэлектрика.

Виды поляризации:

ионная и ионно-релаксационная;
объемная;
дипольно-релаксационная;
электронная и электронно-релаксационная;
спонтанная.

Исходя из конструктивных особенностей, различают трубчатые и цилиндрические, монолитные, пластинчатые и секционные, дисковые, горшкообразные и литые, бочоночные, а также секционные разновидности.

Область применения конденсаторов:

Электроника – радиотехническое и телевизионное оборудование, запоминающие устройства, автоматика и разнообразная телемеханика, телеграфия и телефония.
Электроэнергетика – сварка разрядом, запуск электродвигателей, подавление радиопомех, регулирование напряжения, электроосвещение, отбор энергии, использование в сложных схемах и генераторах, а также защита от напряжения.
Промышленность – добывающая, металлургическая и металлообрабатывающая.
Техника – медицинская, лазерная, электроизмерительная, радиолокационная, фотографическая, автотракторная.

В зависимости от изменения емкости различают постоянные, переменные (изменение осуществляется механически или электрически) и подстроечные конденсаторы (изменение осуществляется разово или периодически).

Источник

Электрическая цепь RC

Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе,
согласно закону Ома, составит U/R, где U — напряжение заряда конденсатора.

Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и
противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:

Решаем дифференциальное уравнение C(dU/dt)= -U/R

Интегрируем:

Из таблицы интегралов здесь используем преобразование

Получаем общий интеграл уравнения: ln|U| = — t/RC + Const.
Выразим из него напряжение U потенцированием: U = e^-t^/RC * e^Const.
Решение примет вид:

U = e^-t^/RC * Const.

Здесь Const — константа, величина, определяемая начальными условиями.

Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону
e^-t^/RC.

Экспонента — функция exp(x) = e^x
e – Математическая константа, приблизительно равная 2.718281828…

Постоянная времени τ

Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U,
в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения U_C и определится выражением:

Тогда напряжение U_C на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:

U_C = U(1 — e^-t/RC)

При t = RC, напряжение на конденсаторе составит U_C = U(1 — e^-1) = U(1 — 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.

Постоянная времени τ = RC

За время τ конденсатор зарядится до (1 — 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 — 1/e³)*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 — 1/e⁵)*100% ≈ 99% значения U.

Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R,
тогда в цепи пойдёт ток разряда конденсатора.

Напряжение на конденсаторе при разряде будет составлять U_C = Ue^-t/τ = U/e^t/τ.

За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.

За время 3τ конденсатор разрядится до (1/e³)*100% ≈ 5% от значения U.
За время 5τ до (1/e⁵)*100% ≈ 1% значения U.

Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.

Замечания и предложения принимаются и приветствуются!

Источник

Заряд конденсатора

Процессы зарядки и разрядки конденсаторов

Емкость и энергия конденсатора

Как зарядить конденсатор

Зарядка конденсатора от источника постоянной ЭДС

Заряд конденсатора, ток

Время, необходимое для зарядки конденсатора

Заряд конденсатора: формула

Время разряда конденсатора

Значение диэлектрика

Синтаксис

Разряд конденсатора

Заряд конденсатора. Ток

Формула

Устройство и принцип работы

Определение заряда

Процессы зарядки и разрядки конденсаторов.

Относительная диэлектрическая проницаемость

Плоский конденсатор.

От чего зависит емкость

Емкость и энергия конденсатора.

Заряд конденсатора от источника постоянной ЭДС

Разряд конденсатора через сопротивление

Значение диэлектрика

Синтаксис

Разряд конденсатора

Электроника для всех

Заряд конденсатора. Ток

Советы и предупреждения

Формула

Определение результирующего сопротивления конденсатора

Похожие посты:

Устройство и принцип работы

Разрядное устройство своими руками

Определение заряда

Процессы зарядки и разрядки конденсаторов.

Относительная диэлектрическая проницаемость

Как разряжать правильно

Плоский конденсатор.

От чего зависит емкость

Виды и области применения

Электрическая цепь RC

Постоянная времени τ

Не пропустите также: