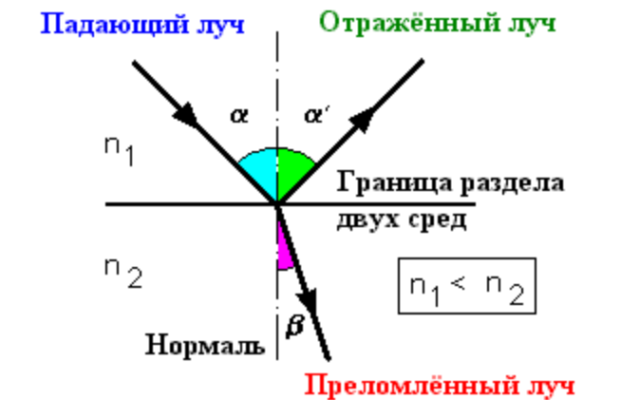
Как найти закон преломления света - AvtoShod.ru - решение различных проблем

Преломление света.

Закон преломления (частный случай).
Обратимость световых лучей.
Закон преломления (общий случай).
Полное внутреннее отражение.
Разберем задачи ЕГЭ по теме: Преломление света.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: закон преломления света, полное внутреннее отражение.

На границе раздела двух прозрачных сред наряду с отражением света наблюдается его преломление — свет, переходя в другую среду, меняет направление своего распространения.

Преломление светового луча происходит при его наклонном падении на поверхность раздела (правда, не всегда — читайте дальше про полное внутреннее отражение). Если же луч падает перпендикулярно поверхности, то преломления не будет — во второй среде луч сохранит своё направление и также пойдёт перпендикулярно поверхности.

к оглавлению ▴

Закон преломления (частный случай).

Мы начнём с частного случая, когда одна из сред является воздухом. Именно такая ситуация присутствует в подавляющем большинстве задач. Мы обсудим соответствующий частный случай закона преломления, а уж затем дадим самую общую его формулировку.

Предположим, что луч света, идущий в воздухе, наклонно падает на поверхность стекла, воды или какой-либо другой прозрачной среды. При переходе в среду луч преломляется, и его дальнейший ход показан на рис. 1.

Рис. 1. Преломление луча на границе «воздух–среда»

В точке падения проведён перпендикуляр (или, как ещё говорят, нормаль) к поверхности среды. Луч , как и раньше, называется падающим лучом, а угол alpha между падающим лучом и нормалью — углом падения. Луч — это преломлённый луч; угол beta между преломлённым лучом и нормалью к поверхности называется углом преломления.

Всякая прозрачная среда характеризуется величиной , которая называется показателем преломления этой среды. Показатели преломления различных сред можно найти в таблицах. Например, для стекла n=1,6 , а для воды n=1,33 . Вообще, у любой среды ; показатель преломления равен единице только в вакууме. У воздуха , поэтому для воздуха с достаточной точностью можно полагать в задачах n=1 (в оптике воздух не сильно отличается от вакуума).

Закон преломления (переход «воздух–среда»).

1) Падающий луч, преломлённый луч и нормаль к поверхности, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно показателю преломления среды:

$frac{displaystyle sinalpha }{displaystyle sinbeta }=n$ . (1)

Поскольку из соотношения (1) следует, что , то есть — угол преломления меньше угла падения. Запоминаем: переходя из воздуха в среду, луч после преломления идёт ближе к нормали.

Показатель преломления непосредственно связан со скоростью распространения света в данной среде. Эта скорость всегда меньше скорости света в вакууме: . И вот оказывается,что

$n=frac{displaystyle c }{displaystyle v }$ . (2)

Почему так получается, мы с вами поймём при изучении волновой оптики. А пока скомбинируем формулы . (1) и (2):

$frac{displaystyle sinalpha }{displaystyle sinbeta }=frac{displaystyle c }{displaystyle v }$ . (3)

Так как показатель преломления воздуха очень близок единице, мы можем считать, что скорость света в воздухе примерно равна скорости света в вакууме . Приняв это во внимание и глядя на формулу . (3), делаем вывод: отношение синуса угла падения к синусу угла преломления равно отношению скорости света в воздухе к скорости света в среде.

к оглавлению ▴

Обратимость световых лучей.

Теперь рассмотрим обратный ход луча: его преломление при переходе из среды в воздух. Здесь нам окажет помощь следующий полезный принцип.

Принцип обратимости световых лучей. Траектория луча не зависит от того, в прямом или обратном направлении распространяется луч. Двигаясь в обратном направлении, луч пойдёт в точности по тому же пути, что и в прямом направлении.

Согласно принципу обратимости, при переходе из среды в воздух луч пойдёт по той же самой траектории, что и при соответствующем переходе из воздуха в среду (рис. 2) Единственное отличие рис. 2 от рис. 1 состоит в том, что направление луча поменялось на противоположное.

Рис. 2. Преломление луча на границе «среда–воздух»

Раз геометрическая картинка не изменилась, той же самой останется и формула (1): отношение синуса угла alpha к синусу угла beta по-прежнему равно показателю преломления среды. Правда, теперь углы поменялись ролями: угол beta стал углом падения, а угол alpha — углом преломления.

В любом случае, как бы ни шёл луч — из воздуха в среду или из среды в воздух — работает следующее простое правило. Берём два угла — угол падения и угол преломления; отношение синуса большего угла к синусу меньшего угла равно показателю преломления среды.

Теперь мы целиком подготовлены для того, чтобы обсудить закон преломления в самом общем случае.

к оглавлению ▴

Закон преломления (общий случай).

Пусть свет переходит из среды 1 с показателем преломления $n_{displaystyle 1}$ в среду 2 с показателем преломления $n_{displaystyle 2}$ . Среда с большим показателем преломления называется оптически более плотной; соответственно, среда с меньшим показателем преломления называется оптически менее плотной.

Переходя из оптически менее плотной среды в оптически более плотную, световой луч после преломления идёт ближе к нормали (рис. 3). В этом случае угол падения больше угла преломления: .

Наоборот, переходя из оптически более плотной среды в оптически менее плотную, луч отклоняется дальше от нормали (рис. 4). Здесь угол падения меньше угла преломления:

Оказывается, оба этих случая охватываются одной формулой — общим законом преломления, справедливым для любых двух прозрачных сред.

Закон преломления.
1) Падающий луч, преломлённый луч и нормаль к поверхности раздела сред, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой среды:

$frac{displaystyle sinalpha }{displaystyle sinbeta }=frac{displaystyle n_{displaystyle 2}}{displaystyle n_{displaystyle 1}}$ . (4)

Нетрудно видеть, что сформулированный ранее закон преломления для перехода «воздух–среда» является частным случаем данного закона. В самом деле, полагая в формуле (4) $n_{displaystyle 1}=1, n_{displaystyle 2}=n$ , мы придём к формуле (1).

Вспомним теперь, что показатель преломления — это отношение скорости света в вакууме к скорости света в данной среде: $n_{displaystyle 1}=c/v_{displaystyle1}, n_{displaystyle 2}=c/v_{displaystyle2}$ . Подставляя это в (4), получим:

$frac{displaystyle sinalpha}{displaystyle sinbeta }=frac{displaystyle v_{displaystyle 1}}{displaystyle v_{displaystyle 2}}$ . (5)

Формула (5) естественным образом обобщает формулу (3). Отношение синуса угла падения к синусу угла преломления равно отношению скорости света в первой среде к скорости света во второй среде.

к оглавлению ▴

Полное внутреннее отражение.

При переходе световых лучей из оптически более плотной среды в оптически менее плотную наблюдается интересное явление — полное внутреннее отражение. Давайте разберёмся, что это такое.

Будем считать для определённости, что свет идёт из воды в воздух. Предположим, что в глубине водоёма находится точечный источник света , испускающий лучи во все стороны. Мы рассмотрим некоторые из этих лучей (рис. 5).

Рис. 5. Полное внутреннее отражение

Луч $SO_{displaystyle 1}$ падает на поверхность воды под наименьшим углом. Этот луч частично преломляется (луч $O_{displaystyle 1} A_{displaystyle 1}$ ) и частично отражается назад в воду (луч $O_{displaystyle 1} B_{displaystyle 1}$ ). Таким образом, часть энергии падающего луча передаётся преломлённому лучу, а оставшаяся часть энергии -отражённому лучу.

Угол падения луча $S O_{displaystyle 2}$ больше. Этот луч также разделяется на два луча — преломлённый и отражённый. Но энергия исходного луча распределяется между ними по-другому: преломлённый луч $O_{displaystyle 2} A_{displaystyle 2}$ будет тусклее, чем луч $O_{displaystyle 1} A_{displaystyle 1}$ (то есть получит меньшую долю энергии), а отражённый луч $O_{displaystyle 2} B_{displaystyle 2}$ — соответственно ярче, чем луч $O_{displaystyle 1} B_{displaystyle 1}$ (он получит большую долю энергии).

По мере увеличения угла падения прослеживается та же закономерность: всё большая доля энергии падающего луча достаётся отражённому лучу, и всё меньшая — преломлённому лучу. Преломлённый луч становится всё тусклее и тусклее, и в какой-то момент исчезает совсем!

Это исчезновение происходит при достижении угла падения $alpha _{0}$ , которому отвечает угол преломления $90^{circ}$ . В данной ситуации преломлённый луч должен был бы пойти параллельно поверхности воды, да идти уже нечему — вся энергия падающего луча целиком досталась отражённому лучу .

При дальнейшем увеличении угла падения преломлённый луч и подавно будет отсутствовать.

Описанное явление и есть полное внутреннее отражение. Вода не выпускает наружу лучи с углами падения, равными или превышающими некоторое значение $alpha _{0}$ — все такие лучи целиком отражаются назад в воду. Угол $alpha _{0}$ называется предельным углом полного отражения.

Величину $alpha _{0}$ легко найти из закона преломления. Имеем:

$frac{displaystyle sinalpha _{0}}{displaystyle sin90^{circ}}=frac{displaystyle 1}{displaystyle n}$ .

Но $sin90^{circ}=1$ , поэтому

$sinalpha _{0}=frac{displaystyle 1}{displaystyle n}$ ,

откуда

$alpha _{0}=arcsinfrac{displaystyle 1}{displaystyle n}$ .

Так, для воды предельный угол полного отражения равен:

$alpha _{0}=arcsinfrac{displaystyle 1}{1,33} approx 48,8^{circ}$ .

Явление полного внутреннего отражения вы легко можете наблюдать дома. Налейте воду в стакан, поднимите его и смотрите на поверхность воды чуть снизу сквозь стенку стакана. Вы увидите серебристый блеск поверхности — вследствие полного внутреннего отражения она ведёт себя подобно зеркалу.

Важнейшим техническим применением полного внутреннего отражения является волоконная оптика. Световые лучи, запущенные внутрь оптоволоконного кабеля (световода) почти параллельно его оси, падают на поверхность под большими углами и целиком, без потери энергии отражаются назад внутрь кабеля. Многократно отражаясь, лучи идут всё дальше и дальше, перенося энергию на значительное расстояние. Волоконно-оптическая связь применяется, например, в сетях кабельного телевидения и высокоскоростного доступа в Интернет.

к оглавлению ▴

Разберем задачи ЕГЭ по теме: Преломление света.

Задача 1. Нижняя грань AC прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина $alpha = 30^{circ}$ . Луч света падает из воздуха на клин перпендикулярно грани AB, преломляется и выходит в воздух через ту же грань AB, но уэе под углом преломления $beta = 90^{circ}$ Определите показатель преломления материала клина. Сделайте рисунок, поясняющий ход луча в клине.

Дано:
$alpha = 30^{circ}$
$beta = 90^{circ}$
n-?
Решение. Решение задач по геометрической оптике необходимо начинать с построения чертежа (рисунка), моделирующего условия, описанные в тексте задачи.

Световой луч падает на прозрачный клин перпендикулярно стороне АВ (см.рис.1). В этом случае, световой луч не преломляется на границе раздела воздух-клин, так как угол падения равен 0, соответственно, угол преломления также равен 0. Следовательно, внутри клина световой луч попадает на нижнюю грань АС, которая представляет собой плоское зеркало. Согласно рис.1 величина угла $alpha_1=180^{circ}-(alpha+90^{circ})=90^{circ}-alpha.$

$alpha_1=90^{circ}-30^{circ}=60^{circ}.$

Тогда угол падения луча на плоское зеркало будет равен
$90^{circ}-alpha_1=90^{circ}-60^{circ}=30^{circ}.$

То есть угол падения равен $alpha=30^{circ}$ .
Согласно закону отражения света, угол падения светового луча равен углу отражения. В треугольнике МКО угол КОМ образован суммой двух углов α, поэтому он равен 60°. Тогда угол падения светового луча на грань АВ также будет равен $2alpha=60^{circ}$ (равенство накрест лежащих углов).
На следующем этапе задачи надо применить закон преломления света, так как луч переходит из одной среды в другую.
$frac{sin{2alpha}}{sinbeta}=frac{1}{n}$
При записи этой формулы учтено, что второй средой является воздух с показателем преломления равным 1, а первой средой является материал клина с показателем преломления n, который необходимо определить. Из последней формулы можно выразить и рассчитать n.

$n=frac{sinbeta}{sin2alpha}$

$n=frac{sin90^{circ}}{sin(2cdot 30^{circ})}=frac{sin90^{circ}}{sin60^{circ}}approx 1,15$

Ответ: 1,15

Задача 2. На тонкую собирающую линзу от удалённого источника падает пучок параллельных лучей (см. рисунок). Как изменится положение изображения источника, создаваемого линзой, если между линзой и её фокусом поставить
плоскопараллельную стеклянную пластинку с показателем преломления n (на рисунке положение пластинки отмечено пунктиром)? Ответ поясните, указав, какие физические закономерности Вы использовали. Сделайте рисунок, поясняющий ход лучей до и после установки плоскопараллельной стеклянной пластинки.

Решение. Рассмотрим ход световых лучей от удаленного источника через линзу при отсутствии плоскопараллельной стеклянной пластинки (см.рис.1).

Луч 1-1ʹ проходит через оптический центр линзы и не преломляется. Луч 2-2ʹ идет через фокус и после прохождения через линзу, идет параллельно главной оптической оси. Пересечение этих двух лучей дает действительное изображение удаленного источника, которое расположено в фокальной плоскости линзы. Этот факт также можно доказать, используя формулу тонкой линзы.

$frac{1}{d}+frac{1}{f}=frac{1}{F} (1)$

Так как источник света расположен на расстоянии то $frac{1}{d}rightarrow 0.$

Тогда формула тонкой линзы (1) примет вид $frac{1}{f}=frac{1}{F},$ следовательно, f=F, т.е. изображение формируется в фокальной плоскости линзы.

Рассмотрим ход световых лучей через плоскопараллельную стеклянную пластинку. Для этого необходимо использовать закон преломления света.

Рис.2

Согласно рис.2 угол падения луча на пластину равен α. Закон преломления света на границе раздела воздух-пластинка имеет вид:

$frac{sinalpha}{sinbeta}=frac{n}{1}=n (1).$

Здесь учтено, что показатель преломления воздуха равен 1, а пластинки n.
При переходе светового луча из пластинки в воздух, закон преломления света будет иметь вид:

$frac{sinbeta}{singamma}=frac{1}{n} (2).$

В этом случае первой средой является пластинка с показателем преломления n, а второй средой будет воздух с показателем преломления равным 1.
Из (1) и (2) выразим и .

Так как правые части этих уравнений равны, то

Отсюда вытекает равенство углов . Следовательно, луч, падающий на стеклянную пластину, выходит из нее, оставаясь параллельным входящему лучу. Но при этом выходящий луч немного смещается вверх.

Исходя из этого можно сделать вывод, что изображение удаленного источника после прохождения через плоскопараллельную стеклянную пластину, не изменится. Из удаленного источника выходит бесконечное количество параллельных лучей, которые собираются в фокальной плоскости линзы.

Ответ: не изменится.

Задача 3. Ученик провел опыт по преломлению света, представленный на фотографии. Как изменится при уменьшении угла падения угол преломления светового пучка и скорость света, распространяющегося в стекле? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшиться
3) не изменится
Запишите в таблицу выбранные цифры для каждой величины. Цифры в ответе могут повторяться.

Угол преломления	Скорость света в стекле

Решение. Для ответа на первый вопрос задачи необходимо применить закон преломления света для границы раздела воздух-стекло.

$frac{sinalpha}{sinbeta}=frac{n}{1}=n.$

Показатель преломления стекла равен n, а воздуха 1.
При уменьшении угла падения α, будет уменьшаться и значение Так как показатель преломления стекла не изменяется, то значение sinbeta так же будет уменьшаться. Поэтому угол преломления уменьшится.

Для ответа на второй вопрос надо учесть, что скорость света в данной среде определяется значением показателя преломления $v_{cp}=frac{c}{n},$ где с – скорость света в вакууме, а n – показатель преломления среды (стекла). Так как эти обе величины не изменяются, то скорость света в стекле так же не изменяется.

Ответ: 23.

Задача 4. Чему равен синус предельного угла полного внутреннего отражения при переходе света из вещества с n_1=1,5 в вещество с n_2=1,2 ?

Решение.

Явление полного внутреннего отражения наблюдается при переходе светового луча из оптически более плотной среды в оптически менее плотную (см.рис.1). Источник света S должен находиться в среде с большим показателем преломления.

Для нахождения синуса угла полного внутреннего отражения необходимо воспользоваться законом преломления света.

$frac{sinalpha_{np}}{sinbeta}=frac{n_2}{n_1} (1)$

При полном внутреннем отражении преломленный луч скользит по границе раздела двух сред и угол преломления $beta=90^{circ}$ . С учетом того, что $sin90^{circ}=1$ уравнение (1) примет вид:

$sinalpha_{np}=frac{1,2}{1,5}=0,8$

$sinalpha_{np}=0,8$

Ответ: 0,8.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Преломление света.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Из прошлых уроков вы уже знаете, что в однородной среде свет распространяется прямолинейно. Но в жизни много ситуаций, когда свет проходит через разные вещества до того, как достигнет наших глаз.

Например, через оконные стекла мы отлично видим все, что происходит на улице. А через стекла в межкомнатных дверях мы можем видеть только размытые силуэты того, что находится за дверью. Тот же самый пример можно привести и с прозрачной и мутной водой.

Значит, получаемое нашими глазами изображение как-то связано с тем, через какие среды проходит свет. Двигаясь прямолинейно в одной среде, он переходит в другую и снова двигается прямолинейно. Что же происходит при этом переходе из одной среды в другую?

Так, вам предстоит узнать новое понятие — преломление света. В ходе данного урока вы узнаете закономерности этого явления, рассмотрите различные опыты и научитесь применять полученные знания для решения задач.

Явление преломления света

Рассмотрим простой опыт. Для него нам понадобится прозрачный стакан с водой и обычный карандаш (рисунок 1).

Рисунок 1. Демонстрация преломления света

Сначала опустим карандаш в воду вертикально (рисунок 1, а). Части карандаша в воздухе и в воде не изменились.

А теперь поменяем угол наклона карандаша (рисунок 2, б). Мы увидим интересную картинку. Нам кажется, что карандаш переломился на границе воды и воздуха.

Что произошло? Мы видим карандаш, потому что на него падает свет от какого-то источника. Его лучи отражаются от карандаша и попадают нам в глаза. Когда мы опустили карандаш в воду под каким-то углом, световые лучи дошли до наших глаз не только через воздух, но еще и через воду в стакане. При этом они поменяли направление своего распространения при переходе из одной среды в другую. В таком случае говорят, что свет преломился.

Преломление света — это явление изменения направления распространения света при переходе из одной среды в другую.

Но, если свет преломляется при переходе из одной среды в другую, почему на рисунке 1 (а) мы все равно видим карандаш без изменений? Чтобы разобраться с этим вопросом, нам необходимо более подробно изучить природу преломления света.

Скорость света и оптическая плотность среды

Свет распространяется в пространстве с определенной скоростью. Эта скорость настолько велика, что нам кажется, будто свет появляется мгновенно. Например, когда в темной комнате мы щелкаем переключателем, и включается свет.

Ученые не только рассчитали значение этой скорости, но и доказали, что скорость света различается в разных средах (таблица 1).

Вещество	$c$, $frac{км}{с}$
Воздух	300 000
Вода	225 000
Стекло	198 000
Сероуглерод	184 000
Алмаз	124 000

Таблица 1. Значения скорости света в различных средах

Значения скорости света в вакууме и воздухе практически не отличаются, поэтому используют одно значение — $300 000 frac{км}{с}$. Эта величина обозначается буквой $c$.

В других же средах наблюдается значительная разница в значениях скорости. Например, в воде скорость света меньше, чем в воздухе. При этом говорят, что вода является оптически более плотной средой, чем воздух.

Оптическая плотность — это величина, которая характеризует различные среды в зависимости от значения скорости распространения света в них.

Если пучок света падает на поверхность, разделяющую две прозрачные среды с разной оптической плотностью, то часть света отразится от этой поверхности, а другая часть проникнет во вторую среду. При этом луч света изменит свое направление — происходит преломление света.

Схема преломления светового луча. Угол преломления

Рассмотрим преломление света более подробно (рисунок 2).

Рисунок 2. Схема преломления светового луча при переходе из воздуха в воду

Перечислим элементы, обозначенные на рисунке 2:

MN — граница раздела воздуха и воды
Луч AO — падающий луч
Луч OB — преломленный луч
CD — перпендикуляр, опущенный к поверхности раздела двух сред и проведенный через точку падения O
Угол AOC — угол падения ($alpha$)
Угол DOB — угол преломления ($gamma$)

Угол преломления — это угол между перпендикуляром, опущенным к границе раздела двух сред в точке падения светового луча, и преломленным лучом.

Направления луча при переходе в воду изменилось. Луч света стал ближе к перпендикуляру CD. Т.е., $gamma < alpha$. Рассмотрим опыт, который нам наглядно демонстрирует этот факт.

Возьмем стеклянный сосуд и наполним его водой. Воду подкрасим флуоресцентной жидкостью. Она будет светится в тех местах, где на нее будет попадать яркий свет — это удобно для наших наблюдений. На дно сосуда поместим плоское зеркало (рисунок 3).

Рисунок 3. Преломление света на опыте с плоским зеркалом

Теперь на поверхность воды с помощью маленького фонарика направим пучок света. Сделаем это таким образом, чтобы пучок света падал под каким-то углом.

Мы увидим, как луч поменяет свое направление на границе воздуха и воды. При этом угол преломления заметно меньше угла падения ($gamma_1 < alpha_1$).

Далее луч отразится от плоского зеркала и снова достигнет границы раздела двух сред. Теперь мы видим, что луч падения заметно меньше луча преломления ($gamma_2 > alpha_2$).

Вода — более плотная оптическая среда, чем воздух. Из всего этого мы можем сделать следующие выводы:

Если свет идет из оптически менее плотной среды в более плотную, то угол преломления всегда меньше угла падения: $gamma < alpha$
Если свет идет из оптически более плотной среды в менее плотную, то угол преломления всегда больше угла падения: $gamma > alpha$

Если в ходе опытов мы будем менять угол падения, то заметим, что угол преломления тоже будет изменяться. При этом вышеописанные нами закономерности будут исполняться.

Показатель преломления

Давайте выясним, как именно углы падения и преломления связаны друг с другом. Рассматривать будем луч света падающий из воздуха в воду.

При увеличении угла падения, будет увеличиваться угол преломления (рисунок 4). Но отношение между этими углами ($frac{alpha}{gamma}$) не будет постоянным.

Рисунок 4. Зависимость угла преломления от угла падения

Постоянным будет оставаться другое отношение этих углов — отношение их синусов:
$frac{sin 30 degree}{sin 23 degree} = frac{sin 45 degree}{sin 33 degree} = frac{sin 60 degree}{sin 42 degree} approx 1.33$.

Полученное число (1.3) называют относительным показателем преломления. Обозначают эту величину буквой $n_{21}$.

Так, для любой пары веществ с разными оптическими плотностями можно записать:

$frac{sin alpha}{sin gamma} = n_{21}$.

Чем больше относительный показатель преломления, тем сильнее преломляется световой луч при переходе из одной среды в другую.

В чем физический смысл этой величины? Ранее мы говорили, что оптическая плотность характеризует вещество по скорости распространения света в нем. Показатель преломления делает то же самое.

Относительный показатель преломления — это величина, показывающая, во сколько раз скорость света в первой по ходу луча среде отличается от скорости распространения света во второй среде:
$n_{21} = frac{upsilon_1}{upsilon_2}$.

Если луч света падает из вакуума или воздуха в какое-то вещество, то используется еще одна величина — абсолютный показатель преломления.

Абсолютный показатель преломления — это величина, показывающая во сколько раз скорость света в вакуумевоздухе больше, чем в данной среде:
$n = frac{c}{upsilon}$,
где $c = 3 cdot 10^8 frac{м}{с}$.

В таблице 2 представлены значения абсолютных показателей преломления некоторых веществ. Иногда их называют относительными показателями преломления относительно воздуха, потому что для воздуха $n = 1$.

Вещество	$n$
Воздух	1.00
Лед	1.31
Вода	1.33
Спирт	1.36
Стекло (обычное)	1.50
Стекло (оптическое)	1.47 — 2.04
Рубин	1.76
Алмаз	2.42

Таблица 2. Абсолютные показатели преломления света различных веществ

Выразим относительный показатель преломления $n_{21}$ через абсолютные показатели преломления $n_1$ и $n_2$:
$n_{21} = frac{upsilon_1}{upsilon_2} = frac{frac{c}{n_1}}{frac{c}{n_2}} = frac{n_2}{n_1}$.

Относительный показатель преломления $n_{21}$ имеет нижний индекс $21$, который читается как: «два один». Этот индекс связан с полученной нами формулой: $n_{21} = frac{n_2}{n_1}$. То есть, относительный показатель преломления $n_{21}$ равен отношению абсолютных показателей $n_2$ к $n_1$. При этом нижние индексы обозначают последовательность сред, через которые проходит световой луч.

Здесь мы вернемся к вопросу о том, почему на рисунке 1 (а) мы не видим преломления.

Если падающий луч падает перпендикулярно на границу раздела двух сред, то он не испытывает преломления.

Доказывается это опытным путем. При любых других углах падения, отличных от $0 degree$, преломление света происходит по вышеописанным закономерностям.

Закон преломления света

Итак, преломление света происходит по определенному закону.

Закон преломления света:
падающий и преломленный лучи и перпендикуляр, проведенный к границе раздела двух сред в точке падения луча, лежат в одной плоскости. При этом отношение синуса угла падения к синусу угла преломления — постоянная величина для двух сред:
$frac{sin alpha}{sin gamma} = frac{n_2}{n_1} = n_{21}$.

Мнимое изображение, образованное преломлением света. Призмы

Преломление света, как и отражение света плоским зеркалом, создает “кажущееся” изменение положение источника света. Мы наблюдали такое изменение в самом первом опыте этого урока на рисунке 1, б.

Но, дело в том, что мнимое положение источника света в случае преломления будет различным для лучей, падающих на границу раздела двух сред под разными углами. Поэтому мнимое положение источника света при преломлении обычно подробно не рассматривают.

Тем не менее, мы часто замечаем эти изменения. Например, в прозрачной воде в закрытых водоемах или в море кажется, что предметы, лежащие на дне и находящиеся в толще воды, находятся на другом расстоянии от нас, чем они есть на самом деле.

Рассмотрим наглядный опыт с монеткой (рисунок 5).

Рисунок 5. Опыт с монеткой

Возьмем неглубокую широкую чашку и положим на ее дно монетку. Выберем такое положение для наблюдения, чтобы она была не видна (рисунок 5, а).

Оставаясь в этой же точке наблюдения, нальем в чашку воду. Теперь монета стала видна (рисунок 5, б). То есть, мы видим не саму монету, а ее мнимое изображение, образованное преломлением света.

В различных оптических приборах используют эти особенности преломления. Часто свет проходит сквозь тело, имеющее форму призмы (рисунок 6, а).

Рисунок 6. Прохождение светового луча через призму

Световой луч, падающий на боковую грань призмы дважды преломляется (рисунок 6, б): при входе в призму и при выходе из нее. Такой луч на выходе из призмы будет отклоняться к основанию треугольника.

В оптических приборах используют не просто призмы, но и их различные сочетания. Например, на рисунке 7 изображены 3 коробки, в которых находятся треугольные призмы.

Рисунок 7. Различные положения призм, используемые для изменения хода световых лучей

Вы можете оценить, как при разных положениях призм изменяется ход лучей на выходе из коробки. При этом падающие лучи во всех трех случаях (а, б, в) были параллельны и имели одинаковое направление.

Примеры задач

Задача №1

Луч света переходит из скипидара в воздух. Определите абсолютный показатель преломления скипидара, если при угле падения, равном $30 degree$, угол преломления равен $45 degree$ (рисунок 8). Чему равна скорость распространения света в скипидаре?

Рисунок 8. Задача на преломление света №1

Дано:
$alpha = 30 degree$
$gamma = 45 degree$
$n_2 = 1$
$c = 3 cdot 10^8 frac{м}{с}$

$n_1 — ?$
$upsilon_1 — ?$

Посмотреть решение и ответ

Скрыть

Решение:

Так как световой луч проходит из скипидара (первая среда) в воздух (вторая среда), мы обозначили абсолютный показатель скипидара как $n_1$, а воздуха как $n_2$.

По закону преломления света:
$frac{sin alpha}{sin gamma} = n_{21} = frac{n_2}{n_1}$.

Для воздуха $n_2 = 1$, поэтому:
$frac{sin alpha}{sin gamma} = frac{1}{n_1}$.

Выразим $n_1$:
$n_1 = frac{sin gamma}{sin alpha}$.

Рассчитаем $n_1$:
$n_1 = frac{sin 45 degree}{sin 30 degree} = frac{frac{sqrt{2}}{2}}{frac{1}{2}} = sqrt{2} approx 1.41$.

По определению абсолютного показателя преломления для скипидара мы можем записать:
$n_1 = frac{c}{upsilon_1}$.

Выразим $upsilon_1$ и рассчитаем:
$upsilon_1 = frac{c}{n_1} = frac{3 cdot 10^8 frac{м}{с}}{1.41} approx 2 cdot 10^8 frac{м}{с}$.

Ответ: $n_1 approx 1.41$, $upsilon_1 approx 2 cdot 10^8 frac{м}{с}$.

Задача №2

Световой луч падает из воздуха в стекло. Абсолютный показатель преломления стекла равен $1.73$. Чему равен угол преломления, если отраженный луч образует с перпендикуляром, опущенным в точку падения луча на границе раздела двух сред, угол, равный $60 degree$?

При решении задачи мы будем использовать рисунок 9.

Рисунок 9. Задача на преломление света №2

$AO$ — падающий луч, а угол $alpha$ — угол падения. Луч $AO$ падает на границу раздела двух сред (воздуха и стекла). Образуются отраженный луч $OB$ и преломленный луч $OC$. Им соответствуют угол отражения $beta$ и угол преломления $gamma$.

Теперь запишем условие задачи и решим ее.

Дано:
$n_1 = 1$
$n_2 = 1.73$
$beta = 60 degree$

$gamma — ?$

Посмотреть решение и ответ

Скрыть

Решение:

По закону отражения света:
$alpha = beta = 60 degree$.

По закону преломления света:
$frac{sin alpha}{sin gamma} = frac{n_2}{n_1}$.

Для воздуха $n_1 = 1$, поэтому:
$frac{sin alpha}{sin gamma} = n_2$.

Выразим синус угла преломления и рассчитаем его:
$sin gamma = frac{sin alpha}{n_2} = frac{sin 60 degree}{1.73} = frac{frac{sqrt{3}}{2}}{1.73} = frac{sqrt{3}}{3.46} approx frac{1.73}{3.46} = 0.5 = frac{1}{2}$.

Если $sin gamma = frac{1}{2}$, то $gamma = 30 degree$.

Ответ: $gamma = 30 degree$.

Задача №3

На дне пруда глубиной $3 space м$ находится источник света. Показатель преломления воды равен $1.33$, а воздуха — $1$. На какой глубине наблюдатель увидит источник света, если он смотрит вертикально вниз с лодки.

Условие задачи дает понять, что в глаз наблюдателя попадает луч, который падает перпендикулярно границе раздела двух сред. В таком случае, преломление наблюдаться не будет. Тем не менее, как и в настоящей жизни, мы все равно увидим преломленное изображение источника света. Он будет казаться ближе. В ходе решения этой задачи вы узнаете, почему так происходит.

Для начала рассмотрим рисунок 10.

Рисунок 10. Задача на преломление света №3

Источник света $S$ находится на глубине $H$. Мы опишем его двумя лучами: $SA$ и $SO$. Луч $SA$ перпендикулярен к границе раздела двух сред. Поэтому он не преломляется. Луч $SO$ достигает границы раздела под некоторым углом. Он образует с перпендикуляром $CD$ угол падения $alpha$. Далее этот луч преломляется под углом преломления $gamma$ и попадает в глаза наблюдателя (точка $B$).

Продолжим преломленный луч до луча $SA$. Этот луч мы будем использовать как перпендикуляр к поверхности воды, чтобы оценивать глубину. Мы получили точку $S_1$ — мнимое изображение источника света. Соответственно длина отрезка $AS$ — это реальная глубина пруда $H$, а длина отрезка $AS_1$ — мнимая глубина $h$.

Обратите внимание, что мы взяли второй луч $SO$ не просто так — он падает под крайне малым углом $alpha$. После преломления мы получаем такой малый угол $gamma$, что он попадает в глаз наблюдателя. Т.е., на рисунке 8 схематическая область увеличена для нашего удобства во много раз. Мы рассматриваем настолько малые углы, что преломленный луч $SB$ достигает глаза, и мы видим мнимое изображение, образованное преломлением света.

Теперь мы можем записать условие задачи и решить ее.

Дано:
$H = 3 space м$
$n_1 = 1.33$
$n_2 = 1$

$h — ?$

Посмотреть решение и ответ

Скрыть

Решение:

Рассмотрим две прямые $AS$ и $CD$. Они параллельны, а прямая $SO$ — секущая. Тогда накрест лежащие углы равны друг другу:
$angle ASO = alpha$.

Запишем тангенс этого угла в прямоугольном треугольнике $ASO$:
$tg alpha = frac{AO}{AS} = frac{AO}{H}$.
Тогда, $AO = H cdot tg alpha$.

Теперь попробуем выразить $AO$ из другого треугольника — $AS_1O$.
Если рассмотрим $S_1O$ как прямую, пересекающую две параллельные прямые, то $angle AS_1O = gamma$.

Запишем тангенс этого угла:
$tg gamma = frac{AO}{AS_1} = frac{AO}{h}$.
Тогда, $AO = h cdot tg gamma$.

Получается, что $H cdot tg alpha = h cdot tg gamma$.
Выразим отсюда мнимую глубину $h$:
$h = H cdot frac{tg alpha}{tg gamma}$.

Так как углы $alpha$ и $gamma$ крайне малы, мы можем смело использовать следующие приближения:
$tg alpha approx sin alpha$,
$tg gamma approx sin gamma$.

Тогда, $h = H cdot frac{sin alpha}{sin gamma} = H cdot frac{n_2}{n_1}$.
Так как $n_2 = 1$, мы можем записать, что $h = frac{H}{n_1}$.

$h = frac{3 space м}{1.33} approx 2.3 space м$.

Ответ: $h = 2.3 space м$.

Источник

В (1621) году голландский математик Виллеброрд Снеллиус опытным путём открыл и сформулировал закон преломления света. Он отметил, что при изменении угла падения угол преломления изменяется так, что постоянным остаётся соотношение синусов этих углов.

Закон преломления света (закон Снеллиуса)

Падающий и преломлённый лучи и перпендикуляр, проведённый к границе раздела двух сред в точке падения луча, лежат в одной плоскости.
Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред, равная относительному показателю преломления:

Явление полного внутреннего отражения

Рассмотрим луч света, который переходит из среды с большим показателем преломления в вещество с меньшим абсолютным показателем преломления (например, из воды в воздух).

Рис. 1. Схема полного внутреннего отражения

В этом случае угол преломления луча больше, чем угол падения. Если увеличивать угол падения, то при некотором предельном угле

αпр

угол преломления становится равным (90)°. При дальнейшем увеличении угла падения луч полностью отражается от границы раздела и не переходит в другую среду. Это явление называется явлением полного внутреннего отражения (рис. 1).

Запишем закон преломления света для

αпр

Обрати внимание!

Явление полного внутреннего отражения наблюдается только при переходе светового луча из среды с большим абсолютным показателем преломления в среду с меньшим абсолютным показателем преломления вещества, а также при угле падения большем или равным углу

αпр

Явление полного внутреннего отражения используется в волоконной оптике — для передачи световых сигналов на большие расстояния. Использование обычного зеркального отражения не дает желаемого результата, так как даже зеркало самого высокого качества (посеребрённое) поглощает часть световой энергии. И при многократном отражении энергия света стремится к нулю.

Рис. 2. Изображение хода луча в световоде

(1) — защитная оболочка

(2) — оболочка (с меньшим показателем преломления)

(3) — сердцевина (с большим показателем преломления)

Оптическое волокно состоит из внутренней сердцевины, окружающей ее оболочки и дополнительного защитного покрытия (защитной оболочки) (рис. 2). Сердцевина — светопередающая часть волокна из стекла или пластика. Чем больше диаметр сердцевины, тем большее количество света может быть передано по волокну. Оболочка обеспечивает переотражение света в сердцевину волокна таким образом, чтобы световые волны распространялись только по сердцевине волокна. При входе в световод падающий луч направляется под углом больше предельного, что обеспечивает отражение луча без потери энергии. Волоконные световоды с успехом применяют в медицине. Например, световод вводят в желудок или в область сердца для освещения или наблюдения тех или иных участков внутренних органов. Использование световодов позволяет исследовать внутренние органы без введения лампочки, то есть исключая возможность перегрева.

Источник

Закон преломления света

4.1

Средняя оценка: 4.1

Всего получено оценок: 544.

4.1

Средняя оценка: 4.1

Всего получено оценок: 544.

Эксперименты показывают, что в однородных средах свет распространяется прямолинейно. Падая на границу раздела двух сред, свет частично отражается, а также частично проходит через границу раздела и распространяется во второй среде. Изменение направления светового луча, возникающего на границе двух сред, называется преломлением (рефракцией).

Принцип Гюйгенса

Для объяснения механизма распространения световых волн, нидерландский ученый Христиан Гюйгенс в 1678 г. сформулировал принцип (постулат, т.е. утверждение принимаемое за истинное без доказательств), названный его именем. Принцип состоит из двух основных положений:

Каждая точка среды, до которой дошла световая волна, сама становится источником вторичных волн;
Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени. Фронт волны – это огибающая фронта вторичных волн.

Рис. 1. Принцип Гюйгенса.

На представленном рисунке изображен фронт световой волны, распространяющийся со скоростью v в два момента времени — t и t+ Δt. Видно, что точки волны в момент времени t являются источниками вторичной волны в момент времени t+ Δt.

Как отражается свет

Из принципа Гюйгенса следует закон отражения света, который формулируется так:

Луч падающий, луч отраженный и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Угол падения α равен углу отражения β.

Рис. 2. Отражение и преломление света на границе двух сред с разными показателями преломления

Как преломляется свет

Угол γ, образованный преломленным лучом и перпендикуляром к границе раздела двух сред, проведенным через точку падения луча, называется углом преломления. Видно, что угол γ не равен углу α.

Закон преломления света был экспериментально открыт в ХVII веке нидерландским физиком Снеллиусом, и формулируется так:

падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред к точке падения луча, лежат в одной плоскости;
отношение синуса угла падения к синусу угла преломления — постоянная величина для двух данных сред.

Формула закона преломления света, количественно описывающая соотношение синусов углов падения и преломления, выглядит так:

$$n21={v1over v2}$$

где n₂₁ — физическая величина, называемая относительным показателем преломления второй среды относительно первой. Эта формула также называется в честь своего первооткрывателя законом Снеллиуса.

Ярким примером явления преломления света является кажущийся излом чайной ложки в стакане воды на границе раздела воздух-вода.

Рис. 3. Сломанная ложка в стакане с водой

Что такое относительный показатель преломления

Экспериментально установлено, что отличие угла преломления от угла преломления связано с изменением скорости распространения световой при переходе из одной среды в другую. Физический смысл показателя преломления — это отношение скорости распространения волн в первой среде v₁ к скорости их распространения во второй среде v₂:

$$n21={v1over v2}$$

Показатель преломления n среды относительно вакуума называется показателем преломления этой среды:

$$n={cover v}$$

где c — скорость света в вакууме, v — скорость света в данной среде.

Экспериментально доказано, что скорость света в вакууме является максимальной скоростью распространения в природе. Значение c равно 300 000 км/сек. Поэтому показатели преломления всех веществ больше единицы.

Таким образом относительный показатель преломления n₂₁ в формуле закона Снеллиуса равен отношению показателей преломления сред n₁ и n₂:

$$ n21={ n2over n1}$$

Из двух сред та среда, которая имеет меньшее значение показателя преломления, называется оптически менее плотной средой. Если свет переходит из оптически менее плотной среды в оптически более плотную, то угол преломления меньше угла падения .

Что мы узнали?

Итак, мы узнали что происходит со световой волной, падающей на границу раздела двух сред с разными показателями преломления. Принцип Гюйгенса, закон Снеллиуса и знание величин показателей преломления позволяют определить углы отражения и преломления на границе раздела двух сред.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Александр Коновалов

5/5

Оценка доклада

4.1

Средняя оценка: 4.1

Всего получено оценок: 544.

А какая ваша оценка?

Источник

Преломление света.

Закон преломления (частный случай).

Обратимость световых лучей.

Закон преломления (общий случай).

Полное внутреннее отражение.

Разберем задачи ЕГЭ по теме: Преломление света.

Явление преломления света

Скорость света и оптическая плотность среды

Схема преломления светового луча. Угол преломления

Показатель преломления

Закон преломления света

Мнимое изображение, образованное преломлением света. Призмы

Примеры задач

Задача №1

Задача №2

Задача №3

Закон преломления света

Принцип Гюйгенса

Как отражается свет

Как преломляется свет

Что такое относительный показатель преломления

Что мы узнали?

Тест по теме

Оценка доклада

Не пропустите также: