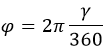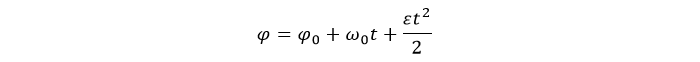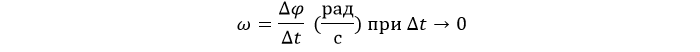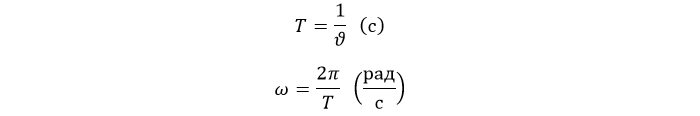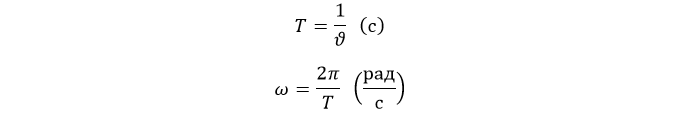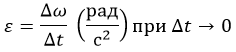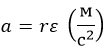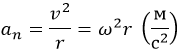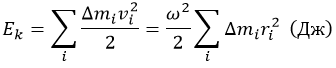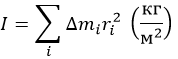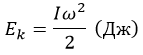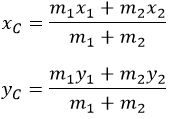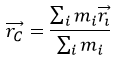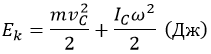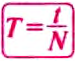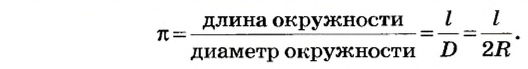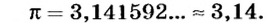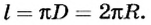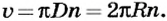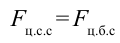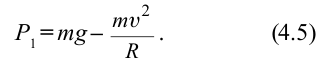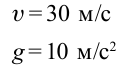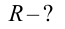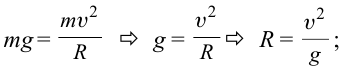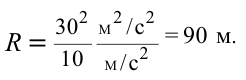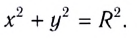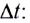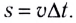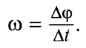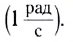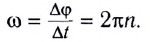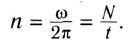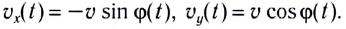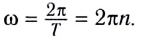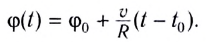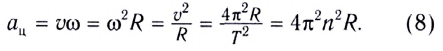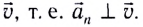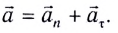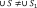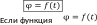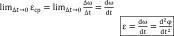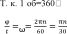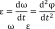Как найти закон движения вращательного движения

В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».

Основные понятия кинематики вращательного движения

Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.

Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.

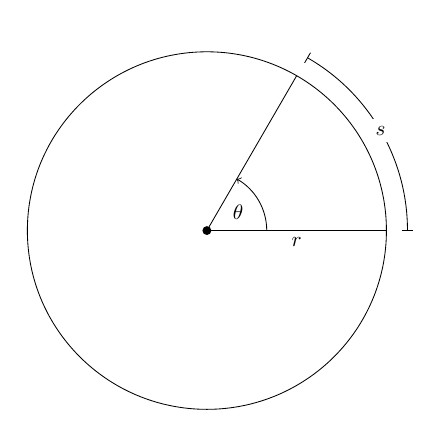
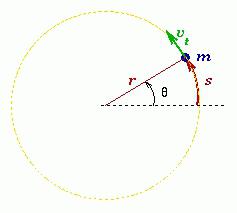
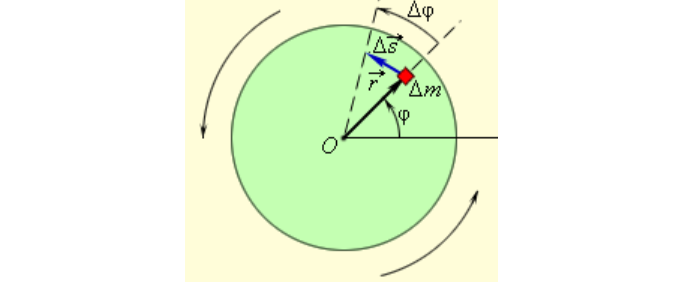
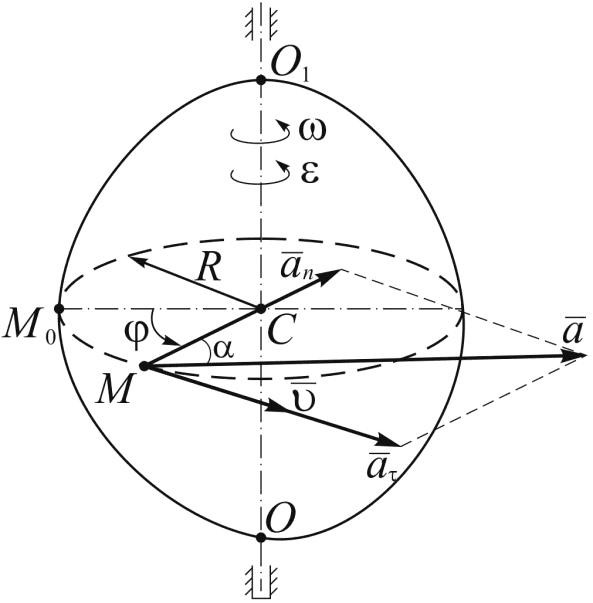
Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.

Через некоторое время радиус повернется относительно исходного положения на угол Δφ.

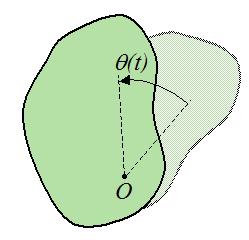
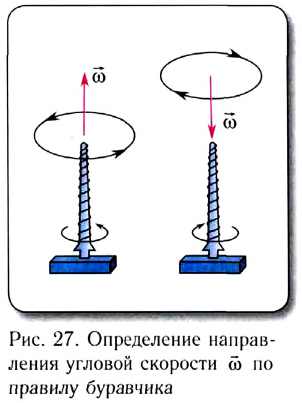
За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:

φ = φ(t).

Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:

ΔS = Δφr.

Основные элементы кинематики равномерного вращательного движения

Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.

Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:

ω = dφ/dt.

Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле

ω = φ/t.

Согласно предварительной формуле размерность угловой скорости

[ω] = 1 рад/с.

Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то

ω = 2π/T,

поэтому период вращения определим следующим образом:

T = 2π/ω.

Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:

ν = 1/T.

Единицы измерения частоты: [ν]= 1/c = 1 c^-1 = 1 Гц.

Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:

ω = 2πν.

Основные элементы кинематики неравномерного вращательного движения

Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.

Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:

ε = dω/dt.

Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.

Если вращательное движение замедлено — dω/dt < 0, то векторы ε и ω противоположно направлены.

Замечание. Когда происходит неравномерное вращательное движение, вектор ω может меняться не только по величине, но и по направлению (при повороте оси вращения).

Связь величин, характеризующих поступательное и вращательное движение

Известно, что длина дуги с углом поворота радиуса и его величиной связана соотношением

ΔS = Δφ r.

Тогда линейная скорость материальной точки, выполняющей вращательное движение

υ = ΔS/Δt = Δφr/Δt = ωr.

Нормальное ускорение материальной точки, что выполняет вращательно поступательное движение, определим следующим образом:

a = υ²/r = ω²r²/r.

Итак, в скалярном виде

a = ω²r.

Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение

a = ε r.

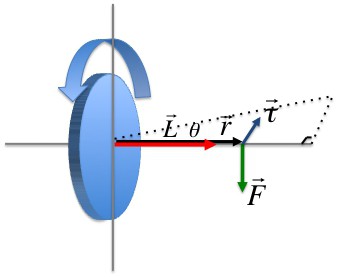
Момент импульса материальной точки

Векторное произведение радиуса-вектора траектории материальной точки массой m_i на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.

Момент импульса материальной точки (L_i) направлен перпендикулярно плоскости, проведенной через r_i и υ_i, и образует с ними правую тройку векторов (то есть при движении с конца вектора r_i к υ_i правый винт покажет направление вектора L_i).

В скалярной форме

L = m_iυ_ir_isin(υ_i,r_i).

Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,

sin(υ_i,r_i) = 1.

Так что момент импульса материальной точки для вращательного движения примет вид

L = m_iυ_ir_i.

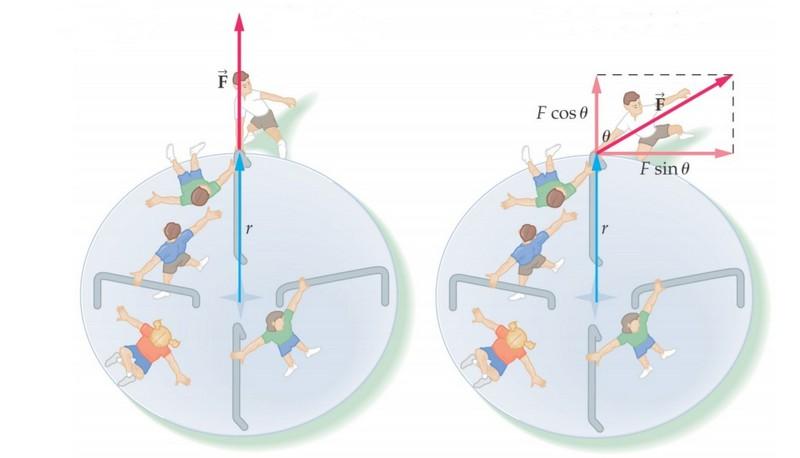
Момент силы, которая действует на i-ю материальную точку

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме

M_i = r_iF_isin(r_i, F_i).

Считая, что r_isinα = l_i, M_i = l_iF_i.

Величина l_i, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы F_i.

Динамика вращательного движения

Уравнение динамики вращательного движения записывается так:

M = dL/dt.

Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.

Момент импульса и момент инерции

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой

L_i = m_iυ_ir_i.

Если вместо линейной скорости подставить ее выражение через угловую:

υ_i = ωr_i,

то выражение для момента импульса примет вид

L_i = m_ir_i²ω.

Величина I_i = m_ir_i² называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:

L_i = I_iω.

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:

L = Iω.

Момент силы и момент инерции

Закон вращательного движения гласит:

M = dL/dt.

Известно, что представить момент импульса тела можно через момент инерции:

L = Iω.

Тогда

M = Idω/dt.

Учитывая, что угловое ускорение определяется выражением

ε = dω/dt,

получим формулу для момента силы, представленного через момент инерции:

M = Iε.

Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.

Теорема Штейнера. Закон сложения моментов инерции

Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I₀ + ma²,

где I₀ — начальный момент инерции тела; m — масса тела; a — расстояние между осями.

Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).

Вращательное движение твердого тела – движение, при котором все точки объекта описывают траекторию в виде окружности. 

Распространенный случай в физике – вокруг покоящейся оси (рис. 1).

Рис. 1 Вращение твердого тела вокруг оси

Линия, соединяющая неподвижные точки, читается осью вращения. Кинематика перемещения в целом аналогична поступательной. Только путь измеряется не в метрах, а в радианах или градусах. 

Последние связаны между собой следующей формулой:

где:

• ϕ – угол в радианах (рад);

• γ – угол в градусах (°).

Закон и уравнение вращательного движения твердого тела

Законы движения также схожи. Для равноускоренного движения:

где:

• ϕ₀ – начальный угол (рад);

• ω₀ – начальная угловая скорость (рад/с);

• t – время (с);

• ε – угловое ускорение (рад/с²).

Под положительным понимают перемещение против часовой стрелки.

Угловая скорость

В обычной жизни вращение оценивается в оборотах за единицу времени. За минуту чаще всего. Для расчетов такие характеристики неудобны. Поэтому определяется так:

Скорость в оборотах ν легко связать с угловой:

где:

ν – скорость в оборотах (1/с).

Используется еще одна важная величина – период вращения T. За это время предмет совершает полный поворот:

Угловое ускорение

Это величина:

В уравнении движения был показан частный случай равноускоренного перемещения. Но это не всегда так. Также ε может принимать отрицательные значения в случае замедления.

Линейные величины

При малых величинах пройденный путь (см. рис. 2) будет равен:

где r – расстояние до центра вращения (м).

Рис. 2 Перемещение

Откуда следует линейная скорость:

Вектор, перпендикулярный отрезку, r. То есть расположенный на касательной к окружности вращения.

И, соответственно, ускорение:

Кроме того, передвижение по кривой линии невозможно без центростремительного ускорения:

Возвратно-вращательное движение

Общий случай раскачивания маятника. Анализ подобных противоположных телодвижений пары объектов порождает некоторые парадоксы.

Возникают странные и дико звучащие названия вроде «безопорного движителя». Выводы в конечном итоге противоречат законам механики Ньютона.

Приверженцы таких рассуждений существуют и доводы имеют право на жизнь. Не все общепринятые взгляды безупречны. Евклидова геометрия тому пример. Теория довольно запутана, и здесь мы ее рассматривать не будем.

С учетом масс

Представив себе, что тело состоит из незначительных масс m_i, получим любопытные результаты. Кинетическая энергия выразится так:

Джоуль (Дж) – единица энергии и работы в системе СИ.

Моментом инерции относительно выбранной оси называется:

или в соответствующей интегральной форме.

Тогда энергия выразится следующим образом:

То есть имеется некий аналог массы. Но последняя является неизменной присущей объекту величиной. Момент же инерции зависит от местонахождения оси.

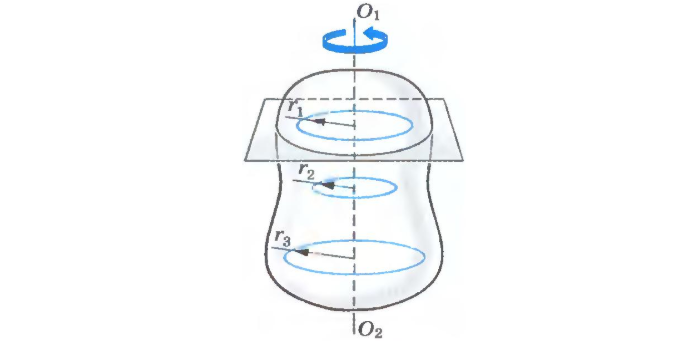
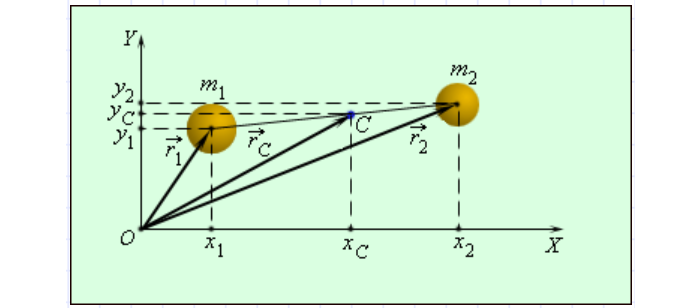
В реальных условиях распространен случай вращения вокруг оси, включающей центр масс. Найдем его для системы, указанной на рис. 3.

Рис. 3 Определение центра масс.

Определится по формулам:

Вектор, направленный из начала координат в центр масс, в общем случае выразится следующим образом:

Можно перевести в интегральную форму. В присутствии гравитации – заодно и центр тяжести.

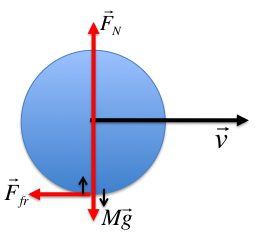
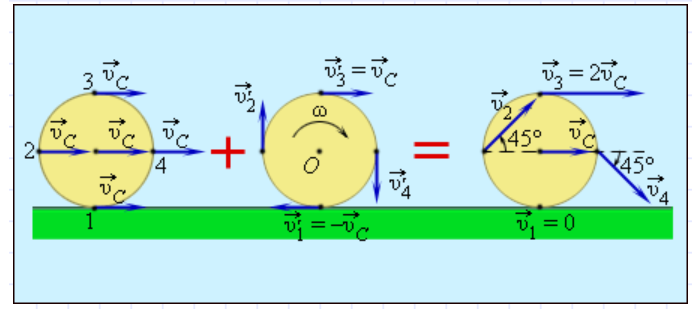
Можно сказать, что общее движение предмета включает поступательное и вращательное. Пример – качение чего-то округлого (рис. 4). При этом все перемещение точек можно исчерпывающе изобразить на рисунке. В таком варианте движение называется плоским. 

Полная кинетическая энергия равна:

где:

• m – масса объекта;

• I_C – момент инерции относительно оси, включающей центр масс.

Рис. 4 Качение колеса

Частные случаи вращательного движения

Рассмотрим несколько:

1. Равномерное (рис. 5), с постоянной скоростью, с нулевым ускорением. 

Выражается уравнением: φ = φ₀ + ωt

Рис. 5 При ε = 0.

2. Равноускоренное. Рассмотрено ранее. Но все же уместны некоторые пояснения (рис. 6).

Рис. 6 ε = const.

3. Вокруг неподвижной оси. Наиболее распространенный в рассмотрении вариант. Как для реальных нужд, так и в теории.

4. Возвратно-вращательное. В математическом выражении напоминает колебания. При подробном рассмотрении вызывает неудобные вопросы.

Заключение

Для разработчиков оборудования тема отнюдь не праздная. Рассматриваются задачи по передаче силового момента (в частности в ременных механизмах). Разбирается механика работы подшипников, гироскопов.

В артиллерии снаряды стабилизируются вращением. Да и расчеты их на прочность связаны со сложным напряженным состоянием в связи с раскручиванием в стволе.

Орбиты планет имеют отношение к рассматриваемой кинематике.

На самом деле все сферы использования данной темы невозможно перечислить, это действительно нужный раздел.

>

Второй закон Ньютона для вращательного движения – главное тождество динамики, помогающее решить основную задачу механики для вращающегося тела: указать угол поворота тела в любой промежуток времени.

Задача механики поступательного движения считается решенной если в любое мгновение легко указать положение материальной точки относительно других тел, при условии, заданной системы отсчета.

Кроме поступательного существует вращательное движение – это такой вид движения при котором каждая точка движется по окружности, центры окружности лежат на одной прямой (оси вращения).

Характеристики вращательного движения:

• Всякая точка абсолютно твердого тела перемещается по дуге круга;
• «Ядра» окружностей расположены вдоль одной линии – ось вращения
• Разные точки передвигаются по разным траекториям;
• Зависимости перемещения по времени представляют отличные значения, изменяющиеся по направлению;
• Углы поворота точек – одинаковы.

Аналоги характеристик поступательного и вращательного движения

Параметры вращательного перемещения необходимо рассматривать, проводя сравнение с характеристиками поступательного.

Справка! При передвижении поступательно: указывается вектор силы, через II закон создателя классической механики – Ньютона выражается векторная величина – ускорение, зная его кинематика помогает выводить координаты x, y, z.

 Последовательность нахождения координат тела в любой момент времени для поступательного перемещения:

1. зная силу F находим ускорение a;
2. из ускорения находи координаты x,y,z.

Пойдем от обратного для вращательного движения:

Найти нам необходимо угла поворота – φ в любой момент времени, для этого используем угловое ускорение ε, а вот аналог силы F мы пока не знаем.

Опишем кинематику вращательного движения.

• Аналог линейной скорости во вращательном движении это угловая скорость ω — выражается отношением:

— угол поворота

— незначительный отрезок времени

• Вспомним формулу линейной скорости υ точки находящейся на вращающемся теле, для этого умножим угловую скорость ω и r — расстояние от оси до искомой точки.

Виды вращательного движения:

1. Равномерное вращение.

Поворот предмета за равные промежутки времени на одинаковые углы говорит о равномерности перемещения. Угловое ускорение отсутствует.

Уравнение движения выглядит:

— угол поворота в любой момент времени,

— начальный угол поворота

Угловая скорость постоянна, но линейная скорость постоянно изменяет направление, а это означает, что существует центростремительное ускорение, направленное по радиусу к центру окружности.

1. Неравномерное вращение

При неравномерном перемещении постоянное угловое ускорение принимает вид:

При низменном , закон изменения угловой скорости получается:

Подставляя полученные данные в формулу движения при равномерном вращении получим:

Вспомним как рассчитать угол поворота тела тремя разными способами:

Первый способ.

Второй способ (через среднюю скорость).

Третий способ:

Сравнение формул вращательного и поступательного перемещения наглядно представлено таблично.

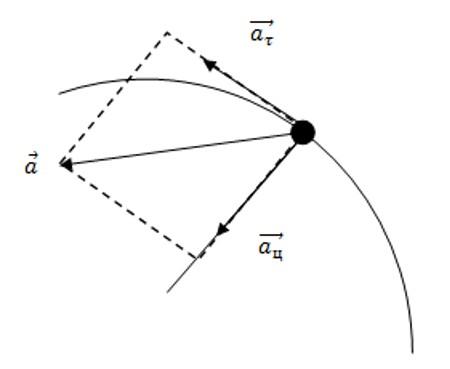
При нахождении точки на теле, неравномерно вращающемся на окружности, ускорение приобретает вид суммы:

— центростремительного и тангенциального

— тангенциального .

Сумма ускорений равна:

Тангенциальное ускорение вычисляется следующим образом

Используя связь υ и ω, получается:

Нужно сформулировать ключевые тождества, включая 2 закон сэра Ньютона для вращательного механического движения, сопутствующие обозначения, необходимые в ходе решения задач.

Вывод второго закона Ньютона для вращательного движения

Пусть тело, характеристиками которого можно пренебречь закреплено на невесомом стержне, 0 – ось вращения, длиной эквивалентной отрезку r.

На материальную точку оказывает воздействие силы ,  – реакция стержня.

— сила реакции нити;

— сила приводящая тело в движение

r — радиус нити

По II закону английского физика Исаака Ньютона второй закон динамики в векторной форме выглядит:

Выбор системы координат: Y – направляется по радиусу, Х – перпендикулярно.

Переписывая главное правило динамики в проекциях на эти оси:

Для этого на рисунке отобразим угол  и выразим через него все проекции.

OX: ,

OY: ,

Из рисунка видно, что  — тангенциальное ускорение, и  – модуль центростремительного ускорения

Вспомним, что тангенциальное ускорение равно:

Перепишем уравнение проекции на ось x с учетом этого знания:

Вычислим угловое ускорение из полученной формулы:

Умножая на дробь на :

Далее надо визуально отобразить на рисунке rsinα.

Как видно из полученного рисунка перпендикуляр d – плечо силы F.

Из построения:

М – момент силы.

Сравнивая с выражением:

I=mr²– мера инертности тела, момент инерции.

Выходит: 2 закон Ньютона представлен для вращательного движения:

Словесная формулировка основного тождества динамики вращательного перемещения:

Алгебраическая сумма моментов сил, действующих на тело тождественно произведению момента инерции тела на его угловое ускорение.

 Внимание!  – не учитывается: направлена вдоль r , проходит через 0.

Практическое применение второго закона Ньютона для вращательного движения

Перемещение путем вращения часто находит практическое применение. Яркие примеры:

• Колеса транспортных средств;
• Шестеренки;
• Роторы электродвигателей.

Простые «мозголомки» из школьного курса физики

Задание 1. Велосипедное колесо

Определить меру инертности у велоколеса диаметром 67 см с массой 1,3 кг? Возможно, не учитывать массу ступицы?

Порядок ответа:

Колесо целесообразно разбить на N мельчайших фрагментов размером Δl с массой Δm.

 Внимание! Внутренней структурой колеса пренебречь нельзя. Поэтому его фрагменты –  материальные точки.

Мера инертности вычисляется из выражения:

Для N частей:

Получается:

 кг х м²

Радиус ступицы много меньше обода колеса, при расчете не учитывается.

Задача 2.  Взаимодействие кинематики и динамики

Материальная точка перемещается по окружности, ее радиальное ускорение изменяется пропорционально четвертой степени времени. Найти n из отношения .

 Внимание! M – действует на точку относительно оси вращения.

Решение:

Записывается второй закон Ньютона для вращательного движения:

Нормальное ускорение:

Выражая угловую скорость:

Учитывая, неизменность расстояния до центра окружности, :

Итог:

Упражнение  3.  Графическое представление

Одно тело вращается по зависимости 1, потом действие момента сил изменяется согласно графику 2. Нужно сравнить угловые скорости в точках A и B.

Процесс размышлений:

Основной закон динамики перемещения путем вращения:

Угловая скорость:

Поскольку тело одно, 1/I неизменно.

Геометрический смысл интеграла – площадь криволинейных трапеций.

Случай 1:

График 2:

Результат:

Получается:

Задание 4.  Шары

Два точечных шарика, обладающие равными массами скреплены тонкой невесомой спицей l. Записать выражение момента инерции системы, относительно оси, перпендикулярно соотносящейся со спицей и центром масс.

Ход рассуждений:

Центр оси расположен между шарами:

Мера инертности I₁:

Мера инертности системы:

Упражнение 5. Гири

Грузы массами 2 и 1 килограмм связаны ниткой, перекинутой через блок, весящий 1 килограмм. Вычислить ускорение перемещения гирь? Рассчитать натяжение нитей?

Справка! Блок считается диском, сделанным из однородного материала. Трением не учитывается.

Поиск решения:

Векторный вид поступательного передвижения:

Перемещение диска – вращение:

М₁– для натяжения нитиТ₁;

М₂– для натяжения нитиТ₂.

Первые 2 равенства надо спроектировать на Х, последнее – Y.  Записать уравнение кинематической связи. Получается система:

Подставляя 4 тождество в 3:

Вычитая (2) из (1), переписывается (5):

Численное значение из выражения (6) подставляется в (1) и (2):

Практическое применение в жизни

Автомобиль

Вопрос:

Ускорится автомобиль, если установить шины большего диаметра?

Ответ:

Нет. Чем больше диаметр шин, тем выше линейное ускорение. Каждый автомобиль обладает максимальным угловым ускорением, соответствующее его мощности. Мощность машины ограничена, увеличение диаметра шин приведет к снижению углового ускорения, линейное не изменится.

«Что-то странная какая-то утка, на курицу похожа…»

«Деревенская» задача:

Домашние птицы: селезень и курица имеют одинаковую длину шага. Почему курица бегает ровно, а селезень перемещается переваливаясь?

Пояснение:

Расстановка лап селезня шире, центр тяжести расположен дальше от опоры, поэтому при ходьбе селезень вынужден делать поворот на больший угол. Момент силы тяжести от опоры увеличивается, соответственно становится больше величины угловых ускорения и скорости.

Гонки

Условие:

Европейские гонки проходят по улицам города, поэтому гонщики не снижая большой скорости совершают резкие повороты. Двигатель гоночных машин расположен посередине авто. Содержание преимущества?

Решение:

Двигатель посередине авто, обладает меньшей мерой инертности относительно центра масс, поэтому поворот осуществляется при меньшем моменте сил.

Фигурное катание

Спортивный запрос:

Зачем фигурист прижимает руки к телу?

Мнение эксперта:

Фигурист, вращаясь вокруг вертикальной оси, прижимает руки к корпусу. Момент инерции уменьшается, момент импульса остается неизменным, угловая скорость увеличивается.

Невесомость

Космическая проблема:

Космонавт находится в невесомости. Как ему совершить поворот на 180˚ вокруг продольной оси?

Распутывание Гордиева узла:

Для поворота космонавт поднимает руку над головой, провоцируя поступательные движения в направлении, противоположенному повороту.

О кошках

Дилемма:

Эмиль Кроткий утверждал: «Кошка мечтала о крыльях: ей хотелось попробовать летучих мышей». Люди не раз пытались подкидывать животное вверх ногами, при этом приземление всегда осуществляется на лапы. Момент внешних сил равен нулю, момент импульса сохраняется. Как кошке удается переворачиваться?

Разгадка:

Момент импульса кошки, находящейся в свободном падении остается постоянным, моменты внешних сил отсутствуют. Вытягивая или прижимая к телу лапы, кошка изменяет меру инертности передней части тела относительно центральной оси от момента инерции задней части тела. Попеременно подтягивая передние или  задние лапы, животное совершает поворот, ускоряющийся вращением хвоста.

Освоение 2 закона Исаака Ньютона с учетом кинематических и динамических характеристик для вращательного механического движения на практических примерах – легкое задание: надо запастись терпением, желанием приобретать знания. Изучать физику лучше вооружившись высказыванием Морихэй Уэсибы: «Двигайся, как луч света, летай, как молния, бей, как гром, вращайся вокруг устойчивого центра!»

Содержание:

Вращательное движение тела:

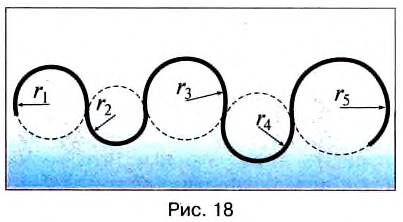
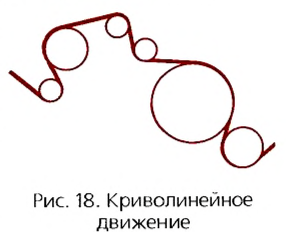
До сих пор мы изучали прямолинейное движение тел, хотя в природе и технике часто совершаются более сложные движения тел — криволинейные, когда траекторией тела является кривая линия. Любую кривую линию всегда можно представить как совокупность дуг окружностей разных радиусов (рис. 18).

Поэтому, изучив движение материальной точки по окружности, сможем в дальнейшем изучать и любые другие криволинейные движения. Кроме того, из всех возможных криволинейных движений в технике широко применяется вращательное движение деталей машин и механизмов, например вращение шестерён машин и станков, деталей, обрабатываемых на токарных станках, валов двигателей, колес машин, фрез, свёрл и т. п. Любая точка этих деталей движется по окружности. Эти две особенности и обусловили обязательное изучение движения по окружности, а именно — равномерное движение тела по окружности.

Движение материальной точки по круговой траектории с постоянной по значению, но изменяющейся по направлению скоростью, называют равномерным движением по окружности.

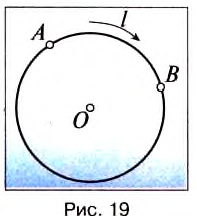
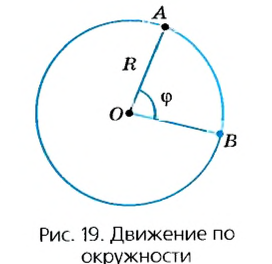
Предположим, что тело равномерно движется по окружности из точки А в точку В (рис. 19). Тогда пройденный им путь — это длина дуги

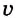
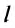
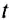
где — скорость движения тела по окружности; — пройденный телом путь (длина дуги);  — время движения тела.

Направление скорости проще всего определить на опыте.

Опыт:

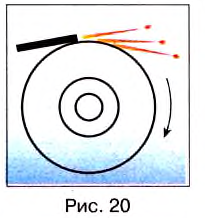
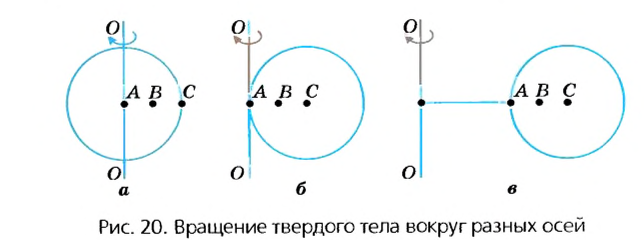
К вращающемуся точильному кругу, прикоснемся железным стержнем. Увидим, что искры из-под стержня летят по касательной к окружности этого круга (рис. 20).

Результат будет таким же в любой точке этого круга. Но каждая искра — это раскалённая частичка, оторвавшаяся от круга и летящая с такой же скоростью, какую она имела в последний момент движения вместе с кругом.

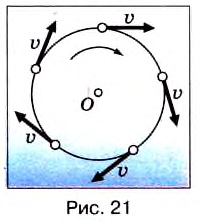
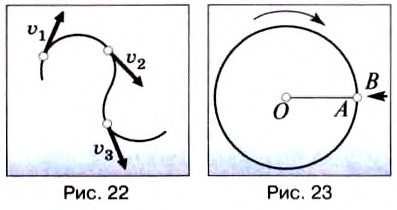
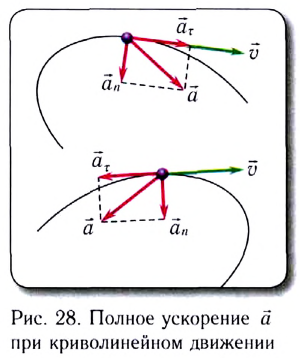
Итак, скорость материальной точки при движении по окружности направлена по касательной к ней в любой точке круга (рис. 21), а с учётом представления кривой на рисунке 18 этот вывод можно распространить на любые криволинейные движения (рис. 22). 

Опыт:

Закрепим на горизонтальной оси О фанерный диск (рис. 23), на котором проведен радиус ОА. Напротив точки А поставим указатель В и будем медленно и равномерно вращать диск. Увидим, что точка А с каждым оборотом диска снова появляется напротив указателя В, т. е. совершает движение, повторяющееся через определенный интервал времени.

Движения, при которых определенные положения материальной точки повторяются через одинаковые интервалы времени, называют периодическими движениями.

Равномерное движение по окружности — это периодическое движение. Периодическое движение характеризуют такими величинами, как период обращения и частота обращения.

Период обращения — это интервал времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности.

Обозначается период обращения большой латинской буквой Т.

Если за время 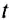материальная точка при равномерном движении по окружности совершает N оборотов, то период обращения определяется формулой:

Единицей периода обращения в СИ является одна секунда (1 с).

Если период обращения равняется 1 с, то материальная точка при равномерном движении по окружности осуществляет один оборот за 1 с.

Частота обращения определяется числом оборотов, которое материальная точка совершает за единицу времени при равномерном движении по окружности

Обозначается частота обращения малой латинской буквой .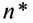

* В научной и учебной литературе частоту обращения еще обозначают малой греческой буквой 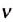(ню).

Если за время материальная точка совершила N оборотов, то, чтобы определить частоту обращения , нужно N поделить на , т. е.:
 а так как = ТN , то .
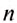
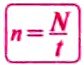
Из последней формулы видно, что частота обращения и период обращения связаны обратно пропорциональной зависимостью, а для определения единицы частоты обращения нужно единицу разделить на единицу периода обращения, т. е. на секунду.

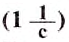
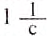
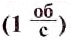
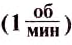
Единицей частоты обращения в СИ является единица, разделённая на секунду .  это частота обращения, при котором за 1 с материальная точка совершает 1 полный оборот, двигаясь равномерно по окружности. В технике такую единицу иногда называют одним оборотом в секунду , часто применяют также единицу один оборот в минуту .

Движение точки по окружности

Движения, происходящие в природе и технике, могут отличаться по изменению значения скоростей и по изменению направления скоростей. Так, например, при движении точки вдоль прямой линии в одном направлении направление скорости не меняется, хотя ее значение может быть различным. В этом случае движение считается неравномерным.

Но движения могут быть и криволинейными, например, точки могут двигаться по окружностям. На рисунке 18 изображена траектория движения точек нити или ленты между круглыми барабанами. Такие траектории можно представить в виде отрезков прямых линий и окружностей разных размеров. Понятно, что такие движения могут быть и равномерными, каждая точка все время будет иметь одинаковую скорость по значению, хотя направление скорости от точки к точке траектории может меняться.

Рассмотрим движение материальной точки по окружности, когда это движение равномерно, т. е. значение скорости остается постоянным (рис. 19). Точка, двигаясь по окружности радиуса R, за определенное время 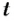переходит из точки А в точку В. При этом отрезок OA поворачивается на угол — угловое перемещение точки. Такое движение можно характеризовать угловой скоростью:

где 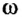(греческая буква «омега») — угловая скорость; (греческая буква «фи») — угловое перемещение.

Угловое перемещение определяется в радианах (рад.). 1 радиан — это такое перемещение, когда траектория движения точки — длина дуги окружности АВ — равна длине радиуса R.

Единицей угловой скорости является радиан в секунду (рад/с).

1 рад/с равен угловой скорости такого равномерного движения по окружности, при котором за 1 с осуществляется угловое перемещение 1 рад.

При определении угловой скорости слово «рад» обычно не пишут, а просто обозначают 1/с (имеется в виду рад/с).

Движение точки по окружности (и вращение твердого тела) характеризуют также такие величины, как период и частота вращения.

Период вращения (Т) — это время, на протяжении которого точка (тело) совершает один полный оборот по окружности. Период вращения:

где t — время вращения, N — количество выполненных оборотов.

Период вращения Т измеряется в секундах. Период равен 1 с, если точка (тело) осуществляет один оборот в секунду. Частота вращения (вращательная частота):

где N — количество совершенных оборотов за время t .

Частота вращения измеряется в оборотах за секунду (об/с).

Частота вращения  определяет количество оборотов точки (тела) вокруг центра (оси вращения) за 1 с.

Еще Архимед установил, что для всех окружностей любого радиуса отношение длины окружности к его диаметру является величиной постоянной. это число обозначили греческой буквой 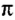(«пи»).

Таким образом, длина окружности

За один оборот материальная точка осуществляет угловое перемещение 2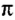 рад.

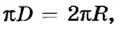
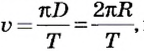
Движение по окружности характеризуется привычным для нас понятием скорости как пути, который проходит точка за единицу времени. В данном случае эта скорость называется линейной. Если учитывать, что за один оборот (время Т) точка проходит путь  то линейная скорость равномерного движения точки по окружности или

Вращение твердого тела

Твердые тела состоят из большого количества частичек. Абсолютно твердыми наукой считаются тела, расстояние между точками которых не изменяется во время явлений, которые с ними происходят. Однако следует иметь в виду, что абсолютно твердых тел в природе нет.

Как упоминалось в § 3, движения твердых тел бывают поступательные и вращательные. Твердые тела могут вращаться вокруг любых осей, в том числе и тех, которые проходят через их центры.

В случае а (рис. 20) ось вращения проходит через центр шара (например, вращаются колеса транспортных средств или Земля в своем суточном вращении вокруг оси). В случае в ось проходит через край шара. В случае в шар находится на определенном расстоянии от оси (например, Земля движется вокруг Солнца или Луна вокруг Земли). В некоторых случаях даже Землю и Луну можно считать материальными точками, а в некоторых случаях это сделать невозможно. Подумайте, в каких?

Что же является наиболее характерным для вращательного движения твердых тел? Очевидно, что при этом все точки этих тел в своем движении описывают окружности, центры которых находятся на осях вращения.

Понятно также, что разные точки тел за одно и то же время проходят по своим траекториям разные расстояния — чем дальше от оси вращения лежат точки, тем больше эти расстояния. Но за одно и то же время угловое перемещение всех точек одинаково. Следовательно, и угловая скорость  для всех точек данного тела также будет одинаковой.

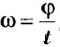
Для характеристики вращательного движения твердых тел используют такие же понятия, что и для движения точки по окружности: период вращения Т — время одного полного вращения; вращательная частота (частота вращения) 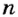— количество полных вращений за единицу времени; угловая скорость со. Кроме основной единицы частоты вращения об/с, используют об/мин, об/ч и т. п.

Период вращения Земли вокруг- Солнца равен в среднем 365 суток, а период вращения Луны вокруг Земли в среднем 28 суток. Изучая физику, астрономию, вы узнаете, что небесные тела, например планеты Солнечной системы, движутся не по окружностям, а по так называемым эллипсам.

Динамика вращательного движения

При просмотре фильмов-боевиков вы могли наблюдать, что при резком вращении руля автомобиля машина опрокидывается. В цирке мотоциклисты катаются по поверхности стен.
Проведем такой опыт. Нальем воду в ведро и раскрутим его в вертикальной плоскости. При определенной скорости вращения вода не выливается из ведра.

Из приведенных выше примеров можно сделать заключение, что существует сила, которая опрокинет машину при резком повороте, удержит мотоциклиста на стене и не даст вылиться воде из ведра при вращении.
Откуда появляется эта сила? От чего зависит ее величина?
Для этого вспомним о возникновении центростремительной силы в теле при равномерном вращательном движении:

По третьему закону Ньютона:

и при вращении появляется также центробежная сила. 
Вот эта центробежная сила опрокинет резко разворачивающуюся машину, удержит воду в ведре при вращении и т.д.

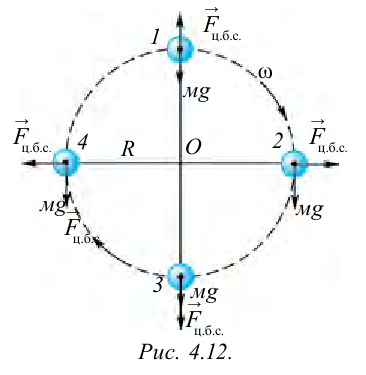
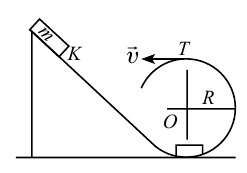
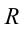
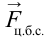
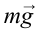
На рисунке 4.12 показаны силы, действующие на тело, которое совершает вращательные движения по кругу радиусом . В точке 1, из-за того что центробежная сила направлена противоположно силе тяжести , вес тела уменьшается:

В точке 3 сила тяжести тела и центробежная сила направлены вниз, т.е. в одном направлении. В этом случае вес тела растет:

Центробежную силу нужно учитывать при вращении тела и в случаях поворота в ходе движения. 
Кроме того, на поворотах дороги под воздействием центробежной силы наблюдается отклонение тела от вертикального положения. Чтобы это не приводило к авариям, велосипедисты или мотоциклисты должны двигаться с небольшим уклоном в сторону от центра вращения (рис. 4.13а).
Для уравновешивания этой силы специально для автомобилей на поворотах строят участки дороги с уклоном с одной стороны (рис. 4.13б). Для трамваев и поездов рельсы на поворотах дороги с внешней стороны круга делаются чуть выше.

• Заказать решение задач по физике

Пример

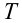
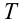
При движении по кругу тело опускается вниз. При каком радиусе круга тело не упадет с точки . Скорость тела в точке равна 30 м/с.
Дано:

Найти:

Решение:

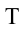
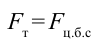
Чтобы тело не упало из точки должно  выполняться следующее условие: 

Ответ: 90 м.

Кинематика вращательного движения

При криволинейном движении материальной точки ее мгновенная скорость направлена по касательной к траектории в данной точке.
Движение тела (МТ) по окружности является частным случаем криволинейного движения по траектории, лежащей в одной плоскости.

Одним из простейших и широко распространенных видов такого движения является движение по окружности с постоянной по модулю скоростью. Это такое движение, при котором тело (МТ) за любые равные промежутки времени описывает одинаковые дуги. Подчеркнем, что при подобном движении скорость точки постоянно меняет свое направление.

Для описания движения по окружности используется ряд физических величин. Рассмотрим некоторые из них.

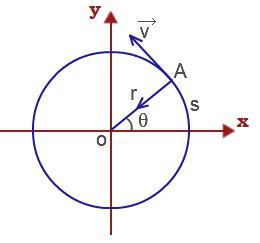
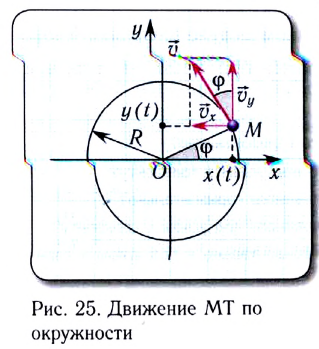
Удобным параметром для определения положения материальной точки М, совершающей движение по окружности радиусом R с центром в начале координат, является угол поворота 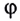(рис. 25)

радиус-вектора точки М. Он отсчитывается от оси Ох против хода часовой стрелки и связан с декартовыми координатами соотношениями:

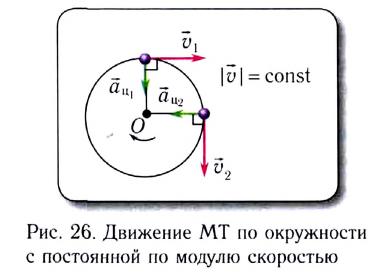
По теореме Пифагора можно найти, что координаты х и у материальной точки в декартовой системе координат удовлетворяют соотношению

Скорость 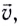с которой материальная точка движется по окружности, называется линейной скоростью (рис. 26).

Проходимый точкой путь s (длина дуги окружности) равен, как и для всякого равномерного движения, произведению модуля скорости v и промежутка времени движения

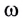
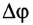
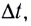
Модуль угловой скорости — это отношение угла поворота к промежутку времени за который этот поворот произошел:

Угловая скорость 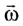 со является величиной векторной. Она направлена вдоль оси вращения материальной точки, и ее направление определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения конца буравчика, рукоятка которого вращается в том же направлении, что и тело (рис. 27).

Единица угловой скорости в СИ — радиан в секунду

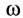
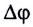
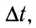
При движении по окружности с постоянной по модулю скоростью v угловая скорость является величиной постоянной и ее модуль равен отношению угла поворота к промежутку времени за который этот поворот произошел:

Здесь n — частота вращения — физическая величина, численно равная числу оборотов N материальной точки в единицу времени:

Единица частоты вращения в СИ — секунда в минус первой степени 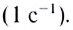Время совершения одного оборота называется периодом вращения Т.

Следовательно, 

В СИ период измеряется в секундах (1с).

При совершении полного оборота 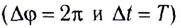период определяется по формуле    

Модуль постоянной линейной скорости тела (МТ), движущегося по окружности, вычисляется по формуле

Проекции скорости 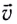(см. рис. 25) с течением времени изменяются по закону

Модуль угловой скорости определяется соотношением

Следовательно, соотношение между модулями линейной и угловой скорости имеет вид

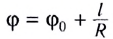
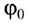
Поскольку (докажите самостоятельно), где — угол поворота радиус-вектора в момент начала движения, то кинематический закон движения МТ но окружности имеет вид

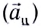
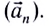
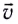
При движении МТ по окружности с постоянной по модулю скоростью ее направление непрерывно изменяется и, следовательно, движение МТ происходит с ускорением, которое называется центростремительным или нормальным Ускорение направлено по радиусу к центру окружности и характеризует быстроту изменения направления скорости с течением  (см. рис. 26). Его модуль определяется формулой

Нормальное ускорение 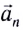в любой момент времени перпендикулярно скорости

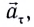
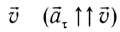
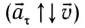
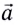
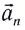
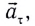
Как и при прямолинейном равноускоренном движении, ускорение называемое тангенциальным (касательным), совпадает с направлением скорости или направлено противоположно ей и поэтому изменяет только модуль скорости. Следовательно, при движении по окружности с непостоянной по модулю скоростью (например, математический маятник) или при любом криволинейном движении полное ускорение 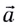можно представить в виде векторной суммы нормального ускорения и тангенциального ускорения направленного по касательной к окружности в данной точке (рис. 28):

Полное ускорение всегда направлено в сторону вогнутости траектории (см. рис. 28).

Модуль полного ускорения находится по теореме Пифагора:

где 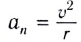 — нормальное ускорение, с которым точка двигалась бы по дуге
окружности радиусом r, заменяющей траекторию в окрестности рассматриваемой точки. Этот радиус r называют радиусом кривизны траектории.

2.2.1. Уравнение (закон) вращательного
движения. Угловая скорость и угловое
ускорение тела.

Вращательным движением твердого
тела называется такое его движение, при
котором остаются неподвижными все его
точки, лежащие на некоторой прямой,
называемой осью вращения.

При этом все остальные точки тела
движутся в плоскостях, перпендикулярных
оси вращения, и описывают окружности,
центры которых лежат на этой оси.

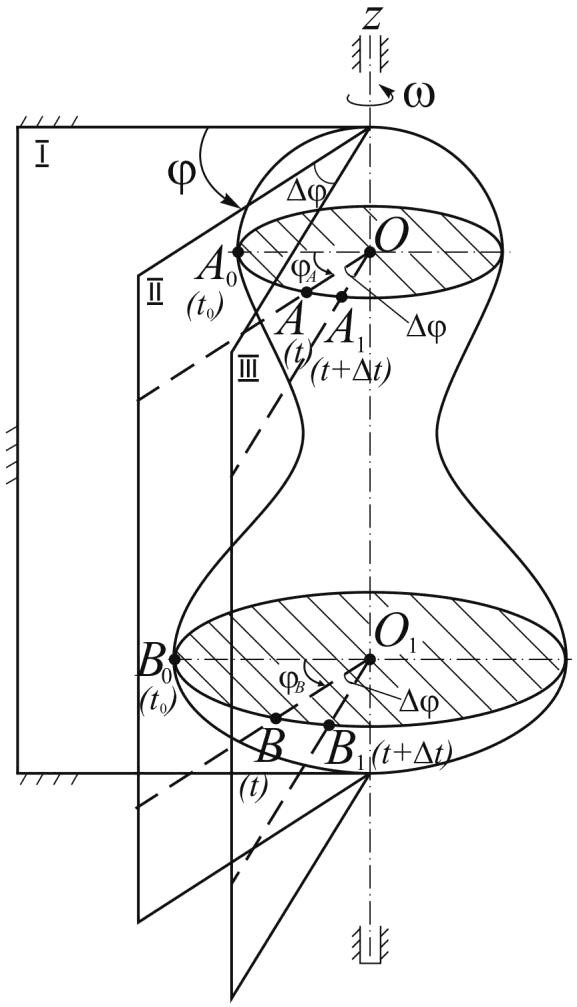
Зададимся направлением оси z (рисунок
7). Проведем через эту ось две полуплоскости:
I – неподвижная полуплоскость; II –
подвижная полуплоскость связана с
твердым телом и вращается вместе с ним.

φ – угол поворота, который выражается
в рад.

ветствующий N оборотам φ=2πN.

При повороте плоскости II на угол φ, точка
A₀ переместится по

А₀А
= S, а точка В₀ по дуге

В₀В
= S₁, причем

.
При этом центральные углы, на которые
повернутся точки A₀ и В₀
данного твердого тела, будут равны, т.е.
φ_А = φ_В = φ.

С
ледовательно,
значение угла поворота φ вполне определяет
положение тела при его вращении вокруг
оси z, т. е. угол φ является однозначной
и непрерывной функцией времени t,
являющейся уравнением (законом)
вращательного движения твердого тела.

(23) известна, то

для каждого момента времени t будет
вполне определено значение угла φ, т.
е. будет известно положение твердого
тела в данный момент.

Пусть в момент времени t тело от
начала отсчета повернулось на угол φ,
а в момент времени t₁=t+∆t
— на угол φ+∆φ. Следовательно, за время
∆t тело повернется на угол ∆φ. Тогда

_ср
– средняя угловая скорость.

Средней угловой скоростью

_ср
называется отношение приращения
угла поворота ∆φ к соответствующему
промежутку времени ∆t, т. е.

(24)

Переходя от выражения (24) к его пре-

делу, при ∆t→0, получим алгебраическую
Рисунок 7 величину угловой скорости. ω=

(25)

Угловой скоростью называется особая
физическая величина, которая характеризует
быстроту изменения угла поворота φ с
течением времени, и численно равна
первой производной от угла поворота по
времени.

Единицей измерения угловой скорости
является рад/с.

При неравномерном вращении тела
происходит изменение угловой скорости.
Пусть в момент времени t угловая
скорость была равна ω, а в момент времени
t₁=t+∆t угловая скорость
имела значение ω1=ω+∆ω,
т. е.

t→ω

t+∆t→ω+∆ω

∆t→∆ω

Отношение

обозначим как среднее угловое ускорение.

Средним угловым ускорением ε_ср
называется отношение приращения угловой
скорости ∆ω к соответствующему промежутку
времени ∆t, т. е.

(26)

Переходя от выражения (26) к его пределу
при ∆t→0, получим алгебраическую
величину углового ускорения вращающегося
тела в любой момент времени t, т. е.

ε=

(27)

Угловым ускорением тела называется
особая физическая величина, характеризующая
быстроту изменения угловой скорости с
течением времени, и численно равна
первой производной от угловой скорости
по времени или второй производной от
угла поворота по времени.

Единицей измерения углового ускорения
является рад/с².

Формулы (23), (25) и (27) характеризуют движение
любой точки вращающегося твердого тела.

2.2.2. Частные случаи вращательного
движения твердого тела.

Равномерное вращение твердого тела.

Вращение тела с постоянной угловой
скоростью называется равномерным, т.
е. ε=0, а ω=const.

Положим, что в начальный момент времени
t₀=0, угол поворота имеет значение
φ0,

тогда

φ — φ₀=ωt

(28)

Выражение (28) является уравнением
(законом) равномерного вращения твердого
тела.

Если φ0=0, то
φ=ωt, откуда угловая скорость равномерного
вращения равна:

(29)

Если φ0
0,
то

, (30)

т. е. угловая скорость равномерного
вращения твердого тела равна отношению

приращения угла поворота за некоторый
промежуток времени к величине этого
промежутка.

В современной технике очень часто
пользуются понятием «частота вращения
твердого тела».

Частотой вращения называется число
оборотов, совершаемых вращающимся телом
за единицу времени (обычно за минуту),
и обозначается n.

= 2π рад, а φ = 2πn, то зависимость между
угловой скоростью ω [c¹] и частотой
вращения n [об/мин] имеет вид:

, т. е.

(31)

Равнопеременное (равноускоренное
и равнозамедленное) вращение твердого
тела.

Вращение тела, при котором ε=const, называется
равнопеременным.

Если абсолютная величина угловой
скорости ω увеличивается, то вращение
называется равноускоренным, а если
уменьшается – равнозамедленным.

Составим уравнение равнопеременного
вращения.

Пусть при t₀=0 угловая скорость
равна ω0. Тогда
из формулы

Т.о. угловая скорость равноускоренного
вращения твердого тела равна

(32)

(33)

В случае равнозамедленного вращения,
в формулах (32)…(34) перед ε должен стоять
знак « — » .

2.2.3. Определение линейных скоростей и
ускорений точек вращающегося твердого
тела.

П
усть
вращение тела задано уравнением

.
Для простоты допустим, что φ0=0.
Составим уравнение движения точки M
по ее траектории (окружности радиусом
R) (рисунок 8).

S=

= R·φ = R·

Точка M помимо угловой скорости
имеет еще и линейную (при движении по
окружности, она называется еще окружной).
Эта скорость направлена по касательной
к траектории и будет равна:

(35)

Вектор линейной (окружной) скорости
любой точки тела, вращающегося вокруг
Рисунок 8 неподвижной оси, равен по
модулю произ-

ведению модуля угловой скорости тела
на кратчайшее расстояние от точки до
оси и направлен в сторону вращения
перпендикулярно к плоскости, проходящей
через точку и ось вращения (по касательной
к траектории).

Ускорение точки M определим по
касательному и нормальному ускорениям.
Продифференцируем выражение (35):

, т. е.

(36)

Касательное (тангенциальное)
ускорение точки по модулю равно
произведению углового ускорения тела
на радиус вращения точки и направлено
по касательной к траектории. будем
иметь

Нормальное (центростремительное)
ускорение любой точки по модулю равно
произведению радиуса вращения точки
на квадрат угловой скорости.

С учетом выражений (36) и (37) полное
ускорение точки будет определяться:

2.2.4. Угловая скорость и угловое ускорение
вращающегося твердого тела как векторы.

До сих пор мы рассматривали ω и ε как
скалярные величины. Введем понятия
векторов угловой скорости и .

Условимся изображать угловую скорость
вращающегося твердого тела вектором,
направляя его от любой точки оси вращения
по этой оси так, чтобы, смотря навстречу
этому вектору, видеть вращение тела,
происходящим в сторону, обратную вращению
часовой стрелки.

Для левой системы координат вектор
угловой скорости направляется в ту
сторону, откуда вращение тела мы будем
видеть происходящим по часовой стрелке.

Рисунок 10. Левая система координат и
правило левого винта

Векторы, направления которых зависят
от принятой системы координат, называются
псевдовекторами.

Вектор углового ускорения характеризует
изменение вектора угловой скорости

в зависимости от времени, т. е.

=

Известно, что направление векторной
производной совпадает с предельным
направлением приращения дифференцируемого
вектора. Т.

к. вектор

имеет постоянное направление, то
направление его приращения ∆ с
направлением самого вектора ускоренное
и противоположно ное.

Если знаки

одинаковые, то вращение

ускоренное (рисунок 11, а). Если знаки

различные, то вращение замедленное
(рисунок 11,

_б).
Рисунок 11

Модуль вектора углового ускорения
определяется по формуле:

Т. к. точки приложения векторов и
выбираются произвольно, то эти векторы
являются скользящими.

2.2.5. Выражения линейной скорости,
касательного и нормального ускорений
точек вращающегося твердого тела в виде
векторных произведений.

Выведем векторное выражение линейной
скорости какой-нибудь точки M,
пользуясь понятием вектора

(рисунок 12). O₁M = R –
радиус вращения т. M.

т. O – полюс, выбранный произвольно
на оси вращения. — радиус-вектор т. M.

— угол между радиус-вектором и вектором
угловой скорости

.

O₁M (пл. ∆OMO₁), (
z).

М
одуль
скорости т. M υ = ω·R, R=ρ·

(из ∆OMO₁). υ=ω·ρ·

(40)

Из векторной алгебры известно, что
векторное произведение двух векторов

=
ω·ρ· (41)

Кроме
того, пл. ∆OMO₁

Сравнивая выражения (1) и (2), получим

(42)

Выражение (42) называется формулой Эйлера
и выражает вектор линейной скорости
точки вращающегося тела, который равен
векторному произведению вектора угловой
скорости тела на радиус- вектор,
проведенный из любой точки, лежащей на
оси вращения тела, в данную точку.

Для получения векторных формул
касательного и нормального ускорений
продифференцируем по времени выражение
(42):

Из сравнения выражений (43) и (44) и рисунка
12 видно, что

(45)

(46)

Докажем по-другому, что первое слагаемое
выражения (43) есть касательное ускорение,
а второе

— центростремительное ускорение.
Известно, что модуль касательного
ускорения

где
–
угол между

Т. е. касательное (вращательное) ускорение
точки твердого тела, вращающегося вокруг
неподвижной оси, равно векторному
произведению вектора углового ускорения
тела на радиус-вектор этой точки
относительно любой точки оси ее вращения.

По аналогии для нормального ускорения
получаем

(49) , (50) т. к.

Из сопоставления (49) и (50) и правила
векторного произведения:

Т. е. нормальное ускорение точки твердого
тела, вращающегося вокруг неподвижной
оси, равно векторному произведению
вектора угловой скорости тела на линейную
(вращательную) скорость этой точки.

Соседние файлы в предмете Теоретическая механика

• #
• #
• #
• #
• #
• #
• #
• #
• #