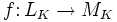Линейный
оператор ,
действующий из пространства
в пространство ,
ставит в соответствие каждому вектору
определенный вектор
из .
При этом вектор
называется образом
вектора
,
а вектор
— прообразом
вектора
при отображении .
Пусть
и
— некоторые базисы линейных пространств
и
соответственно. Тогда ,
и координаты вектора — образа
связаны с координатами вектора — прообраза
соотношением

(7.2.1)
в
котором
— матрица линейного оператора
в паре базисов
и .
В
случае, когда пространства
и
совпадают, базисы
и
также совпадают, и формула (7.2.1) принимает
вид

(7.2.2)
Образом
(областью
значений)
линейного
оператора
называется
множество всех элементов
вида .
Образ линейного оператора является
подпространством пространства
и обозначается .
Размерность образа называется рангом
оператора
и обозначается .
Ядром
линейного оператора
называется
множество всех векторов пространства
,
которые переводятся оператором
в нулевой вектор пространства .
Ядро линейного оператора является
подпространством пространства
и обозначается .
Размерность ядра называется дефектом
оператора
и обозначается .
Сумма
ранга и дефекта оператора
равна размерности пространства
.
Ранг
линейного оператора равен рангу матрицы
этого оператора.
Базис
системы векторов — столбцов матрицы
линейного оператора
образует систему координатных столбцов
базиса образа .
Базис подпространства решений однородной
системы линейных алгебраических
уравнений с матрицей оператора
образует базис ядра .
Пример
1.
Из пространства
с базисом
в пространство
с базисом
действует линейный оператор ,
имеющий в данной паре базисов матрицу

Найдите столбец координат в базисе
образа вектора
и столбец координат в базисе
прообраза вектора .
Решение.
Столбец координат образа вектора
в базисе находим
непосредственно по формуле (7.2.1):

Для
определения прообраза вектора
по той же формуле (7.2.1) имеем

или,
что то же самое,
Отсюда
находим все прообразы
вектора ,
где
— свободная переменная, принимающая
произвольные значения.
Пример
2.
В пространстве с
базисом линейный
оператор
переводит векторы ,
в
векторы ,
соответственно. Найдите матрицу оператора
в
базисе .
Решение.
Пусть 
матрица оператора в
базисе .
Тогда из условий ,
по формуле (7.2.2) имеем 
или,
в подробной записи,
Отсюда
получаем
Следовательно,
.
Пример
3.
Найдите базис ядра и базис образа
линейного оператора пространства ,
если этот оператор задан матрицей 
Решение.
При помощи элементарных преобразований
над строками матрицы
приведём её к ступенчатому виду:

Отсюда
следует, что .
Базис составляют,
например, векторы
и .
Дефект
оператора найдём по формуле
,
т.е.
фундаментальная система решений
однородной системы линейных алгебраических
уравнений с матрицей
будет состоять из одного вектора. Общее
решение однородной системы можно
записать в виде .
Полагая
получаем базисный вектор .
7.2.1.
Линейный оператор переводит
вектор
в вектор.
Найдите образ вектора
и прообраз вектора ,
если
,
,
;
,
,
;
,
,
.
7.2.2.
Линейный оператор в
паре базисов и
имеет матрицу .
Найдите прообраз вектора ,
если

;
б)
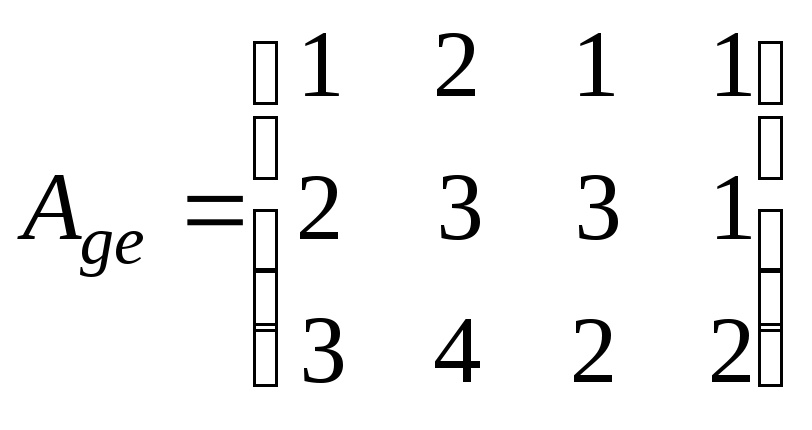
;
в)

.
7.2.3.
Выясните, существует ли линейный оператор
двумерного пространства, переводящий
векторы ,
соответственно в векторы ,
,
и найдите матрицу этого оператора в
базисе ,
:
а)
б)
в)
7.2.4.
Выясните, существует ли линейный оператор
трехмерного пространства, переводящий
векторы ,
,
соответственно в векторы ,
,
,
и найдите матрицу этого оператора в том
же базисе, в котором даны координаты
всех векторов:
а)
б)
7.2.5.
Для указанных линейных операторов
пространства
найдите дефект и ранг, а также постройте
базисы ядра и образа. Каждый оператор
описывается своим действием на
произвольный вектор :
а)
б)
в)
7.2.6.
Найдите образ и ядро оператора
дифференцирования в пространстве .
7.2.7.
В пространстве
рассмотрите разностный
оператор
где
— фиксированное
число, отличное от нуля. Найдите его
образ и ядро.
7.2.8.
Найдите образ и ядро оператора
проектирования (см. задачу 7.1.2) на
параллельно
и оператора отражения (см. задачу 7.1.3) в
параллельно .
7.2.9.
Найдите базис ядра и базис образа
линейного
оператора из ,
заданного в некотором базисе матрицей
:
а)
;
б)
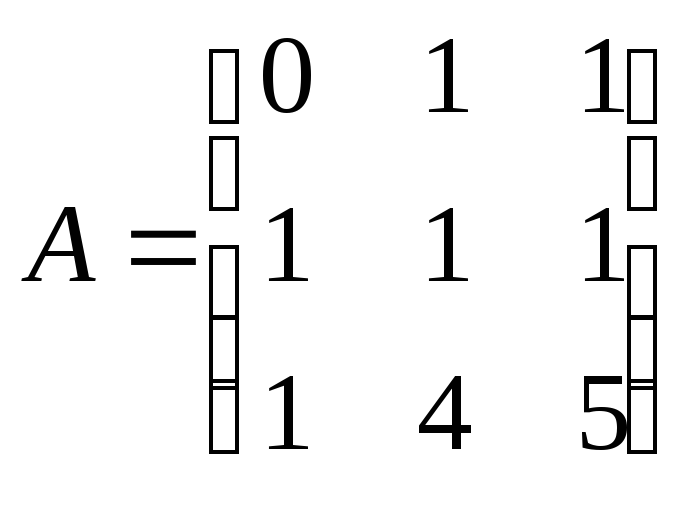
в)
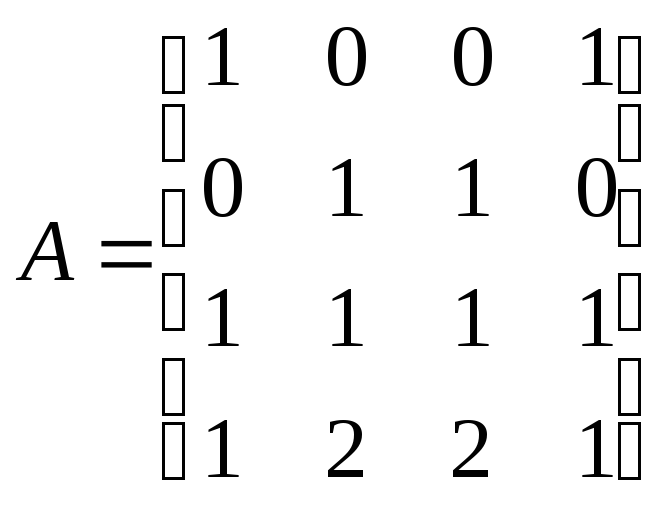
7.2.10.
Найдите размерность линейного пространства
всех линейных операторов, действующих
в
— мерном линейном пространстве
и постройте базис пространства .
Соседние файлы в папке Задачник-2
- #
- #
- #
- #
- #
- #
Задача №1. В арифметическом пространстве [math]mathbb{R}^4[/math] линейный оператор [math]displaystyle varphi[/math] задан матрицей
[math]A= left(!!begin{array}{rrrr} 1 & -2 & 1 & 3\ -2 & 5 & 6 & -12 \ 5 & 9 & 13 & 9 \ -1 & 3 & 7 & -9 end{array}!!right)[/math]
Найти базисы ядра и образа, ранг и дефект линейного оператора. Найти операторы, индуцированныe в ядре и образе.
Решение.
1) По определению ядро линейного оператора [math]displaystyle varphi[/math] ([math]displaystyle ker varphi[/math]) есть множество всех векторов [math]displaystyle x[/math], которые [math]displaystyle varphi[/math] переводит в нулевой вектор. Это означает, что [math]displaystyle ker varphi[/math] состоит из векторов, координаты которыx [math]displaystyle x_1, x_2, x_3, x_4[/math] (в некотором базисе [math]displaystyle { e_1, e_2, e_3, e_4 }[/math]) удовлетворяет условию:
[math]begin{pmatrix} 1 & -2 & 1 & 3\ -2 & 5 & 6 & -12 \ 5 & 9 & 13 & 9 \ -1 & 3 & 7 & -9 end{pmatrix}!!! begin{pmatrix} x_1\ x_2 \ x_3 \ x_4 end{pmatrix}!=! begin{pmatrix} 0\ 0 \ 0 \ 0 end{pmatrix}[/math]. То есть, [math]kervarphi[/math] cooтветствует пространству [math]L[/math] решений системы [math]begin{cases}x_1-2x_2+x_3+3x_4=0,\ -2x_1+5x_2+6x_3-12x_4=0,\ 5x_1+9x_2+13x_3+9x_4=0,\ -x_1+3x_2+7x_3-9x_4=0.end{cases}[/math]
Общим решением системы является семейство векторов [math]left(-frac{15}{4}C , 0, frac{3}{4}C, C right)[/math]. Полагая [math]C=4[/math], находим базис [math]ker varphi[/math]: [math](-15,,0,,3,,4)[/math].
2) Дефектом линейного оператора называется размерность его ядра ([math]dim ker varphi[/math]). Здесь [math]dim ker varphi=1[/math], т.к. в ядре существует лишь один линейно независимый вектор.
Верны ли мои рассуждения?
3) Не знаю, как найти образ линейного отображения [math]varphi[/math] ([math]im varphi[/math]). Подскажите идею.
4) Рангом линейного отображения [math]varphi[/math] называется размерность его образа ([math]dim im varphi[/math]). Здесь всё ясно.
5) Что такое операторы, индуцированные в ядре и образе?
Задача №2. Найти матрицу, область значений и ядро оператора [math]A[/math] проектирования на плоскость [math]x-z=0[/math]. Если [math]x={x_1, x_2, x_3 }[/math], то [math]Ax={x_1-x_2-x_3, -2x_1+3x_2, x_2- x_3 }[/math].
1) Cовершенно не знаю, как найти матрицу. И что означает проектирование на плоскость?
2) Если найду матрицу, то можно найти ядро.
3) Область значений — это синоним образа или что-то другое?
И ещё один вопрос общего характера. Существует ли какое-то обозначение для базиса линейного пространства (как, например, для ядра или размерности)?
Ядро и образ линейного оператора
Пусть линейный оператор , действует из пространства в себя и пусть в линейном пространстве выбраны два базиса: и Разложим “новые” базисные вектора в линейные комбинации “старых” базисных векторов :
Стоящая здесь матрица м столбцом которой является координатный столбец го базисного вектора в “старом” базисе называется матрицей перехода от “старого”базиса к “новому“. Если теперь координаты вектора в “старом” базисе а координаты того же вектора в “новом” базисе то имеет место равенство
Так как разложение по базису единственно, то отсюда следует, что
Получен следующий результат.
Теорема 1.Координаты вектора в базисе и координаты того же вектора в базисе связаны соотношениями (2), где матрица перехода от “старого”базиса к “новому“ .
Посмотрим теперь, как связаны между собой матрицы и одного и того же оператора в различных базисах и пространства Матрицы и определяются равенствами Пусть Это равенство в базисе равносильно матричному равенству
а в базисе матричному равенству ( здесь приняты те же обозначения, что и в (1)). Используя теорему (1), будем иметь
так как столбец произвольный, то отсюда получаем равенство
Доказан следующий результат.
Теорема 2.Если матрица оператора в базисе а матрица того же оператора в базисе то
Замечание 1.Две произвольные матрицы и связанные соотношением где некоторая невырожденная матрица называются подобными матрицами. Таким образом, две матрицы одного и того же оператора в различных базисах подобны.
Пример 1.Матрица оператора в базисе имеет вид
Найти матрицу этого оператора в базисе Вычислить координаты вектора в базисе
Решение. Матрица перехода от старого базиса к новому и обратная к ней матрица имеют вид
поэтому по теореме 2 матрица оператора и новом базисе будет такой:
Далее, вектор имеет следующий координатный столбец в базисе По теореме 1 координатный столбец этого вектора в базисе будет иметь вид
Замечание 2. Можно обобщить этот результат на операторы, действующие из одного линейного пространства в другое. Пусть оператор действует из линейного пространства в другое линейное пространство и пусть в пространстве выбраны два базиса: и а в пространстве – два базиса и Тогда можно составить две матрицы и линейного оператора
и две матрицы и перехода от “старых” базисов к “новым”:
Нетрудно показать, что в этом случае имеет место равенство
Пусть дан линейный оператор действующий из линейного пространства в линейное пространство Следующие понятия бывают полезными при решении линейных уравнений.
Определение 1. Ядром оператора называется множество
Образом оператора называется множество
Нетрудно доказать следующее утверждение.
Теорема 3.Ядро и образ линейного оператора являются линейными подпространствами пространств и соответственно, причем имеет место равенство
Для вычисления ядра оператора надо записать уравнение в матричной форме (выбрав базисы в пространствах и соответственно) и решить соответствующую алгебраическую систему уравнений. Поясним теперь, как можно вычислить образ оператора .
Пусть матрица оператора в в базисах и Обозначим через -й столбец матрицы Принадлежность вектора образу означает, что существуют числа такие, что вектор столбец представляется в виде т.е. является элементом пространства линейных комбинаций столбцов матрицы Выбрав в этом пространстве базис (например, максимальную совокупность линейно независимых столбцов матрицы ), вычислим сначала образ оператора-матрицы : а затем построим образ оператора :
Приведем пример вычисления ядра и образа оператора, действующего из пространства в себя. В этом случае базисы и совпадают.
Пример 2.Найти матрицу, ядро и образ оператора проектирования на плоскость ( трехмерное пространство геометрических векторов).
Решение.Выберем в пространстве какой-нибудь базис (например, стандартный базис ). В этом базисе матрица оператора проектирования находится из равенства Найдем образы базисных векторов. Так как плоскость проходит через ось то
Далее (см. Р10) И аналогично
Значит, матрица оператора имеет вид
Ядро оператора-матрицы вычисляем из уравнения
Образ оператора-матрицы натянут на все линейно независимые столбцы матрицы т.е.
Ядро оператора
,
удовлетворяющее условию линейности
f(αx + βy) = αf(x) + βf(y) .
для всех 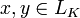
Содержание
Важные частные случаи
Связанные понятия
Примеры
Примеры линейных однородных операторов:
где 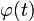
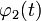
См. также
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Ядро оператора» в других словарях:
Ядро (значения) — Ядро нечто центральное и самое важное, часто круглое. Это слово имеет различные значения в разных областях: Содержание 1 Ядерная физика 2 Биология 3 Науки о Земле 4 Спорт … Википедия
Ядро — Содержание 1 Ядерная физика 2 Биология 3 Науки о Земле … Википедия
ЯДРО — линейного оператора линейное подпространство области определения линейного оператора, состоящее из всех векторов, к рые отображаются этим оператором в нуль. Я. линейного непрерывного оператора, определенного на нек ром топологическом векторном… … Математическая энциклопедия
Ядро интегрального уравнения — Ядром интегрального оператора называется функция двух аргументов , определяющая некий интегральный оператор равенством где пространство с мерой , а принадлежит некоторому … Википедия
Ядро (матем.) — Интегральное уравнение функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро дифференциальном уравнении.… … Википедия
ЯДРО — интегрального оператора функция двух аргументов К( х, у), определяющая интегральный оператор . равенством где хпробегает пространство . с мерой а принадлежит нек рому пространству функций, определенных на X. Г. Л. Литвинов … Математическая энциклопедия
ВЫРОЖДЕННОЕ ЯДРО — ядро линейного интегрального Фредгольма оператора, имеющее вид где Ри Q точки евклидовых пространств. А. Б. Бакушинский … Математическая энциклопедия
ИТЕРИРОВАННОЕ ЯДРО — функция ( х, s) К п( х, s), к рая образуется из данного ядра Кинтегрального оператора по рекуррентным соотношениям: К п наз. n й итерацией, или n м итерированным ядром, ядра K. И. я. иногда наз. повторным ядром. Если ядро Кнепрерывно или… … Математическая энциклопедия
ДЕФИНИТНОЕ ЯДРО — определенное ядро, ядро К( Р, Q )линейного интегрального Фредголъма оператора, удовлетворяющее соотношению где Р, Q точки евклидова пространства, j произвольная суммируемая с квадратом функция, j комплексно сопряженная функция. В зависимости от… … Математическая энциклопедия
ВОЛЬТЕРРА ЯДРО — функция (матрица функция) К(s, t).двух действительных переменных s, t такая, что или при или при Если такая функция является ядром линейного интегрального оператора, действующего в пространстве и сама квадратично суммируема в треугольнике, в к… … Математическая энциклопедия
Как найти базис ядра
Все права защищены 2019
Перепечатка информации возможна только при наличии
согласия администратора и активной ссылки на источник!
Дано четырехмерное пространство (как я понимаю, в нём находится базис, состоящий из четырех векторов). Нужно найти матрицу оператора в четырехмерном пространстве (получается, самим придумать и составить; как я понимаю, она будет состоять из 4 строк и 4 столбцов?), причём размерность ядра Ker равно размерности образа Im и равно 2. Далее необходимо найти исходя из составленной матрицы базис ядра и образа.
Прошу помочь разобраться в этом задании. С этими линейными операторами, ядрами, образами прям совсем туго((
задан 10 Янв 20:35
Достаточно взять любую матрицу 4×4 ранга 2. Для этого пишем первые две строки наугад, чтобы они не были пропорциональными. Скажем, 1 0 -2 3 и 0 1 4 -1. В качестве третьей строки берём любые, которые выражаются через первые две. Можно брать значения a+b, 2a-b, 3a+2b и т.п.
Базис ядра — это базис в пространстве решений однородной системы. Решаем её методом Гаусса, находя два базисных вектора. В качестве базиса образа можно взять любые два столбца, которые не пропорциональны.
Все эти абстрактные понятия на самом деле легко освоить на конкретных примерах.
@falcao вы сделали вывод о том, что ранг матрицы будет равен 2 исходя из размерности образа? Всегда такое правило действует?
@Yu_Ko: здесь оба числа равны 2, поэтому разницы нет. А общее правило такое: если матрица имеет размер nxn и ранг r, то образ имеет размерность r, а размерность ядра равна n-r. Это более или менее очевидно — особенно для образа. Ведь он состоит из столбцов матрицы и всех их линейных комбинаций. А линейно независимых столбцов, дающих базис образа, будет в точности r. Сумма же размерностей образа и ядра равна размерности всего пространства, то есть n.
@falcao как же вы выручаете! Спасибо огромное! Благодаря вам всё прояснилось, чего не добьёшься от нынешних преподавателей в вузе(
@Yu_Ko: форму для того и существует, чтобы смысл разных понятий прояснять. Преподаватели так поступают не от хорошей жизни. Дело в том, что когда в короткий по времени курс надо уложить много разных методов решения задач (включая дифференциальные уравнения, или ряды Фурье), то там поневоле приходится ограничиваться изложением типовых «рецептов». Типа, капусты вот столько, а морковки в 3 раза меньше Тут как бы уже не до кулинарных «изысков»
Построение базисов в ядре и образе линейного оператора.
Речь пойдёт о построении базисов в ядре и образе линейного оператора.
Будут рассмотрены два примера: первый пример с пояснениями; вто-
рой как образец оформления. Значок будет указывать на утверждения, требующие доказательств. Рекомендуется рассматривать эти утверждения как хорошие теоретические задачи для самостоятельного решения. Полный список теоретических задач приведён в конце.
Пусть L векторное пространство, A линейный оператор в L. Ядро (=нуль-пространство) линейного оператора полный прооб-
раз множества <0>, т. е. множество всех векторов, которые переводятся линейным оператором в 0:
Образ (=множество значений) линейного оператора множество всех векторов, у которых есть прообразы относительно A:
Ядро и образ линейного оператора являются подпространствами . Например, если L координатная плоскость (двумерное векторное
пространство с базисом e 1 , e 2 ) и оператор A проектирует радиус-векторы на ось абсцисс (=на линейную оболочку вектора e 1 ) параллельно оси ординат (=параллельно линейной оболочке вектора e 2 ), то ker A ось ординат (линейная оболочка вектора e 2 ), im A ось абсцисс (линейная оболочка вектора e 1 ):
ker A = `(e 2 ), im A = `(e 1 ).
Рассмотрим на примере, как находить базисы ядра и образа линейного оператора, заданного матрицей в некотором базисе.
Пример 1. Дана матрица линейного оператора A в базисе e = (e 1 , e 2 , e 3 , e 4 ):