Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Простые и составные числа
Определение 1
Натуральное число $p$ называется простым числом, если у него только $2$ делителя: $1$ и оно само.
Делителем натурального числа $a$ называют натуральное число, на которое исходное число $a$ делится без остатка.
Пример 1
Найти делители числа $6$.
Решение: Нам надо найти все числа, на которые заданное число $6$ делится без остатка. Это будут числа: $1,2,3, 6$. Значит делителем числа $6$ будут числа $1,2,3,6.$
Ответ: $1,2,3,6$.
Значит, для того, чтобы найти делители числа надо найти все натуральные числа, на которые данное делится без остатка. Нетрудно заметить, что число $1$ будет являться делителем любого натурального числа.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 2
Составным называют число, у которого кроме единицы и самого себя есть другие делители.
Примером простого числа может являться число $13$, примером составного число $14.$
Замечание 1
Число $1$ имеет только один делитель-само это число, поэтому его не относят ни к простым, ни к составным.
Взаимно простые числа
Определение 3
Взаимно простыми числами называются те, у которых НОД равен $1$.Значит для выяснения будут ли являться числа взаимно простыми необходимо найти их НОД и сравнить его с $1$.
Попарно взаимно простые
Определение 4
Если в наборе чисел любые два взаимно просты, то такие числа называются попарно взаимно простыми. Для двух чисел понятия «взаимно простые» и «попарно взаимно простые» совпадают.
«Взаимно простые числа, их свойства» 👇
Пример 2
$8, 15$ — не простые, но взаимно простые.
$6, 8, 9$ — взаимно простые числа, но не попарно взаимно простые.
$8, 15, 49$ — попарно взаимно простые.
Как мы видим, для того, чтобы определить являются ли числа взаимно простыми, необходимо сначала разложить их на простые множители. Обратим внимание на то, как правильно это сделать.
Разложение на простые множители
Например, разложим на простые множители число $180$:
$180=2cdot 2cdot 3cdot 3cdot 5$
Воспользуемся свойством степеней, тогда получим,
$180=2^2cdot 3^2cdot 5$
Такая запись разложения на простые множители называется канонической, т.е. для того чтобы разложить в канонической форме число на множители необходимо воспользоваться свойством степеней и представить число в виде произведения степеней с разными основаниями
Каноническое разложение натурального числа в общем виде
Каноническое разложение натурального числа в общем виде имеет вид:
$m=p^{n1}_1cdot p^{n2}_2cdot dots dots ..cdot p^{nk}_k$
где $p_1,p_2dots dots .p_k$- простые числа, а показатели степеней- натуральные числа.
Представление числа в виде канонического разложения на простые множества облегчает нахождение наибольшего общего делителя чисел, и выступает как следствие доказательства или определения взаимно простых чисел.
Пример 3
Найти наибольший общий делитель чисел $180$ и $240$.
Решение: Разложим числа на простые множества с помощью канонического разложения
$180=2cdot 2cdot 3cdot 3cdot 5$, тогда $180=2^2cdot 3^2cdot 5$
$240=2cdot 2cdot 2cdot 2cdot 3cdot 5$, тогда $240=2^4cdot 3cdot 5$
Теперь найдем НОД этих чисел, для этого выберем степени с одинаковым основанием и с наименьшим показателем степени, тогда
$НОД (180;240)= 2^2cdot 3cdot 5=60$
Составим алгоритм нахождения НОД с учетом канонического разложения на простые множители.
Чтобы найти наибольший общий делитель двух чисел с помощью канонического разложения, необходимо:
- разложить числа на простые множители в каноническом виде
- выбрать степени с одинаковым основанием и с наименьшим показателем степени входящих в состав разложения этих чисел
- Найти произведение чисел, найденных на шаге 2.Полученное число и будет искомым наибольшим общим делителем.
Пример 4
Определить, будут ли простыми, взаимно простыми числами числа $195$ и $336$.
Решение: Воспользуемся для разложения на множители каноническим разложением:
-
$195=3cdot 5cdot 13$
$336=2cdot 2cdot 2cdot 2cdot 3cdot 7=2^4cdot 3cdot 5$
-
$НОД (195;336) =3cdot 5=15$
Мы видим, что НОД этих чисел отличен от $1$, значит числа не взаимно простые. Также мы видим, что в состав каждого из чисел входят множители, помимо $1$ и самого числа, значит простыми числа так же являться не будут, а будут являться составными.
Пример 5
Определить, будут ли простыми, взаимно простыми числами числа $39$ и $112$.
Решение: Воспользуемся для разложения на множители каноническим разложением:
-
$39=3cdot 13$
$112=2cdot 2cdot 2cdot 2cdot 7=2^4cdot 7$
-
$НОД (39;112)=1$
Мы видим, что НОД этих чисел равен $1$, значит числа взаимно простые. Также мы видим, что в состав каждого из чисел входят множители, помимо $1$ и самого числа, значит простыми числа так же являться не будут, а будут являться составными.
Пример 6
Определить будут ли простыми, взаимно простыми числами числа $883$ и $997$.
Решение: Воспользуемся для разложения на множители каноническим разложением:
-
$883=1cdot 883$
$997=1cdot 997$
-
$НОД (883;997)=1$
Мы видим, что НОД этих чисел равен $1$, значит числа взаимно простые. Также мы видим, что в состав каждого из чисел входят только множители, равные $1$ и самому числу, значит числа будут являться простыми.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
- Простые множители
- Разложение на множители онлайн
- Взаимно простые числа
- Проверка онлайн на взаимно простые числа
Взаимно простые числа
Разберемся, что такое взаимно простые числа. Это такие числа, которые не имеют общих делителей, кроме 1 или -1. Можно сформулировать и по другому. У взаимно простых чисел наибольший общий делитель (НОД) равен единице.
Например, числа 5 и 4 — взаимно простые, потому что число 5 имеет делители 1 и 5, а делители четверки: 1, 2 и 4. Общий делитель у них – это единица, а значит, они взаимно просты.
По второму определению: наибольший общий делитель чисел 5 и 4 равен 1, НОД(5,4) = 1, а значит они взаимно простые.
Взаимно простые числа от 1 до 100
Приведем примеры взаимно простых чисел.
2 и 99,
15 и 16,
28 и 57,
29 и 31,
12 и 1,
59 и 97 и т. д.
Чтобы образовывать взаимно простые числа, должно быть, по крайней мере, два числа.
Как проверить, являются ли взаимно простыми числа
По определению взаимно простых чисел, если числа имеют 1 или -1 в качестве единственного общего множителя, то такие числа будут взаимно простыми.
Решим примеры.
Являются ли взаимно простыми числа:
35 и 40
Решение:
Раскладываем оба числа на простые множители.
Множители первого числа: 35 = 5 х 7.
Множители второго числа: 40 = 2 х 2 х 2 х 5.
Общий множитель данных чисел равен 5. Следовательно, 35 и 40 не являются взаимно простыми.
77 и 20
Решение:
Множители первого числа: 77= 7 х 11.
Множители второго числа: 20 = 2 х 2 х 5.
НОД чисел 77 и 20 равен единице, а значит эти числа будут взаимно простыми.
231 и 280
Решение:
При разложении обоих чисел на множители получаем:
231 = 3 х 7 х 11.
280 = 2 х 2 х 2 х 5 х 7.
Наибольший общий делитель этих чисел равен 7, а значит они не взаимно простые.
Свойства взаимно простых чисел
Свойство 1: Число 1 взаимно простое с каждым числом.
Свойство 2: Все простые числа взаимно просты между собой.
Поскольку каждое простое число имеет только два делителя: 1 и само число, единственным общим делителем двух простых чисел будет 1. Например, 11 и 17 — это два простых числа. Множители 11 равны 1, 11, а делители 17 равны 1, 17. Единственный общий делитель равен 1 и, следовательно, они взаимно просты.
Свойство 3: Любые два последовательных числа всегда взаимно просты.
Рассмотрим любые два последовательных числа, например, 2 и 3, 3 и 4 или 14 и 15. У всех этих чисел общий делитель – это единица.
Свойство 4: Сумма любых двух взаимно простых чисел всегда взаимно проста с их произведением.
2 и 3 взаимно просты. Их сумма равна 5 (2+3), а произведение – 6 (2х3). Следовательно, числа 5 и 6 взаимно просты.
Решение примеров.
Являются ли взаимно простыми числа 21 и 24
21 и 24 не являются взаимно простыми числами, потому что имеют множитель равный 3. ( 21 = 3 х 7, 24 = 2 х 2 х 2 х 3).
Являются ли взаимно простыми числа 13 и 11
13 и 11 взаимно простые числа, потому что это простые числа (свойство 2).
Являются ли взаимно простыми числа 17 и 18
17 и 18 взаимно простые числа, потому что это два последовательных числа (свойство 3).
В чем разница между простыми и взаимно простыми числами?
Простое число определяется как число, которое не имеет множителя, кроме 1 и самого себя.
Но взаимно простые числа считаются парами, и два числа взаимно просты, если их общий делитель равен только 1. Их НОД равен единице.
Таким образом, взаимно простые числа – это обязательно 2 или более чисел. Составные числа также могут быть взаимно простыми.
Пример
Числа 25 и 26 – это составные числа (25 = 5 х 5, 26 = 2 х 13). Но они взаимно просты, т.к. это последовательные числа (свойство 3).
Взаимно простыми множителями называются числа, не имеющие общих делителей, кроме единицы. Алгоритм достаточно прост, попробуйте рассмотреть его на примере: разложите на два взаимно простых множителя число 90.

Инструкция
В первую очередь определите, какие вообще есть множители у числа 90, то есть на какие числа его можно разделить без остатка. Начните с единицы и далее проверяйте все числа: вы получите 1, 2, 3, 5, 9, 10, 18, 30, 45.
Попробуйте найти все множители числа 90 другим способом: разложите его на простые множители. Самое малое простое число (после 1) – это 2. Число 90 делится без остатка на него, поэтому оно будет первым среди простых множителей. Далее разделите 90 на 2, вы получите 45. Это число на 2 не делится.
Следующее простое число 3. Разделите 45 на 3 – вы получите 15. Теперь подберите третий множитель. Самое меньшее простое число, на которое можно разделить 15 без остатка, это 3. Значит, это третий множитель. Разделив 15 на 3, вы получите число 5. Оно делится только на само себя, значит, это ваш последний простой множитель. Таким образом, 90 можно разделить на следующие простые множители: 2, 3, 3, 5. Проверьте: перемножьте их между собой, у вас снова получится 90.
Теперь, зная простые множители, найдите все остальные, просто перемножив их между собой в разных сочетаниях. Например, один из составных множителей числа 90 будет число 2х3=6, другой 2х5=10, третий 3х5=15, четвертый 2х3х3=18, пятый 2х3х5=30, шестой 3х3х5=45.
Определите, какие из полученных множителей взаимно простые, то есть не имеют общих делителей (кроме единицы), причем их произведение должно быть равно 90. Так как число 90 может быть получено перемножением четырех чисел 2, 3, 3, 5, то взаимно простыми будут такие числа: 2 и 3х3х5, а также 2х3х3 и 5. Если в обоих множителях появится число 3, то они будут ему кратны, то есть не будут являться взаимно простыми. Таким образом, вы получили две пары взаимно простых множителей для числа 90, это 2 и 45, а также 18 и 5.
Проверьте себя: умножьте 2 на 45, вы получите 90. В то же время, разложив 45 на простые множители (5*3*3), вы поймете, что на 2 это число без остатка не делится. Точно также проверьте вторую пару взаимно простых множителей.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Взаимно простые числа

4.5
Средняя оценка: 4.5
Всего получено оценок: 186.
4.5
Средняя оценка: 4.5
Всего получено оценок: 186.
Взаимно простые числа тема достаточно сложная тема 6 класса математики. Как и простые числа, тема взаимно простых чисел используется для сложения и вычитания дробей. Чтобы не допускать ошибок в этой теме разберемся в вопросе подробнее.
Простые числа
Что такое простое число? Простое число делится только на единицу и на само себя. Например, число 13 является простым, так как нацело делится только на 1 и на 13. Секрет в том, что практически каждое число можно разделить на другое число. Но в простых числах важно именно деление нацело, дробные частные и деление с остатком не рассматривается.
Простые числа в знаменателях дробей означают, что для нахождения общего знаменателя нужно перемножить эти числа между собой. Разложить простые числа на множители невозможно. Поэтому НОД двух простых чисел это их произведение.
Числа, которые содержат в себе больше двух множителей, то есть делятся на несколько чисел, называются сложными. Сложные числа состоят из перемноженных простых.
Взаимно простые числа
Взаимно простыми числами называются числа, наибольший общий делитель которых равен единицы. Доказать факт того, что числа являются взаимно простыми можно только с помощью разложения чисел на простые множители. Если у чисел нет общих множителей, кроме 1, то они будут взаимно простыми.
При этом сами по себе взаимно простые числа могут быть сложными. Важен именно НОД двух чисел.
Нужно учитывать, что взаимно простыми могут быть не только два числа, но и 3, 4, 10 – любое множество чисел может быть взаимно простым.
Как определить взаимно простые числа?
Для того чтобы определить взаимно простые числа, можно воспользоваться двумя алгоритмами:
- Разложить каждое из чисел на множители и искать общие простые множители. Если такие есть, то числа не являются взаимно простыми. Если общих множителей нет, числа можно считать взаимно простыми.
- Делить каждое из чисел поочередно на простые множители. Этот способ проще в исполнении, так как не требует большой внимательности и сосредоточенности. Но такая проверка не подойдет для больших чисел, слишком долгой может получится проверка. Поэтому более надежным будет использовать первый вариант.
Относительно друг друга два простых числа всегда будут взаимно простыми. А если одно из чисел, делится на другое нацело, то эти числа точно не являются взаимно простыми.
Пример
Определим, являются ли взаимно простыми числа 1729 и 282
Определение начинается с разложения на множители:
1729=7*13*19
282=2*3*47
Обратите внимание, что для разложения таких чисел придется использовать метод перебора. Согласно таблице простых чисел каждый множитель проверяется, после чего деление продолжается. Подбирать множители нужно от маленьких чисел к большим, то есть от 2 и выше.
Как видно, общих множителей у двух чисел нет. Это значит, что числа можно считать взаимно простыми. Не нужно пугаться, если среди множителей попадаются достаточно большие числа. Среди учеников существует миф, что простые числа редко бывают больше 20, это не так. Просто такие числа проще использовать в задачах, чтобы набить руку. На экзамене или в контрольной сложность числа для разложения может быть абсолютно любой
Что мы узнали?
Мы поговорили о простых числах. Выяснили, что такое взаимно простые числа и обговорили некоторые их свойства. Привели примеры взаимно простых чисел. Обговорили неправильные мнения по поводу простых и взаимно простых чисел.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Ольга Оль
8/10
-
Валентина Дашинова
8/10
-
Саша Романов
7/10
-
Захар Забанов
10/10
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 186.
А какая ваша оценка?
Калькулятор взаимно простых чисел
Онлайн калькулятор определит являются ли число взаимно простыми, путем нахождения наибольшего общего делителя чисел.
Для определения взаимно простых чисел необходимо указать количество и ввести числа.
Нажмите кнопку рассчитать и калькулятор укажет как определить взаимно простые числа.
Определение взаимно простых чисел
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Ниже описано как определить являются ли числа 35 и 40 взаимно простыми.
- 1 Находим наибольший общий делитель чисел: НОД(35, 40)=5.
- 2 Наибольший общий делитель ≠ 1 следовательно числа не взаимно простые.
Пример Определить являются ли 77 и 20 взаимно простыми числами

Примеры взаимно простых чисел
Рассмотрим на примере как определить взаимно простые числа.
Пример Являются ли числа 42 и 55 взаимно простыми

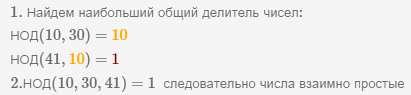
Определим что 3 числа 10, 30, 41 являются взаимно простыми.
Пример Проверить что числа 10, 30, 41 взаимно просты
Смотрите также
Другие страницы


