В
математике изучают различные виды
соответствий. Это не случайно, поскольку
взаимосвязи, существующие в окружающем
нас мире многообразны. Для учителя,
обучающего математике младших школьников,
особую значимость имеют взаимно
однозначные соответствия.
Определение.
Взаимно
однозначным соответствием между
множествами Х и У называется такое
соответствие, при котором каждому
элементу множества Х сопоставляется
единственный элемент множества У и
каждый элемент множества У соответствует
только одному элементу множества Х.
Рассмотрим
примеры взаимно однозначных соответствий.
Пусть
Х – множество кругов, У – множество
квадратов и соответствие между ними
задано при помощи стрелок.
Это
соответствие взаимно однозначное, так
как каждому кружку из множества Х
сопоставляется единственный квадрат
из множества У и каждый квадрат из У
соответствует только одному кружку из
множества Х.
Пример
Пусть
Х – множество действительных чисел, У
– множество точек координатной прямой.
Соответствие между ними таково:
действительному числу сопоставляется
точка координатной прямой. Это соответствие
взаимно однозначное, так как каждому
действительному числу сопоставляется
единственная точка координатной прямой
и каждая точка на прямой соответствует
только одному числу.
В
математике взаимно однозначное
соответствие между множествами Х и У
часто называют взаимно однозначным
отображением множества Х на множество
У.
5. Равномощные множества
Определение.
Множества
Х и У называются равномощными, если
между ними можно установить взаимно
однозначное соответствие.
Если
множества Х и У равномощны,
то пишут Х
У.
Нетрудно
видеть, что множества рассмотренные в
предыдущих примерах равномощны.
Равномощными
могут быть как конечные, так и бесконечные
множества
Равномощные
конечные множества называют еще
равночисленными. В
начальном обучении математике
равночисленность выражается словами
«столько же» и может использоваться
при ознакомлении учащихся со многими
понятиями. Например, чтобы ввести
равенство чисел, сравнивают два множества,
устанавливая между их элементами взаимно
однозначное соответствие. Например,
пишут, что 5 = 5, так как кружков столько
же, сколько квадратов.
Понятие
равночисленности множеств лежит и в
основе определения отношений «больше
на …» и «меньше на…» . Например, чтобы
утверждать, что 6 больше 4 на 2, сравнивают
два множества, устанавливая взаимно
однозначное соответствие между множеством
Х, в котором 4 элемента, и подмножеством
У1
другого множества У, в котором 6 элементов,
и делают вывод: треугольников столько
же, сколько кружков, и еще 2. Другими
словами, треугольников на 2 больше, чем
кружков.
Х
У1
У
Как
уже было сказано, равномощными могут
быть и бесконечные множества.
Пример
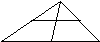
Пусть
Х – множество точек отрезка АВ, У –
множество точек отрезка СD,
причем длины отрезков различны. Так как
между данными множествами можно
установить взаимно однозначное
соответствие, то множества точек АВ и
СD
равномощны.
N
A
M
B
С
M’ D
Пример
Рассмотрим
множество N
натуральных чисел и множество У – четных
натуральных чисел. Они равномощны, так
как между их элементами можно установить
взаимно однозначное соответствие:
N:
1
2
3
…
п …
У:
2
4
6
…
2п
…
Замечание. На
первый взгляд кажется парадоксальным
тот факт, что можно установить взаимно
однозначные соответствия между множеством
и его частью: для конечных множеств
такая ситуация невозможна. Однако в
математике доказано, что для бесконечного
множества А всегда найдется такое его
подмножество В, что между А и В можно
установить взаимно однозначное
соответствие.
Иногда это утверждение считают
определением бесконечного множества.
Определение.
Если
бесконечное множество равномощно
множеству N натуральных чисел, его
считают счетным.
Любое
бесконечное подмножество множества N
счетно: чтобы пронумеровать его элементы,
надо расположить элементы подмножества
в порядке возрастание и нумеровать один
за другим. Так, счетно множество всех
нечетных натуральных чисел, множество
натуральных чисел, кратных 5 и др. Счетными
являются также множества всех целых
чисел, всех рациональных.
Существуют
ли множества, отличные от счетных?
Доказано, что бесконечным множеством,
не равномощным множеству N натуральных
чисел, является множество R всех
действительных чисел.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Мощность конечного множества
- Взаимно однозначное соответствие двух множеств
- Эквивалентность
- Счётные и несчётные множества
- Примеры
Мощность конечного множества
Мощностью конечного множества называют число элементов этого множества.
В общем случае мощность множества A обозначают |A|.
Для конечных множеств чаще встречается обозначение n(A).
Конечные множества легко сравнивать по мощности.
Если n(A) = n(B), то конечные множества A и B равномощны.
Например: Мощность множества A={1;3;5;7} равна n(A)=4.
Мощность множества B = {-3;13;2;4} равна n(B) = 4.
Множества A и B равномощны.
Взаимно однозначное соответствие двух множеств
Говорят, что между множествами A и B установлено взаимно однозначное соответствие, если:
1) каждому элементу множества A соответствует только один элемент множества B;
2) каждый элемент множества B при этом соответствует некоторому элементу множества A;
3) разным элементам множества A соответствуют разные элементы множества B.
Например:
Каждый раз, когда мы «считаем» множество каких-то объектов, мы устанавливаем взаимно однозначно соответствие между этим множеством и подмножеством натуральных чисел от 1 до некоторого n.
С этой точки зрения утверждение
«У Толи три друга: Вася, Коля и Петя» выглядит как соответствие:
Друзья Толи
Вася
Коля
Петя
Эквивалентность
Множества A и B называют эквивалентными (равномощными), если между ними можно установить взаимно однозначное соответствие.
Обозначение: $A sim B$.
Такой подход даёт нам возможность сравнивать по мощности не только конечные, но и бесконечные (!) множества.
Например:
Сравним мощности множеств натуральных и натуральных чётных чисел:
A $ = {n│n in Bbb N },B = {n|n⋮2, n in Bbb N}$
Построим соответствие:
$ begin{matrix} 1 & 2 & 3 & … & n & … \ 2 & 4 & 6 & … & 2n & … \ end{matrix}$
Несмотря на бесконечность обоих множеств и отношение вложенности $B subset A$, получаем взаимно однозначное соответствие, и может утверждать, что множества равномощны |A| = |B| и эквивалентны $A sim B$.
Для мощности натуральных чисел используется специальное обозначение:
|N| = $aleph_0$ – читается «алеф-нуль».
Счётные и несчётные множества
Множество называют счётным, если оно эквивалентно множеству натуральных чисел.
Чтобы доказать счётность множества достаточно придумать правило, по которому нумеруются его элементы.
Например:
Докажем, что множество целых чисел счётно.
Построим соответствие:
$ begin{matrix} 1 & 2 & 3 & 4 & 5 & … & 2n & 2n+1 & … \ 0 & 1 & -1 & 2 & -2 & … & n & -n & … \ end{matrix}$
Получаем взаимно однозначное соответствие между множествами целых и натуральных чисел. Значит, эти множества эквиваленты $Bbb Z sim Bbb N$, и множество $Bbb Z$ счётно.
Что и требовалось доказать.
Множество действительных точек отрезка [0;1] несчётно.
Мощность этого множества равна мощности континуума, $ c gt aleph_0$
Таким образом, множество отрезка [0;1]оказывается мощнее всего множества натуральных чисел.
Любой отрезок [a;b] и отрезок [0;1] эквивалентны.
Мощность любого действительного отрезка равна мощности континуума.
Любое множество, эквивалентное отрезку [0;1], называют континуальным.
Чтобы доказать несчётность множества, нужно показать, что нет таких правил, по которым можно его посчитать. Это значительно сложнее, чем доказать счётность.
Примеры
Пример 1. Среди данных конечных множеств укажите пары эквивалентных:
а) A = {1;3;5}, B = {5;7;9}, C = {0;1}
n(A) = 3, n(B) = 3, n(C) = 2
$A sim B$
б) A = $ {n|n le 3, n in Bbb N }$
B = $ {n|1 lt n lt 5, n in Bbb N }$
C = $ {n||n| le 1, n in Bbb Z }$
Запишем с помощью перечисления:
A = {1;2;3}, B = {2,3,4}
C = {-1,0,1}
n(A) = 3, n(B) = 3, n(C) = 3
$A sim B, B sim C, A sim C$
Пример 2. Пусть A — множество всех окружностей плоскости, B — множество всех правильных треугольников этой плоскости. Каждому треугольнику ставится в соответствие вписанная в него окружность. Является ли это соответствие взаимно однозначным?
Рассматриваем соответствие $B rightarrow A$.
В каждый треугольник можно вписать окружность, и притом только одну. Условие единственности (1) выполняется.
Вокруг каждой окружности можно описать бесконечное количество правильных треугольников, поворачивая их на некоторый угол относительно центра окружности.
Условие (2) не выполняется.
Соответствие не является взаимно однозначным.
Пример 3. Постройте взаимно однозначное соответствие между отрезком [0;1] и отрезком [2;7] с помощью линейной функции.
Искомая функция имеет вид y = kx+b, где
$$x in [0;1], y in [2;7]$$
Прямая проходит через две точки: A(0;2),B(1;7).
Уравнение прямой:
$$ frac{x-x_A}{x_B-x_A} = frac{y-y_A}{y_B-y_A}$$
$$ frac{x}{1} = frac{y-2}{7-2} Rightarrow 5x = y-2 Rightarrow y = 5x+2 $$
$$ x in [0;1] overset {y=5x+2} mapsto y in [1;7] $$
Пример 4*. Постройте взаимно однозначное соответствие между отрезком [0;1] и отрезком [a;b], $a in Bbb R, b in Bbb R$ с помощью линейной функции.
Искомая функция имеет вид y=kx+b, где $x in Bbb [0;1], y in Bbb [a;b]$
Прямая проходит через две точки: A(0;a),B(1;b). Уравнение прямой:
$$ frac{x-x_A}{x_B-x_A} = frac{y-y_A}{y_B-y_A} $$
$$ frac{x}{1} = frac{y-a}{b-a} Rightarrow (b-a)x = y-a Rightarrow y = (b-a)x+a $$
$$ x in [0;1] overset{y = (b-a)x+a} mapsto y in [a;b] $$

Соответствие между множествами А и В называется взаимно однозначным, если каждому элементу множества А соответствует единственный элемент множества В, причем разным элементам множества А соответствуют разные элементы множества В и каждый элемент множества В поставлен в соответствие некоторому элементу множества А. Множества называют эквивалентными (или равномощными), если между ними можно установить взаимно однозначное соответствие. Конечные множества А и В эквивалентны тогда и только тогда, когда количество элементов в них одинаково.
Установление взаимно однозначного соответствия дает возможность сравнивать не только конечные множества, но и, что самое главное, множества с бесконечным числом элементов.
Простейшим среди бесконечных множеств является множество натуральных чисел.
Множество называется счетным, если оно эквивалентно множеству натуральных чисел. Иначе можно сказать, что множество счетно, если все его элементы можно занумеровать всеми натуральными числами.
Пример 1. Множество натуральных чисел N = {1;2;3;…} эквивалентно множеству целых отрицательных чисел А = {-1;-2;-3;…}, причем взаимно однозначное соответствие устанавливается так: каждому числу n є N соответствует число -n є А.
Пример 2. Сопоставим числу n число 2n. Тогда получаем взаимно однозначное соответствие между множеством всех натуральных чисел и множеством всех четных натуральных чисел.
Замечание. Для конечных множеств справедлива формула
m(АUВ) = m(А) + m(В)-m(А∩В), (1)
где m(A), m(В), m(АUВ), m(А∩В) — соответственно число эле¬ментов множеств А, В, АUВ, А∩В.
Пример 3. Экзамен по русскому языку сдавали 300 абитуриентов, оценки 2, 3, 4 получили 280 человек, а оценки 3, 4, 5 получили 200 человек. Сколько человек получили оценки 3 и 4?
Решение.
Введем следующие обозначения:
А — множество абитуриентов, получивших оценки 2, 3, 4;
В — множество абитуриентов, получивших оценки 3, 4, 5.
Тогда АUВ — множество всех абитуриентов; А∩В — множество абитуриентов, получивших оценки 3, 4.
m(А) =280, m(B)=200, m(AUB)=300.
m(А∩В) нужно найти.
Из формулы (1):
m(А∩В) = m(А) + m(В) — m(А∩В);
m( А∩В)=280+200-300=180.
Ответ: {180}.