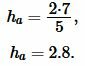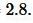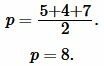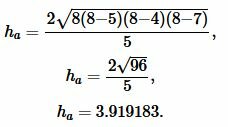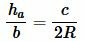Как найти высоту треугольника в базисе

Как найти вектор высоты треугольника

Формулы для нахождения высоты треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

Нахождение высоты треугольника

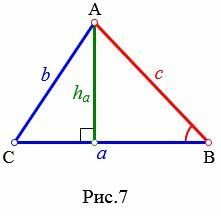
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты h_a, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Примеры задач

Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Как найти вектор высоты треугольника

И в итоге: x+2y+z-9=0
это вы написали уравнение плоскости, проходящей через точку С перпендикулярно АВ.

Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости

I. «Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости»

Нужно найти не длину, а уравнение CH.

II. «Можно воспользоваться двойным векторным произведением. и найти направляющий вектор высоты. »
То есть:
AC
AB

Нужно найти не длину, а уравнение CH. — Если найдёте `H`, то сможете написать уравнение по двум точкам.

Так? — Да. только вычисления не проверял. а в том, что получили, можно сократить на 36.

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Высота треугольника онлайн

С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Открыть онлайн калькулятор

Высота треугольника. Определение

Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).

Теорема о пересечении высот треугольника

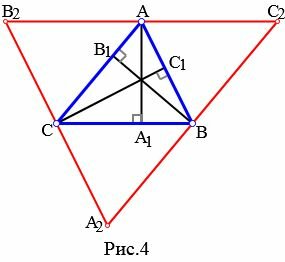
Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.

Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты ( small AA_1 ,) ( small BB_1 ,) ( small CC_1 ) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник ( small A_2B_2C_2. ) Покажем, что точки ( small A, B, C ) являются серединами сторон треугольника ( small A_2B_2C_2. ) ( small AB=A_2C ) так как они являются противоположными сторонами параллелограмма ( small ABA_2C. ) ( small AB=CB_2 ) так как они являются противоположными сторонами параллелограмма ( small ABCB_2. ) Тогда ( small CB_2=CA_2, ) то есть точка ( small C ) является серединой стороны ( small A_2B_2 ) треугольника ( small A_2B_2C_2. ) Аналогично доказывается, что точки ( small A ) и ( small B ) являются серединами сторон ( small B_2C_2 ) и ( small A_2C_2, ) соответственно.

Далее из ( small AA_1⊥BC ) следует, что ( small AA_1⊥B_2C_2 ) поскольку ( small BC ǁ B_2C_2 ). Аналогично, ( small BB_1⊥A_2C_2, ) ( small CC_1⊥A_2B_2. ) Получили, что ( small AA_1,) ( small BB_1, ) ( small CC_1) являются серединными перпендикулярами сторон ( small B_2C_2, ) ( small A_2C_2, ) ( small A_2B_2, ) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.

Точка пересечения высот треугольника называется ортоцентром.

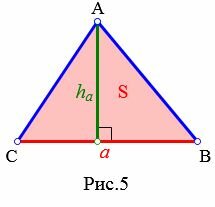
Высота треугольника по основанию и площади

Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).

Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:

.

.

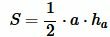
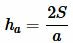(1)

Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника.

Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:

Ответ:

Высота треугольника по трем сторонам

Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):

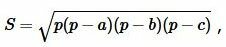(2)

где ( small a, b, c ) стороны треугольника а полупериод ( small p ) вычисляется из формулы:

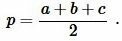(3)

Высота треугольника, отпущенная на сторону ( small a) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:

.

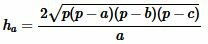(4)

Пример 2. Известны стороны треугольника: ( small a=5, ) ( small b= 4, ) ( small c=7. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Найдем, сначала полупериод ( small p ) треугольника из формулы (3):

Подставляя значения ( small a , b, c ) и ( small p ) в (4), получим:

Ответ:

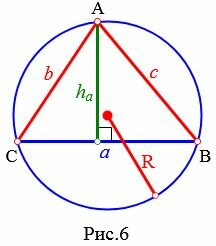
Высота треугольника по двум сторонам и радиусу описанной окружности

Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:

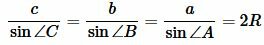(5)

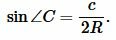(6)

Далее, из теоремы синусов имеем:

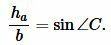(7)

Подставляя (6) в (7), получим:

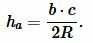(8)

Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:

(small max (b,c) ≤2R Пример 3. Известны стороны треугольника: ( small b=7, ) ( small c= 3 ) и радиус описанной окружности ( small R=4. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Проверим сначала условие (9):

(small max (7,3) ≤2 cdot 4 Ответ: ( small 2frac<5><8>. )

Высота треугольника по стороне и прилежащему к ней углу

Найдем высоту ( small h_a ) треугольника на рисунке 7. Из теоремы синусов имеем:

( small frac<large h_a><large sin angle B>=frac<large c><large sin 90°>, )

Пример 4. Известны сторона ( small c=12 ) треугольника и прилежащий угол ( small angle B=30°. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Для нахождения высоты треугольника подставим значения ( small c=12 ) и ( small angle B=30° ) в (11). Имеем: