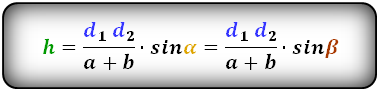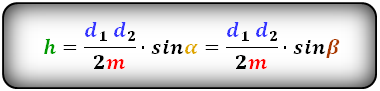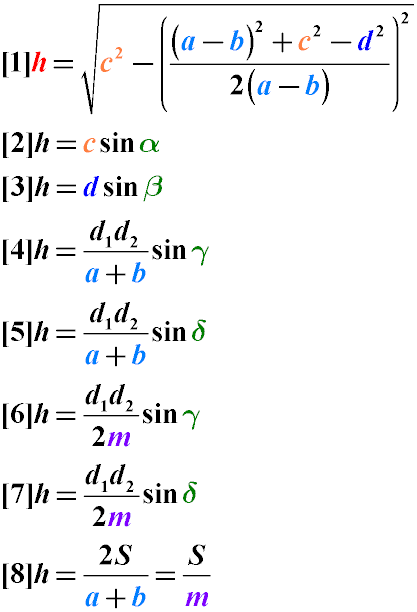Нахождение высоты трапеции: формулы и примеры задач
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту трапеции, а также разберем примеры решения задач для закрепления материала.
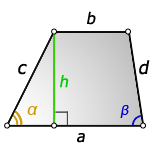
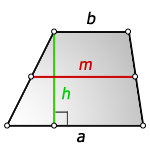
Напомним, высотой трапеции называется отрезок, соединяющий оба ее основания и перпендикулярный им.
Нахождение высоты трапеции
Через длины сторон
Если известны длины всех четырех сторон трапеции, ее высота рассчитывается по формуле ниже:
Через боковую сторону и прилежащий угол
Высоту трапеции можно вычислить, если знать длину любой из ее боковых сторон и значение прилежащего к ней и основанию угла.
Через диагонали и угол между ними
Зная длину оснований трапеции, а также диагоналей и угол между ними, вычислить высоту удастся по формуле:
Если сумму оснований заменить длиной средней линии (m), то формула будет выглядеть следующим образом:
Средняя линия трапеции (m) равняется полусумме ее оснований, т.е m = (a+b) /2.
Через площадь
Высоту трапеции можно вычислить, если известны ее площадь и длины оснований (или средней линии).
Примечание: формулы для нахождения высоты равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Примеры задач
Задание 1
Найдите высоту трапеции, если ее основания равны 9 и 6 см, а боковые стороны – 4 и 5 см.
Решение
Т.к. у нас есть длины всех сторон, мы можем воспользоваться первой формулой для вычисления требуемого значения:
Кстати, т.к. высота равна одной из боковой сторон трапеции, значит она является прямоугольной.
Задание 2
Площадь трапеции равна 26 см 2 . Найдите ее высоту, если основания равны 10 и 3 см.
Решение
В данном случае можно применить последнюю из рассмотренных формул:
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) |
| a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
a — большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Все формулы высоты трапеции
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
1. Формула высоты трапеции через стороны и углы при основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
h — высота трапеции
Формулы длины высоты, ( h ):
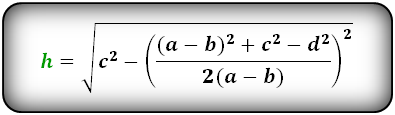
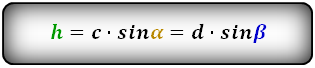
2. Формула высоты трапеции через диагонали и углы между ними
d 1 , d 2 — диагонали трапеции
α , β — углы между диагоналями
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, ( h ):
3. Формула высоты трапеции через площадь
S — площадь трапеции
a , b — основания
h — высота трапеции
m — средняя линия
http://ru.onlinemschool.com/math/formula/trapezium/
http://www-formula.ru/height-trapeze
Определения
Трапеция — это такой четырехугольник, у которого две стороны параллельны (они являются основаниями трапеции, указанные на рисунках a и b), а две другие — нет.
Высота трапеции — это такой отрезок h, который проведен перпендикулярно основаниям.
Нахождение высоты по площади и основаниям
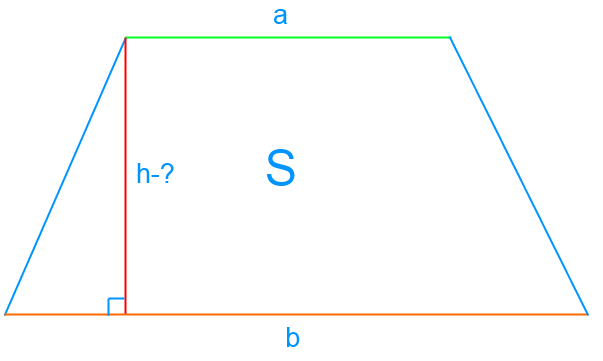
Чтобы вычислить площадь S трапеции мы используем формулу:
[S=frac{((a+b) times h)}{2}]
Здесь h — высота трапеции, а сегменты a и b являются ее основаниями.
Можем найти h:
[h=frac{2 times S}{(a+b)}]
Пример 1
Площадь трапеции S составляет 50 см2, длина ее основания a = 4 см, длина второго основания b равна 6 см, то для нахождения высоты h мы используем формулу:
[h=frac{2 times 50}{(4+6)}=10 mathrm{~cm}]
Ответ: 10 см.
Нахождение высоты, зная площадь и среднюю линию
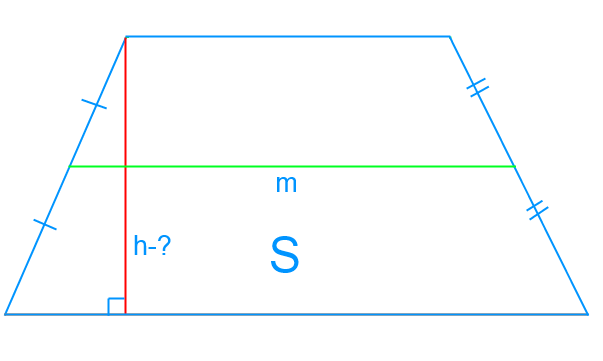
Мы используем формулу, с помощью которой можно рассчитать площадь трапеции:
S = m × h,
Здесь h — это высота трапеции, m — ее средняя линия.
Можем найти h:
[h=frac{S}{m}], будет ответом.
Пример 2
Средняя линия трапеции, обозначенная буквой m, равна 20 см, а площадь S, которая составляет 200 см2. Давайте найдем значение высоты трапеции h.
[h=frac{200}{20}=10 mathrm{~cm}]
Ответ: 10 см
Высота прямоугольной трапеции
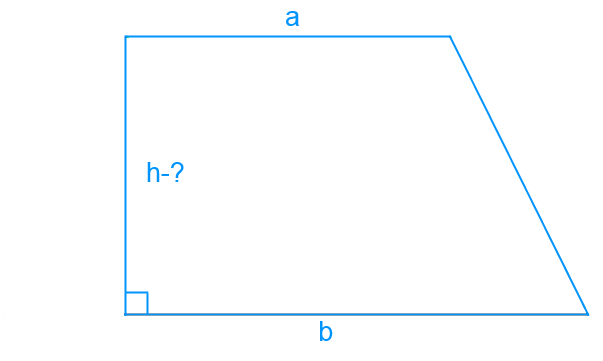
Определение
Диагональ — это сегмент, соединяющий пару противоположных вершин трапеции. Когда трапеция прямоугольная, используя диагональ, мы находим высоту данной фигуры.
Трапецию, одна из боковых сторон которой перпендикулярна основаниям, называют прямоугольной трапецией.
Таким образом, рассмотрим подобную трапецию ABCD, где AD — высота, AC — диагональ, DC-основание. Мы используем теорему Пифагора, которая говорит, что в прямоугольном треугольнике ADC квадрат гипотенузы AC равен сумме квадратов его сторон — катетов AB и BC.
Тогда мы сможем написать:
AC² = AD² + DC².
AD — это катет треугольника, сторона трапеции и, одновременно, ее высота. Так как отрезок перпендикулярен основаниям. Длина катета будет находиться как:
[A D=sqrt{left(A C^{2}-D C^{2}right)}]
Таким образом, у нас есть формула, которая поможет при вычислении найти высоту трапеции AD.
Пример 3
Основания трапеции с прямым углом(DC) равно 14 см, а ее диагональ (AC) равна 15 см, мы будем использовать теорему Пифагора для получения высоты (сторона AD).
Пусть x — неизвестная часть прямоугольного треугольника (AD), тогда
[A C^{2}=A D^{2}+D C^{2}] может быть записан
[15^{2}=14^{2}+x^{2}]
[x=sqrt{left(15^{2}-14^{2}right)}=sqrt{(225-196)}=sqrt{29} mathrm{см}]
Ответ: [sqrt{29} mathrm{см}], что составляет приблизительно 5,385 см
Нет времени решать самому?
Наши эксперты помогут!
Нахождение высоты через стороны
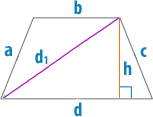
Существует еще один способ найти высоту — через стороны. Помимо высоты в трапеции стоит провести также ее диагональ, которая образует треугольник с прямым углом и даст возможность найти высоты несколькими различными способами через различные треугольники.
Если выразить все длины сторон таких треугольников через стороны трапеции и привести подобные слагаемые, то получится следующая формула:
[mathrm{h}=sqrt{C^{2}-left(frac{(a-b)^{2}+e^{2} d^{2}}{2(a-b)}right)^{2}}]
Пример 4
Дана трапеция, в ней известны основания a и b. Эти основания соответственно равны 4,5 см и 2,5 см. Известны и ее боковые стороны d и c, которые равны 2 см и используем формулу:
[h=sqrt{2^{2}-left(frac{(4,5-2,5)^{2}+2^{2}-2 sqrt{2}^{2}}{2(4,5-2,5)}right)^{2}}=sqrt{4}=2 см]
Ответ: h=2 см.
Высота трапеции
Содержание:
- Что такое трапеция
-
Как найти высоту трапеции
- Через стороны
- Через среднюю линию и площадь
- Через боковую сторону и угол
- Через диагонали, угол между ними и основания
- Через диагонали, угол и среднюю линию
- Через радиус вписанной окружности
- Примеры вычисления
Что такое трапеция
Определение
Трапеция — это геометрическая фигура, которая состоит из двух параллельных и неравных друг другу отрезков (оснований) и боковых сторон.
Все стороны трапеции могут иметь разную величину. Но если ее боковые стороны равны, значит трапеция равнобедренная.
Определение
Высота трапеции — это перпендикуляр, проведенный из любой точки одного основания фигуры до другого.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как найти высоту трапеции
Через стороны
Если нам известны стороны фигуры, мы можем найти ее высоту по формуле:
(h=sqrt{b^2-(frac{{(a-d)}^2+d^2+c^2}{2cdot(a-b)}})^2)
Где h — высота, a — большее основание, b — меньшее основание, c и d — боковые стороны.
Через среднюю линию и площадь
Если в условии есть данные о величине средней линии и площади, можем использовать формулу:
(h=frac Sm)
Где m — средняя линия трапеции.
Через боковую сторону и угол
Когда нам известна величина одной из боковых сторон и угол между этой стороной и большим основанием, используем формулу:
(h=ccdotsinleft(alpharight))
Где alpha — это угол между стороной c и большим основанием a.
Через диагонали, угол между ними и основания
Если нам известны длины обоих диагоналей трапеции, а также угол между ними, можем найти высоту следующим образом:
(h=frac{d_1d_2}{a+b}cdotsinleft(gammaright))
Где (d_1) и (d_2) — диагонали трапеции, а (gamma) — угол между ними.
Через диагонали, угол и среднюю линию
В том случае, если нам известны сразу длины диагоналей, угол между ними и величина средней линии, мы можем узнать высоту трапеции по формуле:
(h=frac{d_1d_2}{2m}cdotsinleft(gammaright))
Через радиус вписанной окружности
Если в трапецию можно вписать окружность, то ее высота будет равна диаметру этой окружности, то есть d=h. Другими словами, высота фигуры будет равна удвоенному радиусу вписанной в нее окружности:
(h=2r)
Где r — радиус выписанной окружности.
Примеры вычисления
Задача 1
Дана трапеция, в которой известны основания a и b. Они равны 4,5 см и 2,5 см. Также известны ее боковые стороны d и c, равные 2 см и (2sqrt2) см соответственно. Найти высоту.
Решение
Чтобы решить эту задачу, используем формулу (h=sqrt{b^2-(frac{{(a-d)}^2+d^2+c^2}{2cdot(a-b)}})^2.)
Подставляем известные значения:
(h=sqrt{2^2-(frac{{(4,5-2,5)}^2+2^2+{(2sqrt2)}^2}{2cdot(4,5-2,5)}}{)^2=}h=sqrt{4-(frac{4+4-8}4}{)^2=sqrt4=2}) см.
Ответ: h=2 см.
Задача 2
Известно, что основания a и b равнобедренной трапеции равны 3 см и 5 см. Площадь фигуры равна 8 см2. Вычислить высоту.
Решение:
Чтобы найти высоту, нужно знать величину средней линии m. Определим ее следующим образом:
(m=frac{a+b}2=frac{3+5}2=4 см.)
Теперь используем формулу (h=frac Sm) и подставим известные значения:
(h=frac84=2) см.
Ответ: h=2 см.
Задача 3
Мы знаем, что сторона c трапеции равна (sqrt2) см, а угол (alpha) между известной стороной и основанием равен 45 градусов. Найти значение высоты.
Решение:
Используем формулу (h=ccdotsinleft(alpharight)) и подставим значения:
(h=sqrt2cdotsinleft(45^circright)=frac{sqrt2cdotsqrt2}2=frac22=1) см.
Ответ: h=1 см.
Задача 4
Даны диагонали трапеции (d_1) и (d_2), равные 2 см и 3 см, а также угол gamma между ними, который равняется 30 градусов. Основания a и b, длина которых 2 см и 1 см соответственно. Найти h.
Решение:
Для решения задачи использует формулу (h=frac{d_1d_2}{a+b}cdotsinleft(gammaright).)
Подставим значения:
(h=frac{2cdot3}{2+1}cdotsinleft(30^circright)=frac63cdotfrac12=1) см.
Ответ: h=1 см.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту трапеции, а также разберем примеры решения задач для закрепления материала.
Напомним, высотой трапеции называется отрезок, соединяющий оба ее основания и перпендикулярный им.
-
Нахождение высоты трапеции
- Через длины сторон
- Через боковую сторону и прилежащий угол
- Через диагонали и угол между ними
- Через площадь
- Примеры задач
Нахождение высоты трапеции
Через длины сторон
Если известны длины всех четырех сторон трапеции, ее высота рассчитывается по формуле ниже:
Через боковую сторону и прилежащий угол
Высоту трапеции можно вычислить, если знать длину любой из ее боковых сторон и значение прилежащего к ней и основанию угла.
Через диагонали и угол между ними
Зная длину оснований трапеции, а также диагоналей и угол между ними, вычислить высоту удастся по формуле:
Если сумму оснований заменить длиной средней линии (m), то формула будет выглядеть следующим образом:
Средняя линия трапеции (m) равняется полусумме ее оснований, т.е m = (a+b)/2.
Через площадь
Высоту трапеции можно вычислить, если известны ее площадь и длины оснований (или средней линии).
Примечание: формулы для нахождения высоты равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Примеры задач
Задание 1
Найдите высоту трапеции, если ее основания равны 9 и 6 см, а боковые стороны – 4 и 5 см.
Решение
Т.к. у нас есть длины всех сторон, мы можем воспользоваться первой формулой для вычисления требуемого значения:
Кстати, т.к. высота равна одной из боковой сторон трапеции, значит она является прямоугольной.
Задание 2
Площадь трапеции равна 26 см2. Найдите ее высоту, если основания равны 10 и 3 см.
Решение
В данном случае можно применить последнюю из рассмотренных формул:
Высота трапеции
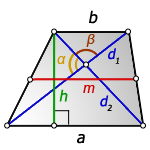
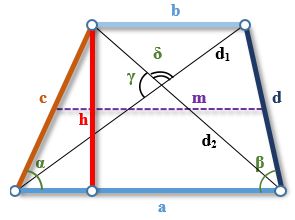
на рисунке обозначены:
a — большее основание трапеции
b — меньшее основание
c,d — боковые стороны трапеции
m — средняя линия трапеции
h — высота трапеции
d1, d2 — диагонали трапеции
α, β — углы между основанием и боковыми сторонами
γ, δ — углы между диагоналями трапеции
Формулы нахождения высоты трапеции
Высоту трапеции можно найти через длины ее сторон, диагоналей, углы между боковыми сторонами и основанием и углы между диагоналями. Также ее можно вычислить через площадь и среднюю линию трапеции:
Высота трапеции равна произведению длины боковой стороны на синус угла между этой стороной и большим основанием трапеции. (Формулы 2 и 3)
Высоту трапеции можно найти как произведение длин диагоналей и синуса угла между ними, деленное на сумму длин оснований трапеции. (Формулы 4 и 5)
Высота трапеции равна произведению длин диагоналей и синуса угла между ними, деленными на удвоенную среднюю линию трапеции (Формулы 5 и 6)
Высоту трапеции можно вычислить как площадь такой трапеции деленную на длину ее средней линии (Формула 
0
Площадь трапеции |
Описание курса
| Трапеция (задачи про основания)