Как найти высоту теплицы огэ 2022

В 2022 учебном году выпускники 9 классов будут сдавать ОГЭ по обновлённым заданиям. Представляем вам вариант тренировочной работы по математике в формате ОГЭ от СтатГрада. Обычно статградовские задания, используемые на пробных тестированиях в школах, максимально приближены к реальным экзаменационным вариантам. Рассказываем, как работать с новыми заданиями про теплицу.

Хотите БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ОГЭ по математике 2023 года — приходите на пробное занятие в Lancman School. Решите продолжить готовиться к ОГЭ вместе с нами весь год — дадим скидку после бесплатного пробного занятия.

Любой вопрос смело пишите сюда. Мы 13 лет готовим к ОГЭ на высокие баллы. Прокачиваем знания даже самых слабых учеников. Гаранитруем получение оценки «5» на ОГЭ. Офисы Курсов ОГЭ Lancman School есть на каждой ветке московского метро.

Если хотите сэкономить, но получить при этом качественную подготовку, записывайтесь на наши онлайн-курсы ОГЭ-2023 по русскому языку, математике, обществознанию и английскому языку.

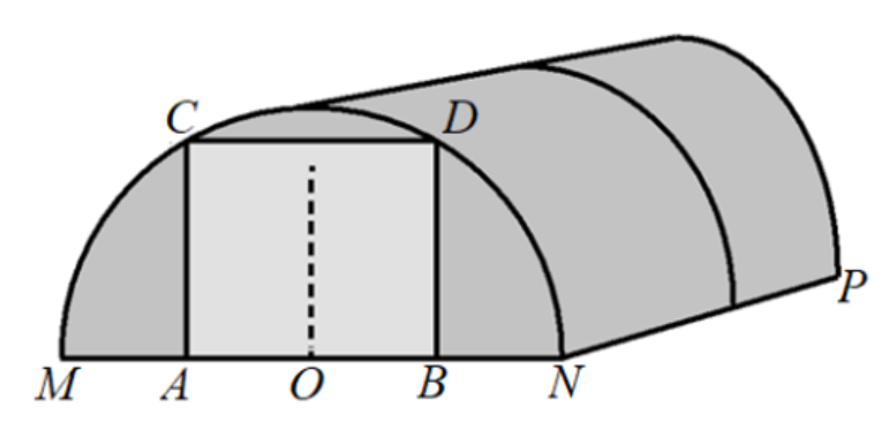
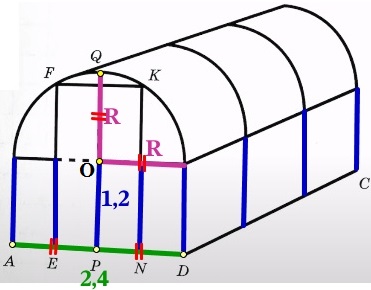
Алексей Юрьевич решил построить на дачном участке теплицу длиной NP = 4,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 5,2 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B — середины отрезков MO и ON соответственно.

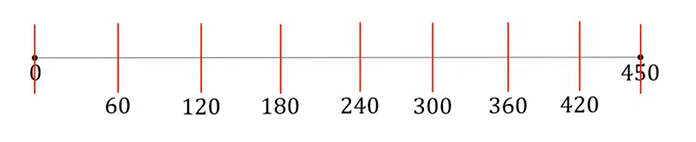
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?

Решение:

Решать подобные задания лучше наглядным способом, то есть нарисовать предварительно дугу и делать на ней необходимые пометки.

Ответ: 9.

2. Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.

Решение:

Длину МN необходимо искать, исходя из дуги, используя формулу длины окружности. Поскольку MN — это полуокружность, то ее длина равна πR.

πR=5,2

3,14R=5,2

R=5,2/3,14

MN=2 × 520/314=520/157

MN=3,31

Ответ: 3,3

3. Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.

Решение:

Площадь участка внутри теплицы представляет собой прямоугольник, и его площадь равна MN × NP.

S=520/157 × 4,5= 2340/157=14,9… При округлению получаем 15.

Можно взять ответ в 3,3 из предыдущего задания для решения.

S=3,3 × 4,5=14,85. При округлении тоже получаем 15.

Ответ: 15.

4. Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.

Решение:

Для начала необходимо посчитать площадь крыши теплицы. Она представляет собой прямоугольник со сторонами, равными 4,5 и 5,2.

S крыши=5,2 × 4,5=23,4

Остаётся посчитать площадь двух полуокружностей (перед и задняя часть теплицы). Вместе это одна окружность — значит, можно не считать площадь 2 раза.

S стенок=3,14 × (260/157)в квадрате=314/100 × 260/157 × 260/157=1352/157

К данной площади необходимо добавить 10%, поскольку плёнки надо купить с запасом. Прибавляем по 10% к уже имеющимся цифрам.

S крыши=25,74

S стенок=9,47…

Складываем и округляем. Получаем примерно 35 метров плёнки.

Ответ: 35.

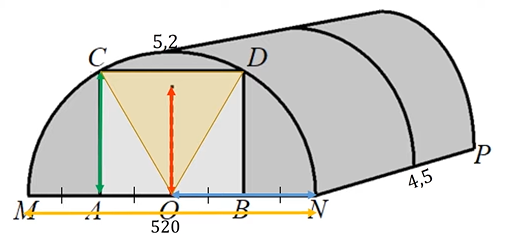
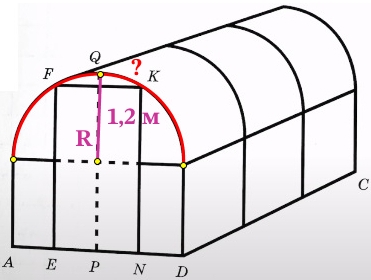
5. Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.

Решение:

Задача геометрическая: нам надо представить, что перед нами равносторонний треугольник.

Итак, перед нами равносторонний треугольник СOD. Найдя его высоту, мы найдём высоту входа в теплицу. Будем использовать формулу высоты равностороннего треугольника. Сторона треугольника COD равна радиусу окружности, которую мы уже знаем (260/157).

h=1,40… Округляем до 1,4.

Ответ: 1,4.

Ваш ребёнок — школьник 1-11 класса? Вы учитель? Отлично! Мы пишем для вас. Узнавайте от нас первыми новости образования, актуальную информацию об экзаменах и просто полезные советы. Кнопка подписки прямо под постом!

Фото: pixabay.com

Источник

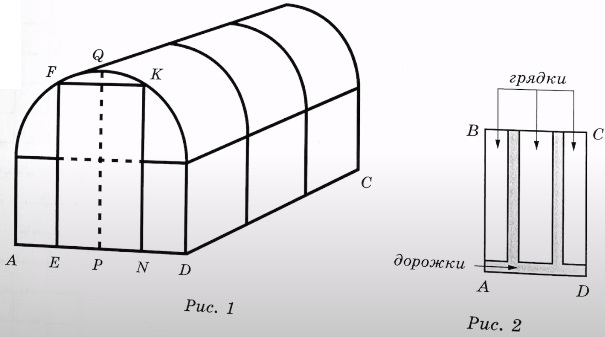
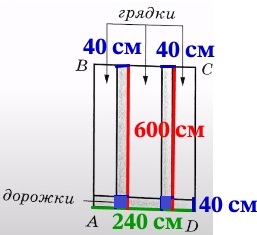
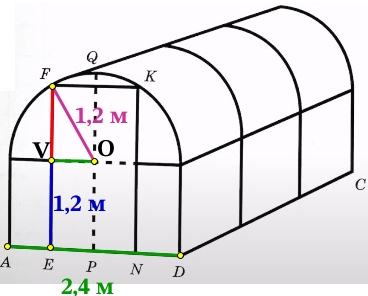
Юрий Борисович начал строить на дачном участке теплицу (рис. 1). Для этого он сделал прямоугольный фундамент длиной 6 м (DC на рис. 2) и шириной 2,4 м (AD на рис. 2). Нижний ярус теплицы имеет форму прямоугольного параллелепипеда, собран из металлического профиля и по длине для прочности укреплён металлическими стойками. Высота нижнего яруса теплицы в два раза меньше её ширины. Для верхнего яруса теплицы Юрий Борисович заказал металлические дуги в форме полуокружностей, которые крепятся к стойкам нижнего яруса. Отдельно требуется купить материал для обтяжки поверхности теплицы. В передней стенке планируется вход, показанный на рис.1 прямоугольником EFKN, где точки E, P и N делят отрезок AD на равные части. Внутри теплицы Юрий Борисович планирует сделать три грядки: одну широкую центральную и две одинаковые узкие по краям, как показано на рис. 2. Между грядками и при входе в теплицу будут дорожки шириной 40 см, для которых надо купить тротуарную плитку размером 20×20 см.

Источник: ОГЭ Ященко 2023 (36 вар)

Задание 1

Найдите высоту теплицы PQ в метрах.

Решение:

Высоту теплицы PQ можно найти следующим образом:

PQ = PO + OQ

РО – это высота нижнего яруса теплицы, который в два раза меньше её ширины AD:

PO = AD/2 = 2,4/2 = 1,2 м

OQ – это радиус полуокружности верхнего яруса теплицы, равный половине ширины теплицы AD (т.к. E, P и N делят отрезок AD на равные части):

R = OQ = PD = AD/2 = 2,4/2 = 1,2 м

Найдём высоту теплицы PQ:

PQ = PO + OQ = 1,2 + 1,2 = 2,4 м

Ответ: 2,4.

Задание 2

Сколько нужно купить упаковок плитки для дорожек, если в каждой упаковке 6 штук?

Решение:

По условию ширина грядок равна 40 см. Длина нижней дорожки, равна ширине теплицы AD = 2,4 м = 240 см. Длины двух других дорожек равны длине теплицы СВ = 6 м = 600 см:

Найдём общую площадь всех трёх грядок:

40·240 + 40·600 + 40·600 = 40·(240 + 600 + 600) = 40·1440 = 57600 см²

Дорожки пересекаются, площадь двух квадратов посчитали дважды, вычтем их:

57600 – 40·40 – 40·40 = 54400 см²

Площадь одной тротуарной плитки равна 20х20 см:

20·20 = 400 см²

Найдём сколько нужно купить:

54400/400 = 136 плиток

В одной упаковке 6 плиток, значит надо купить:

136/6 ≈ 22,6..

Такое количество упаковок нам не продадут, значит надо брать минимум 23 упаковки.

Ответ: 23.

Задание 3

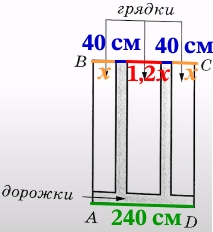
Найдите ширину центральной грядки, если она в 1,2 раза больше ширины узкой грядки. Ответ дайте в сантиметрах.

Решение:

Пусть ширина каждой из узких грядок равна х, тогда ширина центральной грядки 1,2х. Зная все расстояния, составим уравнение и найдём х:

х + 40 + 1,2х + 40 + х = 240
3,2х + 80 = 240
3,2х = 240 – 80
3,2х = 160
х = 160/3,2 = 50 см

Найдём ширину центральной грядки:

1,2х = 1,2·50 = 60 см

Ответ: 60.

Задание 4

Найдите длину металлической дуги для верхнего яруса теплицы. Ответ дайте в метрах, округлив его в большую сторону с точностью до десятых.

Решение:

Длина металлической дуги, это половина длины окружности с радиусом равным 1,2 м. Найдём по формуле длину окружности:

С = 2πR = 2·3,14·1,2

Длина дуги в два раза меньше, округлим в большую сторону до десятых:

frac{С}{2}=frac{2·3,14·1,2}{2}=3,14·1,2=3,768approx 3,8:м

Ответ: 3,8.

Задание 5

Найдите высоту EF входа в теплицу в сантиметрах с точностью до целого.

Решение:

Высоту EF можно найти следующим образом:

EF = EV + VF

EV – это высота нижнего яруса теплицы он равен 1,2 м = 120 см.
Рассмотрим ΔFVO, он прямоугольный, в нём FO = 1,2 м = 120 см, как радиус дуги. VO = EP, как параллельные стороны прямоугольника, и равен 2,4/4 = 0,6 м = 60 см.
В прямоугольном ΔFVO, по теореме Пифагора, найдём VF:

FO² = VF² + VO²
120² = VF² + 60²
120² – 60²= VF²
10800 = VF²
VF = √10800

Найдём высоту EF, в сантиметрах с точностью до целого:

EF = EV + VE = 120 + sqrt{10800} = 120 + sqrt{3cdot 4cdot 9cdot 100}=120+sqrt{3cdot 2^{2}cdot 3^{2}cdot 10^{2}}=120+2cdot 3cdot 10cdot sqrt{3}=120+60cdot sqrt{3}approx 120+60cdot 1,73 approx 120+103,8approx 223,8approx 224: см

По ответам сборника, будет верный любой ответ в диапазоне 222 – 225 см.

Ответ: 224.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.5 / 5. Количество оценок: 352

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

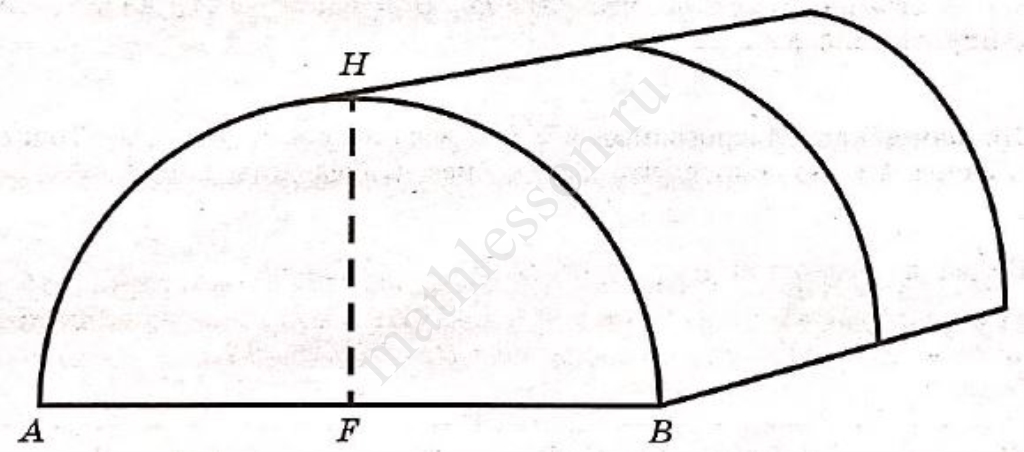
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.

Отдельно требуется купить плёнку для передней и задней стенок теплицы. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 х 20 см. Высота теплицы показана на рисунке отрезком HF.

1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 70 см?

2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 12 штук?

3. Найдите высоту теплицы. Ответ дайте в метрах с точностью до десятых.

4. Найдите площадь участка, отведённого под теплицу. Ответ дайте в квадратных метрах. Результат округлите до целых.

5. Сколько квадратных метров плёнки необходимо купить для передней и задней стенок, если с учётом крепежа её нужно брать с запасом 10 % ? Ответ округлите до десятых.

Источник

Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником BCC₁B₁, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.

Задание 1.

Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?

Задание 2.

Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?

Задание 3.

Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.

Задание 4.

Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.

Задание 5.

Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.

Рассмотрим первые пять задач Варианта 16 из ОГЭ. Математика: типовые экзаменационные варианты:36 вариантов /под ред . И.В. Ященко на нахождение неизвестных величин теплицы.

Сергей Петрович решил построить на дачном участке теплицу длиной 6 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.

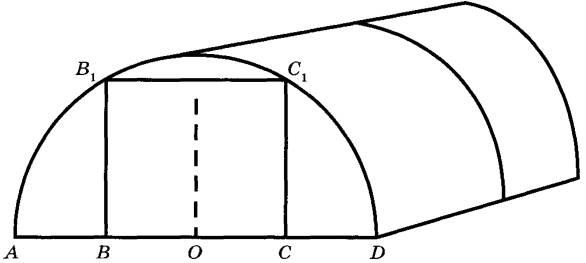
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником 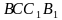, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 50 см, для которых необходимо купить тротуарную плитку размером 25 см х 25 см.

Задание 1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 80 см?

Решение.

Длина теплицы 6 м = 600 см. Разделим эту длину на 80 см и округлим результат до ближайшего наибольшего целого, получим:

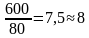
то есть, нужно заказать 8 дуг + 1 первая дуга = 9 дуг.

Ответ: 9.

Задание 2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 10 штук?

Решение.

В теплице 3 грядки, между которыми будут две дорожки. Длина каждой дорожки равна длине теплицы – 600 см, а ширина – 50 см.

Площадь одной дорожки 600∙50 = 30 000 ,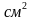

тогда площадь двух дорожек 2∙30 000 = 60 000 .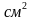

Тротуарная плитка имеет размеры 25х25 см площадь одной плитки 625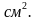 Найдем сколько плиток необходимо для дорожек

площадь двух дорожек : площадь одной плитки

60 000:625 = 96 плиток

Так как плитки продаются в упаковках по 10 штук, то необходимо купить

упаковок

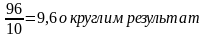
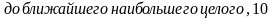
Ответ: 10.

Задание 3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.

Решение.

Ширина теплицы определяется диаметром полуокружности длиной 5 метров. Для вычисления радиуса такой полуокружности можно воспользоваться формулой длины окружности L=2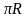 . Нам дана длина полуокружности =5м, следовательно

полная длина окружности будет 10м. Подставим

2*3,14R=10

R=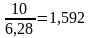 ширина теплицы равна диаметру , поэтому 2*1,592=3,184.

Ответ дать в метрах с точностью до десятых 3,2 м.

Ответ: 3,2.

Задание 4. Найдите ширину узкой грядки, если ширина центральной грядки относится к ширине узкой грядки как 5:3. Ответ дайте в сантиметрах с точностью до десятков.

Решение.

Условно представим теплицу с грядками: две по краям с шириной 3x см и одна центральная с шириной в 5х см. Между ними дорожки шириной 50 см.

Учитывая, что вся ширина теплицы примерно 3,2 м = 320 см, получаем уравнение:

3х+50+5х+50+3х=320,

11х=320-50-50,

Х=220/11

Х=20. Найдите ширину узкой грядки 3х=3*20=60 см.

Ответ: 60.

Задание 5. Сколько квадратных метров пленки необходимо купить дл передней и задней стенок, если с учетом крепежа ее нужно брать с запасом 15% ? Ответ округлите до десятых.

Решение. Ширина теплицы 3,2 м , а радиус 1,6 м

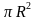
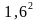
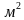
Так как передние и задние части стенок теплицы являются полуокружностями ,то вместе они образуют круг. Площадь круга S= = 3,14* = 8,0384

С учетом крепежа ее нужно брать с запасом 15%

8,0384+0,15*8,0384=9,24416 Ответ округлите до десятых 9,2

Ответ: 9,2

Полное условие в текстовом виде на странице: https://mat-ege.ru/uncategorized/razbor-zadanij-1-5-o-stroitelstve-tepliczy-novyj-format-oge-2020/

Мы в ВК: https://vk.com/onlinemath

Алексей Юрьевич решил построить на дачном участке теплицу длиной NP = 6,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 6,1 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B — середины отрезков MO и ON соответственно.

1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 75 см?

2. Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.

3. Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.

5. Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.

Помощь сайту/каналу: https://mat-ege.ru/pomoshh-sajtu-mat-ege-ru/

Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.

Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?

Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.

Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.

Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.

Спрятать решение

Решение.

Треугольник COD — равносторонний. Высота треугольника COD является высотой входа. Воспользуемся формулой высоты равностороннего треугольника: где a — это сторона треугольника. Таким образом, высота равна:

Ответ: 1,4.

Готовая рабочая тетрадь ОГЭ 2022 по математике 9 класс на задачи с ответами №1-5 про зонты, теплицы, план местности, лист бумаги, шины для подготовки, с подсказками как решать данные задания.

Скачать рабочую тетрадь

Рабочая тетрадь ОГЭ 2022 по математике задачи №1-5

Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 м2. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать пополам таким же образом, получается два листа формата А2.

И так далее. Отношение длины большей стороны к длине меньшей стороны для листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта и при изменении формата листа. В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А3, А5 и А6.

1)Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

2)Сколько листов формата А6 получится из одного листа формата А2?

3)Найдите длину листа бумаги формата А1. Ответ дайте в миллиметрах с округлением до ближайщего целого числа, кратного 10.

4)Найдите ширину листа бумаги формата А1. Ответ дайте в миллиметрах с округлением до ближайшего целого числа, кратного 10.

5)Найдите отношение длины большей стороны листа формата А1 к меньшей. Ответ округлите до десятых.

6)Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.

7)Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 15 пунктов, на листе формата А5? Размер шрифта округлите до целого.

8)Бумагу формата А3 упаковали в пачки по 120 листов. Найдите массу пачки, если масса бумаги площади 1 м2 равна 96 г. Ответ дайте в граммах.

В передней стенке планируется вход, показанный на рисунке прямоугольником BCC1B1, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.

1)Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?

2)Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?

3)Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.

4)Найдите ширину входа в теплицу. Ответ дайте в метрах с точностью до десятых.

5)Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.

6)Найдите высоту входа в теплицу. Ответ дайте в сантиметрах с точностью до десятых.

7)Сколько процентов составляет площадь, отведённая под грядки, от площади всего участка, отведённого под теплицу? Ответ округлите до целых.

Другие тренировочные варианты ОГЭ 2022 по математике 9 класс

Источник

ЗАДАНИЕ «ТЕПЛИЦЫ»

1. Какое
наименьшее количество дуг нужно заказать, чтобы расстояние между соседними
дугами было не более 70 см?

1) Длина теплицы 6 м, переведем м в см
2) Разделим длину теплицы на расстояние между соседними дугами
3) Так как количество дуг не может быть дробным числом, округляем до целого (в большую сторону)
4) НО, при делении не учитывается 1 дуга, от которой идет расчет. Поэтому необходимо к результату прибавить 1 дугу

Ответ: 10

2. Сколько
упаковок притки необходимо купить для дорожек между грядками, если она
продается в упаковках по 8 штук?

1) Найдем площадь одной дорожки между грядками по формуле , при этом длина дорожки равна длине теплицы (6м или 600см), а ширина указана в тексте (60 см)
2) Таких дорожек у нас 2, поэтому умножим площадь одной дорожки на 2
3) Найдем площадь одной плитки по формуле , размеры плитки указаны в тексте (20см20см)
4) Найдем площадь одной упаковки, умножив площадь одной плитки на количество плиток в упаковке
5) Найдем количество упаковок по формуле
6) Так как количество упаковок не может быть дробным числом, округляем до целого (в большую сторону)

Ответ: 3

3. Найдите
ширину входа в теплицу. Ответ дайте в метрах с точностью до десятых.

Работаем с окружностью, диаметр которой AD, ширина входа в теплицу BC это половина отрезка AD, то есть радиус окружности
1) Найдем длину дуги окружности (см. текст: … Сергей Петрович заказал… длиной 5 м каждая…). Форма дуги – полуокружность. Чтобы найти длину дуги, нужно значение полуокружности умножить на 2
2) Найдем радиус окружности из формулы длины дуги окружности , l из прошлого действия =10
3) Округлим до десятых

Ответ: 1,6

4. Найдите ширину центральной
грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в
сантиметрах с точностью до десятков.

Для наглядности изобразим грядки на рисунке, линиями отделены грядки и дорожки в следующей последовательности: грядка – дорожка — центральная грядка – дорожка – грядка.
1) Обозначим узкую грядку за
2) Так как центральная грядка в 2 раза больше узкой, то она будет равна 2x
3) Дорожки между грядками равны по 60 см
4) Вся ширина теплицы равна двум радиусам, умножаем радиус 160см на 2
5) Составляем уравнение
6) Так как за x обозначили ширину узкой грядки, а за 2x широкой, то умножим x на 2

Ответ: 100

5. Внимание!
Это задание может иметь несколько вариантов

5.1.
Сколько процентов составляет площадь,
отведенная под грядки от площади всего участки, отведенного под теплицу? Ответ
округлите до целых.

1) Найдем площадь грядок (2 узкие и 1 центральная: найти площадь каждой по формуле и сложить). Длина теплицы 600см (в тексте), ширину узкой и центральной грядки берем из предыдущей задачи
2) Найдем площадь, отведенную под теплицу по формуле . Длина теплицы 600см (в тексте), ширину теплицы рассчитывали ранее (320см)
3) Найдем сколько % составляет площадь, отведенная под грядки от площади всего участки, отведенного под теплицу
4) Округляем ответ до целых

Ответ: 63

5.2.
Сколько квадратных метров пленки необходимо
купить для передней и задней стенок, если с учетом крепежа ее нужно брать с
запасом 15%. Ответ округлите до десятых

1) Найдем площадь круга (так как передняя и задняя часть теплицы вместе образуют круг) по формуле , радиус берем из предыдущих задач
2) Так как площадь круга это 100%, а с учетом крепежа необходимо брать на 15% больше, то получаем, что необходимо 115% от площади круга. 115% переводим в десятичную дробь 1,15 и умножаем на площадь круга
3) Округляем до десятых

Ответ: 9,2

5.3.
Найдите высоту
входа в теплицу. Ответ дайте в сантиметрах

1) Высота входа в теплицу (пунктирная линия) равна отрезку CC₁
2) Проведем отрезок ОС₁ (радиус окружности, берем из номеров выше)
3) Отрезок ОС равен четвертой части отрезка AD (диаметр, берем из предыдущих номеров)
4) По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов) ищем неизвестный катет
5) Так как корень из 19200 не имеет целого числа, то выделяем часть из под корня
6) Определяем приблизительное значение
7) Вычисляем