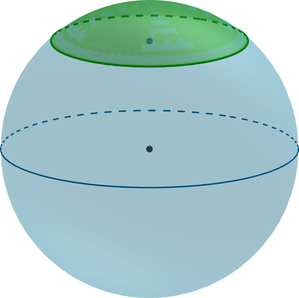
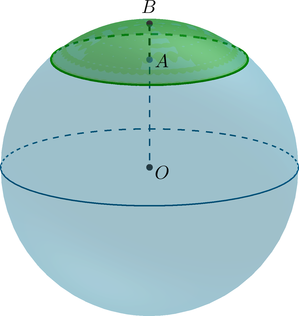
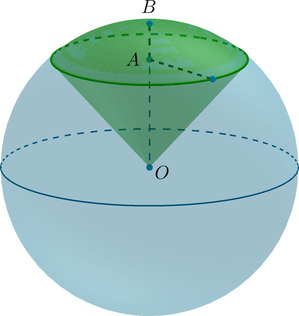
Как найти высоту шарового сектора - AvtoShod.ru - решение различных проблем

({color{red}{{small{textbf{Факт 1. Про шаровой сегмент}}}}})
(bullet) Шаровой сегмент – шасть шара, отсекаемая от него плоскостью ((alpha)).

(bullet) Если (O) – центр шара, (OB=R) – радиус шара, перпендикулярный плоскости (alpha), (A) – центр круга (основания шарового сегмента), а также точка пересечения радиуса (OB) c этим кругом, то
(H=AB) – высота шарового сегмента.
(bullet) Площадь сферического сегмента (часть сферы, отсекаемая от нее плоскостью (alpha)) вычисляется по формуле [S=2pi cdot RH] (bullet) Объем шарового сегмента вычисляется по формуле [V=pi H^2cdot left(R-frac13Hright)]

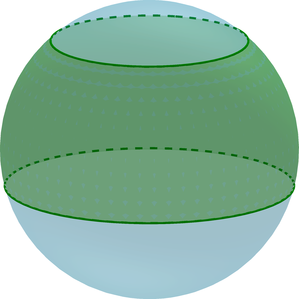
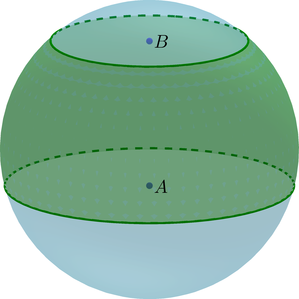
({color{red}{{small{textbf{Факт 2. Про шаровой слой}}}}})
(bullet) Шаровой слой – часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.

(bullet) Основания шарового слоя – это сечения шара плоскостями.
(bullet) Высота (H=AB) шарового слоя – это расстояние между основаниями.
(bullet) Площадь сферической части шарового слоя равна [S=2pi RH] где (R) – радиус шара.
(bullet) Объем шарового слоя равен разности объемов двух шаровых сегментов: [V=V_{A}-V_{B}]

({color{red}{{small{textbf{Факт 3. Про шаровой сектор}}}}})
(bullet) Шаровой сектор – часть шара, ограниченная сферической частью шарового сегмента и боковой поверхностью конуса, имеющего то же основание, что и шаровой сегмент.

(bullet) Если (H=AB), то объем шарового сектора равен [V=dfrac23pi R^2cdot H]

Источник

Как найти объем шарового сегмента?

Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара. Формула объема шарового сектора: V = (2/3)*πR²*h, где h — высота сегмента.

Что такое шаровой сегмент?

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Рисуется большой круг. Круг с центром A — основание шарового сегмента.

Как вычислить объем шара формула?

Формула для вычисления объема шара Объем шара равен четырем третим от его радиуса в кубе помноженого на число пи. где V — объем шара, R — радиус шара, π = 3.

Как найти высоту сегмента шара?

S=πR(2h+r), где h − высота соответствующего шарового сегмента, r − радиус основания шарового сегмента (или конуса), R − радиус шара.

Как найти хорду в окружности?

Формула длины хорды окружности

α = градус
α = радиан
α = x / радиан

Как найти сегмент круга?

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой. P=s+a, где s − длина дуги, a − длина хорды.

Как вычислить площадь сегмента круга?

Площадь сегмента круга

α = градус
α = радиан
α = x / радиан

Как вычислить окружность круга?

Диаметр круга рассчитывается по следующим формулам:

Если нам известна длина: Формула для расчета диаметра круга через его длину: D=P/π
Если нам известна площадь: Формула для расчета диаметр круга через площадь: D=2√S/π
Если нам известен диаметр: Формула для расчета диаметр круга через радиус: D=2R.

Что такое круговой сегмент как можно вычислить его площадь?

Можно воспользоваться приближенной формулой вычисления площади кругового сегмента: S=2/3*(a*h), где a – основание треугольника или длина хорды, h – высота сегмента, которая является результатом разности между радиусом круга и высотой равнобедренного треугольника. … Как правило, за основу берется треугольник.

Как найти площадь сегмента формула?

Площадь сегмента можно найти как разность площадей сектора круга и этого равнобедренного треугольника.

Что такое круговой сегмент?

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

Что такое сегмент в математике?

Сегмент — (от лат. segmentum отрезок, полоса, от seco режу, рассекаю) часть чего либо. В математике Сегмент, или отрезок множество точек прямой, включающее свои концы.

Что такое сегмент в биологии?

Сегмент (биология) — части тела, похожие по строению и расположенные последовательно вдоль продольной оси тела.

Что такое сегмент по анатомии?

segmentum — «отрезок») — анатомический комплекс, состоящий из двух смежных позвонков с соответствующими суставами и мышечно-связочным аппаратом на этом уровне, и одного межпозвонкового диска между этими позвонками. травматологии, мануальной терапии, рентгенологии и др. специальностях медицины.

Что означает слово сегмент?

Сегмент, или отрезок — множество точек прямой, включающее свои концы. Сегмент (геометрия) — плоская фигура, заключённая между кривой и её хордой. Сегмент (стереометрия) — часть тела, ограниченная плоскостью и отсекаемой ею частью поверхности. Как частный случай: шаровой сегмент.

Что такое сегментация целевой аудитории?

Сегментирование целевой аудитории – это разделение аудитории на группы, где они объединены по признаку схожих потребностей (запросов).

Что такое сегмент в бизнесе?

Область рынка, в которой компания имеет возможность занять лидирующие позиции. Бизнес—сегмент — область деятельности, направление специализации компании, в котором она получает и наращивает конкурентные преимущества.

Что такое сектор и сегмент?

Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами. Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.

Что называется сектором?

Сектор круга — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Что такое сектор в информатике?

Се́ктор диска — минимальная адресуемая единица хранения информации на дисковых запоминающих устройствах (НЖМД, дискета, CD). Является частью дорожки диска. Первоначально у большинства устройств размер сектора составляет 512 байт (например, у жестких и гибких дисков), либо 2048 байт (например, у оптических дисков).

Что такое кластер на компьютере?

Кластер (англ. cluster) — в некоторых типах файловых систем — логическая единица хранения данных в таблице размещения файлов, объединяющая группу секторов. … Как правило, это наименьшее место на диске, которое может быть выделено для хранения файла.

Что такое сектор дорожка и кластер магнитного диска?

Сектор диска — минимальная адресуемая единица хранения информации на дисковых запоминающих устройствах (НЖМД, дискета, CD). Является частью дорожки диска. В случае FAT16 для диска объемом 512 Мб кластер будет составлять 8 Кб, до 1 Гб — 16 Кб, до 2 Гб — 32 Кб и так далее. …

Что такое кластер по литературе?

Кластер — это графическая форма организации информации, когда выделяются основные смысловые единицы, которые фиксируются в виде схемы с обозначением всех связей между ними. Он представляет собой изображение, способствующее систематизации и обобщению учебного материала.

Что такое цилиндр на жестком диске?

Цили́ндр у дискового накопителя — совокупность всех дорожек в заданном положении привода. В каждой позиции привода жёсткого диска каждая из головок может считывать свою дорожку (участок поверхности пластины в виде кольца).

Что такое дисковый накопитель?

Накопи́тель на жёстких магни́тных ди́сках, или НЖМД (англ. hard (magnetic) disk drive, HDD, HMDD), жёсткий диск, разг. винчестер — запоминающее устройство (устройство хранения информации, накопитель) произвольного доступа, основанное на принципе магнитной записи.

Сколько секторов в одной дорожке в адресации CHS?

Затем контроллеры стали сообщать, будто в дорожке 63 сектора, а на одной поверхности диска 255 дорожек (максимально допустимые значения), число же головок подбирается сообразно объёму.

Как определяется физический адрес сектора?

Информация на магнитных дисках размещается и передается блоками, которые называются секторами. … Физический адрес сектора на диске определяется триадой [c-h-s], где c — номер цилиндра (cylinder), h — номер рабочей поверхности диска (магнитной головки, head), s — номер сектора на дорожке (sector).

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить объем сегмента шара, а также разберем пример решения задачи для закрепления теоретического материала.

Определение сегмента шара
Формулы для нахождения объема шарового сегмента
- Через радиус шара и высоту сегмента
- Через радиус основания сегмента и его высоту
Пример задачи

Определение сегмента шара

Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.

R – радиус шара;
r – радиус основания сегмента;
h – высота сегмента; это длина перпендикуляра от центра его основания (точка O₂) до точки на поверхности шара.

Формулы для нахождения объема шарового сегмента

Пояснения:

В формулах ниже используется радиус шара (R) или радиус основания сегмента (r). Поэтому, если изначально дан их диаметр (d), то чтобы найти требуемый радиус, нужно соответствующий диаметр разделить на два.
Число π округленно равняется до 3,14.

Через радиус шара и высоту сегмента

Чтобы найти объем (V) сегмента шара, необходимо знать радиус шара и высоту сегмента.

Через радиус основания сегмента и его высоту

Вычислить объем (V) шарового сегмента можно, зная его высоту и радиус основания (круга).

Данная формула получена следующим образом:

Радиус шара можно выразить через радиус основания сегмента и его высоту:

Таким образом, заменив R в первой формуле для расчета объема на выражение выше, получаем:

Пример задачи

Найдите объем сегмента шара, если известно, что его высота равняется 4 см, а радиус шара – 9 см.

Решение

В данном случае с учетом известных значений нам подходит первая формула:

Источник

Сферическая поверхность — это геометрическое место точек (т. е. множество всех точек) в пространстве, равноудалённых от одной данной точки, которая называется центром сферической поверхности.

На рисунке все точки равноудалены от точки (C), радиус (CA) соединяет центр с точкой на сфере.

Рис. (1). Сфера.

Все расстояния от центра до любой точки на сфере одинаковы и равны радиусу. Используя формулу расстояния между точками с данными координатами, можно составить уравнение сферы:

AC=x−x02+y−y02+z−z02=R;AC2=x−x02+y−y02+z−z02=R2;

Шар — это тело, ограниченное сферической поверхностью.

Можно получить шар, вращая полукруг (или круг) вокруг диаметра. Все плоские сечения шара — круги. Наибольший круг лежит в сечении, проходящем через центр шара, и называется большим кругом. Его радиус равен радиусу шара.

Любые два больших круга пересекаются по диаметру шара. Этот диаметр является и диаметром пересекающихся больших кругов.

Через две точки сферической поверхности, расположенные на концах одного диаметра, можно провести бесчисленное множество больших кругов.

Например, через полюса Земли можно провести бесконечное число меридианов.

Рис. (2). Глобус.

Всякое сечение шара плоскостью есть круг (или точка, если плоскость касается шара).

При решении заданий удобнее вместо шара чертить один из больших кругов, а плоскость сечения заменить хордой этого круга.

Рис. (3). Шар и его сечение.

Круговое сечение шара делит его на два шаровых сегмента, а сферу — на две сегментные поверхности.

Часть шара, ограниченная двумя параллельными круговыми сечениями и лежащим между ними сферическим поясом (или зоной), называется шаровой зоной.

Радиусы, проведённые от центра шара к точкам сферы, принадлежащим одной сегментной поверхности, или сферическому поясу, образуют шаровой сектор, он может быть ограничен сферическим сегментом, или зоной, и одной или двумя коническими поверхностями.

Высота шаровой или сферической зоны — это расстояние между плоскостями сечений; высота шарового сегмента, или сегментной поверхности, определяется как расстояние от плоскости сечения до параллельной ей плоскости, касательной к этому сегменту. Высоту шарового сектора определяют как высоту соответствующей сегментной поверхности, или сферического пояса.

Рис. (4). Шар, разделённый на сегменты.

OO1

(= d) — расстояние между центром шара и плоскостью сечения;

(OA = R) — радиус шара;

O1A

(= r) — радиус окружности сечения.

В вычислениях используется теорема Пифагора в прямоугольном треугольнике

AOO1

Рис. (5). Шар и секущая плоскость.

Источники:

Рис. 1. Сфера, © ЯКласс.

Рис. 2. Глобус. Указание авторства не требуется, 2021-06-07, бесплатно для коммерческого использования, https://clck.ru/VLuEU.

Рисунки 3-5. Шар и его сечение; шар, разделённый на сегменты, шар и секущая плоскость, © ЯКласс.

Источник

Комментарии преподавателя

Задача 1 (вычисление объёма шарового сектора)

Найти объём шарового сектора, если известен радиус шара – 75 см, и радиус окружности, лежащей в основании соответствующего шарового сегмента – 60 см (рис. 1).

Рис. 1. Иллюстрация к задаче

Дано: r = 60 см; R = 75 см

Найти:

Решение:

1. Введём обозначения:

– радиус основания сегмента

– радиус шара

– высота шарового сегмента

2. Для того чтобы вычислить объём шарового сектора, необходимо знать радиус шара (он нам известен) и высоту сегмента .

Рассмотрим прямоугольный треугольник . В нём OM – радиус шара, – радиус окружности, а можем найти по теореме Пифагора:

см

3. Найдём высоту сегмента H:

см

4. Подставим в формулу объёма шарового сектора известные величины:

Ответ:

Задача 2 (определение объёма шарового сегмента)

Высота шарового сегмента составляет 0,1 диаметра шара. Определить, какую часть объёма шара составляет объём шарового сегмента.

Дано:

Найти:

Решение:

1. Так как высота H шарового сегмента – это диаметра шара, то:

, где R – радиус шарового сегмента

2. Найдём объём шарового сегмента:

3. Найдём отношение объёма сегмента к объёму шара, то есть узнаем, какую часть объёма шара составляет объём шарового сегмента.

Объём сегмента:

Объём шара:

Отношение объёма сегмента к объёму шара:

Ответ: объём шарового сегмента составляет объёма шара.

Задача 3 (определение объёма шарового сегмента)

В шаре проведена плоскость, которая перпендикулярна диаметру и делит диаметр на два отрезка длиной 6 см и 12 см. Найти объёмы частей, на которые делит плоскость шар.

Рис. 2. Иллюстрация к задаче

Дано: см; см

Найти:;

Решение:

На рисунке 2 изображено осевое сечение шара (окружность) и плоскости (DC), AB – диаметр шара.

1. Диаметр шара равен:

см

Следовательно, радиус шара:

см

2. Плоскость разделила шар на два сегмента, найдём объём меньшего с высотой см. Для этого подставим значение высоты сегмента и радиуса шара в формулу объёма шарового сегмента:

3. Объём второго сегмента можно аналогично найти по формуле объёма шарового сегмента или как разность объёма шара и объёма сегмента с высотой см.

Объём шара:

Ответ: ; .

Разветвление: задача 4

В III веке до нашей эры жил великий учёный своих дней – Архимед. Он сделал множество открытий, но, согласно легенде, больше всего он гордился тем, что получил соотношение между объёмом цилиндра и объёмом вписанного в этот цилиндр шара. Согласно этой же легенде, на могиле Архимеда, которая не сохранилась до наших дней, был изображен цилиндр и вписанный в него шар, а также написано соотношение объёмов цилиндра и шара.

В то время это было великое достижение, так как точных формул для нахождения объёмов цилиндра и шара ещё не было.

Найдём это соотношение.

Рис. 3. Иллюстрация к задаче

, где R – радиус цилиндра; r – радиус шара (рис. 3)

, где H – высота цилиндра, так как шар можно вписать только в равносторонний цилиндр.

Объём шара:

Объём цилиндра:

Отношение этих объёмов:

Отношение площадей этих фигур будет таким же. Докажем это. Площадь шара:

Площадь цилиндра

Отношение этих площадей:

Разветвление: задача 5

Диаметр шара, равный 12 см, разделён в отношении 1:3:4. Через точки деления проведены две параллельные плоскости. Найти объём шарового слоя, отсечённого этими плоскостями (рис. 4).