Автор вопроса: Марат Новиков
Опубликовано: 02/04/2023
Как найти высоту в шаре?
У нас есть 18 ответов на вопрос Как найти высоту в шаре? Скорее всего, этого будет достаточно, чтобы вы получили ответ на ваш вопрос.
- Как найти сегмент шара?
- Как найти объем шарового сектора?
- Как найти высоту в шаре? Ответы пользователей
- Как найти высоту в шаре? Видео-ответы
Отвечает Артём Дадашов
Как найти высоту сегмента в шаре? … Есть две основные формулы: h= R-√(R^2-r^2); h= Sсгм/(2pi*R). Здесь R — радиус сферы, r — радиус основания сегмента, Sсгм — …
Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара. Как можно получить шар?
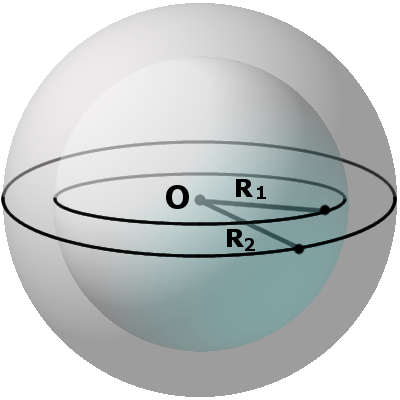
Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Как найти сегмент шара?
Вычисляется по формуле: V = πh²(3R − h)/3. (R — радиус шара, h — высота шарового сегмента, π — число Пи).
Как найти объем шарового сектора?
Формула для расчета объема шарового сектора : V = 2 / 3 * п * R2 * h. п — число п = 3,14. R — радиус шара. h — высота сектора.
Отвечает Анатолий Иванов
V(сегм.) = π H 2 · ( R − H 3 ) , где R — радиус шара, H — высота шарового сегмента.
Отвечает Андрей Вилков
Шар — радиус, объем, площадь, диаметр, окружность … Найти площадь поверхности шарового сегмента, зная радиус и высоту, можно, умножив длину окружности, …
Отвечает Роман Садыков
Через радиус основания сегмента и его высоту
Отвечает Рома Кредо
h – высота сегмента; перпендикуляр от центра основания сегмента до точки на сфере. Формула для нахождения объема сектора шара. Чтобы найти объем шарового …
Отвечает Александр Прямиков
Площадь поверхности шарового сегмента S = 2πRh, в которой R – радиус круга, а h – высота шарового сегмента. Для шарового сегмента также …
Отвечает Ильнар Логинов
дано два шара одинаковой массы один лежит а второй мы сбрасываем на первый (со скоростью Vo) с высоты h, как найти высоту на которую …
Отвечает Даниил Халиков
Основания шарового слоя – это сечения шара плоскостями. ∙ Высота …
7 класс, 17 урок, Медианы, биссектрисы и высоты треугольника
По вопросам размещения рекламы на наших видеороликах — https://api.whatsapp.com/send?phone=77072132054. Решаем …
Как найти высоту трапеции, зная все стороны?
Рассказываю о том, как искать высоту в трапеции, все стороны которой даны. Использую дополнительное построение …
Объем и площадь поверхности шара
Еще все выражение на четыре третьих вот предложили это число на множители чтобы легче найти радиус ну а теперь …
Построение высоты в треугольнике
Created by InShot:https://inshotapp.com/share/youtube.html.
19. Геометрия на ЕГЭ по математике. Высота в прямоугольном треугольнике и ее свойства
7 (495) 984 09 27, +7 (800) 775 06 82 (бесплатный звонок по России) Наш адрес: г. Москва, м. Пушкинская, Страстной …
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить объем сегмента шара, а также разберем пример решения задачи для закрепления теоретического материала.
- Определение сегмента шара
-
Формулы для нахождения объема шарового сегмента
- Через радиус шара и высоту сегмента
- Через радиус основания сегмента и его высоту
- Пример задачи
Определение сегмента шара
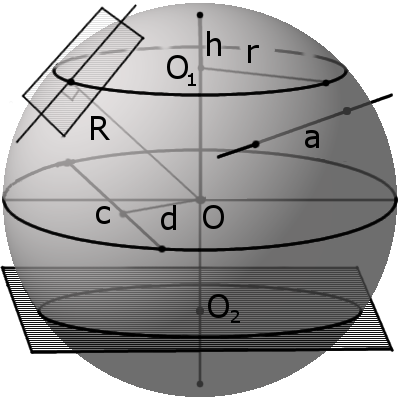
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.
- R – радиус шара;
- r – радиус основания сегмента;
- h – высота сегмента; это длина перпендикуляра от центра его основания (точка O2) до точки на поверхности шара.
Формулы для нахождения объема шарового сегмента
Пояснения:
- В формулах ниже используется радиус шара (R) или радиус основания сегмента (r). Поэтому, если изначально дан их диаметр (d), то чтобы найти требуемый радиус, нужно соответствующий диаметр разделить на два.
- Число π округленно равняется до 3,14.
Через радиус шара и высоту сегмента
Чтобы найти объем (V) сегмента шара, необходимо знать радиус шара и высоту сегмента.
Через радиус основания сегмента и его высоту
Вычислить объем (V) шарового сегмента можно, зная его высоту и радиус основания (круга).
Данная формула получена следующим образом:
Радиус шара можно выразить через радиус основания сегмента и его высоту:
Таким образом, заменив R в первой формуле для расчета объема на выражение выше, получаем:
Пример задачи
Найдите объем сегмента шара, если известно, что его высота равняется 4 см, а радиус шара – 9 см.
Решение
В данном случае с учетом известных значений нам подходит первая формула:
Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Определение.
Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Объём шара:
| V = | 4 | πR3 = | 1 | πD3 |
| 3 | 6 |
Формула. Площадь поверхности сферы через радиус или диаметр:
S = 4πR2 = πD2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:
x2 + y2 + z2 = R2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x0, y0, z0) в декартовой системе координат:
(x — x0)2 + (y — y0)2 + (z — z0)2 = R2
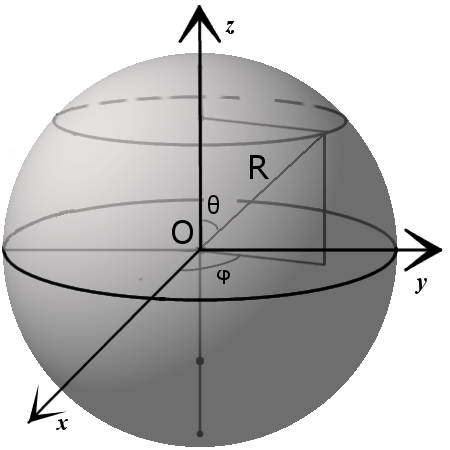
3. Параметрическое уравнение сферы с центром в точке (x0, y0, z0):
x = x0 + R · sin θ · cos φ
y = y0 + R · sin θ · sin φ
z = z0 + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сечение образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d < R
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m < R
Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:
r = √R2 — m2,
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
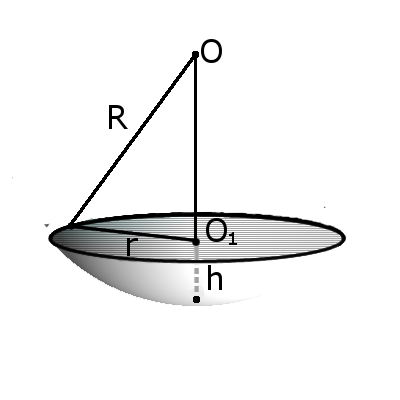
Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2πRh
Формула. Объём сегмента сферы с высотой h через радиус сферы R:
Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.
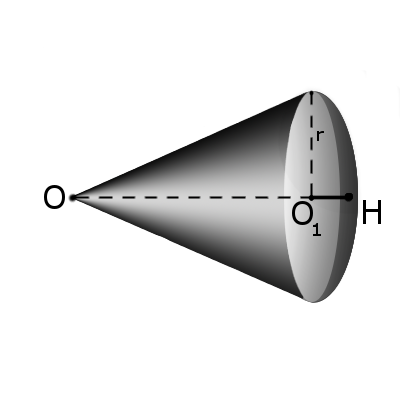
Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Формула. Площадь поверхности сектора S с высотой O1H (h) через радиус шара OH (R):
S = πR(2h + √2hR — h2)
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.
Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.
Рисуется большой круг.
|
|
|
Круг с центром (A) — основание шарового сегмента. (AC = r) — радиус основания шарового сегмента,
(AB = H) — высота шарового сегмента,
(OC = R) — радиус шара.
Площадь сферического сегмента вычисляется по формуле
Объём шарового сегмента вычисляется по формуле
(V(сегм.) =)
πH2
·(R
−H3)
, где (R) — радиус шара, (H) — высота шарового сегмента.
В формулах для сегмента не используется радиус основания сегмента, а используется радиус шара.
Источники:
Рисунки © Якласс
Поскольку шаровой сегмент представляет собой часть сферы, сечение которой находится под прямым углом к оси вращения, следовательно, становится возможным найти объем шарового сегмента, площадь поверхности, периметр сечения сферы и его диаметр, зная радиус и высоту шарового сегмента.
Диаметр шарового сегмента, также как и диаметр сферы, равен удвоенному радиусу тела.
d=2r
Периметр сечения сферы, образующего шаровой сегмент, является длиной окружности с заданным радиусом, и равен удвоенному произведению радиуса на число π.
P=2πr
Чтобы вычислить объем шарового сегмента через радиус и высоту, нужно найти треть произведения числа π и квадрата радиуса на разность утроенного радиуса и высоты.
V=(πh^2 (3R-h))/3
Найти площадь поверхности шарового сегмента, зная радиус и высоту, можно, умножив длину окружности, являющуюся периметром сечения сферы, на высоту шарового сегмента. Так как периметр сечения равен удвоенному произведению числа π и радиуса шарового сегмента, то формула площади поверхности шарового сегмента выглядит следующим образом:
S=2πrh