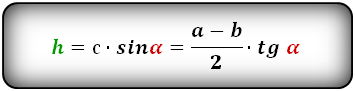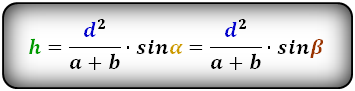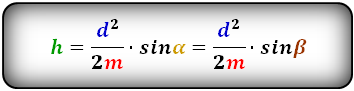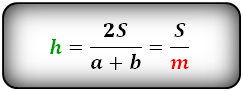В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту равнобедренной (равнобокой) трапеции.
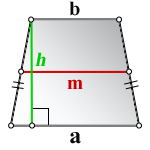
Напомним, высотой трапеции называется перпендикуляр, соединяющий оба ее основания. Также, в равнобедренной трапеции боковые стороны равны.
-
Нахождение высоты равнобедренной трапеции
- Через длины сторон
- Через боковую сторону и прилежащий угол
-
Через основания и прилежащий угол
- Через площадь и основания
- Через диагонали и угол между ними
Нахождение высоты равнобедренной трапеции
Через длины сторон
Зная длины всех сторон равнобедренной трапеции, вычислить ее высоту можно, используя формулу ниже:
Через боковую сторону и прилежащий угол
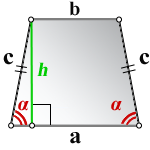
Если известна длина боковой стороны равнобедренной трапеции и угол между ней и основанием фигуры, найти высоту можно следующим образом:
Через основания и прилежащий угол
Вычислить высоту трапеции можно, если известны длины ее оснований и угол при любом из оснований (например, при большем).
Через площадь и основания
Также высоту равнобедренной трапеции удастся найти через ее площадь и длины оснований:
Данная формула может быть представлена в другом виде, если вместо оснований дана средняя линия (m).
m – средняя линия, равняется полусумме оснований, т.е. m = (a+b)/2.
Через диагонали и угол между ними
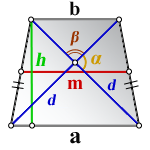
И еще один способ вычислить высоту равнобедренной трапеции, если известны ее диагонали (которые имеют одинаковую длину), угол между ними и основания.
Та же самая формула, но со средней линией (m) вместо суммы оснований:
Примечание: если диагонали равнобедренной трапеции взаимно перпендикулярны, то ее высота равняется половине суммы оснований или, другими словами, средней линии.
1. Формула высоты равнобедренной трапеции через стороны и углы при основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при нижнем основании
h — высота трапеции
Формулы длины высоты, (h ):
2. Формула высоты равнобедренной трапеции через диагонали и углы между ними
d — диагонали трапеции
α , β — углы между диагоналями
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
3. Формула высоты равнобедренной трапеции через площадь
S — площадь трапеции
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 10 октября 2013
-
Обновлено: 13 августа 2021
Что такое трапеция
Определение
Трапеция — это геометрическая фигура, которая состоит из двух параллельных и неравных друг другу отрезков (оснований) и боковых сторон.
Все стороны трапеции могут иметь разную величину. Но если ее боковые стороны равны, значит трапеция равнобедренная.
Определение
Высота трапеции — это перпендикуляр, проведенный из любой точки одного основания фигуры до другого.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
h = Sm
Видео
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 — | ( | (a — b)2 + c2 — d 2 | ) | 2 |
| 2 | 2(a — b) |
5. Формула Герона для трапеции S = a + b √(p — a )(p — b )(p — a — c )(p — a — d ) |a — b | где p = a + b + c + d — полупериметр трапеции.2
Теги
Трапецией принято называть выпуклую четырёхугольную четырехугольник с парой параллельных и двумя не
параллельными сторонами. Отрезки, которые создают параллельные прямы называются «основанием
трапеции», две других стороны играют роль «боковой стороны трапеции». Средняя линия трапеции будет
соединять два центра боковых сторон.
- Высота трапеции через боковую сторону и прилегающий угол
при основании - Высота трапеции через площадь и длины оснований
- Высота трапеции через площадь и среднию линию
- Высота трапеции через основании, диагонали и угол между
диагоналями - Высота трапеции через среднию линию, диагонали и угол между
диагоналями
Как найти высоту при помощи боковой стороны и прилегающего угла при основании
Для вычисления высоты трапеции через боковую сторону и прилегающий угол при основании нужно
воспользоваться нижеприведенной формулой:
h = a · sin α
где h — это искомая высота трапеции, a — известная боковая сторона, sin α — угол
при основании.
Цифр после
запятой:
Результат в:
Пример. Чтобы разобраться с применением формулы, давайте рассмотрим пример. Дана
некая трапеция. Нам известно, что боковая сторона равна 10 сантиметрам, а прилегающих угол
составляет 30 гр. Нам нужно найти высоту данной трапеции. Для решения у нас есть вся нужная
информация и формула выше. Подставляем значения в формулу: h = a · sin, h = 10 · sin 30, h = 10 · 1/2, h = 5 см
Как найти высоту трапецию при помощи длины основания и площади трапеции
Чтобы найти высоту трапеции через известные длины основания и площадь, нужно воспользоваться
формулой:
h = (2S) / (a + b)
где h — это искомая высота трапеции, S — известная площадь фигуры, a и b — длины
обеих оснований.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Нам известно, что в трапеции АВСD основания a и b равны
5 и 10 сантиметров. Площадь фигуры равна 30 квадратных сантиметров. Для решения нужно
воспользоваться формулой. h = (2S) / (a + b), h = (2 х 30) / (5 + 10), h = 60 /15, h = 4 см.
Высота трапеции равна 4 см.
Как найти высоту при помощи диагоналей, углу между диагоналями и средней линией трапеции
Чтобы найти высоту трапеции через среднюю линию, известные диагонали и угол между ними, нужно
прибегнуть к применению выведенной формулы:
h = ((D x d) / (2m)) x sin (α)
где h — это искомая высота трапеции, D и d — известные диагонали, m — средняя
линия, sin(α) — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Дана трапеция с диагоналями 5 и 12 сантиметров.
Известно, что средняя линия фигуры равна 6 см, а угол между диагоналями – 30 градусов. Применив
формулу выше, мы сможем с легкостью найти высоту трапеции. h = ((D x d) / (2m)) x sin (α), h = ((5 x 12) / (2 х 6)) x sin (30), h = (60 /12) x 0.5, h = 2.5 см.
Высота трапеции равна 2.5 см.
Как найти высоту при помощи средней линии и площади трапеции
Чтобы найти высоту трапеции через площадь и среднюю линию воспользуемся выведенной формулой:
h = (2S) / m
где h — это искомая высота трапеции, S — известная площадь фигуры, а m — средняя
линия.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Площадь произвольной трапеции составляет 30 квадратных
сантиметров. Средняя линия фигуры равна 5 см. Нужно найти высоту по формуле. h = (2S) / m, h = (2 х 30) / 5, h = 60 / 5, h = 12 см. 12
см – высота трапеции.
Как найти высоту при помощи известного основания, диагоналей трапеции и угла между диагоналями
Для нахождения высоты трапеции при помощи известного основания, диагонали и углу между диагоналями
используют нижеприведенную формулу:
h = ((Dd) / (a + b)) x sin (α)
где h — это искомая высота трапеции, D и d — известные диагонали, a и b — длины
обеих оснований, sin(α) — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: В трапеции ABCD диагонали равны 10 см каждая. Известно,
что сумма основ фигура равна 20 см. Угол, созданный между диагоналями – 30 градусов. Нужно найти
высоту. Для этого нужно воспользоваться выше предоставленной формулой. h = ((Dd) / (a+b)) x sin (α), h = ((10 х 10) / (20)) x sin (30), h = 5 x sin (30), h = 2.5 см.
Высота трапеции равна 2.5 см
Можно выделить 2 разновидности трапеции:
- Трапеция, в которой одна из боковых сторон лежит под перпендикулярным углом с обеими основами
называется прямоугольной. - Трапеции с равными боковыми сторонами называется равнобедренной.
Высотой трапеции принято называть отрезок, которой показывает самое короткое расстояние между верхним
и нижним основанием фигуры. Существует большое количество математических задач разного уровня
сложности, для решения которых активно применяют высоту. Стоит разобраться со всеми возможными
формулами, которые используются для нахождения высоты трапеции.
Высота трапеции
Содержание:
- Что такое трапеция
-
Как найти высоту трапеции
- Через стороны
- Через среднюю линию и площадь
- Через боковую сторону и угол
- Через диагонали, угол между ними и основания
- Через диагонали, угол и среднюю линию
- Через радиус вписанной окружности
- Примеры вычисления
Что такое трапеция
Определение
Трапеция — это геометрическая фигура, которая состоит из двух параллельных и неравных друг другу отрезков (оснований) и боковых сторон.
Все стороны трапеции могут иметь разную величину. Но если ее боковые стороны равны, значит трапеция равнобедренная.
Определение
Высота трапеции — это перпендикуляр, проведенный из любой точки одного основания фигуры до другого.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как найти высоту трапеции
Через стороны
Если нам известны стороны фигуры, мы можем найти ее высоту по формуле:
(h=sqrt{b^2-(frac{{(a-d)}^2+d^2+c^2}{2cdot(a-b)}})^2)
Где h — высота, a — большее основание, b — меньшее основание, c и d — боковые стороны.
Через среднюю линию и площадь
Если в условии есть данные о величине средней линии и площади, можем использовать формулу:
(h=frac Sm)
Где m — средняя линия трапеции.
Через боковую сторону и угол
Когда нам известна величина одной из боковых сторон и угол между этой стороной и большим основанием, используем формулу:
(h=ccdotsinleft(alpharight))
Где alpha — это угол между стороной c и большим основанием a.
Через диагонали, угол между ними и основания
Если нам известны длины обоих диагоналей трапеции, а также угол между ними, можем найти высоту следующим образом:
(h=frac{d_1d_2}{a+b}cdotsinleft(gammaright))
Где (d_1) и (d_2) — диагонали трапеции, а (gamma) — угол между ними.
Через диагонали, угол и среднюю линию
В том случае, если нам известны сразу длины диагоналей, угол между ними и величина средней линии, мы можем узнать высоту трапеции по формуле:
(h=frac{d_1d_2}{2m}cdotsinleft(gammaright))
Через радиус вписанной окружности
Если в трапецию можно вписать окружность, то ее высота будет равна диаметру этой окружности, то есть d=h. Другими словами, высота фигуры будет равна удвоенному радиусу вписанной в нее окружности:
(h=2r)
Где r — радиус выписанной окружности.
Примеры вычисления
Задача 1
Дана трапеция, в которой известны основания a и b. Они равны 4,5 см и 2,5 см. Также известны ее боковые стороны d и c, равные 2 см и (2sqrt2) см соответственно. Найти высоту.
Решение
Чтобы решить эту задачу, используем формулу (h=sqrt{b^2-(frac{{(a-d)}^2+d^2+c^2}{2cdot(a-b)}})^2.)
Подставляем известные значения:
(h=sqrt{2^2-(frac{{(4,5-2,5)}^2+2^2+{(2sqrt2)}^2}{2cdot(4,5-2,5)}}{)^2=}h=sqrt{4-(frac{4+4-8}4}{)^2=sqrt4=2}) см.
Ответ: h=2 см.
Задача 2
Известно, что основания a и b равнобедренной трапеции равны 3 см и 5 см. Площадь фигуры равна 8 см2. Вычислить высоту.
Решение:
Чтобы найти высоту, нужно знать величину средней линии m. Определим ее следующим образом:
(m=frac{a+b}2=frac{3+5}2=4 см.)
Теперь используем формулу (h=frac Sm) и подставим известные значения:
(h=frac84=2) см.
Ответ: h=2 см.
Задача 3
Мы знаем, что сторона c трапеции равна (sqrt2) см, а угол (alpha) между известной стороной и основанием равен 45 градусов. Найти значение высоты.
Решение:
Используем формулу (h=ccdotsinleft(alpharight)) и подставим значения:
(h=sqrt2cdotsinleft(45^circright)=frac{sqrt2cdotsqrt2}2=frac22=1) см.
Ответ: h=1 см.
Задача 4
Даны диагонали трапеции (d_1) и (d_2), равные 2 см и 3 см, а также угол gamma между ними, который равняется 30 градусов. Основания a и b, длина которых 2 см и 1 см соответственно. Найти h.
Решение:
Для решения задачи использует формулу (h=frac{d_1d_2}{a+b}cdotsinleft(gammaright).)
Подставим значения:
(h=frac{2cdot3}{2+1}cdotsinleft(30^circright)=frac63cdotfrac12=1) см.
Ответ: h=1 см.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так