Как найти высоту правильного октаэдра - AvtoShod.ru

Зная ребро октаэдра, можно найти его высоту, построив прямоугольный треугольник через квадратное основание одной из пирамид, соединив таким образом отрезок, являющийся половиной высоты, с боковым ребром. Через теорему Пифагора, половина высоты будет равна квадратному корню из разности квадратов бокового ребра и половины диагонали квадрата в основании. Приведя в итоге алгебраическими преобразованиями формулу к упрощенному виду, получим, что высота тетраэдра равна боковому ребру, деленному на корень из двух.
h=a/√2

Периметр октаэдра равен сумме всех длин его ребер, а так как ребер у октаэдра 12, то нужно умножить длину одного ребра на двенадцать, чтобы найти периметр.
P=12a

Площадь полной поверхности октаэдра складывается из восьми граней, каждая из которых является равносторонним треугольником. Исходя из этого, площадь октаэдра, зная боковое ребро, равна его квадрату с коэффициентом два корня из трех.
S=2√3 a^2

Чтобы найти объем октаэдра нужно рассчитать объем четырехугольной пирамиды отдельно и умножить его на два, тогда получится, что через боковое ребро объем октаэдра равен ему в кубе, умноженному на корень из двух, деленный на три.
V=(√2 a^3)/3

Поскольку октаэдр является правильным многогранником, в него можно вписать сферу, а также описать сферу около него. Радиусы вписанной и описанной сферы лежат на осях внутри октаэдра, и их можно вычислить по нижеприведенным формулам через боковое ребро.
r=(a√6)/6
R=(a√2)/2

Источник

С помощью данного калькулятора можно найти не только площадь октаэдра, но и другие его величины, такие как высоту, объем, радиус описанной сферы, ребро октаэдра и т. д. Для этого нужно всего лишь заполнить любую ячейку, введя известное значение, и нажать на кнопку “Рассчитать”. Остальные недостающие данные калькулятор рассчитает автоматически. Также в ответах будут даны подробные и понятные формулы вычислений.

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Радиус вписанной сферы (r)

Радиус описанной сферы (R)

Площадь грани октаэдра (Sg)

Округление:

* — обязательно заполнить

Источник

Октаэдр и площадь полной его поверхности: описание, формулы, примеры

Содержание:

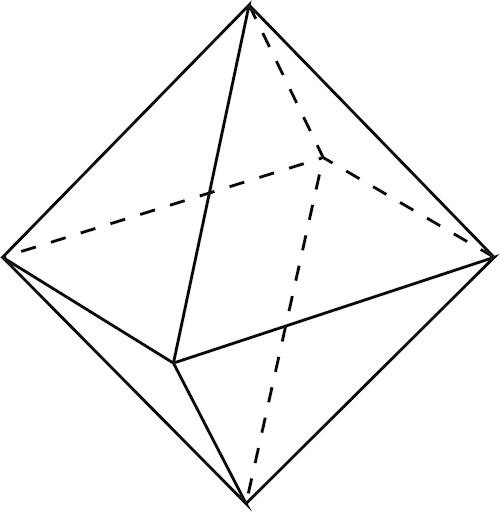
Существует несколько способов определить площадь поверхности октаэдра. Он представляет собой один из пяти правильных многоугольников или так называемых Платоновых тел. Имеет восемь одинаковых граней (поверхностей) в виде равносторонних треугольников, к каждой из его вершин прилагается по четыре грани. Рассмотрим, что собой представляет тело, где встречается в природе, как вычисляется его площадь и объём.

Что такое октаэдр

Свойства октаэдра

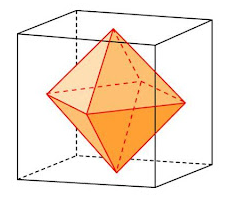
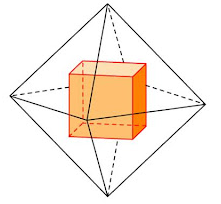
В тело вписывается куб, вершины которого находятся в центрах граней куба.

Симметрия куба и вписанного (описанного) октаэдра совпадают.

Двойственен кубу.

Является полным усечением тетраэдра.

Имеет равные ребра и диагонали.

Состоит из равносторонних треугольников.

Диагонали тела взаимоперпендикулярны, в точке пересечения делятся на равные отрезки.

Октаэдр симметричен, причём 3 оси пролегают через противоположные вершины, 6 – через центры ребер.

Центр симметрии тела расположен в точке пересечения диагоналей.

Ребра равны по длине, поверхности – по площади.

Математические характеристики тела

Как вычислить площадь поверхности октаэдра

Площадь октаэдра равна сумме площадей составляющих его треугольников:

Здесь S_треуг – площадь треугольника.

После подстановки значения получится требуемый результат.

Если известна длина ребра, придётся вычислить площадь треугольников.

Подставляем значение в первое выражение:

Упрощаем: после сокращения дроби на четыре получается формула площади поверхности октаэдра:

2. S = 8 * S_треуг = 2 sqrt <3>a^2.

Существует ещё один способ проведения вычислений. Он менее точный чем предыдущие, однако позволяет обойтись без калькулятора. При приблизительном подсчёте 2 sqrt <3>равняется 3,464 или 3,46.

Здесь a – длина стороны треугольника (равны).

Для примера, имеется фигура октаэдр с длиной стороны 5 см.

S=2sqrt <3>a^2=2*sqrt <3>*5^2=2*sqrt <3>*25=50sqrt <3>approx 86,6 см.

Как вычислить объём правильного октаэдра

Объём показывает размер внутреннего пространства геометрического тела. Объем правильного октаэдра вычисляется, если знаете длину ребра геометрического тела, по формуле:

После проведения приблизительных расчётов frac<sqrt 2> <3>approx 0,47 формула принимает следующий вид :

Рассчитаем двумя методами на примере правильного многоугольника с гранью, равной 5 см:

V= 0,47 * a^3 = 0,47*125 approx 58,93

Значения совпали, во втором случае нужно выполнять гораздо меньше операций. Подходит он только, если не требуется исключительная точность – при округлении до 4-5 знаков после запятой точность снизится.

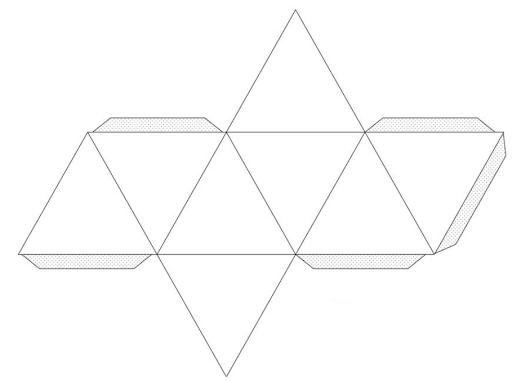
Развёртка

Октаэдр, как большинство гомерических тел, имеет развёртку поверхности – это плоская фигура, полученная путём совмещения поверхности модели с одной плоскостью без пересечения либо наложения граней друг на друга.

Рисунок развёртки октаэдра.

В природе насчитывается 11 разновидностей развёртки октаэдра, позволяющих создать его модель из бумаги или картона. Наиболее распространённая выглядит как восемь одинаковых треугольников. Шесть из них размещено в ряд, к третьему и четвёртому основаниям прилегает ещё по одному, их вершины направлены в противоположные стороны.

Октаэдр.

Октаэдр — один из 5-ти выпуклых правильных многогранников — Платоновых тел.

У октаэдра 8 треугольных граней, 12 рёбер, 6 вершин, к каждой его вершине сходятся 4 ребра.

На примере октаэдра легко проверить формулу Эйлера 6в+8г-12р=2. В каждой из вершин октаэдра сходятся 4 треугольника, т.о., сумма плоских углов у вершины октаэдра равна 240°. Из понятия правильного многогранника делаем вывод, что каждое ребра октаэдра имеет одинаковую длину, а грань — одинаковую площадь.

Обозначим длину ребра октаэдра как а, значит площадь полной поверхности октаэдра (S) и объём октаэдра (V) найдем из таких формул:

Радиус описанной сферы около октаэдра:

Радиус вписанной сферы около октаэдра:

Сумма длин всех ребер равна 24а.

Двугранный угол: α=2ϕ≈109,47°, где .

Свойства октаэдра.

Октаэдр легко вписывается в тетраэдр, при этом 4 из 8-ми граней октаэдра совместятся с 4-мя гранями тетраэдра, каждая из 6-ти вершин октаэдра совместится с центрами 6-ти ребер тетраэдра.

Октаэдр легко вписывается в куб (гексаэдр), при этом каждая из 6-ти вершин октаэдра совместится с центрами 6-ти граней куба.

В октаэдр легко вписать куб, при этом каждая из 8-ми вершин куба будут располагаться в центрах 8-ми граней октаэдра.

У правильного октаэдра есть симметрия O_h, которая совпадает с симметрией куба.

Развёртка октаэдра.

Симметрия октаэдра.

3 из девяти осей симметрии октаэдра проходят сквозь противолежащие

вершины, 6 — квозь середины ребер.

Центр симметрии октаэдра — точка пересечения осей симметрии октаэдра.

3 из девяти плоскостей симметрии тетраэдра проходят сквозь все 4 вершины октаэдра, которые лежат в одной плоскости.

6 плоскостей симметрии проходят через 2 вершины, которые не принадлежат одной грани, и середины противолежащих ребер.

Октаэдр

Древние греки дали многограннику имя по числу граней. «Окто» означает восемь, «хедра» — означает грань (октаэдр – восьмигранник).

Поэтому на вопрос — «что такое октаэдр?», можно дать следующее определение: » Октаэдр это геометрическое тело из восьми граней, каждая их которых — правильный треугольник «.

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .

Октаэдр имеет следующие характеристики:

Тип грани – правильный треугольник;
Число сторон у грани – 3;
Общее число граней – 8;
Число рёбер, примыкающих к вершине – 4;
Общее число вершин – 6;
Общее число рёбер – 12;

Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.

Октаэдр имеет центр симметрии — центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.

Математические характеристики октаэдра

Октаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы октаэдра определяется по формуле:

, где a — длина стороны.

Сфера может быть вписана внутрь октаэдра.

Радиус вписанной сферы октаэдра определяется по формуле:

Площадь поверхности октаэдра

Для наглядности, площадь поверхности октаэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон октаэдра (это площадь правильного треугольника) умноженной на 8. Либо воспользоваться формулой:

Объем октаэдра определяется по следующей формуле:

Октаэдр можно представить в виде двух правильных пирамид с четырехугольным основанием, соединенных друг с другом через это основание.

Вариант развертки

Октаэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка — единая деталь с линиями сгибов.

Древнегреческий философ Платон ассоциировал октаэдр с «земным» элементом воздух, поэтому для построения модели этого правильного многогранника мы выбрали серый цвет.

Заметим, что это не единственный вариант развертки.

Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
— если Вы предполагаете распечатать на цветном принтере — цветная развертка
— если Вы предполагаете использовать для сборки цветной картон — развертка

Классический вариант раскраски предполагает окраску октаэдра четырьмя различными цветами, причем таким образом, что каждая грань имеет свой цвет отличный от соседней и только противоположные не соприкасающиеся друг с другом грани окрашиваются в одинаковые цвета.

Вариант окраски представлен на рисунке. Вы можете скачать развертку с соответствующей раскраской граней.

Видео. Октаэдр из набора «Волшебные грани»

Вы можете изготовить модель октаэдра воспользовавшись деталями для сборки из набора «Волшебные грани».

Сборка многогранника из набора:

Подробная сборка от Алексея Жигулева (youtube-канал PRO)

вращение готового многогранника:

Видео. Вращение правильных многогранников

источники:

http://www.calc.ru/Oktaedr.html

http://mnogogranniki.ru/oktaedr.html

Источник

Чтобы воспользоваться этим простым онлайн-калькулятором и найти ребро октаэдра, необходимо заполнить любой пустующий слот и нажать на кнопку “Рассчитать”. Таким образом можно найти не только ребро октаэдра, но и другие величины, такие как высоту, объем, площадь октаэдра и др. Также в ответе будут даны все формулы расчета в подробном виде, что очень удобно. Сохраните эту шпаргалку по геометрии, чтобы иметь к ней доступ в нужный момент.

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Радиус вписанной сферы (r)

Радиус описанной сферы (R)

Площадь грани октаэдра (Sg)

Округление:

* — обязательно заполнить

Источник

октаэдр

Тип боковых поверхностей	равносторонние треугольники
Количество лиц	8-е
Количество углов	6-е
Количество ребер	12-е
Значок Schläfli	{3.4}
двойной к	Шестигранник (куб)
Сеть тела
Количество разных сетей	11
Количество граней в углу	4-й
Количество углов поверхности	3-й
Октаэдр в формате STL

(Также, особенно австрийский октаэдр [ ɔktaeːdɐ ] (от древнегреческого ὀκτάεδρος oktáedros , немецкий «восьмигранный» ) является одним из пяти Платоновых твердых тел , более точно регулярный полиэдр ( многогранник , многогранник ) с

8 конгруэнтных равносторонние треугольники в боковых поверхностях
12 ребер одинаковой длины и
6 углов, в которых встречаются четыре стороны

Это и равносторонняя четырехсторонняя двойная пирамида с квадратным основанием, которая является правильным поперечным многогранником третьего измерения, и равносторонняя антипризма с равносторонним треугольником в качестве основания .

симметрия

Три квадрата, перпендикулярные друг другу, каждый из которых образует основание двойной пирамиды.

Октаэдр с примерами осей вращения и двух плоскостей симметрии (красной и зеленой) ${ displaystyle C_ {4}, C_ {3}, C_ {2}}$

Из-за своей высокой симметрии — все углы , ребра и поверхности похожи друг на друга — октаэдр является правильным многогранником . Оно имеет:

и является

точка симметрична центру.

Всего группа симметрии октаэдра — группа октаэдра или группа куба — состоит из 48 элементов.

Отношения с другими многогранниками

Октаэдр — это многогранник, двойственный шестиграннику ( кубу ) (рис. 1), и наоборот.

Изображение 2: Два правильных тетраэдра, вписанных в куб, образуют звездный тетраэдр.

Два правильных тетраэдра (см. Рисунок 2: один тетраэдр в красных тонах, другой в зеленых тонах) можно вписать в куб таким образом, чтобы углы были одновременно углами куба, а ребра — диагоналями поверхностей куба. Объединение является звездный тетраэдр

Трехмерное пересечение двух тетраэдров (рис. 3) представляет собой октаэдр с половиной длиной стороны. Если на восьми гранях тетраэдра октаэдра также создать звездный тетраэдр.

Если октаэдр описан правильным тетраэдром (рис. 4), 6 углов октаэдра являются центрами 6 ребер тетраэдра, а 4 из 8 граней октаэдра лежат на боковых гранях одного из двух возможных тетраэдров. Октаэдр получается, когда 4 тетраэдра с одинаковой длиной стороны отрезаны от тетраэдра с двойной длиной ребра.

С помощью октаэдров и куба можно построить множество тел , которые также имеют группу октаэдров в качестве группы симметрии . Так вы, например, получите

усеченный октаэдр с 8 шестиугольников и 6 квадратов
кубооктаэдр с 8 треугольников и 6 квадратов, т.е. с 14 граней , и 12 углов
усеченный куб с 8 треугольников и 6 восьмиугольников

как пересечение октаэдра с кубом (см. архимедовы тела ) и

ромбического додекаэдра с 8 + 6 = 14 углов и 12 пастилок как лица

как выпуклая оболочка соединения октаэдра с кубом .

Формулы

Размеры октаэдра с длиной ребра a
объем	${ displaystyle V = { frac {a ^ {3}} {3}} cdot { sqrt {2}} приблизительно 0 {,} 471 cdot a ^ {3}}$	без твердых углов в углах
Площадь поверхности	${ displaystyle A_ {O} = 2 times a ^ {2} times { sqrt {3}} приблизительно 3 {,} 464 times a ^ {2}}$
Умкугельрадиус	${ displaystyle r_ {u} = h_ {p} = { frac {a} { sqrt {2}}} приблизительно 0 {,} 707 cdot a}$
Радиус краевого шара	${ displaystyle r_ {k} = { frac {a} {2}} = 0 {,} 5 cdot a}$
Inc радиус сферы	${ displaystyle r_ {i} = { frac {a} {6}} cdot { sqrt {6}} приблизительно 0 {,} 408 cdot a}$
Отношение объема к объему шара	${ displaystyle { frac {V} {V_ {UK}}} = { frac {1} { pi}} приблизительно 0 {,} 318}$
Внутренний угол равностороннего треугольника
Угол между соседними гранями	${ displaystyle beta = arccos left (- { frac {1} {3}} right)}$ ${ Displaystyle приблизительно 109 ^ { circ} ; 28 ^ { prime} ; 16 ^ { prime prime}}$
Угол между краем и гранью	${ Displaystyle gamma = 45 ^ { circ}}$
Углы кромки 3D	${ displaystyle delta = 90 ^ { circ}}$
Сплошные углы в углах	${ displaystyle Omega = arccos left ({ frac {17} {81}} right) приблизительно 1 {,} 3594 ; mathrm {sr}}$
Сферичность	${ displaystyle Psi = { sqrt [{3}] { frac { pi} {3 { sqrt {3}}}}} приблизительно 0 {,} 846}$

Расчет правильного октаэдра

объем

Октаэдр в основном состоит из двух собранных пирамид с квадратным основанием и длиной ребра. ${ displaystyle A_ {Gp}}$

Для пирамид и, следовательно, для половины объема октаэдра применяется

${ displaystyle V_ {p} = { frac {1} {3}} cdot A_ {G_ {p}} cdot h_ {p},}$

в нем базовая площадь ( квадрат )

${ displaystyle A_ {G} = a ^ {2},}$

и высота в пирамиде

${ displaystyle h_ {p} = { frac {a} { sqrt {2}}},}$

со вставленными переменными и множителем 2

${ displaystyle { begin {align} V & = 2 cdot left ({ frac {1} {3}} cdot a ^ {2} cdot { frac {a} { sqrt {2}}) } right) \ & = { frac {a ^ {3}} {3}} cdot { sqrt {2}} ; приблизительно 0 {,} 471 cdot a ^ {3} end { выровнено}}}$

Если объем в правильного тетраэдра известна как функция длины кромки, то объем октаэдра также может быть вычислено как разность между объемом в вписанного тетраэдра с длиной ребра и 4 конгруэнтных тетраэдра с длиной ребра . По логике получается такой же объем

${ displaystyle { begin {align} V & = { frac {(2 cdot a) ^ {3}} {12}} cdot { sqrt {2}} - 4 cdot { frac {a ^ {3}} {12}} cdot { sqrt {2}} \ & = { frac {a ^ {3}} {3}} cdot { sqrt {2}} ; приблизительно 0 { ,} 471 cdot a ^ {3} end {align}}}$

Площадь поверхности

Следующее относится к площади поверхности октаэдра (восемь равносторонних треугольников).
${ displaystyle A_ {O}}$

${ displaystyle A_ {O} = 8 cdot { frac { sqrt {3}} {4}} cdot a ^ {2} = 2 cdot a ^ {2} cdot { sqrt {3}} приблизительно 3 {,} 464 cdot a ^ {2}.}$

Высота пирамиды

Высота пирамиды может быть определена с помощью следующего прямоугольного треугольника.
h_p

В боковых длинах этого треугольника (смотрите рисунок в формулах ): боковая высота как гипотенузе, пирамиды высоту как большая сторона и половине длина кромки пирамиды в виде маленькой стороны.
${ displaystyle h_ {s}}$ ${ displaystyle h_ {p}}$ ${ displaystyle { tfrac {1} {2}} cdot a}$

Следующее относится к высоте равностороннего треугольника.
$ч_ {s}$

${ displaystyle h_ {s} = { frac { sqrt {3}} {2}} cdot a}$

и согласно теореме Пифагора применяется

${ displaystyle { begin {align} ; h_ {p} ^ {2} & = h_ {s} ^ {2} - left ({ frac {1} {2}} cdot a right) ^ {2} = h_ {s} ^ {2} - { frac {1} {4}} cdot a ^ {2} = { frac {3} {4}} cdot a ^ {2} - { frac {1} {4}} cdot a ^ {2} ; Rightarrow \ & = { frac {1} {2}} cdot a ^ {2} Rightarrow \ h_ {p} & = { sqrt {{ frac {1} {2}} cdot a ^ {2}}} = { sqrt { frac {1} {2}}} cdot a = { frac {a} { sqrt {2}}} ; приблизительно 0 {,} 707 cdot a. ; end {align}}}$

Угол между соседними гранями

Этот угол, отмеченный (см. Рисунок в формулах ), имеет вершину на одном крае октаэдра. Его можно определить с помощью следующего прямоугольного треугольника.

Длины сторон этого треугольника равны: радиус краевой сферы как гипотенуза, радиус резцовой сферы как большой катет и треть высоты стороны как маленький катет. Это значение определяется положением центра тяжести треугольной области, поскольку геометрический центр тяжести делит высоту треугольника в соотношении 2: 1.
${ displaystyle r_ {k}}$ ${ displaystyle r_ {i}}$ ${ textstyle { frac {1} {3}} cdot h_ {s}}$

Следующее относится к
углу

${ displaystyle { begin {align} ; cos { frac { beta} {2}} & = { frac {{ frac {1} {3}} cdot h_ {s}} {r_ { k}}} = { frac {{ frac {1} {3}} cdot left ({ frac { sqrt {3}} {2}} right) cdot a} { frac {a } {2}}} = { frac {{ frac {1} {6}} cdot { sqrt {3}}} { frac {1} {2}}} = { frac {1} { sqrt {3}}} ; Rightarrow \ cos beta & = cos left ( arccos left ({ frac {1} { sqrt {3}}} right) cdot 2 right) = - { frac {1} {3}} Rightarrow \ beta & = arccos left (- { frac {1} {3}} right) приблизительно 109 ^ { circ} ; 28 ^ { prime} ; 16 ^ { prime prime}. ; End {align}}}$

Угол между краем и гранью

Этот угол, обозначенный как , имеет вершину в одном углу октаэдра. Угол можно определить с помощью следующего прямоугольного треугольника.

Длины сторон этого треугольника равны (см. Рисунок в формулах ): край пирамиды как гипотенуза, высота пирамиды как большой катет и половина диагонали квадрата с длиной стороны / ребром как маленький катет.
${ displaystyle h_ {p}}$ ${ displaystyle { tfrac {d} {2}} = { tfrac {a} { sqrt {2}}}}$

Следующее относится к
углу

${ displaystyle { begin {align} ; cos gamma & = { frac {h_ {p}} { frac {d} {2}}} = { frac { frac {a} { sqrt {2}}} { frac {a} { sqrt {2}}}} = 1 \ гамма & = arccos left (1 right) = 45 ^ { circ}. ; End { выровнено}}}$

Угол 3D кромки

Этот угол, отмеченный значком (см. Рисунок в формулах ), имеет вершину в одном углу октаэдра и соответствует удвоенному углу d. ЧАС. внутренний угол на площади .

Это относится к трехмерному краевому углу октаэдра.

${ displaystyle delta = 90 ^ { circ}.}$

Сплошные углы в углах

Следующая формула, описанная в Platonic Solids, показывает решение для телесного угла

${ displaystyle Omega = 2 pi -2n cdot arcsin left ( cos left ({ frac { pi} {n}} right) cdot { sqrt { tan ^ {2} left ({ frac { pi} {n}} right) - tan ^ {2} left ({ frac { alpha} {2}} right)}} right)}$

С количеством кромок / поверхностей в углу и внутренним углом равностороннего треугольника применяется следующее:
${ Displaystyle {а = 60 ^ { circ}}}$

${ displaystyle { begin {align} { mathsf {(1)}} ; Omega & = 2 pi -2 cdot 4 cdot arcsin left ( cos left ({ frac { pi } {4}} right) cdot { sqrt { tan ^ {2} left ({ frac { pi} {4}} right) - tan ^ {2} left ({ frac {60 ^ { circ}} {2}} right)}} right) Rightarrow \ & = 2 pi -8 cdot arcsin left ({ frac {1} { sqrt {3} }} right) приблизительно 1 {,} 359347638 ; mathrm {sr} \ конец {выровнено}}}$

из-за этого
${ Displaystyle соз ( arcsin х) = { sqrt {1-х ^ {2}}}}$

${ displaystyle { begin {align} { mathsf {(2)}} ; cos ( arcsin x) & = { sqrt {1- left ({ frac {1} { sqrt {3}) }} right) ^ {2}}} = { frac { sqrt {6}} {3}} Rightarrow \ конец {выровнено}}}$

используется в и формуют

${ displaystyle { begin {align} { mathsf {(3)}} ; Omega & = 2 pi -8 cdot arccos left ({ frac { sqrt {6}} {3}} right) приблизительно 1 {,} 359347638 ; mathrm {sr} ; end {align}}}$

упрощение

${ displaystyle { begin {align} { mathsf {(4)}} ; cos Omega & = cos left (2 pi -8 cdot arccos left ({ frac { sqrt { 6}} {3}} right) right) = { frac {17} {81}} Rightarrow \ конец {выровнено}}}$

${ displaystyle { begin {align} { mathsf {(5)}} ; Omega & = arccos left ({ frac {17} {81}} right) приблизительно 1 {,} 359347638 ; mathrm {sr}. ; end {align}}}$

Определение как набор точек

Октаэдр может быть определена как набор из точек в трехмерном евклидовом пространстве , где сумма в абсолютных значениях 3 координат в системе декартовых координат находится в большинстве же большим , как радиус в области . Формально эту сумму можно записать как
${ displaystyle r_ {u} = { tfrac {a} { sqrt {2}}}}$

${ displaystyle left {x in mathbb {R} ^ {3} mid left | x right | _ {1} leq r_ {u} right } = left {( x_ {1}, x_ {2}, x_ {3}) mid left vert x_ {1} right vert + left vert x_ {2} right vert + left vert x_ {3 } right vert leq r_ {u} right }}$

Здесь сумма сумма норма или 1-норма вектора . Для внутренней части применяется октаэдр, а для поверхности применяется . Согласно этому определению, центральная точка октаэдра от начала координат и ее углов , , , , , расположена на 3 -х осях системы декартовых координат .
${ Displaystyle влево | х вправо | _ {1}}$ Икс ${ Displaystyle влево | х вправо | _ {1} <г_ {и}}$ ${ Displaystyle влево | х вправо | _ {1} = г_ {и}}$ ${ displaystyle (r_ {u}, 0,0)}$ ${ displaystyle (-r_ {u}, 0,0)}$ ${ displaystyle (0, r_ {u}, 0)}$ ${ displaystyle (0, -r_ {u}, 0)}$ ${ displaystyle (0,0, r_ {u})}$ ${ displaystyle (0,0, -r_ {u})}$

В более общем смысле, октаэдр, занимающий любую позицию в трехмерном евклидовом пространстве, может быть определен с помощью векторов . Является ли вектор положения в центре и , , ортогональные векторы направления , соединяющие центр октаэдра с 3 углами, поэтому ортогональной системы из трехмерного векторного пространства , то листья суммы из точек октаэдра определяется как количество из векторов vec {u} $mathbb {R} ^ {3}$

${ displaystyle left {{ vec {m}} + t_ {1} cdot { vec {u}} + t_ {2} cdot { vec {v}} + t_ {3} cdot { vec {w}} in mathbb {R} ^ {3} mid left | t right | _ {1} leq r_ {u} right } = left {{ vec {m}} + t_ {1} cdot { vec {u}} + t_ {2} cdot { vec {v}} + t_ {3} cdot { vec {w}} in mathbb {R} ^ {3} mid left vert t_ {1} right vert + left vert t_ {2} right vert + left vert t_ {3} right vert leq r_ {ты прав }}$

обобщение

Аналоги октаэдра в любой размерности называются -мерными кросс-многогранниками и также являются правильными многогранниками . — Мерный многогранник имеет поперечный углы и ограничена по — мерных симплексов (как граней ). Четырехмерным крест многогранник имеет 8 углов, 24 ребер одинаковой длины, 32 равносторонние треугольники , как боковые поверхности и 16 тетраэдров в качестве граней. Одномерное крест многогранника является сегментом , то двумерный крест многогранника является квадратным , и трехмерный крест многогранника является октаэдром.
2 ^ п

Моделью -мерного кросс-многогранника является единичная сфера относительно нормы суммы

left | x right | _1 = left vert x_1 right vert + cdots + left vert x_n right vert

Для $x = (x_ {1}, dots, x_ {n}) in { mathbb R} ^ {n}$

в векторном пространстве . (Замкнутый) кросс-многогранник, следовательно, есть
$mathbb {R} ^ {n}$

количество

$left {x in mathbb R ^ n mid left | x right | _1 le 1 right } = left {(x_1, dots, x_n) mid left vert x_1 right vert + cdots + left vert x_n right vert le 1 right }$

могут быть определены и содержать происхождение.

Объем в n — мерном кросс-многогранника является , где радиус в сфере вокруг происхождения в координатах относительно нормы суммы. Связь может быть доказана с помощью рекурсии и теоремы Фубини . ${ displaystyle { tfrac {(2 cdot r) ^ {n}} {n!}}}$ г> 0

Сети октаэдра

В октаэдре одиннадцать сеток . Это означает, что есть одиннадцать способов развернуть полый октаэдр, разрезав 5 ребер и разложив их в плоскости . Остальные 7 ребер соединяют 8 равносторонних треугольников сетки. Чтобы октаэдр раскрасить так, чтобы никакие соседние грани не были одного цвета, вам понадобится как минимум 2 цвета.

Графики, двойные графики, циклы, цвета

Раскраска иллюстрируется
октаэдром, вписанным в дуальный куб.

Октаэдр имеет неориентированный плоский граф с 6 узлами , 12 ребрами и 8 областями, назначенными ему, который является 4- правильным , т.е. 4 ребра начинаются от каждого узла, так что степень равна 4 для всех узлов. В случае плоских графов точное геометрическое расположение узлов не имеет значения. Однако важно, чтобы края не пересекались. Узлы этого октаэдрического графа соответствуют углам куба.

В узлах октаэдрической графа могут быть окрашены с 3 -х цветов , так что соседние узлы всегда окрашены по- разному. Это означает, что хроматическое число этого графика равно 3. Кроме того, края можно раскрасить в 4 цвета, чтобы смежные края всегда были окрашены по-разному. Это невозможно с 3 цветами, поэтому хроматический индекс для окраски краев равен 4 (рисунок справа иллюстрирует эту окраску).

Двойной граф (куб- граф ) с 8 узлами , 12 ребрами и 6 областями помогает определить необходимое количество цветов для поверхностей или областей . Узлы этого графа назначаются взаимно однозначно (биективно) областям октаэдрического графа и наоборот (см. Биективную функцию и рисунок выше). Узлы кубического графа можно раскрасить в 2 цвета, чтобы соседние узлы всегда были окрашены по-разному, так что хроматическое число кубического графа равно 2. Из этого можно косвенно сделать вывод: поскольку хроматическое число равно 2, для такой окраски поверхности октаэдра или раскраски областей графа октаэдра необходимо 2 цвета.

Раскраска площади графа октаэдра при раскраске двойных узлов графа куба

5 обрезанных ребер каждой сети (см. Выше) вместе с углами ( узлами ) образуют остовное дерево графа октаэдра. Каждая сеть точно соответствует покрывающему дереву и наоборот, так что между сетями и покрывающими деревьями существует взаимно однозначное ( биективное ) присвоение. Если вы рассматриваете сеть октаэдров без внешней области как граф, вы получите двойственный граф с деревом с 8 узлами и 7 ребрами и максимальной степенью узла 3. Каждая область октаэдра назначается узлу сети. дерево. Не каждое теоретико-графовое созвездие (см. Изоморфизм графов ) таких деревьев встречается, но некоторые встречаются более одного раза .

Октаэдрический граф состоит из 32 окружностей Гамильтона и 1488 окружностей Эйлера .

Октаэдрический граф с одной из 32 окружностей Гамильтона

Заполнение помещений октаэдрами

Трехмерное евклидово пространство может быть полностью заполнено с многогранников или Архимеда твердых веществ одинаковой длины кромки. Такое трехмерное плиточные это называется наполнение комнаты . Следующие заливки пространства содержат октаэдры:

Тетраэдр Серпинского

Октаэдр косвенно связан с тетраэдром Серпинского . Тетраэдр Серпинского является трехмерным обобщением треугольника Серпинского . Начальная фигура — тетраэдр . На каждой итерации из его центра вырезается октаэдр с половиной длины ребра. Остается 4 тетраэдра, из каждого из которых вырезан октаэдр и т. Д.

После шага итерации , очевидно, возникли частичные тетраэдры с одинаковой длиной стороны. Количество вырезанных октаэдров с разной длиной стороны составляет .
${ displaystyle 4 ^ {k}}$ ${ displaystyle { frac {4 ^ {k} -1} {3}}}$

Размер этой структуры , хотя это фигура в трехмерном пространстве. При увеличении числа шагов итерации объем фигуры стремится к нулю, но площадь поверхности остается постоянной, поскольку количество боковых поверхностей конгруэнтных частичных тетраэдров увеличивается в четыре раза с каждым шагом итерации, а длина сторон этих боковых поверхностей , которые представляют собой равные треугольники, делятся пополам.

Приложения

Октаэдрические кристаллы квасцов

В химии предсказание геометрии молекул в соответствии с моделью VSEPR может привести к октаэдрическим молекулам . Октаэдр также появляется в кристаллических структурах , таких как гранецентрированная кубическая структура хлорида натрия (координационное число 6), в элементарной ячейке , а также в сложной химии, если 6 лигандов расположены вокруг центрального атома .

Некоторые природные минералы , например Б. квасцы , кристаллизуется в октаэдрической форме.

В ролевых играх используются восьмигранные игральные кости , называемые «D8», то есть игральные кости с 8 гранями.

Смотри тоже

Октаэдрические числа
Дидервинкель
многогранник
Платоново твердое тело

веб ссылки

Евклид: Stoicheia. Книга XIII.14. Октаэдр сферы …
Октаэдр . — Математика

Индивидуальные доказательства

^ Вильгельм Папе , Макс Зенгебуш (аранжировка): Краткий словарь греческого языка . 3-е издание, 6-е впечатление. Vieweg & Sohn, Braunschweig 1914 ( zeno.org [доступ 12 марта 2020 г.]).
↑ Эрик Вайсштейн: Обычный октаэдр. Формула Умкугельрадиуса (12). В: MathWorld Wolfram. Wolfram Web Resource, доступ к 27 июня 2020 года .
↑ Хариш Чандра Раджпут: Твердые углы, образуемые платоновыми телами (правильными многогранниками) в их вершинах. SlideShare, март 2015, доступ к 27 июня 2020 .
↑ Альтернативное выражение для . WolramAlpha, доступ к 27 июня 2020 .
↑ Сусуму Онака, Департамент материаловедения и инженерии, Токийский технологический институт: простые уравнения, определяющие формы различных выпуклых многогранников: правильных многогранников и многогранников, составленных из кристаллографически малоиндексной плоскости
^ Мартин Хенк, Юрген Рихтер-Геберт, Гюнтер М. Циглер, Технический университет Берлина: Основные свойства выпуклых многогранников
↑ Эрик Вайсштейн: Обычный октаэдр. Сети. В: MathWorld Wolfram. Wolfram Web Resource, доступ к 27 июня 2020 года .
↑ Майк Zabrocki: ДОМАШНЯЯ # 3 РЕШЕНИЯ — МАТЕМАТИКА 3260. (PDF) Йоркский университет, математика и статистика, Торонто, 2003, стр . 3 , доступ к 31 мая 2020 .
↑ Эрик Вайсштейн: Октаэдрический граф. В: MathWorld Wolfram. Wolfram Web Resource, доступ к 27 июня 2020 года .
^ Вольфрам MathWorld: Тетрикс
↑ Гайла Чандлер, Хидеки Цуйки: Фотографии: Тетраэдр Серпинского и его дополнение

Источник

Введите данные:

Округление:

Октаэдр и площадь полной его поверхности: описание, формулы, примеры

Содержание:

Что такое октаэдр

Свойства октаэдра

Математические характеристики тела

Как вычислить площадь поверхности октаэдра

Как вычислить объём правильного октаэдра

Развёртка

Октаэдр.

Свойства октаэдра.

Развёртка октаэдра.

Симметрия октаэдра.

Октаэдр

Математические характеристики октаэдра

Вариант развертки

Видео. Октаэдр из набора «Волшебные грани»

Видео. Вращение правильных многогранников

Введите данные:

Округление:

симметрия

Отношения с другими многогранниками

Формулы

Расчет правильного октаэдра

объем

Площадь поверхности

Высота пирамиды

Угол между соседними гранями

Угол между краем и гранью

Угол 3D кромки

Сплошные углы в углах

Определение как набор точек

обобщение

Сети октаэдра

Графики, двойные графики, циклы, цвета

Заполнение помещений октаэдрами

Тетраэдр Серпинского

Приложения

Смотри тоже

веб ссылки

Индивидуальные доказательства

Не пропустите также: