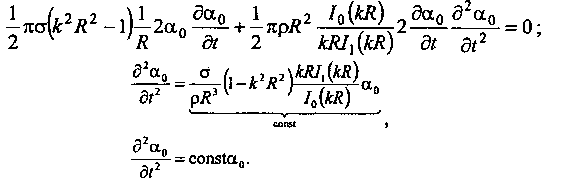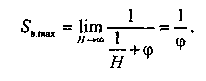Как найти высоту подъема струи

Если вытекающая из отверстия или насадка
струя попадает на неподвижную стенку,
то она с определенным давлением
воздействует на нее. Основное уравнение,
по которому вычисляется давление струи
на площадку, имеет вид

На рис. 5.15 приведены наиболее часто
встречающиеся в практике ограждающие
поверхности (преграды) и уравнения, по
которым вычисляется давление струи на
соответствующую поверхность.

Величина давления струи, естественно,
зависит от расстояния насадка до
преграды. С увеличением расстояния
струя рассеивается и давление уменьшается.
Соответствующие исследования показывают,
что в данном случае струя может быть
разбита на три характерные части:
компактную, раздробленную и распыленную
(рис.5.16).

В пределах компактной части сохраняется
цилиндрическая форма струи без нарушения
сплошности движения. В пределах
раздробленной части сплошность потока
нарушается, причем струя постепенно
расширяется. Наконец, в пределах
распыленной части струи происходит
окончательный распад потока на отдельные
капли.

Рис. 5.15.
Взаимодействие струи жидкости с
неподвижной поверхностью

Рис. 5.16.
Составные части свободной струи

5.8
Распад струи капельной жидкости в
воздухе

Свободной струей называется поток, не
ограниченный твердыми стенками.

Cтруи бывают жидкие и газовые. В зависимости
от условий движения струи могут быть
затопленными и незатопленными.

Струя называется затопленной, если она
движется в среде, однород­ной с массой
струи. К затопленным струям относятся
струи газа, выте­кающие в воздушное
пространство или пространство, заполненное
другим газом, а также водяные струи,
выпускаемые в массу воды или другой
жид­кости.

Струя (жидкая или пенная) называется
незатопленной, если она дви­жется в
газовом пространстве. К незатопленным
струям относятся водяные и пенные
пожарные струи, вытекающие в воздушное
пространство. В практике пожаротушения
наиболее широкое применение нашли
незатоп-ленные водяные струи.

Водяные струи подразделяются на сплошные,
получаемые от ручных и лафетных стволов,
и распыленные, образуемые от специальных
насад­ков-распылителей.

Сплошные водяные струи отличаются своей
компактностью, большой дальностью
полета и сильным динамическим действием.
Строго говоря, сплошные струи получают
при напоре не более 2-3 м. При больших
напо­рах в струе можно выделить две
ее части: сплошную, или компактную, и
раздробленную.

В компактной части сохраняется сплошность
потока, струя имеет ци­линдрическую
или близкую к ней форму, в раздробленной
части нарушает­ся сплошность потока,
струя распадается на все более мелкие
части и рас­ширяется. В раздробленной
части можно выделить две области —
область распада на отдельные крупные
части и область, состоящую из отдельно
ле­тящих капель (распыленная струя).
Понятие компактной части струи явля­ется
относительным, поскольку резкой грани
между нею и раздробленной частью не
существует.

Определение компактной части впервые
сформулировал Фриман в 1888г. Он предложил
за длину компактной части сплошной
водяной струи принимать ту ее часть,
которая несет 75 % всего количества воды
в круге диаметром 26 см и 90 % воды в круге
диаметром 38 см.

Практически деление струи на компактную
и раздробленную части может быть
осуществлено на основании визуального
наблюдения за струей, измерения плотности
струи в различных точках и опыта
использо­вания струй в данной отрасли
техники.

Разрушение струи происходит под влиянием
действующей на нее си­лы тяжести,
сопротивления воздуха и внутренних
сил, вызываемых турбулентностью струи
и коле­бательно-волновым характером
движения жид­кости в ней. На определенной
стадии распада струи в качестве
дополнительных сил, способст­вующих
распылению струи на капли, будут
вы­ступать силы поверхностного
натяжения.

Для создания развитой компактной части
стремятся уменьшить турбулентность и
ликвиди­ровать винтовой характер
движения выходящей из насадка струи
путем применения различных выпрямителей,
устанавливаемых в стволе.

Для уничтожения компактной части, т.е.
получения распыленной струи, применяются
различного рода распылители.

УСТОЙЧИВОСТЬ
ВОДЯНЫХ СТРУЙ ТЕОРЕТИЧЕСКИЙ
АНАЛИЗ ВЛИЯНИЯ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
ЖИДКОСТИ НА УСТОЙЧИВОСТЬ СТРУИ

Вопросы устойчивости поверхности жидких
тел относятся к наиболее сложным вопросам
механики жидкости. Попробуем сначала
разобраться с этим вопросом применительно
к струям жидкости на сравнительно
про­стом идеализированном случае.

Предположим, имеется сплошная
цилиндрической формы струя иде­альной
жидкости. Трение на границе раздела фаз
отсутствует. Силы тяже­сти не влияют
на характер движения жидкости (т.е. силы
тяжести не учи­тываются). Течение
жидкости в струе безвихревое. При
сделанных допу­щениях в системе
координат, движущейся со скоростью
жидкости — жид­кость неподвижна.
Предположим, что в какой-то момент
времени в ре­зультате случайного
малого возмущения поверхность
цилиндрической струи приобрела форму,
описываемую уравнени­ем

где—
волновое число;

— малая величина, т.е.—
длина волны возмущения.

После такого возмущения поверхность
жидкости придет в движение вследствие
действия сил поверхностного натяжения
(т.е., они стремятся сократить поверхность,
но по инерции гребни будут опускаться
ниже нейтральной линии, и поверхность
жидкости придет в колебательное
дви­жение). Следовательно, в выбранной
нами системе координат жидкость в струе
вблизи поверхности также придет в
движение.

Предположим, что это движение безвихревое,
т.е. потенциальное движение (существует
функция

которая удовлетворяет условию

.)

. В случае потенциального движения,
потенциал скорости

удовлетворяет уравнению Лапласа, т.е.

Здесь рассматривается осесимметричная
задача. Поэтому решение удобно проводить
в цилиндрических координатах. В этих
координатах оператор Лапласа, в случае
двухмерного движения, имеет вид:

В данном случае во внимание принимается
тот факт, что движение про­исходит по
углу(т.е.
в касательном направлении к поверхности
отсутству­ет).

Для анализа устойчивости (т.е. будет ли
нарастать во времени ампли­туда
колебаний поверхности или уменьшаться)
воспользуемся энергетиче­ским методом.
Для этого найдем изменение полной
энергии рассматривае­мого жидкого
тела, которая состоит из потенциальной
энергии, обуслов­ленной действием
сил поверхностного натяжения, и
кинетической энергии движущихся частиц
жидкости.

Энергия поверхностного натяжения прямо
пропорциональна величине поверхности.
Поэтому для того чтобы найти изменение
энергии поверхно­стного натяжения
при искривлении поверхности, необходимо
просто най­ти изменение поверхности.

Величинане
остается абсолютно постоянной во время
движения; ее значение должно определяться
условием неизменности заключенного в
цилиндре объема. Жидкость несжимаема
и, следовательно, объем выде­ленного
участка струи постоянен. Будем
рассматривать участок струи дли­ной

Учтем, что

После интегрирования и подстановки
пределов интегрирования полу­чим:

С другой стороны

радиус невозмущенной поверх-

ности струи. Так как W
=const, то

Участок поверхности

Непрерывную функцию можно разложить в
ряд Маклорена:

Разложим функцию

Если х «1, то можно с достаточно
высокой точностью ограничиться первыми
членами разложения

Тогда

Поверхность участка возмущенной струи
длиной X равна:

После подстановки пределов интегрирования
получим:

Так как

V‘
» J

так как

Таким образом, изменение поверхности
на участке струи длиной X
равно

или изменение поверхностина
единицу длины

Изменение потенциальной энергии при
волнообразовании на единицу длины струи
равно:

Еслии
энергия поверхностного натяжения

уменьшится, и при волнообразовании
амплитуда колебаний должна расти, так
как любая система стремится к минимуму
потенциальной энергии.

АНАЛИЗ
ПОЛУЧЕННОГО РЕЗУЛЬТАТА

Выражение для изменения потенциальной
энергии позволяет сделать следующий
принципиальный вывод.

Если

< 1, то по отношению к таким возмущениям
цилиндрическая поверхность струи
неустойчива, так как волнообразование
энергетически выгодно. Что означает kR
< 1 Именно то, что неустойчивость
будет про­являться в том случае, если
длина волны возмущения больше длины
ок­ружности.

По отношению к решению задачи этот вывод
показывает, что мы пра­вильно
предположили, что сс₀ «А.. Практический
же вывод состоит в том, что для того
чтобы получить дальнобойную пожарную
струю, необходимо устранить возмущения
(длинноволновые) на выходе из насадка
(т.е. долж­ны отсутствовать задиры,
забоины и т.д.).

Так как возмущения
не с любой длиной волны приводят к
неустойчиво­сти,
то должны существовать возмущения,
которые особенно быстро приводят к
распаду струи. Для нахождения длины
волны X
таких возмущений
проана­лизируем
полную энергию системы, а для этого
вначале найдем кинетическую энергию.

. ОПРЕДЕЛЕНИЕ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ ЧАСТИЦ ЖИДКОСТИ

В СТРУЕ, ОБУСЛОВЛЕННОЙ
ИХ ДВИЖЕНИЕМ ПОД ДЕЙСТВИЕМ

КОЛЕБАНИЙ ПОВЕРХНОСТИ

Определим кинетическую энергию частиц
жидкости в струе, обуслов­ленную их
движением под действием колебаний
поверхности. Для этого необходимо
получить аналитические выражения для
компонент скорости v_r
и v₂.
Ранее мы отметили, что движение
потенциальное и

Найдем
.
Поскольку в выражении для г — r₀
+ a₀coskz
содержится coskz, то в
выражении для ц/ также должен быть
косинус. Будем искать решение
дифференциального уравнения в виде

Тогда

Подставляя выражение дляв
уравнение , получаем:

Здесь получили дифференциальное
уравнение, исследование которого провел
Фридрих Бессель, построив фундаментальную
систему решений, (уравнение Бесселя
нулевого порядка). Решение уравнения
имеет вид:

где I
₀
Y₀—
функции Бесселя первого и второго
рода нулевого порядка.

при r
= О (на оси
струи) скорость или равна 0 или конечной
величине. Так как при r
= О Y₀ (х)
—> -оо, то С₂ = 0. Поэтому
решение уравнения имеет вид:

где С — постоянная интегрирования
— должна быть найдена из дополни­тельных
физических соображений. Для поверхности

—
радиальная скорость частиц жидкости,
находящихся на поверхности струи

Кинетическаяэнергия частицы жидкости:

на единицу длины струи

ОПРЕДЕЛЕНИЕ СКОРОСТИ
НАРАСТАНИЯ КОЛЕБАНИЙ ПОВЕРХНОСТИ
СТРУИ

Если после наложения возмущения система
(струя) предоставлена са­ма себе и
энергия не подводится, то:

С учетом выражений
для Э_пот
и Э_кин
получим:

или

Решение будем искать в виде:

Подставляя в исходное уравнение,
получаем:

Таким образом, если
,
следовательно,

будетвозрастать
по экспоненциальному закону. Это приведет
к распаду струи на отдельные капли.

График зависимостидля
воды имеет вид

Из графика видно, чтои,
значит,

Рис. 6.2. Зависимость

Таким образом, самое опасное возмущение
(т.е. возмущение, приво­дящее к наиболее
быстрому нарастанию амплитуды колебаний
и, следова­тельно, быстрому распаду
водяной струи) имеет длину волны Х =
9Я (где R — радиус
невозмущенной струи).

ВЛИЯНИЕ ВЯЗКОСТИ ЖИДКОСТИ, СИЛ ТЯЖЕСТИ,
МЕЖФАЗНОГО ТРЕНИЯ НА РАЗРУШЕНИЕ СТРУИ

Для реальных струй необходимо учесть
вязкость, действие сил тяже­сти,
межфазное трение. Задача сильно
усложняется. Кроме того, в реаль­ных
струях, как правило, движение непотенциальное
(турбулентное). Од­нако использованный
подход (анализ изменения потенциальной
и кинети­ческой энергии) к решению
задачи об устойчивости реальных струй
может быть применен. Учет свойств
реальной жидкости приводит к некоторому
изменению величины,
а принципиальные выводы об устойчивости

сохраняются.

Длина непрерывной части струи представляет
собой расстояние, про­ходимое струей
за время нарастания колебаний до такой
степени, что струя распадаетсяСледовательно,
длина непрерывной части зави-

сит от характера возмущений X.
При устранении возмущений длина
ком­пактной струи может быть значительно
увеличена. В случае реальных струй
увеличение все равно ограничено в связи
с действием гравитацион­ной
неустойчивости и межфазного трения.

Уравненэнергии для несжимаемых жидкостей:

Учет вязкости можно выполнить следующим
образом:

где Э -работасил трения в объеме Wза
время t.

При учете вязкости происходит уменьшение
инкремента q колебаний
по абсолютной величине и смещение в
сторону больших длин волн макси­мума
q. Интервал
неустойчивости не меняется (рис. 6.3).
Можно отметить, что полученные результаты
справедливы для малых воз­мущений и,
следовательно, характеризуют их
нарастание в начальный пе­риод.

.
Влияние вязкости жидкости на величину
инкремента
колебаний

Таким образом, цилиндрическая поверхность
жидких струй неустой­чива по отношению
к возмущениям определенной длины волны
(т.е. про­исходит распад на капли) и
существуют возмущения, приводящие к
осо­бенно быстрому распаду струй. Для
воды эти возмущения имеют длину волны


9R.

Межфазное трение, сила тяжести,
турбулентное движение жидкости в струе
способствует более быстрому ее распаду.

ТРАЕКТОРИЯ СПЛОШНОЙ СТРУИ

Рассмотрим случай, когда сплошная струя
вылетает из насадка диа­метром d
с начальной скоростью V₀
и движется в воздушном пространстве
подобно твердому телу, брошенному под
углом к горизонту . Это упрощение
приближенно соответствует участку
струи, на котором со
­храняется цилиндрическая или близкая
к ней форма струи.

Уравнения траектории струи, на которую
действуют силы инерции F_h
тяжести G и
сопротивления воздуха F_k,
могут быть представлены в

виде:

где х,у — координаты частицы струи
в точке траектории; к — коэффициент
сопротивления трению струи в воздухе;
V₀ —
начальная скорость;

— угол наклона ствола к горизонту; d
— диаметр струи (насадка); t
— время, отсчи­тываемое от момента
вылета рассматриваемого жидкого тела
из насадка.

Теоретическая
траектория сплошной струи

Из уравнения определим время:

и, подставив в уравнение (6.2), получим:

Заменяя в формуле V₀
/2g = H,
где Н — напор у насадка, полу­чаем
уравнение траектории в общем виде:

Найденное уравнение представляет собой
непрерывную функцию/(х), имеющую максимум,
следовательно, производная f(x)
при этом значении обращается в нуль,
т.е.

отсюда максимальная
высота подъема струи у_в
будет на
расстоянии х_в
на­чала струи:

Подставляя выражение х_в
в уравнение (6.4), получим максимальное
значение высоты подъема струи у₃:

Из выражения получим формулу для
определения высоты верти­кально
направленной струи, принимая 0 = 90°,

Теоретическую дальность полета струи
x_t
определим из уравнения (6.4) приу = 0:

Из выражения (6.8) видно, что максимальная
теоретическая дальность полета струи
будет при угле & = 45°

Из формул видно, что теоретическая
траектория по своей форме представляет
собой параболу с вершиной в точке В
(х_в;у_а).

В действительности расчет дает хорошее
совпадение с данными, полученными
опытным путем лишь при напорах истечения
Н = 3,5-7 м. При напоре 10 м наибольшая
дальность полета достигается при

= 35 -40 , а при напоре 35 м — при

= 30-34 . Причем наибольшее от­клонение
от теоретической траектории наблюдается
в раздробленной час­ти струи.

Несовпадение теоретических и практических
данных объясняется сложной структурой
струи, недостаточным знанием законов
сопротивле­ния, возникающего при
движении струи в воздухе. В связи с
изменением структуры струи, коэффициент
сопротивления к будет зависеть от
коорди­нат точки траектории струи х
и у, что не учитывалось при получении
фор­мул Поэтому для расчета траекторий
струи используются эм­пирические
данные.

ФОРМУЛЫ ДЛЯ
ПРАКТИЧЕСКОГО РАСЧЕТА ТРАЕКТОРИИ СТРУИ

Вертикальная струя. Для расчета
вертикальной струи обычно поль­зуются
эмпирическими формулами Люгера или
Фримана, полученными в конце XIX
в. при изучении фонтанных и пожарных
струй.

Рассмотрим струю жидкости, которая
вылетает вертикально вверх из

насадка с напором Н = F₀²
/2g и поднимается
на высоту S_B

Потерю высоты, вызванную сопротивлением
воздуха, обозначим че­рез
Н,
а величину компактной части струи S_К.

Высота вертикальной сплошной струи
определится по формуле, предло­женной
Люгером, :

Коэффициент

для насадков пожарных стволов может
быть опреде­лен по эмпирической
формуле

где d — диаметр
выходного сечения насадка, мм. Значение
коэффициента

для различных диаметров насадков
приведены в таблице

Фриман для расчета высоты вертикальных
струй при напорах от 7 до 70 м предложил

Вертикальная струя

фор­мулу

Для практических расчетов формулы
Люгера и Фримана можно счи­тать
равноценными.

Анализируя формулы , можно установить,
что увеличе­ние длины вертикальной
струи связано с увеличением диаметра
насадка и напора перед насадком. Однако
высота струи для каждого отдельного
на­садка не растет неограниченно, а
достигает своей максимальной величины,
после чего высота ее не изменяется, как
бы сильно не увеличивался напор.

Из формулы Люгера найдем, что предельная
величина S, которая
получится при неограниченном увеличении
H, будет равна:

Так как величина ф зависит только от
диаметра , то при больших напорах
увеличение высоты струи возможно только
при увеличении диа­метра насадка.
Применение в пожарном деле лафетных
стволов с насадка­ми большого диаметра
объясняется не только необходимостью
подачи большого количества воды, но и
возможностью подачи воды при обычных
напорах на большое расстояние.

Исследуем теперь формулу Фримана.
Приравнивая первую производ­ную к
нулю, получаем то значение Н, при
котором наблюдается макси­мальная
высота струи:

Величины напоров, с достижением которых
для определенного диа­метра насадков
струя не увеличивается, приведены в
таблице

Решая уравнение относительно Н,
получаем формулу для опре­деления
напора в зависимости от требуемой высоты
струи:

Величину компактной части струи
определяют как часть всей вертикальной
струи:

Значение коэффициента а можно вычислить
по эмпирической форму­ле Лобачева:

Величины коэффициентов а приведены в
табл. 6.3.

Наклонная струя. Для пожаротушения
применяются сплошные струи с различными
углами наклона. Если при одном и том же
напоре у насадка постепенно
изменять угол наклона ствола, то конец
компактной части струи будет
описывать траекторию аЪс, которая
называется огибающей кривой компактной
струи, а наиболее удаленные капли
струи — траекторию а’Ь’с’, называемую
огибающей
кривой раздробленной струи (рис.
6.6). Расстояния по прямой от насадка
до граничных кривых соответственно
называются ра­диусом действия
компактной струи R_K
и радиусом действия раздроблен­ной
струи R_D.

Наклонные струи Расчет наклонных струй
ведут по отношению к величинам S_K
и S_B
для . вертикальных струй.

Огибающая кривая компактной струи аЬс
мало отличается от дуги ок­ружности,
описанной радиусом, который для ручных
стволов диаметром насадка не выше 25 мм
можно принять равным S_K,
т.е.

Для насадков больших диаметров, например,
для лафетных стволов, линия abc
более вытянута вдоль горизонтальной
оси. Для приближенного определения
дальности боя струи с достаточно большим
динамическим эффектом можно воспользоваться
эмпирической формулой Н. П. Гавырина:

где L
— дальность боя струи, м;
—
начальный угол наклона струи к го­ризонту,
градусы; d₀
— диаметр насадка, мм; Н — напор на
выходе из насад­ка,
м. Формула применима при

= 5-32°, d=
5-50 мм иH=
30-80 м.

Рабочая длина
компактных струй ручных стволов,
применяемых для тушения наружных
пожаров, равна, примерно, 17 м. Получение
таких струй для наиболее распространенных
ручных стволов с насадками 13, 16, 19, 22 и
25 мм требует создания напора перед
насадком от 30 до 50 м.

Расстояние от насадка до огибающей
кривой раздробленной струи возрастает
с уменьшением угла наклона R
к горизонту
.
Величину радиуса действия раздробленной
струи определяют по формуле

)

где

— коэффициент, зависящий от угла наклона

Не надо смешивать угол наклона радиуса
действия струи

с углом наклона ствола
.
Угол наклона ствола

для наклонных струй всегда больше угла
наклона R_p
к горизонту. Например, наибольшая
дальность полета струи L
наблюдается при угле наклона ствола

-30°, при этом коэффициент

равен 1,4, а угол
=0.

Зависимость между радиусом действия
компактной части струи, на­пором и
расходом из насадка пожарного ствола
для насадков различных диаметров
приводится в таблице для ручных стволов
и в таблице для ла­фетных стволов.

	Радиусы действия компактной части струи лафетных стволов при угле	наклона
				радиуса действия компактной струи 30
Напор у ствола				Радиус	действия компактной части струи, м, при диаметрах насадков, мм
Я,м	28	32	38	50	63	76	89
	Лк,м	а л/с	Як,м	йл/с	Як.м	йл/с	Лк.м	^л/с	Дк,м	йл/с	Дк,м	йл/с	RKM	йл/с
20	20,2 ■	12,2	20,0	15,9	20,5	22,4	21,0	38,9	—	—	—	—	—	—
25	23,0	13,6	23,5	17,8	24,0	25,1	25,0	43,5	—	—	—	—	—	—
30	26,0	14,9	26,5	19,4	27,0	27,4	28,0	47,5	29,0	76,5	30,5	111,0	32,5	150,0
35	28,	16,2	28,5	21,0	29,5	29,7	31,0	51,5	32,0	82,5	34,0	119,0	36,5	163,0
40	30,0	17,2	30,5	22,5	32,0	31,7	33,0	55,0	35,0	87,3	38,0	127,0	41,0	174,0
45	31,5	18,3	32,5	23,8	34,0	33,6	35,5	58,3	38,0	92,5	41,0	135,0	45,0	184,0
50	33,0	19,3	34,0	25,1	35,5	35,4	37,5	61,4	42,0	97,5	45,0	142,0	49,0	194,0
55	34,0	20,2	36,0	26,0	37,0	37,2	39,0	64,4	44,0	102,0	49,0	149,0	53,0	203,0
60	35,5	21,1	37,0	27,0	38,0	38,2	40,5	67,3	46,0	106,0	52,0	155,0	56,0	212,0
65	36,5	22,0	37,5	28,6	39,0	40,4	41,5	70,0	49,0	111,0	55,0	162,0	60,0	221,0
70	37,0	22,8	37,5	29,7	39,5	41,9	42,5	72,6	52,0	115,0	58,0	168,0	63,0	230,
75	—	—	—	—	40,0	43,4	43,5	75,3	54,0	119,0	60,5	174,0	66,0	238,0
80	—	—	—	—	40,5	44,8	44,5	77,8	56,0	123,0	63,0	179,0	69,0	245,0
85	—	—	—	—	—	—	45,5	80,1	57,0	127,0	65,0	185,0	72,0	253,0
90	—	—	—	—	—	—	46,0	82,5	59,0	131,0	67,0	191,0	74,0	260,0
95	—	—	—	—	—	—	46,5	84,8	60,0	134,0	69,0	196,0	74,5	268,0
100	—	—	—	—	—	—	47,0	87,0	62,0	138,0	70,0	201,0	75,5	274,0

УЧЕНЫЕ ЗАПИСКИ Ц А Г И

Т о м XX 1 98 9 №4

УДК 532.525.2

ИССЛЕДОВАНИЕ ВЫСОТЫ ПОДЪЕМА ВЕРТИКАЛЬНЫХ ЖИДКИХ СТРУЙ

Л. А. Эпштейн

Описаны экспериментальные исследования высоты подъема тонких водяных вертикальных струй, вылетающих в атмосферу с большими скоростями из сопел различного диаметра. Получены и проанализированы зависимости высоты подъема струи от скорости вылета из сопла и его диаметра. Установлены масштабные эффекты, которые приводят к завышению подъема струи при пересчете по Фруду с модели на натуру.

Во второй половине XIX века значительное внимание уделялось жидким струям, образующимся при истечении под давлением через малое отверстие. Соответствующие эксперименты проводились Сава-ром, Магнусом, Плато, Бидоном и др. Теоретические и экспериментальные исследования струй даны в классических работах Рэлея. Исследование жидких струй получило новый импульс в 20—30-х годах XX века в связи с появлением и разработкой двигателей Дизеля. К этому периоду относится ряд фундаментальных работ, проведенных в Германии и США. Изучению подвергались полет и распыление тонких жидких струй, вылетающих под большим давлением из сопла. Как правило, рассматривались небольшие по длине) участки струй вблизи сопла, вопрос об их дальнобойности и высоте подъема не рассматривался. Эти вопросы оказались важными в технике пожаротушения. В литературе имеются незначительные сведения об отдельных исследованиях этих вопросов. Высота, -дальность полета и интенсивность брызговых струй играют существенную роль для движущихся по воде скоростных объектов — гидросамолетов, быстроходных транспортных аппаратов типа глиссеров, судов на воздушной подушке и в специальных задачах, например, при движении колес шасси самолета по мокрому аэродрому, когда возникающие брызги могут повредить конструкцию самолета и двигателя и нарушить нормальную работу последнего. Исследование брызговых потоков в ряде случаев производится на моделях объектов, но вопросы пересчета результатов испытаний моделей на натуру крайне сложны и в литературе освещены мало. Это, в частности, обусловлено тем, что полет брызговых струй связан с сопротивлением воздуха, а последнее в значительной степени определяется характером их дробления, деформациями жидких комплексов и их взаимодействием друг с другом и с окружающим

воздухом. Некоторые сведения и исследования по указанным вопросам содержатся в работах, опубликованных в период 1950—1986 гг., (см. например, [1—3]), однако материалы, учитывающие влияние полученных результатов на высоту, дальность и интенсивность струй, практически отсутствуют.

В настоящей работе описаны и проанализированы проведенные автором опыты по подъему тонких вертикальных водяных струй, вылетающих из сопла со скоростями до 90 м/с.

1. Для образования брызговых струй было изготовлено устройство, показанное на рис. 1. Дюралевый стакан (1) объемом 150 см3 с фланцем (2) и проточкой (3) для герметизирующего резинового кольца (4) крепился к дюралевой пластине—основанию (5). В верхней части стакана были ввернуты на резьбе и краске три штуцера (6), из которых один подсоединялся к манометру (7), другой через редуктор— к баллону сжатого воздуха (8). Третий закрывался заглушкой на резьбе. Во фланец (2) были ввернуты четыре шпильки (9), на которые’садилась латунная крышка (10) с впаянной соосной с ней трубкой (11), не доходившей до дна цилиндра. К верхнему концу этой трубки с помощью накидной гайки крепились сменные сопла (12). Герметизация соединения сопл и трубки достигалась проточкой и кольцевой резиновой прокладкой (13). При проведении опытов стакан

заполнялся водой, сопло снаружи закрывалось заслонкой, перемещавшейся перпендикулярно к его оси, затем в полость стакана от баллона с редуктором подавалось требуемое давление, регистрируемое образцовым манометром (десятиатмосферным или стоатмосферным), после чего на короткое время, порядка секунды, заслонка открывалась и закрывалась. Регистрировалась наибольшая высота образующегося фонтана. При опытах ось сопла была отклонена на несколько градусов от вертикали. Регистрируемое манометром давление в процессе опыта практически не менялось.

Наиболее тонким моментом в проводимых опытах было определение высоты к фонтана, который в своей верхней части состоит из отдельных капель, высота подъема которых не стабильна, а колеблется около некоторого среднего значения. Трудности измерений были также связаны с большими высотами подъема фонтана, которые в проведенных опытах доходили до ~8 метров. С увеличением диаметра струй высота их подъема возрастает. Заметим, что опыты должны проводиться в закрытых помещениях, так как даже небольшой ветер существенно затрудняет измерения и влияет на их результаты. Решение поставленной задачи о создании и измерении высоты фонтана осложняется рядом не принципиальных, но фактически действующих обстоятельств, как, например, коротким временем выброса, затруднениями, связанными с большим количеством опадающей воды, если это время существенно увеличить. Такое увеличение может также сказаться на стабильности показаний манометра. Укажем, что и методы измерения, и само определение высоты фонтана неразрывно связано с многими казалось бы второстепенными факторами, которые могут отразиться не только на точности проводимых опытов, но и характере получаемых зависимостей. В качестве примера мы остановимся ниже на влиянии сочетания метода измерений и устройства крана, открывающего отверстие сопла. В проведенной работе высота к фонтана определялась как среднее арифметическое из высот и Л2 = = к1 + Ак расположения горизонтальной площадки, при которых она смачивается (/ц) или не смачивается (/г2) брызгами. Оказалось, что при значениях к в несколько метров величина АН может быть доведена до —0,15 м, что обеспечивает точность порядка нескольких процентов. При проведении опытов площадка с размерами 0,4ХОД м располагалась с помощью блока или консоли над соплом на различных заданных высотах и фиксировался факт ее смачивания или не-смачивания брызгами. Для фиксации к нижней стороне площадки крепился лист бумаги, предварительно покрытый слоем «побелки». Выбрасываемая вода предварительно слегка подкрашивалась и, попадая на побеленную бумагу, давала четко различимое пятно, размеры этого пятна в известной стеупени характеризовали количество долетевшей жидкости. Если, например, площадка располагалась у верхней границы фонтана, то на ней фиксировалось несколько маленьких самостоятельных пятен, соответствующих попаданию отдельных капель.

При сравнительно малых напорных давлениях рн и диаметрах сопла*, когда скорости и расходы вылетающих струй были невелики, изложенная выше методика изменялась за счет открытия заслонки на время до 10—15 с и опускания подвешенного на блоке щита с бума-

* Давление рн однозначно связано со скоростью вылета струи, Vс —

/— ■ , где С — коэффициент внутренних потерь (£ = 0,3).

рО-К)

гой до появления на нем пятен. Этот путь был несколько более оперативным. Результаты измерения обоими методами удовлетворительно согласовывались между собой.

Забегая несколько вперед (рис. 3), заметим, что высота к фонтана в зависимости от скорости вылета струи vc имеет максимум и растет с увеличением диаметра сопла. Разберем с учетом этих обстоятельств и изложенного выше способа измерения к вопрос о влиянии на зависимость к(ис), получаемую в опытах, устройства крана, отпирающего и запирающего сопло.

Рассмотрим два типа затворных устройств, схематически показанных на рис. 2. В случае крана, при его открытии, давление в точке А возрастает от атмосферного до заданного рн. Размер отверстия сопла сохраняется. В случае заслонки давление в точке А и перед ее открытием и после равно рн, но размер отверстия при открытии возрастает. Предположим, ЧТО ОПЫТ проводится на режиме, где Рп>Рн.х (Рп.м — давление, соответствующее максимуму кривой к(рп)) открывая кран и, следовательно, повышая давление, прежде чем установится рн, получим давление рн.м, и струйка, поднявшись на высоту ктах, смочит индикаторную бумагу. В результате вместо зависимостей на рис. 3 получим зависимости, проведенные штрихами на этом же рисунке. Переменность эквивалентного отверстия при открытии сопла заслонкой не приведет к завышению подъема, так как к (О) —возрастающая функция.

2. Результаты испытаний представлены на рис. 3 в виде проведенных через экспериментальные точки зависимостей высоты к подъема струй от скорости ис истечения из сопла для диаметров сопел £> = = 0,5; 1 и 1,5 мм. Характер зависимостей /г(ус) идентичен для всех диаметров. При некоторой скорости, хотя это кажется парадоксальным, высота к достигает максимума, а с дальнейшим ростом скорости уменьшается и имеет тенденцию приблизиться к горизонтальной асимптоте. Увеличение диаметра сопла для всех скоростей приводит к увеличению к и менее резко выраженному максимуму. Высоты подъема, особенно при больших скоростях, в десятки раз меньше высот, которые были бы при тех же скоростях вылета струй в пу-

VI

стоту. Для этого случая зависимость к’ —проведена на рис. 3

^ £

штрихпунктиром.

На рис. 4 при тех же обозначениях, что и на рис. 3, опытные данные построены в безразмерных координатах: по оси ординат отло-

_ д 1)“^

жено отношение /г = , по оси абсцисс — число Фруда Рг = Рис. 4

и у gD

показывает, что весомость является определяющим фактором только до чисел Рг<50-^100, где безразмерные зависимости к(¥г) для различных диаметров сопел близки между собой. При Рг>100 кривые Я (Рг) для различных диаметров начинают существенно расходиться, причем чем меньше диаметр, тем больше к при том же значении числа Фруда. На этих режимах имеем дело, очевидно, с существенным проявлением «масштабного эффекта», обусловленного взаимодействием струи с окружающим ее воздухом, т. е. с процессами дробления струи и сопротивлением полету образующихся частиц. Зависимость высоты подъема от скорости при полете струи в пустоте, показанная на рис. 3 штрихпунктиром, имеет, очевидно, в безразмерных координатах вид г Рг3

2 ’

Можно сопоставить результаты проведенных опытов с некоторыми схематизированными расчетами. В первом случае предположим, что струя разбивается на сферические капли вскоре после выхода из сопла. Если рассматривать эти капли как твердые частицы, вылетающие вверх с начальной скоростью ис при сопротивлении, пропорциональном квадрату скорости, то высота их подъема может быть определена по известной формуле механики [4]

Й = й1п(, + ^)’ <»

где й — диаметр капли, а & — постоянная:

* = Т^У^4>7’10-4- (2)

Величины р’ и р — плотность воздуха и воды соответственно, а сх — коэффициент сопротивления, который для рассматриваемого диапазона чисел Рейнольдса может быть принят равным —0,5. Результаты расчетов высоты подъема для капель диаметром с( = 0,5; 1; 1,5 и 2 мм по формулам (1) и (2) показаны на рис. 3. Порядок величины подъема согласуется с опытом, если считать, что диаметры капель близки к диаметрам сопла, однако характер зависимостей высоты подъема от скорости существенно различается.

Логично рассмотреть расчеты, в которых наибольший диаметр капель определяется [5] критическим числом Вебера

/оч

^екр = р = 14. (3)

Если найти из (3) (1 и подставить в (1), то получим

(4)

2к?’у ^вкро^ 4 >

На рис. 3 штрихами показана зависимость Н(ис), рассчитанная по {4) при & = 4,7-10-4 и Уе= 14.

Учет дробления по критерию (3) дает общий с экспериментом характер зависимости к(юс) с наличием максимума, но расчетная зависимость получается в отличие от опытов единой для всех диаметров

сопел. Кроме того, расчетные значения к в области больших скоростей вылета струи получаются существенно меньшими, чем в опытах. Это различие растет с ростом диаметра сопла. Таким образом, полное разъяснение физического механизма и теоретический расчет высоты подъема вертикальных струй требует дальнейших исследований.

Если принять струи из сопла .0=1,5 мм за «натуру», а струи из остальных сопел за ее модели в масштабе соответственно = £„/£>*,= = 1,5 и йг=3, то значения коэффициента масштабного эффекта кэфф = Ьл/Нш при моделировании по числу Фруда можно представить в виде зависимостей, показанных на рис. 5, из которых следует, что за счет масштабного эффекта пересчет по Фруду на натуру высоты подъема брызговых струй дает для Рг>100 преувеличенные значения. В условиях проведенных опытов поправочный коэффициент /гЭфф, учитывающий масштабный эффект, близок к 1 для Рг<100, достигает наименьших значений &Эфф = 0,65 при £*=1,5 и £Эфф = 0,4 при &г = 3 в области Рг^ЗОО и с дальнейшим ростом Рг снова увеличивается, принимая ассимптотические значения соответственно &Эфф~0,8 при £*=1,5 и /гЭфф = 0,7 при /гг = 3.

В первом приближении при оценках подъема вертикально летящих брызг от движения колес шасси по мокрому аэродрому (для обычно принимаемого масштаба £г = 5^6), можно считать,что &Эфф~0>5, т. е. что пересчет высоты по масштабу модели дает почти двукратное завышение высоты подъема брызг.

Разработанные методика и аппаратура обеспечили проведение исследований высоты подъема тонких высоконапорных вертикальных водяных струй.

Установлено парадоксальное, на первый взгляд, обстоятельство: с ростом напора или начальной скорости вылета струи высота к ее подъема сначала возрастает, а затем уменьшается и перестает зависеть от напора.

Указанный характер зависимости имеет место для всех испытанных диаметров струй. Причем высота подъема растет с увеличением диаметра и для наибольшего из диаметров £)=1,5 мм достигала /г~7,5 м при ус“30 м/с. С ростом ис величина к несколько уменьшается и при скоростях 60<ис<90 м/с сохраняет постоянную величину.

Моделирование «по Фруду» справедливо только при сравнительно малых числах Рг = < 100; с ростом Рг появляется значитель-

ный масштабный эффект. Ориентировочно для применяемых при исследовании брызгообразования колес шасси масштабов & =/н//м = 5-т-6 коэффициент масштабного эффекта кЭфф = Нн/1гы имеет порядок —• 0,5, т. е. пересчет по Фруду высоты подъема брызг на натуру дает значения, примерно в два раза превышающие действительные.

Приведенные расчетные оценки по порядку величин и характеру зависимостей согласуются с результатами опытов, однако полное разъяснение механизма подъема высоконапорной струи и расчет высоты ее подъема требуют дальнейших исследований вертикальных и наклонных струй.

ЛИТЕРАТУРА

1. Рейнджер А. А., Никол л с И. А. Аэродинамическое дробление капель.— РТК, 1969, т. 7, № 2.

2. Г а р к у ш а В. И., Стасенко А. Л. Численное исследование парокапельных потоков с учетом фазовых переходов, коагуляции и аэродинамического дробления частиц. — Энергетика и транспорт, 1979, № 3.

3. Борисов А. А. и др. О режимах дробления капель и критериях их существования. — ИФМ, 1981, т. XI, № 1.

4. Теоретическая механика. Ч. 1/Под редакцией Н. В. Розе. — М.:

ГТТИ, 1932.

5. Эпштейн Л. А. Методы теории размерностей и подобия в задачах гидромеханики судов. — Л.: Судостроение, 1970.

Рукопись поступила 1/УШ 1988 г.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

высшая-математика — Найти высоту струи над горизонталью