Достаточно знать длину бокового ребра пирамиды, количество сторон многоугольника, лежащего в основании пирамиды, а также длину стороны основания (сторону многоугольника).
В основании правильной пирамиды всегда лежит правильный многоугольник. Любой правильный многоугольник можно вписать в окружность.
Есть такая формула:
a — длина стороны n-угольника (для правильного многоугольника).
L — длина окружности, описывающей этот многоугольник.
n — это количество сторон этого многоугольника
Если выразить эту формулу наоборот, то можно по стороне многоугольника найти длину окружности.
L=a*π/sin(180/n)
Зная длину окружности, можно найти радиус этой окружности:
L=2πR
R=L/(2π)
Подставляя L из первой формулы, получаем:
R = L/(2π) = a*π/(2π*sin(180/n)) = a/(2sin(180/n))
Теперь если приглядитесь к рисунку, то увидите, что радиус описанной окружности является также и катетом в прямоугольном треугольнике (игреком «y» на левой картинке).
А вертикальное ребро пирамиды это гипотенуза этого прямоугольного треугольника.
А искомая нам высота это второй катет этого прямоугольного треугольника.
По теореме Пифагора:
X²=Y²+h²
h²=X²-Y²
h=√(X²-Y²)
X нам известен — это длина боковой стороны пирамиды.
Y тоже известен — это расстояние от одного из углов основания пирамиды до центра пирамиды, и это же радиус описанной вокруг этого многоугольника окружности.
Y=R, а R равен: R=a/(2sin(180/n))
Итак подведём итог:
h=√(X²-Y²) = √(X²-R²) = √(X²-(a/(2sin(180/n)))²)
X — размер боковой стороны (ребра) пирамиды.
n — количество сторон многоугольника в основании.
a — размер стороны этого многоугольника в основании.
Более удобно эту формулу я отразил на рисунке.
УПРАВЛЕНИЕ
ОБРАЗОВАНИЯ
АДМИНИСТРАЦИИ ГОРОДА ХАРЦЫЗСКА
МУНИЦИПАЛЬНАЯ
ОБЩЕОБРАЗОВАТЕЛЬНАЯ ОРГАНИЗАЦИЯ
«ХАРЦЫЗСКАЯ
СРЕДНЯЯ ШКОЛА № 24»
Положение высоты в некоторых видах пирамид
11 класс
Мини – учебник по геометрии
______________________
______________________

Составитель:
учитель
математики
Заставная Н.Н.
г.
Харцызск
2020г.
|
Период: Информационно- познавательный |
Девиз: «Привет, проблема!» |
Механизм: Анализ восприятия |
Доминанта: Анализ, синтез, запоминание |
Внимательно изучи таблицу «Положение высоты в
некоторых видах пирамид». Определи, как ты воспринимаешь и владеешь полученной
информацией.
|
Полностью |
Наполовину |
Непонятно |
ПОЛОЖЕНИЕ
ВЫСОТЫ В НЕКОТОРЫХ ВИДАХ ПИРАМИД
|
|
|
Если в пирамиде Верно и обратное: |
|
|
Если в пирамиде |
|
|
Для решения используют прямоугольный |
|
|
|
|
Если в пирамиде грани Верно и обратное: |
|
|
Если в пирамиде
|
|
|
Для решения используют прямоугольный Для такого вида пирамид справедлива формула:
где |
|
|
|
|
Если в пирамиде |
|
|
Если в пирамиде |
|
|
|
|
Если в пирамиде |
|
|
|
|
Если плоскость |
|
|
|
|
Если плоскость |
|
|
|
Подумай, насколько |
|
|
Прочитай, |
Выдающийся математик — Архимед |
Великий математик, механик и инженер древности Архимед родился в 287
г. до н. э. (предположительно) в Сиракузах — богатом торговом городе Сицилии.
Отцом его был астроном Фидий, который привил сыну с детства любовь к математике,
механике и астрономии. В Александрии Египетской — научном и культурном центре
того времени — Архимед познакомился со знаменитыми александрийскими учеными,
астрономом Кононом, разносторонним ученым Эратосфеном, с которыми потом переписывался
до конца жизни. В знаменитой Александрийской библиотеке Архимед познакомился с
трудами Демокрита, Евдокса и других замечательных греческих геометров, о
которых он упоминал в своих сочинениях.
Уже при жизни Архимеда вокруг его имени создавались легенды, поводом
для которых служили его поразительные изобретения, производившие ошеломляющее
действие на современников.
Всем известен рассказ о том, как Архимед сумел определить, сделана ли
корона царя Гиерона из чистого золота. Благодаря этому случаю был открыт
основной закон гидростатики.
Другая легенда рассказывает, что построенный Гиероном в подарок
египетскому царю Птолемею роскошный корабль Сирокосия, никак не удавалось
спустить на воду. Архимед соорудил систему блоков, с помощью которых он смог проделать
это один, движением руки. Этот случай послужил поводом его крылатых слов
..Дайте мне точку опоры, и я сдвину Землю.
|
|
Архимед |
Знаменитый историк древности Полибий писал: «Такова чудесная сила
одного человека, одного дарования…римляне могли бы быстро овладеть городом, если
бы кто-либо изъял из среды сиракузян одного старца».
Архимед был убит римским солдатом после взятия Сиракуз вследствие
измены.
Плутарх сохранил нам яркий рассказ о его смерти: «К Архимеду подошел
солдат с мечом в руке, что бы убить его. Но Архимед настойчиво просил его подождать
одну минуту, чтобы задача, которой он занимался, не осталась не решенной;
солдат ,которому не было дела до его доказательства, пронзил его своим мечом»
Архимед был замечательным механиком – практиком и теоретиком, но
основным делом его жизни была математика. По словам Плутарха, Архимед был
просто одержим ею. Он забывал о пище, совершенно не заботился о себе. Его
работы относились почти ко всем областям математики того времени.
Так, он нашел все полуправильные многогранники, которые теперь носят
его имя, значительно развил учения о конических сечениях, дал геометрический
способ решения кубических уравнений вида , корни
которых он находил с помощью пересечения параболы и гиперболы Архимед провёл и
полное исследование этих уравнений.
Но главное его внимание было сосредоточено на трех типах проблем.
1.
Определение площадей криволинейных фигур или
объёмов тел. Греки до Архимеда умели находить площади прямолинейных фигур, площадь
круга, объём призмы, пирамиды цилиндра и конуса, но только Архимед нашел общий
метод, позволяющий найти любую площадь или объём. Идеи Архимеда легли в основу интегрального
исчисления. Сам Архимед определил с помощью своего метода площади и объёмы
почти всех тел, которые рассматривались в античной математике. Лучшим своим
достижением он считал определение поверхности и объёма шара. Он просил выбить
на своей могиле шар, вписанный в цилиндр.
2.
Как определить касательную в любой точке кривой.
Древние греки умели находить касательную к окружности, эллипсу, гиперболе и
параболе. Первый общий метод решения и этой задачи был найден Архимедом. Этот
метод лёг в основу дифференциального исчисления.
3.
В математике, физике и астрономии очень важно уметь
находить наибольшие и наименьшие значения изменяющихся величин – их экстремумы.
Например, как среди цилиндров, вписанных шар, найти цилиндр, имеющий наибольшей
объём? Все такие задачи могут быть решены с помощью дифференциального
исчисления. Архимед первым увидел связь этих задач с проблемами определения
касательных и показал, как с их помощью можно решать задачи на экстремумы.
Огромное значение для развития математики имело вычисленное Архимедом
отношение длины окружности к диаметру, т.е. число ,с
большой степенью точности.
Идеи Архимеда почти на две тысячи лет опередили своё время. Только в XVII в. ученые смогли продолжить и развить труды великого греческого
математика. Только тогда было раскрыто их подлинное значение.
Лейбниц, один из творцов дифференциального и интегрального исчислений, писал „Внимательно читая сочинения Архимеда, перестаёшь
удивляться всем новейшим открытиям геометров”
Как Вы считаете, можем ли мы оценить Архимеда, только как учёного, зная его открытия?
Мог ли он совершить их, если бы не имел целью улучшение жизни граждан своего города?
Как Вы считаете, должен ли учёный иметь гражданскую позицию или
заниматься только наукой?
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
|
Период: нормативно — регуляционный |
Девиз: «Освоим изученное!» |
Механизм: добывание, осмысление, нормирование |
Доминанта: мышление, личностная адаптация |
Тебе предстоит решить 5 задач. Выбери уровень
сложности: достаточный (средний) или высокий. Отметь, насколько понятным было
решение каждой задачи, закрась ту часть круга, которая соответствует твоему
уровню понимания решения.
|
Думай Решай Записывай |
|
|
*Достаточный уровень сложности |
**Высокий уровень сложности |
|
Задача |
|
|
Основанием пирамиды является прямоугольник со стороною |
Основанием пирамиды является равнобедренный треугольник, площадь которого |
|
Задача |
|
|
Сторона основания правильной треугольной пирамиды равна 8 |
Основание пирамиды – равнобедренный треугольник с боковой стороной |
|
Задача |
|
|
Основанием пирамиды является правильный треугольник. Одна из боковых |
Основание пирамиды – равнобедренный треугольник с боковой стороной |
|
Задача |
|
|
Основанием пирамиды |
Основание пирамиды |
|
Задача |
|
|
Основанием пирамиды является прямоугольный треугольник с гипотенузой |
В основании пирамиды лежит квадрат. Две боковые смежные грани |
|
Подведи |
|
Подчеркни, во сколько баллов ты оцениваешь свой
результат работы.
1 2 3 4 5
Наклонная высота квадратной пирамиды — это расстояние между ее вершиной, или вершиной , до земли вдоль одной из ее сторон. Вы можете определить наклонную высоту, представив ее как один элемент треугольника. Таким образом, вы можете использовать теорему Пифагора для сравнения высоты наклона с высотой пирамиды и длиной сторон
Нахождение высоты наклона в виде треугольника
Чтобы определить высоту уклона, вы можете понимать высоту уклона как одну линию в прямоугольном треугольнике внутри пирамиды. Две другие линии треугольника будут высотой от центра пирамиды до ее вершины и линией, равной половине длины одной из сторон пирамиды, которая соединяет центр с нижней частью уклона. Длина уклона — это сторона треугольника, противоположная прямому углу — эта сторона называется гипотенузой .
Теорема Пифагора — это математическая формула, которая рассказывает, как разные стороны прямоугольного треугольника связаны друг с другом. Если a и b — две стороны, соединенные прямым углом, а c — гипотенуза, то:
а ^ 2 + б ^ 2 = с ^ 2
«^ 2» в формуле означает, что вы возводите числа в квадрат . Квадрат числа означает, что вы умножаете его на себя. Таким образом, с ^ 2 так же, как с раз с.
Нахождение высоты и базы
Если вы знаете высоту пирамиды и длину одной из сторон ее квадратного основания, вы можете использовать теорему Пифагора для определения высоты наклона. «A» и «b» в теореме будут высотой и половиной длины одной стороны, а «c» будет высотой наклона, поскольку высота наклона является гипотенузой треугольника:
высота ^ 2 + половина длины ^ 2 = наклонная высота ^ 2
Скажем, у вас есть пирамида высотой 4 дюйма и квадратное основание со сторонами 6 дюймов в длину. Чтобы найти половину длины стороны, разделите длину стороны на 2. Таким образом, эта пирамида будет иметь высоту 4 дюйма и половину длины 3 дюйма.
Выравнивание высоты и основания
В теореме Пифагора квадрат гипотенузы равен сумме квадратов двух других сторон. Теперь возведите в квадрат высоту и половину длины и сложите квадратные числа вместе.
Возьмите пирамиду с высотой 4 дюйма и половиной длины 3 дюйма. Квадраты 4 и 3. Помните, что число в квадрате — это число, умноженное на себя. Так:
4 ^ 2 + 3 ^ 2 = высота наклона ^ 2 4 x 4 + 3 x 3 = высота наклона ^ 2
Затем вы добавляете эти два числа вместе:
16 + 9 = высота наклона ^ 2 25 = высота наклона ^ 2
Таким образом, наклонная высота в квадрате равна 25.
Принимая квадратный корень
Теперь вы знаете, что квадрат наклонной высоты — или умноженный на нее — равен 25. Чтобы найти высоту наклонной части, найдите число, умноженное на себя, равное 25. Это называется взятием квадратного корня из 25. Если вы проверяете малые числа, умноженные на себя, вы обнаружите, что 5 умножить на 5 равно 25. Итак:
5 дюймов = наклонная высота
Не всегда можно найти квадратные корни чисел, угадывая и проверяя. Многие числа не имеют точных квадратных корней, поэтому вам может понадобиться калькулятор, чтобы найти приближение.
A square pyramid’s slant height is the distance between its top, or apex, to the ground along one of its sides. You can solve for slant height by visualizing it as one element of a triangle. Doing so, you can use the Pythagorean Theorem to compare slant height to the pyramid’s height and side lengths
Finding Slant Height as a Triangle
To solve for slant height, you can understand slant height as one line in a right triangle inside the pyramid. The triangle’s other two lines will be the height from the center of the pyramid to its apex, and a line half the length of one of the pyramid’s sides that connects the center to the bottom of the slant. The slant length is the side of the triangle opposite to the right angle — this side is called the hypotenuse.
The Pythagorean Theorem is a mathematical formula that tells you how the different sides of a right triangle relate to each other. If a and b are the two sides connected by the right angle, and c is the hypotenuse, then:
a^2 + b^2 = c^2
The «2» in the formula signified that you are squaring the numbers. To square a number means you are multiplying it by itself. So c2 is the same as c × c.
Finding the Height and Base
If you know the height of a pyramid and the length of one of side of its square base, you can use the Pythagorean Theorem to solve for slant height. The «a» and «b» in the Theorem will be height and half the length of one side, and «c» will be slant height, since slant height is the hypotenuse of the triangle:
text{height}^2 + text{half length}^2 = text{slant height}^2
Say you have a pyramid that is 4 inches high, and has a square base with sides 6 inches long. To find half the side length, divide the side length by 2. So this pyramid will have a height of 4 inches and a half length of 3 inches.
Squaring the Height and Base
In the Pythagorean Theorem, the hypotenuse squared is equal to the sum of the squares of the other two sides. Now square the height and the half length, and add the squared numbers together.
Take the pyramid with 4 inch height and 3 inch half length. Square 4 and 3. Remember that a number squared is that number times itself. So:
4^2 + 3^2 = text{slant height}^2 \ (4 × 4) + (3 × 3) = text{slant height}^2
You then add these two numbers together:
16 + 9 = text{slant height}^2 \ 25 = text{slant height}^2
So the slant height squared is equal to 25.
Taking the Square Root
You now know that the slant height squared – or multiplied by itself – is 25. To find the slant height, find the number that, multiplied by itself, equals 25. This is called taking the square root of 25. If you check small numbers multiplied by themselves, you will find that 5 times 5 is equal to 25. So:
sqrt{25} = 5 text{ inches} =text{ slant height}
It’s not always possible to find the square roots of numbers by guessing and checking. Many numbers do not have exact square roots, so you may need a calculator to find an approximation.
Как найти высоту пирамиды
Любое геометрическое тело может быть интересно не только школьнику. В окружающем мире довольно часто встречаются предметы в форме пирамиды. И это не только знаменитые египетские гробницы. Часто говорят о целебных свойствах пирамиды, и кому-то наверняка захочется испытать их на себе. Но для этого надо знать ее размеры, в том числе высоту.

Вам понадобится
- Математические формулы и понятия:
- Определение высоты пирамиды
- Признаки подобия треугольников
- Свойства высоты треугольника
- Теорема синусов и косинусов
- Таблицы синусов и косинусов
- Инструменты:
- линейка
- карандаш
- транспортир
Инструкция
Вспомните, что такое высота пирамиды. Это есть перпендикуляр, опущенный из вершины пирамиды к ее основанию.
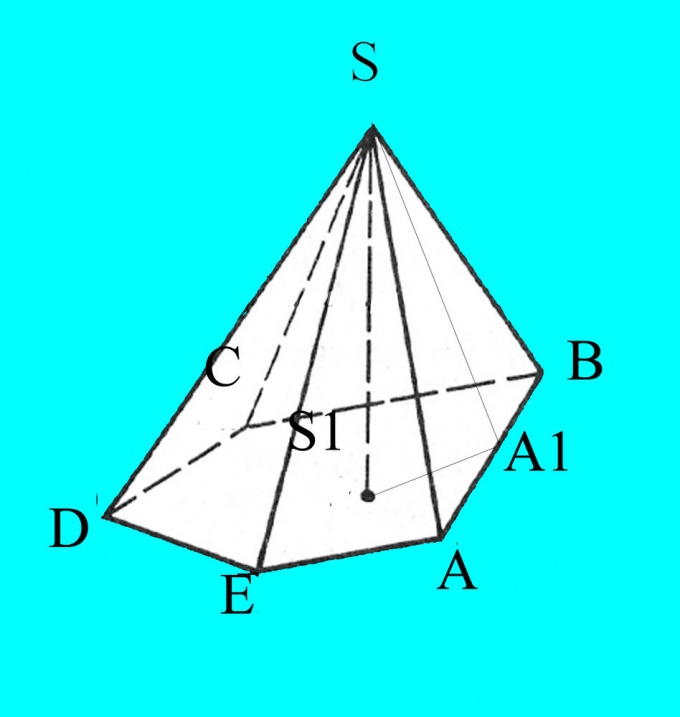
Постройте пирамиду по заданным параметрам. Обозначьте ее основание латинскими буквами А, B, C,D… в зависимости от количества углов. Вершину пирамиды обозначьте S.
Вам известны стороны, углы основания и наклона ребер к основанию. Чертеж получится в проекции на плоскости, поэтому для верности обозначьте на нем известные вам данные. Из точки S опустите высоту пирамиды и обозначьте ее h. Точку пересечения высоты с основанием пирамиды обознчьте S1.
Из вершины пирамиды проведите высоту любой боковой грани. Обозначьте точку ее пересечения с основанием, например, А1. Вспомните свойства высоты остроугольного треугольника. Она делит треугольник на два подобных прямоугольных треугольника. Вычислите косинусы нужных вам углов по формуле
Cos(A) = (b2+c2-a2)/(2*b*c), где а,b и с — стороны треугольника, в данном случае АSB (a=BA,b=AS,c=AB).
Вычислите высоту боковой грани SA1 по косинусу угла АSA1, равного углу SBA из свойств высоты треугольника, и известному боковому ребру AS.
Соедините точки А1 и S1. У вас получился прямоугольный треугольник, в котором вам известна гипотенуза SA1 и угол наклона боковой грани пирамиды к ее основанию SA1S1. По теореме синусов вычислите катет SS1, который одновременно является и высотой пирамиды.
Видео по теме
Обратите внимание
Для вычисления высоты любой пирамиды необходимо сначала вычислить один из боковых треугольников.
В правильной пирамиде высота боковой грани называется апофемой и делит сторону основания пирамиды пополам.
Полезный совет
В правильной пирамиде все стороны наклонены к основанию под одним и тем же углом, поэтому высоту пирамиды можно вычислить и без построения дополнительных треугольников.
Высота боковой грани делит ее на 2 подобных прямоугольных треугольника. Соответственно, угол SAB равен углу А1SB.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
















