Как найти высоту конуса вписанного в шар - AvtoShod.ru

ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

похожие вопросы 5

Источник

��

�� ߣ��,
�� R .

��

�� P – �� , h – �� , r – ��
�� (��.1). �� , �� ţ
�� O . � �� R (��.2), � ��
�� ABP � �� P , �� AB = 2r �
�� PM = h . �� PM ��
�� K . �� PBK – �� , � BM – �� ,
��ģ�� . ��

BM2 = PM· KM, �� r2 = h(2R — h).

�� V(h) – ��ߣ� ��. ��

V(h) = π r2h = π h2(2R — h).

�� , ��
�� V(h) = π h2(2R — h) �� (0;2R) .

�� V’(h) = 0 , ��ģ� ��
V(h) . �� , ��
(0;2R) .

V’(h) = ( π (2Rh2 — h3))‘
= π(4Rh — 3h2) = π h(4R — 3h) = 0.

�� (0;2R) ��
h = R . �� h = R ��
�� . ��, �� (0;R)
�� V(h) ��, � �� (R;2R) – ��.
��, �� h = R ��ߣ� �� . ��

r = = = R.

�� ң� ��, ��, ��

V(h) = π h2(2R — h) =
π · 4· h· h· (2R — h)

π()3
= π · = ,

��ޣ� �� , �� h = 2R — h , �.�. �� h = R .
��, �� ߣ�� h= R .
��

r = = = R.

��

R ; R .

��


web-��
��	�� .�.��
URL	http://zadachi.mccme.ru
��
��	7443

Источник

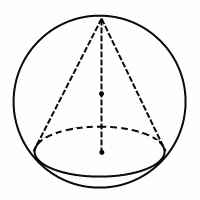
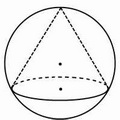
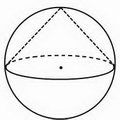
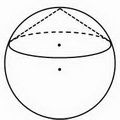
Решение задач на конус, вписанный в шар (конус, вписанный в сферу) сводится к рассмотрению одного или нескольких треугольников.

Конус вписан в шар, если его вершина и окружность основания лежат на поверхности шара, то есть на сфере. Центр шара лежит на оси конуса.

При решении задач на конус, вписанный в шар, удобно рассматривать сечение комбинации тел плоскостью, проходящей через ось конуса и центр шара. Сечение представляет собой большой круг шара (то есть круг, радиус которого равен радиусу шара) с вписанным в него равнобедренным треугольником — осевым сечением конуса. Боковые стороны этого треугольника — образующие конуса, основание — диаметр конуса.

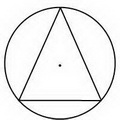
Если угол между образующими острый, центр описанного круга лежит внутри треугольника (соответственно, центр описанного около конуса шара — внутри конуса).

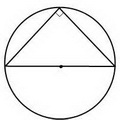
Если угол между образующими прямой, центр круга лежит на середине основания треугольника (центр шара совпадает с центром основания конуса).

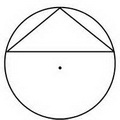
Если угол между образующими тупой, центр круга лежит вне треугольника (центр описанного шара — вне конуса).

Если в условии задачи не сказано, где именно лежит центр описанного шара, желательно рассмотреть, как могут повлиять на решение различные варианты его расположения.

Рассмотрим конуса и описанного около него шара плоскостью, проходящей через ось конуса и центр шара. Здесь SO=H — высота конуса, SB=l — образующая конуса,SO1=O1B=R — радиус шара, OB=r — радиус основания конуса, ∠OSB=α — угол между высотой и образующей конуса.

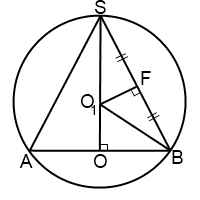
Треугольник SO1B — равнобедренный с основанием SB (так как SO1=O1B=R). Значит, у него углы при основании равны: ∠OSB=∠O1BS=α, и O1F — медиана, высота и биссектриса. Отсюда SF=l/2.

При решении задач на конус, вписанный в шар, можно рассмотреть прямоугольные треугольники SFO1 и SOB. Они подобны (по острому углу S). Из подобия треугольников

$[frac{{SF}}{{SO}} = frac{{S{O_1}}}{{SB}} = frac{{F{O_1}}}{{OB}}.]$

$[frac{{frac{l}{2}}}{H} = frac{R}{l}, Rightarrow frac{l}{{2H}} = frac{R}{l}, Rightarrow {l^2} = 2HR.]$

В прямоугольном треугольнике SOB ∠OBS=90º — ∠OSB=90º-α. По теореме Пифагора

$[S{B^2} = S{O^2} + O{B^2}, Rightarrow {l^2} = {H^2} + {r^2}.]$

В прямоугольном треугольнике O1OB ∠OBO1=90º — ∠O1BS=90º — α — α=90º — 2α.

$[OB = {O_1}B cdot cos angle OB{O_1}]$

$[OB = Rcdotcos ({90^o} - 2alpha ) = Rcdotsin 2alpha , Rightarrow ]$

Если продлить SO до пересечения с окружностью, получим прямоугольный треугольник SBM (∠SBM=90º как вписанный угол, опирающийся на диаметр SM). В нем BO- высота, проведенная к гипотенузе. По свойствам прямоугольного треугольника

$[O{B^2} = SO cdot OM, Rightarrow {r^2} = H cdot (2R - H)]$

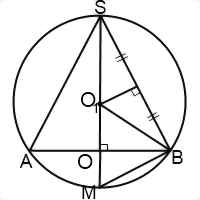
и уже полученное соотношение

$[S{B^2} = SO cdot SM, Rightarrow {l^2} = 2RH.]$

Источник

Выразим параметры вписанного конуса через его переменную высоту H и заданный радиус шара R (константа).

Vконуса = (1/3) SoH.

Радиус ro основания конуса равен:

ro² = R² — (H — R) ².

So = πro² = π * (R² — (H — R) ²).

Получаем формулу объёма:

V = (1/3) * π * (R² — (H — R) ²) * H.

Для нахождения экстремума находим производную объёма по Н и приравниваем нулю.

V’ (H) = (1/3) πH * (4R — 3H) = 0.

Нулю может быть равно только выражение в скобках.

4R — 3H = 0.

Отсюда получаем ответ: высота конуса при максимальном объёме равна H = (4/3) R.

Источник

Вопросы Учеба и наука Математика в шар вписан конус. Найдите высоту…

Даниил

28.05.20

Учеба и наука / Математика

2 ответа

Ответы

Анастасия

5.0

26 отзывов

Рейтинг:
22 609

28.05.20

Яков

0 отзывов

Рейтинг:
4 715

Радиус шара R = 5, радиус конуса r = 4 и высота конуса H связаны соотношением:
R^2 = (H — R)^2 + r^2
Таким образом, получаем:
25 = (H — 5)^2 + 16
(H — 5)^2 = 9
H — 5 = 3
H — 5 = -3
Окончательно получаем:
H = 8, либо H = 2

Ответ: H = 8, либо H = 2

28.05.20

Михаил Александров

4.9

596 отзывов

Рейтинг:
3681 901

Эксперт месяца

Читать ответы

Андрей Андреевич

4.9

834 отзыва

Рейтинг:
482 107

2-й в Учебе и науке

Читать ответы

Eleonora Gabrielyan

4.9

280 отзывов

Рейтинг:
244 836

3-й в Учебе и науке

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

1.Найти угловой коэффициент
касательной к графику функции
f(x) = 2х^2+x в точке хнулевое =-2 ; 2.Напишите уравнение
касательной к графику функции f(x)=-x^2-3x+2 в точке с абциссой хнулевое=-1

2 ответа

15.03.18

Егоров Д.А.

Учеба и наука > Математика

Решено

найти значение выражения (-12.4+8.9)х1.37

1 ответ

19.05.15

таня

Учеба и наука > Математика

Рассчитай расстояние вершины куба до диагонали куба, которая не проходит через эту вершину, если ребро куба — 36 см.

1 ответ

25.03.20

Александр

Учеба и наука > Математика

Вычисли сумму первых 11 членов арифметической прогрессии (an), если даны первые члены: 0;8;…

S11=

1 ответ

21.02.16

Вася

Учеба и наука > Математика

Постройте график функции у=-x^2-2x+3. С помощью графика найдите :
1) промежутки возрастания и убывания функции;
2) наибольшее значение

1 ответ

04.02.18

Вики

Учеба и наука > Математика

Источник

�������

�������

�����

��������� � ���������� �������������

Ответы

Анастасия

Яков

Михаил Александров

Андрей Андреевич

Eleonora Gabrielyan

Не пропустите также:

��

��

��

��