�������
������� ������ � ������ ��������� ������ ����������� ��ߣ��,
���������� � ����� ������� R .
�������
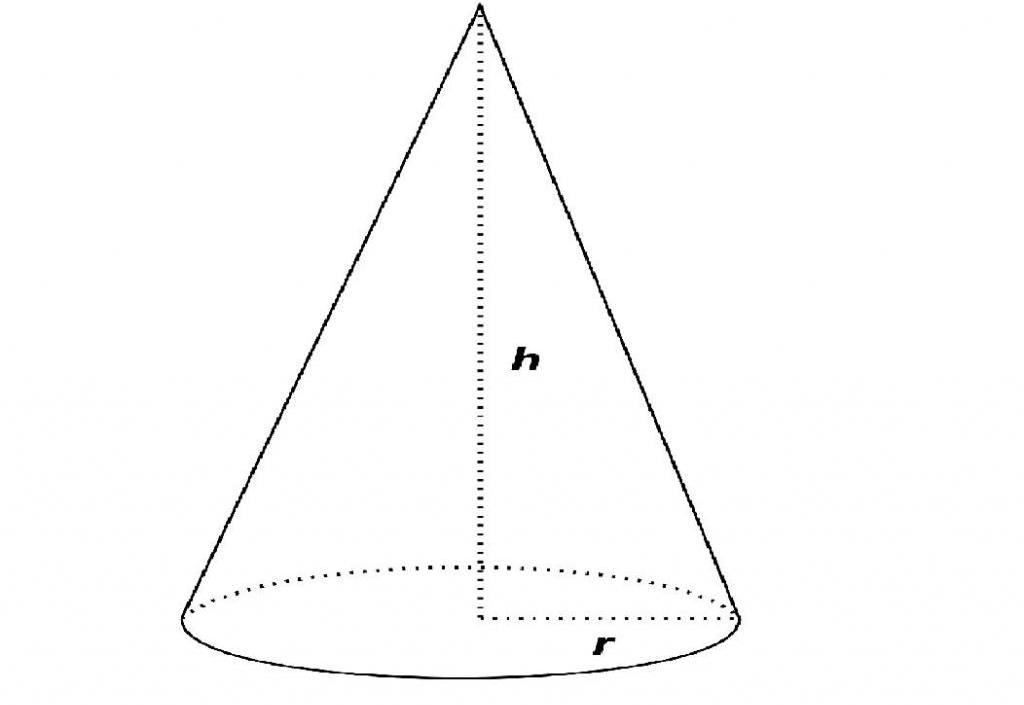
����� P – ������� ������, h – ��� ������, r – ������
��������� (���.1). ���������� ������� ����� ����������, ���������� ����� ţ
����� O . � ������� ��������� ���������� ������� R (���.2), � ������� ������
�������������� ����������� ABP � �������� P , ���������� AB = 2r �
������� PM = h . ��������� ������ PM �� ����������� � ����������� �
����� K . ����� PBK – ������������� �����������, � BM – ��� ������,
�����ģ���� �� ������� ������� ����. �������
BM2 = PM· KM, ��� r2 = h(2R — h).
����� V(h) – ��ߣ� ������. �����
V(h) = π r2h =
π h2(2R — h).
����� �������, ������ �������� � ���������� ����������� ��������
������� V(h) = π h2(2R — h) �� ��������� (0;2R) .
����� ��������� V’(h) = 0 , ���ģ� ����������� ����� �������
V(h) . ���������� ������ �� �� ���, ������� ����������� ����������
(0;2R) .
V’(h) = ( π (2Rh2 — h3))‘
= π(4Rh — 3h2) =
π h(4R — 3h) = 0.
���������� (0;2R) ����������� ������������ ������ ����� ���������
h = R . ��� �������� ����� ����� h =
R �����������
������ ���� � ����� �� �����. ������, �� ���������� (0;R)
������� V(h) ����������, � �� ���������� (R;2R) – �������.
�������������, ��� h = R ��ߣ� ������ ����������. ��� ����
r = =
=
R
.
�������� ����������� ���� ��� �ң� �����, �������, ���
V(h) = π h2(2R — h) =
π · 4·
h·
h· (2R — h)
π(
)3
= π ·
=
,
���ޣ� ��������� �����������, ���� h = 2R — h , �.�. ��� h =
R .
�������������, ���������� �������� ��ߣ�� ������ ����������� ��� h= R .
��� ����
r = =
=
R
.
�����
R ;
R
.
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ���������� | |
| ����� | 7443 |
Как найти высоту конуса. Теория и формулы
Прочитав данную статью, вы узнаете, как найти высоту конуса. Приведенный в ней материал поможет глубже разобраться в вопросе, а формулы окажутся весьма полезными в решении задач. В тексте разобраны все необходимые базовые понятия и свойства, которые обязательно пригодятся на практике.
Фундаментальная теория
Перед тем, как найти высоту конуса, необходимо разобраться с теорией.
Конус — фигура, которая плавно сужается от плоского основания (часто, хотя и необязательно, кругового) до точки, называемой вершиной.
Конус формируется набором отрезков, лучей или прямых, соединяющих общую точку с основанием. Последнее может ограничиваться не только окружностью, но и эллипсом, параболой или гиперболой.
Ось — это прямая (если таковая имеется), вокруг которой фигура имеет круговую симметрию. Если угол между осью и основой составляет девяносто градусов, то конус принято называть прямым. Именно такая вариация чаще всего встречается в задачах.
Если в основе лежит многоугольник, то объект является пирамидой.
Отрезок, соединяющий вершину и линию, ограничивающую основание, называют образующей.
Как найти высоту конуса
Подойдем к вопросу с другой стороны. Для начала используем объем конуса. Чтобы его найти нужно вычислить произведение высоты с третьей частью площади.
Очевидно, что из этого можно получить формулу высоты конуса. Достаточно лишь сделать правильные алгебраические преобразования. Разделим обе части равенства на S и умножим на тройку. Получим:
Теперь вы знаете, как найти высоту конуса. Однако для решения задач вам могут понадобиться и другие знания.
Важные формулы и свойства
Приведенный ниже материал однозначно поможет вам в решении конкретных задач.
Центр массы тела находится на четвертой части оси, начиная от основы.
В проективной геометрии цилиндр — это просто конус, вершина которого находится на бесконечности.
Следующие свойства работают только для прямого кругового конуса.
- Даны радиус основания r и высота h, тогда формула для площади будет выглядеть так: П × r 2 . Соответственно изменится и окончательное уравнение. V = 1/3 × П × r 2 × h.
- Вычислить площадь боковой поверхности можно перемножив число «пи», радиус и длину образующей. S = П × r × l.
- Пересечение произвольной плоскости с фигурой является одним из конических сечений.
Часто встречаются задачи, где необходимо использовать формулу для объема усеченного конуса. Она выводится из обычной и имеет такой вид:
V = 1/3 × П × h × (R 2 + Rr + r 2 ), где: r -радиус нижнего основания, R — верхнего.
Всего этого будет вполне достаточно для решения разнообразнейших примеров. Разве что могут понадобиться знания, не связанные с этой темой, например, свойства углов, теорема Пифагора и другое.
Радиус и высота конуса
Свойства
Через радиус конуса можно найти все параметры конуса, связанные с основанием, а значение высоты позволяет вычислить площади, объемы и все остальные объемные параметры конуса. Так, диаметр конуса равен удвоенному радиусу, периметр окружности в основании вычисляется по стандартной формуле через радиус, равно как и площадь основания. d=2r P=2πr S_(осн.)=πr^2
Прямоугольный треугольник, образованный высотой конуса, радиусом основания и образующей конуса, связывает эти три значения теоремой Пифагора, по которой можно вычислить неизвестную образующую, а также угол между образующей и основанием. Тем временем, угол α рассчитывается из равнобедренного треугольника, сформированного двумя образующими и диаметром из того принципа, что сумма всех углов в треугольнике равна 180 градусам. (рис.40.1, 40.2) l=√(h^2+r^2 ) tanβ=h/r α=180°-2β
Чтобы найти площадь боковой поверхности конуса, необходимо умножить радиус и апофему на число π. Площадь полной поверхности конуса состоит из площади его основания и площади боковой поверхности. В обеих формулах вместо апофемы нужно подставить квадратный корень через высоту и радиус, полученный по теореме Пифагора. S_(б.п.)=πrl=πr√(h^2+r^2 ) S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)=πr(√(h^2+r^2 )+r)
Чтобы найти объем конуса, достаточно знать значения радиуса и высоты, тогда формула объема выглядит как произведение числа π на квадрат радиуса и высоту, деленное на три. V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, зависит не только от радиуса основания конуса и его высоты, но и от образующей, поэтому чтобы вычислить радиус вписанной сферы конуса через радиус конуса и высоту, нужно вместо образующей подставить полученное для нее выше выражение. Радиус описанной сферы может быть представлен сразу формулой только с переменными радиуса и высоты. (рис.40.3, 40.4) r_1=hr/(l+r)=rh/(√(h^2+r^2 )+r) R=(h^2+r^2)/2h
Формула высоты конуса через радиус окружности
Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники . На рисунке 168 осевым сечением конуса является треугольник ABP ( АР = ВР ). Угол АPВ называют углом при вершине осевого сечения конуса .
Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.
Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP ).
Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).
Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением .

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.
ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60 ° ; б) в 90 ° . Найти площадь сечения.
Решени е. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.
Хорда АВ окружности основания стягивает дугу в 60 ° , значит, △ AOB — правильный и АВ = R .
Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S △ ABP = АВ • РC. Имеем: ОР = R (по условию); в △ A OB : ОС = ; в △ ОСР : CP = = .
Тогда S △ ABP = АВ • РС = .
Ответ: а) .
18.3. Касательная плоскость к конусу
Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.
Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.
Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.
18.4. Изображение конуса
Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).
Для достижения наглядности изображения невидимые линии изображают штрихами.
Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.
18.5. Развёртка и площадь поверхности конуса
Пусть l — длина образующей, R — радиус основания конуса с вершиной Р .
Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a ), то получим развёртку поверхности конуса (рис. 176, б ), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса ; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):
α = .
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.
Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле
S бок = α • l 2 , (1)
где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = , получаем:
Таким образом, доказана следующая теорема.
Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼
Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.
S кон = π Rl + π R 2 . (3)
Следствие. Пусть конус образован вращением пря м оугольного треугольника ABC вокруг катета АС (рис. 177). Тогда S бок = π • BC • АВ. Если D — середина отрезка АВ, то AB = 2 AD, поэтому
S бок = 2 π ВС • AD. (4)
Проведём DE ⟂ АB ( E ∈ l = AС ) . Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А ) имеем
= ⇒ BC • AD = DE • АС. (5)
Тогда соотношение (4) принимает вид
S бок = (2 π • DE ) • AC, (6)
т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.
Это следствие будет использовано в п. 19.7.
18.6. Свойства параллельных сечений конуса
Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Доказательств о. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α , параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).
Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β , α || β , то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O 1 = α ∩ РО. Обозначим этот круг F 1 .
Рассмотрим гомотетию с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия отображает основание F конуса на его параллельное сечение — круг F 1 , при этом центр О основания отображается на центр О 1 круга F 1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии точка X отображается на точку X 1 = РX ∩ α . Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:
= = k, (*)
где k — коэффициент гомотетии , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.
А поскольку гомотетия является подобием, то круг F 1 , являющийся параллельным сечением конуса, подобен его основанию.
Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO 1 : Р О , где РO 1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
S сечен : S основ = k 2 = : PO 2 .
18.7. Вписанные в конус и описанные около конуса пирамиды
Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.
Для построения изображения правильной пирамиды, вписанной в конус:
— строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;
— соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;
— выделяют видимые и невидимые (штрихами) линии изображаемых фигур.
На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:
— прямоугольный треугольник (см. рис. 179);
http://geleot.ru/education/math/geometry/calc/cone/radius_and_height
http://reader.lecta.rosuchebnik.ru/demo/8285/data/chapter19.xhtml
ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
Через радиус конуса можно найти все параметры конуса, связанные с основанием, а значение высоты позволяет вычислить площади, объемы и все остальные объемные параметры конуса. Так, диаметр конуса равен удвоенному радиусу, периметр окружности в основании вычисляется по стандартной формуле через радиус, равно как и площадь основания.
d=2r
P=2πr
S_(осн.)=πr^2
Прямоугольный треугольник, образованный высотой конуса, радиусом основания и образующей конуса, связывает эти три значения теоремой Пифагора, по которой можно вычислить неизвестную образующую, а также угол между образующей и основанием. Тем временем, угол α рассчитывается из равнобедренного треугольника, сформированного двумя образующими и диаметром из того принципа, что сумма всех углов в треугольнике равна 180 градусам. (рис.40.1, 40.2)
l=√(h^2+r^2 )
tanβ=h/r
α=180°-2β
Чтобы найти площадь боковой поверхности конуса, необходимо умножить радиус и апофему на число π. Площадь полной поверхности конуса состоит из площади его основания и площади боковой поверхности. В обеих формулах вместо апофемы нужно подставить квадратный корень через высоту и радиус, полученный по теореме Пифагора.
S_(б.п.)=πrl=πr√(h^2+r^2 )
S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)=πr(√(h^2+r^2 )+r)
Чтобы найти объем конуса, достаточно знать значения радиуса и высоты, тогда формула объема выглядит как произведение числа π на квадрат радиуса и высоту, деленное на три.
V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, зависит не только от радиуса основания конуса и его высоты, но и от образующей, поэтому чтобы вычислить радиус вписанной сферы конуса через радиус конуса и высоту, нужно вместо образующей подставить полученное для нее выше выражение. Радиус описанной сферы может быть представлен сразу формулой только с переменными радиуса и высоты. (рис.40.3, 40.4)
r_1=hr/(l+r)=rh/(√(h^2+r^2 )+r)
R=(h^2+r^2)/2h
Пирамида, вписанная в конус
Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина совпадает с вершиной конуса. При этом конус называется описанным около пирамиды.
Около пирамиды можно описать конус тогда и только тогда, когда около ее основания можно описать окружность.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Упражнение 1
Найдите сторону основания правильной треугольной пирамиды, вписанной в конус, радиус основания которого равен 1.
Ответ:
Упражнение 2
Найдите сторону основания правильной четырехугольной пирамиды, вписанной в конус, радиус основания которого равен 1.
Ответ:
Упражнение 3
Найдите сторону основания правильной шестиугольной пирамиды, вписанной в конус, радиус основания которого равен 1.
Ответ: 1.
Пирамида, описанная около конуса
Пирамида называется описанной около конуса, если ее основание описано около основания конуса, а вершина совпадает с вершиной конуса. При этом конус называется вписанным в пирамиду.
В пирамиду можно вписать конус тогда и только тогда, когда в ее основание можно вписать окружность.
Упражнение 1
Найдите сторону основания правильной треугольной пирамиды, описанной около конуса, радиус основания которого равен 1.
Ответ:
Упражнение 2
Найдите сторону основания правильной четырехугольной пирамиды, описанной около конуса, радиус основания которого равен 1.
Ответ: 2.
Упражнение 3
Найдите сторону основания правильной шестиугольной пирамиды, описанной около конуса, радиус основания которого равен 1.
Ответ:
Сфера, вписанная в конус
Сфера называется вписанной в конус, если она касается его основания и боковой поверхности (касается каждой образующей). При этом конус называется описанным около сферы.
В любой конус (прямой, круговой) можно вписать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, вписанной в треугольник, являющийся осевым сечением конуса.
Напомним, что радиус r окружности, вписанный в треугольник, находится по формуле
где S – площадь, p – полупериметр треугольника.
Упражнение 1
В конус, радиус основания которого равен 1, а образующая равна 2, вписана сфера. Найдите ее радиус.
Решение. Треугольник SAB равносторонний. Высота SH равна Площадь S равна Полупериметр p равен 3. По формуле r = S/p получаем
Упражнение 2
В конус, радиус основания которого равен 2, вписана сфера радиуса 1. Найдите высоту конуса.
Решение. Обозначим h высоту SH конуса . Из формулы r = S/p имеем:
где r = 1, a = FG = 4, p =
Решая уравнение
находим
Упражнение 3
Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус вписанной сферы.
Решение. Высота SH конуса равна 1. Образующая .
Полупериметр p равен
По формуле r = S/p , имеем
Ответ:
Упражнение 4
Высота конуса равна 8, образующая 10. Найдите радиус вписанной сферы.
Решение. Радиус основания конуса равен 6. Площадь треугольника SFG равна 48, полупериметр 16. По формуле r = S/p имеем r = 3.
Ответ: r = 3.
Упражнение 5
Можно ли вписать сферу в наклонный конус?
Ответ: Нет.
Сфера, вписанная в усеченный конус
Сфера называется вписанной в усеченный конус, если она касается его основани й и боковой поверхности (касается каждой образующей). При этом усеченный конус называется описанным около сферы.
В усеченный конус можно вписать сферу, если в его осевое сечение можно вписать окружность. Радиус этой окружности будет равен радиусу вписанной сферы.
Упражнение 1
В усеченный конус, радиусы оснований которого равны 2 и 1, вписана сфера. Найдите радиус сферы и высоту усеченного конуса.
Решение. Имеем: A 1 B = A 1 O 1 = 2, A 2 B = A 2 O 2 = 1. Следовательно, A 1 A 2 = 3 , A 1 C = 1.
Таким образом,
Упражнение 2
В усеченный конус, радиус одного основания которого равен 2, вписана сфера радиуса 1. Найдите радиус второго основания.
Решение. Пусть A 1 O 1 = 2. Обозначим r = A 2 O 2 . Имеем: A 1 A 2 = 2+ r , A 1 C = 2 – r . По теореме Пифагора, имеет место равенство из которого следует, что выполняется равенство Решая полученное уравнение относительно r , находим
Упражнение 3
В усеченном конусе радиус большего основания равен 2, образующая наклонена к плоскости основания под углом 60 о . Найдите радиус вписанной сферы.
Решение. Заметим, что осевым сечением конуса, из которого получен усеченный конус, является равносторонний треугольник со стороной 2. Радиус r сферы, вписанной в усеченный конус, равен радиусу окружности, вписанной в этот равносторонний треугольник, т.е.
Упражнение 4
Образующая усеченного конуса равна 2, площадь осевого сечения 3. Найдите радиус вписанной сферы.
Решение. Воспользуемся формулой r = S/p , где S – площадь осевого сечения, p – полупериметр. В нашем случае S = 3 . Для нахождения полупериметра напомним, что для четырехугольника, описанного около окружности, суммы противоположных сторон равны. Значит, полупериметр равен удвоенной образующей цилиндра, т.е. p = 4. Следовательно, r = ¾.
Ответ:
Упражнение 5
Можно ли вписать сферу в усеченный наклонный конус.
Ответ: Нет.
Сфера, описанная около конуса
Сфера называется описанной около конуса, если вершина и окружность основания конуса лежат на сфере. При этом конус называется вписанным в сферу .
Около любого конуса (прямого, кругового) можно описать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, описанной около треугольника, являющимся осевым сечением конуса.
Напомним, что радиус R окружности, описанной около треугольника, находится по формуле
где S – площадь, a , b , c – стороны треугольника.
Упражнение 1
Около конуса, радиус основания которого равен 1, а образующая равна 2, описана сфера. Найдите ее радиус.
Решение. Треугольник SAB равносторонний со стороной 2. Высота SH равна Площадь S равна По формуле R = abc /4 S получаем
Упражнение 2
Около конуса, радиус основания которого равен 4, описана сфера радиуса 5. Найдите высоту h конуса.
Решение. Имеем, OB = 5 , HB = 4. Следовательно, OH = 3. Учитывая, что SO = OB = 5, получаем h = 8.
Ответ: h = 8.
Упражнение 3
Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус описанной сферы.
Решение. Треугольник SAB – прямоугольный, равнобедренный. Следовательно, радиус R описанной сферы равен радиусу основания цилиндра, т.е. R = 1.
Ответ: R = 1.
Упражнение 4
Высота конуса равна 8, образующая 10. Найдите радиус описанной сферы.
Решение. В треугольнике SAB имеем: SA = SB = 10, SH = 8. По теореме Пифагора, AH = 6 и, следовательно, S = 48. Используя формулу R = abc /4 S , получаем
Упражнение 5
Можно ли описать сферу около наклонного конуса?
Ответ: Да.
Сфера, описанная около усеченного конуса
С фера называется описанной около усеченного конуса, если окружност и основани й усеченного конуса лежат на сфере. При этом усеченный к онус называется в писанным в сферу.
Около усеченного конуса можно описать сферу, если около его осевого сечения можно описать окружность. Радиус этой окружности будет равен радиусу описанной сферы.
Упражнение 1
Около усеченного конуса, радиусы оснований которого равны 2 и 1, а образующая равна 2, описана сфера. Найдите ее радиус.
Решение. Заметим, что A 1 O 1 B 2 O 2 и O 1 B 1 B 2 A 2 – ромбы. Треугольники A 1 O 1 A 2 , O 1 A 2 B 2 , O 1 B 1 B 2 – равносторонние и, значит, A 1 B 1 –диаметр. Следовательно, R = 2.
Ответ: R = 2,
Упражнение 2
Радиус меньшего основания усеченного конуса равен 1, образующая равна 2 и составляет угол 45 о с плоскостью другого основания. Найдите радиус описанной сферы.
Решение. Имеем A 2 O 2 = 1, A 1 A 2 = 2, O 1 O 2 = , OO 1 = O 1 C = 1. Следовательно, OO 2 = 1 + и, значит,
Упражнение 3
Радиус одного основания усеченного конуса равен 4, высота 7, радиус описанной сферы 5. Найдите радиус второго основания усеченного конуса.
Решение. Имеем OO 1 = 3 , OO 2 = 4 и, следовательно, O 2 A 2 = 3.
Ответ: 3.
Упражнение 4
Найдите радиус сферы, описанной около усеченного конуса, радиусы оснований которого равны 2 и 4, а высота равна 5.
Решение. Обозначим R радиус описанной сферы. Тогда
Учитывая, что O 1 O 2 = 6, имеем равенство
Решая его относительно R , находим
Упражнение 5
Можно ли описать сферу около усеченного наклонного конуса.
Ответ: Нет.