Как найти высоту конуса через тангенс

Определение конуса.

МОУ СОШ №256 г.Фокино

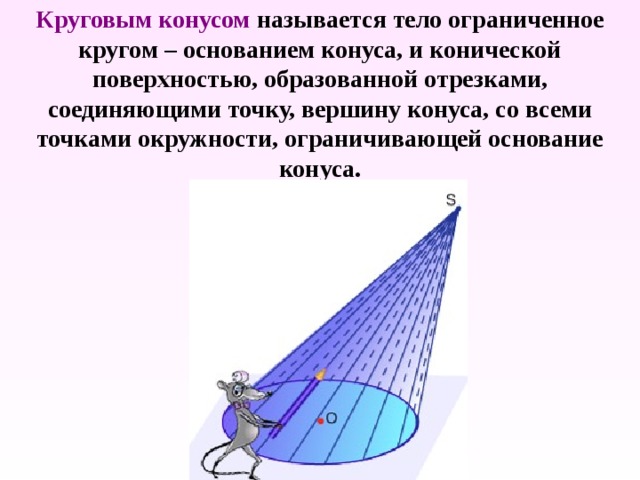
Круговым конусом называется тело ограниченное кругом – основанием конуса, и конической поверхностью, образованной отрезками, соединяющими точку, вершину конуса, со всеми точками окружности, ограничивающей основание конуса.

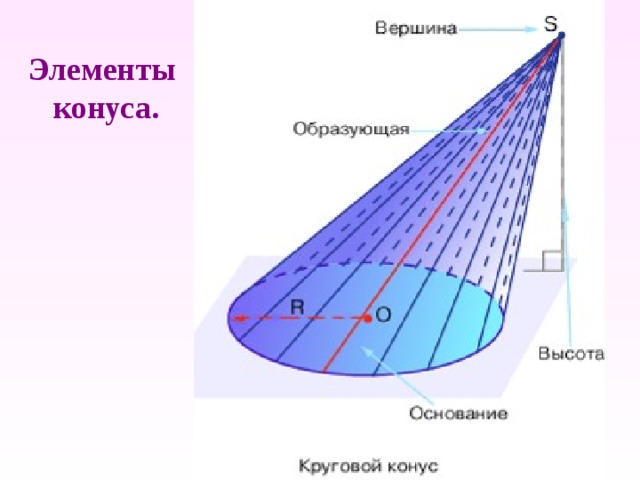
Элементы конуса.

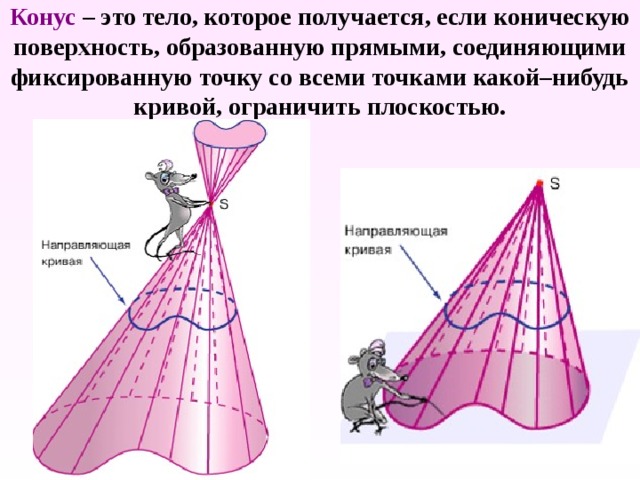
Конус – это тело, которое получается, если коническую поверхность, образованную прямыми, соединяющими фиксированную точку со всеми точками какой–нибудь кривой, ограничить плоскостью.

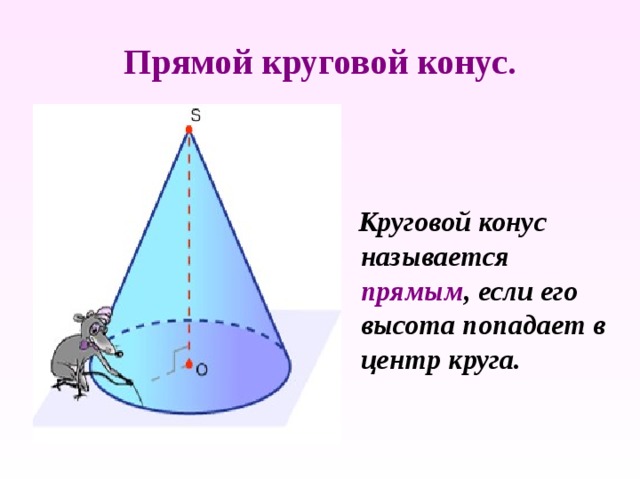
Прямой круговой конус.

Круговой конус называется прямым , если его высота попадает в центр круга.

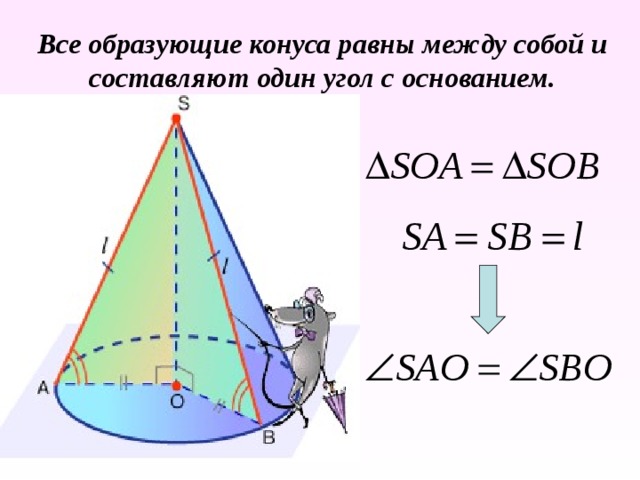
Все образующие конуса равны между собой и составляют один угол с основанием.

?

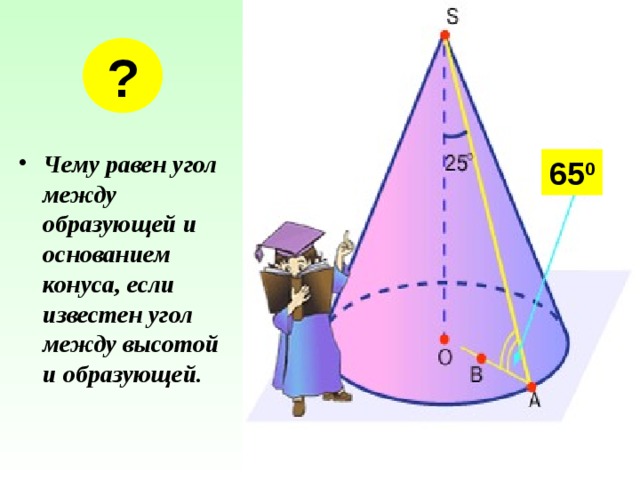
• Чему равен угол между образующей и основанием конуса, если известен угол между высотой и образующей.

65 0

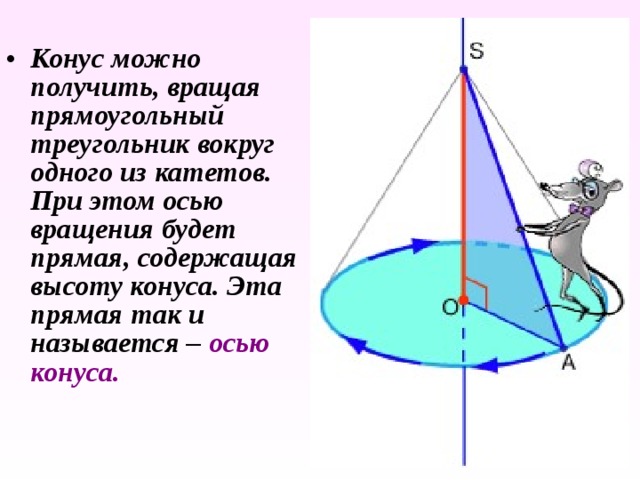
• Конус можно получить, вращая прямоугольный треугольник вокруг одного из катетов. При этом осью вращения будет прямая, содержащая высоту конуса. Эта прямая так и называется – осью конуса.

?

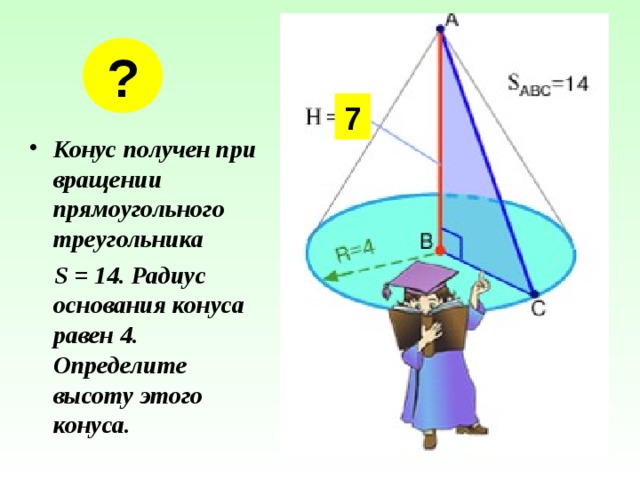
7

• Конус получен при вращении прямоугольного треугольника

S = 14. Радиус основания конуса равен 4. Определите высоту этого конуса.

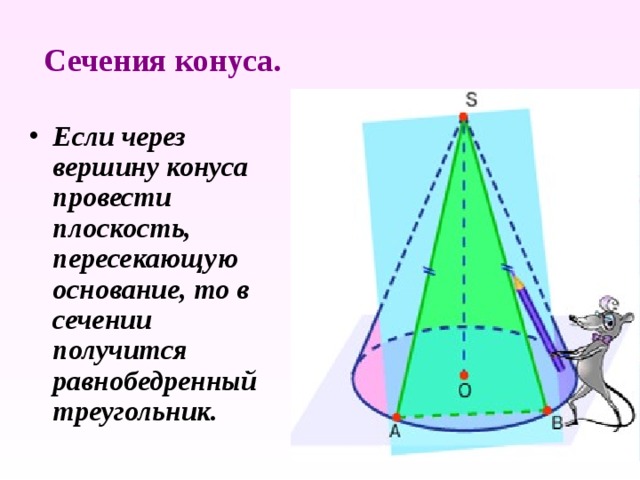
Сечения конуса.

• Если через вершину конуса провести плоскость, пересекающую основание, то в сечении получится равнобедренный треугольник.

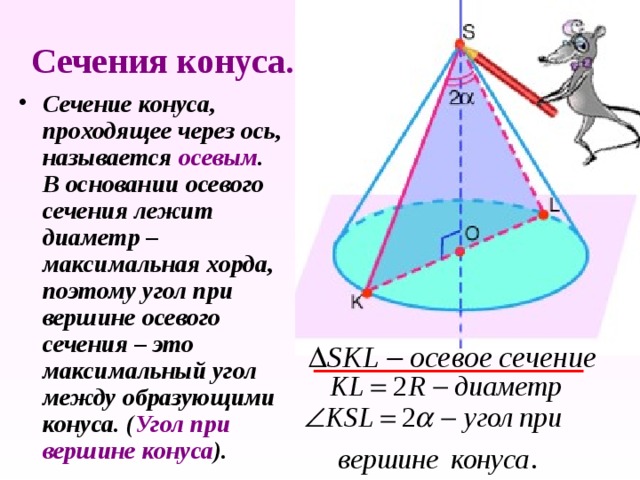
Сечения конуса.

• Сечение конуса, проходящее через ось, называется осевым . В основании осевого сечения лежит диаметр – максимальная хорда, поэтому угол при вершине осевого сечения – это максимальный угол между образующими конуса. ( Угол при вершине конуса ).

?

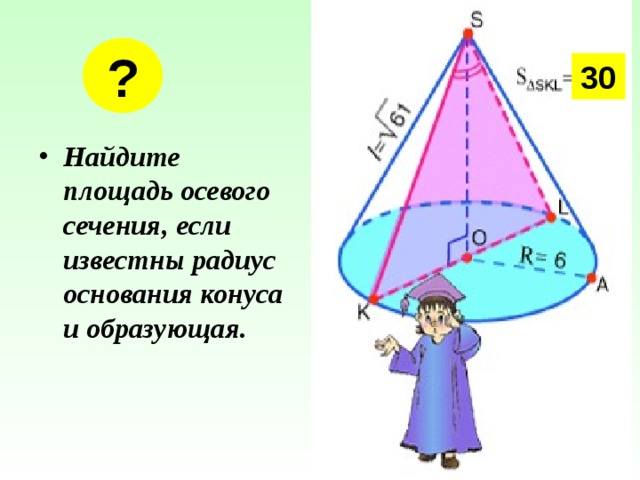
30

• Найдите площадь осевого сечения, если известны радиус основания конуса и образующая.

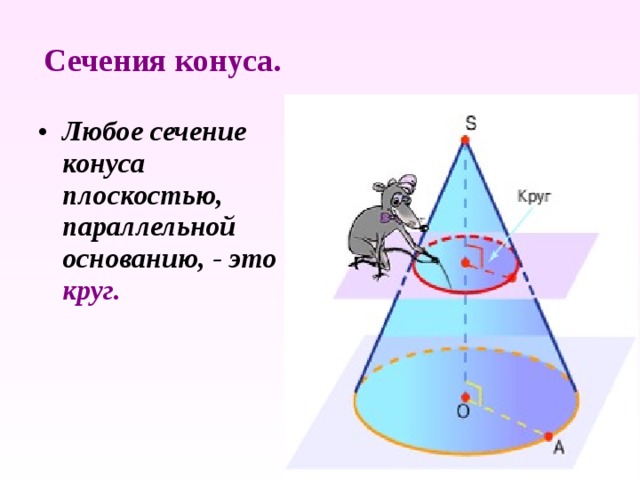
Сечения конуса.

• Любое сечение конуса плоскостью, параллельной основанию, — это круг.

?

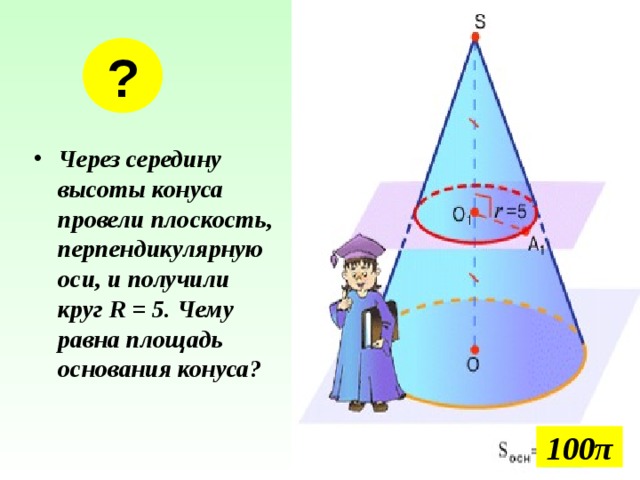
• Через середину высоты конуса провели плоскость, перпендикулярную оси, и получили круг R = 5. Чему равна площадь основания конуса?

100 π

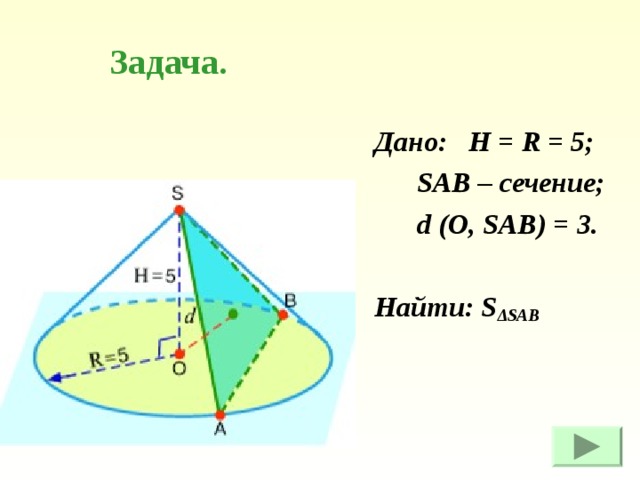
Задача.

Дано: H = R = 5;

SAB – сечение;

d (O, SAB) = 3.

Найти: S ΔSAB

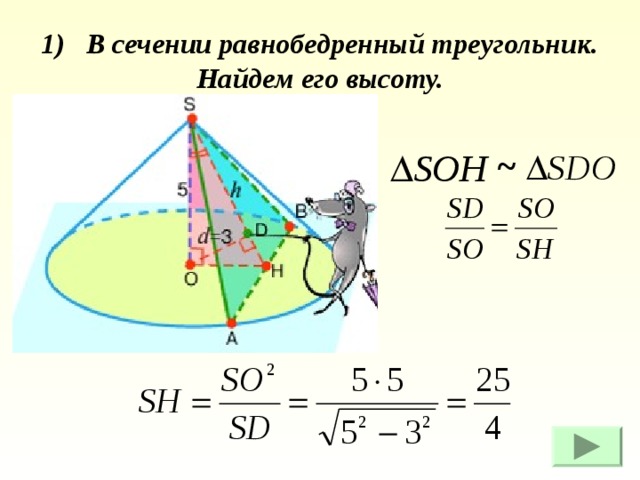
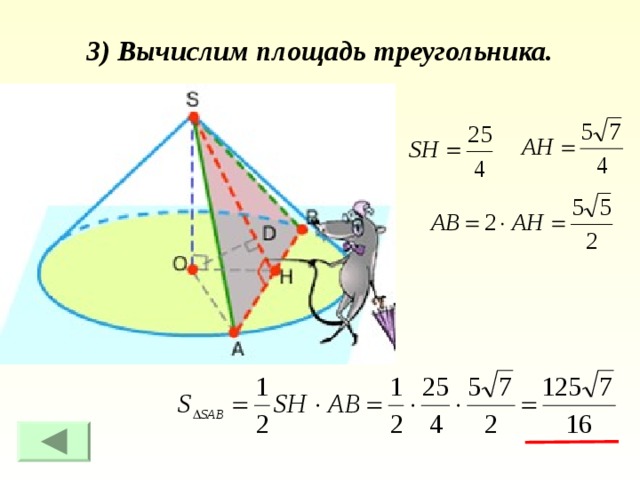
1) В сечении равнобедренный треугольник. Найдем его высоту.

~

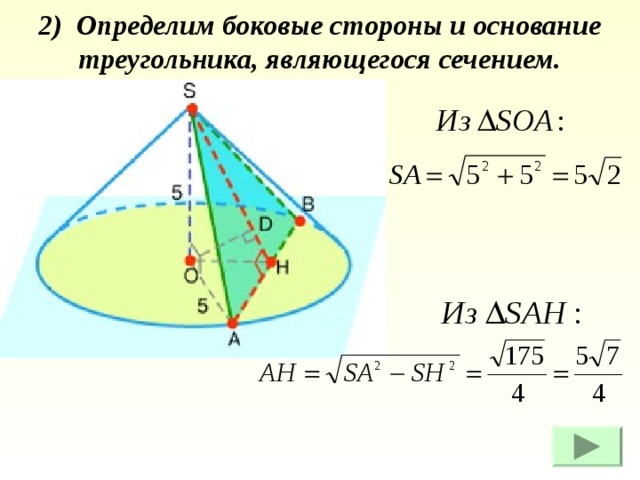
2) Определим боковые стороны и основание треугольника, являющегося сечением.

3) Вычислим площадь треугольника.

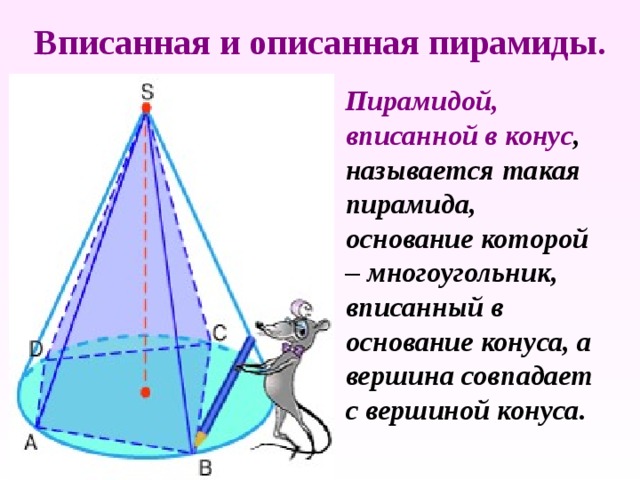
Вписанная и описанная пирамиды.

Пирамидой, вписанной в конус , называется такая пирамида, основание которой – многоугольник, вписанный в основание конуса, а вершина совпадает с вершиной конуса.

?

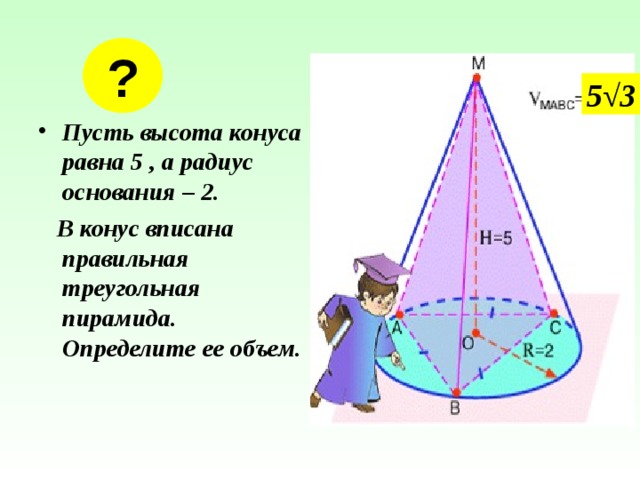
5 √3

• Пусть высота конуса равна 5 , а радиус основания – 2.

В конус вписана правильная треугольная пирамида. Определите ее объем.

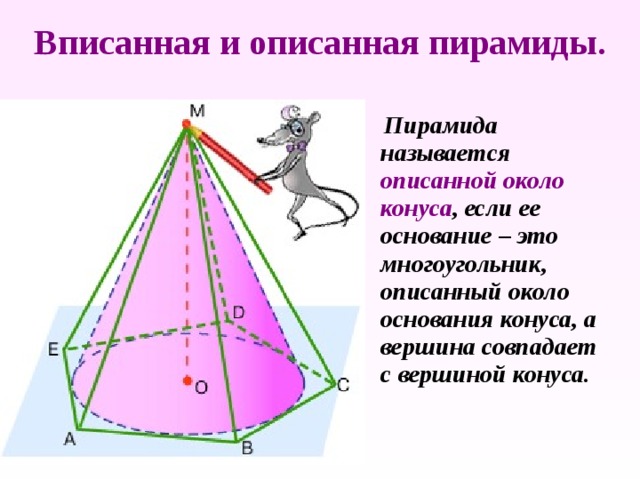
Вписанная и описанная пирамиды.

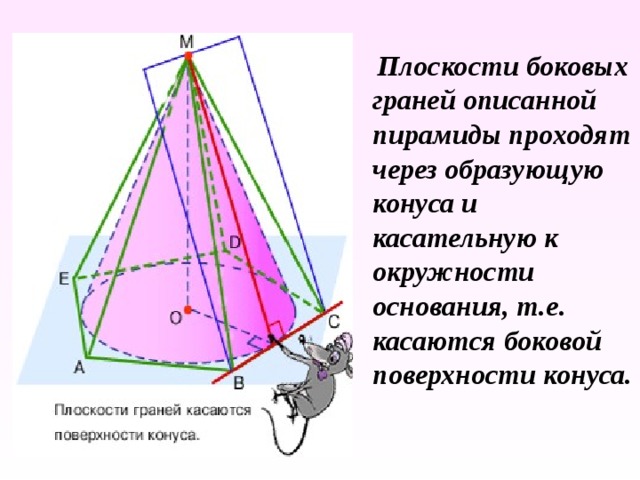
Пирамида называется описанной около конуса , если ее основание – это многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса.

Плоскости боковых граней описанной пирамиды проходят через образующую конуса и касательную к окружности основания, т.е. касаются боковой поверхности конуса.

?

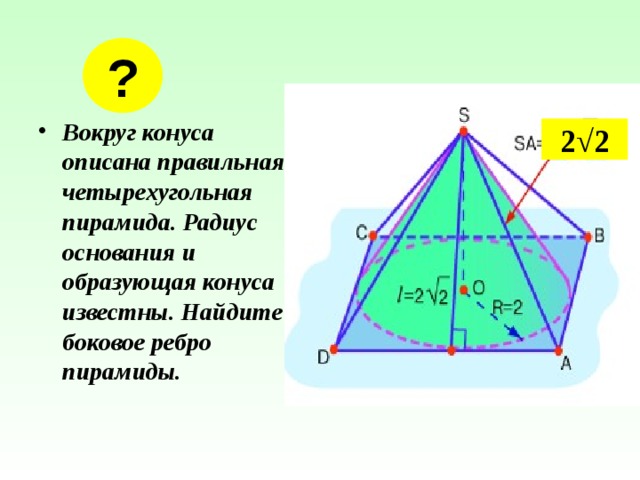
• Вокруг конуса описана правильная четырехугольная пирамида. Радиус основания и образующая конуса известны. Найдите боковое ребро пирамиды.

2√2

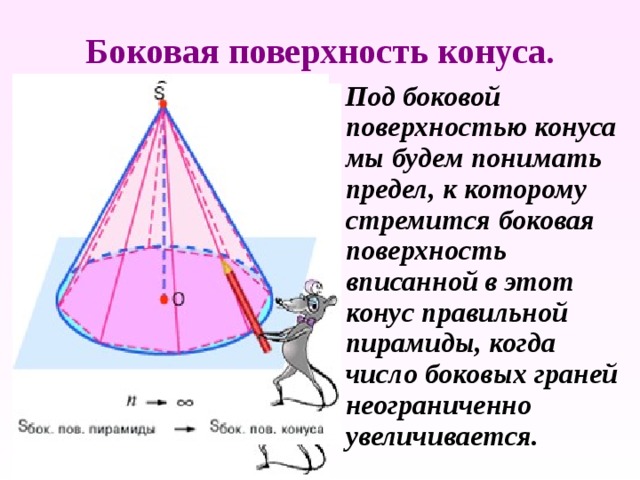
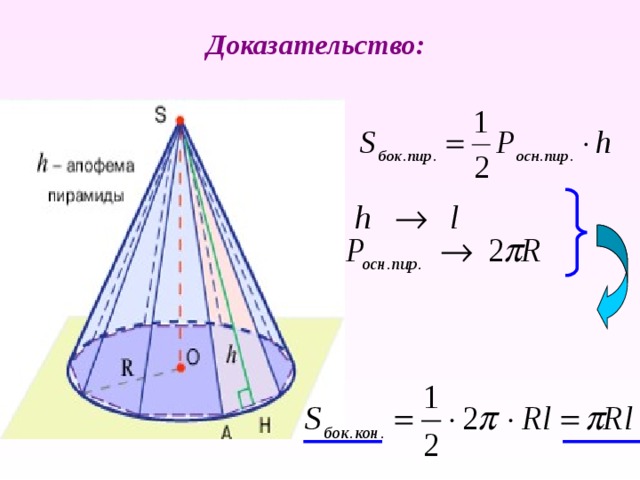
Боковая поверхность конуса.

Под боковой поверхностью конуса мы будем понимать предел, к которому стремится боковая поверхность вписанной в этот конус правильной пирамиды, когда число боковых граней неограниченно увеличивается.

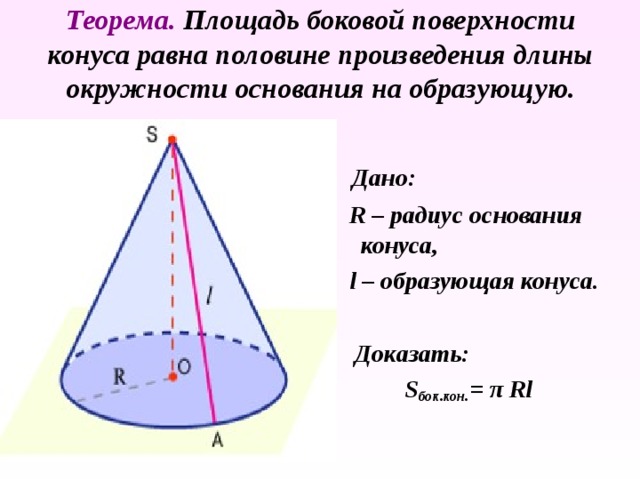
Теорема. Площадь боковой поверхности конуса равна половине произведения длины окружности основания на образующую.

Дано:

R – радиус основания конуса,

l – образующая конуса.

Доказать:

S бок.кон. = π Rl

Доказательство:

?

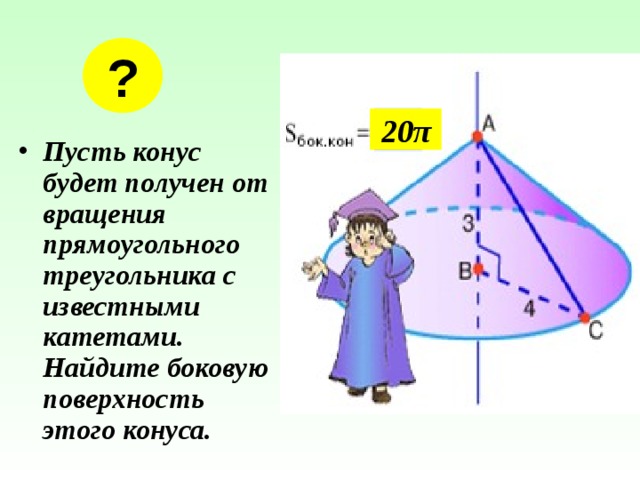
20 π

• Пусть конус будет получен от вращения прямоугольного треугольника с известными катетами. Найдите боковую поверхность этого конуса.

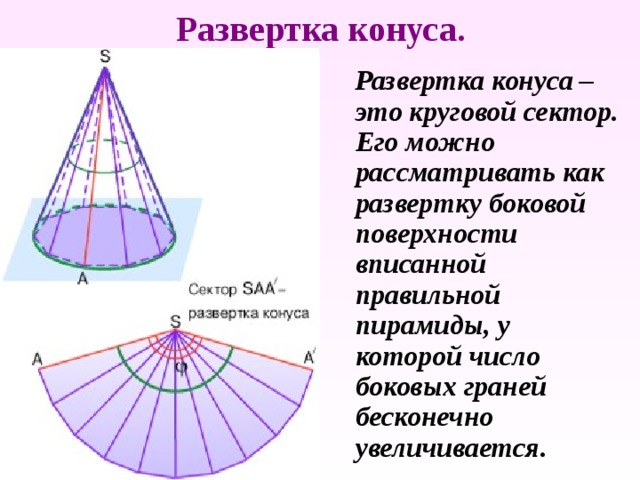
Развертка конуса.

Развертка конуса – это круговой сектор. Его можно рассматривать как развертку боковой поверхности вписанной правильной пирамиды, у которой число боковых граней бесконечно увеличивается.

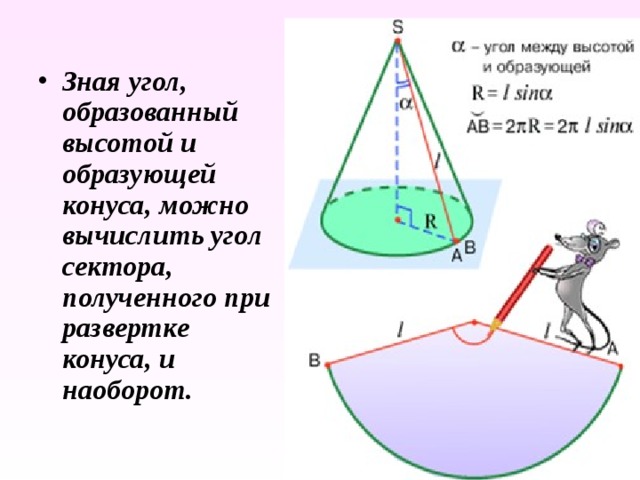
• Зная угол, образованный высотой и образующей конуса, можно вычислить угол сектора, полученного при развертке конуса, и наоборот.

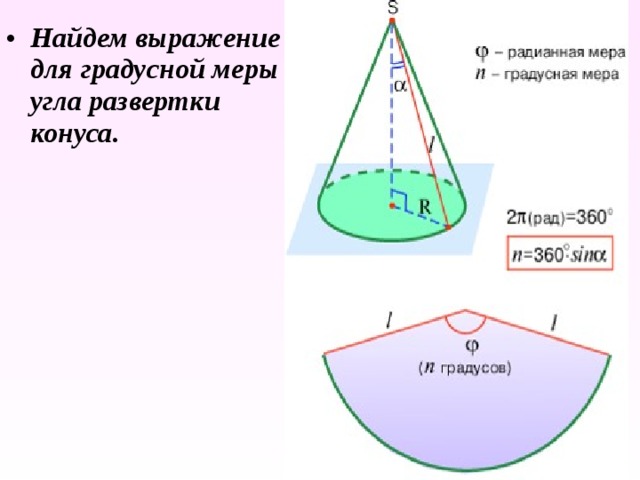
• Найдем выражение для градусной меры угла развертки конуса.

?

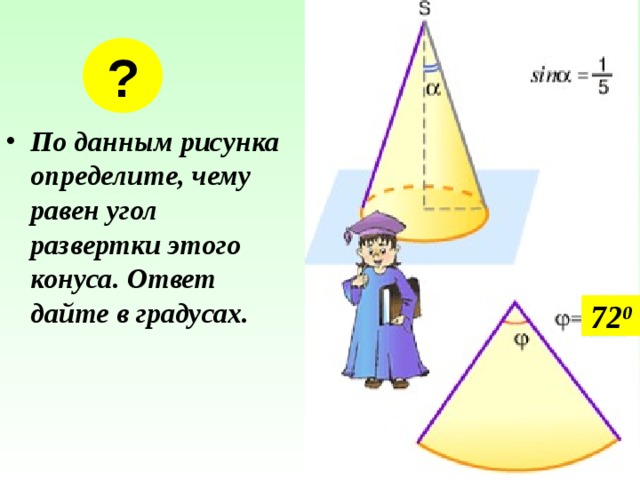
• По данным рисунка определите, чему равен угол развертки этого конуса. Ответ дайте в градусах.

72 0

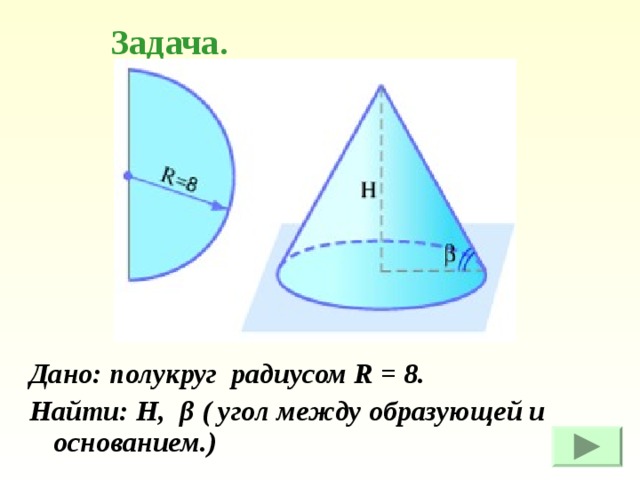
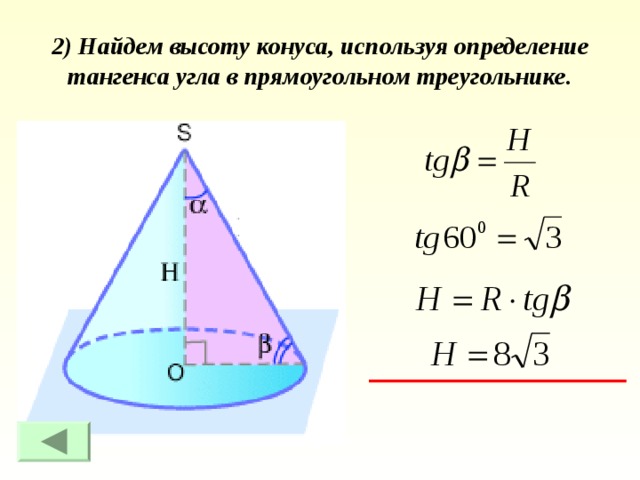
Задача.

Дано: полукруг радиусом R = 8.

Найти: Н, β ( угол между образующей и основанием.)

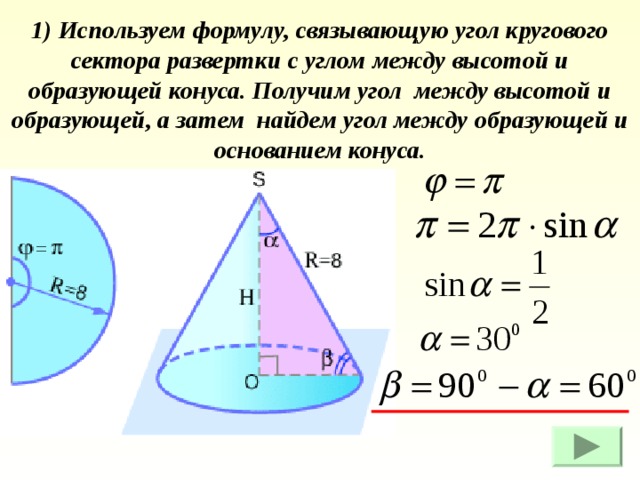
1) Используем формулу, связывающую угол кругового сектора развертки с углом между высотой и образующей конуса. Получим угол между высотой и образующей, а затем найдем угол между образующей и основанием конуса.

2) Найдем высоту конуса, используя определение тангенса угла в прямоугольном треугольнике.

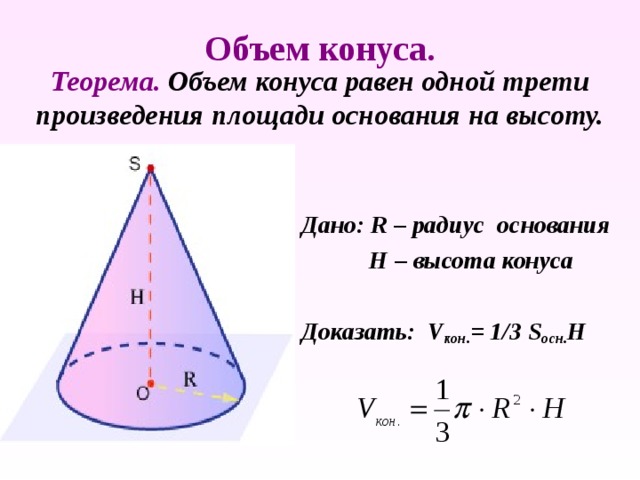
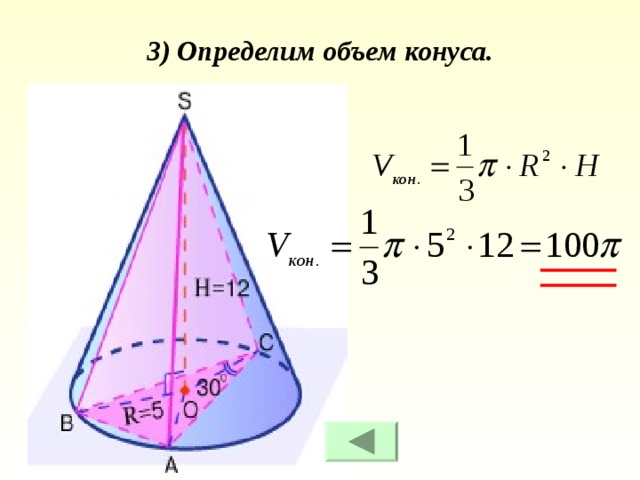
Объем конуса.

Теорема. Объем конуса равен одной трети произведения площади основания на высоту.

Дано: R – радиус основания

Н – высота конуса

Доказать: V кон. = 1/3 S осн. H

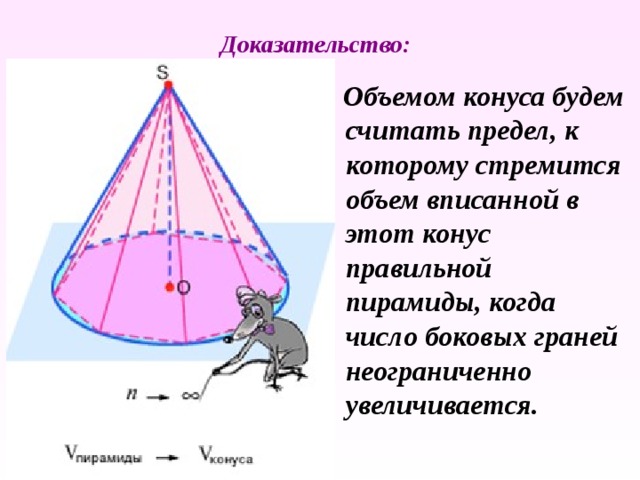
Доказательство:

Объемом конуса будем считать предел, к которому стремится объем вписанной в этот конус правильной пирамиды, когда число боковых граней неограниченно увеличивается.

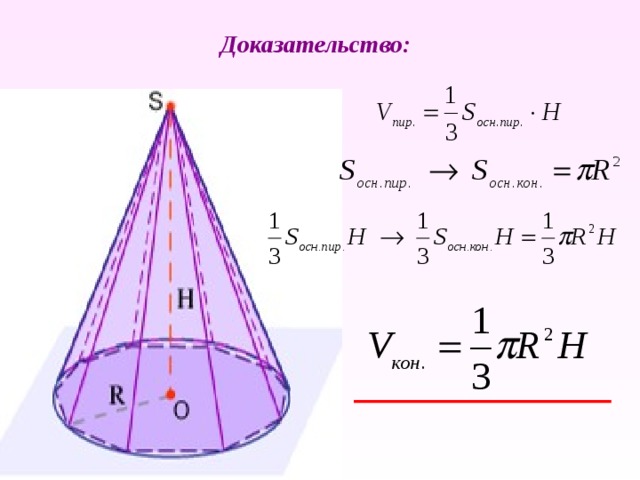
Доказательство:

?

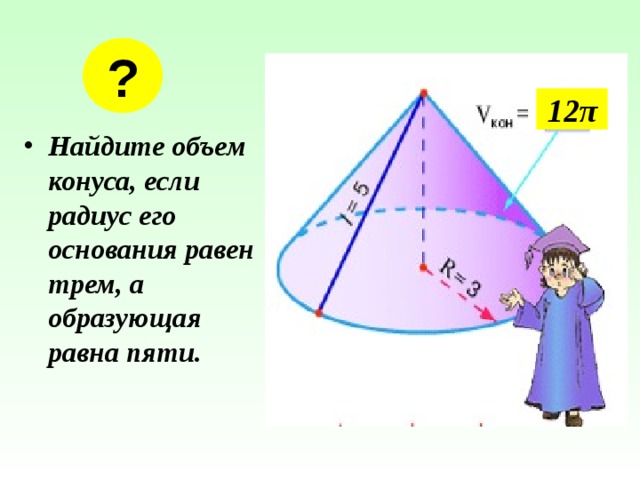
12 π

• Найдите объем конуса, если радиус его основания равен трем, а образующая равна пяти.

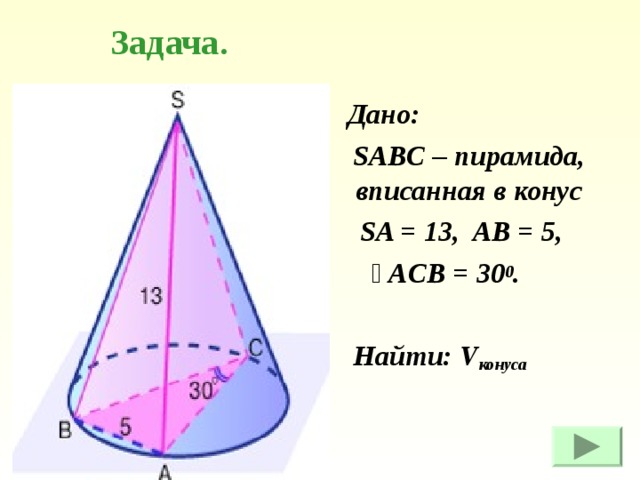
Задача.

Дано:

SABC – пирамида, вписанная в конус

SA = 13, AB = 5,

ے ACB = 30 0 .

Найти: V конуса

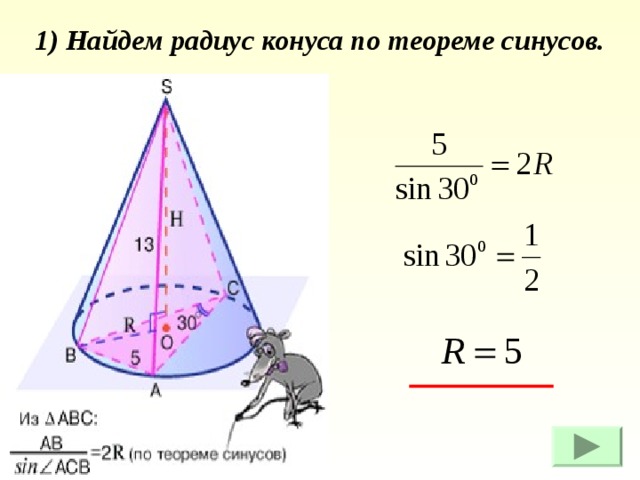
1) Найдем радиус конуса по теореме синусов.

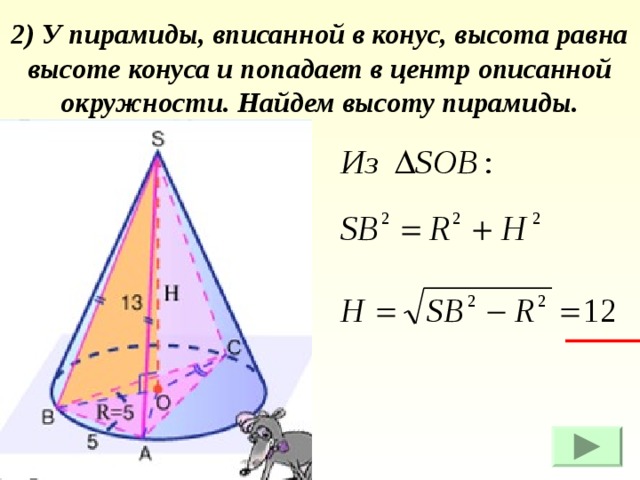
2) У пирамиды, вписанной в конус, высота равна высоте конуса и попадает в центр описанной окружности. Найдем высоту пирамиды.

3) Определим объем конуса.

Прочитав данную статью, вы узнаете, как найти высоту конуса. Приведенный в ней материал поможет глубже разобраться в вопросе, а формулы окажутся весьма полезными в решении задач. В тексте разобраны все необходимые базовые понятия и свойства, которые обязательно пригодятся на практике.

Фундаментальная теория

Перед тем, как найти высоту конуса, необходимо разобраться с теорией.

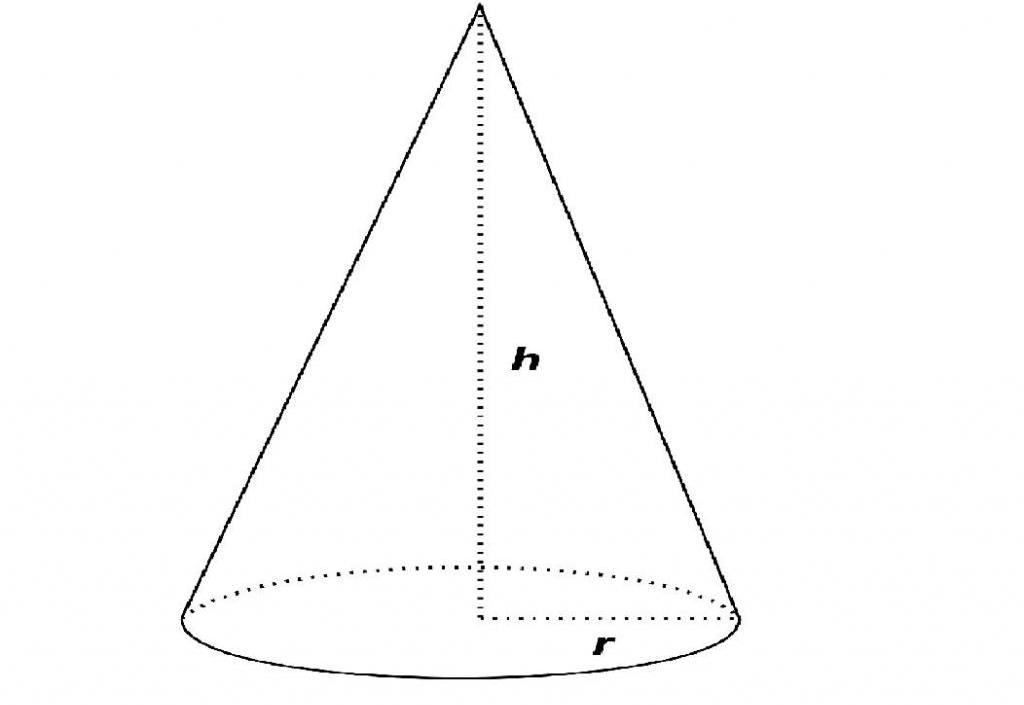
Конус — фигура, которая плавно сужается от плоского основания (часто, хотя и необязательно, кругового) до точки, называемой вершиной.

Конус формируется набором отрезков, лучей или прямых, соединяющих общую точку с основанием. Последнее может ограничиваться не только окружностью, но и эллипсом, параболой или гиперболой.

Ось — это прямая (если таковая имеется), вокруг которой фигура имеет круговую симметрию. Если угол между осью и основой составляет девяносто градусов, то конус принято называть прямым. Именно такая вариация чаще всего встречается в задачах.

Если в основе лежит многоугольник, то объект является пирамидой.

Отрезок, соединяющий вершину и линию, ограничивающую основание, называют образующей.

Как найти высоту конуса

Подойдем к вопросу с другой стороны. Для начала используем объем конуса. Чтобы его найти нужно вычислить произведение высоты с третьей частью площади.

V = 1/3 × S × h.

Очевидно, что из этого можно получить формулу высоты конуса. Достаточно лишь сделать правильные алгебраические преобразования. Разделим обе части равенства на S и умножим на тройку. Получим:

h = 3 × V × 1/S.

Теперь вы знаете, как найти высоту конуса. Однако для решения задач вам могут понадобиться и другие знания.

Важные формулы и свойства

Приведенный ниже материал однозначно поможет вам в решении конкретных задач.

Центр массы тела находится на четвертой части оси, начиная от основы.

В проективной геометрии цилиндр — это просто конус, вершина которого находится на бесконечности.

Следующие свойства работают только для прямого кругового конуса.

• Даны радиус основания r и высота h, тогда формула для площади будет выглядеть так: П × r². Соответственно изменится и окончательное уравнение. V = 1/3 × П × r² × h.
• Вычислить площадь боковой поверхности можно перемножив число «пи», радиус и длину образующей. S = П × r × l.
• Пересечение произвольной плоскости с фигурой является одним из конических сечений.

Часто встречаются задачи, где необходимо использовать формулу для объема усеченного конуса. Она выводится из обычной и имеет такой вид:

V = 1/3 × П × h × (R² + Rr + r²), где: r -радиус нижнего основания, R — верхнего.

Всего этого будет вполне достаточно для решения разнообразнейших примеров. Разве что могут понадобиться знания, не связанные с этой темой, например, свойства углов, теорема Пифагора и другое.

1 ответ:

Читайте также

Зная площадь основания конуса, можно рассчитать радиус, диаметр и периметр основания конуса, преобразовав стандартные формулы.
r=√(S_(осн.)/π)
d=2√(S_(осн.)/π)
P=2πr=2√(πS_(осн.) )

Высота, образующая и радиус конуса соединяются в прямоугольный треугольник, из которого по теореме Пифагора можно найти любое значение, зная остальные два. Угол наклона конуса можно найти из этого же треугольника через отношение тангенса, а уже через него во втором, равнобедренном треугольнике вычислить угол раствора конуса. (рис.40.1,40.2)
l=√(h^2+r^2 )=√(h^2+S_(осн.)/π)
tan⁡β=h/r
α=180°-2β

Вычислить площадь боковой поверхности конуса через площадь основания и высоту можно, заменив радиус и образующую конуса в формуле на соответствующие выражения. Чтобы найти площадь полной поверхности конуса, следует поступить аналогично.
S_(б.п.)=πrl=√(πS_(осн.) (h^2+S_(осн.)/π) )
S_(п.п.)=S_(осн.)+√(πS_(осн.) (h^2+S_(осн.)/π) )

Объем конуса в стандартном виде представляет собой отношение произведения высоты и площади основания к трем, поэтому его можно вычислить сразу через площадь основания и высоту, заданные в условии.
V=1/3 hS_(осн.)

Чтобы найти радиус сферы, вписанной в конус, нужно умножить высоту на выражение, найденное для радиуса, и разделить это на сумму образующей и радиуса. Радиус сферы, описанной около конуса, будет равен образующей во второй степени, деленной на удвоенную высоту. (рис. 40.3, 40.4)
r_1=hr/(l+r)=(h√(S_(осн.)/π))/(√(h^2+S_(осн.)/π)+√(S_(осн.)/π))
R=(h^2+r^2)/2h=(h^2+S_(осн.)/π)/2h

1) Чтобы найти высоту конуса (h) нужно вычислить радиус основания (r):
, где D — диаметр
По формуле Пифагора получаем:
, где l — образующая

2)tgα=f ‘(x)
тк график функции в точке с абсциссой ⇒у=0
x²+2x=0
x=0 x= -2
f ‘(x)=2x +2
tgα=f ‘(0)=2*0 +2 =2