Как найти выражение значение которого является наименьшим

Общая информация

Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.

Для решения такого типа задач необходим определенный «багаж» знаний, поскольку без него вообще не обойтись. В его состав входят следующие элементы:

1. Нахождение области определения функции (ОДФ).
2. Понятие дифференциала и основные методы его нахождения.
3. Умение решать уравнения.
4. Знание графиков простых функций.
5. Основные типы функций, полуинтервал и интервал.

Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.

Наибольшее и наименьшее значение функции на отрезке

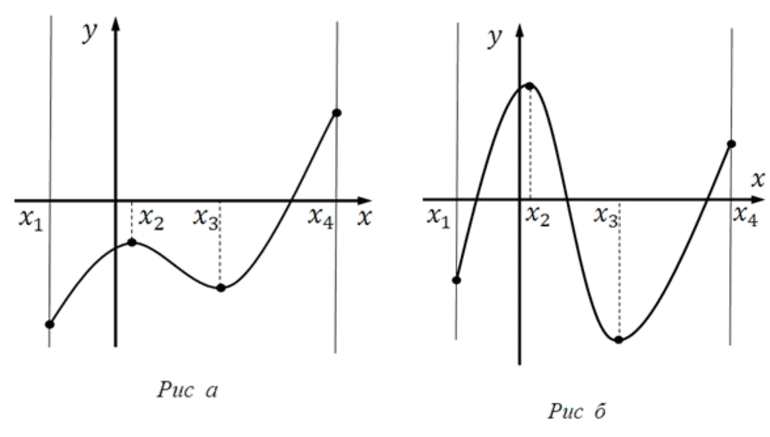
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [—6;6].

Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.

На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [—3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.

Видео

Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале

Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.

1. Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
2. Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
3. Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к , решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям.  Их определяет вид интервала.

• Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b—f(x).
• Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+f(x).
• Если интервал имеет вид  (a;b), то нам надо вычислить односторонние пределы limx→b—f(x),limx→a+f(x).
• Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
• Если интервал выглядит как (—∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→—∞f(x).
• Если —∞; b, то считаем односторонний предел limx→b—f(x) и предел на минус бесконечности limx→—∞f(x)
• Если же —∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x),  limx→—∞f(x).

1. В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4—8 в первой части материала.

Условие: дана функция y=3e1x2+x-6-4. Вычислите ее наибольшее  и наименьшее значение в интервалах  -∞; -4, -∞; -3, (-3;1], (-3;2), [1;2), 2; +∞, [4; +∞).

Решение

Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в :

x2+x-6=D=12-4·1·(-6)=25×1=-1-52=-3×2=-1+52=2⇒D(y): x∈(-∞; -3)∪(-3; 2)∪(2; +∞)

Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.

Теперь выполним дифференцирование функции и получим:

y’=3e1x2+x-6-4’=3·e1x2+x-6’=3·e1x2+x-6·1×2+x-6’==3·e1x2+x-6·1’·x2+x-6-1·x2+x-6′(x2+x-6)2=-3·(2x+1)·e1x2+x-6×2+x-62

Следовательно, производные функции существуют на всей области ее определения.

Перейдем к нахождению стационарных точек. Производная функции обращается в при x=-12. Это стационарная точка, которая находится в интервалах (-3;1] и (-3;2).

Вычислим значение функции при x=-4 для промежутка (-∞; -4], а также предел на минус бесконечности:

y(-4)=3e1(-4)2+(-4)-6-4=3e16-4≈-.456limx→-∞3e1x2+x-6=3e-4=-1

Поскольку 3e16-4>-1, значит, max yx∈(-∞; -4]=y(-4)=3e16-4. Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.

Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:

limx→-3-3e1x2+x-6-4=limx→-3-3e1(x+3)(x-3)-4=3e1(-3-+3)(-3—2)-4==3e1(+)-4=3e+∞-4=+∞limx→-∞3e1x2+x-6-4=3e-4=-1

Значит, значения функции будут расположены в интервале -1; +∞

Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке  x=-12, если x=1. Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к -3 с правой стороны:

y-12=3e1-122+-12-6-4=3e425-4≈-1.444y(1)=3e112+1-6-4≈-1.644limx→-3+3e1x2+x-6-4=limx→-3+3e1(x+3)(x-2)-4=3e1-3++3(-3+-2)-4==3e1(-)-4=3e-∞-4=3·-4=-4

У нас получилось, что наибольшее значение функция примет в стационарной точке max yx∈(3; 1]=y-12=3e-425-4. Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до -4.

Для интервала (-3;2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:

y-12=3e1-122+-12-6-4=3e-425-4≈-1.444limx→-3+3e1x2+x-6-4=-4limx→2-3e1x2+x-6-4=limx→-3+3e1(x+3)(x-2)-4=3e1(2-+3)(2—2)-4==3e1—4=3e-∞-4=3·-4=-4

Значит, max yx∈(-3; 2)=y-12=3e-425-4, а наименьшее значение определить невозможно, и значения функции ограничены снизу числом -4.

Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [1;2) наибольшее значение функция примет при x=1, а найти наименьшее невозможно.

На промежутке (2; +∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка -1; +∞.

limx→2+3e1x2+x-6-4=limx→-3+3e1(x+3)(x-2)-4=3e1(2++3)(2+-2)-4==3e1(+)-4=3e+∞-4=+∞limx→+∞3e1x2+x-6-4=3e-4=-1

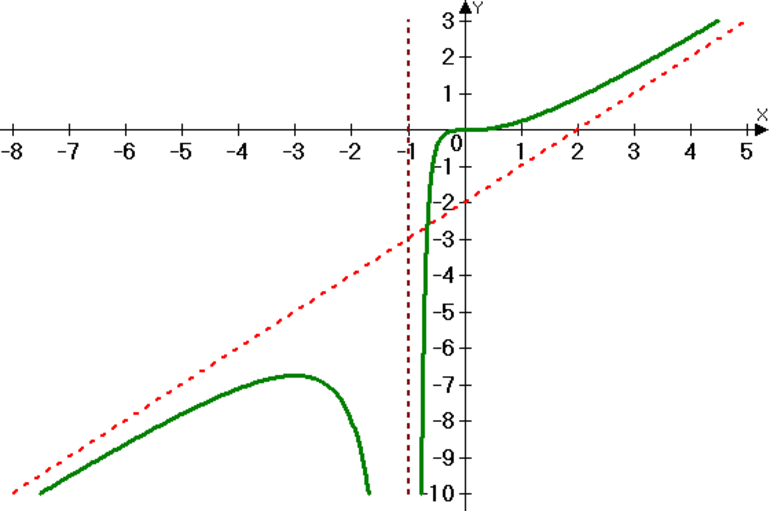
Вычислив, чему будет равно значение функции при x=4, выясним, что max yx∈[4; +∞)=y(4)=3e114-4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y=-1.

Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.

Это все, что мы  хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.

Всё ещё сложно? Наши эксперты помогут разобраться Все услуги

Теги

Как найти наибольшее и наименьшее значение функции

Общая информация

Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.

Для решения такого типа задач необходим определенный «багаж» знаний, поскольку без него вообще не обойтись. В его состав входят следующие элементы:

Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.

Область определения

Область определения какой-либо функции вида y = f(x) — область значений аргумента, при которых она существует. У каждой функции существует два типа неизвестных: зависимые и независимые. К первым следует отнести переменную y, которая зависит от независимой переменной «х». Необходимо отметить, что бывают функции, в которых нет аргумента. Примером их считается функция вида y = const, где const — константа (любое число).

Обозначение интервалов

Результатом решения задач на нахождение ОДЗ является определенный интервал. Важно правильно его обозначать, поскольку это существенно влияет на решение. Нужно руководствоваться следующими правилами:

Очень важно правильно читать интервалы. Например, запись (1;4) читается следующим образом: переменная принимает значения, которые находятся в интервале от 1 не включительно до 4 не включительно. Это числа 2 и 3, поскольку 1 и 4 не входят в промежуток. Запись вида [5;10) читается таким образом: некоторое значение принадлежит интервалу от 5 включительно, до 10 не включительно.

Зависимость от типа

Функции различаются между собой. От этого и зависит нахождение их области определения. Они бывают простыми и сложными. Первые состоят из единичных элементов, а сложные включают в себя несколько типов. Их еще называют составными. Простые классифицируются на три вида:

Рациональные бывают целыми и дробными. Они не включают в себя выражения, содержащие такие элементы: корень, степень, логарифм и тригонометрические функции. D(f) этих функций — все действительные числа (Z). Если она является дробной, то это означает, что в ее числителе и (или) знаменателе находится аргумент, значение которого не должно обращать ее в пустое множество.

Когда под корнем находится выражение, содержащее независимую переменную, то она называется иррациональной. В этом случае D(f) — множество Z, кроме тех, которые превращают выражение под корнем четной степени в отрицательное значение. Функция, представленная степенными выражениями, имеет D(f) = Z, но только тогда, когда значение аргумента не превращает функцию в пустое множество.

Метод нахождения

Для решения любой задачи нужно применять определенные правила. Они называются алгоритмом. Для каждого типа функций существует конкретный вариант решения. Для дробной он является следующим:

В случае, когда выражение является иррациональной функцией, корень которой является четным, следует решать не уравнение, а неравенство. Его значение не должно быть меньше 0. Для логарифмического типа выражение натурального логарифма (ln) должно быть всегда больше 0.

Для sin(x) и cos(x) областью определения является множество значений Z. Однако для tg(x) и ctg(x) следует помнить, что аргумент не должен принимать значение x = (Pi / 2) + Pi * k и x = Pi * k соответственно. Следует отметить, что коэффициент k принадлежит множеству чисел Z.

Для нахождения минимального и максимального значения функции достаточно материала, изложенного выше. Специалисты рекомендуют разобраться с теорией, а затем переходить к практике.

Примеры решений

Дана квадратичная функция y = x^2 + 6x + 9. Необходимо найти наименьшее значение функции квадратного уравнения на отрезке [1;5]. Для этой цели нужно воспользоваться алгоритмом:

Одним из простейших типов задач является следующая: найдите наибольшее значение линейной функции z = 5x + 10 на отрезке [-3;3]. Для ее решения можно также воспользоваться алгоритмом:

Последнюю задачу необязательно решать по алгоритму, поскольку она считается простейшей. Математики рекомендуют тренироваться в нахождении MIN и MAX функции, поскольку только практика позволяет быстро решать задачи.

Таким образом, для нахождения максимального и минимального значений заданной функции необходимо пользоваться специальным универсальным алгоритмом. Кроме того, нужно правильно находить дифференциалы, область определения, а также разбираться в интервалах.

Источник

Что такое наименьшее значение выражения

а) Можно ли при n = 5 написать на доске такие числа, чтобы также выполнялось равенство a₂ = a₅?

б) Можно ли при n = 100 написать на доске такие числа, сумма которых равна 2020?

в) При n = 10 на доске написаны такие числа, сумма которых равна 15. Какое наименьшее значение может принимать сумма их квадратов?

а) Пусть такие числа написаны. Поскольку по условию выполнены равенства и получаем

Следовательно, если также выполняется равенство то Пришли к противоречию.

б) Пусть такие числа написаны. Поскольку при каждом натуральном числе по условию выполнены равенства и получаем

при каждом натуральном числе Значит,

При и при каждом натуральном числе имеем

в) Пусть такие числа написаны. Аналогично доказанному в п. б) получаем

Значит, сумма квадратов всех написанных чисел будет минимальна тогда и только тогда, когда максимально выражение Поскольку функция возрастает при и убывает при наибольшее значение выражения для целых равно 56. Оно достигается при и Таким образом, получаем, что сумма квадратов всех написанных чисел принимает наименьшее значение при и при каждом натуральном числе а также при и при каждом натуральном числе Это значение равно

Ответ: а) нет; б) да; в) 343.

Аналоги к заданию № 561735: 561776 Все

Найдите все значения a, при каждом из которых наименьшее значение функции на отрезке [−1; 3] не меньшее, чем −5.

Потребовать, чтобы наименьшее значение функции было не меньше чем −5 это все равно что потребовать, чтобы все ее значения были не меньше чем −5. То есть неравенство должно выполняться на всем промежутке То есть

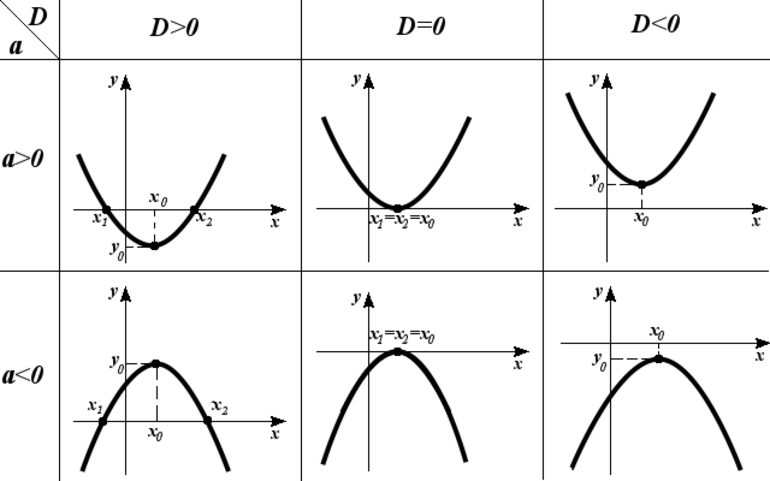
Теперь заметим, что и наоборот — достаточно чтобы эти неравенства выполнялись в нескольких точках, если только одна из них (можно не выяснять какая) будет точкой с наименьшим значением. Поскольку квадратный трехчлен с положительным старшим коэффициентом на любом отрезке принимает наименьшее значение либо в абсциссе вершины параболы — его графика (если эта точка лежит на отрезке) либо в одном из концов отрезка (если не лежит), то нужно проверить следующие неравенства

(верно при ),

(верно при ),

(верно при ).

при то есть при (нас не интересует, поскольку уже установлено что

при то есть при (то есть это обязательно надо проверить, при указанная точка точно лежит на интересующем нас отрезке).

Итак, совмещая все ограничения, получаем

Ответ:

Найдите все значения параметра при каждом из которых наименьшее значение функции больше 1.

При получаем, что График этой функции на рассматриваемом промежутке состоит из двух частей параболы с ветвями, направленными вверх, и осью симметрии При находим а график этой функции на рассматриваемом промежутке — часть параболы с ветвями, направленными вниз.

Наименьшее значение функции может принять только в точках или Поэтому наименьшее значение функции больше 1 тогда и только тогда, когда:

Если то второе неравенство принимает вид откуда Этот промежуток содержит интервал

Если то откуда Значит,

Объединяя найденные промежутки, получаем:

Ответ:

Приведём другое решение.

1. При функция принимает вид: а ее график есть две части параболы с ветвями, направленными вверх и осью симметрии

При функция принимает вид: а ее график есть часть параболы с ветвями, направленными вниз и осью симметрии

Возможные виды графика функции показаны на рисунках.

2. Наименьшее значение функция может принимать только в точках или а если (то есть при ), то в точке

3. Следовательно, наименьшее значение функции больше тогда и только тогда, когда:

Ответ:

Длины сторон прямоугольника ― натуральные числа, а его периметр равен 200. Известно, что длина одной стороны прямоугольника равна n% от длины другой стороны, где n – также натуральное число.

а) Какое наибольшее значение может принимать площадь прямоугольника?

б) Какое наименьшее значение может принимать площадь прямоугольника?

в) Найдите все возможные значения, которые может принимать площадь прямоугольника, если дополнительно известно, что n>100.

а) Так как периметр равен 200, то сумма смежных сторон прямоугольника равна 100. Известно, что наибольшее значение площади прямоугольника при фиксированном периметре достигается в том случае, если он является квадратом. Таким образом, его стороны должны быть равны 50, что не противоречит условию (длины обеих сторон натуральные числа, длина одной стороны равна 100% от длины другой). Значит, наибольшее значение площади прямоугольника равно 2500.

б) Пусть меньшая сторона прямоугольника (или равная другой стороне, если это квадрат) равна тогда другая сторона равна В этом случае площадь прямоугольника равна Графиком данной функции является парабола, ветви которой направлены вниз, а число x не превосходит абсциссы вершины параболы. Следовательно, значение функции будет тем меньше, чем дальше находится число x от абсциссы вершины. Таким образом, наименьшее значение функции достигается при а тогда площадь равна 99. В этом случае условие также соблюдается, так как число 99 равно 9900% от числа 1.

в) Пусть a ― это сторона, n% от которой равны другой стороне. Тогда другая сторона равна Поскольку сумма смежных сторон прямоугольника равна 100, получаем:

Так как a и n ― целые числа, то число 10 000 кратно a.

Возможны три случая:

1) Число a не делится на 5. Тогда оно может быть только степенью двойки, причем не более, чем четвертой, т.е. a может принимать значения 1, 2, 4, 8 или 16, а площадь при этом будет равна, соответственно, 99, 196, 384, 736 или 1344.

2) Число a делится на 5, но не делится на 25. Тогда оно может быть равно 5, 10, 20 или 40. Площадь в этих случаях будет равна, соответственно, 475, 900, 1600 или 2400.

3) Число a делится на 25. В этом случае оно может быть равно только 25. Тогда площадь равна 1875.

Ответ: а) 2500; б) 99; в) 99, 196, 384, 475, 736, 900, 1344, 1600, 1875 или 2400.

Аналоги к заданию № 501400: 501420 511358 Все

Длины сторон прямоугольника ― натуральные числа, а его периметр равен 200. Известно, что длина одной стороны прямоугольника равна n% от длины другой стороны, где n ― также натуральное число.

а) Какое наибольшее значение может принимать площадь прямоугольника?

б) Какое наименьшее значение может принимать площадь прямоугольника?

в) Найдите все возможные значения, которые может принимать площадь прямоугольника, если дополнительно известно, что n >100.

а) Так как периметр равен 200, то сумма смежных сторон прямоугольника равна 100. Известно, что наибольшее значение площади прямоугольника при фиксированном периметре достигается в том случае, если он является квадратом. Таким образом, его стороны должны быть равны 50, что не противоречит условию (длины обеих сторон натуральные числа, длина одной стороны равна 100% от длины другой). Значит, наибольшее значение площади прямоугольника равно 2500.

б) Пусть меньшая сторона прямоугольника (или равная другой стороне, если это квадрат) равна тогда другая сторона равна В этом случае площадь прямоугольника равна Графиком данной функции является парабола, ветви которой направлены вниз, а число не превосходит абсциссы вершины параболы. Следовательно, значение функции будет тем меньше, чем дальше находится число от абсциссы вершины. Таким образом, наименьшее значение функции достигается при а тогда площадь равна 99. В этом случае условие также соблюдается, так как число 99 равно 9900% от числа 1.

в) Пусть ― это сторона, n% от которой равны другой стороне. Тогда другая сторона равна Поскольку сумма смежных сторон прямоугольника равна 100, получаем:

Так как и ― целые числа, то число 10 000 кратно числу a.