Как найти выпуклость функции примеры

Содержание:

• Теоремы о выпуклости функции и точках перегиба
• Схема исследования функции на выпуклость, вогнутость

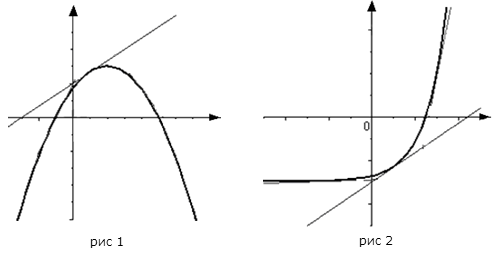
График функции $y=f(x)$, дифференцируемой на интервале
$(a ; b)$, является на этом интервале выпуклым, если график
этой функции в пределах интервала $(a ; b)$ лежит не выше любой
своей касательной (рис. 1).

График функции $y=f(x)$, дифференцируемой на интервале
$(a ; b)$, является на этом интервале вогнутым, если график
этой функции в пределах интервала $(a ; b)$ лежит не ниже любой
своей касательной (рис. 2).

Теоремы о выпуклости функции и точках перегиба

Схема исследования функции на выпуклость, вогнутость

Читать дальше: асимптоты графика функции.

Содержание:

1. Выпуклость графика функции

1. Функция называется выпуклой вверх (вниз) на промежутке, если для любых двух значений из этого промежутка выполняется неравенство

Точки, разделяющие интервалы выпуклости, называются точками перегиба.

2. Если вторая производная функции положительна (отрицательна) на промежутке, то функция является выпуклой вниз (вверх) на этом промежутке.

3. Если — точка перегиба функции и существует, то = 0.

4. Если вторая производная меняет знак при переходе через точку , то точка является точкой перегиба функции

5. Схема исследования функции на выпуклость и точки перегиба’.

1) найти вторую производную функции ;

2) найти точки, в которых вторая производная = 0 или не существует;

3) исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба;

4) найти значения функции в точках перегиба.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Примеры с решением

Пример 1.

Найти точки перегиба и интервалы выпуклости функции

Решение:

В соответствии со схемой исследования (п. 5), найдем Очевидно, при . Знаки второй производной указаны на рис. 8.4.

Функция является выпуклой вверх на интервалах и (так как ) и выпуклой вниз на интервале (0; 1),

( — точки перегиба, так как при переходе через них меняет свой знак.►

Возможно вам будут полезны данные страницы:

Пример 2.

Найти точки перегиба и интервалы выпуклости функции

Решение:

. Вторая производная обращается в нуль в тех же точках , что и в предыдущем примере. Однако, на этот раз знаки второй производной следующие (рис. 8.5).

Таким образом, функция выпукла вниз на всем интервале , и точка не является точкой перегиба. Нетрудно увидеть, что это точка экстремума (максимума) функции. Точка является точкой перегиба. На интервале функция является выпуклой вниз.

Пример 3.

Найти точки перегиба .

Решение:

Имеем Вторая производная обращается в нуль при выполнении равенства . Рис. 8.6 показывает, что при и функция является выпуклой вниз, а при и функция является выпуклой вверх. Точки — точки перегиба.

Выпуклость графика функции

Рассмотрим функцию , имеющую на интервале вторую производную

Вторая производная функции f(x) есть первая производная функции f'(x), поэтому:

1. если на интервале (а; 6), то первая производная f'(x) на этом интервале возрастает;
2. если на интервале (а; &), то первая производная f'(x) на этом интервале убывает.

На рисунках 113—115 изображены графики функций, соответствующие случаю 1.

Объясним это. Для каждого из этих трех графиков при возрастании х от а до Ь тангенс угла между касательной к графику функции и осью Ох возрастает. На рисунке 113 угол а острый для всех значений х из интервала (а; 6); с возрастанием х угол а увеличивается и его тангенс (положительный) увеличивается. На рисунке 114 угол тупой; с возрастанием х угол а увеличивается и его тангенс (отрицательный) увеличивается.

• Наконец, на рисунке 115 тангенс сначала растет, принимая отрицательные значения на интервале (а; с), обращается в нуль в точке х = с, а затем растет, принимая положительные значения на интервале (с; Ь).

Так как в любой точке имеем то рост тангенса угла означает, что на интервале (а; Ь) функция возрастает. Возрастание же первой производной, т. е. возрастание tga, вызвано тем, что вторая производная функции положительна на интервале (а; Ь).

Во всех трех рассмотренных случаях график расположен выше касательной, проведенной в любой его точке.

Справедливо утверждение 1, выражающее геометрический смысл второй производной: если функция на интервале имеет положительную вторую производную fff(x)9 то на этом интервале график функции имеет выпуклость вниз; если же функция f(x) на интервале имеет отрицательную вторую производную то на этом интервале график функции имеет выпуклость вверх.

В случае 1 это утверждение уже разъяснено, а в случае 2 его разъяснение следует из рассмотрения графиков на рисунках 116—118.

Справедливо утверждение 2. Пусть функция f (х) имеет в окрестности точки непрерывную вторую производную Если то функция имеет в точке локальный максимум. Если же , то функция имеет в точке локальный минимум.

Справедливость утверждения 2 следует из доказанной ниже теоремы, если учесть, что из того, что вторая производная отрицательна в точке , в силу предположения о ее непрерывности следует, что она отрицательна в некоторой окрестности этой точки. Из того что вторая производная положительна в точке , в силу ее непрерывности также следует, что она положительна в некоторой окрестности этой точки.

ТЕОРЕМА. Пусть функция f (х) имеет вторую производную на интервале и пусть первая производная этой функции в точке равна нулю: Тогда:

Доказательство.

а) Пусть на интервале Так как вторая производная есть первая производная от первой производной: , то на основании теоремы (п. 5.5) функция на интервале возрастает, но поэтому на интервале на интервале , т. е. первая производная при переходе через точку х0 меняет знак с «-» на «+». Но это означает, что функция в точке имеет локальный минимум.

б) Подобным образом доказывается теорема и в случае , приводящем к локальному максимуму в точке .

Говорят, что точка есть точка перегиба кривой — графика функции , если существует достаточно малое , такое, что для всех кривая находится по одну сторону касательной к кривой в точке с абсциссой , а для всех — по другую. Иными словами, если при переходе х через точка кривой переходит с одной стороны касательной на другую.

Если функция в каждой точке окрестности точки (включая и точку х0) имеет вторую производную , а в точке вторая производная меняет знак с «+» на или с «-» на «+», то точка является точкой перегиба ее графика.

Чтобы найти точки перегиба графика функции на интервале (а; Ь), надо найти вторую производную и решить уравнение

Те корни уравнения (1), которые принадлежат интервалу (а; Ь) и в которых вторая производная меняет знак с «+» на «—» или с «-» на «+», и являются точками перегиба графика функции

Пример с решением

Найдем промежутки выпуклости вверх (вниз) и точки перегиба графика функции

Функция (2) определена для всех

Вычислим вторую производную функции (2). Так как то

Очевидно, что вторая производная функции (2) обращается в нуль в единственной точке отрицательна на интервале , положительна на интервале . Следовательно, точка — точка перегиба графика функции (2).

На интервале график функции (2) имеет выпуклость вверх, а на интервале — выпуклость вниз.

На рисунке 119 изображены график функции (2) в окрестности точки и касательная, проведенная к графику в точке с абсциссой

В
этом пункте приведем определения
выпуклой вниз и выпуклой вверх функции,
точек перегиба, а также сформулируем
необходимые и достаточные условия
выпуклости и наличия точек перегиба.

Пусть
функция

определена на интервале

и пусть

.
Проведем прямую через точки

и

,
лежащие на графике функции

.
Ее уравнение будет

или

Очевидно,

,

.

Определение
5. 12
Функция

называется выпуклой
вверх
(выпуклой
вниз)
на интервале

Геометрически
это означает, что любая точка хорды

(т. е. отрезка прямой

с концами в точках

и

)
лежит не выше (не ниже) точки графика
функции

,
соответствующей тому же значению
аргумента (рис. 35).

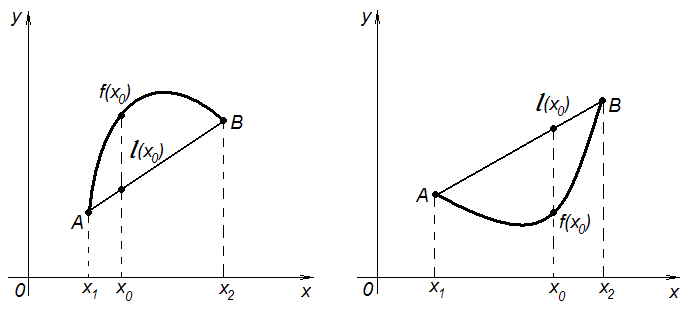
Рис.
35. Выпуклость вверх и выпуклость вниз

Определение
6. 13
Если
вместо

называется строго
выпуклой вверх
(строго
выпуклой вниз)
на интервале

.

Сформулируем
теорему, содержащую необходимые и
достаточные условия выпуклости функции
вверх и вниз.

Теорема
5. 14
Пусть
функция

было

Замечание.
Условие

(
),

является достаточным условием строгой
выпуклости вверх (вниз) функции

на интервале

.

Определим
теперь какая точка является точкой
перегиба функции.

Определение
7. 15
Пусть
функция

называется точкой
перегиба функции

(см. рис. 36).

Рис.
36. Точка перегиба

Сформулируем
необходимые условия существования
точки перегиба.

Теорема
6. 16
(необходимое
условие наличия точки перегиба) Пусть
функция

,
то

.

Приведем
теперь достаточные условия существования
точек перегиба с использованием второй
и третьей производной функции.

Теорема
7. 17
(первое
достаточное условие наличия точек
перегиба) Если функция

.

Если
исследуемая функция имеет третью
производную, то можно использовать
следующий признак существования точек
перегиба.

Теорема
8. 18
(второе
достаточное условие наличия точек
перегиба) Пусть

является точкой перегиба.

Таким
образом, нахождения точек перегиба и
промежутков выпуклости вверх и выпуклости
вниз функции

проводится следующим образом:

• определяется

;

• отыскиваются
те значения

,
при которых

обращается в нуль или не существует,
т.е. решается уравнение

и определяются точки разрывы функции

;

• исследуется
изменение знака

при переходе через эти значения по
следующей схеме

Таблица
8.

Таблица
9.

Значения

,
в которых исследуется знак второй
производной, нужно брать достаточно
близкими к

.
Символ

означает, что в рассатриваемом промежутке
функция

выпукла вверх, символ

означает выпуклость вниз функции. Если
вторая производная сохраняет знак при
переходе через

,
то

не является точкой перегиба.

Пример
16.
Найти интервалы выпуклости и точки
перегиба функции

.

Решение.
Функция определена и по крайней мере
дважды дифференцируема при всех
вещественных

кроме

.
Найдем

:

Получаем,
что вторая производная

равна нулю в точке

,
а в точке

не существует. Исследует знак

на интервалах

,

,

,
для этого заполним следующую таблицу.

Таблица
10.

Получаем,
что

— точка перегиба, при

функция

выпукла вверх, а при

и

— выпукла вниз.

График
функции

изображен на рис. 37.

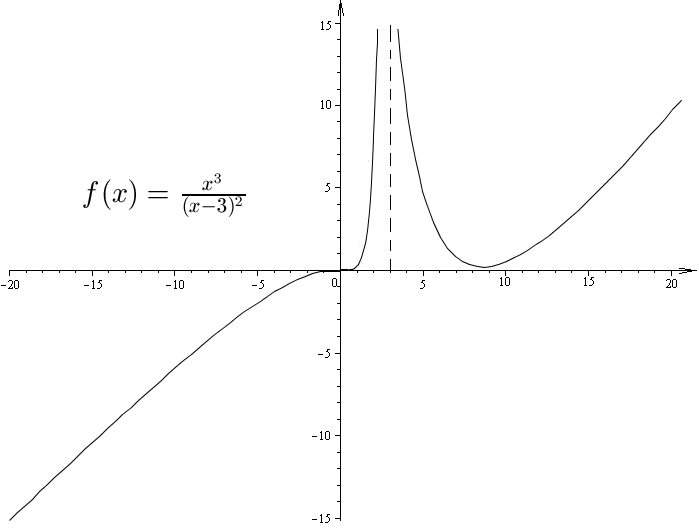
Рис.
37. График функции

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Алгебра и начала математического анализа, 11 класс

Урок №18. Производная второго порядка, выпуклость и точки перегиба.

Перечень вопросов, рассматриваемых в теме

1) Нахождение производной второго порядка;

2) Определение промежутка выпуклости графика функции с помощью алгоритма;

3) Решение прикладных задач с использованием производной второго порядка.

Глоссарий по теме

Возрастание функции. Функция y = f(x) возрастает на интервале X, если для любых х₁ и х₂, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Выпуклость вверх. Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка.

Выпуклость вниз. Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.

Максимум функции. Значение функции в точке максимума называют максимумом функции 

Минимум функции. Значение функции в точке минимума называют минимумом функции 

Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).

Производная второго порядка (вторая производная). Производная второго порядка есть первая производная от производной первого порядка.

Производную определяют, как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к 0, если такой предел существует.

Точка максимума функции. Точку  х₀ называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство  .

Точка минимума функции. Точку  х₀называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство  .

Точка перегиба. Точки, в которых выпуклость вверх меняется на выпуклость вниз или наоборот, называются точками перегиба.

Точки экстремума функции. Точки минимума и максимума называют точками экстремума.

Убывание функции. Функция y=f(x) убывает на интервале X, если для любых х₁ и х₂, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.

Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка.

Алгоритм нахождения интервалов выпуклости графика функции:

1. Найти область определения функции
2. Найти вторую производную функции
3. Найти точки, в которых вторая производная равна нулю или не существует
4. Найти интервалы, на которые область определения функции разбивается этими точками
5. Определить знаки второй производной на каждом интервале
6. Если f ‘‘(х) < 0, то кривая выпукла вверх;

если f ‘‘(х) > 0 то кривая выпукла вниз.

1. Точки, в которых вторая производная меняет знак, — точки перегиба.

Примеры и разбор решения заданий тренировочного модуля

Пример 1.Найти интервалы выпуклости и точки перегиба функции .

Решение:

1. Область определения данной функции D(y) = (-∞; +∞)
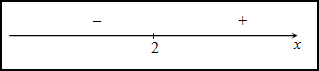
2. Найдем вторую производную функции:
3. при х = 1, х = -1
4. Определим знаки второй производной на каждом интервале (-∞; -1), (-1; 1), (1; +∞), используя метод интервалов (рис. 1).

Рисунок 1 – интервалы на числовой прямой

1. Так как на интервалах (-∞; -1) и (1; +∞) вторая производная положительна, то на этих интервалах функция выпукла вниз.

Так как на интервале (-1; 1) вторая производная отрицательна, то на этом интервале функция выпукла вверх.

Так как при переходе через точки х = 1 и х = -1 вторая производная меняет знак, то эти точки являются точками перегиба.

Ответ: функция выпукла вниз на интервалах (-∞; -1), (1; +∞);

функция выпукла вверх на интервале (-1; 1);

х = 1, х = -1 – точки перегиба.

Пример 2.Найти точки перегиба функции у=sinх

Решение:

Найдем вторую производную заданной функции

У’=соsх

У»= -sinх

Приравняем её к нулю и найдем корни полученного уравнения -sinх=0

В промежутках

Функция у=sinх принимает положительные значения, следовательно, У»= -sinх <0, а в промежутках , sinх <0, следовательно

У» >0. Значит, в точках вторая производная меняет знак и в этих точках график функции у=sinх имеет перегиб

Ответ: точка перегиба

Пример 3.Точка движется по закону S(t) = 3t⁴ – 8t³ + 2t – 3. В какой момент времени ускорение точки будет равно 48?

Решение:

Ускорение — это вторая производная s(t).

Найдем уравнение ускорения.

v=S'(t) = 12t³ – 24t² + 2

a= S»(t) = 36t² – 48t

Остается подставить вместо ускорения его значение равное 48 и решить уравнение.

36t² – 48t=48

36t² – 48t-48=0

При решении один корень получается отрицательный, чего не может быть по условиям задачи, а второй корень равен 2

Ответ: 2

Пример 4. Найдите интервалы выпуклости вверх и выпуклости вниз и точки перегиба функции f(x) = x³ – 6xlnx.

Проверьте свое решение.

Решение:

1. D(f) = (0; +∞)
2. f (x) = (x³ – 6xln x)

1. f (x) = 0 при х = 1, х = -1.

f (x) не существует при х = 0.

С учетом области определения функции, х = 1

1. Так как на интервале (1; +∞) вторая производная положительна, то на этом интервале функция выпукла вниз.

Так как на интервале (0; 1) вторая производная отрицательна, то на этом интервале функция выпукла вверх.

Так как при переходе через точку х = 1 вторая производная меняет знак, то эта точка является точкой перегиба.

Ответ: функция выпукла вниз на интервале (1; +∞);

функция выпукла вверх на интервале (-1; 1);

х = 1– точка перегиба.