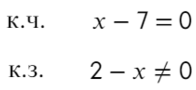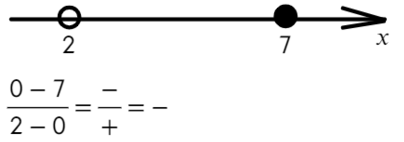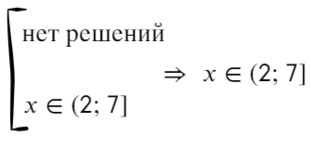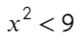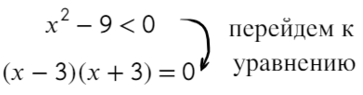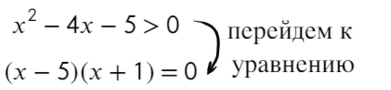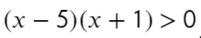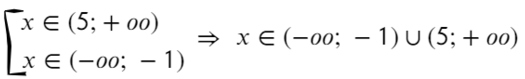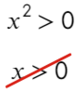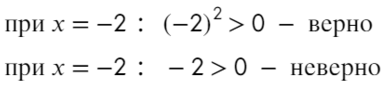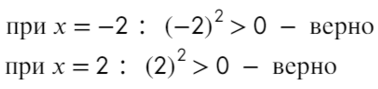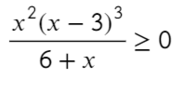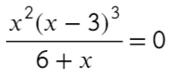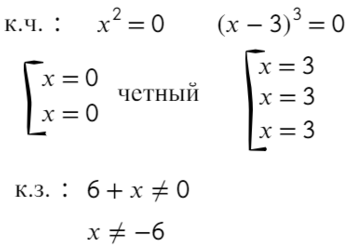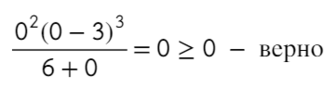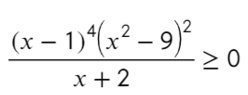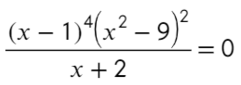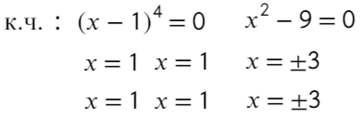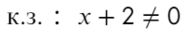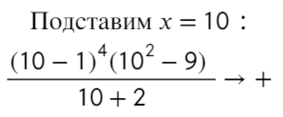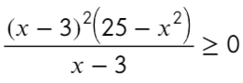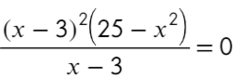Как найти выколотую точку гиперболы на графике - AvtoShod.ru

График функции с переменной в знаменателе

График функции с переменной в знаменателе — следующая группа заданий из номера 23 ОГЭ по математике.

Исследование любой функции начинается с нахождения её области определения.

Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, те значения переменной, при которых знаменатель обращается в нуль, не входят в область определения функции.

В этом случае возможно появление на графике выколотых точек.

Рассмотрим примеры построения графиков функций, содержащих переменную в знаменателе дроби.

1) Постройте график функции

$[ {rm{y = }}frac{{{rm{5x - 8}}}}{{{rm{5x}}^{rm{2}} {rm{ - 8x}}}} ]$

и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.

Решение:

В знаменателе вынесем за скобки общий множитель x:

$[ {rm{y = }}frac{{{rm{5x - 8}}}}{{{rm{x(5x - 8)}}}} ]$

ВАЖНО: прежде чем сократить дробь, следует найти область определения функции!

Дробь имеет смысл, если знаменатель отличен от нуля:

x(5x-8)≠0,

x≠0, x≠8/5.

Область определения функции D(y): x∈(-∞;0)∪(0;8/5)∪(8/5;∞)

(или D(y): x∈R, кроме x=0 и x=8/5).

Теперь сократим дробь на 5x-8:

$[ y = frac{1}{x} ]$

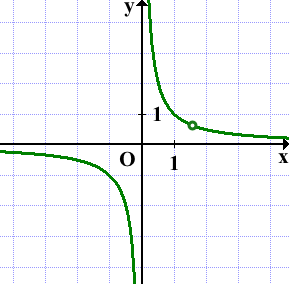
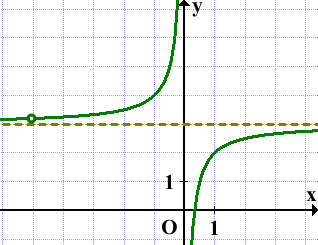
y=1/x — функция обратной пропорциональности. Её график — гипербола. Не забываем про выколотую точку: x≠8/5 (0 не входит в область определения функции y=1/x).

Для построения гиперболы возьмём несколько точек (в том числе, выколотую):

$[ frac{x}{y}left| {frac{{ - 2}}{{ - frac{1}{2}}}} right.left| {frac{{ - 1}}{{ - 1}}} right.left| {frac{{ - frac{1}{2}}}{{ - 2}}} right.left| {frac{{frac{1}{2}}}{2}} right.left| {frac{1}{1}} right.left| {frac{{frac{8}{5}}}{{frac{5}{8}}}} right.left| {frac{2}{{frac{1}{2}}}} right. ]$

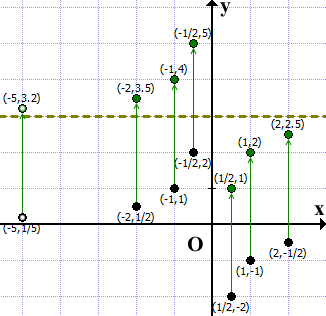
Отмечаем эти точки на координатной плоскости.

Строим гиперболу с выколотой точкой (8/5; 5/8):

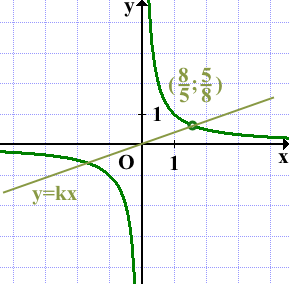
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку:

Чтобы найти k, подставляем координаты выколотой точки

(8/5; 5/8)

в формулу y=kx и находим k:

$[ frac{5}{8} = k cdot frac{8}{5} ]$

$[ k = frac{5}{8}:frac{8}{5} ]$

$[ k = frac{{25}}{{64}} ]$

Ответ : 25/64.

2) Постройте график функции

$[ y = 3 - frac{{x + 5}}{{x^2 + 5x}} ]$

и определите, при каких значениях m прямая y=m не имеет с графиком общих точек.

Решение:

В знаменателе вынесем за скобки общий множитель

$[ y = 3 - frac{{x + 5}}{{x(x + 5)}} ]$

(Не забываем: сначала следует найти область определения функции, и лишь после этого упрощать выражение!)

Ищем область определения функции.

x(x+5)≠0

x≠0; x≠-5;

D(y): x∈(-∞;-5)∪(-5;0)∪(0;∞).

Сокращаем дробь на x+5:

$[ y = 3 - frac{1}{x} ]$

— функция обратной пропорциональности. График — гипербола, полученная из гиперболы

$[ y = - frac{1}{x} ]$

параллельным переносом на 3 единицы вверх вдоль оси Oy.

Сначала найдём несколько точек для построения графика y=-1/x:

$[ frac{x}{y}left| {frac{{ - 5}}{{frac{1}{5}}}} right.left| {frac{{ - 2}}{{frac{1}{2}}}} right.left| {frac{{ - 1}}{1}} right.left| {frac{{ - frac{1}{2}}}{2}} right.left| {frac{{frac{1}{2}}}{{ - 2}}} right.left| {frac{1}{{ - 1}}} right.left| {frac{2}{{ - frac{1}{2}}}} right. ]$

Отметим эти точки на координатной плоскости. Затем каждую из них перенесем на 3 единицы вверх вдоль оси ординат.

Прямая y=0 (ось абсцисс) для гиперболы y=-1/x является асимптотой (то есть прямой, к которой график стремится, но никогда её не достигнет). Асимптоты принято изображать пунктирными линиями. Так как y=0 совпадает с осью Ox, то она изображена сплошной линией. При параллельном переносе на 3 единицы вверх прямая y=0 переходит в прямую y=3. Прямая y=3 — асимптота, поэтому изображаем её пунктиром.

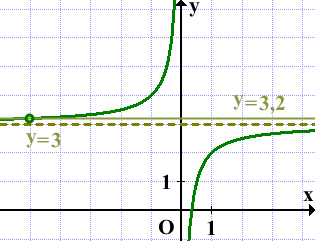
Через полученные точки проведём гиперболу y=3-1/x:

Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку либо совпадает с асимптотой y=3, то есть при m=3,2 и m=3:

Ответ: 3; 3,2.

3) Постройте график функции

$[ y = frac{{(x^2 + 4)(x + 1)}}{{ - 1 - x}} ]$

и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.

Решение:

Найдём область определения функции.

-1-x≠0

x≠-1.

D(y):x∈(-∞;-1)∪(-1;∞).

Преобразуем дробь:

$[ y = frac{{(x^2 + 4)(x + 1)}}{{ - (1 + x)}} ]$

и сократим её на (x+1):

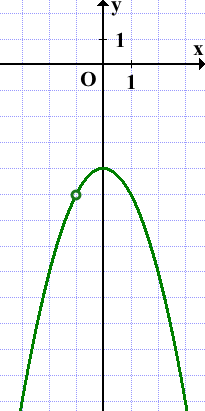
y=-x²-4 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).

График может быть получен из графика функции y=-x² параллельным переносом на 4 единицы вниз вдоль оси Oy (не забываем про выколотую точку! x≠-1):

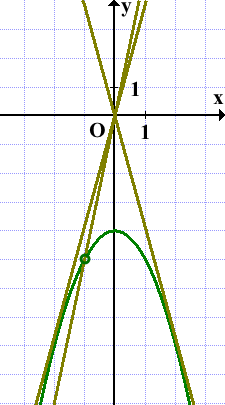
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку либо если она является касательной к параболе:

Значения k в данном случае удобнее искать аналитически, а не с помощью графика.

Прямая y=kx имеет с графиком функции y=-x²-4, где x≠-1 ровно одну общую точку, если система

$[ left{ begin{array}{l} y = - x^2 - 4, \ x ne - 1, \ y = kx \ end{array} right. ]$

имеет одно решение.

Приравниваем правые части равенств:

-x²-4=kx

x²+kx+4=0.

Это квадратное уравнение имеет один корень в двух случаях: либо дискриминант равен нулю, либо дискриминант положителен, но один из корней равен -1.

D=b²-4ac=k²-4·1·4=k²-16.

k²-16=0 при k=4 или k=-4.

Если x=-1, подставив это значение в уравнение, найдём k:

(-1)²+k·(-1)+4=0

k=5.

Ответ: -4; 4; 5.

4) Постройте график функции

$[ y = frac{{(x^2 - 4x + 3)(x^2 - x - 2)}}{{x^2 - 2x - 3}} ]$

и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.

Решение:

Формула функции содержит три квадратных трёхчлена. Чтобы разложить каждый из них на множители, решим три квадратных уравнения и воспользуемся теоремой о разложении квадратного трёхчлена на множители.

1)x²-4x+3=0

x₁=1; x₂=3

x²-4x+3=(x-1)(x-3).

2)x²-x-2=0

x₁=-1; x₂=2

x²-x-2=(x+1)(x-2).

3)x²-2x-3=0

x₁=-1; x₂=3

x²-2x-3=(x+1)(x-3).

$[ y = frac{{(x - 1)(x - 3)(x + 1)(x - 2)}}{{(x + 1)(x - 3)}} ]$

Ищем область определения функции.

(x+1)(x-3)≠0

x≠-1, x≠3.

D(y): x∈(-∞;-1)∪(-1;3)∪(3;∞).

Сокращаем дробь на (x+1)(x+3):

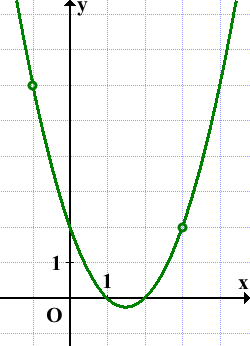
-квадратичная функция. График — парабола ветвями вверх (так как a=1>0).

Координаты вершины параболы

$[ x_o = - frac{b}{{2a}} = - frac{{ - 3}}{{2 cdot 1}} = frac{3}{2} = 1,5; ]$

$[ y_o = (frac{3}{2})^2 - 3 cdot frac{3}{2} + 2 = frac{9}{4} - frac{9}{2} + 2 = - frac{1}{4} = - 0,25. ]$

От вершины — точки (1,5; -0,25) — строим параболу y=x². Поскольку координаты вершины — не целые числа, для построения графика удобно найти дополнительные точки с целыми координатами.

При y=0 (x — 1)(x — 2)=0,

x=1; x=2.

При x=0 y=0²-3·0+2=2.

Находим координаты выколотых точек

При x=-1 y=(-1)²-3·(-1)+2=6,

при x=3 y=3²-3·3+2=2.

Прямая y=m имеет с графиком ровно одну общую точку, если она проходит через одну из выколотых точек либо через вершину, то есть при m=2, m=6 и m=-0,25.

Ответ: -0,25; 2; 6.

Источник

Для того, чтобы хорошо решать это задание, нужно быть знакомым с построением различных графиков функций, в том числе содержащих модуль. Предлагаю тем, кто неуверенно себя чувствует при решении таких заданий, перейти по ссылкам и изучить (или повторить) данные разделы. Задание С3 связано как с исследованием расположения корней квадратного трехчлена, так и с определением области определения функции, и области ее значений. На конкретных примерах мы попробуем научиться решать различные типы таких заданий.

Задача 1. Построить график функции y=x^2+4 и определить, при каких значениях график функции y=kx имеет с графиком 1 общую точку. Построить все такие прямые.

Задача о касательных к параболе

Графиком предложенной функции является парабола, ветви которой направлены вверх и вершина, которую подняли вверх на 4 единицы, лежит на оси ординат. Ее координаты (0;4). Второй график — это прямая, проходящая через начало координат, причем ее наклон может меняться (его определяет коэффициент ). Такая прямая только в одном случае имеет с параболой одну общую точку — если является касательной. Причем, поскольку данная парабола симметрична относительно оси ординат, то к ней можно провести две касательных — с точками касания в первом и третьем квадрантах: Чтобы определить, в какой точке прямая коснется параболы, нужно приравнять обе функции:

Поскольку точка касания — единственная общая точка данных графиков, то дискриминант данного уравнения равен нулю: Откуда k^2=16 и k=pm{4} . Абсциссу точки касания можно найти, если приравнять два уравнения, подставив найденный коэффициент в уравнение прямой: и решить это уравнение: Тогда касание произойдет в точке x=2 и симметричной ей точке x=-2 .

Задача 2. Построить график функции $y=-delim{|}{x^2-4x+3}{|}$ и определить, при каких значениях график функции y=a имеет с графиком три или более общие точки.

График, который подвергнется преобразованиям

Преобразованный график

Строить этот график будем поэтапно: сначала построим график , затем — график функции $y=delim{|}{x^2-4x+3}{|}$ , и, наконец, искомый — $y=-delim{|}{x^2-4x+3}{|}$ : Парабола с ветвями, направленными вверх, стандартной формы, координаты вершины (2;-1) Теперь построим график $y=delim{|}{x^2-4x+3}{|}$ . Поскольку модуль берется от всего выражения, то, чтобы получить этот график, нужно отразить вверх симметрично относительно оси х все точки, имеющие отрицательную ординату. И, наконец, поставив минус, мы «перевернем» весь график вверх тормашками:

«Опрокидываем» преобразованный график

Осталось выяснить, в каком же случае прямая y=a — а это прямая, параллельная оси абсцисс — будет иметь три (или же более) общие точки с графиком построенной нами функции. Прямая показана на рисунке зеленым цветом. Видно, что ниже указанного положения прямая будет иметь только две общие точки с графиком. Если y=-1 , то прямая имеет три точки с графиком — пересекает две его ветви и касается вершины. Выше прямая будет иметь четыре точки пересечения с графиком, однако при y=0 точек пересечения уже снова две. Значит, ответ надо записать так: a in [-1;0)

Задача 3. Построить график функции $y=delim{|}{x^2+2x-8}{|}$ и определить, при каких значениях график функции y=a имеет с ним три и более общие точки.

Исходный график

Окончательный вид

Также построим график в два этапа: саму параболу (координаты ее вершины (-1;-9)), затем отразим всю часть, лежащую ниже оси х, вверх: Тогда три и более (а именно — четыре) общих точки графики $y=delim{|}{x^2+2x-8}{|}$ и y=a будут иметь при a in (0;9]

Задача 4. Построить график функции $y={lbrace}matrix{2}{1}{{{x+4, x<=1}} {x^2-6x+10, x>1}}$ и определить, при каких значениях график функции y=a имеет с ним 2 общие точки.

Из условия ясно, что такой график состоит из двух кусочков. Один из них — прямая, второй — парабола. Первый существует в точке 1 и левее ее, второй — правее этой точки. Нарисуем эти графики:

Кусочная функция

Координаты вершины параболы: $x_0=-{b/2a}=-{-6}/2=3$ ;

Красным показаны прямые y=1 и y=5 — именно они, и только они, имеют две общие точки с построенным графиком. Ответ: a=1 , a=5 .

Задача 5. Построить график функции $y={x^3-x^2+25x-25}/{x-1}$ и определить, при каких значениях график функции y=kx не имеет с графиком общих точек.

Давайте сначала попробуем упростить данное выражение, кроме того, нужно, безусловно, определить область допустимых значений данной функции. ОДЗ: x<>1 . Теперь попробуем упростить данное выражение: $y={x^3-x^2+25x-25}/{x-1}=$ ${x^2(x-1)+25(x-1)}/{x-1}=$ ${(x-1)(x^2+25)}/{x-1}=$ x^2+25

Определение коэффициента наклона касательной

Полученная функция — квадратичная, ее графиком является парабола. Данная парабола симметрична относительно оси y, ее вершина имеет координаты (0; 25). Необходимо заметить, что точка с координатами (1; 26) — выколотая точка (по ОДЗ). Тогда прямая, проходящая через начало координат — а именно таким будет график функции y=kx , не будет иметь с параболой общих точек в трех случаях: если коэффициент меньше, чем у касательной, расположенной справа, или он больше, чем у касательной, расположенной слева, или искомая прямая проходит прямо через выколотую точку. Наверное, проще найти каков этот коэффициент именно в третьем случае: так как прямая проходит через начало координат, достаточно подставить координаты нашей выколотой точки в уравнение прямой и найти : 26=k*1 , откуда k=26 . Проверим, не будет ли такая прямая иметь общих точек с параболой. Приравняем . По сумме коэффициентов это уравнение имеет корень 1, но и второй корень — 25, поэтому такая прямая будет иметь еще одну точку пересечения с параболой. В ответ эту прямую мы не включим. Теперь определим коэффициент наклона касательных, для этого приравняем оба уравнения: , и найдем дискриминант, который должен быть равен нулю при наличии единственной общей точки у двух этих графиков функций: Откуда k^2=100 и Абсциссу точки касания можно найти, если приравнять два уравнения, подставив найденный коэффициент в уравнение прямой: и решить это уравнение: Тогда касание произойдет в точке x=5 и симметричной ей точке x=-5 . Ответ: k<10 , k>-10 .

Задача 6. Построить график функции $y={x-3}/{x^2-3x}$ и определить, при каких значениях он не имеет общих точек с графиком функции y=a .

Гипербола с выколотой точкой

Определим ОДЗ функции: x<>0 , x<>3 . (Для того, чтобы определить ОДЗ, приравняли знаменатель к нулю и решили данное уравнение). Теперь упростим выражение: — видим, что графиком будет обычная гипербола, однако точка x=3 — выколотая точка. В точке x=0 гипербола не существует, оси координат — ее асимптоты (одна из них войдет в ответ). Тогда, если прямая y=a пройдет через выколотую точку, графики не будут иметь общих точек. Найдем : для этого определим ординату выколотой точки: : Ответ: a=1/3 и a=0 .

Задача 7. Построить график функции $y={x-1}/{x^2-x}$ и определить, при каких значениях график функции y=kx имеет с графиком 1 общую точку.

Подбор коэффициента наклона прямой

Определим ОДЗ функции: x<>0 , x<>1 . (Для того, чтобы определить ОДЗ, приравняли знаменатель к нулю и решили данное уравнение). Теперь упростим выражение: — видим, что графиком будет обычная гипербола, однако точка x=1 — выколота. В точке x=0 гипербола не существует, оси координат — ее асимптоты. Тогда, если прямая y=kx пройдет через выколотую точку, графики будут иметь одну общую точку. Найдем : для этого подставим в уравнение прямой абсциссу и ординату выколотой точки: 1=k/1 , k=1 : Ответ: k=1

Задача 8. Построить график функции $y=x^2-4delim{|}{x}{|}+3$ и определить, при каких значениях график функции y=a имеет с ним 2 общие точки.

Построение функции с модулем

Эта функция — функция типа , и чтобы построить график данной функции, необходимо отразить всю часть графика, расположенную справа от оси х, налево: Тогда, если a=-1 , то график y=-1 коснется обеих вершинок нашей «дублированной» параболы, то есть a=-1 — один из ответов. Также, если a>3 , то y=a пересечет обе ветви параболы, то есть все a>3 нас устраивают. Ответ: a=-1 , a>3 .

Задача 9. Построить график функции $y={(x^2-2x)delim{|}{x}{|}}/{x-2}$ и определить, при каких значениях график функции y=c не имеет с ним общих точек.

Кубическая парабола с выколотой точкой

Определим ОДЗ исходной функции: x<>2 . Теперь можно упростить выражение: $y={{(x^2-2x)}delim{|}{x}{|}}/{x-2}=$ .

График представлен на рисунке. Не забудем про выколотую точку — это точка с координатами (2;4). Поэтому, если прямая y=c пройдет именно через эту точку, она не будет иметь общих точек с полученным нами графиком. Ответ: с=4.

Задача 10. Построить график функции и определить, при каких значениях график функции y=kx имеет с ним одну общую точку.

Для того, чтобы построить данный график, необходимо раскрыть модули. С этой целью приравняем подмодульное выражение к нулю, чтобы узнать, в какой точке оно меняет знак: x-1=0 x=1 и x+1=0 x=-1 Нанесем эти точки на числовую прямую и расставим знаки:

У нас получились три интервала, на каждом из которых можно теперь раскрыть модули: 1. 2. 3. Тогда наша функция — кусочно-линейная: .

Она выглядит так:

Кусочно-линейная функция

Зеленым цветом показано одно из возможных положений прямой y=kx . При таком расположении прямой k>1 , и может расти бесконечно. Заметим, что крайнее положение прямой — при k=1. При таком коэффициенте наклона она параллельна правой и левой частям графика, и имеет с ним одну точку пересечения — точку (0;0). Точно так же коэффициент наклона может быть и отрицательным. При этом коэффициент k=-1 — не войдет в ответ, так как в этом случае функция y=kx будет иметь общий отрезок с кусочно-линейной функцией, что не соответствует требованиям задачи. Таким образом,

Ответ: ).

Задача 11. При каких вершины парабол и расположены по одну сторону от оси х?

Обратим внимание на то, что у двух данных парабол ветви направлены в разные стороны: у первой старший коэффициент отрицателен, а у второй — положителен. Поэтому вершины будут лежать по одну сторону от оси, если одна из них будет иметь точки пересечения с осью х, а другая — нет. Иными словами, дискриминант одного квадратного уравнения должен быть положителен, а другого — отрицателен. Это приводит нас к двум системам неравенств:

Дискриминант и наличие пересечений параболы с осью х

${lbrace}matrix{2}{1}{{D_1>0} {D_2<0}}$ .

Или же наоборот: ${lbrace}matrix{2}{1}{{D_1<0} {D_2>0}}$ . Эти два случая изображены на рисунке:

Определим дискриминанты обоих квадратных уравнений:

$D_1=b^2-4ac=16m^2-4(-1)({-}m)=16m^2-4m$

Тогда имеем систему неравенств:

${lbrace}matrix{2}{1}{{16m^2-4m>0} {4m^2+8<0}}$ — решений нет, так как квадрат числа — неотрицателен, и сумма квадрата числа с положительным числом не может быть меньше ноля.

${lbrace}matrix{2}{1}{{16m^2-4m<0} {4m^2+8>0}}$ — в этой системе второе неравенство всегда соблюдается, решение первого — , , 0<m<1/4

Мы рассмотрели один способ решения — с использованием дискриминанта. Есть еще один способ решения такого задания — с помощью координат вершины параболы. Решим последнюю задачу вторым способом.

Нам потребуется определить координаты вершин обеих парабол:

1. $x_0=({-}b)/{2a}=({-}4m)/(-2)=2m$

$y_0=({-}2m)^2+4m*2m-m=4m^2-m$

2. $x_0=({-}b)/{2a}=({-}m)/2=-m$

$y_0=({-}m)^2-2m^2-2=-m^2-2$

Ординаты вершин должны иметь один знак по условию, тогда имеем систему неравенств:

${lbrace}matrix{2}{1}{{4m^2-m<0} {-m^2-2<0}}$

${lbrace}matrix{2}{1}{{4m^2-m>0} {-m^2-2>0}}$ — вторая система решений не имеет, а именно, нет решений у второго неравенства, поэтому решим первую. Второе неравенство первой системы справедливо всегда, осталось решить неравенство:

${4m^2-m<0}$

Решение этого неравенства и есть ответ задачи: 0<m<1/4

До встречи в новых постах, удачи на экзаменах!

Источник

График дробно-рациональной функции. Гипербола.

Функция $y=frac{k}{x}$ . Гипербола. Свойства.

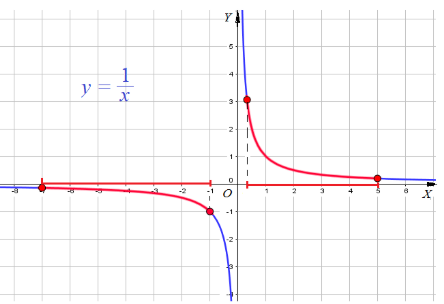
Пример 1: Построить график для функции $y=frac{1}{x}$, $fleft(xright)=frac{1}{x}$

Вычислим значения функции в разнознаковых точках и нанесем точки с вычисленными координатами в системе $XOY$.
$x=1$ $fleft(1right)=1$ $x=frac{1}{2}$ $fleft(frac{1}{2}right)=2$ $x=-1$ $fleft(-1right)=-1$ $x=-frac{1}{2}$ $fleft(-frac{1}{2}right)=-2$
$x=2$ $fleft(2right)=frac{1}{2}$ $x=frac{1}{4}$ $fleft(frac{1}{4}right)=4$ $x=-2$ $fleft(-2right)=-frac{1}{2}$ $x=-frac{1}{4}$ $fleft(-frac{1}{4}right)=-4$
$x=4$ $fleft(4right)=frac{1}{4}$ $x=frac{1}{8}$ $fleft(1right)=8$ $x=-4$ $fleft(-4right)=-frac{1}{4}$ $x=-frac{1}{8}$ $fleft(-frac{1}{8}right)=-8$ .
В системе координат укажем точки $(1;1)$, $(2;1/2)$, $(4;1/4)$, $(1/2;2)$, $(1/4;4)$, $(1/8;8)$, $(-1;-1)$, $(-2;-1/2)$,
Еще точки: $(-4;-1/4)$, $(-1/2;-2)$, $(-1/4;-4)$, $(-1/8;-8)$ . По всем точкам построим кривые — график функции $y=frac{1}{x}$
Функция $y=frac{1}{x}$ не вычисляется при $x=0$, О.Д.З. $xne0$ . График имеет разрыв по вертикальной линии $x=0$. Ветви «прижаты» к ней.
Ветви графика прижимаются к горизонтальной линии $y=0$. Функция $y=frac{1}{x}$ ни при каких $x$ не принимает значение $y=0$

Графиком функции $y=frac{k}{x}$ $kne0$ является гипербола , ветви прижимаются к асимптотическим линиям.

если коэффициент $k > 0$ , в I и III координатных четвертях. Точка $(0;0)$ — центр симметрии.
если $k < 0$ , то во II и IV координатных четвертях. Точка $(0;0)$ — центр симметрии.
Асимптоты: Вертикальная асимптота, линия $x=0$, Горизонтальная асимптота, линия $y=0$

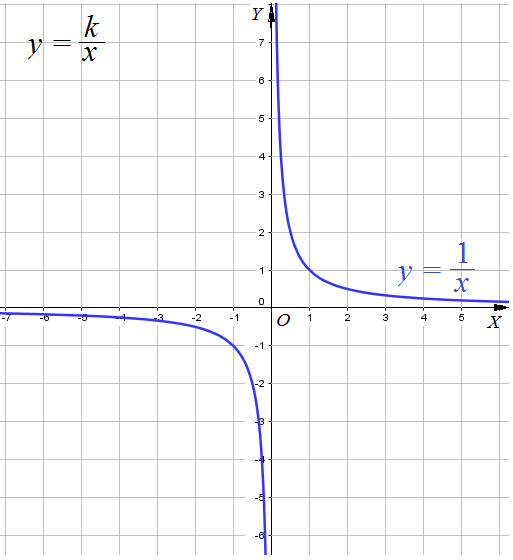
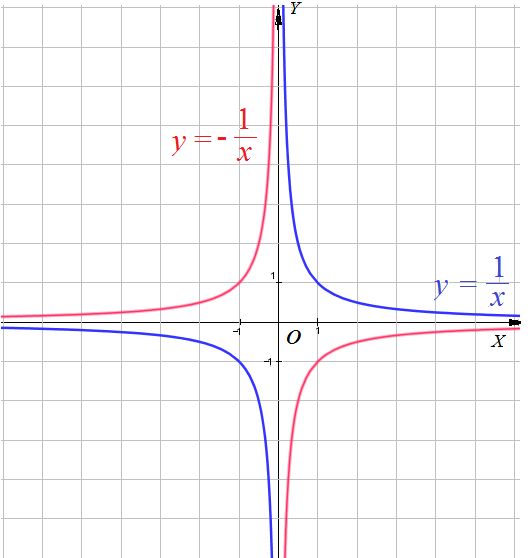
Cвойства функции $y=frac{k}{x}$ при $k > 0$ ( ветви гиперболы расположены в первом и третьем координатных углах) .

Свойство 1: Область Определения Функции — вся числовая прямая , кроме $x=0$.
Свойство 2: $y > 0$ при $x > 0$; $y < 0$ при $x < 0$.
Свойство 3: Функция убывает на промежутках $( — ∞ ; 0 )$ и $( 0 ; + ∞)$
Свойство 4: Функция не ограничена ни снизу, ни сверху.
Свойство 5: Ни наименьшего, ни наибольшего значений $у$ функций нет.
Свойство 6: Функция непрерывна на $( — ∞ ; 0 )$ и $( 0 ; + ∞)$.
Свойство 7: Область значений функции — $( — ∞ ; 0 )$ U $( 0 ; + ∞)$. имеет разрыв в точке $x=0$.

Cвойства функции $y=frac{k}{x}$ при $k < 0$ (ветви гиперболы расположены во втором и четвертом координатных углах).

Свойство 1: Область Определения Функции — вся числовая прямая , кроме $x=0$.
Свойство 2: $y > 0$ при $x < 0$ ; $y < 0$ при $x > 0$.
Свойство 3: Функция возврастает на промежутках $( — ∞ ; 0 )$ и $( 0 ; + ∞)$
Свойство 4: Функция не ограничена ни снизу, ни сверху.
Свойство 5: Ни наименьшего, ни наибольшего значений $у$ функций нет.
Свойство 6: Функция непрерывна на $( — ∞ ; 0 )$ и $( 0 ; + ∞)$
Свойство 7: Область значений функции — объединение $( — ∞ ; 0 )$ U $( 0 ; + ∞)$ . имеет разрыв в точке $x=0$.

Метод Замены для построения Графика Функции.

Мысль: Умеем строить график функции по-проще … используем его для построения функции при «сдвинутых» аргументах и значениях.

Как построить график функции $y=kcdot fleft(xright)$, если известен график функции $y=fleft(xright)$.

График $y=5cdot fleft(xright)$: Растянуть вертикально вверх по оси $OY$ 5 раз все, что над $OX$ графика $y=fleft(xright)$ , $k$ раза.
График $y=5cdot fleft(xright)$: Расстянуть вертикально вниз по оси $OY$ 5 раз все, что под $OX$ графика $y=fleft(xright)$ , $k$ раза.
График $y=frac{1}{3}cdot fleft(xright)$: Сжать по вертикали, оси $OY$ график $y=fleft(xright)$ 3 раза.
Еще способ: Перемасштабирование. Для $y=5cdot fleft(xright)$ … построить $y=fleft(xright)$, изменить масштаб: «1» станет «5», «-2» станет «-10», и т.д.

Как построить график функции $y=-fleft(xright)$, если известен график функции $y=fleft(xright)$.

Эти функции принимают ровно противоположные значения. Значит: график $y=fleft(xright)$ надо отразить по оси $OX$, «перевернуть».

Как построить график функции $y=fleft(x+lright)$, если известен график функции $y=fleft(xright)$.

Построить график $y=fleft(x+lright)$, где $l > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OX$ на $l$ единиц масштаба влево.
Построить график $y=fleft(x-lright)$, где $l < 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OX$ на $l$ единиц масштаба вправо.

Как построить график функции $y=fleft(xright)+m$, если известен график функции $y=fleft(xright)$.

Построить график $y=fleft(xright)+m$, где $m > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OY$ на $m$ единиц масштаба вверх;
Построить график $y=fleft(xright)-m$, где $m > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OY$ на $m$ единиц масштаба вниз.

Как построить график функции $y=fleft(x+lright)+m$, если известен график функции $y=fleft(xright)$.

График функции $y=fleft(x+lright)+m$ можно получить из графика $y=fleft(xright)$ параллельными сдвигами по осям $OX$ и $OY$.

График Дробной Функции.

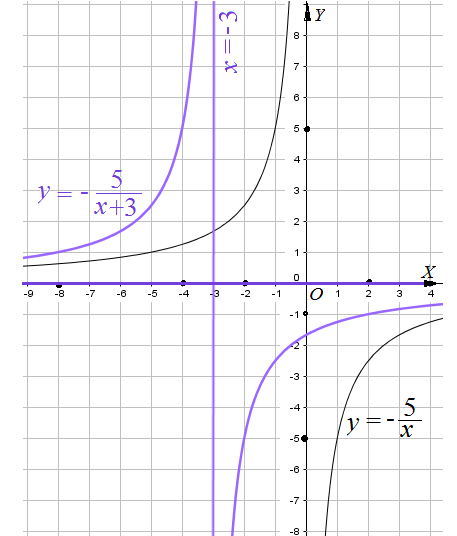
Пример 2: Построить график функции $y=-frac{5}{x+3}$ .

сначала построим график функции $y=-frac{5}{x}$ … от графика $y=frac{1}{x}$ … отразим от $OX$ и растянем по вертикали 5 раз.
сдвинем получившуюся гиперболу вдоль оси $OX$ на $3$ единицы влево, получится требуемый график.
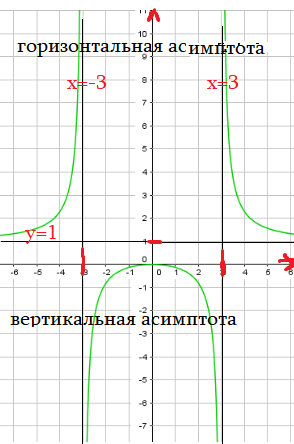
это гипербола с асимптотами $x=-3$; $y=0$. «почему так?» — как мы строим графики?
берем несколько $x$ — точек и находим для каждого свои $y$ — значения в соответствии «с формулой функции».
По точкам проводим график. Очевидно, если, скажем, $x=0,52$ функция $y=-frac{5}{x+3}$ дает какое-то значение,
… то, конечно для $x=3,52$ другая функция, $y=-frac{5}{x}$ дает ровно такое же значение.
значит, точки графиков будут различаться на $3$ единицы по $x$ — координате и совпадать по $y$ — координате.
Ровно так и для всех точек. «Сравни две функции и вообрази их графики: каковы различия и что общего?»

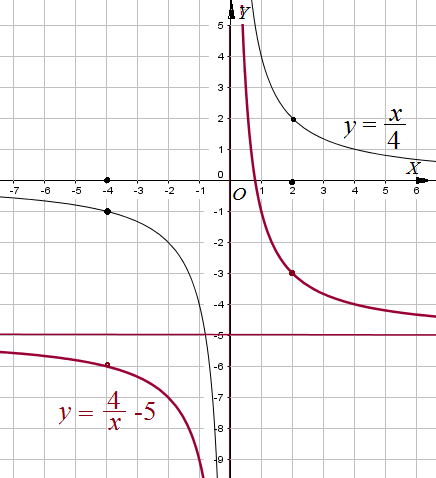
Пример 3: Построить график функции $y=frac{4}{x}-5$ .

Сначала надо построить график функции $y=frac{4}{x}$ . Гиперболу $y=frac{1}{x}$ «растянем» четыре раза.
Сдвинуть получившуюся гиперболу вдоль оси $OY$ на $5$ клеточек вниз. Т.к. каждое значение должно отличаться на 5 единиц.
получится требуемый график. Это гипербола с асимптотами $x=0$; $y=-5$.
Важно знать где пересекается с нулем. Решение, корень $frac{4}{x}-5=0$ дает абсциссу $x=0.8$. Точка графика $left(0,8;0right)$.

Вертикальная асимптота — $x=0$, проходит в полюсе, точке разрыва функции. Точка обнуления знаменателя. Параллельно $OY$.

Горизонтальная асисмптота -$y=-5$, линия, на которую «ложится» график при значениях $х$ около $+-infty$. Параллельно $OX$.

Гипербола — график простой дроби, две асимптоты делят на 4 четверти, ветви гиперболы «зажаты — прижаты» к асимптотическим линиям .

Наклонная асимптота — линия типа $y=2x+3$, к которой «прижимаются» ветви графика «на» или «около» + — бесконечнoсти.

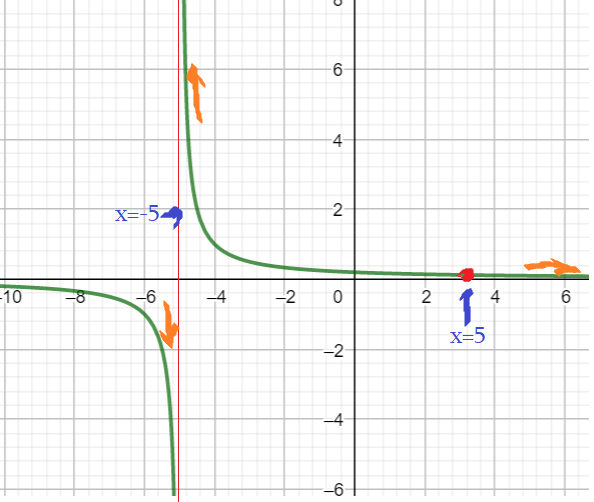
Пример 4: Построить график функции $y=frac{x-5}{x^2-25}$

Если выражение функции упрощается, то следует это сделать. Ибо получится функция проще, легче вычисляемая и рисуемая.
Тождественное преобразование, сокращение $frac{x-5}{x^2-25}=frac{x-5}{(x+5)(x-5)}=frac{1}{x+5}$. Так, что график $y=frac{1}{x+5}$ ?
Не спеши! Мы сократили на $x-5$ , которое незаконно для $x=5$. Нарушается О.Д.З — в исходной функции нет места $x=5$.
Значит: можем строить гиперболу $y=frac{1}{x+5}$ взамен нашей $y=frac{x-5}{x^2-25}$, но «без точки $x=5$».
Точка $x=5$ разрывает «гладкий» график гиперболы. Она называется «выколотая точка с координатами $left(5;0,1right)$».

Важно уметь исследовать функцию — график около точек разрыва. + / — поблизости. Куда тянется?

Исследуем около $x=-5$. Возьмем «близкие» точки $-5,01$ и $-4,99$. Вычислим приближенные значения.
Чуть левее … $fleft(-5,01right)=frac{-5,01-5}{(-5,01)^2-5^2}approx -100$. Чуть правее … $fleft(-4,99right)=frac{-4,99-5}{(-4,99)^2-5^2}approx 100$.
Прямая $x=-5$ — вертикальная асимптота. Ветвь слева прижимается «вниз», к $-infty$ . А справа поднимается вверх к $+infty$.
Около $x=5$. Чуть левее $fleft(4,99right)=frac{4,99-5}{4,99^2-5^2}approx0,101$. $fleft(5,01right)=frac{5,01-5}{5,01^2-5^2}approx0,099$.
Значит, $x=5$ точка разрыва, на графике выколотая точка $left(5;0,1right)$. Т.к. в ней $y=frac{1}{5+5}=0,1$.
«О нулях»: при $x=0$ $y=0,2$ . Но функция нигде не обнуляется, $yne0$. Прямая $y=0$ — горизонтальная асимптота.

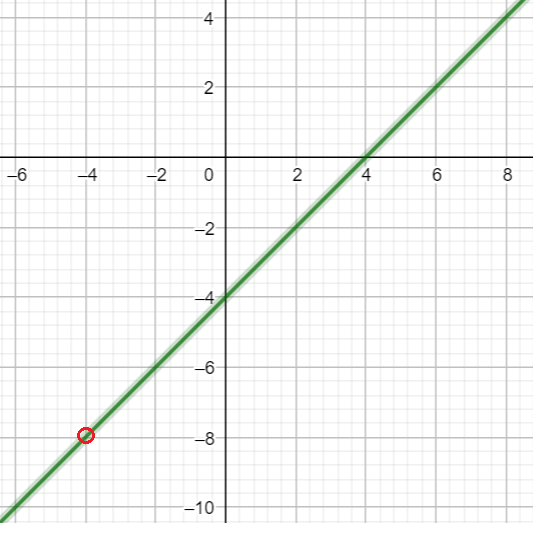
Пример 5: Построить график функции $y=frac{x^2-16}{x+4}$

О.Д.З функции $xne-4$. Оговорив это, со спокойной совестью сократим $y=frac{x^2-16}{x+4}=x-4$.
График нащей функции — прямая линия $y=x-4$ с выколотой точкой $left(-4;-8right)$ при $x=-4$.
«Близко чуть левее»: $x=-4,01$ значение $fleft(-4,01right)=frac{(-4,01)^2-16}{-4,01+4}=-8,01$. Ближе? … Предел $approx-8$.
«О нулях». при $x=0$ $y=-4$ . Обнуление функции $y=0$ при $x=4$ — пересечение с $x$ — осью.

График Дробно — Рациональной Функции.

Определение: дробно-рациональной порядка $left(n;mright)$ называется функция вида $y=frac{acdot x^n+5x^3-x+c}{bcdot x^m-4x^2-7x+d}$

Числитель — многочлен степени $n$ , знаменатель — многочлен степени $m$ . Общий вид: $y=frac{Pleft(xright)}{Qleft(xright)}$

Нули функции — корни числителя $Pleft(xright)=0$ , Асимптоты (полюсы) — корни знаменателя $Qleft(xright)=0$.

Пример 6: Построить график функции $y=frac{x^2}{x^2-9}$.

Функция $fleft(xright)=frac{x^2}{x^2-9}$ — четная: $fleft(xright)=fleft(xright)$ $fleft(8right)=fleft(-8right)$ — Слева и справа от $OY$ симметрично.
Вычисления: $fleft(-4right)=frac{left(-4right)^2}{left(-4right)^2-9}=frac{16}{7}approx2,3$ $fleft(-10right)=frac{100}{91}approx 1,1$ $fleft(-5right)=frac{25}{16}approx 1,6$ $fleft(-3,5right)=frac{12.25}{3,25}approx 3,8$
$fleft(-2right)=fleft(2right)=frac{4}{-5}approx -0,8$ $fleft(-1right)=fleft(1right)approx -0,1$ $fleft(3,5right)approx 3,8$ $fleft(4right)approx 2,3$ $fleft(5right)approx 1,6$ $fleft(10right)approx 1,1$
Наша функция имеет нули в точке $x=0$ , а вертикальные асимтоты — линии $x=-3$ , $x=3$
Асимптота — прямая линия, к которой «прижимается» график функции, «подходя» к ней бесконечно близко.
Чему равно $frac{x^2}{x^2-9}$ при очень больших $x$ ? $xapproxpm1000$ ? Конечно, $yapprox1$ горизонтальная асимптота $y=1$ .
Анализ графика: 1) Обнуляется при $x=0$ . 2) Значение в нуле : $y=frac{x^2}{x^2-9}$ в $x=0$ равно $y=0$.
3) Поведение в разрывах: «чуть левее» полюса $xapprox-3-0,01$ значение $y > 0$ — «большое положительное».
«чуть правее» разрыва $xapprox-3+0,01$ значение функции «большое отрицательное».
Поведение около другого разрыва: когда $x$ «чуть левее» , например $xapprox3-0,01$ , то $y < 0$ ;
когда $x$ «чуть правее» , например $xapprox3+0,01$ , то $y > 0$.
4) Поведение на бесконечности: при $xapproxpminfty$ значение «ложится» около $yapprox1$.
5) Область определения функции — все точки оси $x$ , кроме $x=pm3$
6) Функция положительна $y > 0$ на интервалах $x < -3$ , $x > 3$.
7) Функция отрицательна $y < 0$ на интервалах $-3 < x < 0$ , $0 < x < 3$.

пробaп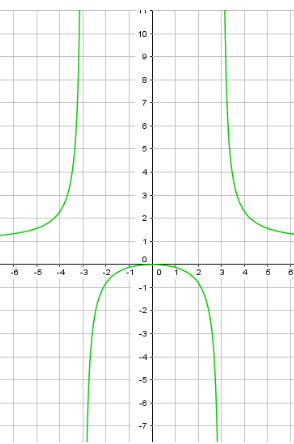

Графический способ решения уравнений

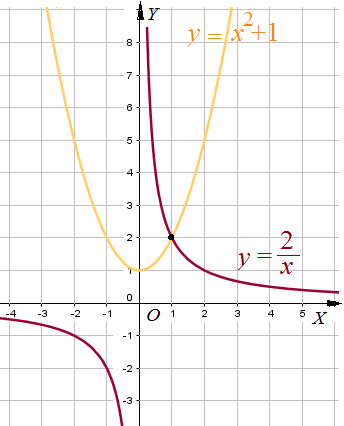
Пример 7: Решить уравнение $frac{2}{x}=x^2+1$ графическим способом.

Рассмотрим две функции : $y=frac{2}{x}$ и $y=x^2+1$ построим гиперболу $y=frac{2}{x}$ и параболу $y=x^2+1$ по
чертежу видно, что графики пересекаются в точке с координатами $left(1;2right)$. если подставить $x=1$ в уравнение,
то равенство выполняется: $frac{2}{1}=1^2+1$ обе функции принимают одно и то же значение $2=2$.
ответ: $x=1$. при таком $x$ графики пересекаются.
«почему?»: при каких $x$ — числах выравниваются обе части уравнения? при тех $x$ — числах, при которых левая
функция и правая функция приобретают одинаковые значения … это то же самое, что графики этих функций
пересекаются в точках с такими $x$ — координатами.

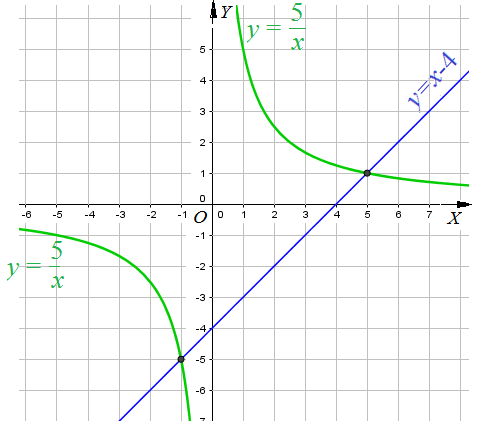
Пример 8: Решить уравнение $frac{5}{x}=x-4$.

рассмотрим две функции: $y=frac{5}{x}$ и $y=x-4$, построим их графики: гиперболу $y=frac{5}{x}$ и прямую $y=x-4$.
по чертежу видно, что гипербола и прямая пересекаются в точках $(-1;-5)$ и $(5;1)$. проверим, подставим
$x=-1$ и $x=5$ в уравнение : $frac{5}{-1}=-1-4$ $Leftrightarrow$ $-5=-5$ и $frac{5}{5}=5-4$ $Leftrightarrow$ $1=1$ . равенство
выполняется, значит данное уравнение имеет два корня — абсциссы точек пересечения графиков.
ответ: $x_1=-1$; $x_2=5$.

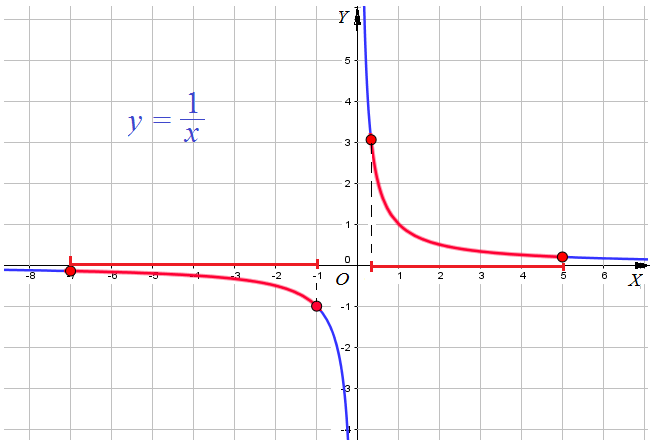
Пример 9: Найти наименьшее и наибольшее значения функции $y=frac{1}{x}$ на отрезках а) $left[frac{1}{3};5right]$ и б) $left[-7;-1right]$.

Построим график функции $y=frac{1}{x}$ .
Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $left[frac{1}{3};5right]$.
Для выделенной части графика находим: наименьшее значение $y=frac{1}{5}$ при $x=5$ , наибольшее $y=3$ при $x=frac{1}{3}$.
Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $left[-7;-1right]$.
Для выделенной части графика находим: наименьшее значение $y=-frac{1}{7}$ при $x=-7$ наибольшее $y=-1$ при $x=-1$.

Пример 10: Доказать, что функция $y=fleft(xright)$ , где $fleft(xright)=frac{4}{x}$

удовлетворяет соотношению $fleft(x-5right)-fleft(x+1right)=1,5cdot fleft(x-5right)cdot fleft(x+1right)$.

Подставим в аргументы функций значения $x-5$ и $x+1$, получим: $fleft(x-5right)=frac{4}{x-5}$ и $fleft(x+1right)=frac{4}{x+1}$ .
распишем левую часть тождества $fleft(x-5right)-fleft(x+1right)=frac{4}{x-5}-frac{4}{x+1}=frac{4left(x+1right)-4left(x-5right)}{left(x-5right)left(x+1right)}=frac{24}{left(x-5right)left(x+1right)}$. аналогично,
с правой стороны получим $1,5cdot fleft(x-5right)cdot fleft(x+1right)=1,5frac{4}{x-5}cdotfrac{4}{x+1}=frac{1,5cdot16}{left(x-5right)left(x+1right)}=frac{24}{left(x-5right)left(x+1right)}$. одинаковые! ч.т.д.

Упражнения

Источник

Обратная пропорциональность — коротко о главном

Определение:

Функция, описывающая обратную пропорциональность, – это функция вида ( displaystyle y=frac{k}{x-a}+b ), где ( kne 0), ( xne 0) и ( xne а)

По-другому эту функцию называют обратной зависимостью.

Область определения и область значений функции:

( Dleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или, что то же самое, ( Dleft( y right)=mathbb{R}backslash left{ 0 right})

( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или ( Eleft( y right)=mathbb{R}backslash left{ 0 right}).

График обратной пропорциональности (зависимости) – гипербола.

Коэффициент ( displaystyle k)

( displaystyle k) – отвечает за «пологость» и направление графика. Чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).

Знак коэффициента ( displaystyle k) влияет на то, в каких четвертях расположен график:

если ( displaystyle k>0), то ветви гиперболы расположены в ( displaystyle I) и ( displaystyle III) четвертях;

если ( displaystyle k<0), то во ( displaystyle II) и ( displaystyle IV).

Коэффициент ( displaystyle a)

Если внимательно посмотреть на знаменатель, видим, что ( displaystyle a) – это такое число, которому не может равняться ( displaystyle x).

То есть ( x=a) – это вертикальная асимптота, то есть вертикаль, к которой стремится график функции

Коэффициент ( b)

Число ( b) отвечает за смещение графика функции вверх на величину ( b), если ( b>0), и смещение вниз, если ( b<0).

Следовательно, ( y=b) – это горизонтальная асимптота.

Алгоритм построения графика функции ( displaystyle y=frac{k}{x-a}+b)

Определяем коэффициенты ( displaystyle k), ( displaystyle a) и ( displaystyle b).
Строим график функции ( displaystyle y=frac{k}{x}) (сначала по 3-4 точкам правую ветвь, потом симметрично рисуем левую ветвь).
График должен быть сдвинут вправо на ( displaystyle a). Но проще двигать не график, а оси, так что ось ( displaystyle Oy) сдвигаем влево на ( displaystyle a).
График должен быть сдвинут вверх на ( displaystyle b). Но проще двигать не график, а оси, так что ось ( displaystyle Ox) сдвигаем вниз на ( displaystyle b).
Старые оси (прямые, которые служили нам осями в пункте 2) оставляем в виде пунктирных линий. Это теперь просто вертикальная и горизонтальная асимптоты.

Что такое функция

Ты помнишь, что функция – это определенного рода зависимость?

Если ты еще не читал тему «Функции», настоятельно рекомендую бросить все и прочитать, ведь нельзя изучать какую-либо конкретную функцию, не понимая, что это такое – функция.

Также очень полезно перед началом этой темы освоить две более простые функции: линейную и квадратичную.

Там ты закрепишь понятие функции и научишься работать с коэффициентами и графиками.

Ну и на всякий случай немного повторим…

Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).

То есть, если у тебя есть функция ( y=fleft( x right)), это значит что каждому допустимому значению переменной ( x) (которую называют «аргументом») соответствует одно значение переменной ( y) (называемой «функцией»).

Что значит «допустимому значению»?

Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции»!

Все дело в понятии «область определения»: для некоторых функций не все аргументы можно подставить в зависимость. Например, для функции ( y=sqrt{x}) отрицательные значения аргумента ( x) – недопустимы.

Функция, описывающая обратную зависимость

Это функция вида ( displaystyle y=frac{k}{x}), где ( kne 0).

По-другому ее называют обратной пропорциональностью: увеличение аргумента вызывает пропорциональное уменьшение функции.

Давай определим область определения. Чему может быть равен ( x)? Или, по-другому, чему он не может быть равен?

Единственное число, на которое нельзя делить – это ( 0), поэтому ( xne 0):

( Dleft( y right)=left( -infty ;0 right)cup left( 0;+infty right))

или, что то же самое,

( Dleft( y right)=mathbb{R}backslash left{ 0 right})

Такая запись означает, что ( x) может быть любым числом, кроме ( 0).

Знак «( mathbb{R})» обозначает множество действительных чисел, то есть всех возможных чисел.
Знаком «( backslash )» обозначается исключение чего-нибудь из этого множества (аналог знака «минус»).
Число ( 0) в фигурных скобках означает просто число ( 0).

Получается, что из всех возможных чисел мы исключаем ( 0)).

Множество значений функции, оказывается, точно такое же: ведь если ( kne 0), то на что бы мы его не делили, ( 0) не получится:

( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или ( Eleft( y right)=mathbb{R}backslash left{ 0 right}).

Также возможны некоторые вариации формулы ( y=frac{k}{x}). Например, ( y=frac{k}{x+a}) – это тоже функция, описывающая обратную зависимость.

Определи самостоятельно область определения и область значений этой функции. Должно получиться:

( Dleft( y right)=left( -infty ;-a right)cup left( -a;+infty right))
( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)).

Давай посмотрим на такую функцию: ( displaystyle y=frac{x-5}{{{x}^{2}}-25}).

Является ли она обратной зависимостью?

На первый взгляд сложно сказать: ведь при увеличении ( x) увеличивается и знаменатель дроби, и числитель, так что непонятно, будет ли функция уменьшаться, и если да, то будет ли она уменьшаться пропорционально?

Чтобы понять это, нам необходимо преобразовать выражение таким образом, чтобы в числителе не было переменной:

( displaystyle y=frac{x-5}{{{x}^{2}}-25}=frac{x-5}{left( x-5 right)left( x+5 right)}=frac{1}{x+5},text{ }xne 5).

Действительно, мы получили обратную зависимость, но с оговоркой: ( xne 5).

Почему так? А потому, что выражение ( left( x-5 right)) было в исходном выражении в знаменателе, поэтому если мы возьмём значение ( x=5) и подставим его в исходную функцию (а ведь именно её нам нужно исследовать), то что мы получим?

Ноль, делённый на ноль. Но ведь на ноль нельзя делить ничего, даже другой ноль. Поэтому ( x) никак не может быть равен ( 5).

Но почему тогда мы также не пишем ( xne -5)? Оно ведь тоже в знаменателе!

А всё потому, что оно как было в знаменателе, так там и осталось, следовательно мы и так видим, что такое значение икса невозможно.

А поэтому — зачем лишний раз писать? Да-да, математики — народ ленивый, без надобности напрягаться не станут:)

Решения

Пример 1

( displaystyle y=1-frac{3}{x+2})

Пример 2

Здесь нужно вспомнить, как квадратный трехчлен раскладывается на множители (это подробно описано в теме «Разложение на множители»).

Напомню, что для этого надо найти корни соответствующего квадратного уравнения: ( displaystyle {{x}^{2}}+4{x}-5=0).

Я найду их устно с помощью теоремы Виета: ( displaystyle {{x}_{1}}=-5), ( displaystyle {{x}_{2}}=1). Как это делается? Ты можешь научиться этому, прочитав тему «Квадратные уравнения».

Итак, получаем: ( displaystyle {{x}^{2}}+4{x}-5=left( x+5 right)left( x-1 right)), следовательно:

( displaystyle y=frac{x+5}{left( x+5 right)left( x-1 right)}=frac{1}{x-1},text{ }xne -5)

Пример 3

Ты уже попробовал решить сам? В чем загвоздка?

Наверняка в том, что в числителе у нас ( displaystyle 2x), а в знаменателе – просто ( displaystyle x).

Это не беда. Нам нужно будет сократить на ( displaystyle left( x+2 right)), поэтому в числителе следует вынести ( displaystyle 2) за скобки (чтобы в скобках ( displaystyle x) получился уже без коэффициента):

( displaystyle y=frac{2{x}-3}{x+1}=frac{2left( x-frac{3}{2} right)}{x+1}=2cdot frac{x-1,5}{x+1}=2cdot frac{x+1-1-1,5}{x+1}=…) дальше сам.

Ответ: ( displaystyle y=2-frac{5}{x+1}).

График обратной пропорциональности

Как всегда, начнем с самого простого случая: ( displaystyle y=frac{1}{x}).

Составим таблицу.

Таблица обратной пропорциональности (зависимости)

( displaystyle mathbf{x})	( displaystyle -3)	( displaystyle -2)	( displaystyle -1)	( displaystyle -0,5)	( displaystyle 0,5)	( displaystyle 1)	( displaystyle 2)	( displaystyle 3)	( displaystyle 4)
( displaystyle mathbf{y})	( displaystyle -frac{1}{3})	( displaystyle -frac{1}{2})	( displaystyle -1)	( displaystyle -2)	( displaystyle 2)	( displaystyle ;1)	( displaystyle frac{1}{2})	( displaystyle frac{1}{3})	( displaystyle frac{1}{4})

Нарисуем точки на координатной плоскости:

Теперь их надо плавно соединить, но как?

Видно, что точки в правой и левой частях образуют будто бы несвязанные друг с другом кривые линии. Так оно и есть.

Это график гиперболы и выглядит он так:

Этот график называется «гипербола» (есть что-то похожее на «параболу» в этом названии, правда?). Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом.

Каждая из них стремится своими концами приблизиться к осям ( displaystyle Ox) и ( displaystyle Oy), но никогда их не достигает. Если посмотреть на эту же гиперболу издалека, получится такая картина:

Оно и понятно: так как ( displaystyle xne 0), график не может пересекать ось ( displaystyle Oy). Но и ( displaystyle yne 0), так что график никогда не коснется и оси ( displaystyle Ox).

Ну что же, теперь посмотрим на что влияют коэффициенты.

На что влияют коэффициенты

Рассмотрим такие функции:

( displaystyle y=frac{1}{x};text{ }y=frac{2}{x};text{ }y=frac{4}{x};text{ }y=-frac{1}{x};text{ }y=-frac{3}{x}):

Ух ты, какая красота!

Все графики построены разными цветами, чтобы легче было их друг от друга отличать.

Итак, на что обратим внимание в первую очередь?

Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси ( displaystyle Ox).

Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат.

А что, если функция выглядит сложнее, например, ( displaystyle y=frac{1}{x-1}+2)?

В этом случае гипербола будет точно такой же, как обычная ( displaystyle y=frac{1}{x}), только она немного сместится. Давай думать, куда?

Чему теперь не может быть равен ( x)? Правильно, ( xne 1). Значит, график никогда не достигнет прямой ( x=1).

А чему не может быть равен ( y)? Теперь ( yne 2). Значит, теперь график будет стремиться к прямой ( y=2), но никогда ее не пересечет.

Итак, теперь прямые ( x=1) и ( y=2) выполняют ту же роль, которую выполняют координатные оси для функции ( displaystyle y=frac{1}{x}).

Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их):

Более подробно о том, как строятся такие графики, мы выучим чуть позже.

А теперь попробуй решить несколько примеров для закрепления.

Обратная пропорциональность в жизни

Где же нам встречается такая функция на практике? Примеров множество. Самый распространенный – это движение: чем больше скорость, с которой мы движемся, тем меньшее время нам потребуется, чтобы преодолеть одно и то же расстояние.

И правда, вспомним формулу скорости: ( displaystyle v=frac{S}{t}), где ( v) – скорость, ( t) – время в пути, ( S) – расстояние (путь).

Отсюда можно выразить время: ( displaystyle t=frac{S}{v})

Пример:

Человек едет на работу со средней скоростью ( 40) км/ч, и доезжает за ( 1) час. Сколько минут он потратит на эту же дорогу, если будет ехать со скоростью ( 60) км/ч?

Решение:

Вообще, такие задачи ты уже решал в 5 и 6 классе. Ты составлял пропорцию:

( displaystyle 60) км/ч – ( 60) мин.

( displaystyle 60) км/ч – ( x) мин.

Далее ты определял, что это обратная пропорциональность, так как чем больше скорость, тем меньше время. Значит, чтобы решить эту пропорцию, нужно поделить числа «крест-накрест»:

( displaystyle frac{40}{x}=frac{60}{60}text{ }Rightarrow text{ }x=40)(мин).

То есть понятие обратной пропорциональности тебе уже точно знакомо. Вот и вспомнили. А теперь то же самое, только по-взрослому: через функцию.

Функция (то есть зависимость) времени в минутах от скорости:

( displaystyle tleft( v right)=frac{S}{v}).

Известно, что ( tleft( 40 right)=60), тогда:

( frac{S}{40}=60text{ }Rightarrow text{ }S=40cdot 60=2400).

Нужно найти ( tleft( 60 right)):

( displaystyle tleft( 60 right)=frac{2400}{60}=40) (мин).

Теперь придумай сам несколько примеров из жизни, в которых присутствует обратная пропорциональность.

Придумал? Молодец, если да. Удачи!

Принципы построения графика обратной пропорциональности (гиперболы)

Теперь давай научимся строить простейшую гиперболу – ( displaystyle y=frac{k}{x}).

Достаточно помнить, как она выглядит, и тогда нам хватит всего трех-четырех точек.

Например, построим гиперболу ( displaystyle y=frac{3}{x}).

Составим таблицу из ( 4) точек, которые принадлежат одной ветке (например, правой):

( x)	( frac{1}{2})	( displaystyle 1)	( displaystyle 3)	( displaystyle 6)
( y)	( displaystyle 6)	( displaystyle 3)	( displaystyle 1)	( frac{1}{2})

Отмечаем точки на рисунке:

Проводим через них плавную линию, которая краями приближается к осям:

Это одна ветвь гиперболы

Проверить правильность построения этой кривой можно так: она должна быть симметрична относительно биссектрисы угла между осями координат:

Отлично, осталось вспомнить, что собой представляет вторая ветвь?

Это точно такая же кривая, расположенная симметрично относительно начала координат. То есть как будто оси теперь направлены не снизу вверх и слева направо, а наоборот: сверху вниз и справа налево, и мы рисуем ту же самую ветвь гиперболы.

Вот:

Еще один полезный факт.

Посмотри на красные точки на графике. Видно, что их абсцисса совпадает с ординатой. Так вот, эти абсцисса с ординатой равны ( sqrt{k}) для правой ветви гиперболы, и ( -sqrt{k}) для левой.

Для функций, у которых ( k) – точный квадрат (например, ( 1), ( 4) или ( displaystyle frac{1}{4})), эту точку, относительно которой ветвь гиперболы симметрична, будет очень легко поставить.

В этом случае достаточно даже трех точек, чтобы построить график.

Например, построим график функции ( displaystyle y=frac{4}{x})

Как и в прошлый раз, начнем с правой ветви.

Точка симметрии: ( displaystyle x=y=2). Выберем еще одну точку, например, ( displaystyle x=1), ( displaystyle y=4). У третьей точки координаты будут наоборот: ( displaystyle x=4), ( displaystyle y=1).

Рисуем:

И теперь симметрично отображаем эту ветвь в третью координатную четверть:

Теперь выясним, что будет, если ( displaystyle k<0)?

Очень просто: если есть график функции с таким же по величине, но положительным ( displaystyle k), то нужно просто отразить его относительно оси ( displaystyle Ox)

То есть правая ветвь теперь будет ниже оси ( displaystyle Ox) (в ( displaystyle IV) четверти), а левая – выше (в ( displaystyle III) четверти).

Принцип построения же останется прежним:

Ну что же, осталось объединить все то, что мы уже выяснили в один алгоритм:

Источник

Закрашенная и незакрашенная точка

Эта ассоциация поможет легко запомнить, выколотая точка или закрашенная на числовой прямой.

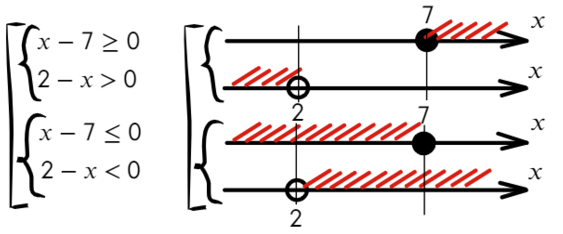
Сравните неравенства, при которых точка заштрихована: x≥a или x≤b и неравенства, в которых точка выколотая: x>a, x или Светлана Иванова, 27 Сен 2012

Сегодня мы узнаем, как использовать метод интервалов для решения нестрогих неравенств. Во многих учебниках нестрогие неравенства определяются следующим образом:

— это неравенство вида которое равносильно совокупности строгого неравенства и уравнения:

В переводе на русский язык это значит, что нестрогое неравенство это объединение классического уравнения и строгого неравенства Другими словами, теперь нас интересуют не только положительные и отрицательные области на прямой, но и точки, где функция равна нулю.

Отрезки и интервалы: в чем разница?

Прежде чем решать нестрогие неравенства, давайте вспомним, чем интервал отличается от отрезка:

— это часть прямой, ограниченная двумя точками. Но эти точки не принадлежат интервалу. Интервал обозначается круглыми скобками: и т.д.;
— это тоже часть прямой, ограниченная двумя точками. Однако эти точки тоже являются частью отрезка. Отрезки обозначаются квадратными скобками: и т.д.

Чтобы не путать интервалы с отрезками, для них разработаны специальные обозначения: интервал всегда обозначается выколотыми точками, а отрезок — закрашенными. Например:

На этом рисунке отмечен отрезок и интервал Обратите внимание: концы отрезка отмечены закрашенными точками, а сам отрезок обозначается квадратными скобками. С интервалом все иначе: его концы выколоты, а скобки — круглые.

Метод интервалов для нестрогих неравенств

К чему была вся эта лирика про отрезки и интервалы? Очень просто: для решения нестрогих неравенств все интервалы заменяются отрезками — и получится ответ. По существу, мы просто добавляем к ответу, полученному методом интервалов, границы этих самых интервалов. Сравните два неравенства:

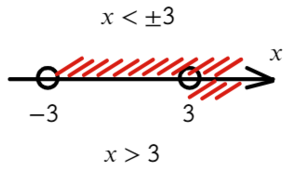
Задача. Решите строгое неравенство:

Решаем методом интервалов. Приравниваем левую часть неравенства к нулю:

( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;

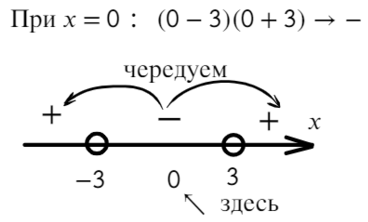
Отмечаем полученные корни на координатной оси:

Справа стоит знак плюс. В этом легко в этом убедиться, подставив миллиард в функцию:

f ( x ) = ( x − 5)( x + 3)

Осталось выписать ответ. Поскольку нас интересуют положительные интервалы, имеем:

Задача. Решите нестрогое неравенство:

Начало такое же, как и для строгих неравенств: работает метод интервалов. Приравниваем левую часть неравенства к нулю:

( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;

Отмечаем полученные корни на координатной оси:

В предыдущей задаче мы уже выяснили, что справа стоит знак плюс. Напомню, в этом легко убедиться, подставив миллиард в функцию:

f ( x ) = ( x − 5)( x + 3)

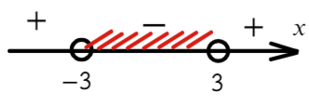
Осталось записать ответ. Поскольку неравенство нестрогое, а нас интересуют положительные значения, имеем:

Итак, основное отличие строгих и нестрогих неравенств:

В строгих неравенствах нас не интересуют концы отрезка, поэтому они отмечаются выколотыми точками. Такие точки никогда не входят в ответ, о чем говорят круглые скобки на первом ответе: x ∈ (−∞; −3) ∪ (5; +∞);
И наоборот, в нестрогих неравенствах концы отрезка входят в ответ. На графике они отмечаются закрашенными точками, а в ответе указываются квадратными скобками: x ∈ (−∞; −3] ∪ [5; +∞).

Вот и вся разница! Просто запомните: в строгих неравенствах точки выколоты, а в нестрогих — закрашены.

Почему бесконечности всегда стоят в круглых скобках

У внимательного читателя наверняка возник вопрос: почему бесконечности отмечаются круглыми скобками даже в нестрогих неравенствах? Например, почему в последней задаче мы пишем

Что ж, это не опечатка. Бесконечность действительно обозначается круглой скобкой, даже если неравенство — нестрогое. Чтобы понять, почему так происходит, достаточно вспомнить определение бесконечности.

— это гипотетическое число, которое больше любого другого числа, участвующего в решении.

Трудность заключается в том, что нельзя работать с бесконечностью напрямую. Мы можем лишь приблизиться к ней, подставляя такие зверские числа, как 1 000 000 и даже 1 000 000 000. Но добраться до самой бесконечности все равно нельзя.

Именно поэтому бесконечность обозначают круглыми скобками. Ведь хотя бесконечность и ограничивает всю числовую прямую, сама она не принадлежит этой прямой.

Ситуация такая же, как с границами интервалов. Рассмотрим все числа из интервала:

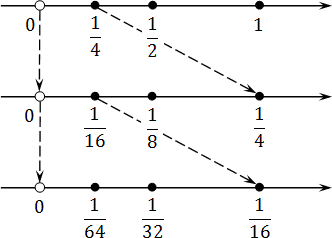
Эта запись означает, что число не принадлежит интервалу, однако любое число, которое больше нуля и меньше единицы — принадлежит. В частности, этому интервалу принадлежат следующие числа:

Попробуем отметить эти числа на координатной прямой. Поскольку каждое следующее число вдвое меньше предыдущего, нам придется несколько раз менять масштаб. Получим вроде этого:

Что дает нам этот график? Оказывается, при достаточно крупном масштабе можно отметить любое число, сколь угодно близкое к нулю. При этом сам ноль никуда не денется — он остается недостижимой границей. Именно это и подразумевается, когда речь заходит о концах интервала.

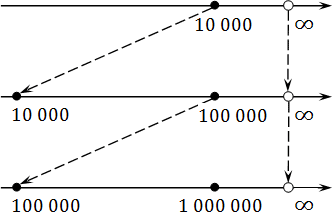
То же самое происходит и с бесконечностью. Разница лишь в том, что масштаб надо не увеличивать, а уменьшать:

Мы можем сколь угодно долго идти к бесконечности, но так и не достигнем ее. Вот почему бесконечности обозначают круглыми скобками, подобно границам интервала.

Примеры решения неравенств

В заключение кратко разберем два нестрогих неравенства. И если в первой задаче еще есть пояснения, то вторая задача будет оформлена именно так, как и надо оформлять настоящее решение.

Как обычно, приравниваем все к нулю:

( x + 8)( x − 3) = 0;
x + 8 = 0 ⇒ x = −8;
x − 3 = 0 ⇒ x = 3.

Теперь рассматриваем функцию, которая находится в левой части неравенства:

f ( x ) = ( x + 8)( x − 3)

Подставим в эту функцию бесконечность — получим выражение вида:

Чертим координатную ось, отмечаем корни и расставляем знаки:

Поскольку мы решаем неравенство или, что то же самое, осталось записать ответ:

x (12 − 2 x )(3 x + 9) ≥ 0

x (12 − 2 x )(3 x + 9) = 0;
x = 0;
12 − 2 x = 0 ⇒ 2 x = 12 ⇒ x = 6;
3 x + 9 = 0 ⇒ 3 x = −9 ⇒ x = −3.

x ≥ 6 ⇒ f ( x ) = x (12 − 2 x )(3 x + 9) → (+) · (−) · (+) = (−) x ∈ (−∞ −3] ∪ [0; 6].

Решение неравенств

Метод интервалов

Перенос знаков

Выбор точек

Система и совокупность

Точка знакопостоянства

Что нельзя делать в неравенстве, даже под пытками:

1) Домножать на знаменатель.

2) Умножать/делить на отрицательное число, не меняя знак.

3) Убирать бездумно логарифм или основание.

Начнем с простого:

Линейные уравнения решаются обычным переносом. Икс в одной части оставим, а числа перенесем в другую:

А само значение −4 нам подходит?

Нет, поэтому ставим круглые скобочки ()

Разберемся со скобками:

Когда мы включаем точку (корень числителя), или стоят знаки нестрогие ( ≥, ≤ ), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,

Если же возьмем пример, где придется делить или умножать на отрицательное число, то знак поменяется:

Ответ: x ∈ ( 0; +oo).

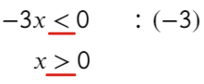
Следующий пример уже с дробью:

Приравняем числитель к нулю и скажем, что знаменатель не равен нулю:

к.ч. (корни числителя)

к.з. (корни знаменателя)

Расставляем корни числителя и знаменателя на одной прямой (сколько решаем неравенств, столько же чертим прямых). Попробуем подставить х = 0, чтобы определить знаки:

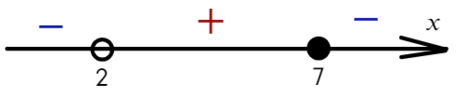
Там, где «0» (перед двойкой), ставим знак «−», а дальше знаки чередуем:

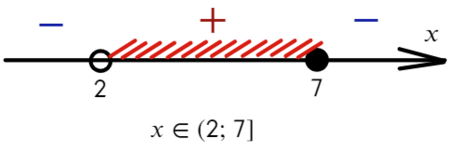
Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+» и закрашенная точка:

Когда мы включаем точку (корень числителя), или стоят знаки (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,

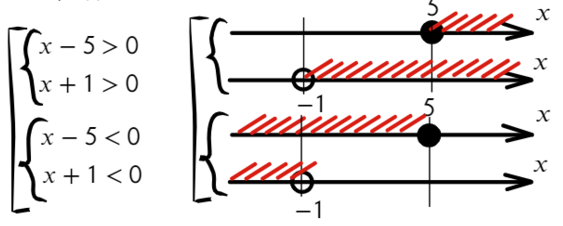
Данный пример можно решить по-другому. Подумаем, когда дробь больше нуля? Конечно, когда числитель и знаменатель — положительные значения или когда оба отрицательные. Поэтому данное неравенство можно разбить на две системы в совокупности:

Отметим на прямой решение каждого неравенства.

Решением совокупности «[» является тот участок, который включен хотя бы в одно неравенство.

Мой любимый пример:

Покажу мастер-класс, как делать не надо. Дома не повторять!

А теперь через метод интервалов разберемся, как сделать правильно:

Там, где ноль, ставим знак «−», рисуем прямую и отмечаем корни каждой скобки. А дальше чередуем:

В данном неравенстве знак меньше, поэтому записываем в ответ промежуток, где знак «−».

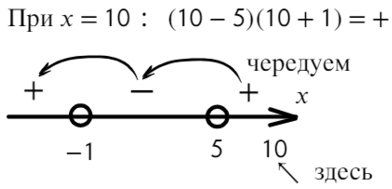
Перейдем к квадратному уравнению:

Разложим на множители и подставим x = 10, чтобы определить знак:

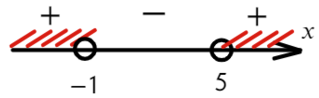
Нам требуются положительные значения:

Второй способ разложить на множители:

Ответ: x ∈ (−oo; −1) ∪ (5; +oo).

А теперь простой, но крайне показательный пример:

Убирать квадрат ни в коем случае нельзя. Простенький контрпример:

Надеюсь, убедил. Вместо знака больше поставим знак равно и попробуем решить методом интервалов:

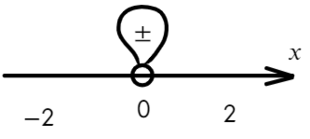
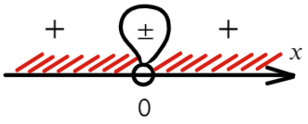
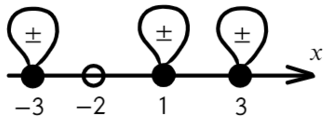
Если корень повторяется четное количество раз, то в этой точке знак меняться не будет. Отмечать будем такую точку восклицательным знаком (а внутри него ±, чуть ниже объясню, зачем это).

В данном неравенстве знак больше, тогда отметим те промежутки, где стоит знак «+».

Только точка «0» не подходит, 0 > 0 — неверно!

Ответ: x ∈ R <0>или x ∈ ( − oo; 0) ∪ (0; +oo).

Переходим на новый уровень:

Все говорят, что домножать на знаменатель нельзя, а я говорю, что буду! (joke)

По методу координат найдем корни числителя и знаменателя:

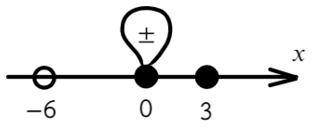
Отметим все корни на одной прямой (сколько неравенств, столько же и прямых). Ноль — корень четной кратности, над ним рисуем восклицательный знак! Если это корень числителя, то точка будет закрашена, если знаменателя — выколота (на ноль делить нельзя).

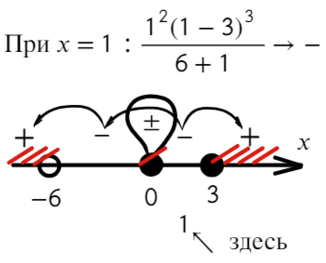
Требуется найти промежутки, где выражение больше или равно нулю. Нам подойдут все «промежутки», где знак плюс. Для этого подставим значение x = 1 и с промежутка [0; 3] начнем расставлять знаки. Там же находится единица.

Вот для чего ставят в восклицательном знаке ±: чтобы не потерять отдельные точки, в данном случае 0.

Ответ: (−oo; − 6) ∪ <0>∪ [ 3; +oo).

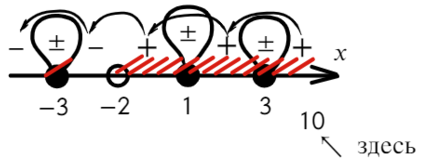
По той же схеме корни числителя и знаменателя:

Определим знак при x = 10 и расставим знаки с промежутка, где присутствует 10:

Все точки от − 2 закрашены, значит эти промежутки можно объединить в один.

Точка x = 3 встречается 3 раза (2 раза в числителе и 1 раз в знаменателе), знак через нее меняться будет! А также эта точка будет выколота, проверь это, подставив в уравнение x = 3. На ноль же делить нельзя?

Узнать ещё

Эта ассоциация поможет легко запомнить, выколотая точка или закрашенная на числовой прямой.

Сравните неравенства, при которых точка заштрихована: x≥a или x≤b и неравенства, в которых точка выколотая: x>a, x<b. В первом случае в самом знаке неравенства есть прямая подсказка, что точку надо заштриховать, уже и штриховать начали, первый штрих сделали: ≥ или ≤. Поэтому и на чертеже на числовой прямой в таких неравенствах — заштрихованная точка:

А в знаках > или < штриха дополнительного нет, значит, и закрашивать точку не надо. Получилась выколотая точка.

С3 ГИА – построение графиков функций.

Задача о касательных к параболе

Графиком предложенной функции является парабола, ветви которой направлены вверх и вершина, которую подняли вверх на 4 единицы, лежит на оси ординат. Ее координаты (0;4). Второй график – это прямая, проходящая через начало координат, причем ее наклон может меняться (его определяет коэффициент ). Такая прямая только в одном случае имеет с параболой одну общую точку – если является касательной. Причем, поскольку данная парабола симметрична относительно оси ординат, то к ней можно провести две касательных – с точками касания в первом и третьем квадрантах: Чтобы определить, в какой точке прямая коснется параболы, нужно приравнять обе функции:

Поскольку точка касания – единственная общая точка данных графиков, то дискриминант данного уравнения равен нулю: Откуда k^2=16 и и решить это уравнение: Тогда касание произойдет в точке x=2 и симметричной ей точке x=-2 .

Задача 2. Построить график функции график функции y=a имеет с графиком три или более общие точки.

График, который подвергнется преобразованиям

Строить этот график будем поэтапно: сначала построим график , затем – график функции

“Опрокидываем” преобразованный график

Осталось выяснить, в каком же случае прямая y=a – а это прямая, параллельная оси абсцисс – будет иметь три (или же более) общие точки с графиком построенной нами функции. Прямая показана на рисунке зеленым цветом. Видно, что ниже указанного положения прямая будет иметь только две общие точки с графиком. Если y=-1 , то прямая имеет три точки с графиком – пересекает две его ветви и касается вершины. Выше прямая будет иметь четыре точки пересечения с графиком, однако при y=0 точек пересечения уже снова две. Значит, ответ надо записать так: a in [-1;0)

Задача 3. Построить график функции график функции y=a имеет с ним три и более общие точки.

Также построим график в два этапа: саму параболу (координаты ее вершины (-1;-9)), затем отразим всю часть, лежащую ниже оси х, вверх: Тогда три и более (а именно – четыре) общих точки графики будут иметь при a in (0;9]

Задача 4. Построить график функции и определить, при каких значениях график функции y=a имеет с ним 2 общие точки.

Из условия ясно, что такой график состоит из двух кусочков. Один из них – прямая, второй – парабола. Первый существует в точке 1 и левее ее, второй – правее этой точки. Нарисуем эти графики:

Координаты вершины параболы:

Красным показаны прямые y=1 и y=5 – именно они, и только они, имеют две общие точки с построенным графиком. Ответ: a=1 , a=5 .

Задача 5. Построить график функции график функции y=kx не имеет с графиком общих точек.

Давайте сначала попробуем упростить данное выражение, кроме того, нужно, безусловно, определить область допустимых значений данной функции. ОДЗ: . Теперь попробуем упростить данное выражение:

Определение коэффициента наклона касательной

Полученная функция – квадратичная, ее графиком является парабола. Данная парабола симметрична относительно оси y, ее вершина имеет координаты (0; 25). Необходимо заметить, что точка с координатами (1; 26) – выколотая точка (по ОДЗ). Тогда прямая, проходящая через начало координат – а именно таким будет график функции y=kx , не будет иметь с параболой общих точек в трех случаях: если коэффициент меньше, чем у касательной, расположенной справа, или он больше, чем у касательной, расположенной слева, или искомая прямая проходит прямо через выколотую точку. Наверное, проще найти каков этот коэффициент именно в третьем случае: так как прямая проходит через начало координат, достаточно подставить координаты нашей выколотой точки в уравнение прямой и найти : 26=k*1 , откуда k=26 . Проверим, не будет ли такая прямая иметь общих точек с параболой. Приравняем . По сумме коэффициентов это уравнение имеет корень 1, но и второй корень – 25, поэтому такая прямая будет иметь еще одну точку пересечения с параболой. В ответ эту прямую мы не включим. Теперь определим коэффициент наклона касательных, для этого приравняем оба уравнения: , и найдем дискриминант, который должен быть равен нулю при наличии единственной общей точки у двух этих графиков функций: Откуда k^2=100 и и решить это уравнение: Тогда касание произойдет в точке x=5 и симметричной ей точке x=-5 . Ответ: , .

Задача 6. Построить график функции он не имеет общих точек с графиком функции y=a .

Гипербола с выколотой точкой

Определим ОДЗ функции: , . (Для того, чтобы определить ОДЗ, приравняли знаменатель к нулю и решили данное уравнение). Теперь упростим выражение: – выколотая точка. В точке x=0 гипербола не существует, оси координат – ее асимптоты (одна из них войдет в ответ). Тогда, если прямая y=a пройдет через выколотую точку, графики не будут иметь общих точек. Найдем : для этого определим ординату выколотой точки: : Ответ: a=1/3 и a=0 .

Задача 7. Построить график функции график функции y=kx имеет с графиком 1 общую точку.

Подбор коэффициента наклона прямой

Определим ОДЗ функции: , . (Для того, чтобы определить ОДЗ, приравняли знаменатель к нулю и решили данное уравнение). Теперь упростим выражение: – выколота. В точке x=0 гипербола не существует, оси координат – ее асимптоты. Тогда, если прямая y=kx пройдет через выколотую точку, графики будут иметь одну общую точку. Найдем : для этого подставим в уравнение прямой абсциссу и ординату выколотой точки: 1=k/1 , k=1 : Ответ: k=1

Задача 8. Построить график функции график функции y=a имеет с ним 2 общие точки.

Построение функции с модулем

Эта функция – функция типа , то график y=-1 коснется обеих вершинок нашей “дублированной” параболы, то есть a=-1 – один из ответов. Также, если y=a пересечет обе ветви параболы, то есть все нас устраивают. Ответ: a=-1 ,.

Задача 9. Построить график функции график функции y=c не имеет с ним общих точек.

Кубическая парабола с выколотой точкой

Определим ОДЗ исходной функции: . Теперь можно упростить выражение: пройдет именно через эту точку, она не будет иметь общих точек с полученным нами графиком. Ответ: с=4.

Задача 10. Построить график функции график функции y=kx имеет с ним одну общую точку.

У нас получились три интервала, на каждом из которых можно теперь раскрыть модули: 1. 2. 3. Тогда наша функция – кусочно-линейная: .

Она выглядит так:

Зеленым цветом показано одно из возможных положений прямой y=kx . При таком расположении прямой , и может расти бесконечно. Заметим, что крайнее положение прямой – при k=1. При таком коэффициенте наклона она параллельна правой и левой частям графика, и имеет с ним одну точку пересечения – точку (0;0). Точно так же коэффициент наклона может быть и отрицательным. При этом коэффициент k=-1 – не войдет в ответ, так как в этом случае функция y=kx будет иметь общий отрезок с кусочно-линейной функцией, что не соответствует требованиям задачи. Таким образом,

Ответ: вершины парабол и расположены по одну сторону от оси х?

Обратим внимание на то, что у двух данных парабол ветви направлены в разные стороны: у первой старший коэффициент отрицателен, а у второй – положителен. Поэтому вершины будут лежать по одну сторону от оси, если одна из них будет иметь точки пересечения с осью х, а другая – нет. Иными словами, дискриминант одного квадратного уравнения должен быть положителен, а другого – отрицателен. Это приводит нас к двум системам неравенств:

Дискриминант и наличие пересечений параболы с осью х

Или же наоборот: . Эти два случая изображены на рисунке:

Определим дискриминанты обоих квадратных уравнений:

Тогда имеем систему неравенств:

– решений нет, так как квадрат числа – неотрицателен, и сумма квадрата числа с положительным числом не может быть меньше ноля.

– в этой системе второе неравенство всегда соблюдается, решение первого – , ,

Мы рассмотрели один способ решения – с использованием дискриминанта. Есть еще один способ решения такого задания – с помощью координат вершины параболы. Решим последнюю задачу вторым способом.

Нам потребуется определить координаты вершин обеих парабол:

– вторая система решений не имеет, а именно, нет решений у второго неравенства, поэтому решим первую. Второе неравенство первой системы справедливо всегда, осталось решить неравенство:

Решение этого неравенства и есть ответ задачи:

Источник

График дробно-рациональной функции. Гипербола.

Упражнения

Обратная пропорциональность — коротко о главном

Что такое функция

Функция, описывающая обратную зависимость

График обратной пропорциональности

На что влияют коэффициенты

Обратная пропорциональность в жизни

Принципы построения графика обратной пропорциональности (гиперболы)

Закрашенная и незакрашенная точка

Отрезки и интервалы: в чем разница?

Почему бесконечности всегда стоят в круглых скобках

Примеры решения неравенств

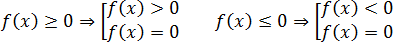
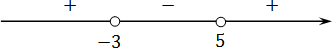
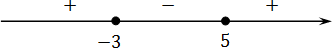
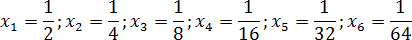
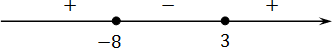
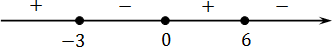
<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://ik-study.ru/uploads/s/v/d/w/vdwu9qwztel6/img/hgsT8tKi.jpg" />Решение неравенств

Метод интервалов

Перенос знаков

Выбор точек

Система и совокупность

Точка знакопостоянства

Узнать ещё

С3 ГИА – построение графиков функций.

Не пропустите также:

Решение неравенств