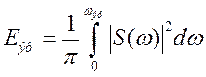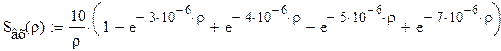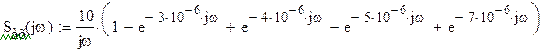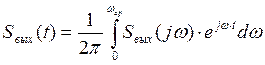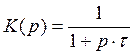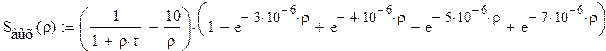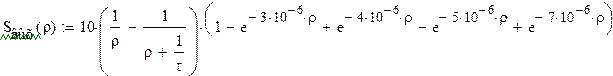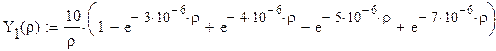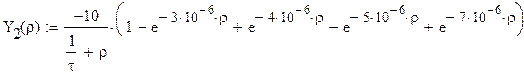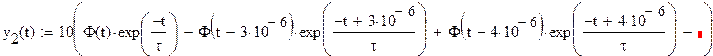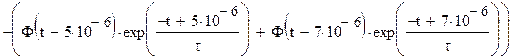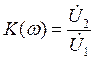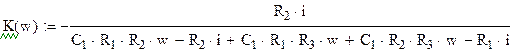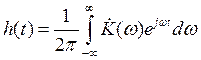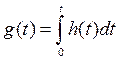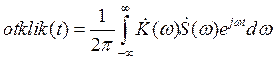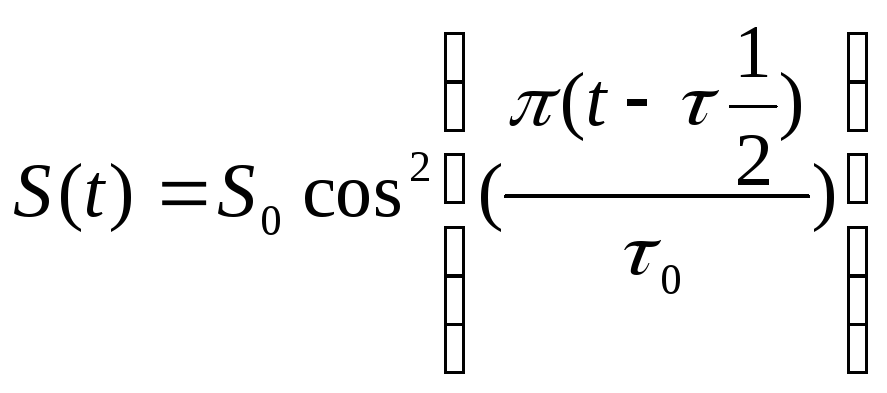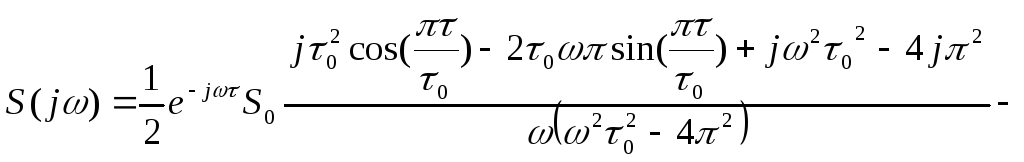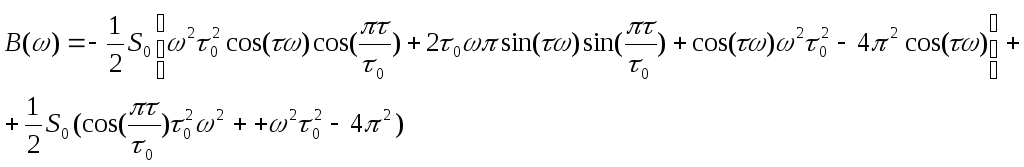Как найти выходной сигнал цепи

5.4.1. Классический метод

5.4.2. Временной метод

5.4.3. Спектральный метод

5.4.4. Операторный метод

Основной задачей анализа является определение реакции (выходного) сигнала цепи при действии на её входе сигнала известной формы. При этом, входной сигнал может быть описан как во временной, так и в частотной области. В связи с этим различают следующие методы анализа: классический, временной (или метод интеграла наложения), спектральный и операторный. Выбор того или иного метода зависит от структуры цепи, вида воздействующего на неё сигнала, формы представления (временная или частотная) входного сигнала.

5.4.1. Классический метод

Классический метод основывается на решении дифференциального уравнения вида (5.16), описывающего линейную цепь. Решение этого уравнения представляет собой сумму двух слагаемых

, (5.19)

где первое слагаемое представляет собой общее решение однородного дифференциального уравнения

, (5.20)

а второе слагаемое – частотное решение (5.16) при , где – правая часть уравнения (5.16). Физически – свободная составляющая полного отклика (выходного сигнала), представляет собой реакцию цепи на отключение(или включение) входного сигнала и характеризует переходные процессы в цепи. Второе слагаемое – вынужденная составляющая, является реакцией цепи после окончания переходных процессов и характеризует установившейся(стационарный) режим преобразования цепью входного сигнала. Обычно, классический метод используется для изучения переходных процессов, что приводит к необходимости решения уравнения (5.20). Общее решение однородного уравнения (5.20) имеет вид

, (5.21)

где , ,…, – постоянные коэффициенты, определяемые начальными условиями,

, ,…, – корни характеристического уравнения:

. (5.22)

Это уравнение имеет ровно n корней, при этом корни могут быть либо вещественными, либо комплексными, что определяет характер переходных процессов. Что же касается , то если входной сигнал является постоянным или периодическим, то после окончания переходных процессов выходной сигнал принимает форму входного сигнала. Так, если представляет собой гармонический сигнал, то также будет гармоническим, отличаясь от входного сигнала амплитудой и начальной фазой.

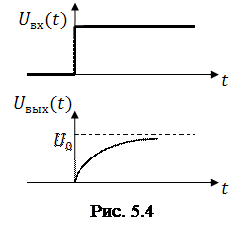
В качестве примера рассмотрим, что собой представляет отклик RC-цепи (рис. 5.3,8) на входной сигнал вида .

Дифференциальное уравнение цепи (5.15) перепишем в виде

,

где – постоянная времени.

Поскольку дифференциальное уравнение имеет порядок n=1, решение однородного уравнения

согласно (5.21), запишется в виде

,

где – корень характеристического уравнения

,

откуда следует . Тогда

.

До поступления входного сигнала ёмкость С разряжена. В момент поступления входного сигнала (скачка) ёмкость не может мгновенно зарядиться до , это произойдёт по мере перехода к установившемуся режиму. Очевидно в установившемся режиме

.

Таким образом, суммарный выходной сигнал

.

Коэффициент найдём из начальных условий. Начальными условиями при исследовании линейных цепей называют значения токов в индуктивностях и напряжений на емкостях в момент времени . Так как в этот момент времени , то можно записать

,

Откуда следует . Тогда окончательно суммарный выходной сигнал

.

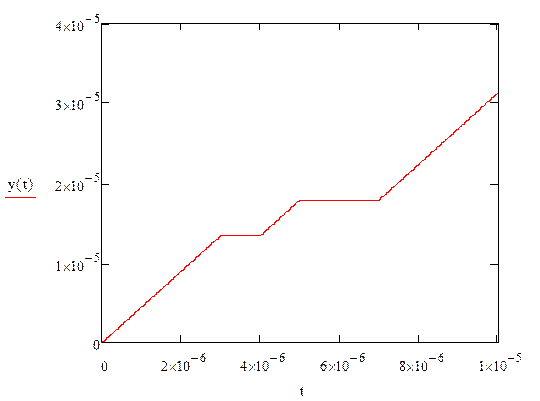
На рис. 5.4. изображены эпюры напряжений на входе и выходе исследуемой RC-цепи.

5.4.2. Временной метод

Временной метод (метод интеграла положения, метод интеграла Дюамеля) основывается на представлении входного сигнала цепи в виде суммы элементарных сигналов вида единичного скачка или очень короткого импульса ( – функции). Тогда, зная отклик линейной цепи на каждый элементарный сигнал и суммируя их можно получить в соответствии с принципом суперпозиции (наложения) полный отклик цепи на входной сигнал сложной формы.

Выберем в качестве элементарного сигнала – функцию. Тогда входной сигнал в соответствии с (1.19) можно записать следующим образом

.

Очевидно, выходной сигнал

.

Так как оператор не зависит от времени, его можно внести под знак интеграла. Тогда, с учётом (5.5)

. (5.23)

Если момент появления входного сигнала , то с учётом того, что выходной сигнал не может появиться ранее входного, выражение (5.23) принимает вид

. (5.24)

Таким образом, сигнал на выходе линейной цепи представляет собой свёртку входного сигнала с импульсной характеристикой цепи. Линейная цепь с постоянными параметрами при преобразовании проводит операцию взвешенного суммирования всех мгновенных значений входного сигнала, начиная с момента и заканчивая текущим моментом времени . Роль весовой функции выполняет импульсная характеристика цепи.

Выражение (5.24) носит название интеграла Дюамеля. Это выражение было получено в предположении, что входной сигнал представлен в виде суммы элементарных сигналов вида – функций. Если входной сигнал представить в виде (1.15) комбинаций сигналов вида единичного скачка, то можно получить другие формы интеграла Дюамеля, в частности

. (5.25)

Здесь – переходная характеристика цепи.

Итак, для использования метода интеграла наложения необходимо знать импульсную характеристику или переходную характеристику . Эти характеристики можно определить несколькими способами. Прямой (непосредственный способ состоит в решении дифференциального уравнения (5.20) в предположении, что входной сигнал является очень коротким импульсом(для определения импульсной характеристики) или сигналом вида единичного скачка( для определения переходной характеристики).

В выше приведённом примере было решено дифференциальное уравнение и найден отклик RC-цепи на воздействие сигнала

.

Очевидно, форма отклика не изменится, если входной сигнал будет единичным скачком, при этом масштаб отклика изменится в раз. Тогда выходной сигнал

, (5.26)

поскольку реакция цепи на единичный скачок является переходной характеристикой. В соответствии с (5.7) определяется импульсная характеристика

(5.27)

Второй способ определения импульсной или переходной характеристики, назовём его косвенным, состоит в использовании однозначного соответствия между импульсной характеристикой и комплексным коэффициентом передачи.

5.4.3. Спектральный метод

При рассмотрении характеристик линейной цепи было получено соотношение (5.10), связывающее спектральные характеристики входного и выходного сигнала с комплексным коэффициентом передачи цепи. Это соотношение лежит в основе спектрального анализа. Если задачей анализа является определение частотных характеристик выходного сигнала, то при известных и использование (5.10) полностью решает эту задачу. В ряде случаев сигнал представлен во временной области и требует найти отклик цепи как функцию времени. При этом использование метода интеграла наложения может быть затруднено сложностью нахождения импульсной характеристики цепи. В то же время комплексный коэффициент передачи найти достаточно просто. Тогда спектральный метод анализа сводится к следующим операциям:

— для входного сигнала прямым преобразованием Фурье находится комплексный спектр ;

— определяется комплексный коэффициент передачи цепи ;

— в соответствии с (5.10) определяется комплексный спектр выходного сигнала ;

— обратным преобразованием Фурье вычисляется форма сигнала на выходе цепи.

Итак, важнейшим условием использования спектрального метода является знание комплексного коэффициента передачи исследуемой цепи. Найти комплексный коэффициент передачи можно, используя методы теории цепей (метод узловых потенциалов или метод контурных токов). Если известно аналитическое описание цепи дифференциальным уравнением (5.16), то комплексный коэффициент передачи находится в соответствии с (5.18). Наконец, цепь можно представить в виде делителя напряжения, элементами которого являются комплексные сопротивления

; ; .

Проиллюстрируем последний подход на примере уже рассматривавшейся выше RC-цепи. Если представить цепь как делитель напряжения, то выходной сигнал представляет собой напряжение на ёмкости С. Тогда, если комплексный ток, протекающий в цепи, то

,

и комплексный коэффициент передачи

,

что совпадает с результатом, полученным в подразделе 5.3.

5.4.4. Операторный метод

Операторный метод является обобщением спектрального метода. В основе метода лежит преобразование Лапласа. Рассмотрим некоторый сигнал , определённый на интервале времени (0, ). Умножим этот сигнал на и полученный новый сигнал подвергнем преобразованию Фурье

.

Обозначая через , получим

. (5.28)

Выражение (5.28) называется односторонним преобразованием Лапласа функции . При этом, называют оригиналом, а изображением.

Нетрудно убедиться, что при выражение (5.28) преобразуется к виду

,

что соответствует преобразованию Фурье. Таким образом если преобразование Фурье представляет собой спектральное разложение сигнала по гармоническим составляющим , то преобразование Лапласа – разложение сигнала по экспоненциально – косинусным составляющим . Действительно, представим

.

Здесь использована формула Эйлера

.

С другой стороны

,

где .

Тогда окончательно

представляет собой экспоненциально – косинусную функцию.

Переход от изображения к оригиналу осуществляется при помощи обратного преобразования Лапласа

. (5.29)

Для значительной части функций широко используемых при описании оригиналов были рассчитаны изображения по Лапласу. Некоторая часть оригиналов и изображений приведена в таблице 5.1.

Поскольку преобразование Лапласа является обобщением преобразования Фурье, то оно обладает теми же свойствами, что и преобразование Фурье. Остановимся на некоторых из них, которые будем использовать в дальнейшем. Пару преобразований (прямое и обратное) будем обозначать следующим образом

.

1. Линейность преобразований Лапласа

(5.30)

2. Свойство временного сдвига

(5.31)

3. Операция дифференцирования

; (5.32)

4. Операция интегрирования

. (5.33)

Применим к обеим частям уравнения (5.16) прямое преобразования Лапласа. Тогда с учётом (5.32), получим

(5.34)

откуда следует

. (5.35)

Это отношение называется передаточной функцией цепи или её операторным коэффициентом. Таким образом, передаточная функция является оператором преобразования линейной цепью в базисе экспоненциально – косинусных сигналов.

Сравним выражение комплексного коэффициента передачи (5.18) с выражением (5.35). Из этого сравнения следует, что комплексный коэффициент передачи является частным случаем при , т.е.

(5.36)

Таким образом, если известна передаточная функция цепи, то операторный метод поиска отклика цепи состоит в следующем:

— находится изображение по Лапласу входного сигнала

; (5.37)

— находится изображение выходного сигнала как произведение

; (5.38)

— определяется оригинал выходного сигнала

. (5.39)

Установим связь между временными характеристиками и передаточной функцией. Произведя в (5.12) замену на , получим

.

Таким образом, передаточная функция и импульсная характеристика связаны между собой преобразованием Лапласа

.

Что касается переходной характеристики, то применяя к (5.8) преобразование Лапласа и учитывая (5.33), получим

.

В заключение отметим, что операторный метод позволяет сводить линейные дифференциальные уравнения вида (5.16) к алгебраическим уравнениям (5.34), что позволяет в ряде случаев упростить анализ цепей. Помимо этого, учитывая широкое распространение таблиц преобразований Лапласа для большого числа функций, можно исключить громоздкие вычисления, непосредственно обращаясь к этим таблицам.

Рассмотрим применение операторного метода на примере анализа определения отклика RC-цепи на входной сигнал вида . Эта задача была решена классическими временными методами. Спектральным методом был найден комплексным коэффициент передачи. Заменив в выражении для цепи на , получим передаточную функцию цепи

.

Следуя операторному методу найдём изображение по Лапласу входного сигнала, воспользовавшись при этом таблицей 5.1

.

Далее, в соответствии с (5.38), определим изображение выходного сигнала

.

И наконец, по таблице 5.1 (позиция 5) находим оригинал

,

что совпадает с полученными ранее результатами.

Тогда эффективную ширину спектра можно определить по
формуле:

Подставляя в данный интеграл ,
находим, что эффективная ширина спектра:

В данном случае мы предполагали лишь положительную
область спектра, но в силу симметричности для всей области спектра эффективная ширина
его умножается на 2.

·  Найти сигнал,
который получается из заданного при воздействии фильтра с прямоугольной АЧХ и
линейной ФЧХ (частота среза  фильтра в МГц и
крутизна  ФЧХ в рад/МГц приведены в табл. 2),
построить временной график полученного сигнала

Таблица
2

Передаточная функция цепи имеет вид:

где— функция включения
Хевисайда.

Исходный сигнал, записанный как линейная комбинация
функций включения:

Представим исходный сигнал в операторном виде,
применив прямое преобразование Лапласа:

Заменив  на , получаем выражение для входного сигнала в
частотной области:

Выражение
для выходного сигнала в частотной области можно получить путем перемножения
комплексной частотной характеристики цепи и входного сигнала.

Тогда
выходной сигнал во временной области может быть получен как обратное
преобразование Фурье от выходного сигнала в частотной области:

График
выходного сигнала имеет вид:

 

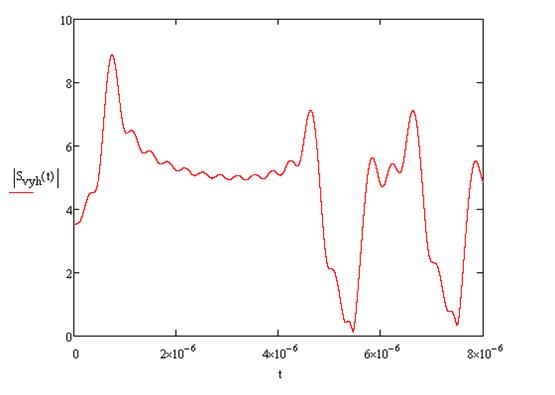График
выходного сигнала

·  Найти сигнал,
который получается из заданного при воздействии RC-фильтра НЧ с
параметрами, указанными в табл. 3 ( в кОм,  в мФ), построить временной график
полученного сигнала

                                    
Таблица 3

Представим исходный сигнал в операторном виде,
применив прямое преобразование Лапласа:

Передаточная функция фильтра в операторном виде:

где — постоянная времени,
которая определяется следующим образом:

Выражение для выходного сигнала можно получить путем
перемножения передаточной функции фильтра и входного сигнала  в операторном
виде:

Преобразуем выражение для :

Т.о. сигнал на выходе можно представить как разность
двух составляющих, одна из которых есть входной сигнал. Найдем обратное
преобразование Лапласа от обоих составляющих:

Откуда:

График выходного сигнала, построенный с помощью
математического пакета MathCAD,
имеет вид:

График
выходного сигнала

2.
Линейные инвариантные к сдвигу цепи

2.1ЛИС-цепь
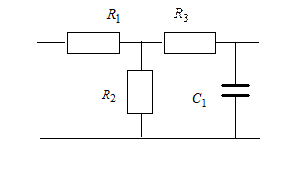
определяется схемой согласно варианту (табл. 4), ее параметры ( в кОм,  в пФ,  в мГн ) – согласно подварианту
(табл. 5).

            Таблица 4Таблица
5

·             2.2    
Требуется:
 Найти комплексную частотную характеристику цепи, построить графики АЧХ и ФЧХ

КЧХ
можно найти как отношение выходного напряжения к входному:

Для нахождения входного напряжения
свернем схему относительно входных зажимов:

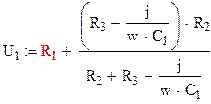Для нахождения выходного напряжения,
воспользуемся методом делителя токов:

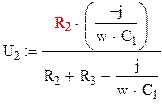Тогда КЧХ:

Построим графики АЧХ и ФЧХ комплексно
частотной характеристики:

 

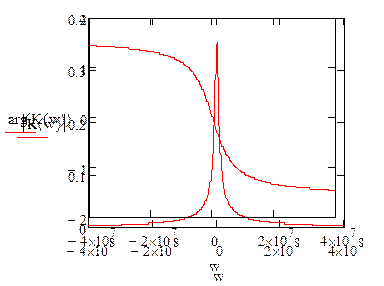·  Найти импульсную
и переходную характеристики, построить графики

Импульсная характеристика – отклик цепи
на дельта функцию. В теории сигналов, КЧХ связана с импульсной характеристикой
парой преобразований Фурье.

Импульсная характеристика цепи:

Построим график импульсной
характеристики:

 

Переходная характеристика – интеграл от импульсной
характеристики с переменным верхним пределом интегрирования:

Построим график переходной характеристики:

 

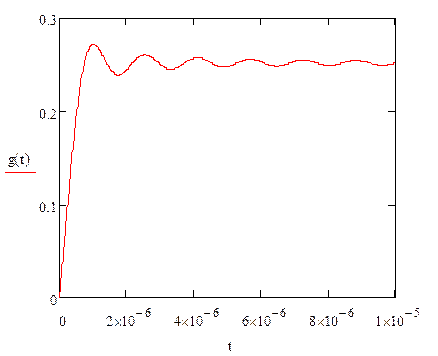·  Найти отклик
цепи на заданный сигнал, построить график

В теории сигналов, отклик цепи может быть найден как
обратное преобразование Фурье от произведения КЧХ на спектральную плотность
сигнала:

Построим график отклика цепи:

 

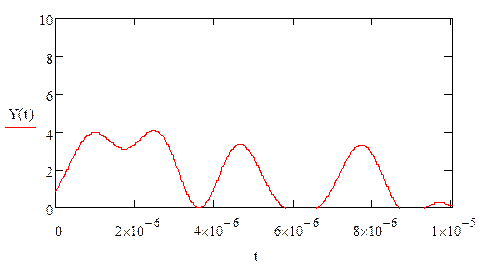Федеральное
агентство по образованию Российской
Федерации

Томский Государственный
Университет Систем Управления и Радиоэлектроники
(ТУСУР)

Кафедра электронных систем

Автоматизации и управления
(ЭСАУ)

Расчёт сигнала на выходе линейной цепи

Пояснительная
записка к курсовому проекту 
по дисциплине 
“Электротехника и электроника”

Студент группы 588-2 
_________А. А. Березников 
«____»_________2010г.

Руководитель

Доцент 
кафедры ЭСАУ 
_________А.А.Шибаев

«____»_________2010г.

                                                             
Томск, 2010

ТЕХНИЧЕСКОЕ ЗАДАНИЕ НА
КУРСОВУЮ РАБОТУ ЧЕТВЕРТОГО СЕМЕСТРА

 по дисциплине «ЭЛЕКТРОТЕХНИКА
И ЭЛЕКТРОНИКА»

Выдано студенту гр. 588-2
Березникову Алексею Алексеевичу

Тема: «Расчет сигнала на выходе
линейной цепи»

Исходные 
данные:

1. Схема линейной цепи,
вариант — 1         
2.  Воздействие s_вх (t) , вариант — 4

 Ход 
выполнения курсовой работы:

1. Исследовать частотные и временные 
свойства линейной цепи, при этом

1.1. Определить и построить АЧХ — K (ω) и ФЧХ — φ (ω) для
заданной цепи.

1.2. Определить и построить 
переходную характеристику линейной 
цепи h(t), проверить выполнение предельных
соотношений между K(ω) и h(t).

1.3. Определить и построить, 
используя известное соотношение 
импульсную реакцию линейной цепи.

1.4. Привести объяснение 
полученных результатов на основе 
физических представлений о свойствах 
данной цепи.

2. Исследовать частотные свойства 
заданного сигнала, при этом

2.1. Записать математические 
модели заданного сигнала для 
двух случаев: непериодический 
сигнал и периодический сигнал, приняв
за период интервал времени Т. Сделать описание временных свойств
сигналов.

2.2. Выполнить спектральный 
анализ непериодического сигнала 
s_вх(t),
воспользовавшись методикой “экспресс
– спектрального анализа”.

2.3. Определить ширину 
спектра непериодического сигнала 
s_вх
(t), задавшись η = 0.9.

2.4. Построить графики 
спектральной плотности S(ω) и фазового спектра φ(ω)

2.5. Выполнить спектральный 
анализ периодического сигнала 
s_вх(t),
при этом амплитуды спектральных составляющих
допустимо определить на основе известного
соотношения, связывающего спектры непериодического
и периодического сигналов.

2.6. Определить ширину 
спектра периодического сигнала 
s_вх(t),
приняв η
= 0.9.

3. Определить сигнал на выходе 
линейной цепи на основе принципа 
суперпозиции 

(одним из двух методов — по выбору)

3.1. Определить сигнал на выходе
линейной цепи на основе принципа суперпозиции
операторным методом или одним из методов
временного интегрирования для случая
непериодического воздействия s_вх(t). По результатам расчёта
построить в едином масштабе времени графики
непериодического воздействия s_вх(t) и отклика s_вых(t) на выходе линейной цепи.

3.2. Исследовать влияние соотношения
между ω_o=1/τ
и Т,
характеризующих инерционные свойства
цепи и временные свойства сигнала на
форму отклика (расчеты выполнить для ω_o·Т = 0,1;
1; 10). Привести объяснение полученных результатов,
основываясь на физических представлениях
о свойствах данной цепи.

4. Компьютерное моделирование.

4.1. С помощью одного из пакетов
прикладных программ выполнить моделирование
частотных и временных свойств заданной
цепи. Промоделировать отклик заданной
цепи на заданное воздействие во временной
области при различных соотношениях между ω_o
и Т: ω_oТ=0,1;1;10.

5. Сделать обобщающие выводы:

5.1. По временным и 
спектральным свойствам линейной 
цепи.

5.2. По временным и 
спектральным свойствам воздействия.

5.3. По сопоставлению результатов 
расчета на основе временных 
(спектральных) методов, сравнивая полученные
аналитические результаты и физические
представления о работе цепи, а также результаты
компьютерного моделирования.

Срок сдачи выполненной работы
на проверку………………………………_____________
2010г.

Задание выдал доцент кафедры ЭСАУ
A.А.Шибаев………………………………….15 февраля
2010г.

СОДЕРЖАНИЕ

1 Введение 5

2 Данные для работы 5

2.1 Схема
линейной цепи 5

3 Исследование частотных и временных
свойств линейной цепи 6

3.1 Определение
АЧХ — K(w) и ФЧХ — j (w) 6

3.2 Определение
переходной характеристики линейной цепи 7

3.3 Определение
импульсной реакции линейной цепи 8

3.4 Объяснение
полученных результатов 9

4 Исследование частотных свойств заданного
сигнала 11

4.1 Математические
модели непериодического и периодического
сигналов 11

4.2 Спектральный
анализ непериодического сигнала 12

4.3 Ширина
спектра непериодического сигнала 13

4.4 Спектральный
анализ периодического сигнала……………………………………14

4.5 Ширина
спектра периодического сигнала 16

5 Определение сигнала на выходе цепи. 18

5.1 Определение
отклика 18

5.2 Исследование
влияния соотношения между w₀ и T 18

6      Моделирование
в пакете MicroCap 8.0 19

6.1. Определение
АЧХ и ФЧХ 19

6.2. Определение
сигнала на выходе линейной цепи 21

7 Обобщающие выводы 22

7.1 Выводы
по временным и частотным свойствам линейной
цепи 22

7.2 Выводы
по временным и частотным свойствам воздействия 22

7.3 Выводы
по результатам расчета сигнала на выходе
цепи 22

7.4 Обобщающий
вывод по проделанной работе 22

Введение

Основной целью работы
является исследование временных и 
частотных свойств заданной цепи,
исследование частотных свойств 
заданных сигналов, а так же определение 
отклика цепи на воздействие (непериодический 
сигнал), применяя один из методов временного
интегрирования. Исходные данные приведены 
ниже.

Исходная цепь

                                       
Входной непериодический сигнал

Входной периодический 
сигнал

w₀=1/CR=1/t; w=2p/T; 
3. Исследование
частотных и временных свойств линейной
цепи.

1. Определение АЧХ и ФЧХ

Найдём передаточную функцию 
K (w):

Приняв wτ=x получим:

Модуль K комплексной передаточной функции
является амплитудно-частотной
функцией цепи (АЧХ). Выделим её из предыдущего
выражения:

Аргумент комплексного
числа 
является фазовой частотной функцией
цепи (ФЧХ). Выделим эту функцию из выражения,
определяющего
(х) для данной цепи при помощи встроенной
функции MathCad, которая вычисляет аргумент
комплексного числа (функции).

Ниже 
приведены графики АЧХ и ФЧХ 
для исследуемой цепи.

1. Определение переходной характеристики

Переходная характеристика
цепи h(t) есть отклик этой цепи на воздействие
на неё единичного скачка напряжения или
тока i(t). Для определения переходной характеристики
можно воспользоваться операторным методом.
По известному изображению комплексной
передаточной функции K(р) можно определить изображение
отклика, т.е. переходной характеристики:

,

где 1/р – изображение
по Лапласу единичной функции (функции
Хевисайда) .

p=wi; 
x=

Полюсами 
в данном выражении являются :

Полученные вычеты:

Переходная характеристика равна
сумме полученных вычетов:

Если приблизительно вычислить значения
простых дробей:

Для удобства построения графика и 
увеличения наглядности пронормируем
h(t) – введем

переменную 

Рис 1.2.1 Переходная
характеристика h(x)

Переходная характеристика
и передаточная функция связаны 
между собой предельными соотношениями:

Предыдущие выражения 
подтверждают выполнение этих соотношений 
для проведённых исследований данной
цепи.

1.   Определение импульсной реакции

Важной характеристикой 
линейной цепи является её импульсная
характеристика g(t). Импульсная характеристика есть
реакция цепи на импульс очень малой длительности
и с достаточно большой амплитудой, которые
определяют его энергию. Фактически этот
импульс математическая абстракция, обозначаемая
как дельта-импульс d(t). Определяется импульсная реакция
цепи исходя из соотношения:

;

Воспользуемся этим соотношением
для вычисления g(t), подставив в него пронормированное h(t):

Рис 1.3.1  Импульсная
реакция цепи g(t)

3.4. Объяснение
полученных результатов на основе физических                                      
представлений о свойствах цепи.

В основе объяснения полученных результатов 
лежит представление о том, что 
идеальный конденсатор при воздействии
на него напряжением с представляет собой разрыв, с ростом
частоты сопротивление конденсатора уменьшается,
и на бесконечно высокой частоте конденсатор
представляет собой короткое замыкание.

Пусть, модуль комплексного сопротивления
обоих конденсаторов равен нулю, эквивалентная
схема цепи для данного случая:

Т.к . на выходе присутствует короткое
замыкание, то всё приложенное напряжение
падает на параллельно соединённых 
резисторах и сигнал на выходе равен 
нулю.

При уменьшении частоты входного сигнала
возрастает модуль комплексного сопротивления
конденсаторов и увеличивается падение
напряжения на них. Т.к. один из конденсаторов
подключен параллельно выходу, то соответственно
увеличивается и выходное напряжение. 
При дальнейшем уменьшении частоты сопротивление
конденсаторов становится больше сопротивления
резисторов и при эквивалентная схема имеет вид

               
:  

Т.е. при 
коэффициент передачи цепи стремится
к 1.

Из фазочастотной характеристики
цепи видно, что выходной  сигнал
по фазе отстает от входного. Максимальный
сдвиг фаз между выходным и входным сигналами
-90⁰ при. Это объясняется тем, что в этом случае
весь ток цепи протекает через емкостные
элементы, как имеющие нулевое сопротивление.
А так как напряжение на емкости отстает
от тока на 90⁰, то и выходное напряжение
будет отставать от входного напряжения
на 90⁰ . При уменьшении частоты входного
сигнала доля емкостной составляющей
в токе, протекающем в цепи, уменьшается
и цепь приобретает всё более резистивный
характер, соответственно и сдвиг фаз
между входным и выходным сигналами уменьшается
и при стремится к 0.

           
Таким образом, данная цепь 
является простым фильтром низких
частот, с коэффициентом передачи, стремящимся
к 1.  

На поведение h(t) и g(t) основное влияние
оказывает конденсатор, подключенный
параллельно выходу цепи,  т.к. второй
конденсатор подключен последовательно
одному из резисторов и параллельно второму.

4. Исследование частотных свойств сигнала

4.1. Математические
модели и временные свойства сигналов

Для непериодического сигнала:

   Где
функция
Хэвисайда

Входной непериодический 
сигнал

                                 
Входной периодический сигнал

Для периодического
сигнала:

Временные свойства: представляет
собой периодически повторяющуюся
последовательность состоящую из линейного
понижения амплитуды с 2E на времени 0 до
Е на времени Т/2, резкого падения до -E и
затем линейного увеличения амплитуды
до 0 длительностью на времени T.

1. Спектральный анализ непериодического сигнала

Спектральный анализ непериодического
сигнала основывается на интегральных
преобразованиях Лапласа, а также равенстве
Парсеваля. Применим преобразование Лапласа
для нахождения комплексной спектральной
функции сигнала, а затем её модуля и аргумента.

Откуда получим комплексную 
спектральную функцию:

График спектральной плотности 
сигнала:

График 
фазового спектра сигнала:

1. Ширина спектра непериодического сигнала

Для
нахождения практической ширины спектра 
непериодического сигнала воспользуемся 
равенством Парсеваля и тем, что 
практическая ширина спектра несет h=0.9) всей энергии сигнала:

где Э – энергия;

h — коэффициент, определяющий
длительность сигнала, h=0.9;

Dw — верхний предел полосы
пропускания, Dw=2pDF.

ΔF=Δx/Δw

Получаем интегральное
уравнение:                       

Решая данное интегральное
уравнение, получаем: . Практическая ширина спектра непериодического
сигнала:

1.  Спектральный анализ периодического сигнала

Периодический
сигнал, разложенный в ряд Фурье,
имеет вид:

где

Найдем коэффициенты ряда.

Итак, разложение в ряд 
Фурье данного сигнала имеет 
вид:

Чётные гармоники у 
данного сигнала отсутствуют.

  Построим график этой функции для
n=50:

Построим 
график амплитудного спектра:

Построим график фазового спектра:

1. Ширина спектра периодического сигнала

  Энергия n-го гармонического колебания
на периоде T равна:

  Средняя мощность n-го гармонического
сигнала определяется как  

Ширину 
спектра для периодического сигнала 
можно найти из соотношения:

,

где  
P_T – средняя мощность сигнала

       
— коэффициент, определяющий длительность
сигнала равный 0,9

       
– мощность постоянной составляющей

       
– мощность отдельной гармонической
составляющей

    
Найдем энергию n-го колебания:

Находим 90% энергии сигнала:

Рассчитаем величины спектральных
составляющих и их мощностей:

Из таблицы видно, что уже 
при n=3 энергия сигнала превышает

Найдем практическую ширину спектра 
сигнала, учитывая, что 
:

5.Определение
сигнала на выходе линейной цепи

1. Определение сигнала на выходе линейной цепи операторным методом

Для определения отклика цепи на
воздействие можно воспользоваться 
операторным методом. Для этого 
необходимо провести обратное преобразование
по Лапласу. Воспользуемся формулой:

,   где

Проведя обратное преобразование
по Лапласу, которое ввиду громоздкости
не приводится, получаем аналитическое
выражение для сигнала на выходе линейной
цепи.

1. Исследование влияния соотношения между w₀ и T

Произведение w₀T характеризует инерционность
заданной цепи по отношению к заданному
сигналу. На рисунке приведены нормированные
графики входного и выходного сигналов
для трех значений соотношения w₀T: 0,1; 1; 10 в одинаковом масштабе.

 Графики входного и выходного 
сигналов для трех значений 

Из графиков видно, что зависимость
формы выходного сигнала от соотношения
такова: чем больше w₀T, тем форма выходного сигнала
ближе к форме входного сигнала. Этого
можно добиться либо увеличением длительности
сигнала, либо уменьшением постоянной

6. Моделирование в пакете
MicroCap 8.0

6.1   Определение АЧХ и ФЧХ

Пакет MicroCap 8.0 предназначен для анализа
и симуляции электрических цепей, различной
сложности. В связи с тем, что в этом пакете
необходимо чтобы все параметры цепи были
определены, присвоим значения: R=1kОм; L=1мГн.
Для анализа частотных свойств заданной
цепи составим в  MC цепь представленную
на рисунке.

Рис. 4.1.1 – Цепь, построенная 
в MicroCap 7.0

АЧХ и ФЧХ цепи, полученные MC:

Как видно, частотные свойства
цепи найденные с помощью MC, совпадают
с теми, что были найдены в пункте 3.1, свидетельствуя
о правильности полученных результатов.

1. Определение сигнала на выходе линейной цепи

Для определения отклика 
цепи на непериодический сигнал, зададим 
этот сигнал при помощи координат.

 В нашем случае 
сопротивление 1 кОм, емкость — 1 нФ ,
поэтому постоянная времени цепи будет
равна τ =1 мкс. w₀T=1.

Найдем отклик цепи для 
трех случаев w₀T=0,1; w₀T=1; w₀T=10, изменяя параметры входного
сигнала. Полученные отклики изображены
на рисунках:

Рис. 4.1.4 – Отклик цепи в 
случае w₀T=0,1

Рис. 4.1.5 – Отклик цепи в 
случае w₀T=1

Рис. 4.1.6 – Отклик цепи в 
случае w₀T=10

Как видно результаты моделирования 
полностью совпадают с результатами
расчетов выполненных в пункте 5.1.

7.Обобщающие выводы

7.1   Выводы
по временным и спектральным свойствам
линейной цепи

В ходе данной работы был 
проведен полный анализ свойств заданной
линейной цепи. Были определены АЧХ 
и ФЧХ, а также отклик сигнала 
на единичный скачок (h(t)), и единичный
импульс (g(t)).

Из анализа АЧХ, видно,
что данная цепь может выступать 
в роли простейшего фильтра низких
частот. Цепь не пропускает сигнал, имеющий
высокую частоту, т.е. АЧХ на этих частотах
приближается к нулю. На частотах, близких
к нулю, коэффициент передачи равен единице.

Отклик на единичный 
скачок значение ноль  в начальный 
момент времени, что обусловлено 
наличием в цепи емкостей, напряжение
на которых не может меняться мгновенно,
и соответственно емкость на малых частотах
будет представлять собой разрыв цепи.
Т.е. сигнал проходит через резистор и
не изменяется. Затем, емкости не пропускают
сигнал, и он проходит без искажений. Через
некоторое время емкости полностью, без
искажений пропускают сигнал.

7.2     Выводы по временным и спектральным
свойствам воздействия 

Исследование сигнала было
разбито на две части. Вначале были исследованы
свойства непериодического сигнала. Были
найдены спектральная плотность и фазовый
спектр непериодического сигнала. Периодический
сигнал может быть получен из непериодического,
если принять период равным T(длительность
непериодического сигнала) и продолжить
его на всей оси.

Для обоих сигналов была
определена практическая ширина спектра.
Было показано, что ширина спектра 
непериодического сигнала близка к 
ширине периодического сигнала.

 7.3    Выводы по результатам расчета
сигнала на выходе цепи

Расчет выходного сигнала 
был произведен операторным методом.
Полученные отклики полностью совпадают
с откликами, полученными при помощи пакета
Micro-Cap 8.0. Таким образом, аналитическое
выражение для отклика было получено верно.

 7.4    Обобщающий
вывод по проделанной работе

В результате работы было проведено 
комплексное исследование заданной
цепи, заданного сигнала, и их взаимодействие.
Был получен отклик линейной цепи
на заданное воздействие. Таким образом,
задание данной курсовой работы было
полностью выполнено.

Как
пример использования спектрального
метода решим задачу о прохождении
экспоненциального видеоимпульса
напряжения
черезRC-цепь,
рассмотренную выше. В данном случае
спектральная плотность входного сигнала
и задача сводится к вычислению интеграла,
входящего в выражение:

.

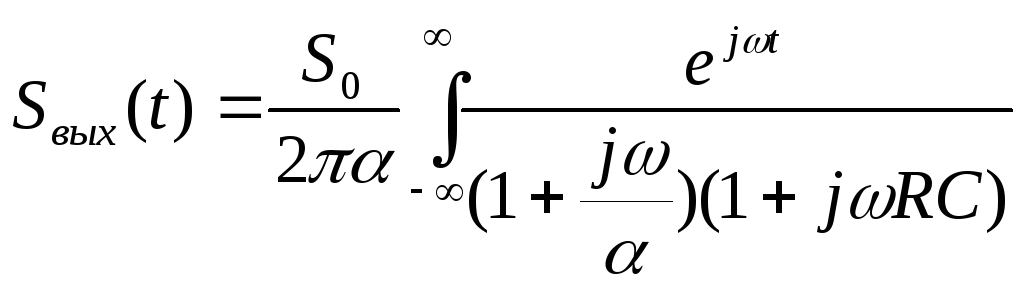
Раскладывая
алгебраическую часть подынтегральной
функции

на
элементарные дроби, имеем:

.

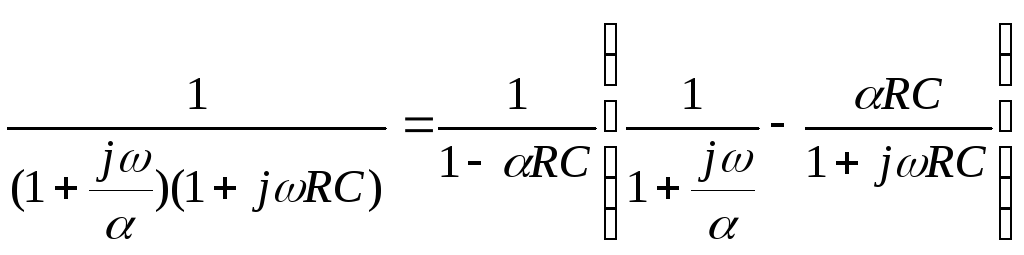
Структура
слагаемых, стоящих в правой части
выражения в скобках, позволяет
непосредственно использовать результат,
полученный при вычислении импульсной
характеристики RC-цепи,
и записать решение при t>0:

(6)

Естественно,
что при t<0

(7)

(10)

2.5. Геометрическая интерпретация процесса

Спектральный
метод позволяет наглядно интерпретировать
преобразования сигналов, которые
происходят при их прохождении через
линейные стационарные системы. Системный
оператор T
– это правило перехода от вектора
некоторого линейного пространства к
новому вектору.
В самом общем случае можно считать, что
операторT
изменяет форму вектора
в.
Нормане будет равна

норме

:

Кроме
того, между векторами и
возникает
некоторый угол.

По
формуле Рэлея, энергия выходного сигнала

,
(16)

где
—
энергетический спектр сигнала на входе.

В
соответствии с формулой (16), выходной
энергетический спектр .

(17)

Величину
(17) называют частотным коэффициентом
передачи по мощности системы на заданной
частоте ω. Поскольку этот коэффициент
вещественный, вычисление энергии
выходного сигнала оказывается гораздо
более простой задачей по сравнению с
поиском самой формы выходного сигнала.

Теперь,
рассмотрев различные методы анализа
линейных цепей и сделав вывод о том, что
наибольшую практическую пользу имеет
спектральный метод анализа из-за своей
простоты и наглядности, приступим к
непосредственному расчёту сигнала на
выходе линейного устройства. Расчёты
приведены в следующих пунктах.

3.
Расчёт амплитудного и фазового спектров
входного сигнала.

В
задании приведён входной сигнал. Он
имеет следующий вид:

S(t)

t

рис.1

где

с,c,
B

Далее
для нахождения спектральной плотности
сигнала S(t)
нам необходимо найти прямое преобразование
Фурье . В нашем случае необходимо
посчитать интеграл:

,

,

.

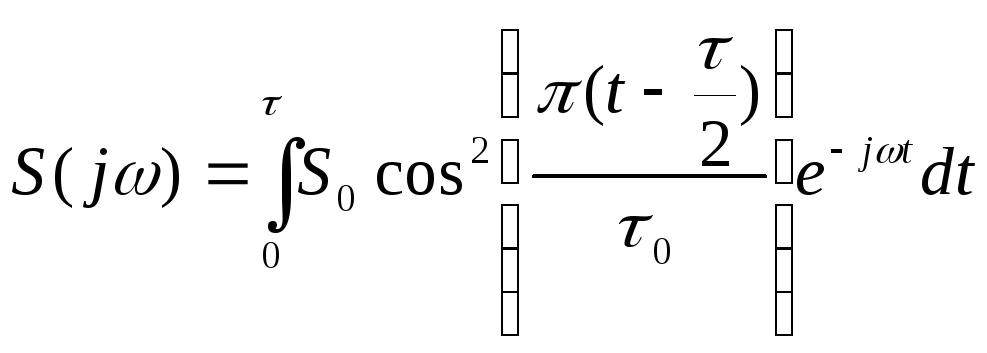
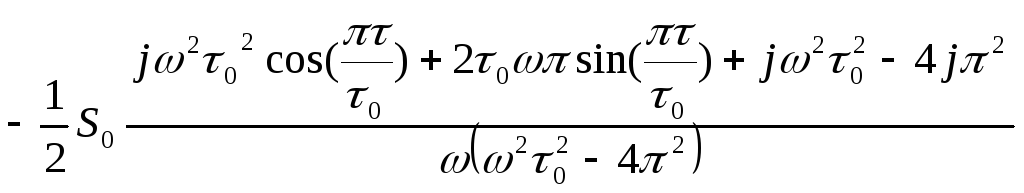
Это
выражение необходимо путём преобразований
привести к виду a+jb.
В итоге получаем:

,

где

Таким
образом, действительная часть спектра
будет равна,а
мнимая часть —.
Знаменательоставлен
для того, чтобы не усложнять конечные
формулы действительной и мнимой частей.

Для
построения амплитудного и фазового
спектров сигнала приводим наше выражение
к виду
,
гдеи—
модуль и аргумент спектра входного
сигнала соответственно. В нашем случае,.

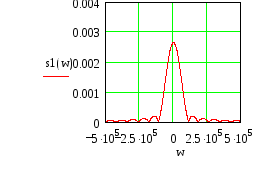
По
этим данным строятся графики амплитудного
и фазового спектров входного сигнала.

Амплитудный
спектр входного сигнала

Фазовый
спектр входного сигнала