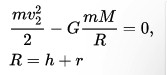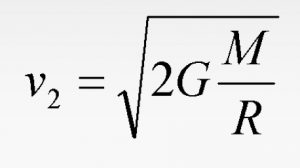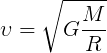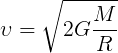Вычисление первой космической скорости на Марсе – задача несложная и описывается простыми физическими формулами. Именно эта скорость дает возможность летательному аппарату покинуть поверхность красной планеты и двигаться по ее орбите. А создание таких аппаратов – одна из важнейших целей в проектах по колонизации и исследованиям планеты Марс.
Даем определение космическим скоростям первой, второй
Чтобы ракета смогла попасть в космическое пространство, ей необходимо придать нужное ускорение и разогнать до скорости, которая позволит преодолеть силу земной гравитации.
Первая космическая скорость – это скорость, которую должен поддерживать объект, чтобы сохранять свое положение на орбите, двигаясь горизонтально над поверхностью планеты не снижаясь на нее и без ущерба для круговой траектории.
На Земле она составляет 7,9 километров в секунду. У Марса – меньше – 3,53 км в сек., так как масса Марса почти в два раза отличается от земной. Более подробно о расчетах этих величин расскажем ниже.
Но для межпланетных перемещений недостаточно вывести объект на орбиту. Нужно еще придать ему достаточный импульс, чтобы двигаться дальше, по параболе, полностью игнорируя силу планетного тяготения. Такая скорость считается 2-ой космо-скоростью. Другие ее названия – скорость освобождения, убегания или параболическая.
Вторая космическая скорость – это наименьшая скорость, которую должен развить объект, чтобы преодолеть силу притяжения центральной планеты и покинуть ее замкнутую орбиту.
Цифровые величины второй космической скорости для Марса, Земли равняются 5 км/с и 11,2 км/с соответственно.
Формулы вычисления этих двух космических скоростей получаются из основного закона классической теории тяготения Ньютона, который дает возможность с большой точностью рассчитать многие параметры и характеристики небесных объектов и звездных скоплений.
В результате изучения теории тяготения тел, установлено, что гравитационная сила притяжения двух объектов находится в прямой пропорциональности от масс этих тел и в обратной зависимости от расстояния между объектами:
F гр – это сила гравитации, m1, m2 – массы взаимодействующих тел, r – дистанция между ними. Важную роль в этой формуле имеет G – гравитационная постоянная:
Вычисление космических скоростей первой и второй
Для подсчета и определения первой космической скорости на Марсе воспользуемся уравнением движения, или II законом Ньютона:
В нашем примере F – сила притяжения, удерживающая тело на орбите, m – масса тела, a – его ускорение.
Ускорение при движении тела по окружности является центростремительным и равняется v2/r, где v – и есть 1-ая космическая скорость. В итоге после замены получаем формулу:
М – масса Марса, G – гравитационная константа, r – радиус орбиты.
Из этого равенства находим:
Зная массу Марса и другие величины, подставляем в формулу и получаем, что 1-ая космическая скорость Марса примерно равна:
v1 = 3,5 м/с = 3,53 км/с = 12728 км/ч = 2,2 мили/с = 7909 миль/ч
Продолжим расчет для второй космической скорости на Марсе. Формулу для нее получаем, пользуясь законом сохранения энергии, который описывает падение небесного объекта на планету из бесконечности:
Здесь r – радиус планеты, h – высота тела над планетой, M – масса Марса, G – гравитационный коэффициент, v – вторая космическая скорость.
Цифровое значение G стремительно мало и приводит к тому, что силы притяжения тел с маленькими массами, не ощутимы, что мы и наблюдаем у предметов на нашей планете Земле. Но для огромных астрономических тел гравитация и ее сила имеет первостепенное значение.
Решаем уравнение и находим v:
Таким образом, используя значения марсианских параметров, находим, что вторая космическая скорость для Марса составляет:
v2 = 5000 м/с = 18000 км/ч = 5 км/с = 3,11 мили/с = 11185 миль/ч
Соотношение обоих космических скоростей получается таким:
Кстати, если скорость летающего объекта имеет горизонтальное направление, по значению превышает 1-ую космическую, но меньше 2-ой космической, то тело будет двигаться по эллиптической орбите.
Формы орбит, по которым движутся улетающие объекты от планеты, представляют собой виды конических сечений:
- окружность – для тел, обладающих 1-ой;
- эллипс – при скорости, чуть меньше 2-ой;
- парабола – при 2-ой;
- гипербола – больше, чем 2-ая.
В школьных учебниках можно встретить множество интересных задач на космическую тематику. Многие из них начинаются словами: найдите вторую космическую скорость, вычислите значение первой для звезды, выведите формулу для расчета скорости летательного аппарата вокруг Марса и т.д.
Как вычислить нужные параметры и скорости – задачи типичные, и решаются с помощью выведенных выше формул.
Другие космические скорости – третья, четвертая и пятая
Кроме 1-ой и 2-ой космических скоростей (v1, v2) существуют и другие понятия – v3, v4 и v5. Все эти космические скорости – это скорости движения и характеристики летающих объектов или аппаратов в гравитационных полях астрономического пространства и действия небесных тел и систем – спутников, астероидов, звезд, комет, планет, галактик и звездных скоплений.
Все тела в космосе подчиняются закону всемирного тяготения, который был открыт одним из основоположников физики Исааком Ньютоном в 1666 году. Гравитация заставляет небесные тела притягиваться. Благодаря этим силам планеты удерживаются в системах, движутся вокруг звезд, а звезды собираются в галактики, формируя Вселенную. Кстати, физическая природа гравитации до сих не нашла полного объяснения. Механизм гравитационного взаимодействия до сих пор не разгадан учеными и не создана подходящая модель действия сил притяжения.
Критические космические скорости помогают ракетам и аппаратам вырваться из цепкого гравитационного влияния и отправиться в открытое пространство Вселенной. В результате их действия получается:
- v1 – предмет становится спутником небесного объекта, вращаясь на относительно небольшой высоте от его поверхности;
- v2 – в этом случае аппарат способен преодолеть силу гравитации и сможет удалиться от планеты;
- v3 – при таких скоростях аппарат уже может выйти за пределы не только гравитационного поля планеты, но и всей планетной системы (например, Солнечной), оторвавшись от притяжения центральной звезды;
- v4 – позволяет покинуть целую галактику;
- v5, v6 и тд. – понятие, можно сказать из области фантастики, скорость, которая позволяет улететь в любую точку любой другой галактики и даже Вселенной, уйти за пределы невиданной гравитации.
Первые две скорости помогают исследовать нашу солнечную систему и ее окрестности. Но их явно недостаточно, чтобы совершать путешествия свободно и быстро во всем космическом пространстве, которое раскрывается нам. Придет время, когда человечеству будут доступны другие сверхскорости. Но для этого нужно открыть иные источники дешевой энергии, а это пока за пределами наших возможностей.
Пригодилась информация? Плюсани в социалки!
- Связь Марса с Землей – сколько идет сигнал до красной планеты?
- Сравнение Марса и Земли, какая планета больше и в чем их отличие
- Как посчитать сколько мне лет на Марсе
Из школьного курса физики мы помним, что первая космическая скорость Земли – это показатель, которого необходимо достичь, чтобы объект мог выйти на эллиптическую орбиту вращения вокруг планеты. Это же, собственно, касается и любого массивного космического тела. В свою очередь, вторая космическая скорость – это предел, необходимый для того, чтобы полностью покинуть гравитационное поле планеты.
Вторая космическая скорость зависит от ряда параметров и для каждого космического объекта – отличается. Давайте рассмотрим, по какому принципу она вычисляется, и разберем примеры для крупных планет Солнечной Системы, Солнца и Луны.
Как рассчитать вторую космическую скорость
Вторая космическая скорость зависит от массы и радиуса небесного тела. Условно можно себе представить, что для ее расчета можно пойти от обратного решения задачи. То есть, вычислить скорость с какой объект будет падать на планету из космоса. По модулю это и будет вторая космическая скорость.
Итак, учитывая закон сохранение кинетической и потенциальной энергий при движении тел, можно вывести такую формулу в падающем объекте на небесное тело:
Где m – масса стартующего объекта, М – масса небесного тела, R – сумма радиуса планеты и высоты расположение объекта над поверхностью, G – гравитационная постоянная, V – искомая вторая космическая скорость. Таким образом, из формулы можно вычислить V:
Это и будет решение нашей задачи со знанием всего двух параметров – радиуса небесного тела и его массы.
Вторая скорость для разных небесных тел
Итак, попробуем на основании выведенной формулы рассчитать вторую космическую скорость для разных небесных тел Солнечной Системы, учитывая что их радиус и массу мы знаем.
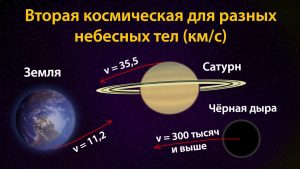
Начнем с самого простого – Земли. Радиус нашей планеты равен 6,37 тысяч километров, а масса – 5,97 х 10²³ кг. Подставляем в нашу формулу и получаем – вторая космическая скорость Земли равна 11,2 километра в секунду. Именно до таких цифр нужно разогнать гипотетический объект, чтобы он покинул зону гравитационного притяжения нашей планеты.
Теперь можно перейти к нашей звезде и посчитать вторую космическую скорость для Солнца. Радиус его равен 696 тысяч километров, а масса 1,989 х 10³⁰ кг. Расчеты по формуле дают результат в 617,7 километров в секунду! До такой скорости нужно разогнать предмет, чтобы он смог покинуть нашу Солнечную Систему и попасть в межзвездное пространство.
Теперь попробуем вычислить показатель для остальных планет системы. Итак, радиус и масса Меркурия составляют соответственно 2,438 тысяч километров и 330 х 10²¹ кг. Подставив в формулу цифры, получаем вторую космическую скорость Меркурия 4,3 км/с.
Идем далее и получаем такие цифры – вторая космическая скорость Венеры – 11,2 километров в секунду, Марса – 5,0 км/с, Юпитера – 61 км/с, Сатурна – 36 км/с, Нептуна – 24 км/с, Урана – 22 км/с, Луна – 2,4 км/с.
Таким образом, мы видим, что преимущественно чем массивнее планета (а вернее, чем плотнее, потому что радиус тоже важен) – тем больше нужна скорость, чтобы объект мог вырваться за пределы гравитационного влияния.
Показательными и интересными также являются примеры третей и четвертой космических скоростей. Что это за параметры? Если говорить грубо – то третья космическая скорость, это вторая космическая для Солнца, но высчитываемая вблизи Земли. Простыми словами – какую скорость нужно развить с Земли, чтобы покинуть Солнечную Систему? Посчитав по формуле, получим 16,65 километров в секунду.

Здесь приведены формулы и примеры расчета первой и второй космической скорости для небесных тел произвольной массы и радиуса.
Для быстрого расчета можно воспользоваться онлайн-калькулятором.
Первая космическая скорость
Первая космическая скорость — это скорость, которую нужно придать телу, масса которого пренебрежительно мала по сравнению с массой планеты,
чтобы это тело стало спутником планеты и вращалось вокруг нее по круговой траектории. Примечание: если скорость будет выше заданной (но меньше второй космической), то траектория орбиты будет
не круговой, а эллипсоидной.
Формула первой космической скорости:
где
G — гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10-11 м3/(кг*с2), или Н*м2/кг2
R — радиус небесного тела
M — масса небесного тела
Вторая космическая скорость
Вторая космическая скорость — это минимальная скорость, которой должно обладать тело, чтобы преодолеть гравитационное притяжение планеты и покинуть замкнутую орбиту вокруг нее.
Формула второй космической скорости:
где
G — гравитационная постоянная
R — радиус небесного тела
M — масса небесного тела
Пример:
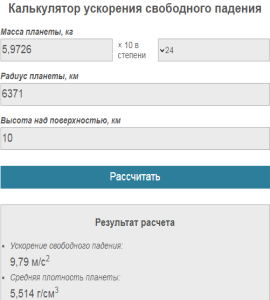
Масса планеты Земля составляет 5,9726*1024 кг, средний радиус — 6371 км (или 6371000 м). Подставив эти значения в формулы первой и второй
космических скоростей, мы получим значение соответственно 7 910 м/с и 11 187 м/с.
Теперь рассчитаем значение космических скоростей для планеты Нептун. Масса Нептуна — 1,0243*1026 кг. средний радиус — 24 622 км (24 622 000 м).
В итоге получим значения — 16 663 м/с и 23 565 м/с.
Значения для Марса (6,4171*1023 кг и 3389,5 км) будет 3 555 м/с и 5 027 м/с.
Для Венеры (4,8675*1024 кг и 6051,8 км) — 7 327 м/с и 10 362 м/с соответственно.
Калькулятор космических скоростей
Другие формулы
Если мы подбросим камень в воздух – он упадет на Землю. Если у самолета на высоте 10 километром отключаться двигатели – он тоже упадет на Землю. Но спутники и космические корабли, что мы запускаем в космос, не падают. Почему?
Все дело в том, с какой скоростью тот или иной объект удаляется от планеты. Хватит ли этому объекту энергии преодолеть притяжение планеты.
Оглавление
- 1 Первая космическая скорость
- 1.1 Расчет
- 2 Вторая космическая скорость
- 2.1 Расчет
- 3
- 4 Третья космическая скорость
- 4.1 Расчет
- 5 Четвертая космическая скорость
- 6 Пятая космическая скорость
- 7 Почему спутники не падают на Землю
Первая космическая скорость
Это та самая минимальная скорость для выхода корабля или спутника на круговую орбиту, равную радиуса планеты, без учета вращения планеты и сопротивления ее атмосферы.
Если скорость будет превышать первую, но не достигнет второй космической скорости, то траектория тела из круговой начнет переходить в эллиптическую.
Впервые такую скорость смог достичь первый искусственный спутник Земли «Спутник-1» СССР 4 октября 1957 года.
Расчет
Вторая космическая скорость
Это минимальная скорость, которую следует придать телу для того, чтобы оно покинуло замкнутую орбиту и смогло улететь от небесного тела за пределы его гравитационного поля.
Иными словами, для Земли, это та скорость, с которой должны двигаться космические аппараты (КА) для полетов к другим объектам Солнечной системы: Луны, Марса и т.д.
Движение тела на второй космической скорости происходит по параболической траектории.
Впервые такую скорость развил Советский космический аппарат Луна-1 2 января 1959 года, чтобы преодолеть расстояние от Земли до Луны и изучить наш естественный спутник.
Расчет
Третья космическая скорость
Такую скорость необходимо придать телу, чтобы оно смогло покинуть Солнечную систему. Так как 99,8% массы Солнечной системы приходится на Солнце, то можно сказать, что КА надо преодолеть гравитационное притяжение Солнца.
Расчет
Для Солнечной системы это величина равна 16,650 км/с.
Самое выгодное расположение космодрома для подобного запуска – максимально близко к экватору, так как на экваторе самая большая скорость собственного вращения Земли вокруг своей оси и направление движения в сторону вращения Земли и в сторону орбитального движения Земли по орбите.
КА «Новые горизонты» покинул атмосферу Земли со скоростью близкой к третьей космической – 16,26 км /с. Относительно Солнца он имел скорость 45 км/с. Такой скорости недостаточно, чтобы покинуть Солнечную систему. Но благодаря гравитационному маневру у Юпитера, «Новые горизонты» добавил еще 4 км/с, что позволило ему покинуть Солнечную системы, предварительно показав нам карликовую планету Плутон.
Четвертая космическая скорость
Эта та скорость, которая позволит покинуть галактику в данной точке.
Четвертая космическая в основном не зависит от месторасположения Земли в Млечном пути. Она зависит от расположения и плотности звездного вещества в окрестностях Солнечной системы. А эти данные пока мало изучены.
Для нашей части галактики четвертая космическая скорость примерно равна 550 км/с.
Пятая космическая скорость
Эта скорость редко применима и является больше «фантазией», так как такую скорость необходимо развить для путешествия на другую планету в другую звездную систему, независимо от их взаимного расположения, с траекторией перпендикулярно плоскости эклиптики.
Для Земли эта скорость будет равна 43,6 км/с.
Почему спутники не падают на Землю
Этот вопрос поднимался в самом начале статьи. Теперь давайте на него ответим.
На спутник на орбите действует сила тяжести со стороны Земли. И под действием этой силы спутнику логичнее упасть.
Но, он летит вокруг Земли с первой космической скоростью – 7,9 км/с. Вспомните, чем больше скорость – тем сложнее затормозить. Вот и здесь, спутник и хотел бы упасть, но он не может затормозить и просто пролетает мимо Земли по инерции, тем самым продолжая бесконечное падение.
То есть, спутники падают, но промахиваются и не попадают в Землю.
Еще больше космоса и интересных фактов в телеграмм-канале.