Извлечение корня из комплексных чисел
Чтобы извлечь корень n из комплексного числа необходимо:
- Найти модуль комплексного числа |z|.
- Найти аргумент комплексного числа φ.
Затем записать ответ в виде
- Решение онлайн
- Видеоинструкция
Например, для необходимо ввести 1+i и 3. Корень числа вводится как sqrt, например sqrt(3).
см. также Как решать уравнения с комплексными числами, Алгебраическая форма записи комплексного числа.
Все вычисления с комплексными числами можно проверить в онлайн режиме с помощью калькулятора Web2.
Примечание:
- abs — модуль комплексного числа |z|. Пример:
abs(-5.5-6.6i) - arg — аргумент комплексного числа φ. Пример:
arg(5.5+6.6i)
Пример №1. Найдите .
Решение:
Находим тригонометрическую форму комплексного числа z = 1 + i: x = Re(z) = 1, y = Im(z) = 1 > 0,
,
.
Таким образом, – тригонометрическая форма комплексного числа z = 1 + i.
Извлекаем (k = 0, 1, 2). Итак,
Пример №2. Найдем корень из комплексного числа. . Для этого перейдем в тригонометрическую форму
x=-1, y=-1.
,
.
Такой тангенс у двух углов и
.
Так как х и у отрицательны, то угол находится в третьей четверти . n=3,
m=0,1,2.
Подставим m=0
Подставим m=1
Подставим m=2
Онлайн калькулятор предназначен для вычисления корня
-ой степени из комплексного числа, с описанием подробного хода решения на русском языке. Для нахождения корня
-ой степени, сначала необходимо выбрать (алгебраическую, тригонометрческую или показательную)
форму представления комплексного числа. Далее приведены минимальные теоретические сведения, необходимые для понимания решения, выдаваемого калькулятором.
Согласно теории, корень
-ой степени из любого числа
()
имеет ровно
значений. Например:
Пример, по интереснее:
где
— мнимая единица. Можете попробовать возвести все значения в куб, и действительно получите
. Возникает вопрос: как найти все
значений корня
-ой степени из числа? Для этого необходимо использовать формулу Муавра, причем комплексное число должно быть записано в тригонометрической форме. Наш калькулятор автоматически осуществит перевод введенного числа в тригонометрическую форму, если потребуется.
Комплексные числа по-шагам

Примеры комплексных выражений
- Деление комплексных чисел
-
(1-2i)/(1+4i)
- Умножение комплексных чисел
-
(5+4i)*(8-2i)
- Комплексные уравнения
-
z - |z| = 2 + i
-
(i + 5)*z - 2*i + 1 = 0
- Возведение комплексного числа в степень
-
i^15
-
(1 - 2*i)^32
- Квадратный корень из комплексного числа
-
sqrt(1-24*i)
- Кубический корень
-
cbrt(1-24*i)
- Корни четвертой и пятой степени
-
(1-11*i)^(1/4)
-
(1-11*i)^(1/5)
- Мнимая и действительная часть
-
im(re(x) + y)
- Комплексно-сопряженное число
-
conj(1 + 4j)
-
(3/2-3*sqrt(3)/2*i)/conj(-5/2-1/3*i)
- Реальная часть комплексного числа
-
re(1+I)
- Мнимая часть
-
im(1+I)
- Модуль комплексного числа
-
absolute(1+I)
- Аргумент
-
arg(1+I)
- Комплексный знак числа
-
sign(1+I)
Что умеет?
- Простые операции с комплексными числами
- Выполнять деление с подробным решением
- Находить разные формы комплексных чисел:
- Алгебраическую
- Тригонометрическую
- Показательную
- Модуль и аргумент комплексного числа
- Комплексно-сопряжённое к данному
- Геометрическую интерпретацию комплексного числа
Подробнее про Комплексное число
.
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- — умножение
- 3/x
- — деление
- x^2
- — возведение в квадрат
- x^3
- — возведение в куб
- x^5
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- — число Пи
- e
- — основание натурального логарифма
- i
- — комплексное число
- oo
- — символ бесконечности
Комплексные корни
Решение уравнений
При решении многих задач в математике, физике, электротехнике часто возникает необходимость в решении уравнений с комплексными корнями, извлечении корней из комплексных чисел.
Пусть дано комплексное число z, из которого надо извлечь корень n. Для этого находим модуль |z| и аргумент (ф) комплексного числа.
Корень числа находим по формуле:
Результатом решения квадратных уравнений вида ах2 + by + с = 0 с комплексными коэффициентами являются комплексные корни 2-го порядка.
Для решения квадратного трехчлена необходимо вычислить дискриминант (D):
D = b2 — 4ac, затем найти корни, которые зависят от знака D. Квадратное уравнение имеет 2 корня.
- если D больше 0, уравнение имеет 2 вещественных корня;
- при D = 0 у уравнения 1 корень х = -b / 2а;
- при D меньше 0 — 2 мнимых корня (вещественных корней нет).
Общая формула:
Любое уравнение вида имеет п комплексных корней. Часть из них, возможно и все, — действительные.
Существует универсальный способ извлечения корней из любого комплексного числа.
Пусть дано уравнение , где w — комплексное число. Найти все n корней уравнения (z0, z1, z2, …z n-1) можно по формуле:
|w| — модуль комплексного числа w, ф — его аргумент, k = 0, 1, 2, …n-1
С помощью онлайн калькулятора вы сможете быстро вычислять комплексные корни заданного многочлена.
Комплексные корни и степени чисел онлайн
| Основание степени. Произвольное число |
| Значение степени. В том числе комплексное число |
| Точность вычисления. Количество знаков после запятой |
| Вы ввели следующее выражение |
| Результат вычисления степени |
| Результат выражения (альтернативный вывод) со всеми корнями |
Этот онлайн калькулятор рассчитывает любые степени действительных или комплексных чисел.
Поможет Вам рассчитать корень комплексного числа, возвести в степень действительное или комплексное выражение.
Рассчитывает степень любого числа
Хотелось бы заметить, что возведение любого действительного числа в дробную степень, не так сложно как может показаться на первый взгляд.
то есть, если мы хотим возвести число 3 в степень
то решение такое
Итого
Если речь идет о комплексных числах, то возведение степень и извлечени корня осуществляется по уравнению Муавра.
Формулы следующие:
Для возведения в степень

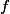
Для извлечения корня
где p = 0, 1, …, k—1.
Есть еще третий возможный вариант, когда не только основание является комплексным числом, но и степень этого числа также число комплексное.
Конечно возникает желание использовать формулу Муавра и преобразовать её, для наших нужд, но мы воспользуемся первым вариантом вычисления степеней.
то есть вот этой формулой
Формула расчета логарифа комплексного числа известна
здесь k — может принимать любые целые значения, поэтому говорят, что логарифм комплексного числа многозначен.
Для практических целей используется главное значение(k=0)
Формула расчета экспоненты комплексного числа тоже
Таким образом у нас есть всё, что бы рассчитать на практике комплексную степень комплексного числа.
Синтаксис
Если используете XMPP клиент: step_i <запрос>
Если используете этот сайт: <запрос>
где запрос — состоит из двух чисел. Сначала идет основание потом в другом окне степень.
Основание может быть как действительным числом так и комплексным, положительным или отрицательным
Комплексное значение пишется как x:y где х- действительная часть числа, а y- мнимая часть, но можно написать и в нормальном виде через символ i
Степень может быть быть целым числом,как положительным так и отрицательным.
Степень может быть выражена также степенью двух целых чисел например 1/2 или -5/7. В таком случае альтернативный вывод покажет Вам, все 2 или все 7 корней соответственно.
Степень может быть комплексным числом записанным как в нормальной форме через символ i, так и через сокращенную запись x:y, где x- действительная часть числа, y — мнимая часть числа
Замечание: В поле можно вводить только числа и никак не выражение, если у Вас есть желание посчитать вот такое выражение
то эта страница вам не поможет, Вам надо использовать универсальный калькулятор комплексных чисел
где x- это основание, а y-степень
Примеры
Например: взять степень 2/5 от комплексного числа 1-2.5i
Пишем 1:-2.5 2/5 или если делаете запрос через Jabber step_i 1:-2.5 2/5
Ответ получим
Комплексное число 1:-2.5 в степени 2/5 равно
Действительная часть: 1.3209 Комплексная часть: -0.6812
Действительная часть: 1.0560 Комплексная часть: 1.0457
Действительная часть: -0.6682 Комплексная часть: 1.3275
Действительная часть: -1.4690 Комплексная часть: -0.2253
Действительная часть: -0.2396 Комплексная часть: -1.4667
Интересно, а чему будет равна мнимая единица в степени мнимой единицы?
пишем i i
и получаем что
возведем еще одно число в комплексную степень.
число 1+i в комплексную степень 1-i
результат вот такой

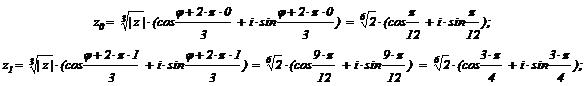
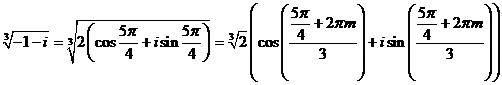
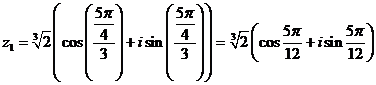
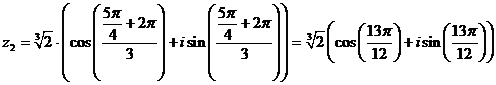
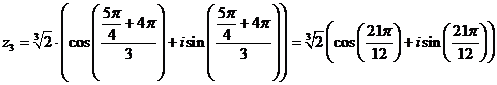
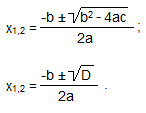
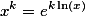
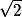
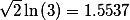
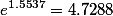
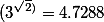
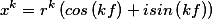
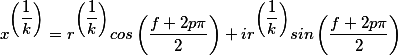
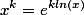
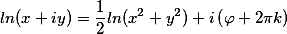
)
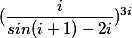
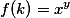
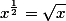
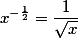
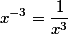
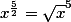

^{1-i}=2.8078792972606+1.3178651729012i)