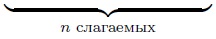При
решении задач на смешанное соединение проводников обычно составляют так
называемые эквивалентные схемы, выделяя участки с последовательным и
параллельным соединением.
Пример
1.
Сопротивление R1,2 заменило
выделенный участок цепи, в котором два проводника соединены параллельно.
Тогда
мы можем найти сопротивление этого участка с параллельным соединением
проводников:
А теперь видно,
что проводники R1,2 и R3 соединены
последовательно. Общее сопротивление равно R = R1,2 + R3 = 4 +
2 = 6.
Пример
2.
В данном случае
нужно развернуть схему, двигаясь от точки к точке. Видно, что в точке Б схема
разветвляется, а в точке В ветви соединяются. Таким образом,
эквивалентные схемы будут иметь вид:
R2, R3 и R4 соединены
последовательно. Поэтому R2,3,4 = R2 + R3 + R4 = 1 + 10
+ 1 = 12
R2,3,4 и R5 соединены
параллельно. Поэтому
И в последней
схеме проводники соединены последовательно. R = R2-5 + R1 + R6 = 1 + 4,8
+ 1 = 6,8.
Пример
3.
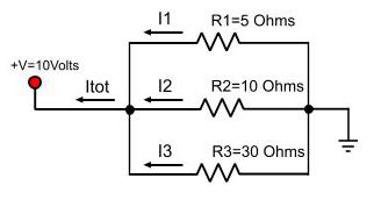
Найти распределение токов и напряжений в цепи.
Решение.
Так
как известны сила тока и сопротивление на первом участке, то можно найти
напряжение на нем: U1 = I1 R1 = 1 ∙ 10
= 10 B.
Первый
и второй проводники соединены параллельно. Значит, напряжение на них одинаково,
т.е. U1 = U2 = 10 В. Так
как первый и второй проводники имеют одинаковое сопротивление, то сила
тока на них одинакова: I2 = 1 А. При
параллельном соединении I1,2 = I1 + I2 = 2 А.
Участки
1-2, 3-4-5 и 6-7 соединены последовательно между собой, значит I3,4,5 = I6,7 = I1,2 = 2 A.
Найдем
общее сопротивление участка 3-4-5:
R3,4,5
= 3 Ом.
Тогда можно найти напряжение на 3-4-5, при параллельном соединении оно
одинаково на всех участках. U3,4,5 = I3,4,5 ∙R3,4,5 = 2 ∙ 3 =
6 В.
U3 = U4 = U5 = 6 В. Зная
напряжение на каждом из участков и сопротивление, можно найти силу тока на
каждом участке.
Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.).
Определение эквивалентного сопротивления
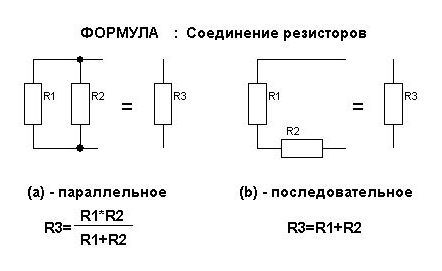
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.
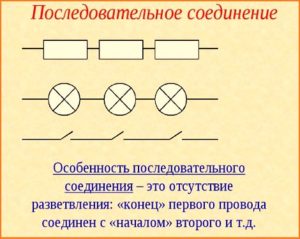
Последовательное соединение элементов
Параллельное соединение резисторов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
I = U/R.
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
R = U/I.
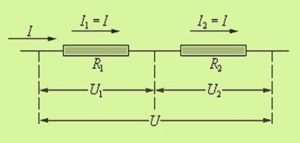
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
I = I1= I2= … = In.
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
U = U1 + U2+ … + Un.
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Схема смешанного соединения резисторов
Схема смешанного соединения обладает свойствами схем последовательного и параллельного соединения резисторов. В этом случае элементы частично подключаются последовательно, а другая часть соединяется параллельно. На представленной схеме резисторы R1 и R2 включены последовательно, а резистор R3 соединен параллельно с ними. В свою очередь резистор R4 включается последовательно с предыдущей группой резисторов R1, R2 и R3.
Расчет сопротивления для такой цепи сопряжен с определенными трудностями. Для того чтобы правильно выполнить расчеты используется метод преобразования. Он заключается в последовательном преобразовании сложной цепи в простейшую цепь за несколько этапов.
Если для примера вновь использовать представленную схему, то в самом начале определяется сопротивление R12 резисторов R1 и R2, включенных последовательно: R12 = R1 + R2. Далее, нужно определить сопротивление резисторов R123, включенных параллельно, по следующей формуле: R123=R12R3/(R12+R3) = (R1+R2)R3/(R1+R2+R3). На последнем этапе выполняется расчет эквивалентного сопротивления всей цепи, путем суммирования полученных данных R123 и сопротивления R4, включенного последовательно с ним: Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4.
В заключение следует отметить, что смешанное соединение резисторов обладает положительными и отрицательными качествами последовательного и параллельного соединения. Это свойство успешно используется на практике в электрических схемах.
Параллельное соединение резисторов
Напряжение при последовательном и параллельном соединении резисторов
Параллельное соединение
КПД источника тока
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.
Практическое применение
Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
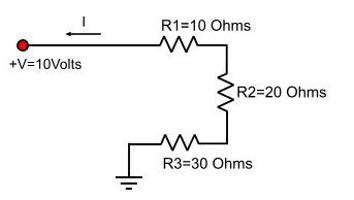
Простое соединение
Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
Советуем изучить Управляемый стабилизатор напряжения tl431 (on semiconductor)
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Расчёт при смешанном соединении устройств
Внутреннее сопротивление — формула
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Расчет смешанного соединения резисторов.
Расчет начинают от дальнего участка цепи по отношению к источнику питания. Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ
. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.
Суть данного метода заключается в уменьшении
количества элементов в цепи с целью
упрощения схемы
и, соответственно, упрощению расчета общего сопротивления.
Разберем схему смешанного соединения из семи резисторов
:
Самым дальним участком схемы оказались резисторы R6
и
R7
, соединенные
параллельно
:
Вычисляем их общее сопротивление используя формулу параллельного
соединения:
Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6
с суммарным сопротивлением равным
30, 709 кОм
.
Продолжим расчет и следующим дальним участком схемы оказались резисторы R5
и
R6
, соединенные
последовательно
:
Вычисляем их общее сопротивление используя формулу последовательного
соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):
Схема уменьшилась еще на один элемент и приняла вид:
Теперь дальним участком оказались резисторы R4
и
R5
соединенные
параллельно
:
Вычисляем их общее сопротивление:
Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно
. Таким образом мы максимально упростили схему и привели ее к удобному расчету.
Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного
соединения, и получаем общее сопротивление всей цепи:
Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения. Удачи!
Источник
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
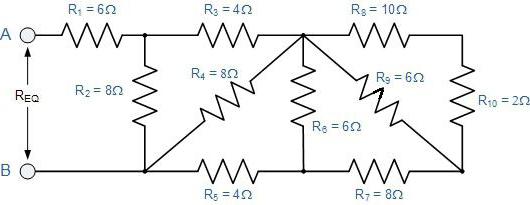
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
U = 24 В.
Требуется рассчитать токи на всех резистивных элементах.
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD:
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Задана электрическая цепь постоянного тока смешанного соединения,состоящая из 10 резисторов. Значения сопротивления резисторов и номер схемы для соответствующего варианта указаны в таблице №1.
Определить: эквивалентное сопротивление участка цепи Rэкв ; мощность P, напряжение U, силу тока I на входе цепи; токи Ii и напряжения Ui на всех элементах цепи. В ходе решения выполнить несколько проверок полученных результатов по законам Кирхгофа.
Таблица №1
| №
варианта |
№
схемы |
P | U | I | R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 |
| Вт | В | А | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | ||
| 1 | 1 | ? | 150 | ? | 6 | 3 | 8 | 12 | 15 | 12 | 2 | 10 | 15 | 5 |
| 2 | 2 | ? | 300 | ? | 10 | 40 | 2 | 10 | 20 | 15 | 60 | 7 | 15 | 30 |
| 3 | 3 | ? | 240 | ? | 20 | 30 | 60 | 20 | 20 | 5 | 25 | 50 | 8 | 36 |
| 4 | 4 | ? | 360 | ? | 2 | 5 | 3 | 20 | 60 | 30 | 7 | 15 | 60 | 6 |
| 5 | 5 | ? | 200 | ? | 2 | 13 | 30 | 10 | 20 | 4 | 8 | 3 | 6,5 | 60 |
| 6 | 6 | ? | 300 | ? | 10 | 20 | 60 | 4 | 5 | 15 | 45 | 6 | 2 | 3 |
| 7 | 7 | ? | 500 | ? | 3 | 15 | 15 | 8 | 7 | 10 | 10 | 10 | 30 | 20 |
| 8 | 8 | ? | 300 | ? | 20 | 5 | 4 | 8 | 7 | 3 | 15 | 30 | 6 | 10 |
| 9 | 9 | ? | 600 | ? | 15 | 30 | 15 | 10 | 40 | 10 | 45 | 2 | 9 | 5 |
| 10 | 10 | ? | 300 | ? | 0,2 | 0,8 | 2 | 4 | 5 | 6 | 30 | 60 | 2 | 15 |
| 11 | 11 | ? | 360 | ? | 60 | 12 | 15 | 30 | 15 | 3 | 1 | 60 | 5 | 30 |
| 12 | 12 | ? | 150 | ? | 5 | 8 | 10 | 20 | 40 | 23 | 25 | 5 | 15 | 35 |
| 13 | 1 | ? | ? | 40 | 15 | 30 | 20 | 30 | 20 | 12 | 10 | 5 | 10 | 60 |
| 14 | 2 | ? | ? | 40 | 3 | 6 | 8 | 10 | 20 | 15 | 60 | 17 | 10 | 60 |
| 15 | 3 | ? | ? | 20 | 10 | 20 | 60 | 15 | 30 | 4 | 30 | 60 | 2 | 60 |
| 16 | 4 | ? | ? | 18 | 15 | 5 | 40 | 10 | 20 | 30 | 10 | 15 | 30 | 4 |
| 17 | 5 | ? | ? | 100 | 10 | 10 | 20 | 5 | 8 | 8 | 20 | 1 | 1 | 6 |
| 18 | 6 | ? | ? | 100 | 6 | 24 | 8 | 40 | 20 | 20 | 10 | 7,5 | 15 | 7,5 |
| 19 | 7 | ? | ? | 50 | 5 | 15 | 15 | 7 | 8 | 5 | 10 | 15 | 6 | 3 |
| 20 | 8 | ? | ? | 20 | 20 | 4 | 5 | 1 | 3 | 5 | 30 | 15 | 14 | 6,6 |
| 21 | 9 | ? | ? | 20 | 6 | 3 | 8 | 9 | 4,5 | 10 | 7 | 7 | 4 | 4 |
| 22 | 10 | ? | ? | 30 | 1 | 2 | 3 | 4 | 5 | 30 | 60 | 3 | 2 | 4/3 |
| 23 | 11 | ? | ? | 20 | 6 | 8 | 24 | 6 | 3 | 4 | 5 | 30 | 10 | 60 |
| 24 | 12 | ? | ? | 80 | 1 | 2 | 3 | 12 | 12 | 0,5 | 5 | 6 | 7 | 2 |
| 25 | 1 | ? | ? | 20 | 10 | 15 | 14 | 12 | 15 | 20 | 4 | 7 | 15 | 30 |
| 26 | 2 | 1620 | ? | ? | 6 | 3 | 3 | 2 | 5 | 30 | 15 | 14 | 20 | 12 |
| 27 | 3 | 2000 | ? | ? | 60 | 10 | 20 | 40 | 10 | 1 | 20 | 12 | 5 | 10 |
| 28 | 4 | ? | ? | 30 | 5 | 10 | 15 | 15 | 30 | 15 | 10 | 20 | 12 | 3 |
| 29 | 5 | 3200 | ? | ? | 20 | 15 | 10 | 12 | 15 | 20 | 30 | 2 | 5 | 40 |
| 30 | 6 | ? | 280 | ? | 20 | 4 | 5 | 20 | 40 | 20 | 10 | 12 | 4 | 6 |
| 31 | 7 | 50000 | ? | ? | 22 | 2 | 8 | 5 | 15 | 10 | 20 | 30 | 10 | 40 |
| 32 | 8 | 1440 | ? | ? | 20 | 60 | 10 | 0,4 | 0,6 | 1 | 15 | 30 | 9 | 4 |
| 33 | 9 | ? | ? | 40 | 15 | 30 | 15 | 10 | 40 | 10 | 45 | 2 | 9 | 5 |
| 34 | 10 | 2250 | ? | ? | 2 | 3 | 10 | 10 | 12 | 15 | 20 | 30 | 10 | 8 |
| 35 | 11 | ? | ? | 16 | 60 | 12 | 15 | 30 | 15 | 3 | 1 | 60 | 5 | 30 |
| 36 | 12 | 1280 | ? | ? | 5 | 8 | 10 | 20 | 40 | 10 | 15 | 8 | 10 | 12 |
ЗАДАЧА №2. Однофазные цепи переменного тока.
Неразветвлённая цепь переменного тока, показанная на соответствующем рисунке, содержит активные и реактивные сопротивления, величны которых заданы в таблице №2. Кроме того извесен один из дополнительных параметров. Определить следующие величины, если они не заданы в таблице параметов.
1. полное сопротивление цепи Z;
2. напряжение, приложенное к цепи U;
3. силу тока в цепи I;
4. сдвиг фаз φ;
5. активную P, реактивную Q и полную S мощности, потребляемые цепью;
6. начертить в масштабе векторную диаграмму и пояснить ее построение.
Таблица №2
| №
варианта |
№
схемы |
R1 | R2 | Дополнительный параметр | ||||
| Ом | Ом | Ом | Ом | Ом | Ом | |||
| 1 | 1 | 8 | 4 | 18 | — | 2 | — | I = 10 A |
| 2 | 2 | 16 | — | 5 | 6 | 8 | — | Q= 135 ВАР |
| 3 | 3 | 4 | — | 9 | — | 3 | 3 | U = 20 B |
| 4 | 4 | 10 | 14 | 18 | — | 20 | 30 | UR2 = 28 B |
| 5 | 5 | 32 | — | 20 | 20 | 6 | 10 | I = 4 A |
| 6 | 6 | 4 | — | 5 | 6 | 3 | — | I = 5 A |
| 7 | 7 | 8 | — | 12 | — | — | 6 | P = 72 Вт |
| 8 | 8 | 2 | 6 | — | 10 | 4 | — | U = 20 B |
| 9 | 9 | 3 | — | — | — | 1 | 4 | Q= 125 ВАР |
| 10 | 10 | 8 | — | — | — | 4 | 2 | U = 80 B |
| 11 | 1 | 1 | 2 | 8 | — | 4 | — | S = 1000 ВА |
| 12 | 2 | 3 | — | 10 | 12 | 26 | — | P1 = 48 Вт |
| 13 | 10 | 12 | — | 22 | — | 2 | 4 | P = 72 Вт |
| 14 | 3 | 40 | — | 50 | — | 12 | 8 | QL1 = 48 ВАР |
| 15 | 4 | 40 | 20 | 20 | — | 80 | 20 | QC1 = — 320 ВАР |
| 16 | 5 | 32 | — | 25 | 15 | 8 | 8 | UL1 = 125 B |
| 17 | 6 | 8 | — | 10 | 15 | 9 | — | QC1 = — 320 ВАР |
| 18 | 7 | 4 | — | 5 | — | — | 9 | P = 256 Вт |
| 19 | 8 | 10 | 6 | — | 20 | 8 | — | I = 4 A |
| 20 | 9 | 8 | — | — | — | 4 | 2 | S = 50 ВА |
| 21 | 10 | 4 | — | 10 | — | 3 | 4 | P = 64 Вт |
| 22 | 1 | 8 | 4 | 6 | — | 22 | — | P1 = 32 Вт |
| 23 | 2 | 4 | — | 3 | 6 | 12 | — | S = 500 ВА |
| 24 | 3 | 12 | — | 16 | — | 10 | 6 | UL2 = 160 В |
| 25 | 4 | 6 | 2 | 10 | — | 1 | 3 | P = 200 Вт |
| 26 | 5 | 80 | — | 10 | 10 | 40 | 40 | QL2 = 40 ВАР |
| 27 | 6 | 4 | — | 10 | 15 | 9 | — | Q= 1600 ВАР |
| 28 | 7 | 4 | — | 5 | — | — | 8 | Q= -192 ВАР |
| 29 | 8 | 6 | 2 | — | 4 | 10 | — | Q= -24 ВАР |
| 30 | 9 | 16 | — | — | — | 8 | 4 | P = 64 Вт |
| 31 | 10 | 12 | — | 4 | — | 12 | 8 | U = 100 B |
| 32 | 1 | 2 | 2 | 4 | — | 8 | — | Q1 = -96 ВАР |
| 33 | 2 | 8 | — | 2 | 2 | 10 | — | QC1 = — 20 ВАР |
| 34 | 3 | 24 | — | 28 | — | 35 | 25 | S = 1000 ВА |
| 35 | 4 | 30 | 34 | 32 | — | 50 | 30 | UC1 = 500 В |
| 36 | 5 | 40 | — | 10 | 10 | 20 | 20 | QL2 = 20 ВАР |
ЗАДАЧА №3. Трехфазные цепи переменного тока.
Три группы сопротивлений соединили «звездой» с нулевым проводом и включили в трехфазную сеть переменного тока с линейным напряжением Uл ном. Активные сопротивления в фазах А, В и С соответственно равны RA, RB, RC; реактивные – XA, XB, Xc. Характер реактивных сопротивлений указан на схеме цепи (индуктивное или ёмкостное). Линейные токи в нормальном режиме равны IA, IB, IC. Фазы нагрузки потребляют активные мощности PA, PB, PC и реактивные мощности QA, QB, QC. Начертить схему цепи для каждого варианта. Определить величины, отмеченные в таблице №3 прочерками. Начертить в масштабе векторную диаграмму цепи. Из векторной диаграммы определить ток в нулевом проводе.
Таблица №3
Это
комбинация последовательного и
параллельного соединения сопротивлений.
Рассмотрим способы расчета смешанного
соединения:
1).
Вычисление эквивалентного сопротивления.
2).
Определение токов по формуле «разброса»
Поливанова.
3).
Определение токов методом подобия или
пропорциональных величин.
1.
Рис. 1.10
R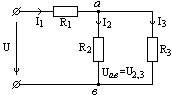
;RЭ=R1+R2,3;
I1=;U2,3
=
I1R2,3
=
U – I1R1;
Рис.
1.10
I2=,I3=
,I1
=
I1
+
I3
проверка.
2.
Рис. 1.10
R=R1+
,
где
Ri
Rk
– сумма попарных произведений из трех
сопротивлений.
|
I |
U |
|
I |
В |
|
I |
3. Метод применим
только для линейных цепей, т.е. таких в
которыхR, L,
Состаются постоянными и не зависят
от величины проходящего через них тока
[3].
Для
этих цепей при смешанном соединении
ток любой ветви пропорционален входному
напряжению Ik
= ak
U,
при этом ак
для
каждой ветви имеет свое значение (см.
формулы Поливанова).
Метод
имеет смысл применять для смешанного
соединения с большим количеством ветвей,
если требуется определить сразу токи,
не вычисляя R,
например для следующей схемы (рис. 1.11):
|
Рис. |
При (I |
Затем,
используя законы Ома и Кирхгофа, находят
токи и напряжения на остальных участках,
постепенно приближаясь к источнику.
Наконец находят новое значение входного
напряжения U,
вычисляют коэффициент подобия К=и на него умножают все ранее вычисленные
токи и напряжения.
2. Расчет сложных цепей
Сложной
называется такая электрическая цепь,
которая не может быть сведена к смешанному
соединению сопротивлений. К сложным
относятся также цепи, содержащие
источники энергии в разных параллельных
ветвях.
Примером
сложной цепи может быть мостовая схема.
Существует
несколько методов расчета сложных
цепей, но все они основаны на законах
Кирхгофа.
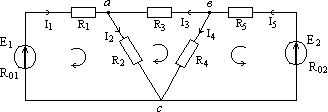
2.1. Непосредственное применение законов Кирхгофа
Пусть
дана следующая цепь (рис. 2.1):
Рис.
2.1
Произвольно
намечают стрелками направление токов
в ветвях и круговыми стрелками направление
обхода независимых контуров.
Число неизвестных
токов будет равно числу ветвей. Вначале
составляем уравнения по Iзакону Кирхгофа. Их число равно числу
узлов без одного (независимые уравнения).
Остальные
уравнения составляются по II закону
Кирхгофа с соблюдением знаков (+) и ()
для ЭДС и токов в зависимости от
направления обхода контура [4].
С
учетом сказанного составляем систему
уравнений для заданной схемы:
I
I2
+
I3
=
0,
I5–I3–I4=0,
I1(R01
+
R1)
+ I2R2
=
E1,
(2.1)
I4R4
–
I2R2
–
I3R3
=
0,
I5(R02
+
R5)
+
I4R4
=
E2.
Решая
эту систему, сразу находим токи в ветвях.
Если ток получается с (),
то его истинное направление противоположно
выбранному.
Сложную систему
уравнений надо решать с помощью
определителей
Ik=
,
или иным математическим
способом.
2.2 Метод контурных токов
Для
сложных цепей, содержащих более 2-х
узлов, метод контурных токов является
наиболее простым и универсальным, ибо
он значительно сокращает число уравнений
по сравнению с непосредственным
применением законов Кирхгофа. Впервые
предложен Максвеллом.
Для примера
рассчитаем сложную цепь предыдущего
раздела.
Сущность
метода заключается в том, что сложная
цепь рассматривается как совокупность
соприкасающихся ячеек или контуров
(отличие от независимых контуров
предыдущего метода).
Каждой
ячейки приписывается некоторый контурный
ток произвольного направления, а ток в
общей ветви находится, как алгебраическая
сумма контурных токов (рис. 2.2). При таком
условии I-й
закон Кирхгофа удовлетворяется
автоматически и составлять по нему
уравнение не надо (Iк
= 0,
превращается в тождество 0
= 0).
Однако,
при составлении уравнений по II закону
Кирхгофа нужно помнить одну особенность.
Алгебраическая сумма ЭДС каждой ячейки
равна алгебраической сумме произведений:
а)
контурного тока данной ячейки на сумму
сопротивлений всех ветвей этой ячейки;
б)
контурных токов всех ячеек, смежных с
данной, на соответствующие сопротивления
общих ветвей. Правило знаков ЭДС и токов
остается прежним, причем контур обходится
в направлении собственного контурного
тока.

(R01+R1+R2)IbR2=E1, Iста=Ia, Iас=Ia–Ib,
Ib
(R2+R3+R4)–IaR2+IcR4=0, Iав=Ib, Iбс=Ib+Ic,
(2.1)
Ic
(R02+R5+R4)+IbR4=E2. Iспб=Ic.
Токи
во внешних ветвях цепи равны соответствующим
контурным, в общих ветвях – их
алгебраическая сумма [5]. Число ячеек
всегда значительно меньше числа ветвей,
отсюда число уравнений в системе меньше,
чем при непосредственном применении
законов Кирхгофа (3 вместо 5 в приведенном
примере).
Сложную систему
уравнений лучше решать с помощью
определителей.
Соседние файлы в папке Практикум
- #
- #
Смешанное соединение
Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
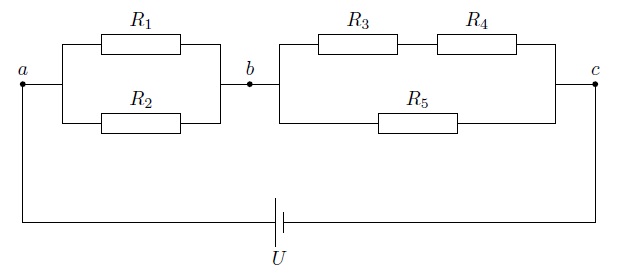
Рассмотрим пример смешанного соединения проводников (рис. ).
Рис. Смешанное соединение
Пусть
В,
Ом,
Ом,
Ом,
Ом,
Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков
и
. Сопротивление участка
:
Ом.
Участок
является параллельным соединением: два последовательно включённых резистора
и
подключены параллельно к резистору
. Тогда:
Ом.
Сопротивление цепи:
Ом.
Теперь находим силу тока в цепи:
A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:

B.
(Заметим попутно, что сумма этих напряжений равна
В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора
и
находятся под напряжением
, поэтому:

A.
(В сумме имеем
А, как и должно быть при параллельном соединении.)
Сила тока в резисторах
и
одинакова, так как они соединены последовательно:
А.
Стало быть, через резистор
течёт ток
A.
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Последовательное и параллельное соединение резисторов
Напряжение при последовательном и параллельном соединении резисторов
Какое соединение проводников называется параллельным
Сопротивление при последовательном и параллельном соединении резисторов
Параллельное соединение
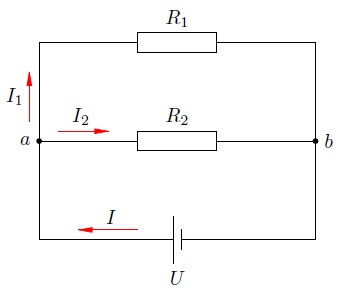
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).
Рис. 5. Параллельное соединение
Резисторы подсоединены к двум точкам:
и
. Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от
к
(по направлению тока) называется неразветвлённой частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.
1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения
и
на резисторах
и
равны разности потенциалов между точками подключения:
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку
за время
из неразветвлённого участка поступает заряд
. За это же время
из точки
к резистору
уходит заряд
, а к резистору
— заряд
.
Ясно, что
. В противном случае в точке
накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:
что и требовалось.
3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть
— сопротивление разветвлённого участка
. Напряжение на участке
равно 
. Поэтому:
Сокращая на
, получим:
(1)
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами
, но разными поперечными сечениями
и
. Тогда это соединение можно рассматривать как проводник той же длины
, но с площадью сечения
. Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти
:
(2)
К сожалению, в общем случае
параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
(3)
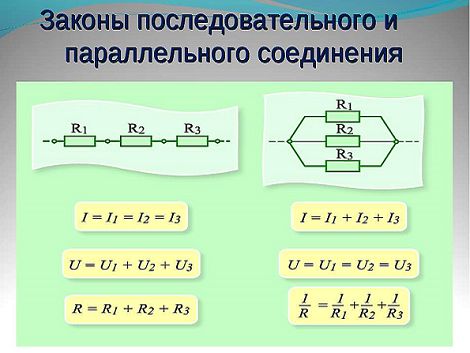
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех
резисторов одинаковы и равны
. Тогда:
откуда
Мы видим, что сопротивление участка из
параллельно соединённых одинаковых проводников в
раз меньше сопротивления одного проводника.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора
и
, соединённых последовательно и подключённых к источнику постоянного напряжения
(рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Рис. 4. Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.
1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике.
Действительно, напряжение
на участке
— это работа поля по переносу единичного заряда из точки
в точку 
на участке
— это работа поля по переносу единичного заряда из точки
в точку
. Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки
в точку
, то есть напряжение
на всём участке:
Можно и более формально, без всяких словесных объяснений:
3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.
Пусть
— сопротивление участка
. По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения
, но с разными длинами
и
.
Сопротивления проводников равны:
Эти два проводника образуют единый проводник длиной
и сопротивлением
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Разница между последовательным и параллельным соединением, преимущества и недостатки
Принципиальные отличия между последовательным и параллельным соединение проводников по ключевым электротехническим параметрам приведены в таблице:
| Параметр/тип соединения | Последовательное | Параллельное |
| Электросопротивление | Равняется сумме электросопротивлений всех электропотребителей. | Меньше значения электросопротивления каждого отдельного из подключенных электроприборов. |
| Напряжение | Равняется совокупному вольтажу всех электропотребителей. | Одинаковая величина на всех участках электроцепи. |
| Сила тока | Одинаковая величина на всех участках электроцепи. | Равняется совокупному значению токов на каждом из приборов. |
За счет своих особенностей каждый из типов сборки цепей имеет свои преимущества и недостатки. Это позволяет использовать данные способы для решения разных электротехнических задач.
Плюсы и минусы последовательного соединения
Основными преимуществам электроцепей из последовательно соединенных приборов являются их следующие особенности:
- простота проектирования и построения схемы;
- низкая стоимость комплектации;
- возможность подключения приборов, рассчитанных на меньшее рабочее напряжение, по сравнению с номинальным напряжением сети;
- выполнение функции регулирования тока – обеспечивает равномерные нагрузки на все приборы.
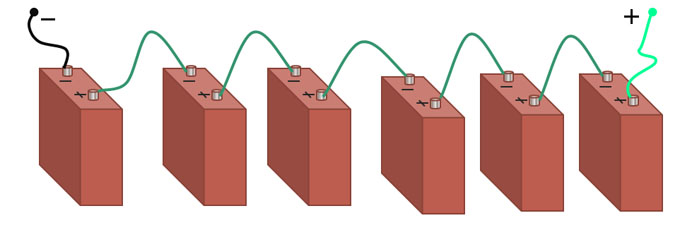
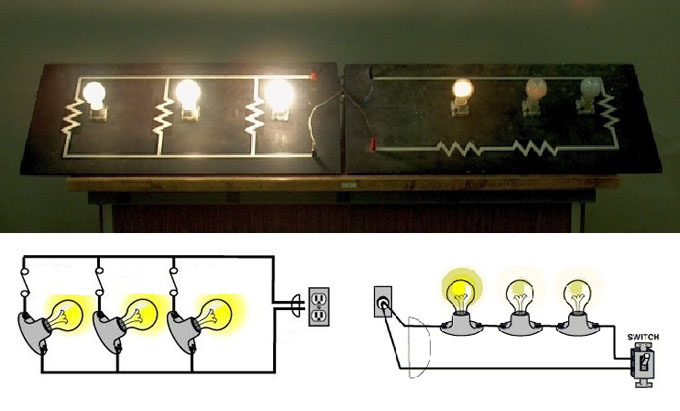
Однако у этого способа компоновки электросхемы есть и серьезные недостатки. Главным из них является ненадежность цепи из последовательно соединенных проводников. При выходе из строя любого из подключенных приборов, происходит отключение всей цепи.
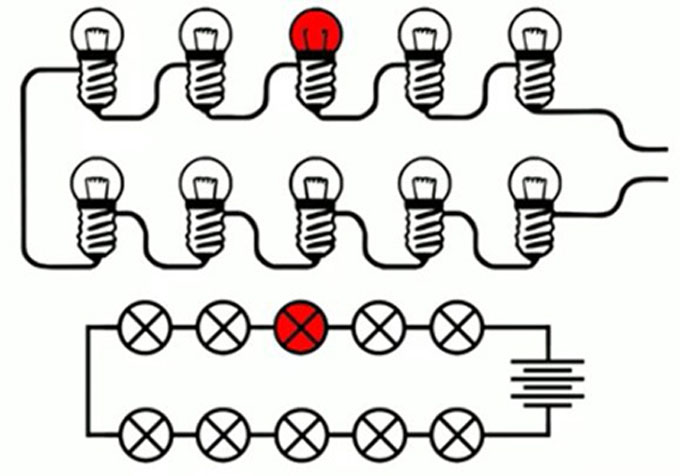
Кроме того, минусом является снижение напряжения при увеличении количества подключенных потребителей. Примером может служить последовательное соединение нескольких ламп. Чем больше осветительных приборов подключено таким способом к источнику электропитания, тем менее яркий свет они будут давать.
Плюсы и минусы параллельного соединения
При использовании параллельного соединения проводников обеспечиваются такой набор преимуществ:
- стабильность напряжения на электроприборах, вне зависимости от их числа;
- возможность включения или отключения отдельных участков в нужный момент без нарушения работы всей электроцепи;
- надежность – при выходе одного или нескольких компонентов из строя сама электроцепь продолжает сохранять работоспособность.

Недостатком является более сложный расчет и сложная схема, использование которой повышает стоимость комплектации электросети.
Не допускается подключение приборов, с номинальным рабочим вольтажом меньше сетевого. Параллельное соединение аккумуляторов с разным значением вольтажа связано с перетеканием тока в АКБ с меньшей его величиной, что может вызывать ускоренный износ батареи.
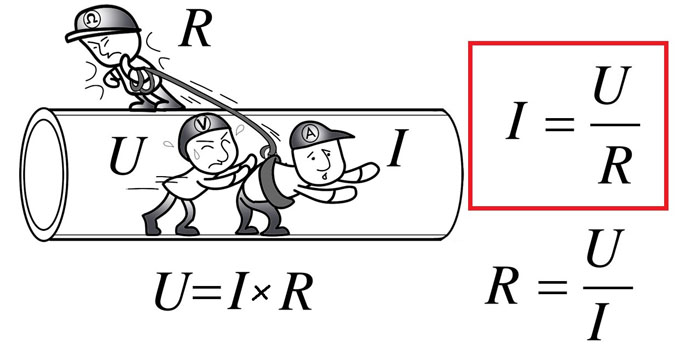
Закон Ома для участка цепи
Одним из ключевых электротехнических законов можно назвать закон Ома для участка цепи. Именно этим законом объясняются отличия, которые существуют для параллельного и последовательного соединения проводников.
Формулируется он таким образом:
Сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника.
Записывается он следующей формулой:
I = U/R, где
I – сила тока, (А);
U – вольтаж, (В);
R – электросопротивление, (Ом).
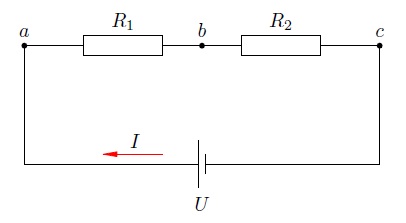
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- Закон ома параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Как различить эти два соединения?
Внимательно посмотрите на схему. Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.
Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.
Формулы для силы тока
О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину силы тока в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.
Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:
Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.
Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при параллельном соединении проводников:
Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.
Формулы для напряжения
Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.
Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:
Другая ситуация складывается, если рассматривается параллельное соединение резисторов. Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:
Формулы для электрического сопротивления
Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.
Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:
- последовательно, значит, нужно равенство для напряжения — Iобщ * Rобщ = I1 * R1 + I2 * R2;
- параллельно необходимо пользоваться формулой для силы тока — Uобщ / Rобщ = U1 / R1 + U2 / R2 .
Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны. Значит, их можно сократить. То есть получаются такие выражения:
- R общ = R 1 + R 2 (для последовательного соединения проводников).
- 1 / R общ = 1 / R 1 + 1 / R 2 (при параллельном соединении).
При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.
Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.
Работа тока
Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t, где А — работа тока, t — время его прохождения по проводнику.
Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U 1 + U 2) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.
Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А 1 + А 2.
Мощность тока
При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I. После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р 1 + Р 2.
То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.
Смешанное соединение проводников в электрической цепи
На практике сборку электроцепей, как правило, проводят таким метод, который предусматривает смешанное соединение проводников. Это комбинированное решение, которое сочетает оба способа. Обычно для монтажа основной сети используют параллель, а отдельные потребители при необходимости объединяют в последовательную сеть.
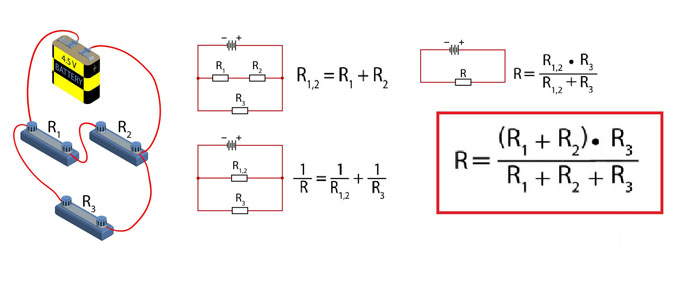
При расчете и сборке смешанных соединений сопротивлений обязательно должны учитываться особенности, преимущества и недостатки обоих методов подключения. В ходе проектирования, схему целесообразно разбить на отдельные части и выполнить расчет в по физическим законам, которые справедливы для последовательного и параллельного соединения. После этого, составные части объединяют в единую схему.
Способы соединения резисторов, решение задачи смешанного соединения проводников: видео
Смешанное соединение резисторов
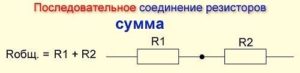
Смешанное соединение резисторов – это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.
Пример цепи со смешанным соединением резисторов:
Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:
Определяется общее сопротивление участков с параллельным соединением резисторов.Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление.После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений.Далее рассчитывается сопротивление полученной простой схемы.Определяется общее сопротивление участков с параллельным соединением резисторов.Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление.После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений.Далее рассчитывается сопротивление полученной простой схемы.
PS:
Параллельное соединение резисторов используется для получения меньшего сопротивления из имеющихся простейших радиоэлектронных элементов. При таком способе соединения складываются проводимости. Поэтому чем больше параллельно включенных резисторов, тем ниже получается общее сопротивление или выше проводимость соответственного участка электрической цепи – носителям электрических зарядов легче его преодолеть.
Последовательное соединение резисторов используется с целью большего ограничения протеканию электрическому току, то есть приводит к повышению сопротивления соответственного участка электрической цепи или для снижения ее проводимости.
Важнейшим параметром резистора является мощность рассеивания. При любом способе соединения, не важно, при последовательном, при параллельном или при смешанном, происходит сложение мощностей рассеивания отдельных резисторов. Поэтому все вместе они способны рассеять больше тепла, а соответственно и пропустить большие токи не перегреваясь, что широко применяется в радиолюбительской практике.
Предыдущая
РазноеЭлектромагнитное излучение – невидимый убийца.
Следующая
РазноеКак правильно соединить провода между собой
Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике. Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов. Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.
Рисунок 1. Соединение резисторов.
Смешанное соединение резисторов. Расчет смешанного соединения
Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.
В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.
Смешанное соединение
встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.
И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.
топологические понятия, элементы, схема замещения
2.Законы Ома и Кирхгофа для цепей постоянного тока
3.Последовательное, параллельное и смешанное соединение потребителей
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
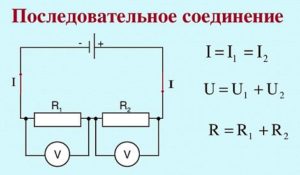
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I. Напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3,
Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
4.Расчёт цепи постоянного тока методами контурных токов и узловых потенциалов
Метод контурных токов. В основе лежит 2-й закон Кирхгофа. Суть метода в ведении фиктивных контурных токов и их расчёт.
1.Определение числа уравнений: у=в-ви.т-(n-1).
В-число ветвей, ви.т-с источником тока,n-число узлов.
2.Составляем уравнения для неизвестных контурных токов в общем виде.
3.Определяем неизвестные коэффициенты левой и правой части (Е и R).
4.Подставив коэффициенты, решаем уравнения, находим токи контуров.
5.Определяем через контурные токи токи в ветвях.
Метод узловых потенциалов. В основе лежит 1-й закон Кирхгофа. Определяем потенциалы узлов цепи с последующим определением токов в ветвях, используя закон Ома для участков цепи.
1.Подготовка схемы. Обозначим узлы. Потенциал одного из них принимаем за 0.
2.Составляем уравнения потенциалов в общем виде:
Фи1*g11 + фи2*g12 = I11 – для первого узла
Фи1g21 + фи*g22 = I22 – для второго узла
3.Определяем неизвестные проводимости gmn –сумма проводимостей ветвей, подходящих к узлу n.
4.Подставив, решаем уравнения, находим фи1 и фи2.
5.Произвольно выбираем направления токов и, используя закон Ома для участка цепи определяем эти токи: In = (фиX-фиY+En)/Rn.
Расчет смешанного соединения резисторов.
Расчет начинают от дальнего участка цепи по отношению к источнику питания. Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ
. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.
Суть данного метода заключается в уменьшении
количества элементов в цепи с целью
упрощения схемы
и, соответственно, упрощению расчета общего сопротивления.
Разберем схему смешанного соединения из семи резисторов
:
Самым дальним участком схемы оказались резисторы R6
и
R7
, соединенные
параллельно
:
Вычисляем их общее сопротивление используя формулу параллельного
соединения:
Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6
с суммарным сопротивлением равным
30, 709 кОм
.
Продолжим расчет и следующим дальним участком схемы оказались резисторы R5
и
R6
, соединенные
последовательно
:
Вычисляем их общее сопротивление используя формулу последовательного
соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):
Схема уменьшилась еще на один элемент и приняла вид:
Теперь дальним участком оказались резисторы R4
и
R5
соединенные
параллельно
:
Вычисляем их общее сопротивление:
Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно
. Таким образом мы максимально упростили схему и привели ее к удобному расчету.
Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного
соединения, и получаем общее сопротивление всей цепи:
Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения. Удачи!
Виды соединений потребителей.
Различают последовательное, параллельное и смешанное соединение потребителей.
Припоследовательном соединении потребителей конец первого потребителя присоединяется к началу второго, конец второго – к началу третьего и т.д.
Рисунок 9 – Схема последовательного соединения потребителей
1) Сила тока на всех потребителях одинаковая
2)
Общее сопротивление равно сумме сопротивлений отдельных потребителей
3) Напряжение на зажимах цепи равно сумме падений напряжений на отдельных её участках .
При необходимости уменьшить U и I приемника последовательно ему подключают резистор.
Вывод: при выходе из работы одного элемента вся цепь обесточивается, и при изменении сопротивления одного из них меняется ток во всей цепи и напряжение на каждом элементе.
При параллельном соединении элементов цепи все начала собираются в одну точку, а концы в другую точку и включаются в электрическую цепь, образуя параллельные ветви.
Рисунок 10 – Схема параллельного соединения потребителей
1) Общий ток равен сумме токов параллельных ветвей
2) Напряжение на всех потребителях включенных параллельно одинаковое
3) Общее сопротивление будет меньше наименьшего из включенных параллельно
Из закона Ома для участка цепи
—
для двух потребителей
Если сопротивление потребителей равны, то
Вывод:
При выходе из строя одного потребителя остальные остаются включенные в цепь.
Все приемники находятся под одним напряжением независимо от их мощности (сопротивления).
Смешанным называется такое соединение потребителей, когда в цепи имеются одновременно и параллельное и последовательное их соединение.
Цепь постепенно упрощают, заменяя эквивалентным (равноценным) сопротивлением, используя формулы для последовательного и параллельного соединения потребителей.
Дата добавления: 2017-11-21; ;
Похожие статьи:
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»: