In graph theory, a clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent, that is, they are connected by an edge of the graph. The number of cliques in a graph is the total number of cliques that can be found in the graph.
The Mathematics behind cliques in a graph involves the concept of adjacency matrices and graph theory. An adjacency matrix is a matrix representation of a graph where each row and column corresponds to a vertex in the graph and the elements of the matrix indicate whether there is an edge between the vertices.
For example, in an undirected graph with 5 vertices, the adjacency matrix would be a 5×5 matrix where a 1 in position (i, j) indicates that there is an edge between vertex i and vertex j, and a 0 indicates that there is no edge.
1 1 1 0 0
1 1 1 0 0
1 1 1 1 1
0 0 1 1 1
0 0 1 1 1
To find the number of cliques in a graph using an adjacency matrix, you can use a graph algorithm such as the Bron–Kerbosch algorithm, which is an efficient method for enumerating all cliques in an undirected graph.
The Bron–Kerbosch algorithm works by iterating over all possible subsets of the vertices and checking if they form a clique. It does this by using the adjacency matrix to check if every pair of vertices in the subset is adjacent (i.e., connected by an edge). If they are, then the subset forms a clique and is added to the list of cliques.
Example 1:
Consider the following graph:
Example 1
This graph has three cliques: {1, 2, 3}, {3, 4, 5}, and {1, 2, 4, 5}.
To find the number of cliques in a graph, graph traversal algorithms such as depth-first search (DFS) or breadth-first search (BFS) can be used to visit all the vertices and check for cliques at each vertex.
For example, you could start at vertex 1 and perform a DFS to explore the graph. When you reach vertex 3, you know that the vertices 1, 2, and 3 form a clique. You can then continue the DFS to explore the remaining vertices and check for cliques at each vertex.
Alternatively, you could use a graph algorithm specifically designed to find cliques, such as the Bron–Kerbosch algorithm. This algorithm is an efficient method for enumerating all cliques in an undirected graph.
Example 2:
Consider a simple undirected graph with 4 vertices and 6 edges, as shown below:
Example 2
To count the number of cliques in this graph, we can use the following formula:
Number of cliques = n * (n – 1) / 2 – m + 1 where n is the number of vertices in the graph and m is the number of edges. Plugging in the values for this graph, we get:
Number of cliques = 4 * (4 – 1) / 2 – 6 + 1 = 2So there are 2 cliques in this graph.
This formula works because it counts the number of possible pairs of vertices in the graph (n * (n – 1) / 2), and then subtracts the number of edges to account for overcounting. Finally, it adds 1 to account for the fact that a single vertex on its own is also considered a clique.
This formula only works for undirected graphs, and it may not give the correct result for graphs with multiple edges or self-loops. It is also not practical for large graphs, as the time complexity of this approach is O(n^2). However, it can be a useful tool for quickly counting the number of cliques in small graphs
Approaches:
- Brute-force search: One approach is to simply enumerate all possible cliques in the graph and count them. This approach has a time complexity of O(3^n), where n is the number of vertices in the graph, so it is only practical for very small graphs.
- Bron-Kerbosch algorithm: The Bron-Kerbosch algorithm is a pivot-based algorithm that uses a recursive approach to find all cliques in a graph. It has a time complexity of O(3^(n/3)), where n is the number of vertices in the graph, and a space complexity of O(n).
- Tomita algorithm: The Tomita algorithm is another pivot-based algorithm that uses a recursive approach to find all cliques in a graph. It has a time complexity of O(4^(n/4)), where n is the number of vertices in the graph and a space complexity of O(n).
- Pivot Bron-Kerbosch algorithm: The pivot Bron-Kerbosch algorithm is an improvement over the Bron-Kerbosch algorithm that uses a pivot element to prune the search space and reduce the time complexity. It has a time complexity of O(2^n), where n is the number of vertices in the graph, and a space complexity of O(n^2).
- Hybrid algorithm: The hybrid algorithm is a combination of the Bron-Kerbosch and Tomita algorithms that uses both pivoting and recursion to find all cliques in a graph. It has a time complexity of O(2^n), where n is the number of vertices in the graph and a space complexity of O(n^2)
- Approximation algorithms: Another approach is to use approximation algorithms, which are designed to find a good approximation of the number of cliques in a graph in polynomial time. These algorithms may not find all cliques in the graph, but they can be useful in cases where the exact number of cliques is not necessary.
- Parallelization techniques: It is also possible to improve the performance of the above algorithms by using parallelization techniques, such as multi-threading or distributed computing, to divide the work across multiple processors. However, these approaches may have additional overhead costs and may not be suitable for all types of graphs.
Which approach is best for your specific problem will depend on the size of the graph and the desired time and space complexity. You should choose the approach that best meets your needs and constraints.
Observation behind the Approaches:
The different approaches to finding the number of cliques in a graph are based on different observations and techniques. Here are some observations behind these approaches:
- Brute-force search: This approach simply enumerates all possible cliques in the graph and counts them. It is based on the observation that a clique is a subset of the vertices of the graph that are all connected to each other.
- Bron-Kerbosch algorithm: The Bron-Kerbosch algorithm is based on the observation that a clique can be found by starting with a vertex and then expanding to include its neighbors, as long as they are all connected to each other. The algorithm uses a pivot element to prune the search space and reduce the time complexity.
- Tomita algorithm: The Tomita algorithm is based on the observation that a clique can be found by starting with a vertex and then expanding to include its neighbors, as long as they are all connected to each other. The algorithm uses a pivot element to prune the search space and reduce the time complexity.
- Pivot Bron-Kerbosch algorithm: The pivot Bron-Kerbosch algorithm is an improvement over the Bron-Kerbosch algorithm that uses a pivot element to prune the search space and reduce the time complexity. It is based on the observation that many cliques in a graph share common vertices, and by using a pivot element to focus the search on these vertices, it is possible to reduce the time complexity of the algorithm.
- Hybrid algorithm: The hybrid algorithm combines the Bron-Kerbosch and Tomita algorithms and uses both pivoting and recursion to find all cliques in a graph. It is based on the observation that both of these algorithms are effective at finding cliques, and by combining them, it is possible to find all cliques in a graph more efficiently.
- Approximation algorithms: Approximation algorithms are based on the observation that it is often sufficient to find a good approximation of the number of cliques in a graph, rather than the exact number. These algorithms use techniques such as random sampling or graph partitioning to find a good approximation in polynomial time.
- Parallelization techniques: Parallelization techniques are based on the observation that it is often possible to improve the performance of an algorithm by dividing the work across multiple processors. These techniques can be used to speed up the execution of the above algorithms by dividing the search space among multiple threads or processes
Here is a simple algorithm in Python to find the number of cliques in an undirected graph:
Python3
from collections import defaultdict
def find_cliques(graph):
cliques = []
visited = set()
def dfs(node, clique):
visited.add(node)
clique.add(node)
for neighbor in graph[node]:
if neighbor not in visited:
dfs(neighbor, clique)
for node in graph:
if node not in visited:
clique = set()
dfs(node, clique)
if len(clique) > 1:
cliques.append(clique)
return cliques
graph = {
'A': ['B', 'C', 'D'],
'B': ['A', 'C', 'D'],
'C': ['A', 'B', 'D'],
'D': ['A', 'B', 'C'],
'E': ['F'],
'F': ['E']
}
cliques = find_cliques(graph)
print(f'Number of cliques: {len(cliques)}')
print(f'Cliques: {cliques}')
Java
import java.util.*;
public class CliqueFinder {
static List<Set<String>> findCliques(Map<String, List<String>> graph) {
List<Set<String>> cliques = new ArrayList<>();
Set<String> visited = new HashSet<>();
for (String node : graph.keySet()) {
if (!visited.contains(node)) {
Set<String> clique = new HashSet<>();
dfs(node, graph, visited, clique);
if (clique.size() > 1) {
cliques.add(clique);
}
}
}
return cliques;
}
static void dfs(String node, Map<String, List<String>> graph, Set<String> visited, Set<String> clique) {
visited.add(node);
clique.add(node);
for (String neighbor : graph.get(node)) {
if (!visited.contains(neighbor)) {
dfs(neighbor, graph, visited, clique);
}
}
}
public static void main(String[] args) {
Map<String, List<String>> graph = new HashMap<>();
graph.put("A", Arrays.asList("B", "C", "D"));
graph.put("B", Arrays.asList("A", "C", "D"));
graph.put("C", Arrays.asList("A", "B", "D"));
graph.put("D", Arrays.asList("A", "B", "C"));
graph.put("E", Arrays.asList("F"));
graph.put("F", Arrays.asList("E"));
List<Set<String>> cliques = findCliques(graph);
System.out.println("Number of cliques: " + cliques.size());
System.out.println("Cliques: " + cliques);
}
}
C++
#include <iostream>
#include <vector>
#include <set>
#include <map>
using namespace std;
vector<set<string>> findCliques(map<string, vector<string>> graph) {
vector<set<string>> cliques;
set<string> visited;
for (auto node : graph) {
if (visited.find(node.first) == visited.end()) {
set<string> clique;
dfs(node.first, graph, visited, clique);
if (clique.size() > 1) {
cliques.push_back(clique);
}
}
}
return cliques;
}
void dfs(string node, map<string, vector<string>> graph, set<string>& visited, set<string>& clique) {
visited.insert(node);
clique.insert(node);
for (string neighbor : graph[node]) {
if (visited.find(neighbor) == visited.end()) {
dfs(neighbor, graph, visited, clique);
}
}
}
int main() {
map<string, vector<string>> graph;
graph["A"] = {"B", "C", "D"};
graph["B"] = {"A", "C", "D"};
graph["C"] = {"A", "B", "D"};
graph["D"] = {"A", "B", "C"};
graph["E"] = {"F"};
graph["F"] = {"E"};
vector<set<string>> cliques = findCliques(graph);
cout << "Number of cliques: " << cliques.size() << endl;
cout << "Cliques: [";
for(auto clique:cliques) {
for(auto it:clique){
cout << it << ",";
}
cout << "]";
}
return 0;
}
C#
using System;
using System.Collections.Generic;
class CliqueFinder {
static List<HashSet<string>> FindCliques(Dictionary<string, List<string>> graph) {
List<HashSet<string>> cliques = new List<HashSet<string>>();
HashSet<string> visited = new HashSet<string>();
foreach (string node in graph.Keys) {
if (!visited.Contains(node)) {
HashSet<string> clique = new HashSet<string>();
Dfs(node, graph, visited, clique);
if (clique.Count > 1) {
cliques.Add(clique);
}
}
}
return cliques;
}
static void Dfs(string node, Dictionary<string, List<string>> graph, HashSet<string> visited, HashSet<string> clique) {
visited.Add(node);
clique.Add(node);
foreach (string neighbor in graph[node]) {
if (!visited.Contains(neighbor)) {
Dfs(neighbor, graph, visited, clique);
}
}
}
public static void Main(string[] args) {
Dictionary<string, List<string>> graph = new Dictionary<string, List<string>>();
graph.Add("A", new List<string>() { "B", "C", "D" });
graph.Add("B", new List<string>() { "A", "C", "D" });
graph.Add("C", new List<string>() { "A", "B", "D" });
graph.Add("D", new List<string>() { "A", "B", "C" });
graph.Add("E", new List<string>() { "F" });
graph.Add("F", new List<string>() { "E" });
List<HashSet<string>> cliques = FindCliques(graph);
Console.WriteLine("Number of cliques: " + cliques.Count);
Console.WriteLine("Cliques: " + cliques);
}
}
Javascript
function findCliques(graph) {
let cliques = [];
let visited = new Set();
for (let node in graph) {
if (!visited.has(node)) {
let clique = new Set();
dfs(node, graph, visited, clique);
if (clique.size > 1) {
cliques.push(clique);
}
}
}
return cliques;
}
function dfs(node, graph, visited, clique) {
visited.add(node);
clique.add(node);
for (let neighbor of graph[node]) {
if (!visited.has(neighbor)) {
dfs(neighbor, graph, visited, clique);
}
}
}
let graph = {
'A': ['B', 'C', 'D'],
'B': ['A', 'C', 'D'],
'C': ['A', 'B', 'D'],
'D': ['A', 'B', 'C'],
'E': ['F'],
'F': ['E']
};
let cliques = findCliques(graph);
console.log(`Number of cliques: ${cliques.length}`);
console.log(`Cliques: ${cliques}`);
Output
Number of cliques: 2
Cliques: [{'D', 'B', 'C', 'A'}, {'E', 'F'}]
The time complexity of the find_cliques function provided in the code is O(n+m), where n is the number of vertices in the graph and m is the number of edges. This is because the function performs a depth-first search (DFS) on the graph, which takes time proportional to the number of vertices and
The auxiliary space of this function is O(n) because it uses a set to store the visited vertices and a list to store the cliques, both of which have sizes proportional to the number of vertices in the graph.
Note: that the time and space complexity of this function may be different if the graph is represented differently, for example as an adjacency matrix instead of an adjacency list. The time and space complexity of an algorithm can also depend on the specific implementation and the specific input.
Time and space complexity of each approach:
| Approach | Time Complexity | Space Complexity |
|---|---|---|
| Bron-Kerbosch algorithm |
O(3^(n/3)) |
O(n) |
| Tomita algorithm |
O(4^(n/4)) |
O(n) |
| Pivot Bron-Kerbosch algorithm |
O(2^n) |
O(2^n) |
| Hybrid algorithm |
O(2^n) |
O(2^n) |
- The Bron-Kerbosch algorithm and the Tomita algorithm are both pivot-based algorithms that use a recursive approach to find all cliques in a graph.
- The Pivot Bron-Kerbosch algorithm is an improvement over the Bron-Kerbosch algorithm that reduces the time complexity by using a pivot element to prune the search space.
- The hybrid algorithm is a combination of the Bron-Kerbosch and Tomita algorithms that uses both pivoting and recursion to find all cliques in a graph.
- It is worth noting that the time complexity of these algorithms can be improved by using parallelization techniques or approximative algorithms, but these approaches may not find all cliques in the graph and may have additional overhead costs.
Last Updated :
16 Feb, 2023
Like Article
Save Article
| Определение: |
| Встреча в середине (англ. Meet-in-the-middle) — это метод решения уравнения вида , где и , который работает за время , где — время построения множества , — время поиска элемента в множестве , удовлетворяющее решению при заданном , или проверка, что такого не существует. |
Meet-in-the-middle разбивает задачу пополам и решает всю задачу через частичный расчет половинок. Он работает следующим образом: переберем все возможные значения и запишем пару значений в множество. Затем будем перебирать всевозможные значения , для каждого из них будем вычислять , которое мы будем искать в нашем множестве. Если в качестве множества использовать отсортированный массив, а в качестве функции поиска — бинарный поиск, то время работы нашего алгоритма составляет на сортировку, и на двоичный поиск, что дает в сумме .
Содержание
- 1 Задача о нахождении четырех чисел с суммой равной нулю
- 1.1 Реализация
- 2 Задача о рюкзаке
- 2.1 Алгоритм
- 2.2 Реализация
- 3 Задача о количестве полных подграфов в графе
- 3.1 Алгоритм решения
- 4 Задача о нахождении кратчайшего расстояния между двумя вершинами в графе
- 4.1 Алгоритм решения
- 5 См. также
- 6 Источники информации
Задача о нахождении четырех чисел с суммой равной нулю
Дан массив целых чисел . Требуется найти любые числа, сумма которых равна (одинаковые элементы могут быть использованы несколько раз).
Например : . Решением данной задачи является, например, четверка чисел или .
Наивный алгоритм заключается в переборе всевозможных комбинаций чисел. Это решение работает за . Теперь, с помощью Meet-in-the-middle мы можем сократить время работы до .
Для этого заметим, что сумму можно записать как . Мы будем хранить все пар сумм в массиве , который мы отсортируем. Далее перебираем все пар сумм и проверяем бинарным поиском, есть ли сумма в массиве .
Реализация
// sum — массив сумм a + b, cnt — счетчик массива sum function findsum(int[N] A): String for a = 0..N - 1 for b = 0..N - 1 sum[cnt].res = A[a] + A[b] sum[cnt].a = a sum[cnt].b = b cnt++ sort(sum, key = "res") // сортируем sum по полю res for c = 0..N - 1 for d = 0..N - 1 if сумма - (A[c] + A[d]) есть в массив sum index = индекс суммы -(A[c] + A[d]) return (sum[index].a, sum[index].b, A[c], A[d]) return "No solution"
Итоговое время работы .
Если вместо отсортированного массива использовать хэш-таблицу, то задачу можно будет решить за время .
Задача о рюкзаке
Классической задачей является задача о наиболее эффективной упаковке рюкзака. Каждый предмет характеризуется весом ( ) и ценностью (). В рюкзак, ограниченный по весу, необходимо набрать вещей с максимальной суммарной стоимостью. Для ее решения изначальное множество вещей N разбивается на два равных(или примерно равных) подмножества, для которых за приемлемое время можно перебрать все варианты и подсчитать суммарный вес и стоимость, а затем для каждого из них найти группу вещей из первого подмножества с максимальной стоимостью, укладывающуюся в ограничение по весу рюкзака. Сложность алгоритма . Память .
Алгоритм
Разделим наше множество на две части. Подсчитаем все подмножества из первой части и будем хранить их в массиве . Отсортируем массив по весу. Далее пройдемся по этому массиву и оставим только те подмножества, для которых не существует другого подмножества с меньшим весом и большей стоимостью. Очевидно, что подмножества, для которых существует другое, более легкое и одновременно более ценное подмножество, можно удалять.
Таким образом в массиве мы имеем подмножества, отсортированные не только по весу, но и по стоимости. Тогда начнем перебирать все возможные комбинации вещей из второй половины и находить бинарным поиском удовлетворяющие нам подмножества из первой половины, хранящиеся в массиве .
Реализация
// N — количество всех вещей, w[N] — массив весов всех вещей, cost[N] — массив стоимостей всех вещей, R — ограничение по весу рюкзака. function knapsack(int[N] w, int[N] cost, int R): int sn = N / 2 fn = N - sn for mask = 0..2 ** sn - 1 for j = 0..sn if j-ый бит mask == 1 first[i].w += w[j] first[i].c += cost[j] sort(first, key = "w") // сортируем first по весу for i = 0..2 ** sn - 1 if существует такое подмножество с индексом j, что first[j].w first[i].w and first[j].c first[i].c удалим множество с индексом i из массива first for mask = 0..2 ** fn - 1 for j = 0..fn if j-ый бит mask == 1 curw += w[j + sn] curcost += cost[j + sn] index = позиция, найденная бинарным поиском в массиве first, подмножества с максимальным весом, не превыщающим R - curv if first[index].w R - curw and first[index].c + curcost ans ans = first[index].c + curcost return ans
Итоговое время работы .
Задача о количестве полных подграфов в графе
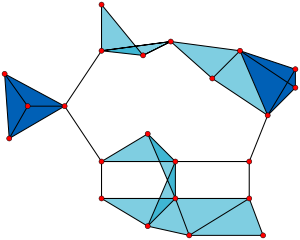
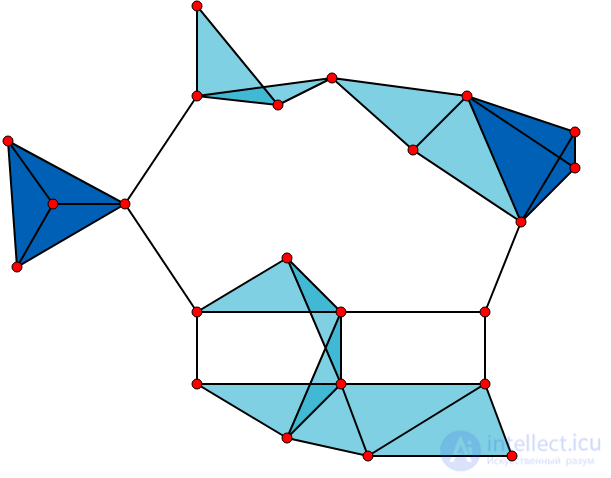
Граф с 23 × 1-вершинными кликами (сами вершины), 42 × 2-вершинными кликами (отрезки), 19 × 3-вершинными кликами (светло-синие и тёмно-синие треугольники) и 2 × 4-вершинными кликами (тёмно-синие зоны). Всего 86 клик.
Дан граф , в котором вершин. Требуется подсчитать количество клик.
Наивное решение — перебор всех возможных подграфов и проверка для каждого, что он является кликой, сложность —
Этот алгоритм можно улучшить до . Для этого нужно в функции перебора хранить маску вершин, которые мы ещё можем добавить. Поддерживая эту маску, можно добавлять только «нужные» вершины, и тогда не нужно будет в конце проверять подграф на то что он — клика. Добавлять вершину можно за , используя побитовое И текущей маски и строчки матрицы смежности добавляемой вершины.
Алгоритм решения
Разбиваем граф на графа и по вершин. Находим за все клики в каждом из них.
Теперь надо узнать для каждой клики графа количество клик графа , таких, что их объединение — клика. Их сумма и есть итоговый ответ.
Для одной клики графа может быть несколько подходящих клик в . О клике мы «знаем» только маску вершин графа , которые ещё можно добавить. Для каждой такой маски в нужно предподсчитать ответ.
С помощью динамического программирования предподсчитаем для каждой маски вершин графа количество клик, вершины которых являются подмножеством выбранной маски. Количество состояний — . Количество переходов: . Асимптотика — .
Для каждой клики (в том числе и пустой) графа прибавим к глобальному ответу предподсчитанное количество клик, которые можно добавить к (в том числе и пустых). Асимптотика: .
Итоговая сложность:
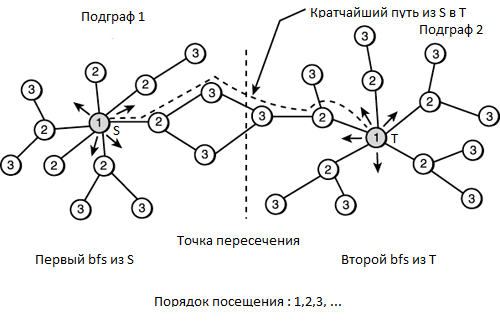
Задача о нахождении кратчайшего расстояния между двумя вершинами в графе
Нахождение кратчайшего расстояния между двумя вершинами
Еще одна задача, решаемая Meet-in-the-middle — это нахождение кратчайшего расстояния между двумя вершинами, зная начальное состояние, конечное состояние и то, что длина оптимального пути не превышает .
Стандартным подходом для решения данной задачи, является применение алгоритма обхода в ширину. Пусть из каждого состояния у нас есть переходов, тогда бы мы сгенерировали состояний. Асимптотика данного решения составила бы . Meet-in-the-middle помогает снизить асимптотику до .
Алгоритм решения
1. Сгенерируем BFS-ом все состояния, доступные из начала и конца за или меньше ходов.
2. Найдем состояния, которые достижимы из начала и из конца.
3. Найдем среди них наилучшее по сумме длин путей.
Таким образом, BFS-ом из двух концов, мы сгенерируем максимум состояний.
См. также
- Обход в ширину
- Целочисленный двоичный поиск
Источники информации
- infoarena.ro — Meet-in-the-middle
- g6prog.narod.ru — Лекции по информатике (36 страница)
- wikipedia.org — Clique
Напомним, что клика
— это максимальный по включению вершин
полный подграф графа. В оптимизационной
форме задача о клике выглядит следующим
образом:
Дан граф G = (V, E).
Необходимо найти наибольшую клику графа
(клику графа с наибольшим для этого
графа числом вершин).
Используем обозначение
ϕ(G) — размер наибольшей клики в графе G.
Тогда задачу о клики можно переформулировать
в форме распознавания следующим образом:
Дан граф G = (V, E) и целое
число b > 0. Правда ли, что ϕ(G) ≥ b.
То есть необходимо
ответить на вопрос, существует ли в
графе в графе G полный подграф с b
вершинами.
Докажем N P -полноту
задачи о клике, сведя к ней известную
нам N P — полную задачу о выполнимости.
ВЫПОЛНИМОСТЬ ∝
КЛИКА.
Покажем, что задача
о выполнимости сводится за полиномиальное
время к задаче о клике.
Пусть нам поставлена
следующая задача о выполнимости: дана
конъюнктивная нормальная форма A = D1 ∧
D2 ∧
… ∧
Dk, где Di — дизъюнкт, i = 1, k. Построим
граф G = (V, E) следующим образом:
V (G) = {(α, i) | α — литерал в Di}, E(G) = {((α,
i), (β, j)) | i /= j, α /= β}.
1)Пусть A выполнима.
Значит на определенном наборе значений
переменных A = 1. Тогда в каждом дизъюнкте
Di найдется хотя бы один литерал αi = 1.
Рассмотрим вершины (αi, i) и (αj , j) при
i /= j. Поскольку на выбранном наборе
значений переменных αi = 1 и αj = 1, то αi /=
αj . Следовательно, вершины (αi, i) и (αj ,
j) соединены ребром в графе G. Таким
образом, множество вершин {(αi, i) | i = 1, k}
порождает полный подграф в графе G.
2) Пусть теперь в графе
G есть клика размера k с вершинами (α1,
1), (α2, 2), …(αk, k). Тогда αi /= αj , ∀i,
j = 1, k. Следовательно, можно таким
образом подобрать значения переменных,
чтобы все αi принимали значение 1
одновременно. Следовательно, A — выполнима.
Итак, мы показали, что
формула A является выполнимой тогда и
только тогда, когда в графе G имеется
клика размера k.
Осталось заметить,
что построение графа G можно выполнить
за полиномиальное время от размера
СКНФ A.
Переформулированная
в форме распознавания задача о клике
принадлежит классу NP , так как, если
ответ на задачу «да» и нам дано
множество вершин, образующих полный
подграф в графе G, мы можем за полиномиальное
время проверить, правда ли каждая из
этих вершин смежная с каждой. Задача о
клике является NP – полной
задачей.
-
Алгоритмы поиска клики
Поскольку задача о
клике является NP – полной
задачей, эффективного алгоритма поиска
Клики, скорее всего, нет. По крайней
мере, пока не доказано, что P=NP.
Однако всегда можно перебрать все
подмножества размера k
во множестве вершин V и
проверить, есть ли среди них клика. Для
этого потребуется Ω(k^2*сочетания
из V
по k)
действий (V
– число вершин в графе). При любом
фиксированном k
эта величина полиноминально зависит
от размера графа G.
Однако в общей постановке задачи k
может быть любым числом, не превосходящим
|V|,
и алгоритм не является полиноминальным.
Алгоритм
Брона – Кербоша.
Одним из самых быстрых
алгоритмов поиска клики был признан
алгоритм Брона – Кербоша. Разработанный
голландскими математиками Броном и
Кербошем в 1973 году.
Алгоритм использует
тот факт, что всякая клика в графе
является его максимальным по включению
полным подграфом. Начиная с одиночной
вершины (образующей полный подграф),
алгоритм на каждом шаге пытается
увеличить уже построенный полный
подграф, добавляя в него вершины из
множества кандидатов. Высокая скорость
обеспечивается отсечением при переборе
вариантов, которые заведомо не приведут
к построению клики, для чего используется
дополнительное множество, в которое
помещаются вершины, которые уже были
использованы для увеличения полного
подграфа.
Алгоритм оперирует
тремя множествами вершин графа:
Множество compsub —
множество, содержащее на каждом шаге
рекурсии полный подграф для данного
шага. Строится рекурсивно.
Множество candidates —
множество вершин, которые могут увеличить
compsub
Множество not — множество
вершин, которые уже использовались для
расширения compsub на предыдущих шагах
алгоритма.
Алгоритм является
рекурсивной процедурой, применяемой к
этим трем множествам.
ПРОЦЕДУРА extend
(candidates, not):
1 ПОКА candidates НЕ пусто
И not НЕ содержит вершины, СОЕДИНЕННОЙ
СО ВСЕМИ вершинами из candidates, ВЫПОЛНЯТЬ:
2 Выбираем вершину v
из candidates и добавляем ее в compsub
3 Формируем new_candidates
и new_not, удаляя из candidates и not вершины, не
СОЕДИНЕННЫЕ с v
4 ЕСЛИ
new_candidates и new_not пусты
5 ТО
compsub – клика
6 ИНАЧЕ
рекурсивно вызываем
extend (new_candidates, new_not)
7 Удаляем v из compsub и
candidates, и помещаем в not
Вычислительная
сложность линейна относительно количества
клик в графе. В
работе ученых Стэндфордского университета
«The
worst-case
time
complexity
for
generating
all
maximal
cliques
and
computational
experiments»
(Худшая по времени сложность для
вычисления максимальных кликов и
вычислительные эксперименты) было
показано, что в
худшем случае алгоритм работает
за O(3^n/3),
где n — количество вершин в графе.
Список
использованной литературы.
Соседние файлы в предмете Дискретная математика
- #
- #
- #
- #
- #
- #
Привет, Вы узнаете про клика, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
клика , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
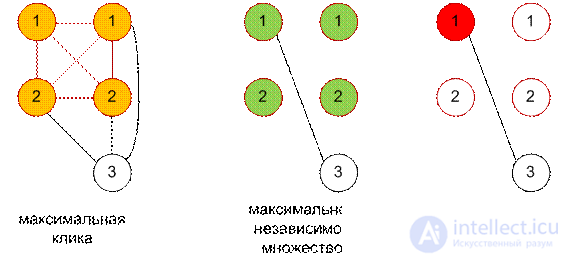
Кликой неориентированного графа называется подмножество его вершин, любые две из которых соединены ребром. Клики являются одной из основных концепций теории графов и используются во многих других математических задачах и построениях с графами. Клики изучаются также в информатике — задача определения, существует ли
клика данного размера в графе (Задача о клике) является NP-полной. Несмотря на эту трудность, изучаются многие алгоритмы для поиска клик.
Хотя изучение полных подграфов началось еще с формулировки теоремы Рамсея в терминах теории графов Эрдешем и Секерешем . Термин «клика» пришел из работы Люка и Пери , использовавших полные подграфы при изучении социальных сетей для моделировании клик людей, то есть групп людей, знакомых друг с другом . Клики имеют много других приложений в науке, и, в частности, в биоинформатике.
Граф с 23 кликами, содержащими 1 вершину (вершины графа), 42 кликами, состоящими из 2 вершин (ребра графа), 19 кликами, состоящими из 3 вершин (закрашенные треугольники) и двумя кликами, состоящими из 4 вершин (темно-синие области).
Шесть ребер не входят ни в один треугольник и 11 светло-голубых треугольников образуют максимальные клики.
Две темно-синие 4-клики являются как наибольшими, так и максимальными, и кликовое число графа равно 4.
Определения
Кликой в неориентированном графе называется подмножество вершин
, такое что для любых двух вершин в
существует ребро, их соединяющее. Это эквивалентно утверждению, что подграф, порожденный
, является полным.
Максимальная клика или клика, максимальная по включению — это клика, которую нельзя расширить добавлением в нее вершин. Иначе говоря, в данном графе нет клики большего размера, в которую она входит.
Наибольшая клика или клика, максимальная по размеру — это клика максимального размера для данного графа.
Кликовое число графа
— это число вершин в наибольшей клике графа
. Число пересечений графа
— это наименьшее число клик, вместе покрывающих все ребра графа
.
Противоположное клике понятие — это независимое множество в том смысле, что каждая клика соответствует независимому множеству в дополнительном графе. Задача о покрытии кликами[en] состоит в нахождении как можно меньшего числа клик, содержащих все вершины графа.
Связанный термин — это биклика, полный двудольный подграф. Двудольная размерность графа — это минимальное число биклик, необходимых для покрытия всех ребер графа.
Математика
Математические результаты относительно клик включают следующие.
Некоторые важные классы графов можно определить их кликами:
- Хордальный граф — это граф, вершины которого могут быть упорядочены в порядке совершенного исключения; порядке, при котором соседи каждой вершины
идут после вершины
.
- Кограф — это граф, все порожденные подграфы которого имеют свойство, что любая наибольшая клика пересекается с любым наибольшим независимым множеством в единственной вершине.
- Интервальный граф — это граф, наибольшие клики которого можно упорядочить так, что для любой вершины
, клики, содержащие
, идут последовательно.
- Реберный граф — это граф ребра которого могут быть покрыты кликами без общих ребер, притом каждая вершина будет принадлежать в точности двум кликам.
- Совершенный граф — это граф, в котором кликовое число равно хроматическому числу в каждом порожденном подграфе.
- Расщепляемый граф — это граф, в котором некоторый набор клик содержит по крайней мере одну вершину из каждого ребра.
- Граф без треугольников — это граф, в котором нет других клик кроме вершин и ребер.
Кроме того, многие другие математические построения привлекают клики графов. Среди них:
Близкая концепция к полным подграфам — это разбиения графов на полные подграфы и полные миноры графа. В частности, теорема Куратовского[en] и теорема Вагнера характеризуют планарные графы путем запрещения полных и полных двудольных подграфов и миноров, соответственно.
Информатика Задача о клике
В информатике задача о клике — это вычислительная задача нахождения максимальной клики или клик в заданном графе. Задача является NP-полной, одной из 21 NP-полных задач Карпа . Она также сложна для параметрического приближения[en] и трудно аппроксимируема. Тем не менее разработано много алгоритмов для работы с кликами, работающих либо за экспоненциальное время (такие как алгоритм Брона — Кербоша), либо специализирующиеся на семействах графов, таких как планарные графы или совершенные графы, для которых задача может быть решена за полиномиальное время.
Бесплатное программное обеспечение для поиска максимальной клики
Ниже приведен список свободно распространяемого программного обеспечение для поиска максимальной клики.
| Название | Лицензия | Язык API | Короткое описание |
|---|---|---|---|
| NetworkX | BSD | Python | приближенное решение, смотри процедуру max_clique (недоступная ссылка) |
| maxClique | CRAPL | Java | точные алгоритмы, реализации DIMACS |
| OpenOpt | BSD | Python | точные и приближенные решения, возможность указать ребра, которые должны быть включены (MCP) |
Перейти к навигацииПерейти к поиску
Задача о клике относится к классу NP-полных задач в области теории графов. Впервые она была сформулирована в 1972 году Ричардом Карпом.
Кликой в неориентированном графе называется подмножество вершин, каждые две из которых соединены ребром графа. Иными словами, это полный подграф первоначального графа. Размер клики определяется как число вершин в ней. Задача о клике существует в двух вариантах: в задаче распознавания требуется определить, существует ли в заданном графе G клика размера k, в то время как в вычислительном варианте требуется найти в заданном графе G клику максимального размера.
NP-полнота
NP-полнота задачи о клике следует из NP-полноты задачи о независимом множестве вершин. Легко показать, что необходимым и достаточным условием для существования клики размера k является наличие независимого множества размера не менее k в дополнении графа. Это очевидно, поскольку полнота подграфа означает, что его дополнение не содержит ни одного ребра.
Другое доказательство NP-полноты можно найти в книге «Алгоритмы: построение и анализ».
Алгоритмы
Как и для других NP-полных задач, эффективного алгоритма для поиска клики заданного размера на данный момент не найдено. Полный перебор всех возможных подграфов размера k с проверкой того, является ли хотя бы один из них полным, — неэффективен, поскольку полное число таких подграфов в графе с v вершинами равно биномиальному коэффициенту
Другой алгоритм работает так: две клики размера n и m «склеиваются» в большую клику размера n+m, причем кликой размера 1 полагается отдельная вершина графа. Алгоритм завершается, как только ни одного слияния больше произвести нельзя. Время работы данного алгоритма линейно, однако он является эвристическим, поскольку не всегда приводит к нахождению клики максимального размера. В качестве примера неудачного завершения можно привести случай, когда вершины, принадлежащие максимальной клике, оказываются разделены и находятся в кликах меньшего размера, причем последние уже не могут быть «склеены» между собой.
Теорема Кенига. В двудольном графе размер максимального паросочетания равен размеру минимального вершинного покрытия.
Из теоремы Кенига следует, что
размер максимальной клики =
размер максимального независимого множества в дополняющем графе =
количество вершин графа – размер минимального вершинного покрытия =
количество вершин графа – размер максимального паросочетания в дополняющем графе
Пример
Рассмотрим второй пример. Размер максимальной клики графа равен 4. Размер максимального независимого множества в дополняющем графе равен 4.
Применение
Много различных задач биоинформатики смоделированы с помощью клик. Например, Бен-Дор, Шамир и Яхини[10] моделировали задачу разбиения на группы экспрессии генов, как задачу поиска минимального числа изменений, необходимых для преобразования графа данных в граф, сформированный несвязными наборами клик. Танай, Шаран и Шамир[11] обсуждают похожую задачу бикластеризации данных экспрессии генов, в которой кластеры должны быть кликами. Сугихара[12] использовал клики для моделирования экологических ниш в пищевых цепях. Дей и Санков[13] описывают задачу описания эволюционных деревьев, как задачу нахождения максимальных клик в графе, в котором вершины представляют характеристики, а две вершины соединены ребром, если существует идеальная история развития[en], комбинирующая эти две характеристики. Самудрала и Молт[14] моделировали предсказание структуры белка как задачу нахождения клик в графе, вершины которого представляют позиции частей белка, а путем поиска клик в схеме взаимодействия белок-белок[en], Спирит и Мирни [15] нашли кластеры белков, которые взаимодействуют тесно друг с другом и имеют слабое взаимодействие вне кластера. Анализ мощности графа[en] — это метод упрощения сложных биологических систем путем нахождения клик и связанных структур в этих системах.
В электротехнике Прихар [16] использовал клики для анализа коммуникационных сетей, а Паул и Унгер [17] использовали их для разработки эффективных схем для вычисления частично определенных булевских функций. Клики используются также в автоматических генерациях тестовых шаблонов[en] — большая клика в графе несовместимости возможных дефектов дает нижнюю границу множества тестовов[18]. Конг и Смит [19] описывают применение клик для поиска иерархических структур в электрических схемах.
В химии Родес и соавторы[20] использовали клики для описания химических соединений в химической базе данных[en], имеющих высокую степень похожести. Кул, Крипен и Фризен[21] использовали клики для моделирования позиций, в которых два химических соединения связываются друг с другом.
Вау!! 😲 Ты еще не читал? Это зря!
- Флаговый комплекс
В общем, мой друг ты одолел чтение этой статьи об клика. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое клика
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Анализ комбинации жадного алгоритма поиска клики с частичным перебором вершин графа
Время на прочтение
4 мин
Количество просмотров 3.1K
Доброго времени суток.
В свободное время провёл небольшое исследование.
В теории графов известен жадный алгоритм поиска кликового числа. Далеко не всегда он даёт верный результат. Под катом проводится анализ результатов работы жадного алгоритма при его комбинации с частичным перебором множеств вершин на графах из «DIMACS benchmark set».
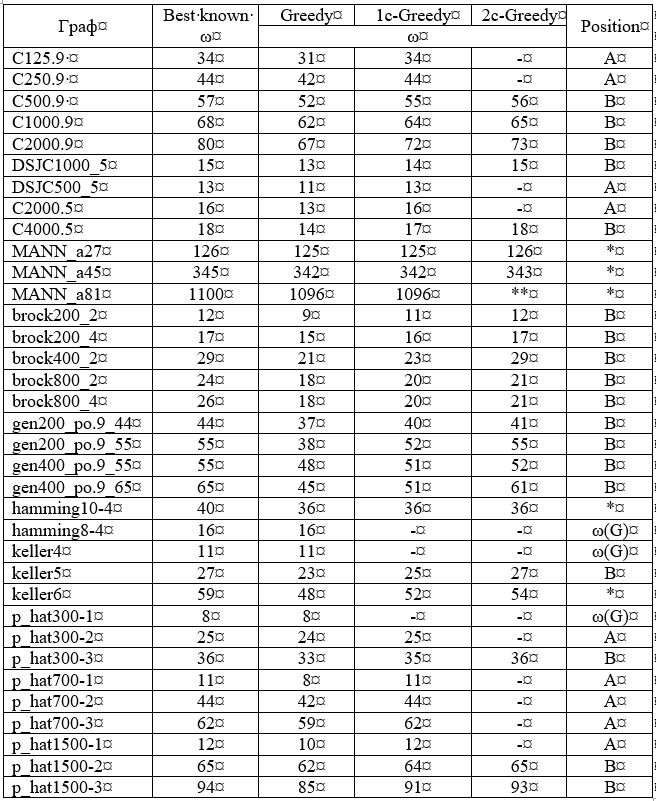
В столбце «Best known» таблицы 1 приведены размеры известных на данный момент максимальных клик указанных графов. В столбце «Greedy» указаны значения размеров максимальных клик, найденных жадным алгоритмом. Жадный алгоритм выдаёт верный ответ лишь в 3 случаях из 35.
Примечание – в реализованном программном коде жадный алгоритм выбирает вершину с наибольшим значением смежности. Если найдено несколько подобных вершин, выбирается первая найденная. Назовём процедуру жадного алгоритма Greedy(A), где А – номер массива (матрицы смежности), к которому применяется алгоритм. Изначальный массив проиндексируем как А0.
Таблица 1 – Результаты работы алгоритма, реализованного на языке Pascal.
** — не анализировалось ввиду большого размера графа.
Сделаем следующий шаг, а именно: будем поочерёдно брать все N вершин графа, отсекая при этом не смежные. Обозначим полученные массивы как Аm, где m – номер выбранной вершины. Такую процедуру в алгоритме обозначим как DelNotAdj(m).
К получаемым подграфам снова применим процедуру Greedy(Аm). Результаты (максимальный размер найденных клик) приведены в столбце «1c-Greedy». Можно заметить, что найденных верных результатов стало больше, а именно 8 из 35.
Теперь рассмотрим парные комбинации смежных вершин. Алгоритмически это будет означать, что мы дважды применим процедуру DelNotAdj(m). Сначала для изначального графа А0, затем для каждой из вершин получаемых Аm. Обозначим получаемые подграфы как Аmx. И вновь воспользуемся Greedy(Аmx). Результаты (максимальный размер найденных клик) приведены в столбце «2-Greedy».
Были также проанализированы комбинации из 3-х вершин (3c-Greedy) для графов C500.9 и C1000.9 с соответствующими результатами ω(C500.9)=57, ω(C1000.9)=66.
На некоторое время отложим анализ результатов работы алгоритмов и рассмотрим их теоретическую временную сложность.
В реализации на языке Pascal процедура жадного алгоритма Greedy(A) имеет временную сложность порядка O(n2), где n – количество вершин в исходном графе. Перебор всех вершин графа усложняет алгоритм в n раз, перебор комбинаций из 2-х – в раз и т.д. вплоть до полного перебора
, где ω(G) – размер максимальной (искомой) клики. В последнем случае применение жадного алгоритма лишено смысла.
Возникает вопрос, как определить, каким перебором можно ограничиться? Из таблицы 1 невозможно выявить четкую закономерность, однако попытаемся осуществить условную классификацию.
Построим графики некоторых найденных значений (рисунок 1). По оси абсцисс отложим значения порядка временной сложности O(n), по оси ординат – возможные значения найденных размеров клик ω от 1 до ω(G) – максимального значения, ωGR – размер клики, найденной жадным алгоритмом в исходном графе.
Рисунок 1
Позиционные обозначения групп построенных графиков приведены в столбце «Position» таблицы 1 для соответствующих графов. ꞷ(G) обозначены графы, для которых жадный алгоритм выдаёт верный результат без перебора. В группу «А» попали графы, для которых уже однократный перебор вершин приводит к нахождению клики заданного размера.
В группу «B» вошли графы, требующие для нахождения верного ответа 2-х и более кратный перебор.
В группу «*» вошли графы, имеющие «полку», т.е. найденные значения размеров клик начиная с просто жадного алгоритма и до перебора 2, 3 и более комбинаций вершин не изменяются. Затем следует увеличение значения ω. Такое поведение обозначено на рисунке отрезками ωGRCFG.
Можно утверждать, что для конкретной вершины и, следовательно, для всего графа в целом, график зависимости размера найденной максимальной клики от количества переборов не будет убывать. Т.е. перебрав все комбинации из вершин, смежных выбранной, мы получим результат не хуже, чем при переборе комбинаций из 2-х вершин.
Обозначим «алгоритмом» последовательность действий по нахождению клики заданного размера, такую что:
- На первом шаге к исходному графу А0 применяется «жадный» алгоритм. Полученное значение размера клики обозначим как ωGR.
- На втором шаге применим последовательно «жадный» алгоритм к подграфам Аm, образованным каждой m вершиной исходного. При этом подграф Аm не должен содержать вершин, не смежных выбранной. Максимальное найденное значение размера клики обозначим как ωGR+1.
- На третьем шаге применим последовательно «жадный» алгоритм к подграфам Аmn, образованным комбинациями смежных m-й и n-й вершин исходного графа А0. При этом подграф Аmn не должен содержать вершин, не смежных n-й и m-й вершинам. Максимальное найденное значение размера клики обозначим как ωGR+2.
- Максимальные найденные значения размеров клик для комбинаций 3-х, 4-х,…, y-вершин обозначим как ωGR+3, ωGR+4,…, ωGR+y соответственно.
- Кликовое число для графа А0 — ω(G).
Предлагается две гипотезы. Первая относится к графам группы «А» и «B» может быть сформулирована следующим образом:
Предположим, что значение размера клики, найденной жадным алгоритмом в исходном графе равно ωGR. Если при однократном переборе вершин с последующим приложением к образованным ими подграфам жадного алгоритма найдено хотя бы одно значение ωGR+1 большее ωGR, то клика искомого размера может быть найдена с временной сложностью порядка 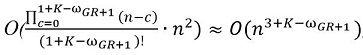
Для группы под «*» гипотеза выглядит так:
В общем случае последовательность значений размеров найденных «алгоритмом» клик ωGR, ωGR+1, ωGR+2,…, ω(G) неубывающая. При этом данная последовательность может иметь не более одного промежутка, такого, что каждый последующий элемент равен предыдущему. Если такой промежуток существует, то его нижняя граница равна ωGR.
Проиллюстрировать данную гипотезу можно следующим образом: не существует последовательности значений ωGR, ωGR+1, ωGR+2,… такой, что она образует «промежуточную полку» (отрезки ωGRCDE рисунка 1).
В случае корректности второй гипотезы из неё могут существовать два следствия:
Следствие 1. Если при работе «алгоритма» найдено значение ωGR+y, большее
ωGR+y-1, то клика искомого размера может быть найдена с временной сложностью порядка 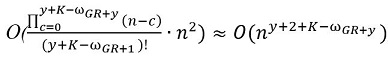
Данное свойство является обобщением первой гипотезы.
Следствие 2. Если на y-м шаге найдено такое же значение ωGR+y, что и на предыдущем шаге, т.е. ωGR+y=ωGR+y-1, следовательно, найденное значение ωGR+y является кликовым числом ω(G) для исходного графа.
Если изложенное повторяет чью-то работу, я не со зла, буду рад ссылке для ознакомления. Еще больше буду рад, если кто-то теоретически сможет доказать или опровергнуть предложенные гипотезы.


.png)