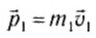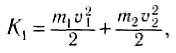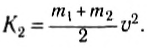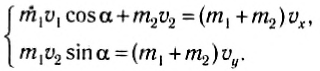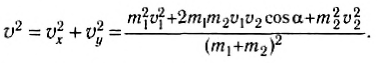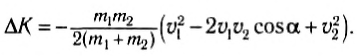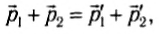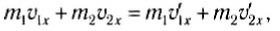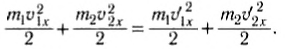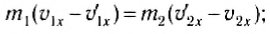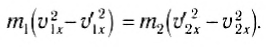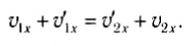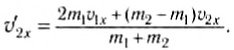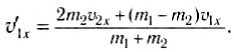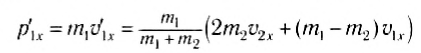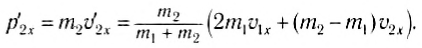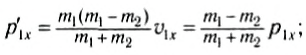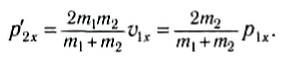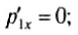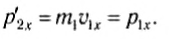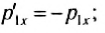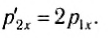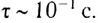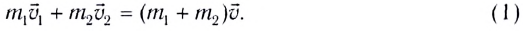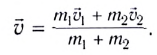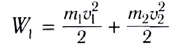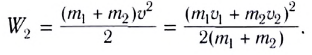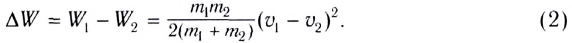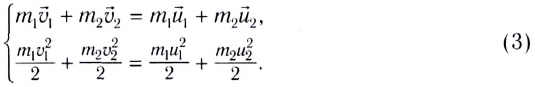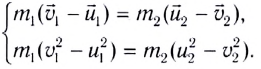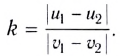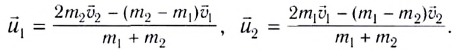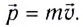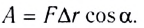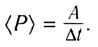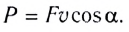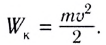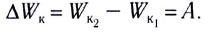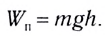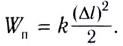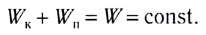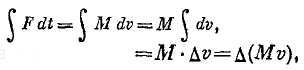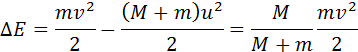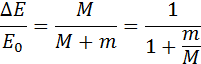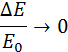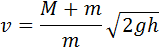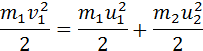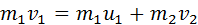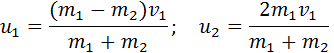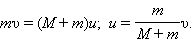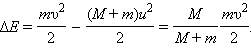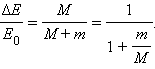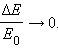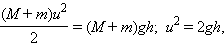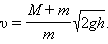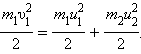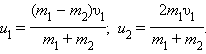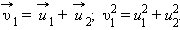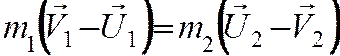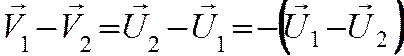Длительность удара
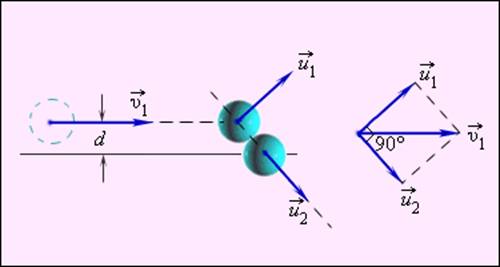
Задача 1. Оценить время упругого удара твердых тел, рассматривая столкновение стержня, налетающего торцом на неподвижную недеформируемую стенку (рис.).
Чаще всего в задачах считают, что упругий удар твердых тел происходит мгновенно, но совершенно очевидно, что это предположение является идеализацией. Столкновение реальных тел всегда занимает конечный промежуток времени $tau$. В самом деле, если бы изменение импульса тела при столкновении происходило мгновенно,
$F = frac{mDelta v}{t_{rightarrow infty}}$,
то сила взаимодействия тел при ударе была бы бесконечно большой, чего, естественно, не бывает.
От чего же может зависеть длительность столкновения?
Допустим, что мы рассматриваем отражение упругого тела от недеформируемой стенки. При столкновении кинетическая энергия тела в течение первой половины столкновения превращается в потенциальную энергию упругой деформации тела. В течение второй половины происходит обратное превращение энергии деформации в кинетическую энергию отскакивающего тела. Такая идея была заложена в задаче тестирования 2005 г. Решите эту задачу, для осмысления этого момента.
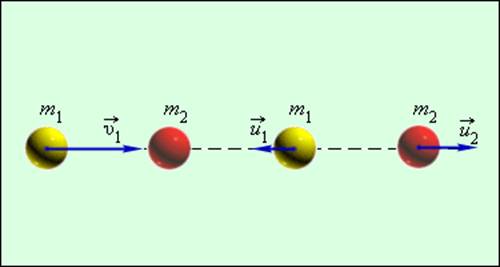
Задача 2. Две абсолютно упругие шайбы массами m1 = m2 = 240 г каждая скользят поступательно по гладкой горизонтальной поверхности навстречу друг другу со скоростями, модули которых v1 = 21 м/с и v2 = 9,0 м/с . Максимальное значение потенциальной энергии E упругой деформации шайб при их центральном столкновении равно … Дж.
Поэтому очевидно, что упругие свойства тела играют определенную роль при столкновении. Итак, можно ожидать, что длительность удара зависит от модуля Юнга материала тела Е, его плотности $rho$ и его геометрических размеров. Возможно, что длительность удара $tau$ зависит и от скорости v, с которой тело налетает на преграду. Нетрудно убедиться, что оценить время столкновения с помощью одних только соображений размерности не удастся. Действительно, если даже взять в качестве налетающего тела шар, размеры которого характеризуются только одним параметром — радиусом R, то из величин Е, $rho$, R и v можно составить бесчисленное множество выражений, имеющих размерность времени:
$tau = sqrt{frac{rho}{E}} cdot f(frac{rho v^2}{E})$, (1)
где $f$ — произвольная функция безразмерной величины $frac{rho v^2}{E}. Поэтому для нахождения $tau$ необходимо динамическое рассмотрение.
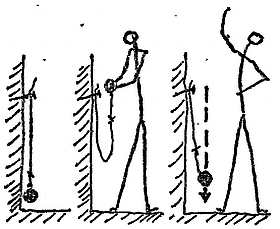
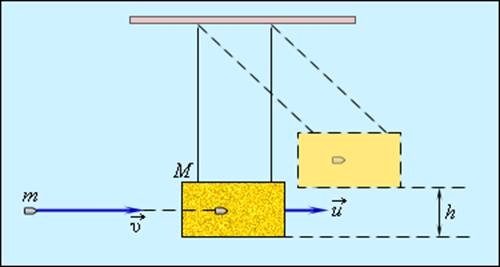
Проще всего такое рассмотрение провести для тела, имеющего форму длинного стержня. Пусть стержень, движущийся со скоростью $v$, налетает торцом на неподвижную стенку. При соприкосновении торцевого сечения стержня со стенкой скорости лежащих в этом сечении частиц стержня мгновенно обращаются в нуль. В следующий момент времени останавливаются частицы, расположенные в соседнем сечении, и т. д.
Участок стержня, частицы которого к данному моменту уже остановились, находится в деформированном состоянии. Другими словами, в этот момент времени деформированной оказывается та часть стержня, до которой дошла волна упругой деформации, распространяющаяся по стержню от места контакта с преградой. Эта волна деформации распространяется по стержню со скоростью звука $u$. Если считать, что стержень пришел в соприкосновение со стенкой в момент времени t = 0, то в момент времени t длина сжатой части стержня равна $ut$. Эта часть стержня на рис. а заштрихована.
В незаштрихованной части стержня скорости всех его частиц попрежнему равны $u$, а в сжатой (заштрихованной) части стержня все частицы покоятся. Первый этап процесса столкновения стержня со стенкой закончится в тот момент, когда весь стержень окажется деформированным, а скорости всех его частиц обратятся в нуль (рис. б).
В этот момент кинетическая энергия налетающего стержня целиком превращается в потенциальную энергию упругой деформации. Сразу после этого начинается второй этап столкновения, при котором стержень возвращается в недеформированное состояние. Этот процесс начинается у свободного конца стержня и, распространяясь по стержню со скоростью звука, постепенно приближается к преграде. На рис. в
стержень показан в тот момент, когда незаштрихованная часть уже не деформирована и все ее частицы имеют скорость $v$, направленную влево. Заштрихованный участок по-прежнему деформирован, и скорости всех его частиц равны нулю. Конец второго этапа столкновения наступит в тот момент, когда весь стержень окажется недеформированным, а все частицы стержня приобретут скорость $v$, направленную противоположно скорости стержня до удара. В этот момент правый конец стержня отделяется от преграды: недеформированный стержень отскакивает от стенки и движется в противоположную сторону с прежней по модулю скоростью (рис. г).
Энергия упругой деформации стержня при этом целиком переходит обратно в кинетическую энергию. Из изложенного ясно, что длительность столкновения τ равна времени прохождения фронта волны упругой деформации по стержню туда и обратно:
$tau = frac{2l}{u}$, (2)
где l — длина стержня. Определить скорость звука в стержне $u$ можно следующим образом.
Рассмотрим стержень в момент времени t (рис. а), когда волна деформации распространяется влево. Длина деформированной части стержня в этот момент равна $ut$. По отношению к недеформированному состоянию эта часть укоротилась на величину $vt$, равную расстоянию, пройденному к этому моменту еще недеформированной частью стержня. Поэтому относительная деформация этой части стержня равна $frac{v}{u}$.
На основании закона Гука
$frac{v}{u} = frac{1}{E} cdot frac{F}{S}$, (3)
где S — площадь поперечного сечения стержня, F — сила, действующая на стержень со стороны стенки, Е — модуль Юнга.
Поскольку относительная деформация $v/u$ одинакова во все моменты времени, пока стержень находится в контакте с преградой, то, как видно из формулы (3), сила F постоянна. Для нахождения этой силы применим закон сохранения импульса к остановившейся части стержня. До контакта с преградой рассматриваемая часть стержня имела импульс $rho Sut cdot v$, а в момент времени t ее импульс равен нулю. Поэтому
$rho Sut cdot v = Ft$. (4)
Подставляя отсюда силу F в формулу (3), получаем
$u = sqrt{frac{E}{rho}}$. (5)
Теперь выражение для времени $tau$.
Деформация столкновения стержня со стенкой (2) принимает вид
$tau = 2l cdot sqrt{frac{rho}{E}}$. (6)
Время столкновения $tau$ можно найти и иначе, воспользовавшись для этого законом сохранения энергии. Перед столкновением стержень недеформирован и вся его энергия — это кинетическая энергия поступательного движения $frac{1}{2}mv^2$. Спустя время $tau$/2 с начала столкновения скорости всех его частиц, как мы видели, обращаются в нуль, а весь стержень сказывается деформированным (рис. б). Длина стержня уменьшилась на величину $Delta l$ по сравнению с его недеформированным состоянием (рис. д).
В этот момент вся энергия стержня — это энергия его упругой деформации. Эту энергию можно записать в виде
$W = frac{1}{2}kDelta l^2$
где k — коэффициент пропорциональности между силой и деформацией: $F = kDelta l$.
Этот коэффициент с помощью закона Гука выражается через модуль Юнга E и размеры стержня:
$sigma = frac{F}{S} = frac{Delta l}{l}E, F = SEfrac{Delta l}{l}$ и $F = kDelta l$,
отсюда
$k = frac{ES}{l}$. (7)
Максимальная деформация $Delta l$ равна тому расстоянию, на которое перемещаются частицы левого конца стержня за время $tau$/2 (рис. д). Так как эти частицы двигались со скоростью $v$, то
$Delta l = frac{vtau}{2}$. (8)
Приравниваем кинетическую энергию стержня до удара и потенциальную энергию деформации. Учитывая, что масса стержня $m = rho Sl$, и используя соотношения (7) и (8), получаем
$frac{rho Slv^2}{2} = frac{ES}{2l} cdot (frac{vtau}{2})^2$,
откуда для $tau$ снова получаем формулу (6). Это время столкновения обычно очень мало.
Например, для стального стержня (E = 2 x 1011 Па, $rho$ = 7,8 x 103 кг/м3) длиной 28 см вычисление по формуле (6) дает $tau$ = 10-4 с. Силу F, действующую на стенку во время удара, можно найти, подставляя скорость звука в стержне (5) в формулу (4):
$F = Svsqrt{rho E}$. (9)
Видно, что сила, действующая на стенку, пропорциональна скорости стержня перед ударом. Но для применимости приведенного решения необходимо, чтобы механическое напряжение стержня F/S не превосходило предела упругости материала, из которого изготовлен стержень. Например, для стали предел упругости (F/S)max = 4 x 108 Па. Поэтому максимальная скорость v стального стержня, при которой его соударение с преградой все еще можно считать упругим, оказывается согласно формуле (9) равной 10 м/с. Это соответствует скорости свободного падения тела с высоты всего лишь 5 м. Укажем для сравнения, что скорость звука в стали $u$ = 5000 м/с, т. е. $v << u$. Время столкновения стержня с неподвижной преградой (в отличие от силы) оказалось не зависящим от скорости стержня.
Этот результат, однако, не является универсальным, а связан со специфической формой рассматриваемого тела. Например, для упругого шара время столкновения со стенкой зависит от его скорости. Динамическое рассмотрение этого случая оказывается более сложным. Связано это с тем, что и площадь соприкосновения деформированного шара со стенкой, и действующая на шар сила в процессе столкновения не остаются постоянными.
Содержание:
Столкновения:
Наиболее общим явлением, наблюдаемым в природе, является взаимодействие материальных тел. Бильярдные шары, сближаясь, в момент соприкосновения взаимодействуют друг с другом. В результате этого меняются скорости шаров, их кинетические энергии. О таком взаимодействии шаров говорят как об их столкновениях.
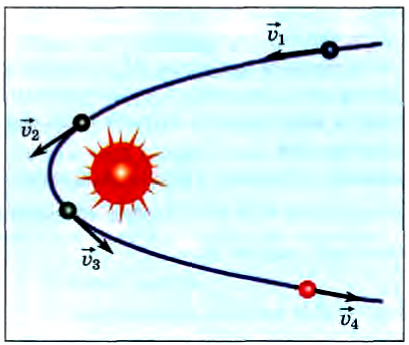
Но понятие «столкновение» относится не только к взаимодействиям, происходящим в результате соприкосновения материальных тел. Комета, прилетевшая из отдаленных областей пространства и прошедшая в окрестности Солнца, меняет свою скорость и удаляется. Этот процесс также является столкновением. хотя непосредственного соприкосновения между кометой и Солнцем не произошло, а осуществлено оно было посредством сил тяготения.
Характерная особенность этого взаимодействия, дающая нам возможность рассматривать его как столкновение, заключается в том, что область пространства, в котором оно произошло, относительно мала. Заметное изменение скорости кометы происходит вблизи Солнца (рис. 129).
Приведенные примеры позволяют нам дать следующее определение столкновения.
Что такое столкновение
Столкновением называется взаимодействие двух и большего числа тел, которое происходит в относительно малой области пространства в течение относительно малого промежутка времени. Вне этого промежутка времени можно говорить о начальных и конечных импульсах тел, когда тела можно считать невзаимодействующими.
Столкновение материальных тел часто называется ударом. Удар определяется как процесс, при котором изменяются импульсы соударяющихся тел без существенного изменения их положений. Это частный случай столкновения, например столкновение шаров, шайб, автомобилей и т. п.
Процессы столкновения являются чрезвычайно сложными. Например, при столкновении двух шаров в момент их соприкосновения начинается деформация шаров. В результате часть кинетической энергии переходит в потенциальную энергию деформации. Затем энергия деформации снова превращается в кинетическую, однако не полностью — часть энергии превращается во внутреннюю. Кроме того, после столкновения шары будут вращаться по иному, чем до столкновения.
Главный интерес при рассмотрении столкновений заключается в знании не самого процесса, а результата. Ситуация до столкновения называется начальным состоянием, а после — конечным. Между величинами, характеризующими начальное и конечное состояния, соблюдаются определенные соотношения. независящие от детального характера взаимодействия. Такими величинами. в частности, являются импульс и энергия системы тел.
В зависимости от характера изменения кинетической энергии тел все столкновения делятся на упругие и неупругие.
Если при столкновении кинетическая энергия тел сохраняется, то столкновение называется упругим, если же не сохраняется — неупругим.
Рассмотрим вначале абсолютно неупругое столкновение (абсолютно неупругий удар). Это частный случай неупругого столкновения, при котором после столкновения тела «слипаются» и движутся вместе.
Пусть в некоторой инерциальной системе отсчета первое тело массой m1 движется до столкновения со скоростью υ1, а второе тело массой m2 — со скоростью υ2. Следовательно, импульсы тел до столкновения равны соответственно:
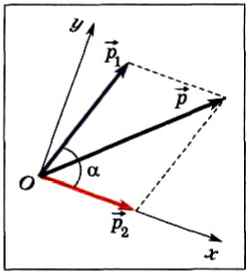
Процесс столкновения обычно наглядно представляют с помощью векторной диаграммы импульсов (рис. 130). Нетрудно убедиться, что кинетическая энергия системы не сохраняется. До столкновения она составляет:
после столкновения —
Изменение кинетической энергии:
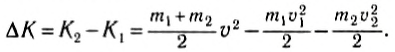
Для расчета выберем оси координат так, как показано на рисунке 130, и спроектируем на них равенство (1). B результате получим:
Рис. 130
Отсюда легко находится квадрат скорости тел после столкновения:
Подставив полученное выражение в (2), получим после несложных преобразований:
Как видно, кинетическая энергия системы уменьшилась. Часть кинетической энергии превратилась в теплоту.
Если тела при столкновении не «слипаются», то скорости тел после столкновения можно найти из закона сохранения импульса:
где штрихом отмечены импульсы тел после столкновения.
При этом кинетическая энергия может как уменьшаться, так и увеличиваться. Последнее происходит, например, при различных взрывах. В этом случае часть внутренней энергии превращается в кинетическую энергию осколков.
Как уже отмечалось, при упругом столкновении выполняется закон сохранения импульса и механической энергии.
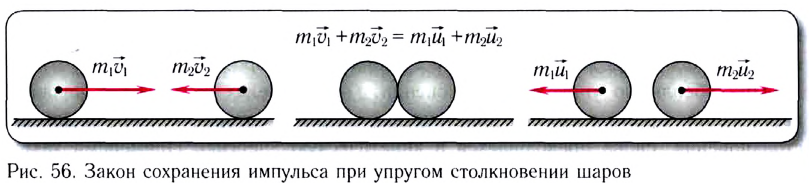
Рассмотрим вначале лобовое столкновение, т. е. такое столкновение, при котором импульсы тел до и после столкновения параллельны некоторой прямой. Эту прямую мы примем за ось Ox (рис. 131). Закон сохранения импульса в этом случае примет вид:
а закон сохранения кинетической энергии —
Из этих уравнений найдем скорости тел после удара. Для этого перепишем (3) и (4) следующим образом:
Воспользовавшись тем, что a2 — b2 = (a-b)(a + b), из выражений (5) и (6) легко получить:
Выразив отсюда, например, 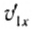
Аналогично:
Проекции импульсов тел после столкновения равны соответственно:
и
Проанализируем полученные выражения для некоторых частных случаев.
Предположим, что тело 2 до столкновения покоилось, т. е. 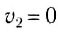
Тогда
При равных массах тел m1 = m2 получим:
Значит, первое тело остановится, а второе придет в движение с таким же импульсом.
Теперь предположим, что масса второго тела намного больше массы первого. Тогда, пренебрегая m1 по сравнению с m2 , получим:
Значит, первое тело отскочит назад с таким же по модулю импульсом, а тело 2 получит импульс, равный удвоенному значению импульса первого тела.
Найдем кинетическую энергию тел после столкновения для случая, когда 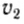
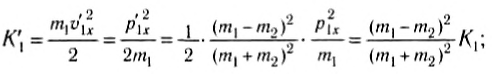
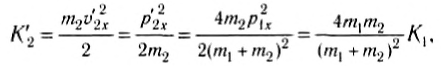
где K1 — кинетическая энергия первого тела до столкновения.
Из полученных выражений следует, что при m1 = m2 первое тело останавливается, а второе приобретает ту же энергию. Если масса второго тела m2 намного больше массы первого m1 то из (10) и (11) следует, что 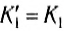
- Заказать решение задач по физике
Главные выводы:
- Столкновением называется взаимодействие двух и большего числа тел, которое происходит в относительно малой области пространства в течение относительно малого промежутка времени.
- Удар определяется как процесс, при котором изменяются импульсы соударяющихся тел без существенного изменения их положений.
- Столкновение тел называется упругим, если кинетическая энергия тел сохраняется. При неупругом столкновении кинетическая энергия тел не сохраняется.
- При столкновениях тел выполняется закон сохранения импульса.
Определение столкновения
Законы сохранения энергии и импульса позволяют провести теоретическое исследование процессов столкновения тел без описания сил, действующих между ними.
Под столкновениями понимают механические процессы взаимодействия между телами, происходящие за очень короткий промежуток времени. При этом силы взаимодействия между сталкивающимися телами настолько велики, что внешними силами, действующими на систему, можно пренебречь.
Вследствие того, что длительность столкновения мала по сравнению со временем наблюдения, различают механические состояния до и после столкновения, причем тела, находящиеся на большом расстоянии друг от друга, считают свободными.
Длительность столкновения бильярдных шаров 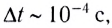
Различают упругие (абсолютно упругие) и неупругие столкновения. В первом случае не происходит выделения теплоты, и механическая энергия сохраняется. Во втором случае выделяется некоторое количество теплоты, поэтому механическая энергия после столкновения уменьшается.
Примером упругих столкновений служат столкновения металлических шаров, а примером неупругих — столкновения пластилиновых шаров, которые при этом слипаются и продолжают движение как одно целое.
Для макроскопических тел в большей степени характерными являются неупругие столкновения, в то время как для физики элементарных частиц, ядер атомов, молекул определяющую роль играет упругое взаимодействие.
Если в процессе столкновения тел на них не действуют внешние силы, то к телам применим закон сохранения импульса, а во многих случаях — и закон сохранения механической энергии. Именно эти законы позволяют, зная скорости тел до столкновения, определить их скорости после столкновения, совершенно не интересуясь тем, что происходило во время него.
При абсолютно неупругом столкновении скорости обоих взаимодействующих тел оказываются одинаковыми. Примером таких тел являются тела из различных пластичных веществ. Такое столкновение можно наблюдать, если подвесить тары из пластилина, развести их в разные стороны и отпустить. После столкновения они оба будут двигаться вместе с одинаковой скоростью.
При абсолютно упругом столкновении в обоих телах не остается никаких деформаций. Кроме того, вся кинетическая энергия, которой тела обладали до столкновения, снова превращается в кинетическую энергию. Примерами таких тел являются шары из стали или слоновой кости.
Рассмотрим простейшее столкновение — центральное, когда скорости тел находятся на линии, соединяющей их центры. Очень часто такое столкновение называют лобовым.
Скорость движения 
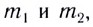
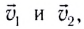
Откуда находим
Определим «потери» механической энергии, найдя кинетическую энергию
тел до столкновения:
и после столкновения:
Тогда часть механической энергии, перешедшая во внутреннюю, определяется выражением:
Следовательно, она зависит от масс сталкивающихся тел и относительной скорости 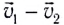
Задача о центральном абсолютно неупругом столкновении впервые была решена Дж. Валлисом в 1669 г.
При абсолютно упругом столкновении двух тел массами 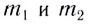
Здесь 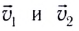
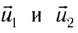
Преобразуем систему уравнений (3), перенеся в правую часть все величины, относящиеся к первому телу, а в левую — ко второму:
Разделив второе уравнение на первое, получим
Перепишем это уравнение в виде 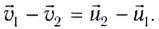
Из него следует, что при центральном абсолютно упругом столкновении тел любой массы их относительная скорость до и после столкновения не изменяется.
Теперь можно дать еще одно определение неупругого столкновения: если относительная скорость тел при центральном столкновении изменяется, то такое столкновение называется неупругим.
Меру неупругости k можно определить как отношение относительных скоростей сталкивающихся тел после и до столкновения:
Она называется коэффициентом восстановления и впервые была измерена Ньютоном в 1687 г. В частности, Ньютон получил значения коэффициента для стали k = 0,55 и стекла k = 0,94, которые приводят и современные справочники.
Абсолютно неупругим является столкновение, при котором скорости тел после столкновения равны 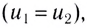
Решая уравнение (4) совместно с первым уравнением системы (3), находим скорости тел после столкновения:
На самом деле при столкновении всегда происходят «потери» механической энергии, т. е. переход части ее в теплоту. Но при малых «потерях» действительный процесс достаточно хорошо описывается абсолютно упругим столкновением.
Задача о центральном абсолютно упругом столкновении впервые была решена X. Гюйгенсом и К. Реном в 1669 г.
Отметим, что осуществить центральное, или лобовое, столкновение на практике очень трудно. Подавляющее число столкновений являются нецентральными.
Основные формулы
Импульс тела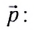
Закон изменения импульса системы тел:
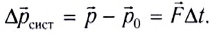
Закон сохранения импульса системы тел:
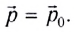
Работа:
Средняя мощность:
Мгновенная мощность:
Кинетическая энергия:
Теорема о кинетической энергии:
Потенциальная энергия:
Потенциальная энергия упруго деформированного тела:
Закон сохранения механической энергии:
- Рычаг в физике
- Блоки в физике
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Механическое давление в физике
«Действие равно противодействию.»
Ньютон
«Если он не погасит свои фары, то я не погашу свои.»
«ЗАДАЧИ»
А. Снаряд массой 1 кг движется горизонтально со скоростью 600 м/сек. Какую силу он развивает?
В. 10-тонный грузовик, движущийся со скоростью 48 км/час, врезается в стену и останавливается. Какова сила столкновения?
Эти вопросы кажутся разумными, да и ответы на них как будто имеют важное значение. На самом же деле в той форме, в какой эти вопросы поставлены, они бессмысленны. Движущийся снаряд не создает усилия в направлении своего движения и не нуждается в приложении силы, чтобы двигаться; авторы задачи пытаются ввести вас в заблуждение, в котором пребывали греки и средневековые последователи Аристотеля. Неизменное движение не связано ни с какой силой, а чтобы придать телу ускорение, к нему нужно приложить силу извне. Даже зная изменение скорости, как в «задаче» В, мы не сможем ответить на поставленный вопрос, поскольку не знаем, за какой промежуток времени происходит это изменение скорости, и, следовательно, не можем вычислить ускорение[121].
Кажущаяся разумность этих задач вызвана ошибочным представлением о силе и движении. Когда мы говорим «ошибочным», мы не просто осуждаем одну точку зрения и воздаем должное другой, мы снова обращаемся к эксперименту, рассматривая его как критерий правильности. Ни один инженер или физик не в состоянии создать прибор или аппарат для измерения «силы» снаряда в полете.
Прикрепленные к снаряду пружинные весы вообще не покажут никакой силы, пока снаряд движется свободно. Мгновенные фотографии самого снаряда не обнаружат ни растяжения, ни сжатия, т. е. отсутствие напряжений. А поскольку попытки измерить «силу» не дают результата, мы не можем считать понятие «силы» в этом случае сколько-нибудь полезным. Если же движущийся снаряд (или движущийся грузовик) сталкивается с каким-нибудь предметом и изменяет скорость, то это связано с реальной силой, с усилием, которое вы можете почувствовать, с чем-то таким, что можно измерить пружинными весами или обнаружить по производимым деформациям. Фотографии снаряда, снятые во время столкновения его со стальной стеной, обнаруживают заметное сжатие и используются для оценки действовавшей силы[122].
Вычисление силы по изменению количества движения Если мы считаем, что соотношение F = M∙a дает в обобщенной форме верное описание поведения природы, то, зная массу тела М и ускорение а, можно вычислить действующую на тело силу. Так поступают в задачах, встречающихся в технике и почти во всех областях физики, от астрономии до физики атома.
В приведенной выше «задаче» В известна масса, но мы не можем найти ускорение, пока нам не сказали, за какой промежуток времени скорость грузовика изменилась с 48 км/час до нуля. Необходимо знать продолжительность столкновения. Предположим, нам известно, что столкновение длится 0,1 сек. Тогда силу можно вычислить следующим образом:
УСКОРЕНИЕ = Δv/Δt = [(0 при неподвижном грузовике) — (48 км/час)] / 0,1 сек = — 48 км/час / 0,1 сек = —13,2 м/сек / 0,1 сек = —132 м/сек2
Знак минус показывает, что движение замедленное. Знак минус у величины силы показывает, что она направлена против движения и «отнимает» у грузовика то количество движения, которым он обладал. Таким образом,
СИЛА F = M∙a = (10 000 кг)∙(—132 м/сек/сек) = 1 320 000 кг∙м/сек2 ~= 132000 кГ.
Такова сила толчка, с которой стена действует на автомобиль против его движения, заставляя его остановиться. С помощью соотношения F = M∙a можно получить ответ, но это, так сказать, окольный путь. Нам даны масса, изменение скорости и время, требуется найти силу. Нельзя ли изменить соотношение F = M∙a и придать ему другую форму, такую, чтобы в него входили F, t, m и изменение v. Это легко сделать, и мы получим соотношение
F∙t = Δ(Mv),
которое, как показано ниже, представляет собой закон F = M∙a, записанный в иной форме. Попробуем им воспользоваться.
СИЛА∙ВРЕМЯ = Изменение (масса∙скорость),
F∙t = Δ(Mv).
Тогда
F∙(0,1 сек) = Δ(Mv) = — (10 000 кг х 0)конечное значение Mv — (10 000 кг х 13,2 м/сек) начальное значение Mv
Вот каким образом соотношение F = M∙a приобретает тот вид, который фактически был дан ему Ньютоном. (Мы предполагаем, что масса М при изменении количества движения остается неизменной.)
Простой вывод
F = M∙a = M∙(v — v0)/t
в соответствии с определением ускорения.
Умножим обе части равенства на t:
F∙t = M∙(v — v0) = Mv — Mv0,
= (Новое значение Mv) — (Старое значение Mv),
поскольку М остается неизменным:
F∙t = Изменение Mv, т. е. Δ(Mv),
Сжатый вывод
(Здесь мы пользуемся для обозначения длительности действия силы символом Δt вместо t.)
F = M∙a = M∙Δv/Δt
F∙Δt = M∙Δv,
= Δ(Mv)
поскольку М постоянна;
F∙Δt = Δ(Mv), или изменению величины (Mv).
Вывод с использованием математического анализа
F = M∙a = M∙Δv/Δt
Поскольку М постоянна.
Если F постоянна, то левая часть записывается в виде 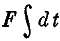
Значит,
F∙Δt = Δ(Mv)
Если F непостоянна, то , «импульс силы», дает произведение (среднее значение силы)∙Δt. Тогда можно записать:
(Среднее значение F)∙Δt = Δ(Mv).
Если М непостоянна (например, масса ракеты, выбрасывающей в полете продукты сгорания), соотношение F = M∙a непригодно, но изменение количества движения Δ(Mv) по-прежнему равно или произведению
(Среднее значение F)∙Δt
Это возвращает нас к определению силы
F = d(Mv)/dt
т. е. сила равна скорости изменения количества движения. Такова первоначальная формулировка Ньютона, которая справедлива даже в теории относительности.
Проработайте предлагаемую ниже задачу на соотношение
F∙Δt = Δ(Mv)
Соотношение F∙Δt = Δ(Mv) представляет собой фактически иную форму записи соотношения F = M∙a и во многих случаях быстрее приводит к цели. Силы следует выражать в ньютонах. Если воспользоваться этим соотношением для вычисления силы, то ответ автоматически получится в ньютонах.
Задача 1(а)
Человек в течение 1/50 сек прикладывает силу 200 ньютон к летящему футбольному мячу, в котором содержится в общей сложности 0,500 кг материала. Насколько быстрее будет двигаться мяч после такого удара?
Приложенная сила равна ___ ньютон.
Время Δt, в течение которого действует сила, равно ___ сек.
Следовательно, увеличение количества движения должно быть равно ___, ньютон∙сек.
(Примечание. Ньютон∙сек должно быть то же самое, что килограмм∙метр/сек.)
Следовательно, поскольку М = 0,500 кг, увеличение скорости должно быть равно ___ м/сек.
Задача 1(б)
Футболист ударяет по покоящемуся мячу массой 0,5 кг и сообщает ему скорость 14 м/сек. Соприкосновение между ногой и мячом длится 1/50 ceк. Вычислите силу, действовавшую при этом столкновении.
[Вместо более утомительного способа, которым вы решали задачу 9 в гл. 7, воспользуйтесь здесь соотношением F∙Δt = Δ(Mv).]
Изменение количества движения равно ___ кг∙м/сек (или ньютон∙сек). Следовательно, действующая сила должна быть равна ___ ньютон.
Эта же сила в «плохих» единицах равна приблизительно ___ кГ.
Задача 1(в)
Футболист ударяет по мячу массой 1/2 кг, летящему на него со скоростью 10 м/сек. Мяч отскакивает назад со скоростью 14 м/сек. Столкновение длится 1/50 сек. Вычислите среднюю действующую силу. (Скорость и количество движения — векторы. Обратите внимание на употребление знаков плюс и минус.)
v0 = —10 м/сек, v = + 14 м/сек, t = 1/50 сек.
За 1/50 сек. количество движения меняется от ___ до ___ кг∙м/сек.
Изменение количества движения равно ___ кг∙м/сек.
Следовательно, действующая сила равна = ___. ___ (единицы) ~= ___ кГ.
Количество движения
Мы называем произведение Mv «количеством движения» (это очень удобная величина, и ею широко пользуются в физике).
Тогда соотношение F∙t = Δ(Mv) гласит: «Сила, умноженная на время ее действия, равна изменению количества движения»[123].
При внезапном изменении количества движения время зачастую мало и его записывают в виде Δt, имея в виду «изменение времени дня», например короткий интервал времени между 3 час. 42 мин. 4,60 сек. и 3 час. 42 мин. 4,72 сек. Значит, мы можем писать
F∙Δt = Δ (количество движения), или Δ(Mv).
Единицы
Поскольку соотношение F∙t = Δ(Mv) получено из соотношения F = M∙a, то силу F нужно выражать в тех же абсолютных единицах — ньютонах. Если М дано в кг, a v — в м/сек, то количество движения Mv будет выражено в килограммах, умноженных на м/сек. Это записывают в таком виде[124]: кг∙м/сек. Если Mv выражено в кг∙м/сек, а t — в сек, то F должна быть в ньютонах[125].
Прыжки и столкновения
Попытаемся применить соотношение F∙Δt = Δ(Mv) в задачах о прыжках, совершаемых людьми, и о столкновениях автомобилей. Мы воспользуемся этим соотношением при решении приводимых ниже задач, а также при построении молекулярной теории газов, где оно позволит нам сделать важные предсказания.
В соотношении F∙Δt = Δ(Mv) величина F представляет собой реальную силу, именно ту силу, которая необходима, чтобы произвести заданное изменение количества движения за указанный промежуток времени Δt. Если пол, стена или что-то еще не развивают силы, то количество движения движущегося тела не изменится.
За короткое время может произойти большое изменение Mv, например, когда прыгун опускается на землю или когда автомобиль врезается в стену. В этом случае Δ(Mv) велико, a Δt мало
F∙(малое Δt) = большое Δ(Mv).
Таким образом, сила F должна быть очень велика. При столкновениях развиваются огромные силы, и, хотя они действуют в течение лишь очень коротких промежутков времени, эти силы способны причинить большой ущерб. Чтобы уменьшить F и предотвратить плачевные последствия, нужно увеличивать Δt. Для этого следует при прыжке сгибать ноги в коленях и надевать мягкую обувь, этой же цели служат эластичные предохранительные маты.
Вратари надевают особые перчатки и, задерживая мяч, следят за тем, чтобы их рука отходила назад для удлинения промежутка времени Δt, в течение которого мяч останавливается. В гл. 7, где была приведена задача о прыжке человека на пол, скорость человека изменялась от 5 м/сек до нуля примерно за 1/100 сек.
В этом случае соотношение F∙Δt = Δ(Mv) дает
F∙(1/100 сек) = (100 кг х 0) — (100 кг х 5 м/сек) =
= —500 кг∙м/сек (или ньютон∙сек),
= —50 000 ньютон
(F выражается в ньютонах, поскольку массу мы выражаем в кг, v — в м/сек; F должна быть выражена в абсолютных единицах)
~= 5000 кГ, или 5 тонн силы.
Это настолько большая сила, что действие ее со стороны пола на ступни, которое передается на позвоночник, недопустимо даже в течение 1/100 сек. Не пытайтесь прыгать с таким резким приземлением — можете поплатиться серьезными телесными повреждениями. Но прыжок с высоты 1,2 м можно сделать вполне безопасным. Для этого достаточно просто согнуть ноги в коленях, увеличив Δt в 10–20 раз по сравнению с 1/100 сек и тем самым уменьшив в 10–20 раз силу F.
Футболист, сообщая мячу массой 0,5 кг скорость 20 м/сек ударом ноги, длящимся 1/100 сек, прикладывает к мячу силу, которая дается соотношением
F∙1/100 = (0,5 кг х 20 м/сек) — (0,5 кг х 0)
F = 10/0,01 = 1000 ньютон ~= 100 кГ.
Носок бутсы должен быть очень крепким.
Борец, когда его бросают на ковер, пытается по возможности удлинить время «приземления», расслабив мышцы и распределяя удар об пол на ряд последовательных столкновений, в которых участвовали бы лодыжки, колени, бедра, ребра, плечи.
Перераспределение количества движения
При столкновении тел происходит обмен количеством движения, перераспределение количества движения между телами.
Понаблюдайте за описанным ниже опытом и установите, приобретается или теряется количество движения при столкновениях.
ДЕМОНСТРАЦИОННЫЙ ОПЫТ
Опыт 1. Тележка, движущаяся по рельсовому пути, наклоненному для компенсации трения, налетает на неподвижную тележку; обе тележки сцепляются буферами и продолжают двигаться вместе. На первой тележке укреплена полоска картона, и с помощью фотоэлемента и часов можно определить скорость тележки. Второй фотоэлемент с часами позволяет определить скорость сцепленных тележек после столкновения.
На фиг. 194 показана схема такого опыта.
Фиг. 194. Столкновения.
Часы I показывают время, за которое картонная полоска на тележке А проходит мимо фотоэлемента до столкновения. Часы II показывают время прохождения картонной полоски мимо фотоэлемента после столкновения, когда тележки сцепляются.
Тележка А массой 2,00 кг налетает на стоящую неподвижно тележку В, масса которой равна 4,00 кг. После столкновения тележки сцепляются (суммарная масса их оказывается равной 6,00 кг) и продолжают двигаться вместе с меньшей скоростью. Перед столкновением картонная полоска длиной 0,5 м, укрепленная на тележка А (которая двигалась равномерно), прошла мимо первого фотоэлемента за 0,40 сек. (Мимо второго фотоэлемента тележка А прошла бы тоже за 0,40 сек до столкновения). После столкновения картонная полоска прошла мимо второго фотоэлемента за 1,20 сек. (Полоска была укреплена на тележке А, но поскольку обе тележки после столкновения оказались сцепленными, время прохождения мимо второго фотоэлемента характеризует скорость обеих тележек.) Таким образом, до столкновения:
Скорость тележки А = 0,50 м/0,40 сек = 1,25 м/сек,
Скорость тележки В = 0 м/сек;
После столкновения:
Скорость сцепленных тележек А + В = 0,50 м/1,20 сек = 0,417 м/сек.
Вычислим теперь суммарное количество движения до и после столкновения и посмотрим, приобретается ли количество движения при столкновении или теряется:
до столкновения
Количество движения тележек = (2,00 кг)∙(1,25 м/сек)Тележка А + (4,00 кг)∙(0 м/сек)Тележка В неподвижна = 2,500 кг∙м/сек.
после столкновения:
Количество движения сцепленных тележек = (6,00 кг)∙(0,417 м/сек), = 2,502 кг∙м/сек.
Совпадение в этом случае получилось превосходное, но мы оперировали здесь выдуманными числами. Вам стоит посмотреть как можно больше настоящих демонстрационных опытов, и нужно знать их результат. Все реальные опыты показывают, что в пределах точности, которую обеспечивают приборы, количество движения не приобретается, не теряется, а происходит лишь обмен количеством движения или перераспределение его между телами.
Этот вывод не зависит от рода столкновения. Идет ли речь о легком упругом соударении, столкновении, при котором тела «склеиваются» друг с другом, или о страшном столкновении, сопровождающемся превращением огромных количеств кинетической энергии в теплоту, — все равно количество движения сохраняется. Это дает нам очень важный путеводный принцип, позволяющий произвести анализ столкновений:
ПРИОБРЕТЕННОЕ КОЛИЧЕСТВО ДВИЖЕНИЯ = ПОТЕРЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
или в другой форме:
СУММАРНОЕ КОЛИЧЕСТВО ДВИЖЕНИЯ НИКОГДА НЕ МЕНЯЕТСЯ
Столкновения и закон сохранения количества движения
Столкновения играют очень важную роль: бомбардировка стенок сосуда молекулами газа, производящего на сосуд давление изнутри; рассеяние атомов гелия на ядре атомов золота при прохождении через золотую фольгу; лобовые соударения нейтронов с атомами водорода, которые позволяют определить массу нейтрона; выбивание быстрыми электронами других электронов из атомов и даже соударения световых квантов, когда они, подобно пулям, налетают на электроны, — все это столкновения, к который мы можем с успехом применить наше новое правило и получить какие-то новые знания или глубже понять те или иные явления.
Мы считаем, что это же правило применимо и к «столкновениям» на расстоянии, таким, как гравитационное влияние Солнца на Земле, воздействия одной планеты на другую, медленные и спокойные «столкновения» Луны с нашим океаном, которые мы называем приливами. Действующие силы могут отличаться в деталях, но всеми столкновениями и взаимодействиями управляет, по-видимому, одно и то же правило, сформулированное Ньютоном в такой форме, что его можно было распространить на атомную физику и включить в новое осмысление мира, которое содержится в эйнштейновской теории относительности. Это правило гласит:
ПРИ ЛЮБОМ ВЗАИМОДЕЙСТВИИ В ЗАМКНУТОЙ СИСТЕМЕ (НА КОТОРУЮ НЕ ДЕЙСТВУЕТ ИЗВНЕ РЕЗУЛЬТИРУЮЩАЯ СИЛА) КОЛИЧЕСТВО ДВИЖЕНИЯ, РАССМАТРИВАЕМОЕ КАК ВЕКТОР, СОХРАНЯЕТСЯ.
Количество движения — вектор
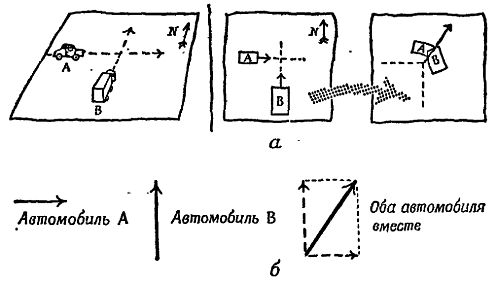
В каждой части соотношения F∙Δt = Δ(Mv) содержится векторная величина. Сила есть вектор, время же не имеет направления в пространстве — это просто число (скажем, число тиканий часов), которое нужно рассматривать как множитель; скорость — вектор, а масса не имеет направления. Масса — это «скаляр», простое число (вроде числа тележек), которое нужно опять-таки рассматривать как множитель. (Умножение скорости 3 м/сек, направленной на восток, на 2 кг дает 6 кг∙м/сек, направленные на восток.) Поэтому мы предполагаем, что импульс силы F∙Δt и количество движения Мv — векторы; эксперимент это подтверждает. Полная формулировка второго закона Ньютона содержит указание на это обстоятельство: сообщаемое ускорение и, следовательно, производимое изменение количества движения совпадают по направлению с направлением приложенной силы. Это может показаться не очень существенным при лобовых столкновениях, когда все движение происходит по одной прямой, но в случае столкновений, происходящих под другими углами, нужно рассматривать количество движения как вектор. Когда сталкиваются автомобили, движущиеся в разных направлениях, и между ними происходит обмен количеством движения, оказывается, что величины Mv подчиняются правилу сложения векторов. На фиг. 195 показано столкновение автомобиля А, движущегося на восток, с автомобилем В, движущимся на север по обледенелой ровной дороге. После столкновения автомобили будут двигаться под некоторым углом к первоначальным направлениям их движения. При этом они будут обладать количеством движения, которое представляет собой векторную сумму количеств движения обоих автомобилей до столкновения.
Фиг. 195. Количество, движения как вектор.
а — движение автомобилей до и после столкновения; б — диаграмма векторов количества движения автомобиля А, автомобиля В и обоих автомобилей вместе.
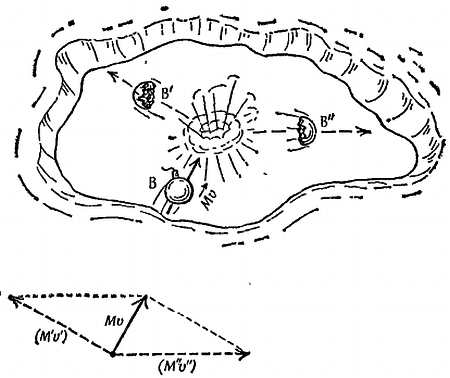
На фиг. 196 показана бомба, скользящая по льду. Бомба разрывается на два осколка, количества движения которых при векторном сложении дают в сумме количество движения бомбы при ее скольжении по льду до взрыва[126].
Фиг. 196. Бомба на льду.
Внизу показана векторная сумма количеств движения обоих осколков.
Чтобы проверить векторный характер закона сохранения количества движения, оставим модель железной дороги с вагончиком и будем наблюдать за столкновением брикетов сухого льда на столе, покрытом листом алюминия. Можно также использовать маятники — стальные шары, подвешенные на длинных нитях[127]. В любом случае мы обнаруживаем, что количества движения после столкновения складываются по правилу сложения векторов, и их сумма равна сумме количеств движения до столкновения. Можно поступить и по-другому: проанализировать наши измерения, разложив каждое Mv на компоненты по двум взаимно перпендикулярным направлениям. Если первоначально двигалось лишь одно тело, то целесообразно выбрать ось х в направлении этого движения, а ось у перпендикулярно к оси х, затем можно разложить все количество движения на х— и у-компоненты. Тогда мы обнаружим, что сумма х-компонент после столкновения равна количеству движения до столкновения, а обе у-компоненты после столкновения равны и противоположны друг другу по направлению.
Может показаться, что рисование и анализ траектории сталкивающихся тел в подобных случаях дело надуманное и бесполезное. Но мы умеем фотографировать траектории отдельных атомов и частей атомов, претерпевающих столкновения, анализ же таких траекторий имеет огромное значение в атомной физике. Электроны, заряженные атомы гелия и другие атомные частицы, пролетая через так называемую камеру Вильсона (о ней рассказано в гл. 39[128]), оставляют отчетливые следы. Если происходит столкновение, то след обнаруживает резкий излом, появляется новый, отходящий в сторону след частицы, испытывающей отдачу, обычно атома газа, в который попала налетающая частица. Зная массы сталкивающихся атомов или атомных частиц, путем построения векторной диаграммы можно извлечь важные сведения о скоростях (количествах движения). Если же известны скорости, то векторная диаграмма позволяет определить отношения масс.
Задача 2. Столкновение ядер
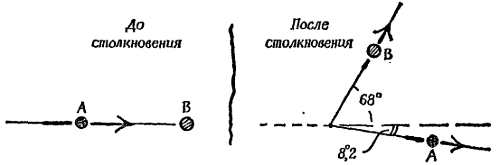
Измерения, выполненные на реальном снимке следов в камере Вильсона, для быстрой альфа-частицы А (ядра гелия), налетающей на неподвижную частицу В (скорости даны в произвольных единицах), позволили получить следующие данные[129]:
До столкновения частица А двигалась со скоростью 2,00 единицы в 1 сек. После столкновения частица А двигалась со скоростью 1,90 единицы в 1 сек в направлении, составляющем 8°,5 с направлением ее первоначальной траектории.
Частица В двигалась после столкновения со скоростью 1,25 единица в 1 сек под углом 68° к направлению первоначальной траектории А (следы обеих частиц образуют Y-образную вилку с углом 76°,5).
Требуется установить природу частицы В, сопоставив ее массу с массой частицы А согласно приведенной ниже методике. Для удобства воспользуемся относительной шкалой атомных масс, принятой в химии, в которой масса ядра гелия А равна 4,0 «атомным единицам массы» (а. е. я,). Тогда, если бы частица В была ядром кислорода, ее масса равнялась бы, 16,0 а. е. м.; в случае азота масса частицы В составляла бы 14,0 а. е. м.; в случае гелия — 4,0 а. е. м., в случае тяжелого водорода — 2,0 а. е. м.; масса ядра обычного водорода равна 1,0 а. е. м.
При определении массы частицы В воспользуйтесь предлагаемым перечнем. (Если у вас получится в ответе какое-нибудь дробное число, например 0,2 или 5,3, то это значит, что вы открыли новую атомную частицу, которую следовало бы как-то назвать в вашу честь.)
а) Начертите на большом листе бумаги в подходящем масштабе векторную диаграмму количеств движения следующим образом: проведите векторы количества движения частицы А до и после столкновения и отметьте количество движения, которое должна приобрести частица В, чтобы в целом количество движения сохранялось.
б) Измерьте вектор количества движения частицы В и, воспользовавшись приведенными данными о скорости, вычислите массу частицы, В.
в) При построении вы, вероятно, воспользовались углом 8,3°, а не 68°. В этом случае измерьте подходящий угол на вашей диаграмме и сравните его с углом 68°. (Получающееся совпадение служит частичной проверкой правил сложения и сохранения количества движения, из которых вы исходили при построении диаграммы.)
Фиг. 197. К задаче 2
г) Если вы знакомы с понятием кинетической энергии тела, которая равна 1/2 mv2 (см. гл. 26[130]), то рассмотрите эту задачу еще раз. Возьмите 4,00 в качестве массы частицы А, а в качестве массы частицы В полученное вами значение и посмотрите, сохраняется ли кинетическая энергия. Если она сохраняется, то взаимодействие представляет собой простое упругое столкновение без каких-либо ядерных превращений. Если же кинетическая энергия не сохраняется, то при взаимодействии должна поглощаться или выделяться ядерная энергия.
Законы сохранения
Что бы ни происходило, количество движения, которое потеряло одно тело, приобретается каким-нибудь другим телом (или телами): векторная сумма количеств движения никогда не меняется.
Чтобы придать этому правилу универсальный характер, необходимо, как мы теперь знаем, учитывать количество движения, уносимое электромагнитными полями, например световыми волнами, и хотя мы по-прежнему вычисляем количество движения в виде произведения (масса)∙(скорость), мы учитываем релятивистское свойство массы возрастать по мере ускорения движения.
Релятивистское изменение массы незаметно при обычных скоростях, даже при астрономически больших значениях скорости, но оно приводит к возрастанию массы и количества движения до бесконечно больших значений, когда мы наблюдаем атомные частицы со скоростями, приближающимися к скорости света.
Это простое правило проверки баланса — суммарное Mv после столкновения равно суммарному Mv до столкновения — делает количество движения чрезвычайно важной и удобной для расчетов величиной. Изучение механики движущихся тел, будь то планеты или атомы, похоже на выслеживание банды преступников, которые постоянно меняют свой внешний облик. Сыщик выискивает признаки, которые можно, пользуясь услугами тайных агентов, распознать и проследить при любых изменениях внешнего облика (специфическая форма уха, золотой зуб, хромота и т. д.).
Ученые установили, что в механике такой неизменной характеристикой является масса: масса сохраняется, говорят они. В течение столетий считали, что вещество неразрушимо и что химические превращения представляют собой лишь обмен частицами вещества.
Тщательное взвешивание химических веществ в колбе до и после химических реакций не обнаружило измеримых изменений общей массы; поэтому ученые выдвинули утверждение о сохранении массы (которое, как они считали, означает сохранение вещества) в качестве универсального правила. Однако этого правила оказалось недостаточно для полного количественного описания столкновений (а в последнее время мы убедились в том, что правило это в его простейшей форме само по себе неверно). В качестве меры движения тела появилось количество движения Mv, когда было установлено, что эта величиа сохраняется. Цепляясь за величину Mv, как за самый надежный ключ к пониманию движения и его измерению, мы по-прежнему рассматриваем сохранение количества движения как прочную основу механики.
Теперь мы располагаем двумя правилами для любой замкнутой[131] системы:
ПРИ ЛЮБОМ ВЗАИМОДЕЙСТВИИ СУММАРНАЯ МАССА М ОСТАЕТСЯ НЕИЗМЕННОЙ
(масса М — скаляр). Это правило называется законом сохранения массы.
ПРИ ЛЮБОМ ВЗАИМОДЕЙСТВИИ СУММАРНОЕ КОЛИЧЕСТВО ДВИЖЕНИЯ Mv ОСТАЕТСЯ НЕИЗМЕННЫМ
(количество движения — вектор). Это правило называется законом сохранения количества движения.
Эти правила позволяют нам делать предсказания или извлечь полезные сведения из измерений. Они представляют собой в известном смысле сущность физики и дают возможность привести природу в стройную систему. (Они напоминают правила проверки бухгалтерского баланса, например: итоговая сумма в графе «приход» должна быть равна итоговой сумме в графе «расход».)
Существуют ли другие подобные правила? Сохраняются ли также величины Mv2, Mv3 и т. д.? Измерения М и v при столкновениях показывают, что величины Mv3 и Mv4 безусловно не сохраняются, поэтому к ним не проявляют интереса и не присваивают им названий. Что же касается величины Mv2, то она представляет интерес: в некоторых случаях она сохраняется, а в других случаях переходит в иные формы весьма важной и удобной характеристики, которую мы называем энергией. Величине Mv2, или, вернее, величине 1/2 Mv2! присвоено наименование кинетическая энергия. Мы вернемся к ней в одной из последующих глав.
Изменение количества движения дается произведением (сила)∙(время). Мы увидим, что изменение кинетической энергии дается произведением (сила)∙(расстояние). Это простое произведение, содержащее силу и размер, и нет ничего удивительного, что величиной 1/2 Mv2 удобно пользоваться.
ПРИМЕРЫ ИЗМЕНЕНИЙ КОЛИЧЕСТВА ДВИЖЕНИЯ
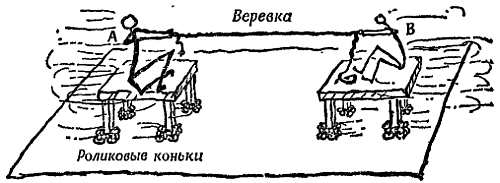
Опыт 2. Грубый опыт со столами на колесах. Студенты А и В сидят на двух столах, снабженных колесиками на шарикоподшипниках (роликовых коньках). Оба стола в начальный момент неподвижны и достаточно удалены друг от друга. Студенты тянут за веревку, и столы сближаются (фиг. 198), пока не столкнутся.
Фиг. 198. Грубый эксперимент.
Если массы (студент + стол) не равны, то туго натянутая веревка сообщает им неодинаковые ускорения. Сближаясь, обе массы приобретают неодинаковые скорости. При столкновении они сводят к нулю количество движения друг друга, и движение прекращается.
Опыт иллюстрирует изменение количества движения, но не дает доказательства его сохранения, если только не измерять приобретаемые количества движения.
Задача 3.
При сближении столов в описанном выше демонстрационном опыте веревка все время туго натянута, ее тянут к себе оба студента или один из них. Предположим, что:
а) студент А крепко держит свой конец веревки, а студент В тянет веревку к себе, поддерживая натяжение постоянным и равным 100 ньютон, или
б) студент В крепко держит свой конец веревки, а студент А тянет веревку к себе, поддерживая натяжение постоянным и равным 100 ньютон, или
в) студенты А и В тянут веревку каждый к себе, поддерживая натяжение постоянным и равным 100 ньютон.
Какие различия вы рассчитываете заметить для этих трех случаев:
1) В относительном движении обоих столов?
2) В движении студента А и стола, на котором он сидит?
(Указание. Студент А и стол обладают определенной массой, к которой приложена сила 100 ньютон.)
3) В количестве веревки, накапливающемся на каждом столе?
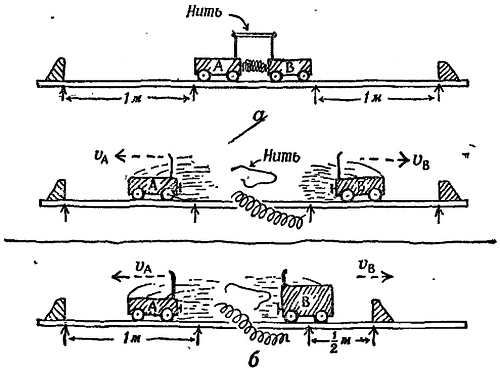
Опыт 3. Тележки, расталкиваемые пружиной (фиг. 199).
Фиг. 199. Движение тележек, расталкиваемых пружиной.
Две игрушечные тележки помещены посередине рельсового пути, у которого компенсировано трение для движения тележек в разные стороны. Между тележками помещена сжатая пружина, которая стремится оттолкнуть их друг от друга, но тележки связаны нитью. Когда нить пережигают, пружина расталкивает тележки, сообщая каждой из них некоторое количество движения; затем пружина перестает действовать, и тележки движутся равномерно.
Если тележки обладают одинаковыми массами, то, как показывают эксперименты, они движутся с равными и противоположно направленными скоростями, например: если тележка А проходит 1 м до какой-то отметки, то тележка В проходит за это же время 1 м в противоположном направлении. Значит, поскольку скорости равны и противоположно направлены (v и —v), а массы равны, количество движения Mv, приобретаемое тележкой В, равно и противоположно по направлению количеству движения —Mv, приобретаемому тележкой А.
Если масса тележки В вдвое больше массы тележки А, то тележка В приобретает вдвое меньшую скорость; если тележка А проходит 1 м, то тележка В проходит за это же время 1/2 м. Если в этом случае тележка А приобретает количество движения —Mv, то тележка В приобретает количество движения 2M(1/2v), направленное в противоположную сторону.
В каждом из этих случаев изменения количества движения равны и противоположны друг другу. Опыты с другими массами, например, когда тело с массой М налетает на тело с массой 3М или тело с массой 2М налетает на тело с массой М, дают аналогичные результаты.
Опыт 4. Опыт с тележками, связанными посредством растянутой пружины (фиг. 200). Этот опыт с игрушечными тележками представляет собой видоизменение опыта 2.
Фиг. 200. Движение тележек навстречу друг другу под действием растянутой пружины.
Две тележки, удаленные друг от друга, помещены на ровный рельсовый путь и соединены длинной растянутой пружиной. После того как тележки отпускают, они сближаются, сталкиваются и сцепляются крючками. Если обе тележки в начальный момент, когда их отпускают, находятся в состоянии покоя, то после столкновения обе сцепленные тележки также будут покоиться.
Мы говорим, что обе массы приобретают равные и противоположно направленные количества движения, которые взаимно уничтожаются при столкновении. Это происходит независимо от того, равны массы тележек или не равны.
Опыт 5. Измерение скорости полета ружейной пули. Если выпущенная из ружья пуля пробивает деревянный брусок и застревает в нем, происходит неупругое столкновение — энергия движения пули в основном превращается в теплоту, но количество движения пули целиком передается бруску. Чтобы измерить скорость пули, вычисляют количество движения, как показано в задаче 4.
Задача 4. Измерение скорости ружейной пули
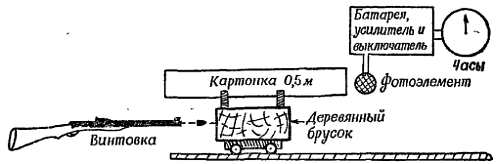
Пуля, выпущенная из ружья, летит горизонтально и попадает в деревянный брусок, положенный на тележку, которая перемещается по рельсовому пути с компенсированным трением (фиг. 201).
Фиг. 201. Измерение скорости ружейной пули на основе сохранения количества движения.
Тележка первоначально покоится, затем пуля застревает в дереве и тележка движется по рельсам с постоянной скоростью. Полоска из картона длиной 0,50 м, укрепленная на тележке, проходит мимо фотоэлемента за 0,80 сек, масса пули, извлеченной из деревянного бруска, равна 0,00300 кг (или 3 г). Масса бруска и тележки, вместе взятых, равна 2,997 кг. Чтобы найти первоначальную скорость пули, обозначьте ее через V м/сек и воспользуйтесь законом сохранения количества движения.
а) Чему равна скорость тела (брусок + тележка + пуля) после столкновения?
б) Обозначьте скорость пули до столкновения через V м/сек. Чему равно количество движения пули до столкновения?
в) Чему равно количество движения тела (брусок + тележка) в состоянии покоя до столкновения?
г) Чему равно суммарное количество движения до столкновения?
д) Чему равна масса всех трех тел, вместе взятых, после столкновения?
е) Чему равно количество движения всех трех тел, вместе взятых, после столкновения?
ж) Воспользуйтесь в качестве исходного предположения законом сохранения количества движения и запишите ваше предположение в виде уравнения, используя полученные выше результаты. Найдите значение V.
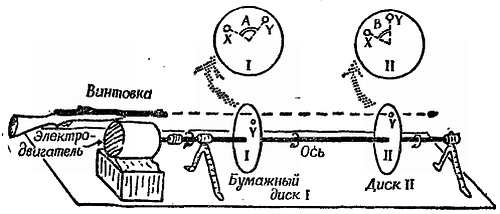
Этот метод используют на практике в баллистике. (Деревянный брусок не укрепляют на тележке, а обычно подвешивают в виде маятника. При этом изменяется геометрия опыта, но принцип, лежащий в его основе, остается прежним.) Метод основав на предположении о сохранении количества движения; скорость пули можно измерить и другими способами; получаемые при этом результаты совпадают с нашими. На фиг. 202 показан принципиально иной метод измерения, который может служить проверкой результата, полученного предыдущим методом. Пуля пролетает через два бумажных диска, укрепленных на оси, вращающейся с известной скоростью, и оставляет в дисках отверстие Y. При неподвижной оси с помощью выстрела проделываются «стандартные отверстия» X. Угловое смещение отверстий (А — В) служит мерой времени пролета пули.
Фиг. 202. Другой метод измерения скорости ружейной пули.
Третий закон Ньютона
Если мы уверены, что количество движения Mv сохраняется (никогда не теряется и не создается вновь, а происходит лишь обмен количеством движения между телами), то можно сделать вывод, что два тела, которые сталкиваются или взаимодействуют между собой, должны действовать друг на друга с равными и противоположно направленными силами. Это третий закон движения Ньютона:
ДЕЙСТВИЕ РАВНО ПРОТИВОДЕЙСТВИЮ
Вот доказательство этого утверждения.
Предположим, что два тела, А и В (фиг. 203), сталкиваются друг с другом (или обмениваются количеством движения каким-нибудь иным способом). Обозначим изменение количества движения тела А через Δ(Mv)A, а изменение количества движения тела В — через Δ(Mv)В. Тогда, если количество движения сохраняется, Δ(Mv)A и Δ(Mv)В должны быть равны и противоположно направлены
Δ(Mv)В = — Δ(Mv)A
(То же можно записать и по другому: полное изменение количества движения, Δ(Mv)A + Δ(Mv)В, должно быть равно нулю.)
Но для тела А изменение количества движения равно
Δ(Mv)A = (Сила, действующая на A)∙Δt,
а для тела В изменение количества движения равно
Δ(Mv)В = (Сила, действующая на В)∙Δt
Физ. 203. Силы, действующие во время столкновения.
При столкновении со стороны каждого тела, действует на другое одна сила.
Время Δt одно и то же для обоих тел, поскольку столкновение тела А с телом В не может длиться больше, чем столкновение тела В с телом А (Δt — это просто продолжительность столкновения обоих тел).
Следовательно, если количество движения сохраняется, то
(Сила, действующая на A)∙Δt = —(Сила, действующая на В)∙Δt,
или
(Сила, действующая на A) = —(Сила, действующая на В)∙Δt.
Таким образом, (сила, действующая на А) и (сила, действующая на В) равны и противоположны друг другу,
ДЕЙСТВИЕ РАВНО ПРОТИВОДЕЙСТВИЮ.
Существует мнение, что сохранение количества движения — это экспериментально установленный факт, и поэтому считают, что третий закон Ньютона хорошо проверен на опыте. Другие рассматривают третий закон как аксиому, своего рода предварительную формулировку способа, которым мы собираемся исследовать природу. Они предостерегают нас, заявляя, что сохранение количества движения нельзя доказать экспериментально. Можно лишь получить иллюстрацию этого принципа, поскольку те же или аналогичные эксперименты, которые берутся для вычисления Mv, мы используем для измерения масс.
Независимо от того, рассматриваем ли мы третий закон Ньютона как экспериментальный факт или основную аксиому, мы пользуемся им во всех областях физики, этот закон формирует наше мышление, не приводя к противоречиям. Сам Ньютон не провозглашал торжественное рождение третьего закона и не пытался внедрять его императивно. Он сформулировал его как рабочую гипотезу, которой собирался пользоваться, приняв ее для построения механики; однако он подверг эту гипотезу еще тщательной проверке, проводя опыты по столкновению маятников. (Прочтите описание экспериментов Ньютона, данное им самим, и обратите внимание, как остроумно он справился с сопротивлением воздуха.)
Если вы понимаете смысл третьего закона, а часто его понимают неправильно и даже неправильно излагают в учебниках, то, пожалуй, сможете пользоваться им не хуже самого Ньютона.
Мощный инструмент для решения задач
Теперь вы видите, каким мощным инструментом может служить закон сохранения количества движения при решении задач. Если в системе происходят какие-то явления, то между одной частью системы и другой ее частью могут возникать многочисленные внутренние силы, но они появляются в виде пар равных и противоположно направленных сил (третий закон Ньютона). Поэтому они не могут изменить результирующего количества движения. Мы можем проводить расчеты общего характера, не зная о внутренних деформациях и перемещениях и не заботясь о них. Когда мы делим нашу систему на две части, например при рассмотрении столкновения, и говорим, что количество движения, приобретенное одной частью, должно быть отнято у другой, нам не нужно ничего знать о силах, которыми обусловлен этот обмен количеством движения. Эти силы представляют собой пары равных и противоположно направленных сил действия и противодействия. Они являются источником равных и противоположно направленных количеств движения независимо от того, постоянны эти силы или быстро возрастают и снова убывают по величине, возникают эти силы при внезапном столкновении или в результате слабого гравитационного притяжения, приводит действие этих сил к колебаниям молекул (теплота), закручиванию пружин (потенциальная энергия) или полному восстановлению первоначальной энергии движения. Так, если пуля вылетает с большой скоростью из ружья и попадает в деревянный брусок, лежащий на абсолютно гладком столе, то скорость скольжения бруска (вместе с пулей) можно вычислить, зная массы и первоначальную скорость пули и предполагая, что количество движения сохраняется. Для расчета не нужно знать в деталях, что происходило с пулей. Как правило, пуля пробивает древесные волокна, разрывая их, в результате чего температура волокон повышается, и в конце концов вся энергия движения пули растрачивается, превращаясь в теплоту. Если пуля ударится о кусок металла, находящийся внутри деревянного бруска, то пуля нагреется сама и может расплавиться. Внутрь деревянного бруска можно поместить приспособление, которое захватывало бы пулю так, чтобы при этом энергия ее движения расходовалась на сжатие пружины или вызывала вращение небольшого колеса. В любых случаях конечная скорость бруска будет одной и той же при условии, что пуля застревает в нем.
Столкновение и «соприкосновение» — слово, которое вводит в заблуждение
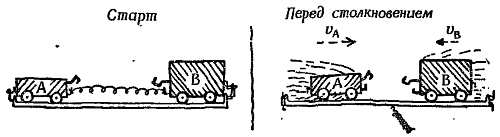
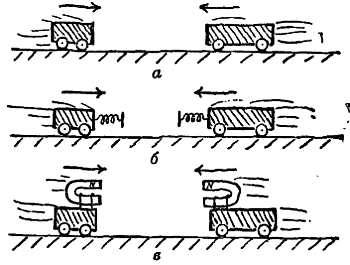
Толкните навстречу друг другу две тележки, стоящие на рельсовом пути «без трения» (фиг. 204).
Фиг. 204. Столкновения.
а — удар; б — пружинные буфера; в — взаимное отталкивание магнитов.
Тележки будут двигаться с постоянными скоростями, пока не произойдет столкновение, сопровождающееся ударом; затем после очень кратковременного соприкосновения тележки отскакивают одна от другой, обладая другими скоростями, но с тем же самым суммарным количеством движения. Если снабдить тележки буферами из хороших стальных пружин, то столкновение будет более продолжительным и мы сможем подробно изучить его отдельные стадии. Конечные скорости, которыми обладают тележки, оттолкнувшись друг от друга, могут быть больше, чем при столкновении, но количество движения опять-таки сохраняется. Количество движения сохраняется на любой промежуточной стадии столкновения: оно равно суммарному количеству движения тележек перед началом столкновения. Во время столкновения, когда тележки максимально сближаются и пружины сжаты сильнее всего, тележки и пружины движутся все вместе с одной и той же скоростью; эту скорость можно вычислить, поскольку известны общая масса и суммарное количество движения. Мы могли бы приспособить какую-нибудь защелку для сцепления тележек в этот момент, измерить скорость сцепленных тележек и проверить наш расчет. Это может служить проверкой закона сохранения количества движения. Именно это мы и делали в демонстрационном опыте со сталкивающимися тележками, о котором говорилось в начале этой главы (стр. 310). Сделаем теперь «столкновение» еще более мягким — поместим на каждой тележке по большому магниту так, чтобы они отталкивали друг друга. Тогда при сближении тележек магниты, подобно пружине, будут отталкивать друг друга все сильнее и сильнее. Тележки разъедутся в противоположные стороны, не соприкоснувшись, а количество движения при этом опять-таки сохранится. На первый взгляд кажется, что здесь не было настоящего столкновения. Тем не менее в действительности — это типичное столкновение, модель жесткого столкновения, при котором оба тела приходят в контакт, только эта модель выполнена в большом масштабе, с замедленным движением сталкивающихся тел. При столкновении любого типа (магниты, пружины, соприкосновение при ударе) на определенной стадии сближения сталкивающихся тел развиваются равные и противоположно направленные силы, которые «расталкивают» оба тела в противоположные стороны и действуют до тех пор, пока тела снова не удалятся одно от другого.
Магнитное отталкивание начинает ощущаться на довольно больших расстояниях и сильно возрастает на малых расстояниях между телами. Насколько тележки должны приблизиться друг к другу, чтобы направление их движения изменилось под действием взаимного отталкивания магнитов, зависит от начальных скоростей. В широком интервале скоростей взаимного отталкивания магнитов оказывается вполне достаточно.
Когда тела при столкновении приходят в соприкосновение, сопровождающееся ударом, возникают такие же силы, но на значительно меньших расстояниях. Это «близкодействующие» атомные силы, которые практически равны нулю, пока атомы на поверхности одного тела не приблизятся к атомам на поверхности другого тела на очень малое расстояние, значительно меньшее диаметра молекул. Тогда-то и появляются большие силы отталкивания, которые становятся еще значительнее при более тесном сближении[132]. Это и есть соприкосновение тел, внезапное появление сил отталкивания на очень малом расстоянии между телами. «Прикосновения» одного атома к другому не происходит. В масштабе атомов существуют лишь силовые поля, которые отталкивают и притягивают атомы или части атомов, причем интенсивность этих полей резко меняется с расстоянием. Нажмите пальцем на стол, и вы почувствуете, как атомы стола начнут отталкивать атомы вашего пальца, когда палец окажется на очень близком расстоянии от поверхности стола. Как бы сильно или слабо вы ни прижимали палец к столу, вы испытываете лишь небольшое отталкивание, которое передается мышечной ткани пальца и воздействует на нервные окончания[133].
Помимо больших сил, которые, как об этом говорилось выше, развиваются на очень малых расстояниях, между пальцем и столом нет никакого «соприкосновения», или «контакта», — эти термины вызывают отчетливое и в то же время ошибочное представление. Ваш палец, наделенный чувством осязания, напоминает своего рода щуп, который инженеры, занимающиеся исследованиями конструкций, называют «тензодатчиком».
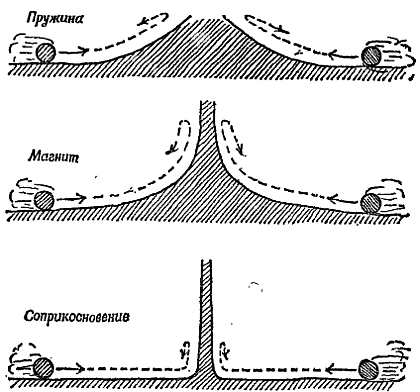
Для иллюстрации столкновений можно предложить другой способ. Заменим тележки катящимися шарами и не будем создавать силы отталкивания, а заставим шары вкатываться вверх по склону соответствующего профиля. На фиг. 205 показаны такие склоны для трех случаев, которые мы только что рассмотрели.
Фиг. 205. Потенциальный барьер.
Симметричный потенциальный барьер соответствует случаю двух одинаковых шариков, сближающихся с одинаковыми скоростями. Одна шар можно поместить на оси симметрии, а другой изобразить катящимся по направлению к первому.
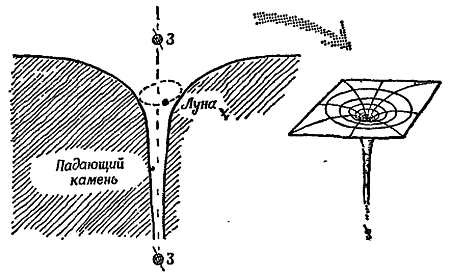
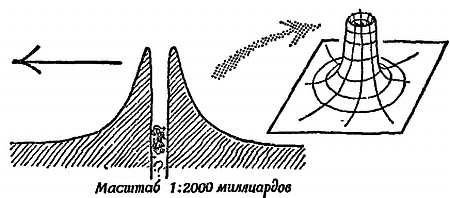
Обратите внимание, что в случае жесткого удара склон оказывается очень крутым, но это не вертикальная стена. (Кривые, описывающие профили этих склонов, называются потенциальными диаграммами, потому что высота склона в каждой точке характеризует потенциальную энергию, запасаемую пружиной, магнитным полем или полем атомных сил во время столкновения, см. гл. 26[134]. Такие потенциальные диаграммы, или потенциальные барьеры, очень полезны при рассмотрении столкновений в ядерной физике. В случае сил притяжения потенциальный барьер превращается в потенциальную яму. На фиг. 206 показана потенциальная яма, создаваемая полем тяготения Земли, а на фиг. 207 — потенциальная яма для случая атомного ядра с потенциальным барьером снаружи.)
Фиг. 206. Потенциальная яма для случая поля тяготения Земли.
Орбита Луны показана в масштабе 1/100 миллиардов.
Фиг. 207. Потенциальная яма и потенциальный барьер для случая атомного ядра.
Таким образом, все столкновения по существу одинаковы. Различие заключается в форме силового поля и не нарушает общего подхода, основанного на законе сохранения количества движения. Все силовые поля, с которыми мы имеем дело в физике, по-видимому, действуют с одинаковыми и противоположно направленными силами: таковы гравитационные силы притяжения, электрические силы отталкивания и притяжения, магнитные силы (которые, как мы считаем, возникают при движении электрических зарядов), а также молекулярные и атомные силы, которые, согласно нашим представлениям, имеют электрическую природу. Пока нам известно очень немногое о ядерных силах.
Поскольку в основе всего нашего подхода к изучению сил и движения лежит принцип «Действие равно противодействию», очень важно понять его смысл.
Смысл принципа «действие равно противодействию»
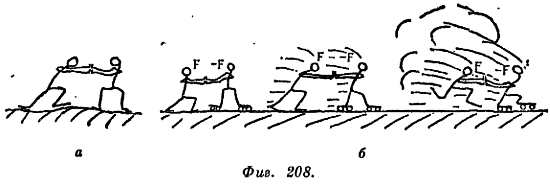
Вы не можете толкнуть меня, не почувствовав сами ответного толчка. Предположим, что мы взялись за руки и вы толкаете меня с силой 100 ньютон в направлении на восток (фиг. 208, а). Автоматически я должен толкнуть вас с силой 100 ньютон в направлении на запад (фиг. 208, б). Не может быть одной силы без наличия второй. Попытка произвести толчок приводит либо к появлению обеих сил, либо обе отсутствуют.
Если мы совершаем равномерное или ускоренное движение, то силы по-прежнему будут равны и противоположно направлены.
Если вы стоите на роликовых коньках, а я, не отрывая рук, вас все время толкаю, то вы приобретете ускорение. Чтобы не отстать, мне, толкая вас, придется бежать все быстрее и быстрее. Но при этом вы по-прежнему будете действовать на меня с такой же силой, с какой я действую на вас, независимо от нашего движения. Обе эти силы равны и противоположно направлены, но это значит, что вообще нет результирующей силы. Мое усилие — это сила, приложенная к вам, и вы чувствуете ее. Сам факт, что при этом вы тоже толкаете меня, не есть действие силы, приложенной к вам. Из двух сил на вас действует только мое усилие. Если это усилие не уравновешивается другими внешними силами, которые также действуют на вас, то вы будете двигаться с ускорением[135].
Парадокс с телегой и лошадью
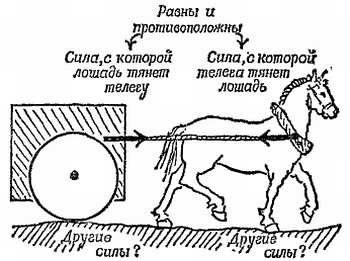
Предположим, что лошадь везет телегу. Тогда телега тянет назад лошадь с такой же точно силой, с какой лошадь тянет телегу вперед (фиг. 209).
Фиг. 209. Задача о лошади и телеге.
Но как же они вообще движутся? Если вас мучает этот вопрос, прочтите приведенные ниже рассуждения; в противном случае их можно без большого ущерба опустить.
Недоумение возникает в связи с тем, что не всегда дают себе труд внимательно разобраться в том, какая сила на что действует. Предположим, что лошадь тянет телегу вперед с силой 100 ньютон. Эта сила действует только на телегу, стремясь придать ей ускорение. Сам факт, что лошадь прилагает силу к телеге, не означает, что сила приложена к лошади. К лошади приложена сила 100 ньютон, с которой телега тянет лошадь назад; эта сила приложена только к лошади. Каждая из этих двух сил действует только на одно тело — на то, которое эта сила тянет, стремясь придать ему ускорение, но силу развивает другое тело.
Лошадь развивает силу 100 ньютон в одном направлении, эта сила действует на телегу.
Телега развивает силу 100 ньютон в противоположном направлении, эта сила действует на лошадь.
Телега. На телегу действуют и другие силы: трение о землю и сопротивление воздуха. Если обе эти силы трения, приложенные к телеге, как раз уравновешивают силу тяги лошади, то результирующая сила, приложенная к телеге, равна нулю и телега будет оставаться в состоянии покоя или двигаться с постоянной скоростью. В этом случае
Сила тяги лошади — Сопротивление трения = Нуль.
Следовательно, ускорение отсутствует. Если сила тяги лошади превышает сопротивление трения, то
Бóльшая сила тяги лошади — Трение = Результирующая сила, направленная вперед (которая сообщает телеге ускорение).
Лошадь. В то же самое время телега тянет лошадь назад, и, чтобы двигаться вперед, лошадь должна отталкивать дорогу назад, заставляя тем самым дорогу толкать ее вперед (еще одна пара равных и противоположно направленных сил). Отталкиваясь от дороги, лошадь испытывает со стороны дороги действие силы, толкающей ее вперед. Если
Сила, с которой дорога толкает лошадь вперед — Сила тяги со стороны телеги — Сопротивление воздуха, испытываемое лошадью = Нуль,
то лошадь движется с постоянной скоростью. Если же лошадь отталкивается от дороги сильнее, так что
Бóльшая сила, с которой дорога толкает лошадь вперед — Сила тяги со стороны телеги — Сопротивление воздуха = Результирующая сила, направленная вперед (которая действует на лошадь),
то лошадь будет двигаться с ускорением.
«Хорошо, — можете возразить вы, — но если рассматривать лошадь и телегу вместе, то почему обе силы (+100 ньютон и —100 ньютон) не уничтожают взаимно друг друга?» Разумеется, так оно и есть. Обе силы взаимно уничтожаются и способствуют движению вперед лошади и телеги не больше, чем усилия человека, тянущего себя одной рукой за другую, помогают ему бежать. Система (лошадь + телега) испытывает направленное вперед усилие со стороны дороги, действующей на лошадь, и сопротивление сил трения. Движение системы зависит от того, что больше.
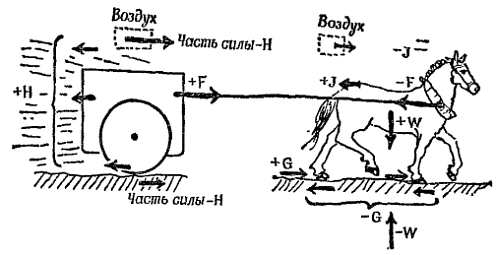
На каждое тело (лошадь), (телега), (лошадь + телега) действует несколько сил. Третий закон Ньютона не говорит о том, являются ли две основные силы, действующие на любой из этих объектов, равными и противоположно направленными. Он требует, чтобы силы взаимодействия для каждой пары тел на фиг. 210 были равны и противоположно направлены.
Фиг. 210. Расположение сил в задаче о лошади и телеге.
Для каждой пары тел мы имеем равные и противоположно направленные силы.
Сила, с которой лошадь тянет телегу, +F и Сила, с которой телега тянет лошадь, — F равны и противоположны.
Другие силы,
действующие в горизонтальной плоскости:
Сила, с которой дорога толкает лошадь, +G и Сила, с которой лошадь толкает дорогу, — G равны и противоположны;
Сумма сил трения, приложенных к телеге, +H и Сумма сил, действующих на дорогу и воздух со стороны телеги, — Н равны и противоположны;
Сила сопротивления воздуха, приложенная к лошади, +J и Сила, действующая на воздух со стороны лошади, — J равны и противоположны;
действующие в вертикальной плоскости:
Сила притяжения лошади Землей, +W и Сила притяжения Земли лошадью, — W равны и противоположны
Такая же пара сил определяет взаимодействие телега — Земля. Но каково соотношение между силами F и G или F и Н, это совсем другой вопрос, который не имеет ничего общего с третьим законом Ньютона. (В то же время, складывая все силы, действующие на одно тело, например силы F и Н, которые действуют на телегу, можно с помощью второго закона Ньютона предсказать ускорение тела.)
«Действие равно противодействию» — почти аксиома
При построении небесной и земной механики Ньютону пришлось иметь дело с притяжением Земли, приложенным к Луне, и с притяжением Луны, действующим на Земле. Если бы мы не могли утверждать, что подобные силы равны и противоположно направлены, то развитие механики сильно осложнилось бы, а то и вовсе стало бы невозможным, даже, пожалуй, лишенным смысла.
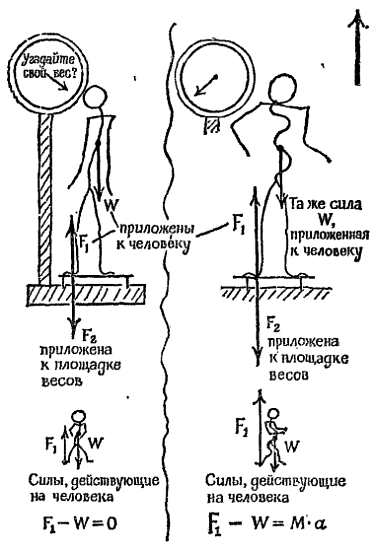
Дело в том, что это свойство сил лежит в основе нашего способа рассмотрения сил в механике. Взвешиваясь, вы фактически измеряете силу давления ваших ступней на площадку весов. Но вы стремитесь измерить силу притяжения вашего тела Землей, и если вы находитесь в состоянии равновесия, то сила земного притяжения уравновешивается реакцией площадки весов. Итак, мы хотим измерить силу земного притяжения W (фиг. 211).
Фиг. 211. Опыт со взвешиванием в ускоренно движущемся лифте.
слева — лифт неподвижен; справа — лифт движется с ускорением.
Мы предполагаем (первый закон Ньютона), что в состоянии равновесия W = —F1, где F1 — реакция площадки весов. Далее (третий закон Ньютона), сила F1 равна и противоположна силе F2 давления тела на площадку весов, и весы измеряют силу F2. Третий закон Ньютона ничего не говорит о соотношении между силой W и любой из сил F1 и F2. Он говорит только о том, что F1 и F2 равны и противоположны друг другу, (Разумеется, самой силе W отвечает равная и противоположная сила реакции, направленная вверх, — притяжение, которое испытывает огромная Земля со стороны вашего тела.)
Если вся эта система тел движется ускоренно вверх (как в лифте в начале подъема), то сила F1 должна быть больше силы W, так что результирующая сила [F1—W] будет придавать ускорение вверх и вашему телу в соответствии с соотношением F = M∙a; но сила F2 по-прежнему будет равна силе F1 и противоположна ей по направлению. В этом случае весы измерят F2 (или F1), но не W.
Демонстрация действия и противодействия
Если равенство действия и противодействия кажется очевидным[136] проявлением симметрии, вы можете рассматривать его как тривиальный факт, своего рода 2 + 2 = 4, и вывести отсюда закон сохранения количества движения. Но большинство ученых считает такой подход чрезмерно наивным и полагает, что равенство действия и противодействия нельзя доказать, не измеряя количества движения.
ОБОДРЯЮЩИЕ ОПЫТЫ
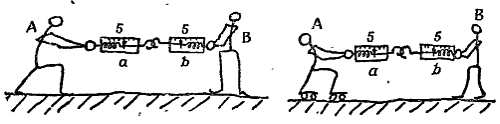
Можно предложить несколько опытов, которые если и не доказывают равенства действия и противодействия, то во всяком случае иллюстрируют этот принцип. Опыты, изображенные схематически на фиг. 213 и 214, кажутся на первый взгляд удачными, но их можно истолковать как проверку самих пружин, проверку, которая ничего не доказывает, если только мы не примем в качестве допущения то, что стремимся доказать.
Фиг. 213. Попытки продемонстрировать принцип «действие равно противодействию».
Показания пружинных динамометров а и b одинаковы, даже если А и В (либо один из них) стоят на роликовых коньках и движутся с ускорением. Динамометр а показывает силу человека A, а динамометр b — силу человека В. Но откуда динамометры знают, чью силу они измеряют?
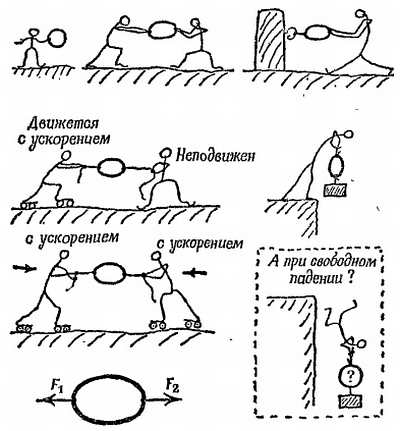
Опыт 6. Пожалуй, лучшим из этих опытов следует считать тот, где меньше всего деталей, запутывающих рассмотрение. На фиг. 214 показан опыт с кольцом из пружинной стали, который демонстрирует силы, возникающие при деформации кольца.
Соображения симметрии не позволяют нам приписать деформацию кольца действию усилия, приложенного именно с одного конца, а не с другого, а заставляют поверить в то, что тянущие силы равны и противоположно направлены. Кольцо деформируется в один и тот же симметричный овал независимо от того, действует ли на него стена или люди, покоятся ли они или движутся любым образом. (В лучшем случае эти опыты приносят нам успокоение. В худшем случае — это надувательство, цель которого заставить нас думать.) Мысль о том, что этот опыт может дать какое-то подтверждение третьего закона Ньютона, все же соблазнительна. Представим себе, что кольцо из пружины становится все тоньше и тоньше, пока его масса не окажется практически равной нулю. В таком случае даже при движении с ускорением на кольцо не должна действовать результирующая сила (первый закон Ньютона). Поэтому обе действующие на кольцо силы должны быть равны и противоположно направлены. Означает ли это, что третий закон Ньютона доказан? Отнюдь нет. Это совсем не те силы, равенство которых мы хотим доказать, а силы, приложенные со стороны разных тел к одному и тому же телу! Мы же хотим узнать, равно ли противодействие кольца, приложенное к одному из тел, силе, приложенной к кольцу со стороны этого тела, и направлено ли оно противоположнотянущей силе.
Ситуация, описываемая третьим законом Ньютона, характерна для каждого конца нашего кольца. Другими словами, дело обстоит еще хуже! Этот результат предостерегает от той опасности, которую таит в себе чересчур смелый подход к доказательствам.
Фиг. 214. Действие и противодействие?
Симметрия кольца дает основание считать, что силы F1 и F2 равны и противоположны друг другу. Это верно, но это на самом деле не те силы, о которых говорится в третьем законе Ньютона.
Всеобщий закон сохранения количества движения
Отныне мы будем рассматривать принцип действие равно противодействию как рабочее правило и, следовательно, будем предполагать, что количество движения всегда сохраняется (если только новые экспериментальные данные не заставят нас изменить свою точку зрения). Кажущиеся противоречия, вроде таинственного «возникновения» количества движения, когда стоящий неподвижно человек вдруг переходит на быструю ходьбу, нас не смущают, мы считаем, что ступни человека придают огромной Земле такое же количество движения, направленное в противоположную сторону, назад. Опыт с подвижной «дорогой» (небольшой платформой на роликах) убеждает нас в правильности этого вывода. Когда человек, стоящий на платформе, делает шаг вперед, платформа начинает двигаться назад (фиг. 215).
Фиг. 215. Сохранение количества движения.
а — человек начинает бежать по подвижной «дороге», платформе на роликах; б — игрушечный поезд движется по ободу колеса, когда поезд трогается по рельсам, колесо испытывает отдачу в обратном направлении.
Такой же результат дает опыт с игрушечным электрическим поездом, движущимся по кольцевому рельсовому пути. Путь уложен на велосипедном колесе с вертикальной осью и свободно вращается. Как только поезд трогается, рельсы начинают двигаться в обратном направлении.
Мы придерживаемся той точки зрения, что закон сохранения количества движения справедлив для молекул, атомов и даже для составных частей атомов. Мы считаем, что этот закон применим ко всем соударениям молекул, в том числе к неупругим столкновениям, когда один атом налетает на другой и выбивает из него какие-нибудь частицы. Этот принцип оказывается настолько плодотворным, что если бы мы натолкнулись на случай, когда количество движения «исчезает», обращается в «ничто» (скажем, при атомном превращении), то могли поддаться искушению придумать какую-то крошечную невидимую частицу, которая уносит недостающее количество движения. Нам пришлось бы выдумать особого рода «демона», встав, вообще говоря, на опасный путь. Антинаучный подход? Да, если вы не найдете иных обоснований для введения демона или применений его!
Мы действительно сталкиваемся с необъяснимым исчезновением количества движения, когда радиоактивный атом выбрасывает электрон — бета-частицу.
В ядерной физике нам пришлось прибегнуть к помощи такого демона — крошечного «нейтрино», частицы, не обладающей ни массой, ни электрическим зарядом, по которым можно было бы обнаружить ее присутствие. В течение многих лет нейтрино оставалось невидимым, и многие действительно считали, что его невозможно обнаружить. Но тогда честно ли было утверждать, что нейтрино существует? Возможно, мы поступали неразумно, рассматривая нейтрино как реально существующую частицу, но как способ устранения незначительных и в то же время существенных нарушений закона сохранения количества движения гипотеза нейтрино была, по-видимому, ничуть не хуже любого другого способа выражения опытной истины. Гипотеза содействовала ясности мышления, и мы поручили нейтрино сразу несколько дел: помимо количества движения, нейтрино уносило некоторую порцию энергии и момент количества движения, восстанавливая баланс и этих величин. Это сделало его более приемлемым: право же, однорукому демону не место в науке! Недавно замечательные поиски физиков-экспериментаторов увенчались успехом: нейтрино было обнаружено. Наш демон занял подобающее место в принятой нами системе классификации научных фактов.
Проработайте предлагаемые задачи, заполняя пропуски, оставленные для ответов.
Задачи на сохранение количества движения
Вычислите полное количество движения в заданном направлении до столкновения, затем вычислите полное количество движения после столкновения. Обозначьте неизвестную вам скорость или силу через X, затем приравняйте суммарное количество движения до столкновения и после столкновения (т. е. предположите, что количество движения сохраняется) и решите уравнение относительно X.
Задача 5
Автомобиль массой 1500 кг, движущийся со скоростью 6 м/сек, догоняет грузовик массой 2000 кг, движущийся со скоростью 3 м/сек в том же направлении, и врезается в грузовик. Найдите скорость, с которой будут двигаться обе машины вместе.
Количество движения всегда сохраняется (т. е. суммарное количество движения не меняется при любом столкновении).
Начальное количество движения легкового автомобиля =
= (___)∙(___)∙____ (единицы)
Начальное количество движения грузовика =
= (___)∙(___)∙____ (единицы)
После столкновения суммарная масса равна ___ кг.
Обозначим скорость обеих машин, движущихся вместе после столкновения, через X м/сек.
Следовательно, количество движения обеих соединившихся машин, выраженное через X, равно (___)∙____ (единицы)
Поскольку суммарное количество движения в направлении вперед одинаково до и после столкновения, то ___ + ___ = ___ м/сек.
Следовательно, решая уравнение относительно X, получаем:
Конечная скорость Х = ___ м/сек.
Задача 6
Автомобиль массой 1500 кг, движущийся со скоростью 6 м/сек, сталкивается «в лоб» с автомобилем массой 2000 кг, движущимся со скоростью 3 м/сек. Найдите скорость обоих автомобилей после столкновения.
Суммарное количество движения до столкновения = количеству движения автомобиля 1 + количество движения автомобиля 2 = ___ + ___ ∙ ___ (единицы)
(Количество движения — вектор, обращайте внимание на знаки плюс и минус.)
Обозначив конечную скорость через X, получим:
Количество движения обоих автомобилей = ___ ∙ ___ (единицы)
Исходя из предположения, что количество движения сохраняется, получим уравнение ___ = ___
Следовательно, конечная скорость X равна ___ м/сек.
Задача 7
На грузовик массой 2000 кг, движущийся в северном направлении со скоростью 30 км/час по обледенелой дороге, налетает легковой автомобиль массой 1000 кг, движущийся по боковой улице в восточном направлении со скоростью 45 км/час. Вычислите скорость обеих машин, указав ее величину и направление.
Примечание. Не переводите километры в метры. Для закона сохранения количества движения это не имеет значения, поскольку ________________
Количество движения грузовика = ___∙___ (единицы) к ___ (направление)
Количество движения легкового автомобиля = ___∙___ = (единицы) к ___ (направление)
Сумма[137] обоих количеств движения представляет собой количество движения, величина которого ___∙___ (единицы), а направление определяется tgA = ___, где угол А — это угол между суммой и северным направлением[138]. На рисунке tgA равен h/b.
Если конечная скорость равна V км/час, то
Конечное количество движения = ___∙___ (единицы)
Если количество движения (вектор) сохраняется, то V должно быть равно ___ км/час.
Задача 8
Орудие массой 100 кг, стоящее неподвижно на абсолютно гладкой поверхности, выпускает горизонтально снаряд массой 1 кг со скоростью 300 м/сек. Найдите скорость отдачи орудия.
Снаряд при вылете из орудия обладает количеством движения ___∙___ (единицы)
Количество движения орудия должно быть
___________________________________
(такое жe? равное и противоположно направленное? большее? меньшее?)
Следовательно, скорость орудия должна быть равна ___ м/сек.
Задачи на изменение количества движения
Задача 9
Человек хочет оторвать от прочной веревки длиной 1 м 20 см кусок длиной 30 см. Он повреждает веревку в том месте, где намерен ее разорвать, затем подвешивает к нижнему концу кусок железа массой 1 кг и привязывает верхний конец веревки к гвоздю, вбитому в стену (фиг. 216).
Фиг. 216. К задаче 9.
Потом человек поднимает кусок железа на высоту гвоздя (при этом веревка свободно свешивается, образуя петлю) и отпускает его. Груз свободно падает, пролетая 1 м 20 см, и туго натягивает веревку резким рывком. Судя по раздавшемуся при этом звуку, рывок длится примерно 1/100 ceк. Веревка разрывается. Оцените величину разрывающей силы.
Задача 10
а) Молоток массой 1 кг, движущийся со скоростью 3 м/сек, ударяет по гвоздю. Гвоздь вошел в твердое дерево и продвигается на очень небольшое расстояние. Молоток отскакивает с малой скоростью. Электронный прибор для измерения промежутков времени показывает, что соприкосновение молотка с гвоздем длится примерно 2/100 сек. Оцените среднее значение силы, действующей на гвоздь во время соприкосновения с молотком.
б) Представьте себе, что молоток ударяет по пружинящему гвоздю и соприкосновение также длится 2/100 сек, но молоток отскакивает от гвоздя почти с той же скоростью, с какой он двигался по направлению к гвоздю, близкой к 3 м/сек. Оцените среднее значение силы, действующей на гвоздь во время соприкосновения с молотком. (Примечание. Если вы получите в ответе нуль, то, очевидно, сделали что-нибудь неправильно. Попробуйте для контроля вставить палец между молотком и гвоздем.)
Задача 11
Реактивный двигатель установлен неподвижно в аэродинамической трубе, в которой воздух движется со скоростью 100 м/сек. Двигатель забирает 18 кг воздуха в секунду; воздух входит в двигатель со скоростью 100 м/сек. После сжатия и нагрева воздух выбрасывается со скоростью 500 м/сек.
а) Чему равна сила тяги двигателя в ньютонах?
б) Чему равна сила тяги двигателя в кГ?
в) Предположим, что двигатель, о котором идет речь, установлен на самолете, летящем со скоростью 100 м/сек (~=360 км/час), и забирает воздух с такой же скоростью. Сила тяги будет примерно такая же, и теперь она толкает самолет вперед со скоростью 100 м/сек (с учетом действия остальных двигателей).
Из следующей главы вы узнаете, что мощность такого двигателя можно рассчитать, помножив силу тяги на скорость.
1) Оцените мощность этого двигателя в «плохих» единицах, кГ∙м/сек.
2) Оцените мощность двигателя в «лошадиных» силах, принимая во внимание, что 1 л. с. = 90 кГ∙м/сек.
Задача 12
Современные зубные врачи пользуются для удаления трудноизвлекаемой пломбы устройством, показанным на фиг. 217.
Фиг. 217. К задаче 12.
Металлический груз В свободно скользит по гладкому металлическому стержню R. В верхней части стержня имеется крючок, которым зацепляют за пломбу. В нижней части стержня сделан металлический упор, чтобы груз не слетал со стержня. Врач зацепляет крючком за пломбу, поднимает груз кверху и затем отпускает его.
Предположим, что груз в таком приспособлении представляет собой кусок металла массой 1 кг и что максимальная скорость этого груза в конце его падения равна 0,5 м/сек.
а) Предположим, что челюсти пациента плотно сжаты и груз останавливается в течение 1/1000 сек. Оцените силу рывка.
б) Предположим, что пациент слегка наклоняет голову, удлиняя время торможения груза до 1/100 сек. Оцените силу рывка в атом случае.
в) Предположим, что приспособление снабжено резиновой прокладкой W, которую можно насадить на стержень так, чтобы она легла на упор. К чему приведет наличие такой прокладки?
Задача 13
Пловец, масса которого 100 кг, способен оттолкнуться от края бассейна с силой 250 кГ.
а) Какую скорость можно приобрести при таком толчке за 1/10 сек?
б) Почему бы не порекомендовать пловцу отталкиваться подобным образом в течение 3/10 сек?
Задача 14
Вор, масса которого (вместе с добычей) равна 125 кг, убегая, налетает на спящую собаку. Столкновение длится примерно 0,1 сек, в результате чего скорость бегущего сократилась на 1,5 м/сек. Какую силу испытывает нога человека?
Задача 15
Отряд завоевателей, штурмующих средневековую крепость, атакует главные ворота с помощью тарана — бревна, масса которого равна 400 кг. Бревно держат на плечах двенадцать человек, которые устремляются в сторону ворот со скоростью 3 м/сек, направив бревно торцом к воротам. Как только таран достигает ворот, нападающие, остановившись, отпускают таран, и он скользит по нашитой на их плечах гладкой кожаной накладке. Таран ломает ворота, отталкивая их на 15 см, прежде чем останавливается.
а) Подсчитайте силу, с которой таран действует на ворота во время столкновения.
б) Один из защитников крепости заявляет: «Если бы моим людям позволили надавить на ворота изнутри, они смогли бы сохранить их. Каждый из них может приложить силу 50 кГ». Сколько потребуется защитников крепости, чтобы спасти ворота?
в) Один из нападающих забыл отпустить таран и зацепился за него. Что произойдет с ним? Проделайте приблизительный расчет.
Задачи на сохранение количества движения
Задача 16
Человек массой 100 кг, движущийся на коньках по гладкому льду со скоростью 10 м/сек, сталкивается лицом к лицу с другим человеком массой 100 кг, стоящим неподвижно. Оба человека, сцепившись, движутся вместе.
а) С какой скоростью они будут двигаться?
б) Предположим, у обоих имеются крупные магниты, которые с большой силой притягивают их друг к другу, когда конькобежец приближается к человеку, стоящему неподвижно. Как это повлияет на скорости обоих людей непосредственно перед столкновением?
в) Предположим, что магниты создают такое же отталкивание. Как оно повлияет на конечную скорость обоих людей? Почему?
Задача 17
Человек массой 100 кг стоит на одном конце длинной плоскодонной лодки, покоящейся на озере. Внезапно он начинает бежать по дну лодки к противоположному концу. Масса лодки (+ количество воды, которая движется вместе с ней) равна 50 кг. Наблюдатель на берегу отмечает, что человек бежит мимо него со скоростью 3 м/сек.
а) Какую скорость лодки зафиксирует этот наблюдатель?
б) С какой скоростью бежит человек по лодке, по его собственному мнению?
Задача 18
Средневековая пушка массой 200 кг устанавливается у края плоской крыши высокой башни. Пушка выпускает ядро массой 5 кг горизонтально. Ядро опускается на расстоянии 300 м от основания башни. Пушка, колеса которой вращаются без трения, тоже движется и падает на землю (фиг. 218).
Фиг. 218. К задаче 18.
а) На каком расстоянии по горизонтали упадет пушка на землю от того места, где она отделилась от крыши? (Примечание. Никаких других данных нет.)
б) Почему размеры крыши башни не входят в расчет?
Задача 19
(Примечание. Приведенная ниже задача кажется довольно глупой, но ее полезно разобрать, имея в виду изучение столкновений молекул.)
Белка массой 1/2 кг сидит на абсолютно гладкой, обледенелой, горизонтальной, плоской крыше. Человек бросает в белку камень массой 1/10 кг, камень летит горизонтально со скоростью 6 м/сек.
1) Белка хватает камень и удерживает его. Вычислите:
а) движущуюся массу до и после захвата камня;
б) количество движения до захвата камня;
в) скорость отдачи белки (вместе с ее грузом); при этом следует исходить из предположения о сохранении количества движения.

3) Объясните, почему в вопросе 2 ответ не изменится, если белка задержит на несколько секунд камень, прежде чем бросить его обратно.
Задача 20
Человек массой 100 кг прыгает с пристани с горизонтальной скоростью 4 м/сек в шлюпку массой 50 кг (в эти 50 кг входит то количество воды, которое движется вместе с лодкой). До прыжка человека лодка покоится (фиг. 219).
Фиг. 219. К задаче 20.
а) Вычислите скорость, с которой лодка вместе с человеком отходит от пристани.
б) Какое расстояние пройдет лодка за 3 сек от того момента, когда в нее прыгнул человек, если пренебречь сопротивлением воды и воздуха?
Задача 21.
а) Мальчик массой 50 кг стоит на плоту массой 500 кг. Плот неподвижен. Он может плыть по поверхности, озера с очень малым трением. Мальчик сначала стоит неподвижно, а потом идет с постоянной скоростью 1 м/сек (по отношению к берегу) и продолжает идти в течение 20 сек. На какое расстояние переместится за это время плот?
б) Предположим, что мальчик идет вдвое быстрее в течение вдвое меньшего промежутка времени. На какое расстояние переместится плот?
в) Предположим, что мальчик идет со скоростью v м/сек в течение t сек. Масса мальчика m кг, а плота М кг. Найдите расстояние, на которое перемещается плот, выразив его через v, t, m, M.
в) Рассмотрите ответы на первые два вопроса, проанализировав третий.
Задача 22.
В настоящей главе описан метод измерения скорости полета ружейной пули (стр. 321). Вы можете сами проделать аналогичное измерение в лаборатории. Для этого потребуется движущаяся по рельсе без трения тележка, на которую положен большой деревянный брусок. Вместо фотоэлемента воспользуйтесь секундомером. Опишите измерения, которые вы стали бы проводить; покажите, как вы будете вычислять скорость пули по результатам измерений.
Задачи на количество движения и силу
Задача 23
Что такое базука? Объясните, почему держащий ее человек не испытывает отдачи при стрельбе.
Задача 24
Два велосипедиста, Альберт и Бертрам, едут рядом по горизонтальному участку дороги со скоростью 3 м/сек, не работая педалями. Альберт — взрослый человек, его масса 80 кг, а Бертрам — мальчик, и его масса 50 кг. В последующих вычислениях трением можно пренебречь. Альберт дает Бертраму толчок в направлении вперед, после чего скорость Бертрама оказывается 6 м/сек.
а) Какова будет после этого скорость Альберта?
б) Бертрам замечает, что толчок длится 2 сек. Каково среднее значение силы, с которой Альберт его толкнул?
Задача 25.
Массивная металлическая болванка покоится на абсолютно гладкой поверхности стола.
1) Шар из слоновой кости массой 1 кг бросают горизонтально в болванку. Происходит лобовое столкновение, и шар отскакивает.
2) Опыт повторяют с куском глины массой 1 кг, его бросают с той же скоростью. После лобового столкновения кусок глины падает и остается неподвижным.
3) С той же скоростью бросают кусок липкой глины массой 1 кг. При лобовом столкновении глина прилипает к металлической болванке и движется вместе с ней.
а) В каком случае (случаях) металлическая болванка приобретает наибольшую скорость: в 1, 2 или 3?
б) В каком случае (случаях) металлическая болванка приобретает наименьшую скорость?
в) Объясните, как вы станете доказывать правильность ваших ответов на вопросы (а) и (б).
Задача 26
Фирма, изготовляющая пулеметы, пишет в своей рекламе: «Наш пулемет настолько эффективен, что способен держаться в воздухе под действием направленного вниз непрерывного потока выпускаемых пуль». (фиг. 220).
Фиг. 220. К задаче 26.
Воспользовавшись приведенными ниже данными и указаниями, выясните, с какой скоростью должен стрелять пулемет.
Масса пулемета 25 кг. Масса каждой стальной пули составляет 1/10 кг, скорость пули при вылете 1300 м/сек.
При взрыве пуля выталкивается вниз по стволу, и одновременно развивается равная и противоположно направленная сила отдачи, приложенная к пулемету. (Сила эта не постоянная, а прерывистая, толчок возникает каждый раз при вылете пули. Однако, если такие толчки следуют один за другим с очень большой частотой, мы можем мысленно сгладить их и получить непрерывно действующую силу. Именно этой «сглаженной» силой здесь и пользуются.)
Предположим, скорость стрельбы составляет X пуль в секунду.
а) Вычислите количество движения, уносимое пулями за промежуток времени 10 сек.
б) Вычислите силу отдачи.
в) Предполагая, что этой силы отдачи как раз достаточно, чтобы поддерживать пулемет висящим в воздухе, вычислите скорость стрельбы.
Задача 27. Второй закон Ньютона в случае переменной массы
По горизонтальному участку пути движется товарный поезд.
Случай I. Поезд движется равномерно с постоянной скоростью.
Случай II. Поезд движется равноускоренно по прямому горизонтальному участку пути.
Случай III. Поезд, который первоначально покоился, внезапно трогается.
Случай IV. Поезд проходит с постоянной скоростью под неподвижным желобом; по желобу в открытые вагоны ссыпают уголь (падающий вертикально), который увеличивает массу поезда, при этом машинист принимает все меры, чтобы при загрузке скорость поезда поддерживалась постоянной.
Для каждого из четырех перечисленных случаев ответьте на следующие вопросы:
а) Изменяется ли количество движения поезда? (Дайте четкое обоснование вашему ответу.)
б) Если да, то какое внешнее тело или источник обусловливает появление силы, необходимой для этого изменения?
в) Какие силы действуют на уголь в случае IV, когда он достигает вагона, попадает в вагон и опускается на дно?
В свете рассмотренной только что задачи соотношение F = Δ(Mv)/Δt представляется более удачным вариантом формулировки второго закона Ньютона, чем соотношение F = M∙a. Почему?
Задача 28.
На плоту, покоящемся на поверхности озера, стоит мальчик. Мальчик начинает шагать по плоту, описывая большой круг, и продолжает двигаться по кругу с постоянной скоростью. (Сопротивлением воды можно пренебречь.)
Как будет вести себя плот? (Попытайтесь сообразить, что произойдет. Ответ будет подсказан в гл. 22[139])
I am afraid that a numerical solution is also difficult. None of the methods mentioned by you and others will work correctly if you don’t have correct initial approximations of the solution, and you could easily miss the first solution. As the function is a combination of trigonometric functions with incommensurable pulsations, the behavior of the distance function is cahotic. And you can have double or near-double roots, which are hard to find.
So you have to sample the function in a systematic way (in constant steps), staying below the Nyquist frequency of both signals, and look for crossings of the minimum distance. At the same time, look for changes of sign of the derivative, and consider the first change event.
If you find a change of sign of the derivative, refine that zero and check if it causes a crossing of the function itself, compared to the other sampled points. I would recommend regula falsi, as it is a safe method to refine a root inside an interval.
When you have found a crossing, refine by regula falsi.
Определение времени соударения шаров
Лабораторная работа № 8
Цель работы – определить скорость соударяющихся шаров, время соударения, среднюю силу соударения.
Приборы и принадлежности: экспериментальная установка для изучения упругого центрального удара шаров.
Описание экспериментальной установки


Принцип работы установки состоит в следующем. При замыкании ключа К1, в положении 1 происходит зарядка конденсатора С (ключ К3 замкнут). Переключая К1 в положение 2, конденсатор можно разрядить через гальванометр (показание гальванометра n0). Для того, чтобы разрядить конденсатор при разомкнутом ключе К3 необходимо шары 1 и 2 привести в соприкосновение, что и происходит во время удара. Так как время соударения короткое, то кондесатор разряжается не полностью, а частично (максимальное показание гальванометра n1).
Общие положения
Идеально упругих ударов в природе не существует, т.к. всегда часть энергии затрачивается на необратимую деформацию тел и увеличение их внутренней энергии. Однако для некоторых тел (стальных шаров) потерями механической энергии можно пренебречь.

Если рассмотреть последнее уравнение применительно к удару, то:
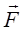
∆ 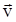


Рассмотрим систему тел, состоящую из двух шаров, подвешенных на практически нерастяжимых нитях (рисунок 2). Массы шаров одинаковы m1=m2.


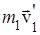



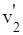
Из закона сохранения механической энергии получим:
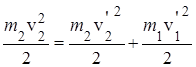

Отсюда

Так как под действием удара 1–й шар начал двигаться, то 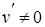

Определение времени соударения шаров
Шары при ударе замыкают электрическую цепь, составленную из заряженного конденсатора, сопротивления и гальванометра. В течение времени соударения шаров конденсатор будет разряжаться через гальванометр. Время соударения может быть отождествлено со временем разрядки конденсатора. Конденсатор разряжается по закону

где С – емкость конденсатора; R – сопротивление цепи при разрядке; t – время разрядки; Q0 – начальный заряд конденсатора; Q – заряд, оставшийся на конденсаторе к моменту времени t (в нашем случае в момент времени t=t).
Поэтому время соударения t равно:


где n0 – показание гальванометра при полной разрядке конденсатора; n1 – показание гальванометра при разряженном конденсаторе за время соударения; b – коэффициент пропорциональности.
Пользуясь этими соотношениями, получаем окончательно

Источник
Упругие и неупругие соударения
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).
Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью 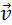
Обозначим скорость ящика с застрявшей в нем пулей через 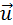
При застревании пули в песке произошла потеря механической энергии:
Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:
Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.
При m > М) отношение
Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:
где h – максимальная высота подъема маятника. Из этих соотношений следует:
Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
В общем случае массы m1 и m2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u1 и u2 – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:
Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u1 и u2 шаров после столкновения:
В частном случае, когда оба шара имеют одинаковые массы (m1 = m2), первый шар после соударения останавливается (u1 = 0), а второй движется со скоростью u2 = υ1, т. е. шары обмениваются скоростями (и, следовательно, импульсами).
Если бы до соударения второй шар также имел ненулевую скорость (υ2 ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ2 относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ1‘ = υ1 – υ2. Определив по приведенным выше формулам скорости u1 и u2 шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.
Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.
Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).
Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние
После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей 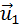
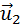
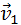
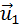
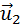
Первое из этих равенств означает, что векторы скоростей 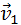
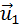
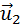
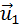
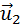
Источник
На каком принципе основан метод определения времени соударения шаров
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).
Ударом (или столкновением ) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).
Обозначим скорость ящика с застрявшей в нем пулей через 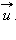
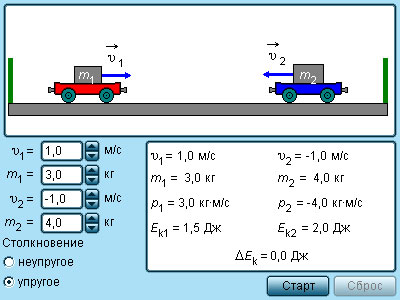 |
При застревании пули в песке произошла потеря механической энергии:
Отношение – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:
Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.
При 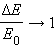
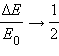
Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:
где – максимальная высота подъема маятника. Из этих соотношений следует:
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
В общем случае массы и соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости и шаров после столкновения:
Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.
Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).
После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей 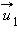
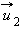
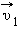
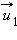
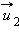
Источник
Изучение закона соударения шаров. Определение времени упругого удара и средней силы соударения шаров
Страницы работы
Содержание работы
ИЗУЧЕНИЕ ЗАКОНА СОУДАРЕНИЯ ШАРОВ.
Цель работы: на примерах упругого и неупругого ударов проверить закон сохранения импульса и определить количественные характеристики соударения шаров.
Приборы и принадлежности: установка FPM-08, набор шаров, линейка, весы, пресс форма, пластилин.
Законы сохранения являются основными законами природы и составляют основу современной физики. К ним относятся: закон сохранения импульса (количества движения), закон сохранения энергии, закон сохранения момента импульса, закон сохранения электрического заряда и др.
В замкнутой системе имеет место закон сохранения импульса – вектор импульса замкнутой системы, с течением времени не изменяется.
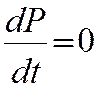
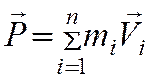
где 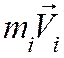
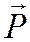
Из формулы (1) следует, что в замкнутой системе взаимодействующие тела только обмениваются импульсом, а изменение количества движения как целого не наблюдается.
Закон Сохранения и превращения энергии утверждает, что при любых процессах, протекающих в изолированной системе, ее полная энергия не изменяется. Возможно только превращение энергии из одной формы в другую.
Энергия является общей мерой различных форм движения материи. Различают два вида механической энергии – кинетическую 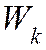
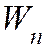
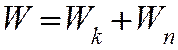
где W– механическая энергия системы.
Превращение кинетической энергии в потенциальную и обратно наблюдается при абсолютно упругом ударе. Ударом называется явление конечного изменения скорости твердых тел за весьма малый промежуток времени, возникающее при столкновении движущихся тел. Физические явления при столкновениях тел довольно сложны. Сталкивающиеся тела деформируются, возникают упругие силы и силы трения, в телах возбуждаются колебания, волны и т.д.
Процесс удара можно разбить на две фазы. Первая фаза – сжатие материала: центры масс сталкивающихся тел сближаются. В момент наибольшей деформации, скорость сближающихся тел обращается в нуль, кинетическая энергия переходит в потенциальную энергию упругой деформации и частично в другие виды энергии.
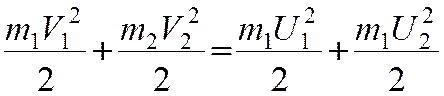
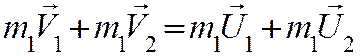
Переписав эти неравенства в виде
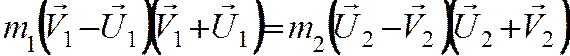
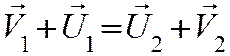
или
Откуда следует, что при абсолютно упругом ударе шаров, относительная скорость их меняет свое направление на противоположное, оставаясь неизменной по величине.
Для количественной оценки уменьшения относительной скорости, вводиться коэффициент восстановления по скорости
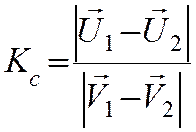
Посредством  можно характеризовать упругие свойства того или оного материала. Наряду с коэффициентом восстановления относительной скорости вводят коэффициент восстановления кинетической энергии
можно характеризовать упругие свойства того или оного материала. Наряду с коэффициентом восстановления относительной скорости вводят коэффициент восстановления кинетической энергии
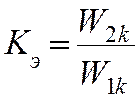
где 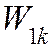
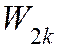
Коэффициенты 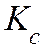
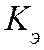
В данной работе проверяется равенство (4) и определяются величины (5) и (6).
Источник