Динамика и кинематика — это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.
Основная формула динамики
Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:
F¯ = m*a¯
Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.
В случае движения вращения второй закон Ньютона записывается в виде:
M = I*α
Здесь M и I — моменты силы и инерции, соответственно, α — угловое ускорение.
Формулы кинематики
Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:
a = Δv/Δt;
v = v0 ± a*t;
S = v0*t ± a*t2/2
Здесь v0 — значение начальной скорости тела, S — пройденный за время t путь вдоль прямолинейной траектории. Знак «+» следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак «-«. Это важный момент.
Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:
α = Δω/Δt;
ω = ω0 ± α*t;
θ = ω0*t ± α*t2/2
Здесь α и ω — угловые ускорение и скорость, соответственно, θ — угол поворота вращающегося тела за время t.
Линейные и угловые характеристики друг с другом связаны формулами:
a = α*r;
v = ω*r
Здесь r — радиус вращения.
Движение по наклонной плоскости: силы
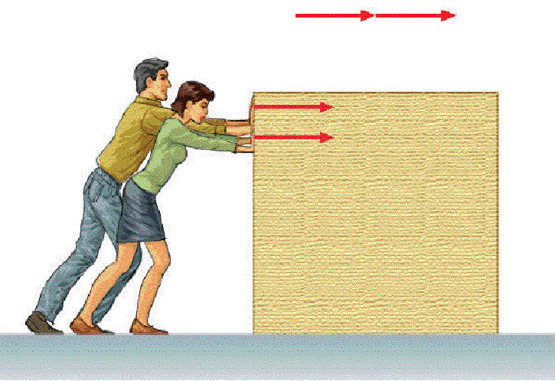
Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.
Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:
- тяжести;
- реакции опоры;
- трения качения и/или скольжения;
- натяжение нити;
- сила внешней тяги.
Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.
Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.
Методика решения
Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.
Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:
Ff = µ*N
Где N — реакция опоры, µ — коэффициент трения, не имеющий размерности.
Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:
F = m*g*sin(φ) — µ*m*g*cos(φ) = m*g*(sin(φ) — µ*cos(φ)) = m*a
Здесь φ — это угол наклона плоскости к горизонту.
Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.
В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:
F = m*g*sin(φ) — Fr = m*a
Где Fr — сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, Fr создает следующий момент:
M = Fr*r = I*α
Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.
Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.
Задача на движение бруска по наклонной плоскости
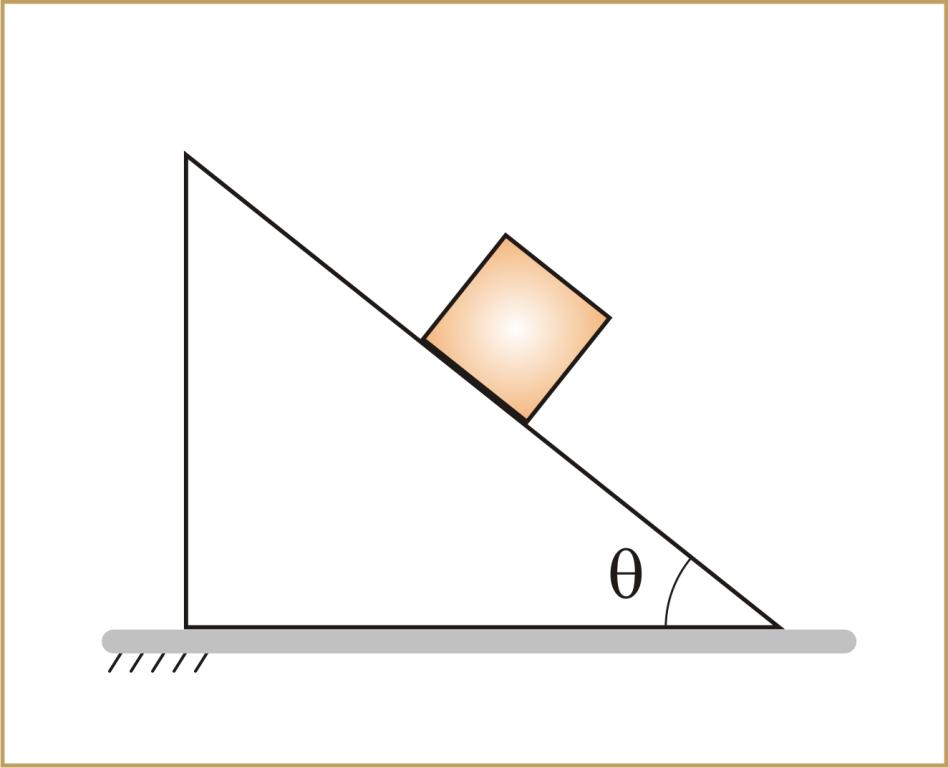
Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.
Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:
m*g*(sin(φ) — µ*cos(φ)) = m*a =>
a = g*(sin(φ) — µ*cos(φ)) ≈ 4,162 м/с2
Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:
S = a*t2/2
Откуда следует выразить время, и подставить известные значения:
t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с
Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.
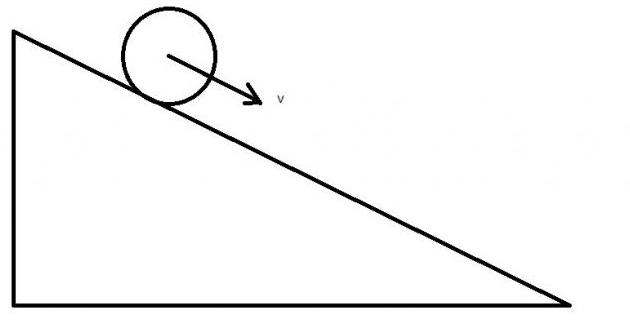
Задача со скатывающимся по плоскости цилиндром
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.
Запишем соответствующие уравнения:
m*g*sin(φ) — Fr = m*a;
Fr*r = I*α = I*a/r
Момент инерции I цилиндра вычисляется по формуле:
I = 1/2*m*r2
Подставим это значение во вторую формулу, выразим из нее силу трения Fr и заменим полученным выражением ее в первом уравнении, имеем:
Fr*r = 1/2*m*r2*a/r = >
Fr = 1/2*m*a;
m*g*sin(φ) — 1/2*m*a = m*a =>
a = 2/3*g*sin(φ)
Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.
Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:
S = a*t2/2 =>
t = √(2*S/a)
Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:
v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))
Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.
Ответ:
Объяснение:
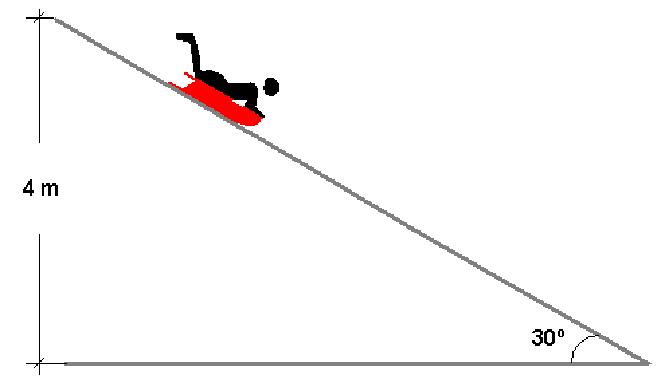
По принципу независимости движения: за такое же время, тело, брошенное горизонтально, упадет на землю при свободном падении:
t₁ = √ (2·h / g ) = √ (2·0,8/10) = √ (0,16) = 0,4 с
Но…
Тело движется под углом к горизонту, поэтому реальное время:
t = t₁ / sin α = 0,4 / 0,5 = 0,8 с
Замечание:
Если взять угол очень малым, например, α = 1·10⁻⁶ рад
то, учитывая, что для малых углов sin α ≈ α
имеем:
t = 0,4/1·10⁻⁶ = 400 000 с или более 100 часов.
А если бросим тело горизонтально? (α = 0)? Получим движение тела по инерции :)))
Ответ:
0,8 с
Объяснение:
Скатываться с наклонной плоскости тело заставляет действующая на него сила тяжести. Эта сила разлагается на две проекции — нормальную, она не вносит вклад в ускорение тела вдоль наклонной плоскости и продольную, а эта составляющая силы как раз сообщает телу ускорение, направленной вдоль наклонной плоскости. Опуская промежуточные рассуждения, можно утверждать что величина ускорения тела вдоль наклонной плоскости равна
м/с²
Так как тело скатывается из состояния покоя, то его перемещение вдоль наклонной плоскости
Откуда, время скатывания
Путь s есть ни что иное, как длина наклонной плоскости
м
Подставляя все в формулу для времени, получим
с.
Приложения:

Так как к данной задаче необходим рисунок, то лучше будет фото с решением и с дополнительными комментариями.
Как я понял из условия, в первом случае нам дан максимальный угол, при котором тело ещё может удержаться на наклонной плоскости. Используя этот факт найдём первым действием коэффициент трения. Далее, рассмотрим второй случай, где тело уже двигается под действием разницы сил проекции силы тяжести и силы трения. Применяя второй закон Ньютона составляем уравнение, откуда выражаем ускорение тела.
Зная ускорение, мы применяем формулу пути при равноускоренном движении с нулевой начальной скоростью, откуда выражаем время. Сводим всё в одну общую формулу, подставляем числовые значения и производим расчёт.
Очень важно отметить, что при построении чертежа необходимо соблюсти масштаб. Силы тяжести в обеих случая должны быть равной длины, а вот сила реакции опоры N должна быть равна по длине проекции силы тяжести на прямую, через которую проходит N.
В первом случае сила трения будет по длине равна проекции силы тяжести на ось, параллельную плоскости. Величина силы трения на двух рисунках также должна отличаться, ибо постоянен для двух рисунков лишь коэффициент трения, а сила реакции опоры N2 будет меньше, чем N1 (т.к. N=mg*cos(a), а при возрастании величины угла его косинус уменьшается), соответственно сила трения на первом рисунке будет немного больше, чем на втором.
2014-06-01
Какое время больше — спуска тела по наклонной-плоскости с высоты $h$ (при нулевой начальной скорости) или подъема с такой начальной скоростью, что тело останавливается на той же высоте $h$?
Решение:
Предположим сначала, что трение отсутствует. Тогда вследствие закона сохранения энергии скорость тела $v$ после спуска по наклонной плоскости с высоты $h$ равна скорости, которую нужно сообщить телу, чтобы оно поднялось на ту же высоту $h$. Поскольку при подъеме и спуске ускорение по модулю одинаковое, время подъема будет равно времени спуска.
При учете силы трения скольжения скорость $v_{1}$ тела после спуска в конце пути меньше скорости $v$ (из-за работы силы трения), а скорость $v_{2}$, которую нужно сообщить телу для подъема, больше и по той же причине. Поскольку спуск и подьем происходят с постоянными (хотя и разными) ускорениями, а пройденные пути одинаковы, то время спуска $t_{1}$ и время подьема $t_{2}$ найдем из уравнений
$s=v_{1}t_{1}/2, s=v_{2}t_{2}/2$,
где $s$ — длина проходимою вдоль наклонной плоскости пути. Так как выполняется неравенство $v_{1} < v_{2}$, то легко получим, что $t_{1} > t_{2}$. Таким образом, при наличии силы трения скольжения время спуска с высоты $h$ больше времени подъема на ту же высоту.
При решении задачи не принималась во внимание сила сопротивления воздуха. Тем не менее легко показать, что если наряду с силой тяжести и силой нормальной реакции наклонной плоскости имеется сила сопротивления воздуха, то независимо от конкретного вида последней время спуска всегда будет больше времени подъема. Действительно, если тело в процессе подъема оказалось на промежуточной высоте $h^{prime}$, то, чтобы оно смогло подняться на высоту $h$, его скорость $v^{prime}$ на высоте $h^{prime}$ при наличии силы сопротивления должна быть больше, чем при движении без сопротивления — часть кинетической энергии при последующем подъеме перейдет в теплоту. При спуске с высоты $h$ тело, оказавшись на высоте $h^{prime}$ из-за работы силы сопротивления будет иметь скорость $v^{prime prime}$, которая меньше скорости тела, спускающегося в отсутствие силы сопротивления. Таким образом, проходя одну и ту же точку наклонной плоскости, на подъеме тело имеет скорость большую, чем на спуске. Поэтому небольшой участок наклонной плоскости вблизи точки $h^{prime}$ тело на подъеме пройдет быстрее, чем на спуске. Разбивая весь путь тела на небольшие участки, видим, что на подъеме каждый такой участок будет пройден телом быстрее, чем на спуске. Следовательно, и общее время подъема будет меньше времени спуска.