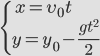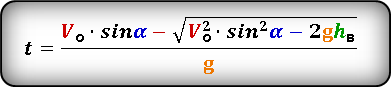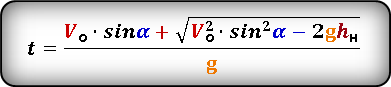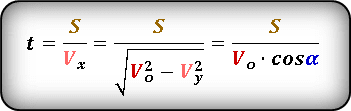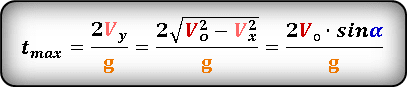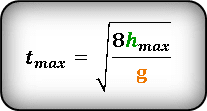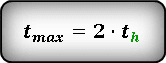Как найти время полета в физике - AvtoShod.ru - решение различных проблем

Движение тела, брошенного горизонтально или под углом к горизонту.

Это движение в плоскости, поэтому для описания движения необходимо 2 координаты.
Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).

Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное.

Движение тела, брошенного горизонтально.

Выразим проекции скорости и координаты через модули векторов.

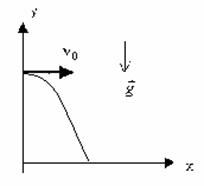
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:

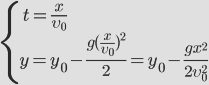
— между координатами квадратичная зависимость, траектория – парабола!

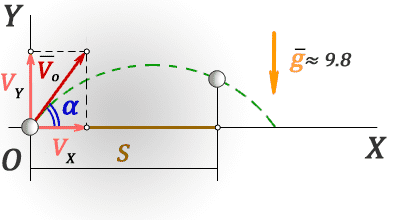
Движение тела, брошенного под углом к горизонту.

Порядок решения задачи аналогичен предыдущей.

Решим задачу для случая х₀=0 и y₀=0.

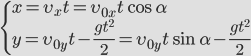
Движение тела, брошенного под углом к горизонту.

Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):

Мы получили квадратичную зависимость между координатами. Значит траектория — парабола.

Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.

Время полета:

Следовательно, для решения этой задачи необходимо решить уравнение

Оно будет иметь решение при t=0 (начало движения) и

Зная время полета, найдем максимальное расстояние, которое пролетит тело:

Дальность полета:

Из этой формулы следует, что:

— максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45⁰;

— на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.

Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело.
Время, за которое тело долетит до середины, равно: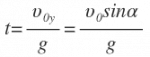

Время подъема:

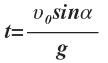
Тогда:

Максимальная высота:

Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна

Угол, под которым направлен вектор скорости в любой момент времени:

Источник

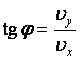
Решение задачи по физике: как найти время полета тела?

Одной из типичных задач в физике является поиск времени полета тела, брошенного под углом к горизонту. В этой статье мы рассмотрим, как решать такую задачу.

Шаг 1: Определение начальных условий

Первым шагом необходимо определить начальные условия задачи. Важно знать начальную скорость и угол броска тела. Обозначим начальную скорость как V₀ и угол броска как α.

Шаг 2: Разложение начальной скорости

Для решения задачи по физике нужно разложить начальную скорость тела на горизонтальную и вертикальную составляющие. В результате получаем:

V₀х = V₀cosα
V₀у = V₀sinα

Где V₀х и V₀у — горизонтальная и вертикальная составляющие начальной скорости соответственно.

Шаг 3: Использование уравнения движения

С помощью уравнения движения можно найти время полета тела. Уравнение движения для вертикальной составляющей равно:

y = V₀yt - 1/2gt²

Где y — вертикальное перемещение тела, g — ускорение свободного падения, t — время полета.

Так как перемещение тела в момент падения на землю равно нулю, то уравнение принимает вид:

0 = V₀ys - 1/2gt²

Отсюда можно выразить время полета:

t = 2V₀ys / g

Шаг 4: Подстановка значений

Окончательный шаг — подставить значения начальной скорости и угла броска в уравнение.

t = 2V₀sinα / g

Вывод

Решение задачи по физике на нахождение времени полета тела сводится к определению начальных условий (начальная скорость и угол броска), разложению начальной скорости на составляющие, использованию уравнения движения и подстановке найденных значений. В результате можно найти время полета тела.

Источник

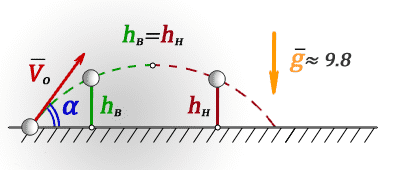
1. Найти время полета тела на определенной высоте

h_в — высота на восходящем участке траектории

h_н — высота на нисходящем участке траектории

t — время в момент которого тело находится на высоте h_в или h_н

V_o — начальная скорость тела

α — угол под которым брошено тело

g ≈ 9,8 м/с² — ускорение свободного падения

Формула для определения значения времени, за которое тело поднялось на определенную высоту, на восходящем участке траектории

Формула для определения значения времени, за которое тело поднялось на определенную высоту, на нисходящем участке траектории

Таким образом, одному значению высоты будет соответствовать два значения времени, одно при подъеме, второе при падении.

2. Найти время полета тела пролетевшее определенное расстояние

S — расстояние пройденное по горизонтали

t — время за которое тело прошло расстояние S

V_o — начальная скорость тела

V_x — проекция начальной скорости на ось OX

V_y — проекция начальной скорости на ось OY

α — угол под которым брошено тело

g ≈ 9,8 м/с² — ускорение свободного падения

Формула для определения значения времени, за которое пройдено определенное расстояние

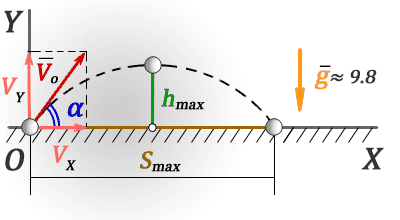
3. Значение времени при максимальных значениях высоты и дальности

S_max — максимальная дальность по горизонтали

h_max — максимальная высота

t_max — время всего полета

t_h — время за которое тело поднялось на максимальную высоту

V_o — начальная скорость тела

V_x — проекция начальной скорости на ось OX

V_y — проекция начальной скорости на ось OY

α — угол под которым брошено тело

g ≈ 9,8 м/с² — ускорение свободного падения

Формула для определения значения времени, затраченное на весь полет, если известна начальная скорость или ее проекции

Формула для определения значения времени, на максимальной высоте

Т. к. траектория движения тела симметрична относительно линии максимальной высоты, следовательно — время всего полета, в два раза больше времени затраченного при подъеме на максимальную высоту

Подробности

Опубликовано: 20 июля 2015

Обновлено: 13 августа 2021

Источник

Что такое движение тела брошенного под углом к горизонту

Определение

Движением тела под углом к горизонту в физике называют сложное криволинейное перемещение, которое состоит из двух независимых движений, включая равномерное прямолинейное движение в горизонтальном направлении и свободное падение по вертикали.

В процессе подбрасывания объекта вверх под углом к горизонту вначале наблюдают его равнозамедленный подъем, а затем равноускоренное падение. Скорость перемещения тела, относительно поверхности земли, остается постоянной.

Направление

На графике изображено схематичное движение тела, которое подбросили под углом к горизонту. В этом случае α является углом, под которым объект начал свое перемещение. Характеристики такого процесса будут следующими:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Направление вектора скорости тела, которое подбросили под определенным углом к горизонту, будет совпадать с касательной к траектории его перемещения.
Начальная скорость отличается от направления горизонтальной линии, а обе ее проекции не равны нулю.
Проекция скорости в начале движения на ось ОХ составляет (V_{ox}=V_{0}cos alpha).
Проекция начальной скорости на ось ОУ равна (V_{oy}=V_{0}sin alpha).
Проекция мгновенной скорости на ось ОХ следующая: (V_{x}=V_{0}cos alpha).
Проекция мгновенной скорости на ось ОУ обладает нулевым значением и рассчитывается следующим образом: (V_{x}=V_{0}sin alpha-gt).
Ускорение свободного падения на ось ОХ обладает нулевой проекцией, или (g_{x}=0).
Проекция ускорения свободного падения на ось ОУ равна (–g), или (g_{y}=-g).

К числу кинематических характеристик движения тела, которое подбросили под углом к горизонту, относят модуль мгновенной скорости в определенное время t. Данный показатель можно рассчитать с помощью теоремы Пифагора:

(V=sqrt{V^{2}_{x}+V^{2}_{y}})

Минимальная скорость тела будет замечена в самой верхней точке траектории, а максимальная величина данной характеристики будет достигнута, когда объект только начинает перемещаться, а также в точке падения на поверхность земли. Время подъема представляет собой время, необходимое для достижения телом верхней точки траектории. За полное время объект совершает полет, то есть перемещается от начальной точки к точке приземления.

Дальность полета является перемещением объекта по отношению к оси ОХ. Такую кинематическую характеристику обозначают буквой l. По отношению к оси ОХ тело перемещается, сохраняя постоянство скорости.

Определение

Горизонтальным смещением тела называют смещение данного объекта, относительно оси ОХ.

Расчет горизонтального смещения тела в какой-либо момент времени t выполняют с помощью уравнения координаты х:

(x=x_{0}+V_{0x}t+frac{gxt^{2}}{2})

Зная следующие условия:

(x_{0}=0);
проекция ускорения свободного падения, относительно оси ОХ, также имеет нулевое значение;
проекция начальной скорости на ось ОХ составляет (V_{0}cos alpha).

Записанная формула приобретает следующий вид:

(x=V_{0}cos alpha t)

Мгновенной высотой принято считать высоту, на которой находится объект в определенный момент времени t. Наибольшей высотой подъема является расстояние от поверхности земли до верхней точки траектории движения тела под углом к горизонту.

Вывод формулы, как найти угол и дальность полета

Перемещение объекта, который был брошен под углом к горизонту, необходимо изобразить с помощью суперпозиций, характерных для двух типов движений:

равномерное горизонтальное движение;
равноускоренное перемещение в вертикальном направлении с ускорением свободного падения.

Движение тела

Скорость тела будет рассчитываться таким образом:

(v_{0x}=v_{x}=v_{0} cos alpha =const)

(v_{0y}=v_{0}sin alpha)

(v_{y}=v_{0}sin alpha-gt)

Уравнение координаты записывают в следующем виде:

(x=v_{0}cos alpha times t)

(y=v_{0}sin alpha times t-frac{gt^{2}}{2})

В любое время значения скорости тела будут равны:

(v=sqrt{v_{x}^{2}+v_{y}^{2}})

Определить угол между вектором скорости и осью ОХ можно таким образом:

(tan beta =frac{v_{y}}{v_{x}}=frac{v_{0}sin alpha -gt}{v_{0}cos alpha })

Время подъема на максимальную высоту составляет:

(t=frac{v_{0}sin alpha }{g})

Максимальная высота подъема будет рассчитана следующим образом:

(h_{max}=frac{v_{0}^{2}sin ^{2}alpha}{2g})

Полет тела будет длиться определенное время, которое можно рассчитать с помощью формулы:

(t=frac{2v_{0}sin alpha }{g})

Максимальная дальность полета составит:

(L_{max}=frac{v_{0}^{2}sin 2alpha }{g})

Примеры решения задач

В примерах, описывающих движение тела, на которое действует сила тяжести, следует учитывать, что а=g=9,8 м/с².

Задача 1

Небольшой камень был брошен с ровной горизонтальной поверхности под углом к горизонту. Необходимо определить, какова максимальная высота подъема камня при условии, что, спустя 1 секунду после его начала движения, скорость тела обладала горизонтальным направлением.

Решение

Направление скорости будет горизонтальным в верхней точке перемещения камня. Таким образом, время, за которое он поднимется, составляет 1 секунду. С помощью уравнения времени подъема можно представить формулу произведения скорости в начале полета на синус угла, под которым бросили камень:

(V_{0}sin alpha =gt)

Данное равенство следует подставить в уравнение для расчета максимальной высоты, на которую поднимется камень, и выполнить вычисления:

(h=frac{V_{0}sin ^{2}alpha }{2g}=frac{(gt)^{2}}{2g}=frac{gt^{2}}{2}=frac{10times 1}{2}=5)

Ответ: максимальная высота подъема камня, который бросили под углом к горизонту, составляет 5 метров.

Задача 2

Из орудия выпустили снаряд, начальная скорость которого составляет 490 м/с, под углом 30 градусов к горизонту. Нужно рассчитать, какова высота, дальность и время полета снаряда без учета его вращения и сопротивления воздуха.

Решение

Систему координат и движение тела можно представить схематично:

Задача

Составляющие скорости, относительно осей ОХ и ОУ, будут совпадать во время начала движения снаряда:

(V_{0x}=V_{0} cos alpha) сохраняет стабильность значения в любой промежуток времени во время всего перемещения тела.

(V_{0y}=V_{0}sin alpha) будет меняться, согласно формуле равнопеременного движения (V_{y}=V_{0}sin alpha-gt).

В максимальной точке, на которую поднимется снаряд:

(V_{y}=V_{0}sin alpha-gt_{1}=0)

Из этого равенства следует:

(t=frac{V_{0sin alpha }}{g})

Полное время полета тела будет рассчитано по формуле:

(t=2t_{1}=frac{2V_{0}sin alpha }{g}=50)

Высота, на которую поднимется снаряд, определяется с помощью уравнения равнозамедленного перемещения тела:

(h=V_{0y}t_{1}-frac{gt_{1}^{2}}{2}=frac{V_{0}^{2}sin ^{2}alpha }{2g}=3060)

Дальность полета снаряда будет рассчитана таким образом:

(S=V_{0x}t=frac{V_{0}^{2}sin 2alpha }{g}=21000)

Ответ: высота составляет 3060 метров, дальность полета равна 21000 метров, время движения составит 50 секунд.

Источник

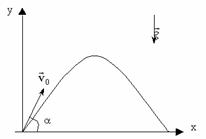
Движение тела, брошенного под углом к горизонту, — движение тела в двумерной системе координат (по двум осям) при изначальном направлении начальной скорости под углом к горизонту. Данное движение является сложным видом механического движения с криволинейной траекторией. Такие типы движений принято рассматривать в проекции на оси выбранной системы координат. В нашем конкретном случае возьмём декартову систему координат и запустим тело под углом displaystyle alpha к оси ОХ (рис. 1).

Рис. 1. Тело бросили под углом к горизонту

Классическая постановка задач на подобную тематику: тело бросили под углом $displaystyle {{upsilon }_{0}}$ к горизонту с начальной скоростью $displaystyle {{upsilon }_{0}}$ , найти различные параметры движения.

Первое, что мы сделаем, это попробуем данное сложное движение представить как сумму простых (рис. 2).

Рис. 2. Тело бросили под углом к горизонту (максимальная высота подъёма, путь по горизонтали, движение)

Рассмотрим само движение. После броска траектория движущегося тела представляет собой параболу (докажем позже). Выберем произвольную точку на параболе и укажем ускорение, с которым движется тело в данный момент (ускорение свободного падения). Направление данного ускорения — вертикально вниз. Проекции данного ускорения на ось ОХ ( $displaystyle {{c}^{2}}$ (м/ $displaystyle {{g}_{y}}=-10$ ), а на ось OY ( $displaystyle {{c}^{2}}$ (м/ $displaystyle {{c}^{2}}$ ).

Тогда, вдоль оси ОХ, тело движется равномерно (т.к. ускорение вдоль этой оси равно 0). Более сложным является движение тела вдоль оси OY: между точками A и B тело движется замедляясь, при этом движение равнозамедленное. Между точками B и C движение равноускоренное (рис.2, подписи). Исходя из установленного вида движения, можем решать задачу.

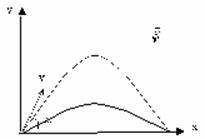
Рис. 3. Тело бросили под углом к горизонту (проекции скоростей)

Для рассмотрения движения тела вдоль осей, введём начальные скорости движения тела вдоль выбранных нами осей (рис. 3). На рисунке представлена часть траектории в самом начале движения. Начальные скорости движения вдоль осей обозначим $displaystyle {{upsilon }_{0y}}$ и $displaystyle left| {{{vec{upsilon }}}_{0}} right|$ . Исходя из треугольника, катетами которого являются наши проекции (можно построить параллельным переносом), а гипотенузой — модуль вектора начальной скорости ( $displaystyle left| {{{vec{upsilon }}}_{0}} right|$ ), можем найти значения необходимых нам проекций:

Вернёмся к рисунку 2. Попробуем найти полное время полёта ( $displaystyle {{t}_{max }}$ ). Для этого воспользуемся тем, что вдоль оси OY тело движется равнозамедленно, а в точке B движение вдоль этой оси и вовсе останавливается. Таким образом, конечная скорость в этой точке вдоль оси OY равна 0. Тогда, исходя из движения:

$displaystyle 0={{upsilon }_{0y}}-gfrac{{{t}_{max }}}{2}$ (3)

$displaystyle frac{{{t}_{max }}}{2}$ — т.к. время движения от точки А до B, и от B до C одинаково. Тогда:

$displaystyle {{t}_{max }}=frac{2{{upsilon }_{0y}}}{g}$ (4)

И, учитывая (2):

$displaystyle {{t}_{max }}=frac{2{{upsilon }_{0}}sin alpha }{g}$ (5)

Перейдём к вопросу о максимальной дальности броска в горизонтальном направлении ( $displaystyle {{S}_{max }}$ ).

Вдоль горизонта тело движется равномерно (рис. 2). Тогда путь, проделанный телом за время $displaystyle {{t}_{max }}$ :

$displaystyle {{S}_{max }}={{upsilon }_{0x}}{{t}_{max }}$ (6)

А с учётом (1) и (5):

$displaystyle frac{2upsilon _{0}^{2}sin alpha cos alpha }{g}$ = $displaystyle frac{upsilon _{0}^{2}sin (2alpha )}{g}$ = $displaystyle frac{upsilon _{0}^{2}sin (2alpha )}{g}$ (7)

Перейдём к максимальной высоте полёта ( $displaystyle {{H}_{max }}$ ). Данный параметр связан с движением тела вдоль оси OY, которое, как мы выяснили, является равноускоренным/равнозамедленным. Рассмотрим участок BC: для него вдоль соответствующей оси тело без начальной скорости движется с ускорением ( $displaystyle frac{{{t}_{max }}}{2}$ ) в течение времени $displaystyle frac{{{t}_{max }}}{2}$ , формируем уравнение:

$displaystyle {{H}_{max }}=frac{g{{left( {}^{{{t}_{max }}}!!diagup!!{}_{2}; right)}^{2}}}{2}=frac{g{{left( {{t}_{max }} right)}^{2}}}{8}$ (8)

С учётом (5):

$displaystyle frac{upsilon _{0}^{2}{{sin }^{2}}alpha }{2g}$ = $displaystyle frac{upsilon _{0}^{2}{{sin }^{2}}alpha }{2g}$ (9)

Таким образом, ряд параметров движения при броске под углом к горизонту можно вычислить, зная лишь начальные параметры броска.

Рис. 4. Тело бросили под углом к горизонту (конечная скорость)

Далее попробуем найти конечную скорость движения (при таких движениях, конечная скорость — скорость при подлёте к Земле). Рассмотрим конечную точку движения С (рис. 4). Скорость тела направлена под неким углом displaystyle beta . Построим проекции данного вектора на оси OX и OY. На основании построенного треугольника реализуем теорему Пифагора для поиска модуля полной конечной скорости:

$displaystyle left| {vec{upsilon }} right|=sqrt{upsilon _{x}^{2}+upsilon _{y}^{2}}$ (10)

Найдём компоненты вектора displaystyle left| {vec{upsilon }} right| . Т.к. движение вдоль оси OX равномерное, значит, $displaystyle {{upsilon }_{x}}={{upsilon }_{0x}}$ , используя (1):

$displaystyle {{upsilon }_{x}}={{upsilon }_{0}}cos alpha$ (11)

Движение вдоль оси OY от точки B в точку C равноускоренное, причём, без начальной скорости за время $displaystyle frac{{{t}_{max }}}{2}$ , тогда:

$displaystyle {{upsilon }_{y}}=gfrac{{{t}_{max }}}{2}$ (12)

Используя (5), получим:

$displaystyle {{upsilon }_{y}}=gfrac{2{{upsilon }_{0}}sin alpha }{2g}={{upsilon }_{0}}sin alpha$ (13)

Подставим (12) и (13) в (10):

$displaystyle {{upsilon }_{0}}sqrt{{{(cos alpha )}^{2}}+{{(sin alpha )}^{2}}}$ = $displaystyle {{upsilon }_{0}}$ = $displaystyle {{upsilon }_{0}}$ (14)

Для избавления от тригонометрических функций мы воспользовались основным тригонометрическим тождеством. Таким образом, доказано, что конечная скорость такого движения равна начальной, кроме того, из треугольника видно, что тело подлетело к земле под углом displaystyle beta =alpha .

Вывод:

для движения тела, брошенного под углом к горизонту, выведены добавочные формулы: (5), (7), (9), которые могут существенно упростить решение задачи.
представлен один из общих способов нахождения скорости при криволинейном движении (через теорему Пифагора и поиск компонент вектора).

Источник

Решение задачи по физике: как найти время полета тела?

Шаг 1: Определение начальных условий

Шаг 2: Разложение начальной скорости

Шаг 3: Использование уравнения движения

Шаг 4: Подстановка значений

Вывод

Что такое движение тела брошенного под углом к горизонту

Вывод формулы, как найти угол и дальность полета

Примеры решения задач

Не пропустите также: